Introducción
En esta ocasión estudiaremos la potencia de un punto con respecto a una circunferencia, esta es una herramienta que nos permite establecer una medida de la distancia de un punto a una circunferencia dada.
Potencia de un punto respecto a una circunferencia
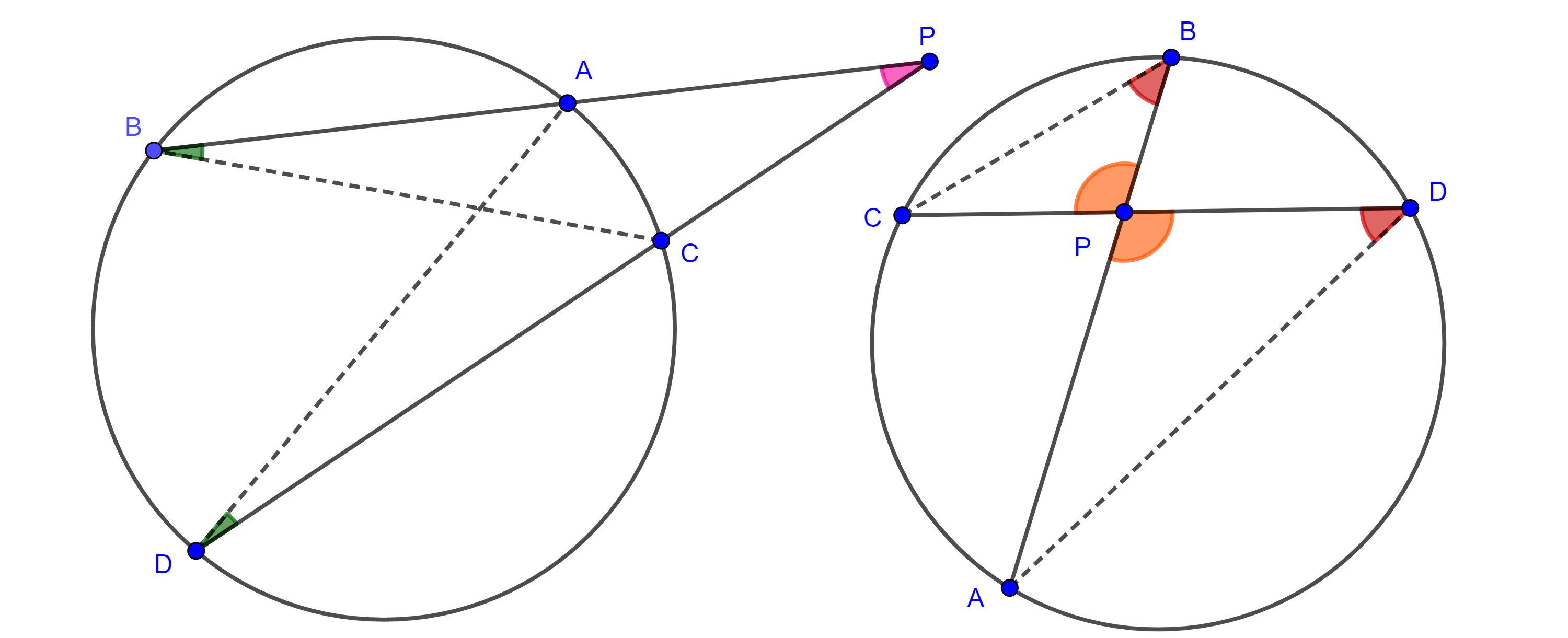
Teorema 1. Sea $\Gamma$ una circunferencia y $P$ un punto en el plano, por $P$ tracemos una secante a $\Gamma$, con intercesiones en $A$ y en $B$, entonces el número $PA \times PB$ es independiente de la secante que tracemos.
Demostración. Consideremos dos secantes desde $P$, $PAB$ y $PCD$, consideremos los triángulos $\triangle PAD$ y $\triangle PCB$, tenemos que $\angle CDA = \angle CBA$, pues abarcan el mismo arco de circunferencia.
Si $P$ es un punto exterior a $\Gamma$, $\angle APC$ es un ángulo común de los triángulos considerados.
Si $P$ es un punto interior a $\Gamma$, $\angle APD = \angle BPC$ por ser opuestos por el vértice.
Por criterio de semejanza AA, $\triangle PAD \sim \triangle PCB$,
$\Rightarrow \dfrac{PA}{PC} = \dfrac{PD}{PB}$
$\Rightarrow PA \times PB = PC \times PD$.
$\blacksquare$
Definición. Al valor constante $PA \times PB$, se le conoce como la potencia de $P$ respecto a la circunferencia $\Gamma$.
Otras expresiones para la potencia
Proposición 1. Sea $P$ un punto en el plano y $(O, R)$ una circunferencia, entonces la potencia de $P$ respecto a $(O, R)$ es igual a $|OP^2 – R^2|$.
Demostración. Por $P$ tracemos la secante $AB$ a $(O, R)$ que pasa por $O$.
Si $P$ es exterior $PA \times PB = (OP – OA)(OP + OB) = (OP – R)(OP + R) = OP^2 – R^2$.
Si $P$ es interior $PA \times PB = (OA – OP)(OP + OB) = (R – OP)(OP + R) = R^2 – OP^2$.
$\blacksquare$
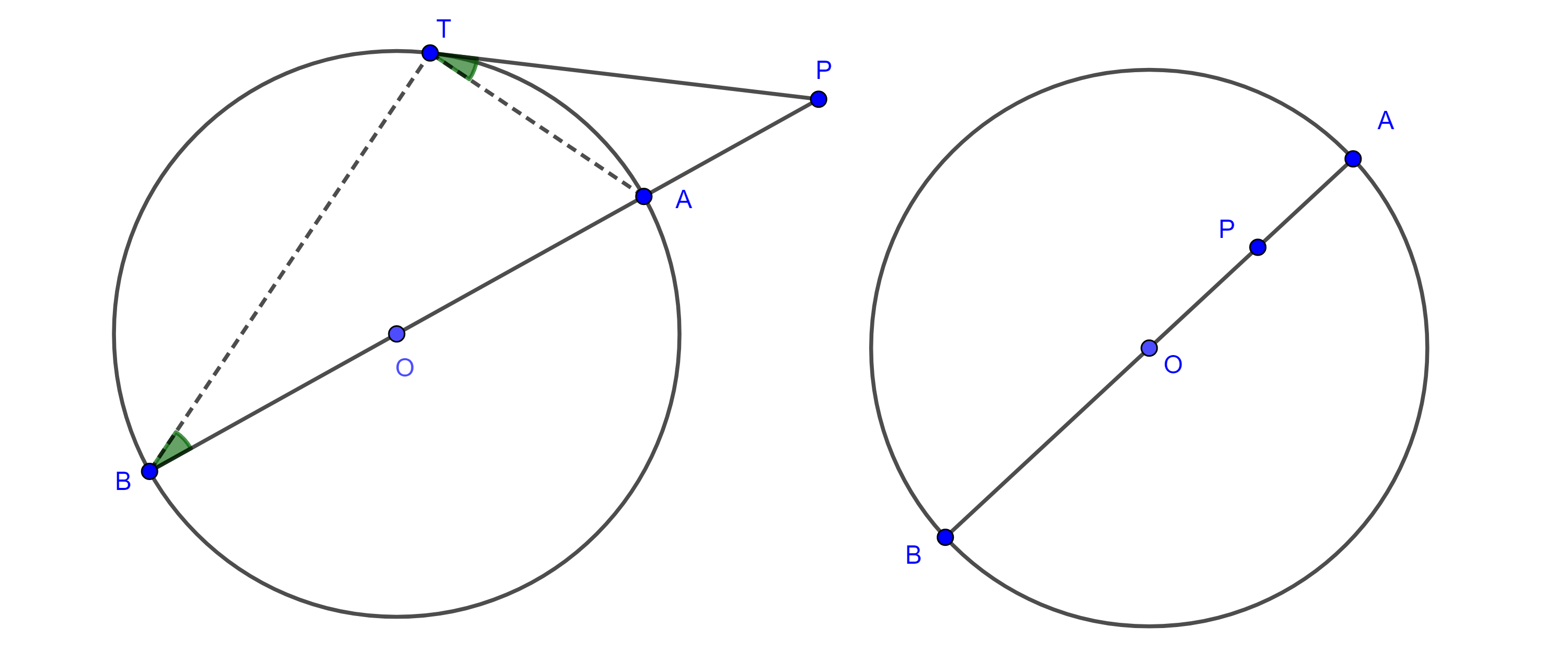
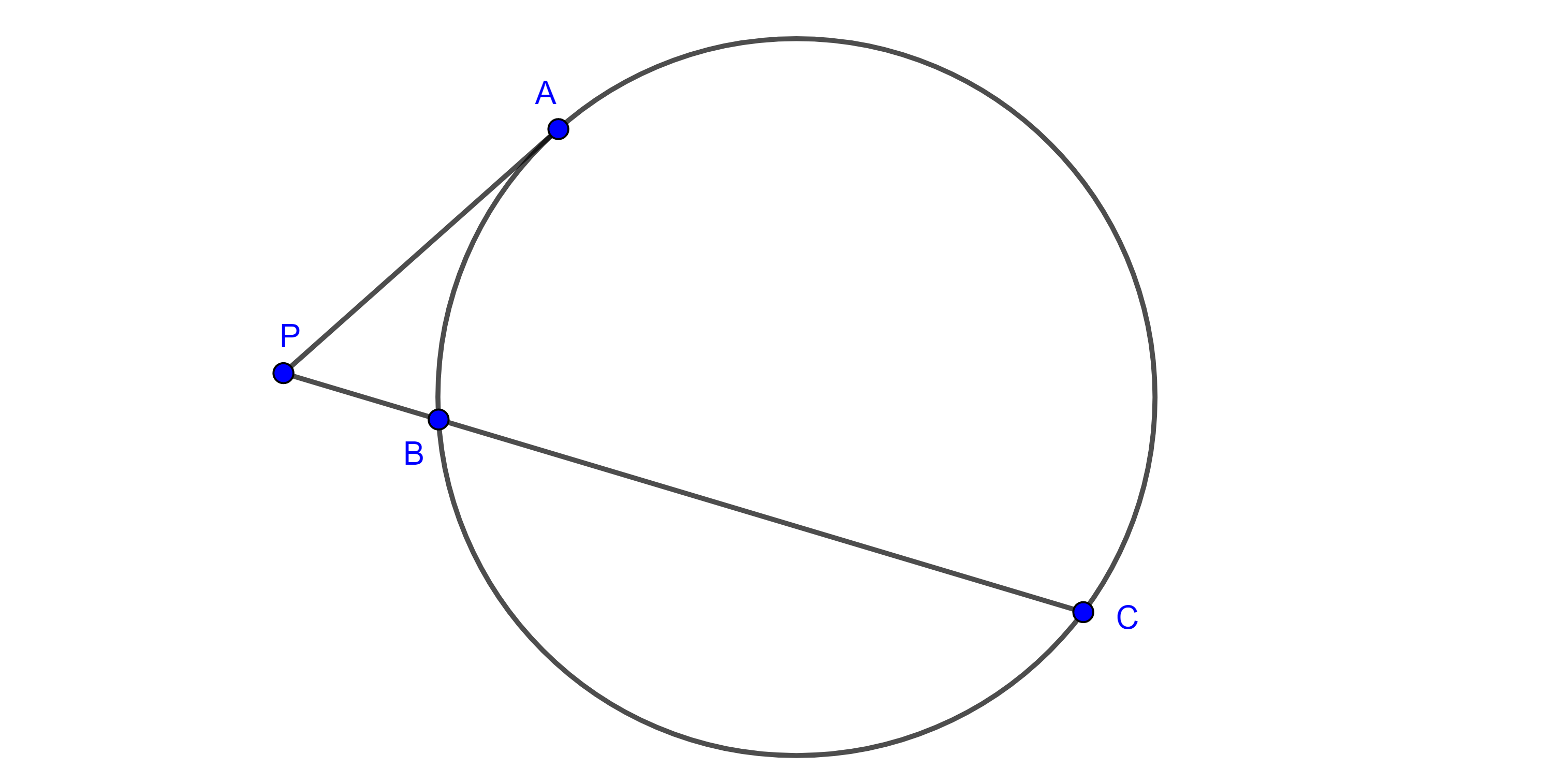
Proposición 2. Si $P$ es un punto exterior a una circunferencia $\Gamma$, entonces el cuadrado del segmento tangente $PT$ a $\Gamma$ es igual a la potencia de $P$ respecto a $\Gamma$.
Demostración. Tracemos una secante $PAB$ por $P$ a $\Gamma$ (figura 2), consideremos $\triangle PAT$ y $\triangle PTB$, como el ángulo semiinscrito $\angle ATP$, abarca el mismo arco que el ángulo inscrito $\angle ABT$, entonces son iguales, además $\angle TPA$ es un ángulo común a ambos triángulos.
Por criterio de semejanza AA, $\triangle PAT \sim \triangle PTB$,
$\Rightarrow \dfrac{PA}{PT} = \dfrac{PT}{PB}$
$\Rightarrow PA \times PB = PT^2$
$\blacksquare$
Teorema de las cuerdas
Teorema 2. Considera dos segmentos $AB$, $CD$ que se intersecan en $P$, entonces $A$, $B$, $C$ y $D$ son cíclicos si y solo si $PA \times PB = PC \times PD$.
Demostración. Supongamos que $A$, $B$, $C$, y $D$ son cíclicos, tanto si $P$ es interno o externo a la circunferencia, por el teorema 1, $PA \times PB = PC \times PD$.
Ahora supongamos se cumple $PA \times PB = PC \times PD$,
$\Rightarrow \dfrac{PB}{PD} = \dfrac{PC}{PA}$.
En caso de que $P$ este en la extensión de ambos segmentos (izquierda figura 3), $\angle APC$ es un ángulo común de los triángulos $\triangle PCB$ y $\angle PAD$.
En caso de que $P$ este contenido en ambos segmentos (derecha figura 3), entonces $\angle BPC = \angle APD$ por ser opuestos por el vértice.
Por criterio de semejanza LAL, $\triangle PCB \sim \triangle PAD$ $\Rightarrow \angle CDA = \angle CBA$.
Sabemos que el lugar geométrico de los puntos que subtienden ángulos iguales con el segmento $AC$, es un arco de circunferencia que pasa por $A$ y $C$. Por lo tanto, $A$, $B$, $C$ y $D$ son cíclicos.
$\blacksquare$
Formula de Euler
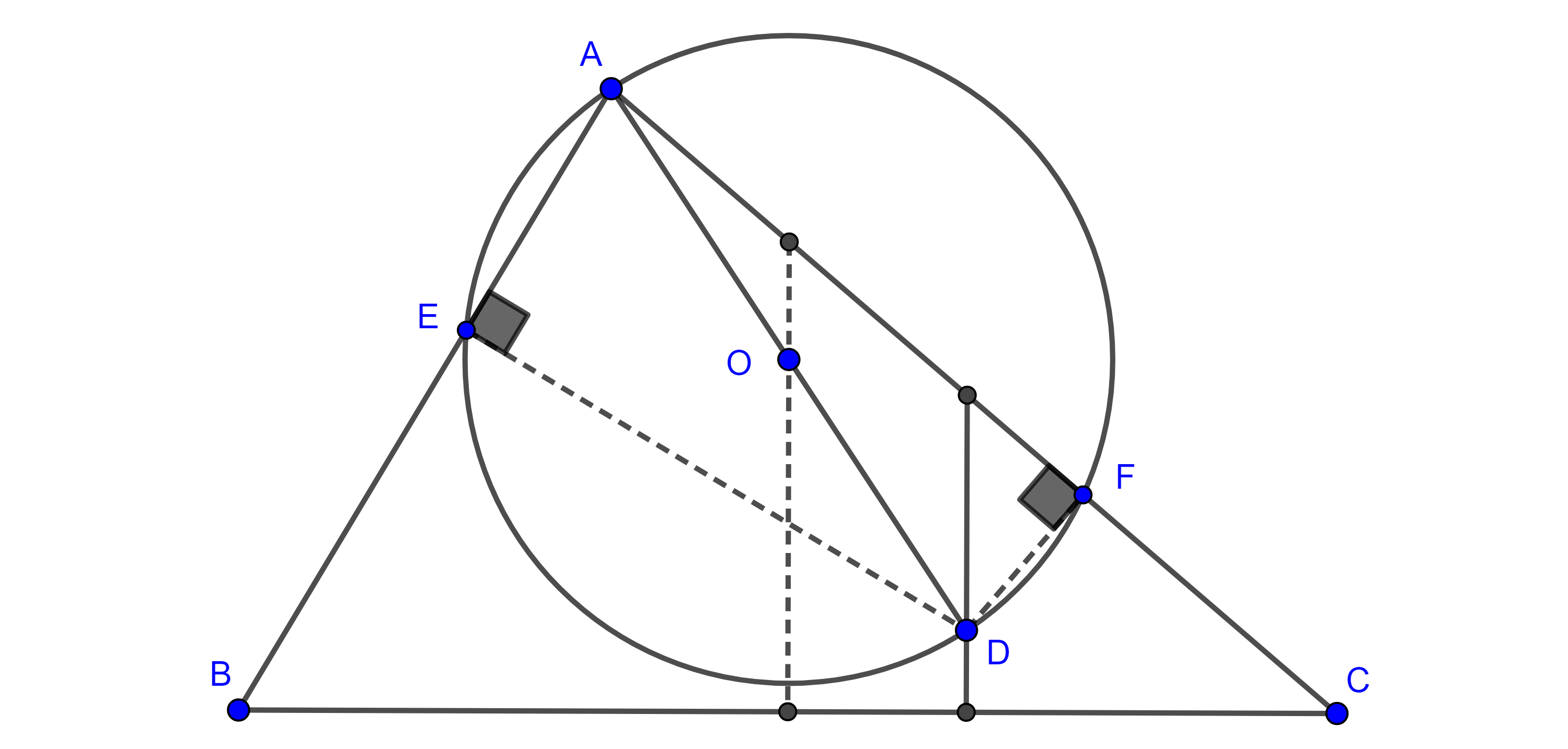
Teorema 3, formula de Euler. Considera el circuncírculo $(O, R)$ y el incírculo $(I, r)$ de un triángulo $\triangle ABC$, entonces $IO^2 = R(R – 2r)$.
Demostración. Sea $K = AI \cap (O, R)$, entonces $\angle BAK = \angle KAC$, pues $AK$ es bisectriz de $\angle A$.
$\angle KAC = \angle KBC$, pues abarcan el mismo arco, por lo tanto $\angle BAK = \angle KBC$.
$\Rightarrow \angle KBI = \angle KBC + \angle CBI = \angle BAK + \angle CBI = \dfrac{\angle A + \angle B}{2}$.
El ángulo $\angle BIK$ es un ángulo exterior de $\triangle BAI$, por lo que es igual a la suma de los ángulos no adyacentes a el,
$\angle BIK = \angle IBA + \angle BAI = \dfrac{\angle A + \angle B}{2}$
$\Rightarrow \angle BIK = \angle KBI$.
Por lo tanto $\triangle IKB$ es isósceles.
Por otro lado, considera $K’ = KO \cap (O, R)$, $Z = AB \cap (I, r)$, $\triangle BK’K$ es rectángulo, pues $KK’$ es diámetro.
Notemos que $\angle ZAK = \angle BAK = \angle BK’K$, pues abarcan el mismo arco, entonces por criterio de semejanza AA, $\triangle ZAI \sim \triangle BK’K$
$\Rightarrow \dfrac{AI}{K’K} = \dfrac{ZI}{BK}$
$\Rightarrow \begin{equation} AI \times BK = K’K \times ZI = 2Rr. \end{equation}$
Por la proposición 1, la potencia de $I$ con respecto a $(O, R)$
$\Rightarrow \begin{equation} AI \times KI = R^2 – IO^2. \end{equation}$
Haciendo el cociente de $(1)$ y $(2)$ tenemos que $\dfrac{BK}{KI} =\dfrac{2Rr}{R^2 – IO^2}$.
Como $\triangle IKB$ es isósceles entonces $BK = KI$
$\Rightarrow IO^2 – R^2 = –2Rr$
$\Rightarrow IO^2 = R^2 – 2Rr = R(R – 2r)$.
$\blacksquare$
Reciproco de la formula de Euler
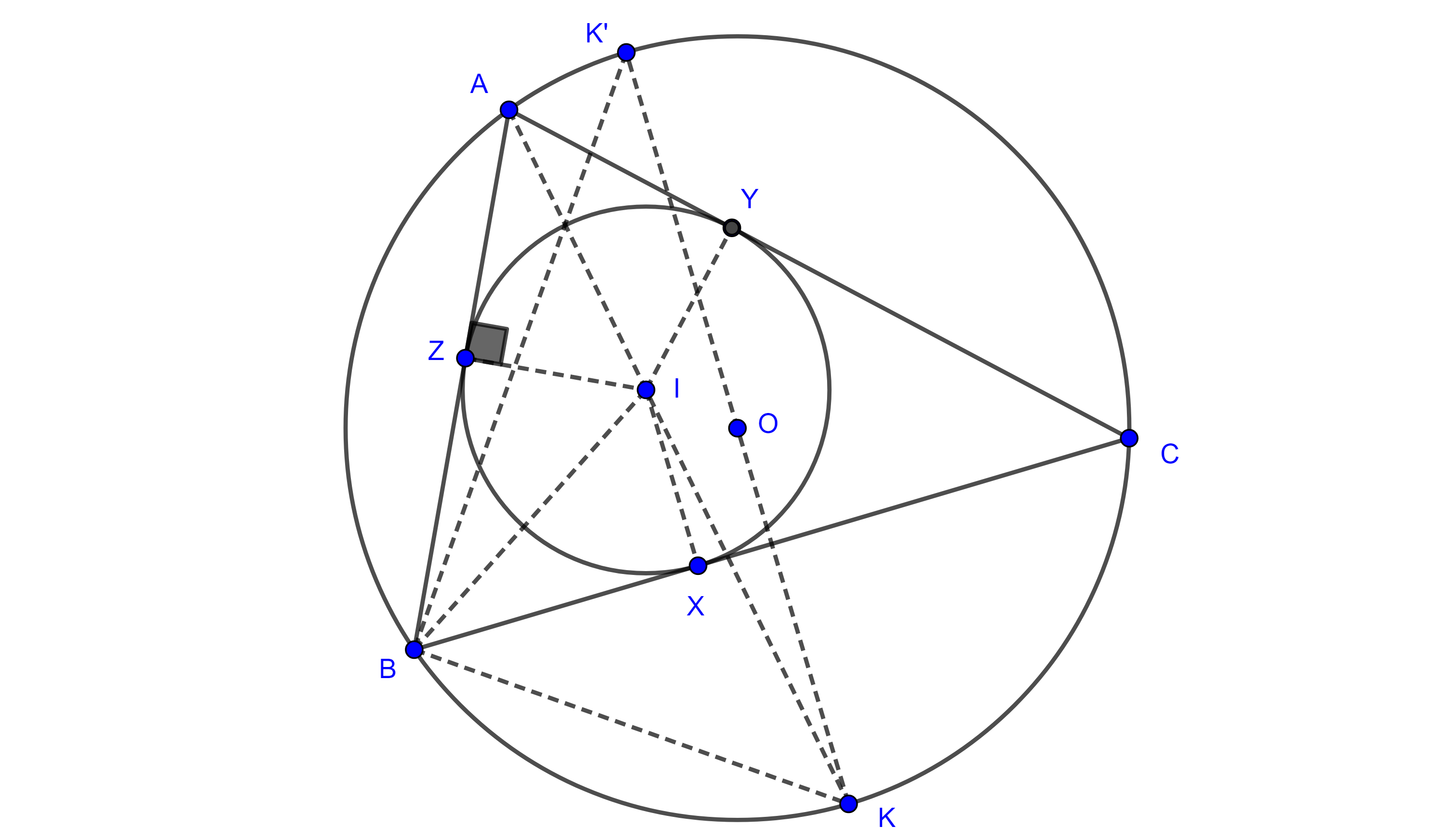
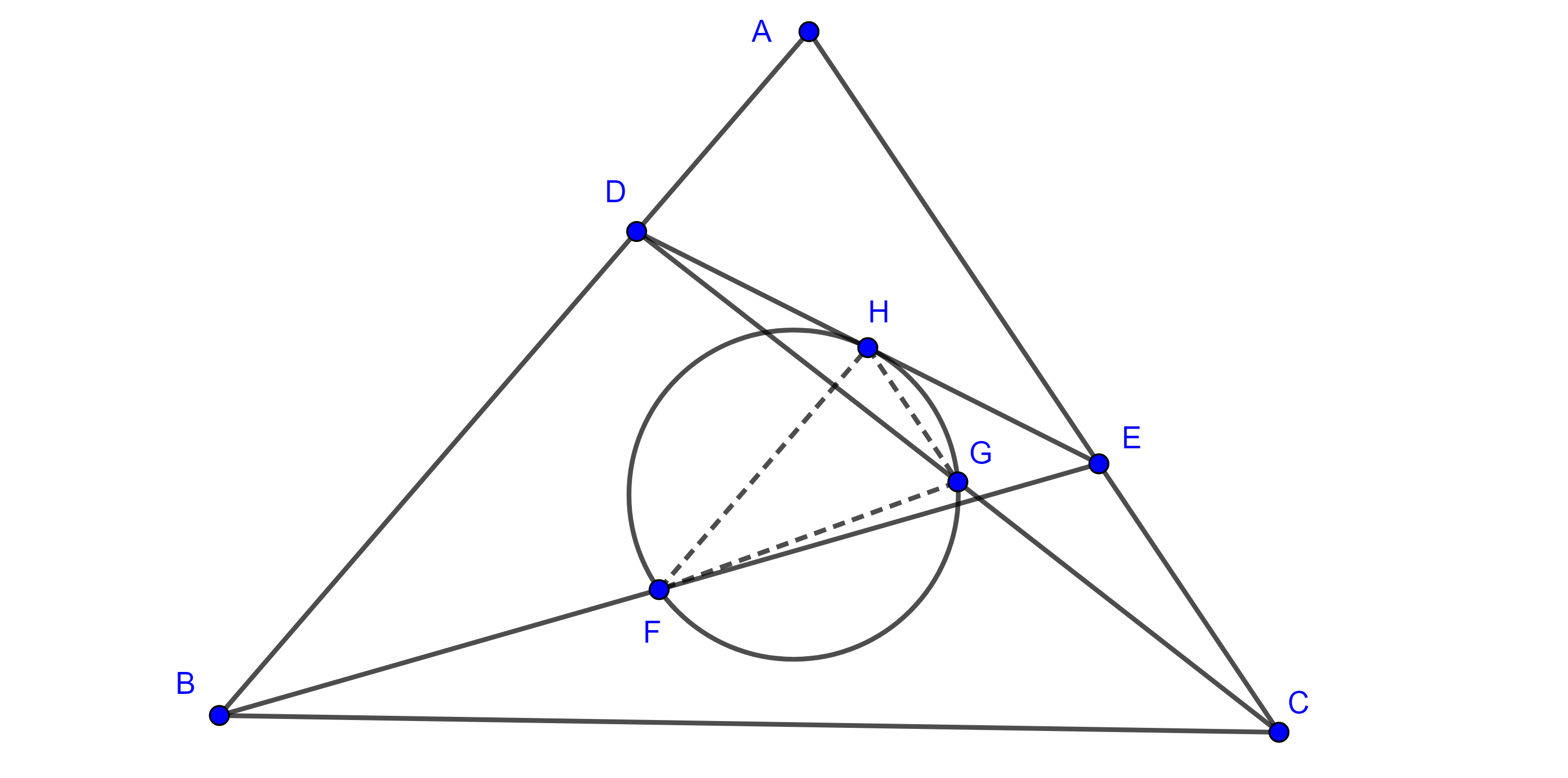
Teorema 4. Sean $(O, R)$, $(I, r)$, dos circunferencias tal que $(I, r)$ está en el interior del círculo $(O, R)$ y tal que la distancia entre sus centros cumple la igualdad $IO^2 = R(R – 2r)$, entonces existen una infinidad de triángulos inscritos en $(O, R)$ y circunscritos en $(I, r)$.
Demostración. Dado que varios argumentos son iguales a los del teorema 3 solo serán mencionados, nos guiaremos en la figura 4.
Desde cualquier punto $A \in (O, R)$ trazamos las tangentes a $(I, r)$ que intersecan a $(O, R)$ en $B$ y $C$, sea $K = AI \cap (O, R)$, usando la igualdad dada y la potencia de $I$ respecto de $(O, R)$ obtenemos,
$\begin{equation} AI \times IK = R^2 – IO^2 = 2Rr. \end{equation}$.
Sean $Z$ e $Y$ los puntos de tangencia de $AB$ y $AC$ con $(I, r)$ respectivamente, por criterio hipotenusa-cateto los triángulos rectángulos $\triangle AIZ$ y $\triangle AIY$ son congruentes por lo que $AK$ es bisectriz de $\angle A$.
Sea $K’ = KO \cap (O, R)$, como $\triangle BKK’$ es rectángulo y $\angle BK’K = \angle ZAI$, por criterio de semejanza AA, $\triangle ZAI \sim \triangle BK’K$ y tenemos que
$\dfrac{AI}{K’K} = \dfrac{ZI}{BK}$
$\Rightarrow \begin{equation} AI \times BK = K’K \times ZI = 2Rr. \end{equation}$
Por $(3)$ y $(4)$ tenemos $AI \times IK = AI \times BK$
$\Rightarrow IK = BK$
Así $\triangle IKB$ es isósceles y $\angle KBI = \angle BIK$, pero
$\angle KBI = \angle KBC + \angle CBI = \dfrac{\angle A}{2} + \angle CBI$ y $\angle BIK = \dfrac{\angle A}{2} + \angle IBA$,
$\Rightarrow CBI = IBA$.
Sea $X$ pie de la perpendicular a $BC$ desde $I$, entonces por criterio de congruencia ALA, $\triangle IZB \cong \triangle IXB$ $\Rightarrow IZ = IX$.
Por lo tanto, $BC$ es tangente a $(I, r)$ en $X$, así $\triangle ABC$ está inscrito en $(O, R)$ y circunscrito en $(I, r)$.
$\blacksquare$
Lema de Haruki
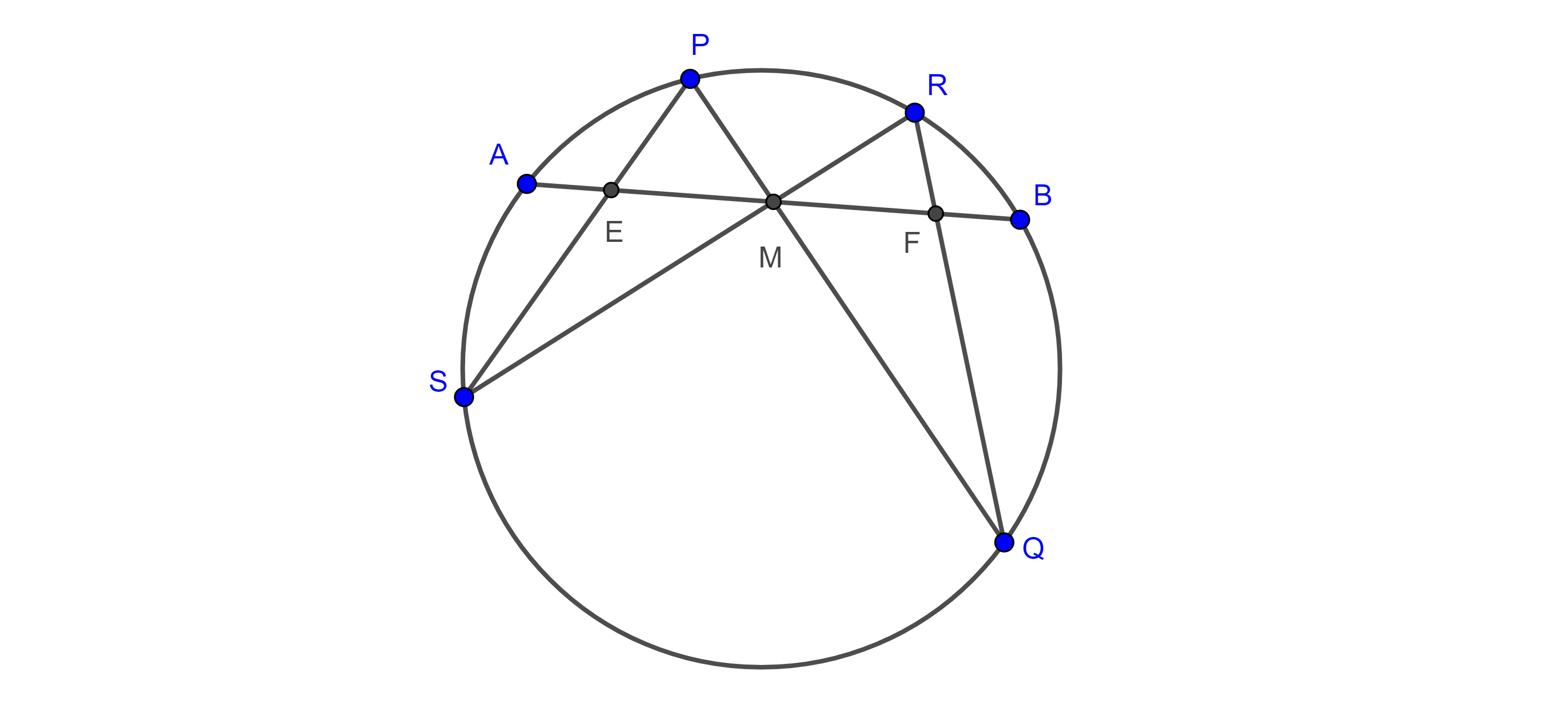
Lema de Haruki. Sean $AB$ y $CD$ dos cuerdas de una circunferencia $\Gamma_1$ que no se intersecan considera $P$ un punto variable en el arco $\overset{\LARGE{\frown}}{BA}$ que no contiene a $C$ y a $D$. Sean $E = PC \cap AB$ y $F = PD \cap AB$, entonces el numero $\dfrac{AE \times FB}{EF}$, es independiente de la posición de $P$ en el arco $\overset{\LARGE{\frown}}{BA}$.
Demostración. Consideremos $\Gamma_2$ circuncírculo de $\triangle PED$ y sea $G = AB \cap \Gamma_2$, entonces $\angle EPD = \angle EGD$, pues abarcan el mismo arco.
Entonces $\angle AGD = \angle EGD = \angle EPD = \angle CPD$, esté último ángulo es fijo mientras $P$ varié en el arco $\overset{\LARGE{\frown}}{BA}$.
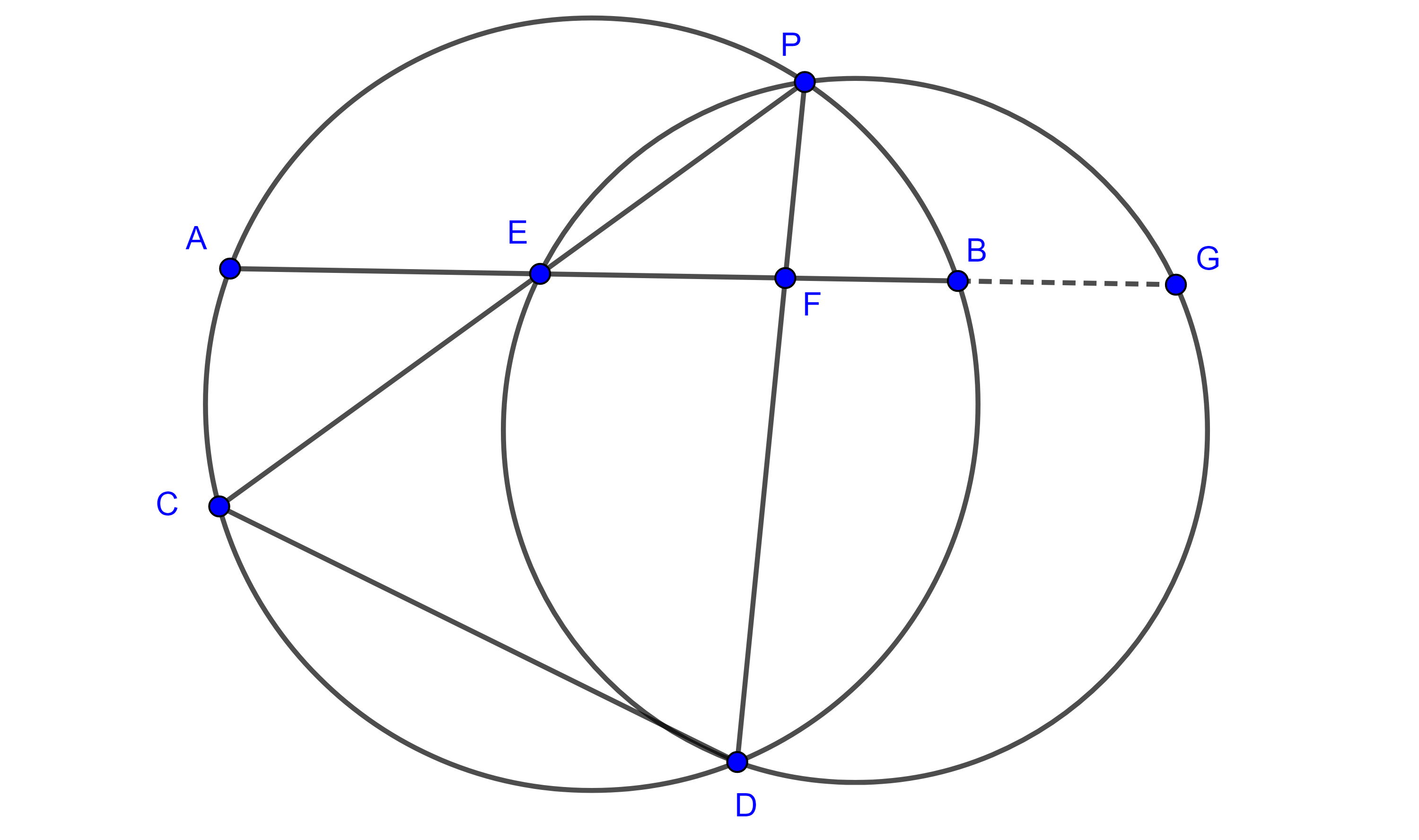
$A$ y $D$ son puntos fijos y $G$ siempre está sobre la recta $AB$, $G$ es un punto fijo, por lo tanto, el valor $BG$ es fijo.
Por otro lado, calculamos la potencia de $F$ respecto de ambas circunferencias
$FA \times FB = FP \times FD$ y $FE \times FG = FP \times FD$
$\Rightarrow (AE + FE) FB = FP \times FD = EF (FB + BG)$
$\Rightarrow \dfrac{AE \times FB}{EF} = BG$.
$\blacksquare$
Mas ejemplos
Problema 1. Sean $\triangle ABC$ y $D$ un punto interior del triángulo tal que $BE \times BA = CA \times CF$ donde $E$ y $F$ son los pies de las perpendiculares a $AB$ y $AC$ trazados desde $D$, encuentra el lugar geométrico de $D$.
Solución. Como $\angle DEA = \angle AFD = \dfrac{\pi}{2}$, entonces $AD$ es diámetro de una circunferencia que pasa por $E$ y $F$, por lo que el centro $O$ de dicha circunferencia $\Gamma(O)$ es el punto medio de $AD$.
Por la proposición 1, la potencia de $B$ y $C$ respecto a $\Gamma(O)$ es
$OB^2 – R^2 = BE \times BA = CA \times CF = OA^2 – R^2$,
$\Rightarrow OB = OC$.
Esto implica que el conjunto $R$, de los puntos medios del segmento $AD$, esta contenido en la mediatriz del segmento $BC$, así el lugar geométrico de los puntos $D$, está en homotecia con centro en $A$ y razón $2$ con el conjunto $R$, esto es una recta paralela a la mediatriz de $BC$ y que esta en el interior de $\triangle ABC$.
$\blacksquare$
Observación. Notemos que si $D$ es un punto exterior de $\triangle ABC$ entonces $B$ y $C$ podrían situarse en lugares distintos respecto de $\Gamma(O)$, es decir uno fuera y otro dentro, por lo que la igualdad $OB = OC$ no seria cierta.
Problema 2. Considera $\triangle ABC$ y $(O, R)$ su circuncírculo, sean $D \in AB$ y $E \in AC$, sean $F$, $G$ y $H$ los puntos medios de $BE$, $CD$ y $DE$ respectivamente, si $DE$ es tangente al circuncírculo de $\triangle FGH$, muestra que $OD = OE$.
Como el ángulo semiinscrito $\angle DHF$ y el ángulo inscrito $\angle HGF$ abarcan el mismo arco, son iguales entre si.
Dado que $HF$ es un segmento medio de $\triangle BDE$ entonces $HF \parallel BD$ y $2HF = BD$
$\Rightarrow \angle DHF = \angle HDA$
$\Rightarrow \angle HGF = \angle HDA$.
De manera análoga podemos ver que $\angle GFH = \angle AED$ y que $HG \parallel EC$ y $2HG = EC$.
Por criterio de semejanza AA, $\triangle FGH \sim \triangle EDA$, entonces
$\dfrac{AE}{HF} = \dfrac{AD}{HG}$
$\Rightarrow \dfrac{AE}{\dfrac{BD}{2}} = \dfrac{AD}{\dfrac{EC}{2}}$
$\Rightarrow AE \times EC = AD \times BD$.
Por lo tanto, $D$ y $E$ tienen la misma potencia respecto a el circuncírculo de $\triangle ABC$.
Por la proposición 1, $R^2 – OD^2 = R^2 – OE^2$, $\Rightarrow OD = OE$.
$\blacksquare$
Más adelante…
Para concluir con los temas básicos de geometría de la circunferencia en la siguiente entrada hablaremos sobre el teorema de Ptolomeo que nos da una condición necesaria y suficiente para que un cuadrilátero convexo sea cíclico, este teorema nos ayudara mas adelante a demostrar algunas identidades trigonométricas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Dos segmentos $PA$ y $BC$ se intersecan en $P$, si $PA^2 = PB \times PC$, muestra que $PA$ es tangente al circuncírculo de $\triangle ABC$ en $A$.
- $\triangle ABC$ es un triangulo rectángulo con $\angle A = \dfrac{\pi}{2}$, sea $D \in BC$ el pie de la altura por $A$, considera $\Gamma_1$ el circuncírculo de $\triangle ADC$ y $\Gamma_2$ una circunferencia tangente a $\Gamma_1$ externamente y tangente a $AB$ y $BC$ en $E$ y $F$ respectivamente, muestra que $CE = CF$.
- Considera $(O, R)$, $(I, r)$ y $(I_a, r_a)$, el circuncírculo, el incírculo y alguno de los excÍrculos respectivamente de un triangulo, muestra que:
$i)$ $OI_a^2 = R(R + 2r_a)$,
$ii)$ $II_a^2 = 4R(r_a – r)$. - Sean $\triangle ABC$, $D \in BC$ el pie de la altura por $A$ y $H \in AD$. Muestra que $H$ es el ortocentro de $\triangle ABC$ si y solo si $DB \times DC = AD \times HD$.
- Teorema de la mariposa. Sea $AB$ una cuerda de una circunferencia y $M$ su punto medio. Por $M$ trazamos otras dos cuerdas $PQ$ y $RS$, sean $E = PS \cap AB$ y $F = RQ \cap AB$. Prueba que $M$ es el punto medio de $EF$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curco: Circunferencias homotéticas.
- Siguiente entrada del curso: Teorema de Ptolomeo.
- Otros cursos.
Fuentes
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 1-11.
- Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 27-31.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 118-124.
- Geometría interactiva
- Wikipedia
- Cut the Knot
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»