Archivo de la etiqueta: Plano fase

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con cero como valor propio

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Vamos a finalizar esta serie de entradas referentes al plano fase de sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ estudiando el caso cuando el sistema tiene al menos un cero como valor propio.

En las entradas anteriores revisamos los casos cuando los valores propios son reales distintos y no nulos, son complejos o se repiten, por lo que el caso que revisaremos en esta entrada es el último por estudiar. En todos los casos anteriores el punto de equilibrio es único y se encuentra en el punto $(0,0)$ del plano fase. Sin embargo, cuando el cero es un valor propio de la matriz asociada al sistema resultará que no habrá un único punto equilibrio, sino que tendremos una infinidad de dichos puntos. Es por eso que dejamos este caso al final.

Veremos cómo se distribuyen los puntos de equilibrio en el plano fase. Finalmente las curvas solución serán muy fáciles de dibujar según el análisis que realizaremos de la solución general al sistema, que será de la forma $$\textbf{X}(t)=c_{1}\begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}+c_{2}e^{\lambda_{2} t}\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}$$ donde $(u_{1},u_{2})$ es un vector propio asociado al valor propio $\lambda_{1}=0$ y $(v_{1},v_{2})$ es un vector propio asociado al valor propio $\lambda_{2} \neq 0$ (si $\lambda_{2}=0$ la solución general se simplifica aún más y es igualmente sencillo hacer el análisis del plano fase).

Dicho lo anterior, vamos a comenzar.

Plano fase para sistemas con cero como valor propio

En el primer video analizamos el plano fase para un sistema de ecuaciones de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando este tiene a cero como un valor propio asociado.

En el segundo video dibujamos el plano fase de algunos sistemas en particular que tienen al menos un valor propio igual a cero.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

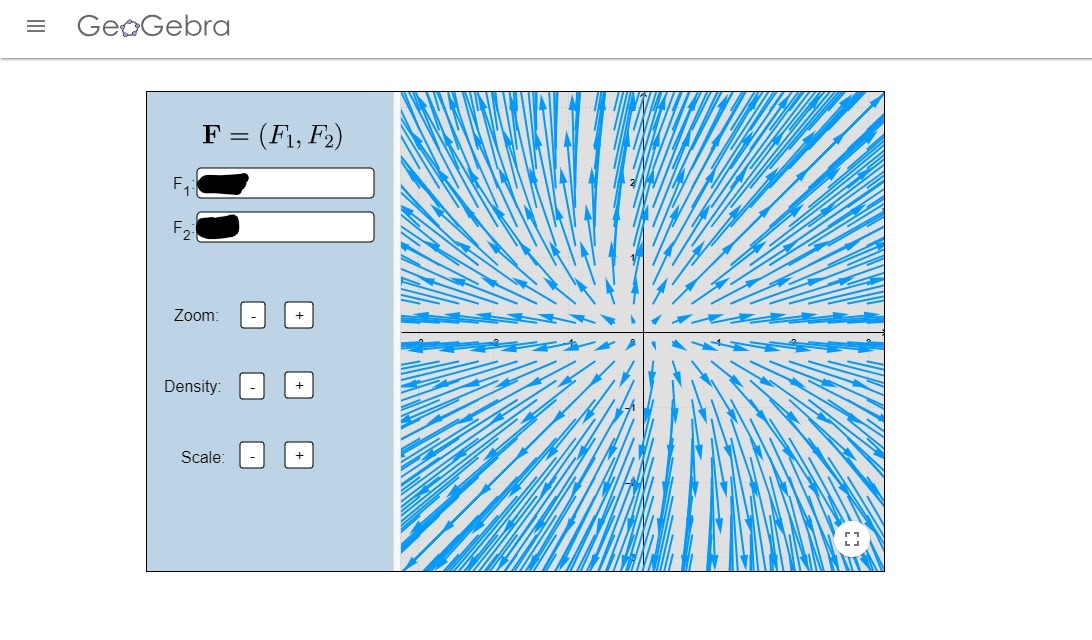
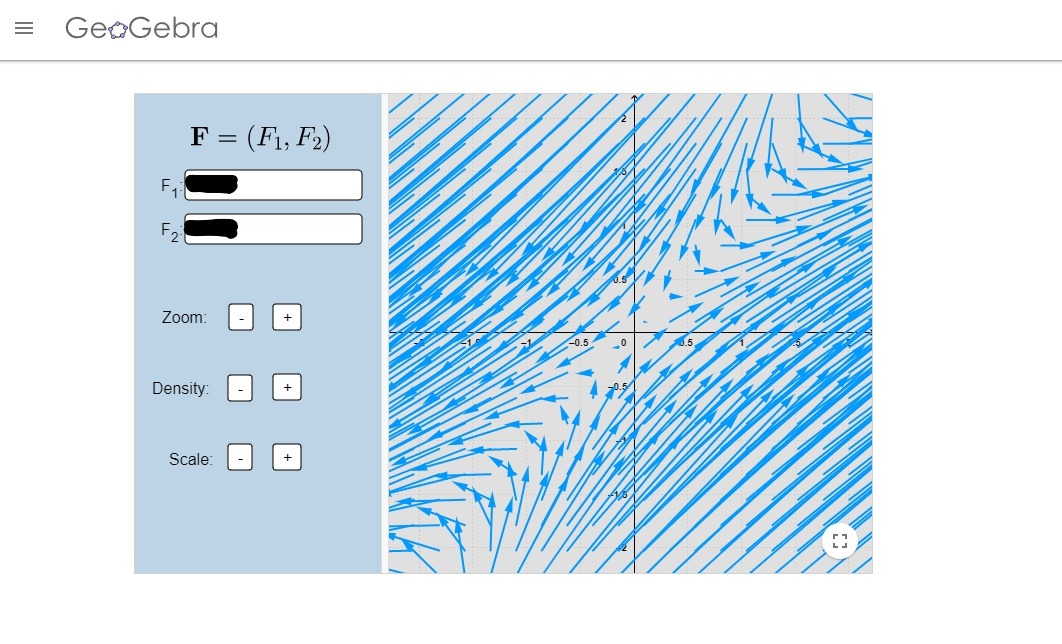
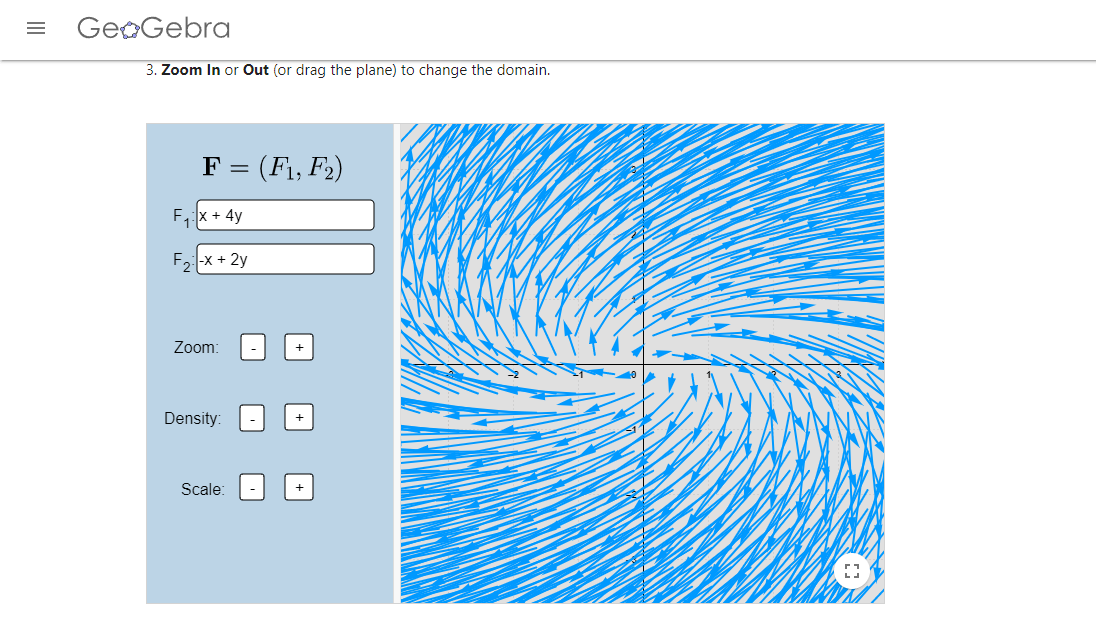
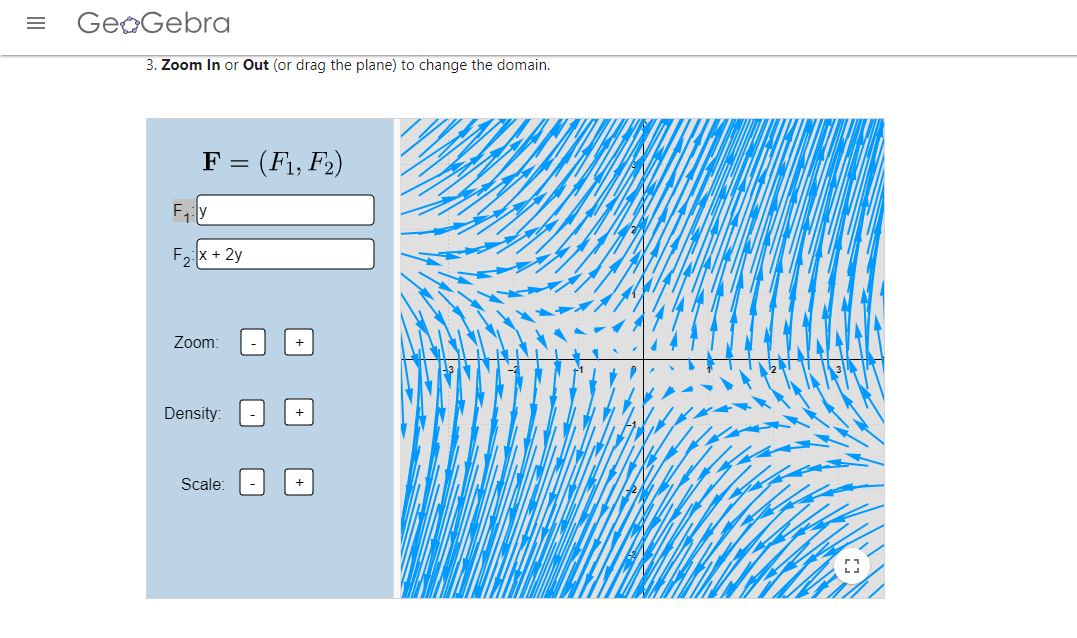
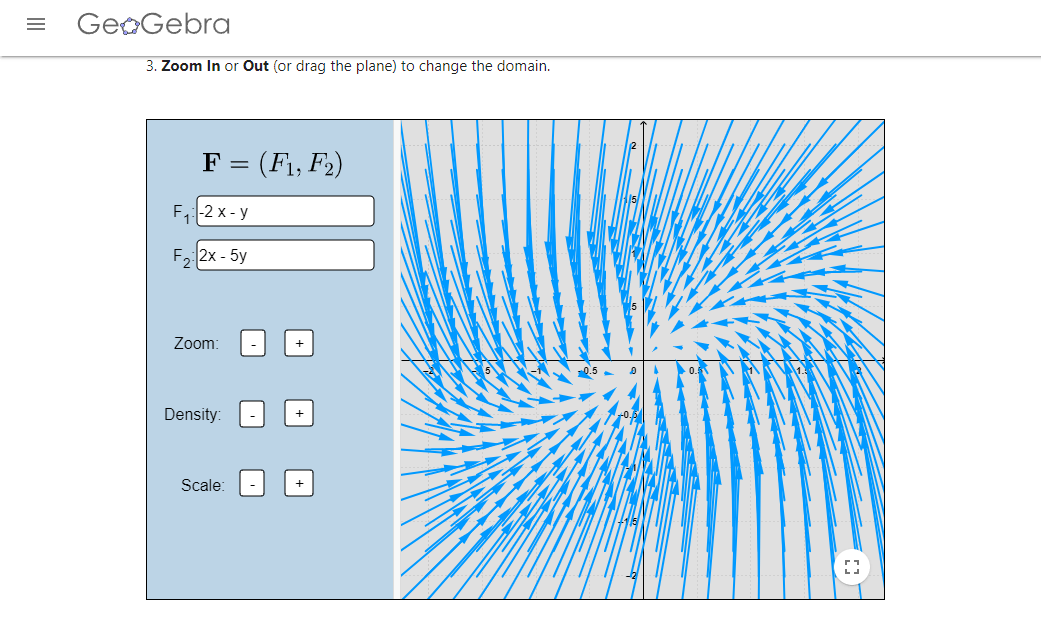
Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Encuentra todas las matrices de tamaño $2 \times 2$ diagonalizables cuyo único valor propio es cero.
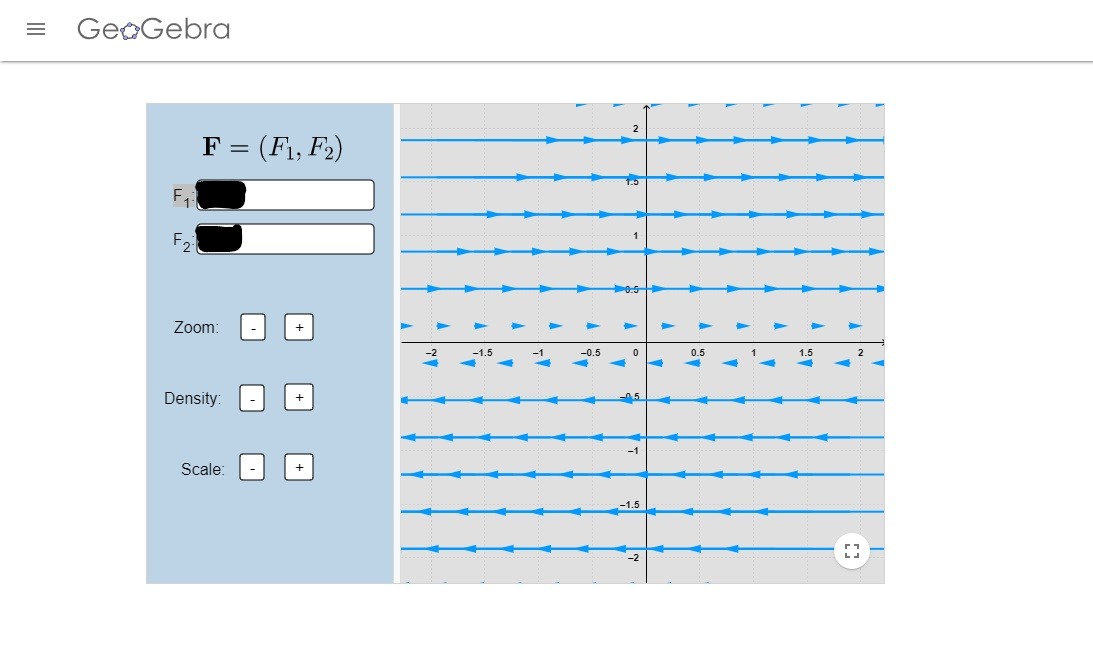
  • Encuentra todos los sistemas de ecuaciones lineales homogéneos con coeficientes constantes cuyo campo vectorial se ve de la siguiente manera:
Campo vectorial 1 cero valor propio
Campo vectorial. Elaboración propia.
  • En el segundo video dibujamos los planos fase de los siguientes sistemas $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -1 & 1 \\ 1 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$ $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 2 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$ ¿Qué puedes decir acerca de los puntos de equilibrio en cada caso? ¿Son estables, asintóticamente estables, inestables, o ninguno de los tres?
  • Encuentra la solución general del siguiente sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 2 \\ 0 & 5 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Resuelve el siguiente sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 5 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general y dibuja el plano fase del siguiente sistema: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 4 & 6 \\ -2 & -3 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$

Más adelante

Hemos terminado de estudiar el plano fase para sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes. Determinamos el comportamiento de las soluciones en el plano y la estabilidad de los puntos de equilibrio en función de los valores propios del sistema.

Estamos a punto de comenzar a estudiar sistemas no lineales, al menos de manera cualitativa (ya que estos sistemas no los sabemos resolver analíticamente). Pero antes vamos a hacer un resumen de todo el análisis realizado recientemente en un dibujo que clasifica las formas del plano fase según dos características de la matriz asociada al sistema: la traza (que es la suma de los elementos en la diagonal) y su determinante.

¡Hasta la próxima!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con valores propios repetidos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En las dos entradas anteriores estudiamos el plano fase para un sistema de dos ecuaciones homogéneas con coeficientes constantes de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuyos valores propios son reales distintos no nulos o complejos. Analizamos el comportamiento de las soluciones en el plano fase y también la estabilidad del punto de equilibrio. Clasificamos los puntos de equilibrio en repulsores, atractores, puntos silla, centros, repulsores espirales y atractores espirales, según sea el caso.

Continuamos en esta entrada revisando el plano fase para sistemas de ecuaciones del mismo tipo, pero ahora consideraremos el caso cuando dicho sistema tiene valores propios repetidos. Sabemos que existen dos casos: cuando la matriz asociada al sistema es diagonalizable y cuando no lo es.

Si la matriz asociada es diagonalizable veremos que el plano fase tiene una forma muy sencilla. En efecto, como la solución general es de la forma $$\textbf{X}(t)=c_{1}e^{\lambda_{1} t} \begin{pmatrix} 1 \\ 0 \end{pmatrix}+c_{2}e^{\lambda_{2} t} \begin{pmatrix} 0 \\ 1 \end{pmatrix}.$$ Veremos que todo vector en $\mathbb{R}^{2}$ es un vector propio del sistema, y por tanto las soluciones (no triviales) en el plano fase son rayos que salen del origen.

Si la matriz asociada al sistema no es diagonalizable entonces la solución general tiene la forma $$\textbf{X}(t)=c_{1}e^{\lambda t}\begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}+c_{2}e^{\lambda t}\left(\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}+t\left(\textbf{A}-\lambda\textbf{Id}\right)\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}\right)$$ donde $\lambda$ es el único valor propio del sistema, $(u_{1},u_{2})$ su único vector propio y $(v_{1},v_{2})$ es un vector propio generalizado. En este caso, solo tenemos una solución de línea recta en el plano fase, así que veremos cuál es el comportamiento de las demás soluciones.

Por supuesto, veremos algunos ejemplos para terminar de entender las ideas presentadas.

Plano fase para sistemas con valores propios repetidos

En el primer video estudiamos el plano fase de manera general para sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando este tiene un único valor propio. Consideramos los casos cuando la matriz asociada al sistema es diagonalizable y cuando no lo es.

En el segundo video dibujamos el plano fase de algunos sistemas de ecuaciones con un único valor propio.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Sea $\textbf{A}$ una matriz de tamaño $2\times 2$ con entradas reales. Muestra que $\textbf{A}$ es diagonalizable y con único valor propio si y sólo si $\textbf{A}=\begin{pmatrix} \lambda & 0 \\ 0 & \lambda \end{pmatrix}$.
  • Encuentra la solución general y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 4 & -4 \\0 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Resuelve y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 3 & -4 \\1 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Resuelve y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -6 & -5 \\5 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}.$$

Más adelante

Estamos a punto de finalizar el estudio del plano fase para sistemas de dos ecuaciones con coeficientes constantes. Sin embargo, aún nos falta un caso, que es cuando el sistema tiene un valor propio igual a cero. El plano fase para este tipo de sistemas es peculiar ya que el sistema tiene infinitos puntos de equilibrio. En la siguiente entrada estudiaremos este caso particular.

¡No te lo pierdas!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con valores propios complejos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos a estudiar el plano fase para sistemas de dos ecuaciones homogéneas con coeficientes constantes de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ En particular, revisamos el caso cuando los valores propios del sistema son reales distintos y no son cero. Vimos que el comportamiento de las curvas y la estabilidad del punto de equilibrio dependen del signo de los valores propios. Así, cuando los signos difieren tenemos un punto silla (inestable), cuando los dos valores propios son negativos tenemos un atractor (punto de equilibrio asintóticamente estable) y finalmente, cuando ambos valores propios son positivos el punto de equilibrio es un repulsor (inestable).

Es turno ahora de analizar el plano fase para sistemas cuyos valores propios son complejos. Sabemos que si $\lambda_{1}=\alpha + \beta i$ es un valor propio del sistema, entonces su conjugado $\lambda_{2}=\alpha – \beta i$ también es un valor propio. Además la solución general a dichos sistemas tiene la forma $$\textbf{X}(t)=c_{1}e^{\alpha t}\left(\cos{\beta t}\begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}-\sin{\beta t}\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}\right)+c_{2}e^{\alpha t}\left(\sin{\beta t} \begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}+\cos{\beta t} \begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}\right)$$ donde los vectores $(u_{1},u_{2})$ y $(v_{1},v_{2})$ son vectores tales que $$\textbf{w}=(u_{1},u_{2})+i(v_{1},v_{2})$$ es un vector propio para $\lambda_{1}$.

Estudiaremos las soluciones cuando $t \rightarrow \infty$. La forma del plano fase va a depender de la parte real $\alpha$ de los valores propios (nota que los dos valores propios tienen la misma parte real), por lo que distinguiremos tres casos, según $\alpha$ sea positivo, negativo o cero. Finalmente clasificaremos a los puntos de equilibrio según su estabilidad.

Plano fase para sistemas con valores propios complejos

En el primer video estudiamos de manera general el plano fase para sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuyos valores propios son complejos. Analizamos tres casos: cuando la parte real de los valores propios es positiva, negativa o cero.

En el segundo video resolvemos y dibujamos el plano fase para distintos sistemas con valores propios complejos.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Prueba que la función $$\textbf{X}(t)=\begin{pmatrix} (c_{1}u_{1}+c_{2}v_{1})\cos{\beta t}+(c_{2}u_{1}-c_{1}v_{1})\sin{\beta t} \\ (c_{1}u_{2}+c_{2}v_{2})\cos{\beta t}+(c_{2}u_{2}-c_{1}v_{2})\sin{\beta t} \end{pmatrix}$$ es periódica, con período $\frac{2\pi}{\beta}$, donde $c_{1},c_{2},u_{1},u_{2},v_{1},v_{2}$ son valores constantes.
  • De acuerdo al ejercicio anterior, concluye que si un sistema homogéneo con coeficientes constantes tiene un valor propio complejo $\lambda_{1}=\beta i$ con vector propio asociado $\textbf{w}=(u_{1},u_{2})+i(v_{1},v_{2})$, entonces las curvas en el plano fase son cerradas.
  • Considera ahora la función $$\textbf{X}(t)=e^{\alpha t}\begin{pmatrix} (c_{1}u_{1}+c_{2}v_{1})\cos{\beta t}+(c_{2}u_{1}-c_{1}v_{1})\sin{\beta t} \\ (c_{1}u_{2}+c_{2}v_{2})\cos{\beta t}+(c_{2}u_{2}-c_{1}v_{2})\sin{\beta t} \end{pmatrix}$$ con $\alpha \neq 0$. Prueba que los puntos en el plano que son imagen de valores periódicos bajo la función del primer ejercicio se quedan contenidos en una recta. Concluye el comportamiento espiral de las soluciones a sistemas de ecuaciones con valores complejos cuya parte real es distinta de cero.
  • Prueba que el punto de equilibrio del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & b \\ -b & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ es un centro.
  • Resuelve y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 2 & 1 \\ -2 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ -1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ -5 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$

(Recuerda que puedes apoyarte del campo vectorial asociado para dibujar el plano fase).

Más adelante

Seguimos avanzando en el estudio del plano fase para sistemas homogéneos con coeficientes constantes. Ya sabemos la forma de las soluciones para sistemas cuyos valores propios son reales distintos y no nulos, o complejos. En la próxima entrada continuaremos revisando el plano fase, pero ahora para sistemas que tienen valores propios repetidos.

¡Hasta la próxima!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con valores propios reales distintos no nulos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En las dos entradas anteriores revisamos los conceptos esenciales para poder estudiar el plano fase del sistema de ecuaciones de primer orden homogéneas con coeficientes constantes $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Revisamos el campo vectorial asociado al sistema, que para los sistemas que estamos considerando se reduce al campo $\textbf{F}(x,y)=(ax+by, cx+dy)$. A cada $(x,y)$, el campo asocia un vector anclado en dicho punto, que además será tangente a las curvas solución. Si observamos el campo vectorial en el plano, entonces podemos darnos una idea aproximada de cómo se verían las curvas solución, y por tanto, el plano fase completo. Por otra parte estudiamos la estabilidad de los puntos de equilibrio, que son aquellos donde el campo vectorial se anula, es decir, cuando $\textbf{F}(x,y)=(0,0)$. De ellos depende el comportamiento del resto de las soluciones en el plano fase.

Con estos ingredientes, estamos listos para poder dibujar los planos fase de casi cualquier sistema de dos ecuaciones con coeficientes constantes. Como sabemos, la solución general a estos sistemas depende de los valores propios de la matriz asociada. Analizaremos el comportamiento de dichas soluciones, comenzando en esta entrada con el caso cuando los valores propios del sistema son reales distintos y no nulos. Después de cada análisis podremos hacer un dibujo esquemático de cómo se ven las soluciones en el plano fase.

¡Vamos a comenzar!

Plano fase para sistemas con valores propios reales distintos no nulos

En el primer video analizamos de manera general el comportamiento de las soluciones a sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando estos tienen valores propios reales distintos y no nulos. Dependiendo del signo de los valores propios será la forma del plano fase.

En el segundo video resolvemos un ejemplo por cada caso analizado en el video anterior.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Prueba que si el determinante de la matriz asociada es cero, entonces el sistema tiene al menos un valor propio $\lambda=0$.
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 4 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general al sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 5 & -1 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Posteriormente grafica la curva correspondiente a la condición inicial $$\textbf{X}(0)=\begin{pmatrix} 2 \\ 1 \end{pmatrix}.$$
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Relaciona cada sistema de ecuaciones con la imagen correspondiente a su plano fase:
  1. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 3 & -2 \\ 2 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  2. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  3. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -1 & 1 \\ 0 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
Campo vectorial valores propios reales uno
Campo vectorial. Elaboración propia
Campo vectorial valores propios reales dos
Campo vectorial. Elaboración propia
Campo vectorial valores propios reales tres
Campo vectorial. Elaboración propia

Más adelante

En esta entrada logramos dibujar el plano fase para sistemas cuyos valores propios son reales distintos y no nulos. El siguiente paso será considerar aquellos sistemas que tienen valores propios complejos. Nuevamente dividiremos el análisis en tres casos, dependiendo del signo de la parte real de los valores propios. Eso lo haremos en la siguiente entrada.

¡No te la pierdas!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Puntos de equilibrio y estabilidad para sistemas de dos ecuaciones de primer orden

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos el estudio a la teoría cualitativa de sistemas de dos ecuaciones de primer orden, definiendo el plano fase del sistema que es el plano $x(t)-y(t)$ junto con todas las curvas que representan a las soluciones al sistema de ecuaciones, vistas como funciones de $\mathbb{R}$ a $\mathbb{R}^{2}$. Una vez que escribimos al sistema de ecuaciones en la forma $$\dot{\textbf{X}}=\textbf{F}(x,y)$$ notamos que la función $\textbf{F}(x,y)$ puede ser vista como una función de $\mathbb{R}^{2}$ a $\mathbb{R}^{2}$. Más aún, podemos ver que a cada punto $(x,y)$ podemos anclar el vector $\textbf{F}(x,y)$ en el plano $x(t)-y(t)$. Este es el campo vectorial asociado al sistema, el cual nos da la información de cómo se ven las curvas solución y su comportamiento.

Para poder dibujar el plano fase de la forma más fiel posible aún debemos estudiar los puntos donde el campo $\textbf{F}$ se anula. A estos puntos los llamaremos puntos de equilibrio. De ellos dependerá casi por completo el comportamiento de las soluciones en el plano fase, por lo que estudiaremos su estabilidad. Es decir, veremos el comportamiento de las soluciones cercanas a los puntos de equilibrio conforme cambia la variable independiente $t$. Finalizaremos estudiando el plano fase de diversos sistemas e interpretando la estabilidad de los puntos de equilibrio según se recorren las curvas solución.

Puntos de equilibrio de sistemas de ecuaciones de primer orden

Definimos los puntos de equilibrio de un sistema de ecuaciones de primer orden y analizamos varios ejemplos. Además, probamos que $$\textbf{X}(t)=\begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix}$$ es solución al sistema de ecuaciones lineal homogéneo con coeficientes constantes $$\dot{\textbf{X}}=\textbf{A}\textbf{X}$$ si $(x_{0},y_{0})$ es punto de equilibrio del sistema.

Estabilidad de puntos de equilibrio

Definimos los conceptos de puntos de equilibrio estables, asintóticamente estables e inestables. Mediante el plano fase estudiamos la estabilidad de puntos de equilibrio de diversos sistemas de ecuaciones.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Considera el sistema lineal homogéneo con coeficientes constantes $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Muestra que si $\det{A} \neq 0$, entonces el único punto de equilibrio del sistema es $(0,0)$.
  • Considera nuevamente el sistema del ejercicio anterior $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Supongamos que $$\textbf{A}=\begin{pmatrix} a & b \\ c &d \end{pmatrix}$$ con $a\neq 0$ y $\det{A}=0$. ¿Qué puedes decir acerca de los puntos de equilibrio del sistema?
  • Encuentra un sistema de ecuaciones no lineales de primer orden sin puntos de equilibrio.
  • Calcula los puntos de equilibrio de los siguientes sistemas: $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 4 \\ -2 & 7 \end{pmatrix}+\begin{pmatrix} 2 \\ 2 \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$
  • Determina la estabilidad de los puntos de equilibrio, según los campos vectoriales que aparecen a continuación:
estabildidad campo vectorial uno
Campo vectorial uno. Elaboración propia
estabilidad campo vectorial dos
Campo vectorial dos. Elaboración propia
estabiliddad campo vectorial tres
Campo vectorial tres. Elaboración propia

Más adelante

Una vez que conocemos los puntos de equilibrio de un sistema de ecuaciones de primer orden y definimos la estabilidad de estos, es momento para analizar el plano fase de los sistemas de dos ecuaciones con coeficientes constantes. Afortunadamente el plano fase y la estabilidad del (único) punto de equilibrio quedará determinado por la forma de los valores propios del sistema.

Comenzaremos en la siguiente entrada con el caso cuando el sistema tiene dos valores propios reales distintos y no nulos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»