Archivo de la etiqueta: morfismo

Álgebra Moderna I: Núcleo e Imagen de un Homomorfismo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

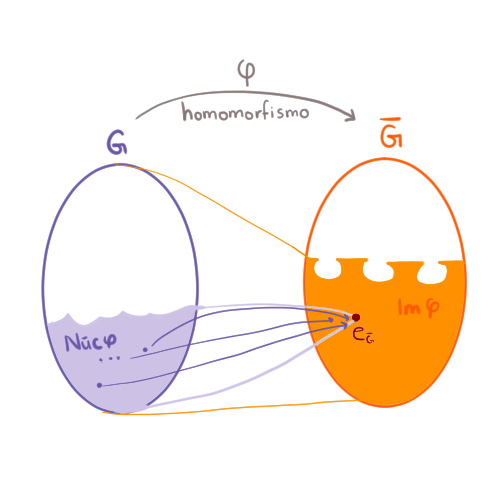
Estamos trabajando con homomorfismos, que son funciones entre dos grupos que respetan sus operaciones. Entre las propiedades que vimos, está que el neutro del dominio siempre va al neutro del codominio. Es decir, al menos hay un elemento que, bajo el homomorfismo, cae en el neutro del codominio.

Para esta entrada consideraremos a la colección de todos los elementos del dominio que van al neutro del codominio. A este subconjunto, lo llamamos el núcleo de $\varphi$. Por otro lado, podemos tomar todos los elementos del dominio, aplicarles $\varphi$ y tomar el subconjunto que resulta en el codominio, a esto le llamamos la imagen de $\varphi$. Estos dos subconjuntos van a ser importantes en el estudio de los homomorfismos.

La imagen muestra que para $\varphi: G\to \bar{G}$ un homomorfismo, el núcleo $\text{Núc }\varphi \subseteq G$ y la imagen $\text{Im }\varphi \subseteq \bar{G}$.

El núcleo y la imagen de un homomorfismo

Comencemos definiendo formalmente los subconjuntos.

Definición. Sean $G, \bar{G}$ grupos, $\varphi: G \to \bar{G}$ un homomorfismo. Definimos al núcleo de $\varphi$ como
\begin{align*}
\text{Núc } \varphi = \{g\in G | \varphi(g) = e_{\bar{G}}\}.
\end{align*}

Es decir, es el conjunto de todos los elementos de $G$ que, bajo $\varphi$ van a dar al neutro de $\bar{G}$.

Notación. Es común, por el nombre en alemán, denotar al $\text{Núc } \varphi$ como $\text{Ker }\varphi$, es llamado el Kernel de $\varphi$.

Definición. La imagen de $\varphi$ es
\begin{align*}
\text{Im } \varphi = \{\varphi(g) | g \in G\}.
\end{align*}

Notemos que $\text{Núc }\varphi \subseteq G$ y $\text{Im }\varphi \subseteq \bar{G}$.

Ejemplos.

Ejemplo 1. Tomemos el homomorfismo $\varphi: S_n \to \{+1,-1\}$ con $\varphi(\alpha) = sgn\, \alpha$ para toda $\alpha\in S_n$. Veamos quién es el núcleo de $\varphi$:
\begin{align*}
\text{Núc }\varphi &= \{\alpha\in S_n | \varphi(\alpha) = +1\} \\
&= \{\alpha\in S_n | sgn\in\alpha = +1\} = A_n.
\end{align*}
Si tomamos el caso no trivial, con $n>1$,
\begin{align*}
\text{Im }\varphi = \{+1,-1\}.
\end{align*}
Ya que $\varphi((1)) = 1$ y $\varphi((1\,2)) = -1$.

Ejemplo 2. Sea $n \in \z^+$. Consideremos el homomorfismo $\varphi: \z \to \mathbb{C}^*$ con
\begin{align*}
\varphi(m) = \left(e^{\frac{2\pi i}{n}}\right)^m \quad \forall m\in \z.
\end{align*}
Buscamos describir su núcleo y su imagen.
\begin{align*}
\text{Núc }\varphi &= \{m\in \z| \varphi(m) =1\}\\
&= \{m\in\z | \left(e^{\frac{2\pi i}{n}}\right)^m = 1\} = n\z.
\end{align*}
La última igualdad se da porque ya sabemos que $e^{2\pi i} = 1$, más aún $e^{\theta i} = 1$ si y sólo si $\theta$ es un múltiplo de $2\pi$, entonces $ \left(e^{\frac{2\pi i}{n}}\right)^m = 1$ si y sólo si $m$ es un múltiplo de $n$.

Ahora la imagen:
\begin{align*}
\text{Im }\varphi &= \{\varphi(m)| m \in \z\} \\
&= \{\left(e^{\frac{2\pi i}{n}}\right)^m | m\in \z\} = \left< e^{\frac{2\pi i}{n}}\right>.
\end{align*}

El núcleo y la imagen son subgrupos

Ahora, probaremos que el núcleo y la imagen de un homomorfismo no son sólo subconjuntos del dominio y codominio respectivamente, si no que son subgrupos.

Teorema. Sean $G, \bar{G}$ grupos, $\varphi:G\to\bar{G}$ un homomorfismo.

  1. $\text{Núc }\varphi \unlhd G$.
  2. $\text{Im }\varphi \leq \bar{G}$.
  3. $\varphi$ es un monomorfismo si y sólo si $\text{Núc }\varphi = \{e_G\}$.

Demostración.
Sean $G,\bar{G}$ grupos, $\varphi: G \to \bar{G}$ un homomorfismo.

  1. P.D. $\text{Núc }\varphi \unlhd G$.
    Primero probaremos que $\text{Núc }\varphi \leq G$.

    Como $\varphi$ es un homomorfismo, $\varphi(e_G) = e_{\bar{G}}$. Entonces $e_G \in \text{Núc }\varphi$.

    Si $a,b\in\text{Núc }\varphi$.
    \begin{align*}
    \varphi(ab^{-1}) &= \varphi(a) \varphi(b^{-1}) &\varphi \text{ es un homomorfismo}\\
    &=\varphi(a)(\varphi(b))^{-1} & \text{Proposición de homomorfismo} \\
    &= e_{\bar{G}}e_{\bar{G}}^{-1} = e_{\bar{G}} & a,b \in \text{Núc }\varphi
    \end{align*}
    Entonces $ab^{-1} \in \text{Núc }\varphi$. Por lo tanto $\text{Núc }\varphi \leq G$.

    Además, si $a\in G$ y $n\in\text{Núc }\varphi$:
    \begin{align*}
    \varphi(ana^{-1}) &= \varphi(a)\varphi(n)\varphi(a^{-1}) &\varphi\text{ es un homomorfismo}\\
    &= \varphi(a)\varphi(n)(\varphi(a))^{-1} &\text{Proposición}\\
    & = \varphi(a) e_{\bar{G}}(\varphi(a))^{-1} &n \in \text{Núc }\varphi \\
    &= \varphi(a) (\varphi(a))^{-1} = e_{\bar{G}}
    \end{align*}
    Así, $ana^{-1}\in \text{Núc }\varphi$. Esto nos dice que el núcleo de $\varphi$ es cerrado bajo conjugación. Por lo tanto $\text{Núc } \varphi \unlhd G$.
    $\newline$
  2. P.D. $\text{Im }\varphi \leq \bar{G}$.
    Primero veamos que el neutro de $\bar{G}$ está en $\text{Im }\varphi$. Esto pasa porque
    $$e_{\bar{G}} = \varphi(e_{G}) \in \text{Im }\varphi.$$

    Ahora, si $c,d\in \text{Im }\varphi$, entonces $c = \varphi(a), d = \varphi(b)$ para algunos $a,b\in G$.
    \begin{align*}
    ad^{-1} = \varphi(a)(\varphi(b))^{-1} &= \varphi(a)\varphi(b^{–1}) &\text{Proposición}\\
    &= \varphi(ab^{-1}) \in \text{Im }\varphi &\varphi\text{ es un homomorfismo}
    \end{align*}
    Por lo tanto $\text{Im }\varphi \leq \bar{G}$.
    $\newline$
  3. P.D. $\varphi$ es un monomorfismo si y sólo si $\text{Núc }\varphi = \{e_G\}$.

    $|\Rightarrow]$ Supongamos que $\varphi$ es un monomorfismo (un homomorfismo inyectivo).
    Como $\text{Núc }\varphi \leq G$, entonces $\{e_G\}\subseteq \text{Núc }\varphi$.
    Ahora, si $g\in \text{Núc }\varphi$, por la proposición anterior,
    \begin{align*}
    \varphi(g) = e_{\bar{G}} = \varphi(e_G).
    \end{align*}
    Y como $\varphi$ es inyectiva, $g = e_G$. Por lo tanto, $\text{Núc }\varphi = \{e_G\}$.

    $[\Leftarrow|$ Supongamos que $\text{Núc }\varphi =\{e_G\} $.
    Sean $a,b\in G$ tales que $\varphi(a) = \varphi(b)$. Entonces
    \begin{align*}
    e_{\bar{G}} &= \varphi(b)(\varphi(a))^{-1} \\
    &= \varphi(b)\varphi(a^{-1}) &\text{Proposición}\\
    &= \varphi(ba^{-1}) &\varphi\text{ es un homomorfismo}
    \end{align*}
    Entonces $ba^{-1} \in \text{Núc }\varphi = \{e_G\}$, así $ba^{-1} = e_G$, esto implica que $b = a$.
    Por lo tanto $\varphi$ es un monomorfismo.

$\blacksquare$

Observemos que el inciso 3 del teorema nos da una herramienta para determinar si un homomorfismo es inyectivo o no usando el núcleo.

Proyección Canónica

Ahora, tomando un grupo y un subgrupo normal, definiremos un epimorfismo de un grupo al grupo cociente.

Proposición. Sea $G$ un grupo, $N$ un subgrupo normal de $G$. La función $\pi_:G\to G/N$ con $\pi(a) = aN$ para toda $a\in G$, es un epimorfismo tal que $\text{Núc }\pi = N$.

Esta función se conoce como la proyección canónica.

Demostración.
Sea $G$ un grupo, $N\unlhd G$, $\pi: G\to G/N$ con $\pi(a) = aN$ para cualquier $a\in G$.

Veamos que $\pi$ es un homomorfismo
Sean $a,b \in G$, entonces
\begin{align*}
\pi(ab) = abN = (aN)(bN) = \pi(a)\pi(b).
\end{align*}

Ahora veamos que es suprayectivo. Esto es debido a que dado $aN\in G/N$, $$aN = \pi(a).$$

Por lo tanto $\pi$ es un epimorfismo.

Finalmente,
\begin{align*}
\text{Núc }\pi = \{a\in G| \pi(a) = e_{G/N}\} = \{a\in G| aN = N\} = N.
\end{align*}

$\blacksquare$

Ahora veamos un corolario que se desprende directamente de lo que acabamos de ver.

Corolario. Todo subgrupo normal es el núcleo de un homomorfismo. De hecho, es el núcleo de un epimorfismo.

Ejemplos

Para terminar veamos unos ejemplos

Ejemplo 1. Tomemos $\varphi:(\r,+) \to (\mathbb{C}^*, \cdot)$ con $\varphi(x) = e^{xi}$ para toda $x\in\r$. Toma 2 min para pensar porqué es un homomorfismo.

Veamos el núcleo y la imágen de $\varphi$:
\begin{align*}
\text{Núc }\varphi &= \{x\in\r | \varphi(x) = 1\} \\
&= \{x\in\r | e^{xi} = 1\} \\
&= \{2\pi n | n \in \z\} = \left< 2\pi\right>.\\\\
\text{Im }\varphi &= \{\varphi(x) | x \in \r\} \\
& =\{e^{xi} | x\in\r\} \\
&= \{z\in \mathbb{C} | |z| = 1\} = \s^1.
\end{align*}
¿Cómo es $\r/\left<2\pi\right>$?
Tomemos $a,b\in \r$.
\begin{align*}
a + \left< 2\pi\right> = b + \left< 2\pi\right> &\Leftrightarrow a-b \in \left< 2\pi\right> \\
&\Leftrightarrow a-b= 2\pi n,\, n\in \z.
\end{align*}
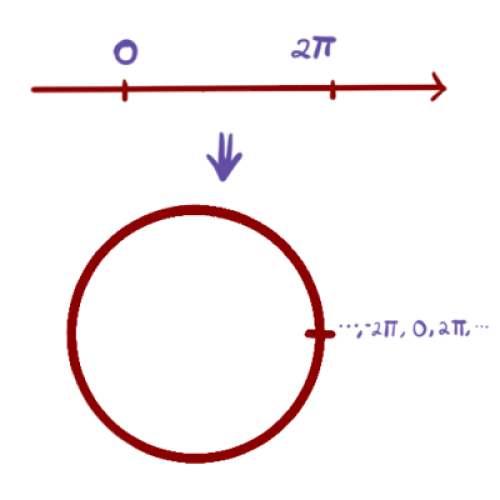
Si lo anterior nos dice que dos números $a,b$ están en la misma clase si y sólo si difieren por un múltiplo de $2\pi$. Si lo pensamos en la recta numérica, nos dice que el $0$ y $2\pi$ quedan indentificados en la misma clase. Intuitivamente podríamos pensar que estamos doblando la recta numérica para obtener una circunferencia donde $0$ y $2\pi$ están en el mismo punto.

Así, $\r/\left< 2\pi\right> = \{a+\left< 2\pi\right> | a\in [0,2\pi)\}$.

Representación gráfica del ejemplo 1.

Ejemplo 2. Consideremos $\varphi: (\r^*,\cdot)\to (\r^*,\cdot)$ con $\varphi(x) = |x|$ para toda $x \in \r^*$ (recuerda que $\r^*=\r\setminus \{0\}$).
\begin{align*}
\text{Núc }\varphi &= \{x\in\r^* | \varphi(x) = 1\} \\
&= \{x\in\r^*| |x| = 1\} = \{+1,-1\}.\\\\
\text{Im }\varphi &= \{\varphi(x) | x \in \r^*\} \\
& =\{|x| | x\in\r^*\} = \r^+. \\
\end{align*}
¿Cómo es $\r^*/\{+1,-1\}$?
Tomemos $a,b\in \r^*$.
\begin{align*}
a\{+1,-1\}= b\{+1,-1\} &\Leftrightarrow a^{-1}b \in \{+1,-1\} \\
&\Leftrightarrow a^{–1}b=\pm 1 \Leftrightarrow b = \pm a.
\end{align*}
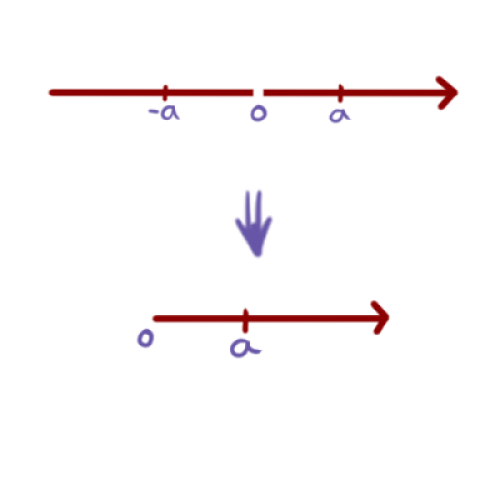
Entonces, dos clases laterales van a ser iguales si y sólo si sus representantes difieren a lo más sólo por el signo.

Lo que hicimos fue tomar a los reales sin el cero y estamos identificando a cada número real $a$ con su inverso aditivo. Entonces la imagen de $\varphi$ en realidad es como si dobláramos la recta por el 0 e identificamos a los reales negativos con su correspondiente positivo.

Así, $\r^*/ \{+1,-1\} = \{a \{+1,-1\} | a\in \r^+\}$.

Representación gráfica del ejemplo 2.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $\varphi:GL(2,\r) \to \r^*$ el homomorfismo tal que $\varphi(A) = \text{det }A$. Encuentra el núcleo y la imagen de $\varphi$.
  2. Sean $G,\bar{G}$ grupos y $\varphi: G\to\bar{G}$ un homomorfismo. ¿Es $ \text{Im }\varphi$ normal en $\bar{G}$? Prueba o da un contraejemplo.
  3. Sean $G,\bar{G}$ grupos y $\varphi: G\to \bar{G}$ un homomorfismo. Sean también, $H\leq G, \bar{H}\leq \bar{G}$.
    • ¿Qué puedes decir de $\varphi[H] = \{\varphi(h) | h \in H\}$?¿Y si $H\unlhd G$?
    • ¿Qué puedes decir de $\varphi^{-1}[\bar{H}] = \{g\in G| \varphi(g) \in \bar{H}\}$? ¿Y si $\bar{H}\unlhd\bar{G}$?
  4. En cada inciso calcula $\text{Núc } \varphi, \text{Im }\varphi, G/\text{Núc}$ y analiza cómo se relacionan:
    • $G$ grupo, $\varphi: G \to G$, con $\varphi =\text{id}_G $.
    • $G$ grupo, $\varphi: G \to G$, con $\varphi(g) = e_G$ para toda $g\in G$.
    • $\varphi: (\mathbb{C}^*, \cdot) \to (\r^*, \cdot)$, con $\varphi(z) = |z|$ para toda $z\in\mathbb{C}^*$.
    • $\varphi: \z \times \z \to \z\times\z$, con $\varphi(x,y) = (x,0)$ para toda $(x,y)\in \z\times\z$.

Más adelante…

Ahora que ya tenemos muy claras las definiciones de núcleo e imagen de un homomorfismo, comenzaremos a ver teoremas que relacionan lo que vimos aquí con isomorfismos y grupo cociente.

Entradas relacionadas

Álgebra Moderna I: Homomorfismo, Monomorfismo, Epimorfismo, Isomorfismo y Automorfismo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Lo sé, el título parece un trabalenguas. Pero ten paciencia, en realidad no es tan complicado.

A lo largo de este curso hemos estado trabajando con grupos, ahora vamos a pensar en funciones que respetan de alguna manera la estructura de los grupos.

Tomemos por ejemplo el grupo de Klein, $V = \{(0,0), (1,0), (0,1),(1,1)\}$, es un grupo que tiene un neutro $(0,0)$ y los otros tres elementos comparten que: tienen orden 2, si se suman consigo mismos obtenemos el neutro y si sumamos dos, obtenemos el tercero:

\begin{align*}
(1,0) + (1,0) &= (0,0)\\
(0,1) + (0,1) &= (0,0)\\
(1,1) + (1,1) &= (0,0).
\end{align*}

\begin{align*}
(1,0) + (0,1) &= (1,1)\\
(0,1) + (1,1) &= (1,0)\\
(1,1) + (1,0) &= (0,1).
\end{align*}

Por otro lado, podemos tomar el conjunto $P = \{(1), (1\, 2)(3\,4), (1\,3)(2\,4), (1\,4)(2\,3)\}$. $P$ es un grupo que tiene un neutro $(1)$ y los otros tres elementos comparten que: tienen orden 2, si se componen consigo mismos obtenemos el neutro y si componemos dos, obtenemos el tercero:

\begin{align*}
(1\, 2)(3\,4)(1\,2)(3\,4) &= (1)\\
(1\,3)(2\,4)(1\,3)(2\,4) &= (1)\\
(1\,4)(2\,3)(1\,4)(2\,3) &= (1).
\end{align*}

\begin{align*}
(1\, 2)(3\,4)(1\,3)(2\,4) &= (1\,4)(2\,3)\\
(1\,3)(2\,4)(1\,4)(2\,3) &= (1\, 2)(3\,4)\\
(1\,4)(2\,3)(1\, 2)(3\,4) &= (1\,3)(2\,4).
\end{align*}

¿Suena familiar? Bueno, esto es porque a pesar de que son grupos distintos, con elementos y operaciones muy diferentes, estructuralmente son iguales.

Para formalizar esta idea, nos gustaría observar que existe una correspondencia entre los dos grupos. Esta correspondencia es biyectiva y además tiene que respetar la estructura de las operaciones. Entonces sería algo así:

\begin{align*}
(0,0) &\longrightarrow (1)\\
(1,0) &\longrightarrow (1\, 2)(3\,4)\\
(0,1) &\longrightarrow (1\,3)(2\,4)\\
(1,1) &\longrightarrow (1\,4)(2\,3).
\end{align*}

En este caso decimos que $V$ y $P$ son isomorfos. Lo definiremos formalmente más adelante, por ahora es importante que observes que esta correspondencia mantiene la estructura de las operaciones de los grupos. Así, este es el objetivo de la entrada, definir y trabajar con funciones (no necesariamente biyectivas) que mantengan las operaciones de dos grupos. Estas funciones son llamadas homomorfismos.

¿Qué son todos estos homomorfismos?

Primero, comencemos definiendo lo más general. Una función que mantenga las operaciones entre grupos.

Definición. Sean $(G,*), (\bar{G}, \bar{*})$ grupos. Decimos que la función $\varphi:G \mapsto \bar{G}$ (ó $\varphi: (G,*)\mapsto (\bar{G},\bar{*})$) es un homomorfismo de grupos si
$$\varphi(a*b) = \varphi(a) \bar{*} \varphi(b) \quad \forall a,b\in G.$$

Se puede decir que $\varphi$ «abre» a la operación.

Definiciones varias.

Ahora, le agregaremos condiciones a $\varphi$. Dependiendo de qué condición extra cumpla, el homorfismo tomará otro nombre.

  • Si el homomorfismo $\varphi$ es inyectivo se llama monomorfismo.
  • Si el homomorfismo $\varphi$ es suprayectivo se llama epimorfismo.
  • Si el homomorfismo $\varphi$ es biyectivo se llama isomorfismo.
  • Un isomorfismo de un grupo en sí mismo se llama automorfismo.

Notación. Si $\varphi$ es un isomorfismo decimos que $G$ es isomorfo a $\bar{G}$ y lo denotamos como $G \cong \bar{G}$.

Puede parecer mucho vocabulario nuevo, así que guarda esta entrada para recordar qué es cada uno.

Ejemplos.

Ejemplo 1.Tomemos $\varphi: (\z , +) \mapsto (\z_n,+)$ con $\varphi(a) = \bar{a}$ para toda $a\in \z$. Es decir, $\varphi$ manda a cada entero a su clase módulo $n$.

Veamos qué sucede con la suma :
$\varphi(a+b) = \overline{a+b} = \bar{a} + \bar{b} = \varphi(a) + \varphi(b)$ para toda $a,b \in \z$.

Además, dado $\bar{a} \in \z_n, \bar{a} = \varphi(a)$. Entonces $\varphi$ es suprayectiva.
Por lo tanto $\varphi$ es un epimorfismo.

Ejemplo 2. Sea $n \in \n^+$.
Tomamos $\varphi: (S_n, \circ) \mapsto (S_{n+1}, \circ)$ donde para cada $\alpha \in S_n$ se define $\varphi(\alpha) \in S_{n+1}$ tal que
\begin{align*}
\varphi(\alpha)(i) =
\begin{cases}
\alpha(i) & \text{si } i \in \{1,…,n\} \\
n+1 & \text{si } i = n+1
\end{cases}
\end{align*}

Es decir, se mantienen las permutaciones de $S_n$ pero se consideran como elementos de $S_{n+1}$ pensando que dejan fijo a $ n+1$.

Ahora veamos qué sucede con el producto, sean $\alpha, \beta \in S_n$:
\begin{align*}
\varphi(\alpha)\varphi(\beta) (i) &= \varphi(\alpha)(\varphi(\beta)(i)) \\
& = \begin{cases} \alpha(\beta(i)) & \text{si } i \in \{1, … , n\} \\
n+1 & \text{si } i = n+1
\end{cases} \\
&= \varphi(\alpha\beta)(i)
\end{align*}

Además, si $\varphi(\alpha) = (1)$ entonces $\alpha(i) = i$ para todo $i \in \{1, …, n\}$. Así $\alpha = (1).$ Por lo que $\varphi$ es inyectiva.
En conclusión, $\varphi$ es un monomorfismo.

Ejemplo 3. Sea $\varphi: (\r, +) \mapsto (\r^+, \cdot)$ con $\varphi(x) = e^x$ para todo $x\in\r$.
Entonces, para la suma de dos elementos en el dominio $x,y \in \r$ tendríamos,
$$\varphi(x+y) = e^{x+y} = e^x e^y = \varphi(x) \varphi(y).$$
Sabemos que $\psi: \r^+ \mapsto \r$ con $\psi(y) = \ln(y)$ para toda $y \in \r^+$ es la inversa de $\varphi$, así $\varphi$ es biyectiva.
Por lo tanto $\varphi$ es un isomorfismo.

Ejemplo 4. Veamos un ejemplo más abstracto. Sea $G$ un grupo y $g\in G$. Y, dadas $x,y \in G$, definimos
$\gamma_g(xy) = g(xy) g^{-1} = (gxg^{-1}) (gyg^{-1}) = \gamma_g (x) \gamma_g(y).$
Además, para toda $x \in G$,
\begin{align*}
\gamma_g \circ \gamma_{g^{-1}} (x) = \gamma_g (g^{-1}x g ) = g(g^{-1} x g) g^{-1} = x \\
\gamma_{g^{-1}} \circ \gamma_{g} (x) = \gamma_{g^{-1}} (g x g^{-1} ) = g^{-1}(g x g^{-1}) g = x .
\end{align*}
Donde, $g^{-1}$ existe porque $G$ es un grupo. Así, lo anterior nos indica que $\gamma_g$ es un homomorfismo invertible, que además tiene como dominio y codominio a $G$.

Por lo tanto $\gamma_g$ es un automorfismo.

Propiedades de los homomorfismos

Proposición. El inverso de un isomorfismo es un isomorfismo.

Demostración.

Sean $(G, *), (\bar{G}, \bar{*})$ grupos, $\varphi:G\mapsto \bar{G}$ es un isomorfismo.
Tomemos $c,d \in\bar{G}$.

Como $\varphi$ es suprayectiva, existen $a,b \in G$ tales que $\varphi(a) = c$ y $\varphi(b) = d$.

\begin{align*}
\varphi^{-1} (c \bar{*}d) &= \varphi^{-1} \left( \varphi(a) \bar{*} \varphi(b) \right) \\
&= \varphi^{-1}\left( \varphi(a * b)\right) & \varphi \text{ es un homomorfismo}\\
& = \varphi^{-1} \circ \varphi (a*b)\\
& = a * b & \text{Composición de inversas}\\
& = \varphi^{-1}(c) * \varphi^{-1}(d) & \text{Pues }\varphi(a) = c,\, \varphi(b) = d
\end{align*}

Así, $\varphi^{-1}$ es un homomorfismo y como es biyectivo por ser invertible, entonces $\varphi^{-1}$ es un isomorfismo.

$\blacksquare$

Proposición. La composición de homomorfismos es un homomorfismo.

Demostración.

Sean $(G,*), (\bar{G}, \bar{*}), (\tilde{G}, \tilde{*})$ grupos. También, sean $\varphi: G \mapsto \bar{G}$ y $\psi: \bar{G} \mapsto \tilde{G}$ homomorfismos.

Dados $a,b \in G$,

\begin{align*}
\psi \circ \varphi(a*b) &= \psi (\varphi (a*b)) \\
&= \psi(\varphi(a)\,\bar{*}\, \varphi(b)) &\varphi\text{ es homomorfismo}\\
&= \psi(\varphi(a)) \,\tilde{*}\, \psi(\varphi(b)) & \psi\text{ es homomorfismo} \\
&= \psi\circ\varphi(a)\, \tilde{*} \,\psi\circ\varphi(b)
\end{align*}

Por lo tanto $\psi\circ\varphi$ es un homomorfismo.

$\blacksquare$

Observaciones.

  • Para todo $G$ grupo, $G\cong G$. (Es decir, $G$ es isomorfo a sí mismo).
  • Si $G, \bar{G}$ son grupos y $G \cong \bar{G}$, entonces $\bar{G}\cong G$.
  • Si $G, \bar{G}, \tilde{G}$ son grupos, $G \cong \bar{G}$ y $\bar{G} \cong \tilde{G}$, entonces $G\cong \tilde{G}.$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $D_{2n} = \left<a,b\right>$ el grupo diédrico formado por las simetrías de un $n$-ágono, con $a$ la rotación de $\displaystyle\frac{2\pi}{n}$ y $b$ la reflexión con respecto al eje $x$. Sea $\varphi: D_{2n} \to D_{2n}$ tal que $\varphi(a^ib^j) = b^j$. ¿Es $\varphi$ un homomorfismo?
  2. Sean $X$ y $Y$ dos conjuntos con la misma cardinalidad. ¿Qué relación hay entre $S_X$ y $S_Y$?
  3. Sea $V = \{e, (1\,2)(3\,4), (1\,3)(2\,4), (1\,4)(1\,3)\} \leq S_4$. Encuentra $H\leq S_4$, $H\neq V$ pero isomorfo a $V$. ¿Es $H$ normal en $S_4$?

Más adelante…

Los homomorfismos son una parte importante de las matemáticas, porque respetar las operaciones es una característica sencilla a simple vista, pero lo suficientemente compleja para que las funciones que la cumplan sean muy interesantes. Los homomorfismos nos permiten cambiar de espacios de trabajo sin mucho problema.

Por otro lado, tal vez ya sabes que las matemáticas de este curso (y de la mayoría de los cursos en este blog) están fundamentadas en la Teoría de Conjuntos. Esta teoría nos permite construir a los objetos matemáticos a partir de conjuntos. Como curiosidad, tal vez te interese saber que existe otra teoría llamada Teoría de Categorías, que generaliza lo anterior, y en la que la generalización de un homomorfismo es llamado morfismo.

Aunque estén definidos de manera diferente, los homomorfismos de esta entrada y los morfismos de la Teoría de Categorías son, en intuición, lo mismo. Esto refuerza la idea de que los homomorfismos son en realidad más importantes de lo que parecen.

Pero bueno, regresemos a nuestro curso: en la siguiente entrada continuaremos viendo el comportamiento de los homomorfismos.

Entradas relacionadas