(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

La Unidad 2 empieza con algunas definiciones nuevas. Veremos un ejemplo específico de grupo, primero definiremos qué es una permutación y luego, el conjunto de todas las permutaciones, al que llamaremos grupo simétrico junto con la composición. Este grupo es importante porque más adelante descubriremos que los grupos se pueden visualizar como subgrupos de grupos de permutaciones.

Primeras definiciones

Definición. Una permutación de un conjunto $X$ es una función biyectiva de $X$ en $X$.

Notación. Denotaremos por $S_X$ al conjunto

$$\begin{array}{r}{S}_X=\{\sigma :X\to X|\sigma \text{ es biyectiva}\}.\end{array}$$

Si $X=\{1,\dots ,n\}$, $S_X$ se denota por $S_n$. Si tomamos $\alpha ,\beta \in S_X$ la composición de $\alpha$ seguida de $\beta$ se denota por $\beta \alpha$.

Observación 1. $S_X$ con la composición es un grupo, se llama el Grupo Simétrico.

Observación 2. $|S_n|=n!$

Definición. Sea $\alpha \in S_n$, $i\in \{1,2,\dots ,n\}$.

Decimos que $\alpha$ mueve a $i$ si $\alpha (i)\ne i$, y que $\alpha$ fija a $i$ si $\alpha (i)=i$. El soporte de $\alpha$ es

$$\begin{array}{r}\text{sop }\alpha =\{i\in \{1,\dots ,n\}:\alpha (i)\ne i\}.\end{array}$$

Ejemplo

Sea $\alpha \in S_{10}$, definida como

$$\begin{array}{r}\alpha =\left(\begin{array}{cccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10\\ 8& 3& 1& 7& 2& 6& 4& 5& 9& 10\end{array}\right).\end{array}$$

La matriz es una manera de representar una permutación, la fila de arriba son todos los elementos de $X=\{1,2,3,4,5,6,7,8,9,10\}$ y la fila de abajo está formada por las imágenes bajo $\alpha$ de cada elemento de la fila de arriba. Es decir, la matriz de $\alpha$ se puede leer como: «$\alpha$ manda al $1$ al $8$», «el $2$ lo manda al $3$», etc. Entonces tenemos que, $\alpha$ mueve a $1,2,3,4,5,7,8$ y fija al $6,9,10$. Así

$$\begin{array}{r}\text{sop }\alpha =\{1,2,3,4,5,7,8\}.\end{array}$$

Definición de ciclo

Definición. Sea $\alpha \in S_n$, $r\in \mathbb{Z}$, $r>1$. Decimos que $\alpha$ es un ciclo de longitud $r$ o un $r$-ciclo si existen $i_1,\dots ,i_r\in \{1,\dots ,n\}$ distintos tales que $\text{sop }\alpha =\{i_1,\dots ,i_r\}$ y

Diremos que la permutación $\text{id}\in S_n$ es un ciclo de longitud $1$ o un $1$-ciclo. Los ciclos de longitud dos se llaman transposiciones.

Las transposiciones son muy importantes porque, como veremos más adelante, nos permitirán describir a las demás permutaciones.

Notación.

• Un $r$-ciclo $\alpha$, tal que cada $i_j$ va a $i_{j+1}$ para cada $j\in \{1,\dots ,r-1\}$ y $i_r$ regresa a $i_1$ se denota como $\alpha =(i_1{i}_2\dots i_r)$.
• Además, denotamos como $r=\text{long }\alpha$ a la longitud de $\alpha$.

Ejemplos

1. $\alpha \in S_8$ con $\alpha =\left(\begin{array}{cccccccc}1& 2& 3& 4& 5& 6& 7& 8\\ 1& 4& 3& 5& 8& 2& 7& 6\end{array}\right)$.

En este caso, $\alpha$ es un $5-$ciclo y $\text{long }\alpha =5$.
Observemos que el ciclo se puede comenzar a escribir con cualquier elemento de su soporte, siempre y cuando se cumpla la regla de correspondencia establecida.

2. Ahora, consideremos $\beta \in S_8$ como

Si componemos $\beta$ con el $\alpha$ del ejemplo anterior obtenemos:

$$\begin{array}{rl}\alpha \beta & =(24586)(35)=(245386).\end{array}$$

Para verificar qué ésta es efectivamente la composición de $\beta$ seguida de $\alpha$, tenemos que observar a dónde manda a cada elemento:

• Comenzamos con el $2$ (esto es arbitrario, se puede comenzar con el número que sea), observamos que $\beta$ lo deja fijo, entonces nos fijamos a dónde lo manda $\alpha$, en este caso, el $2$ es mandado al $4$. Así, $\alpha \beta$ manda al $2$ en el $4$.
• Repetimos el proceso con el $4$, $\beta$ lo deja fijo y $\alpha$ lo manda al $5$. Así, $\alpha \beta$ manda al $4$ en el $5$.
• Ahora con el $5$, $\beta$ manda al $5$ en $3$, entonces ahora vemos a dónde manda $\alpha$ al $3$, en este caso lo deja fijo. Así, $\alpha \beta$ manda al $5$ en el $3$.
• Entonces ahora tenemos que observar a dónde es mandado el $3$ después de la composición. Primero, $\beta$ manda el $3$ al $5$ y $\alpha$ manda el $5$ al $8$, por lo tanto $\alpha \beta$ manda el $3$ al $8$.
• Así continuamos con todos los elementos que aparezcan en la composición hasta terminar.
  
  Ahora, veamos qué sucede con $\beta \alpha$. El proceso es análogo:
  $$\begin{array}{rl}\beta \alpha & =(35)(24586)=(358624).\end{array}$$
  Por lo tanto $\alpha \beta \ne \beta \alpha$.

3. En $S_5$. Podemos considerar la siguiente permutación: $(1234)(245)$. A esta permutación la podemos simplificar usando el mismo procedimiento que en el ejemplo 2.

Observamos a dónde lleva cada uno de sus elementos:

• Comencemos con el 2, la primera parte de la permutación, lleva el 2 al 4 y, la segunda parte lleva el 4 al 1.
• Ahora veamos a dónde va el 1. La primera parte lo deja fijo y la segunda lo lleva al 2. Entonces obtenemos una permutación $(12)$. Pero todavía falta ver el resto de elementos.
• Ahora, veamos qué sucede con el 3. La primera parte lo deja fijo y la segunda lo manda al 4.
• La primera parte de nuestra permutación manda el 4 al 5 y, el 5 se queda fijo.
• Por último, el 5 es mandado al 2 por la primera parte de la permutación y, la segunda parte manda al 2 en el 3. Por lo tanto, el 5 regresa al 3. Esto se puede escribir como:

$$\begin{array}{r}(1234)(245)=(12)(345).\end{array}$$

Es decir:

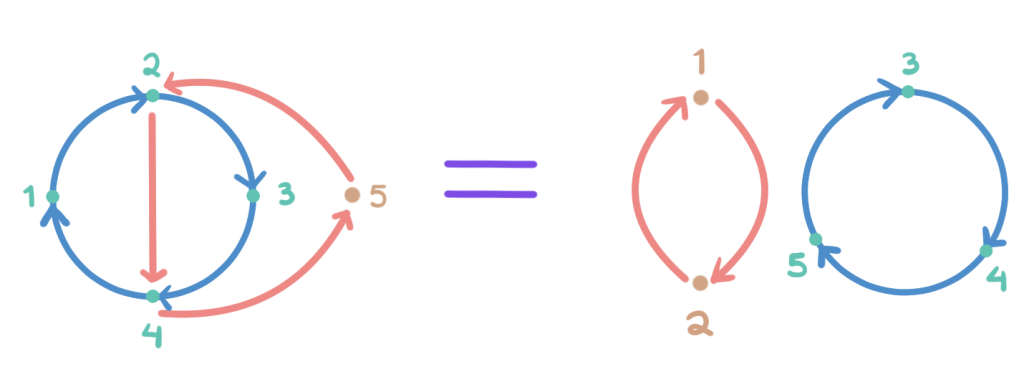
Este ejemplo nos permite intuir que en ocasiones las permutaciones se pueden simplificar.

Observación. Si $n\ge 3$, entonces $S_n$ no es abeliano.

Tarea moral

1. Demostrar la observación 1: $S_X$ con la composición es un grupo, se llama el Grupo Simétrico.
2. Sea $X$ un conjunto infinito, $H$ la colección de permutaciones de $S_X$ que mueven sólo un número finito de elementos y $K$ la colección de permutaciones que mueven a lo más $50$ elementos. ¿Son $H$ y $K$ subgrupos de $S_X$?
3. Considera los siguientes elementos de $S_{10}$
   $$\begin{array}{rl}\alpha & =\left(\begin{array}{cccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10\\ 10& 4& 3& 2& 9& 7& 5& 1& 6& 8\end{array}\right)\\ \\ \beta & =\left(\begin{array}{cccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10\\ 10& 9& 8& 7& 6& 5& 4& 3& 2& 1\end{array}\right).\end{array}$$
   Encuentra $\alpha \beta ,\beta \alpha ,{\alpha }^{-1}$ y ${\beta }^{-1}$.
4. Sea $a\in S_n,$ con $n>2$. Si $\alpha$ conmuta con toda permutación de $S_n$ ¿puedes decir quién debe ser $\alpha$?
   

Más adelante…

Por el momento continuaremos hablando de las permutaciones. El último ejemplo visto nos da la noción de permutaciones disjuntas, este tema es el que profundizaremos en la siguiente entrada, pero por el momento ¿puedes imaginarte de qué se trata?

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Palabras.
• Siguiente entrada del curso: Permutaciones disjuntas.
• Resto de cursos: Cursos.