Introducción

En las entradas anteriores platicamos de cómo resolver sistemas de ecuaciones lineales complejos, y de como pasar de coordenadas polares a rectangulares y viceversa. Ahora veremos un método más para resolver problemas de ecuaciones lineales en los complejos en tres variables. Además, haremos problemas de práctica de estos temas.

La regla de Kramer para tres variables

Cuando platicamos de resolver problemas de ecuaciones lineales complejas en dos variables, vimos que si el determinante no era $0$, entonces podíamos dar la solución de manera explícita. A esto se le conoce como la regla de Kramer. Veremos ahora cuál es la versión de esta regla para tres variables. A continuación enunciamos el método, y más abajo, en el video, se explica un poco más a detalle.

Proposición. Consideremos el siguiente sistema lineal de ecuaciones complejas en variables $x$, $y$ y $z$.
\begin{align*}
ax+by+cz&=j\\
dx+ey+fz&=k\\
gx+hy+iz&=l.
\end{align*}

Supongamos que el determinante $\Delta=\begin{vmatrix} a & b & c\\ d & e & f\\ g & h & i \end{vmatrix}$ no es $0$. Entonces, el sistema tiene una única solución, dada por
\begin{align*}
x&=\frac{\begin{vmatrix} j & b & c\\ k & e & f\\ l & h & i \end{vmatrix}}{\Delta},\\
y&=\frac{\begin{vmatrix} a & j & c\\ d & k & f\\ g & l & i \end{vmatrix}}{\Delta},\\
z&=\frac{\begin{vmatrix} a & b & j\\ d & e & k\\ g & h & l \end{vmatrix}}{\Delta}.
\end{align*}

No veremos la demostración de esta técnica, pues es uno de los temas que estudiarás en álgebra lineal con más generalidad. Sin embargo, veremos algunos ejemplos de cómo se aplica.

Problemas de ecuaciones lineales

Para comenzar, resolveremos un sistema de ecuaciones de dos variables.

Problema. Resuelve en $\mathbb{C}$ el siguiente sistema de ecuaciones:
\begin{align*}
iz+2w&=3+4i\\
2z-iw&=6-3i.
\end{align*}

Pasemos ahora a un ejemplo con tres variables. El el ejemplo 328 del libro Álgebra Superior de Bravo, Rincón, Rincón.

Problema. Resuelve en $\mathbb{C}$ el siguiente sistema de ecuaciones.
\begin{align*}
z_1+z_2+z_3&=6+4i\\
iz_1+(1+i)z_2+(1-i)z_3&=7+4i\\
z_i+iz_2-z_3&=2i.
\end{align*}

El problema está resuelto en los siguientes dos videos.

Problemas de cambio de coordenadas

Finalmente, veremos algunos problemas de cambio entre coordenadas polares y coordenadas rectangulares. Recordemos que la figura clave para cambiar entre coordenadas es la siguiente:

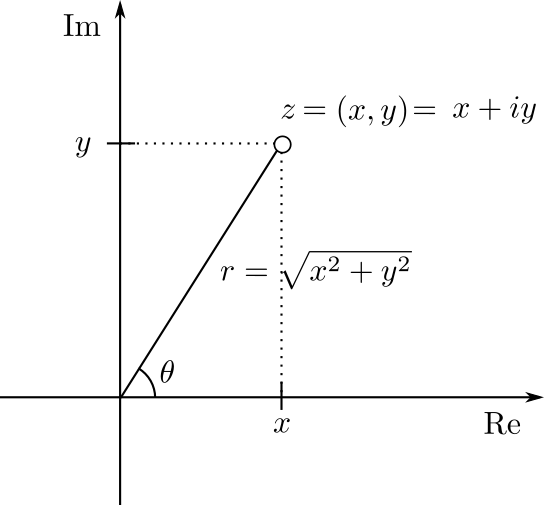
Problema. Calcula las coordenadas rectangulares del complejo cuyas coordenadas polares son $r=\sqrt{2}$ y $s=45^\circ$, y del complejo cuyas coordenadas polares son $r=3$ y $s=90^\circ$.

Problema. Expresa $7+7i$ y $4+2i$ en coordenadas polares.

Más adelante…

Tarea moral

Entradas relacionadas

• Ir a: Álgebra Superior II
• Entrada anterior del curso: Cambio de coordenadas y forma polar de un complejo
• Entrada siguiente del curso: Multiplicación en forma polar y fórmula de De Moivre

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»