Archivo de la etiqueta: composición de funciones

Cálculo Diferencial e Integral I: Suma, producto, cociente y composición de funciones

Por Karen González Cárdenas

Deja un comentario

Introducción

Ya que hemos visto el concepto de función, en esta entrada veremos cómo están definidas las operaciones de suma, producto y cociente. De igual modo, definiremos la composición entre un par de funciones. Para dejar más claras dichas operaciones, daremos ejemplos.

Operaciones de funciones

Definición (operaciones): Sean $f: D_{f}\subseteq \r \rightarrow \r$, $\quad g: D_{g}\subseteq \r \rightarrow \r$. Definimos las siguientes operaciones como:

  • $f+g: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
    $$(f+g)(x)= f(x)+g(x)\quad \text{.}$$
  • $\alpha f: D_{f}\subseteq \r \rightarrow \r \quad$ y $\quad \alpha \in \r$
    $$(\alpha f)(x)= \alpha f(x)\quad \text{.}$$
  • $fg: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
    $$(fg)(x)= f(x)g(x)\quad \text{.}$$
  • $\begin{multline*} \frac{f}{g}: D_{f/g} \subseteq \r \rightarrow \r \end{multline*}$
    \begin{equation*}
    \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\quad \text{.}
    \end{equation*}
    donde $D_{f/g}=D_{f} \cap (D_{g} – \left\{x \in D_{g}: g(x)=0 \right\})$

Notación: Cuando escribamos $f-g$ hacemos referencia a:
$$f-g=f+ (-g) \quad \text{.}$$

Ejemplos

Consideremos a las siguientes funciones:
\begin{align*}
f: \r – \left\{-1\right\} &\rightarrow \r & g: \r &\rightarrow \r & h: \r &\rightarrow \r^{+}
\end{align*}
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}
Notación: Usamos $\r^{+}$ para referirnos al conjunto de los números reales positivos.

Realizaremos las siguientes operaciones para ejemplificar lo visto anteriormente:

  • $$(f+g)(x)= f(x)+g(x)= \frac{1}{x+1} + x^{3}+3$$
    con $D_{f+g}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$
  • $$(fg)(x)= f(x)g(x)=\left(\frac{1}{x+1}\right)(x^{3}+3)=\frac{x^{3}+3}{x+1}$$
    con $D_{fg}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$
  • Si $\alpha = – 4$:
    $$(\alpha g)(x)= \alpha g(x)= -4(x^{3}+3)=-4x^{3}-12$$
    con $D_{\alpha g}= D_{g}= \r$
  • $$\left(\frac{g}{h}\right)(x)=\frac{g(x)}{h(x)}=\frac{x^{3}+3}{x^{2}+2x+1}$$
    como $D_{g/h}=D_{g} \cap (D_{h} – \left\{x \in D_{h}: h(x)=0 \right\})$
    Observemos que $x^{2}+2x+1 = (x+1)^{2}$ por lo que $(x+1)^{2}=0$ cuando $x=-1$.
    Así el dominio sería:
    $$D_{g/h}=\r \cap (\r- \left\{-1 \right\})= \r – \left\{-1\right\}$$
  • $$(h-g)(x)=h(x)-g(x)=x^{2}+2x+1-(x^{3}+3)=x^{2}+2x+1-x^{3}-3$$
    con $D_{h-g}= D_{h} \cap D_{g}= \r \cap \r= \r$

Composición de funciones

Definición (composición): Consideremos a las funciones $g: A \rightarrow B$ y $f: B \rightarrow C$ definimos a la composición de $g$ seguida de $f$ como:

$$f \circ g: A \rightarrow C$$
$$(f \circ g)(x)= f(g(x)),$$
observamos que la composición sólo está definida si $Im_g \subseteq D_f$, por lo que $g(x) \in B$.
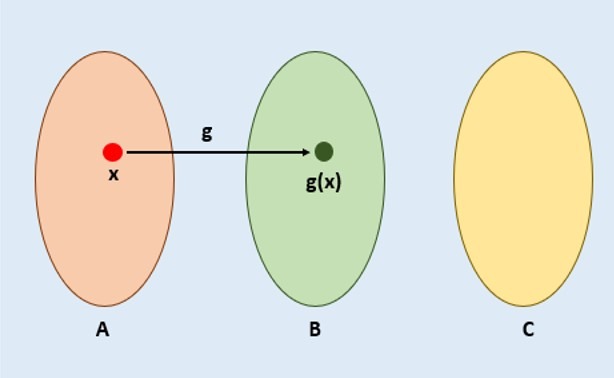
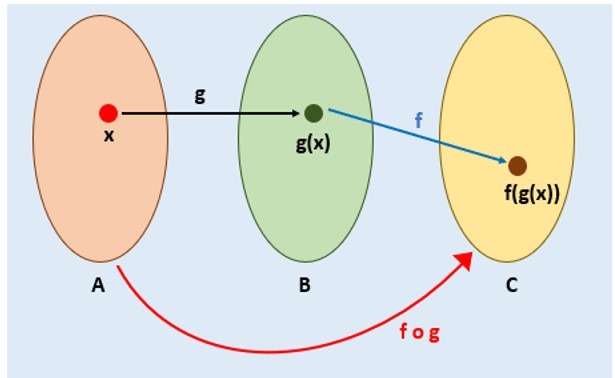
En el siguiente diagrama podemos ver más claramente cómo funciona la composición $f \circ g$:

PASO 1

Primero tomamos $x \in A$ a la cual le aplicamos la función $g$ para así obtener $g(x) \in B$.

PASO 2

Ahora tomamos a $g(x) \in B$ para aplicarle la función $f$ y finalmente obtener $f(g(x)) \in C$.

DIAGRAMA PARA $f \circ g$

Así la composición de $f \circ g$ se vería como en el diagrama anterior.

Observación: La composición no es conmutativa, es decir, ocurre que:
$$f \circ g \neq g \circ f\quad \text{.}$$

Ejemplos

Retomando las funciones:
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}

Realicemos las siguientes composiciones de funciones para tener más claro cómo funciona lo antes explicado:

  • Ejemplo 1:
    \begin{align*}
    (g \circ f)(x)&= g(f(x))\\
    &= g\left(\frac{1}{x+1} \right)\\
    &= \left( \frac{1}{x+1} \right)^{3} +3\\
    &= \frac{1}{(x+1)^{3}}+3
    \end{align*}
    Así tenemos que la composición obtenida es:
    \begin{equation*}
    (g \circ f)(x)=\frac{1}{(x+1)^{3}}+3
    \end{equation*}
  • Ejemplo 2:
    \begin{align*}
    (f \circ h)(x)&= f(h(x))\\
    &= f((x^{2}+2x+1))\\
    &= \frac{1}{(x^{2}+2x+1)+1}\\
    &=\frac{1}{x^{2}+2x+2}
    \end{align*}
    Por lo que la composición quedaría como:
    \begin{equation*}
    (f \circ h)(x) = \frac{1}{x^{2}+2x+2}
    \end{equation*}

Más adelante

Ahora que ya hemos definido las operaciones entre funciones y la composición, en la siguiente entrada veremos qué características debe cumplir una función para poder determinar si es inyectiva, sobreyectiva o biyectiva. Del mismo modo, examinaremos el concepto de función inversa, donde haremos uso de la composición de funciones y algunas condiciones.

Tarea moral

  • Si tenemos a las funciones $f : \r \rightarrow \r$ y $g : \r \rightarrow \r^{+}$ definidas como siguen:
    $$ f(x) = x-8$$
    $$g(x)= x^{4}$$
    Realiza las siguientes operaciones:
    • $f + g$
    • $f – g$
    • $fg$
    • $\frac{g}{f}$
    • $g \circ f$
  • Da una función $f$ y una función $g$ que ejemplifiquen que la composición no es conmutativa:
    $$f \circ g \neq g \circ f\quad \text{.}$$
  • Demuestra que la composición es asociativa, es decir,
    $$f\circ (g \circ h)= (f\circ g) \circ h\quad \text{.}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»