Archivo de la etiqueta: centroide

Geometría Moderna I: Medianas y centroide

Por Rubén Alexander Ocampo Arellano

Introducción

En la entrada puntos nobles del triangulo, vimos que las medianas de un triangulo concurren en un punto, al que llamamos centroide, y que este punto tiene la propiedad de trisecar a las medianas. En esta entrada estudiaremos algunas propiedades más de las medinas y el centroide.

Medianas como los lados de un triángulo

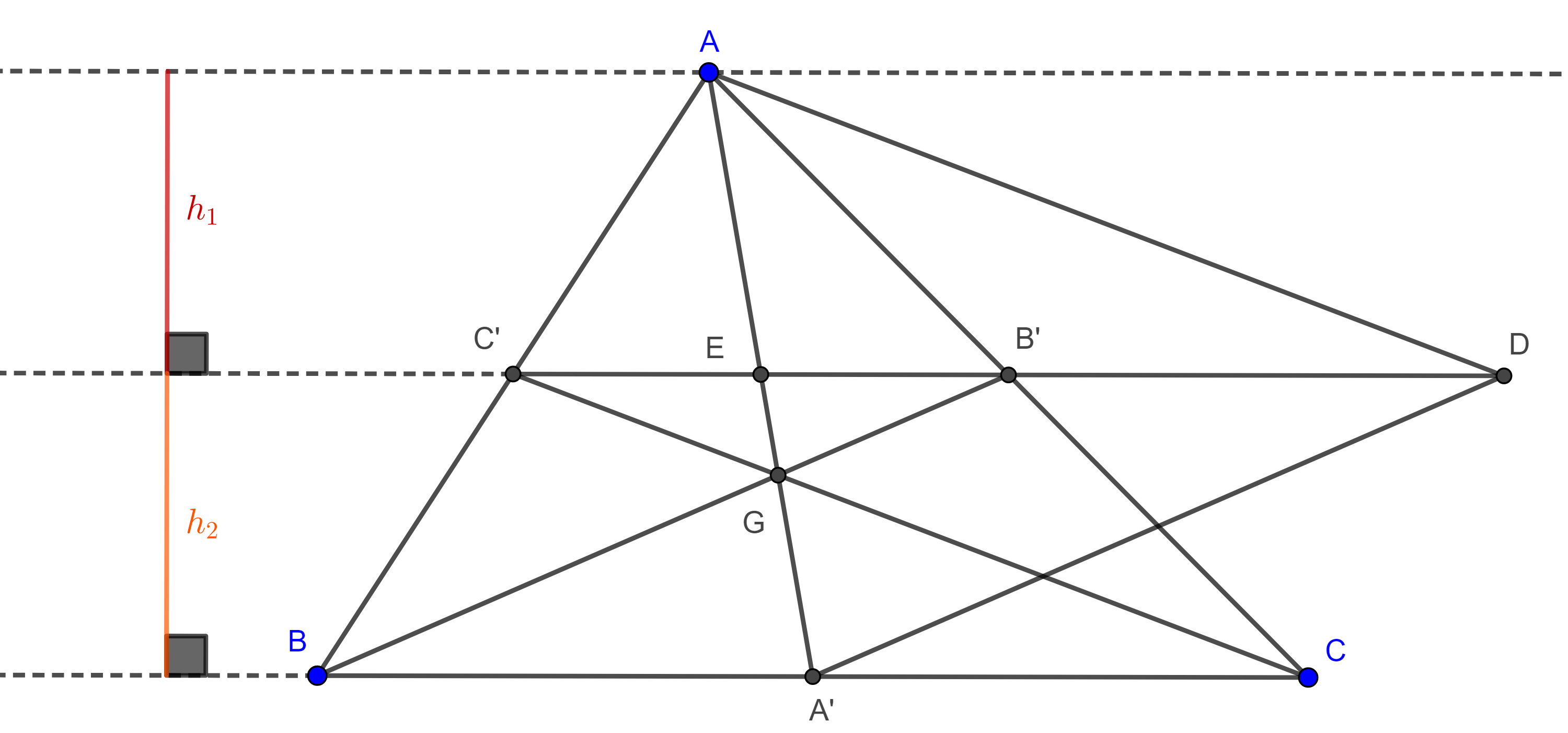
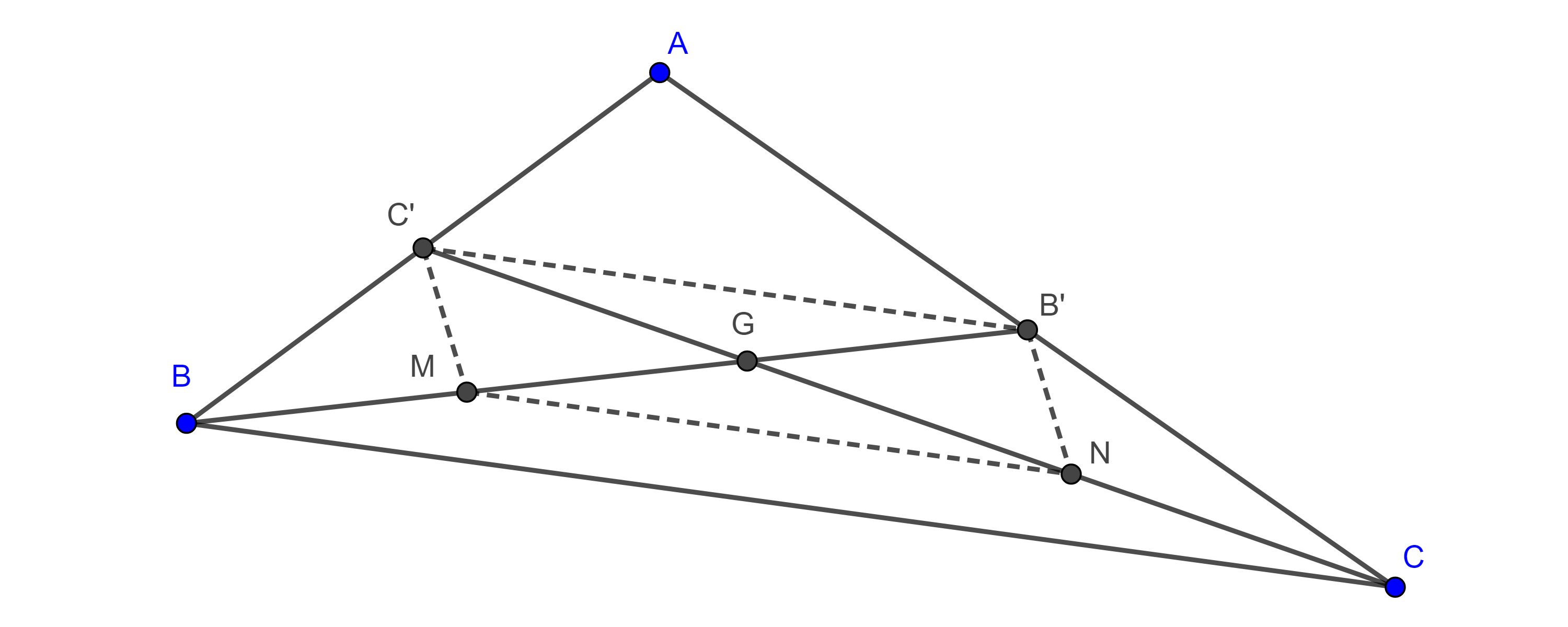
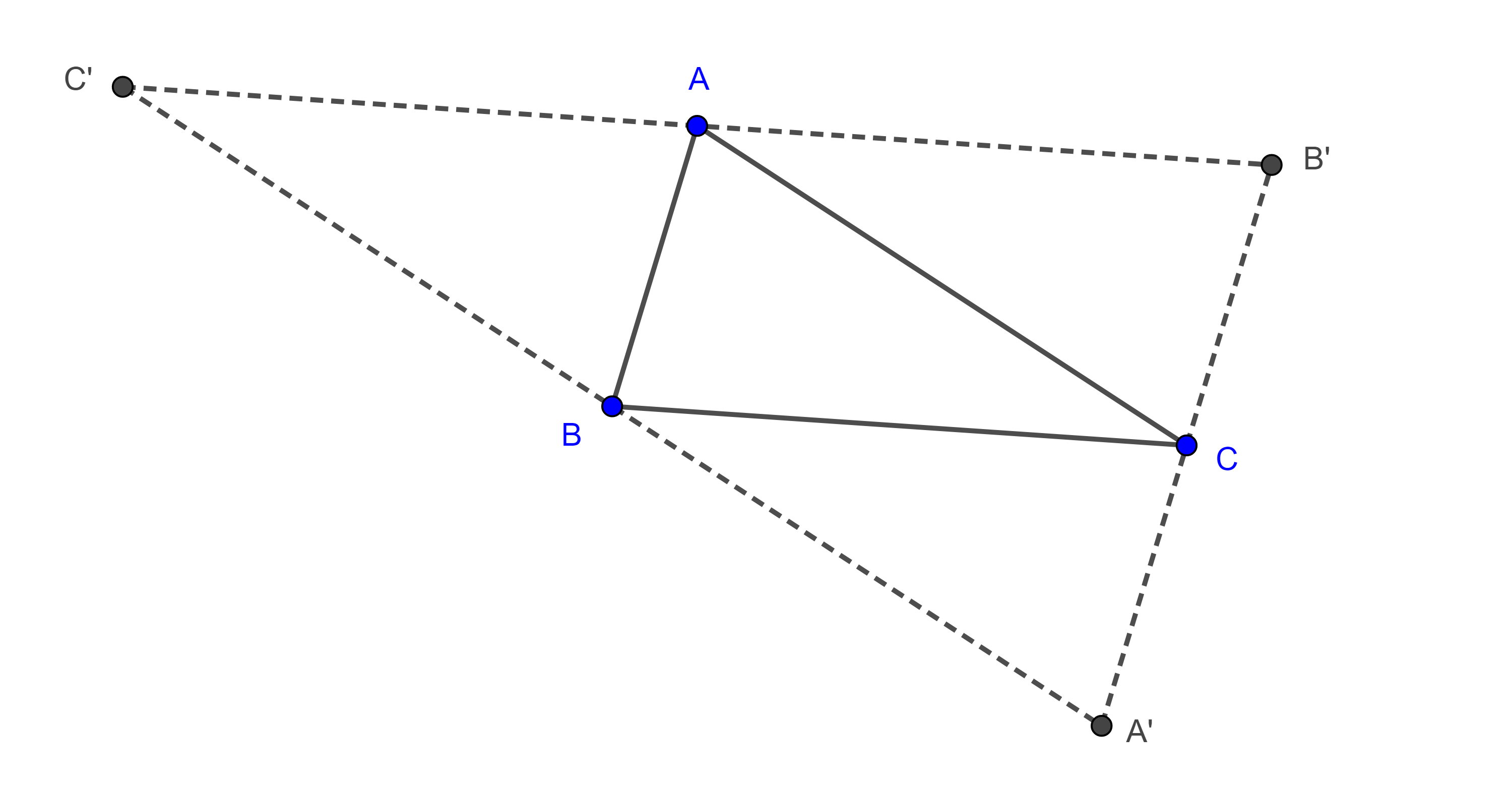
Teorema 1. Si con las medianas de un triángulo dado construimos otro triangulo, entonces cada mediana del triángulo construido es igual a tres cuartos uno de los lados del triángulo dado.

Demostración. Sean $△ A B C$ y $A A ´$ , $B B^{'}$ y $C C^{'}$ las medianas del triángulo.

Construimos $D \in C^{'} B^{'}$ tal que $C^{'} B^{'} = B^{'} D$ , como $C ´ B ´$ es un segmento medio de $△ A B C$ entonces $C^{'} B^{'} ∥ B C$ y $2 C^{'} B^{'} = B C$ .

Lo anterior implica que $B^{'} B A^{'} D$ es un paralelogramo y por lo tanto $B B^{'} = A^{'} D$ .

Como las diagonales de $A C^{'} C D$ se cortan en su punto medio entonces $A C^{'} C D$ es un paralelogramo, por lo tanto, $C C^{'} = A D$ , entonces los lados de $△ A A^{'} D$ son las medianas de $△ A B C$ , por criterio LLL, cualquier otro triangulo con los mismos lados será congruente con $△ A A^{'} D$ .

Sea $E = A A^{'} \cap C^{'} B^{'}$ , como $A^{'} C^{'}$ es un segmento medio de $△ A B C$ entonces $A C^{'} A^{'} B^{'}$ es un paralelogramo, por lo tanto, $E$ es el punto medio de $A A^{'}$ y de $C^{'} B^{'}$ .

Por lo anterior tenemos que $D E$ es mediana de $△ A D A^{'}$ y que $D E = \frac{3}{4}$ , pues por construcción $C^{'} B^{'} = B^{'} D$ .

Dado que $C^{'} D = B C$ $\Rightarrow D E = \frac{3}{4} B C$ .

Con una construcción similar podemos ver que las otras medianas de $△ A D A^{'}$ son iguales a $\frac{3}{4} A C$ y $\frac{3}{4} A B$ .

Observación. Notemos que si seguimos este proceso de construir triángulos con las medianas del triángulo anterior obtenemos dos grupos de triángulos semejantes, un grupo conformado por el primer, el tercer, el quinto triángulo etc. En el otro grupo estarían el segundo, el cuarto triángulo … ambos con razón de semejanza $\frac{3}{4}$ .

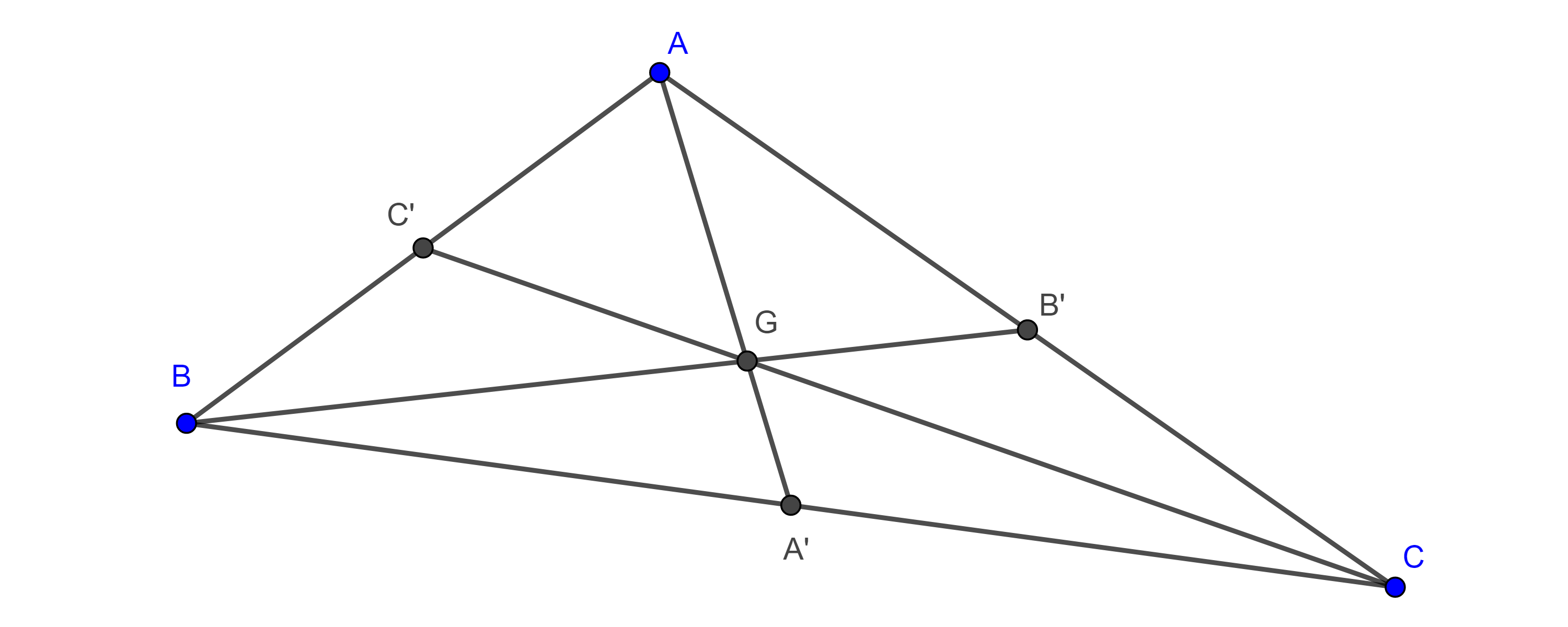
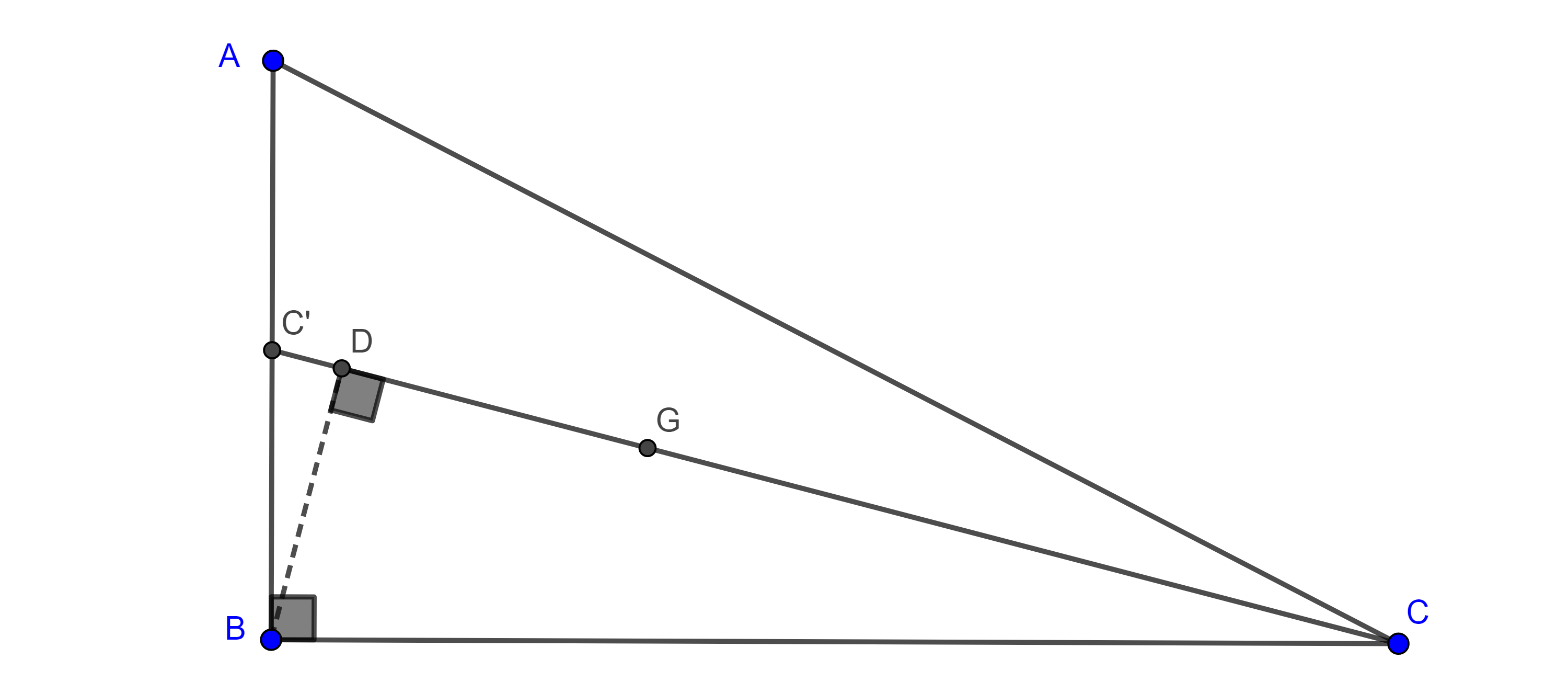
Corolario 1. El área de un triángulo construido con las medianas de un triángulo dado, es igual a tres cuartos el área del triángulo dado.

Demostración. El área de $△ A D A^{'}$ (figura 1) es igual a la suma de las áreas de $△ E D A$ y $△ E D A^{'}$ que tienen la misma base $E D$ y la suma de sus alturas es igual a la altura de $△ A B C$ y por el teorema 1, $D E = \frac{3}{4} B C$ .

Por lo tanto,
$(△ A D A^{'}) = (△ E D A) + (△ E D A^{'}) = \frac{E D \times h_{1}}{2} + \frac{E D \times h_{2}}{2}$
$= \frac{3}{4} \frac{B C (h_{1} + h_{2})}{2} = \frac{3}{4} (△ A B C)$ .

Construcciones

Problema 1. Construir un triángulo dadas las longitudes de sus medianas $m_{a}$ , $m_{b}$ y $m_{c}$ .

Por el teorema 1, sabemos que las medianas del triángulo cuyos lados son $m_{a}$ , $m_{b}$ y $m_{c}$ , están en proporción $\frac{3}{4}$ a los lados del triángulo buscado.

Para encontrar las medianas del triángulo con lados $m_{a}$ , $m_{b}$ y $m_{c}$ , podemos construir este triangulo y luego sus medianas o podemos calcular sus longitudes con el teorema de Apolonio.

Después, multiplicamos cada valor obtenido por $\frac{4}{3}$ y así obtendremos los lados del triangulo requerido.

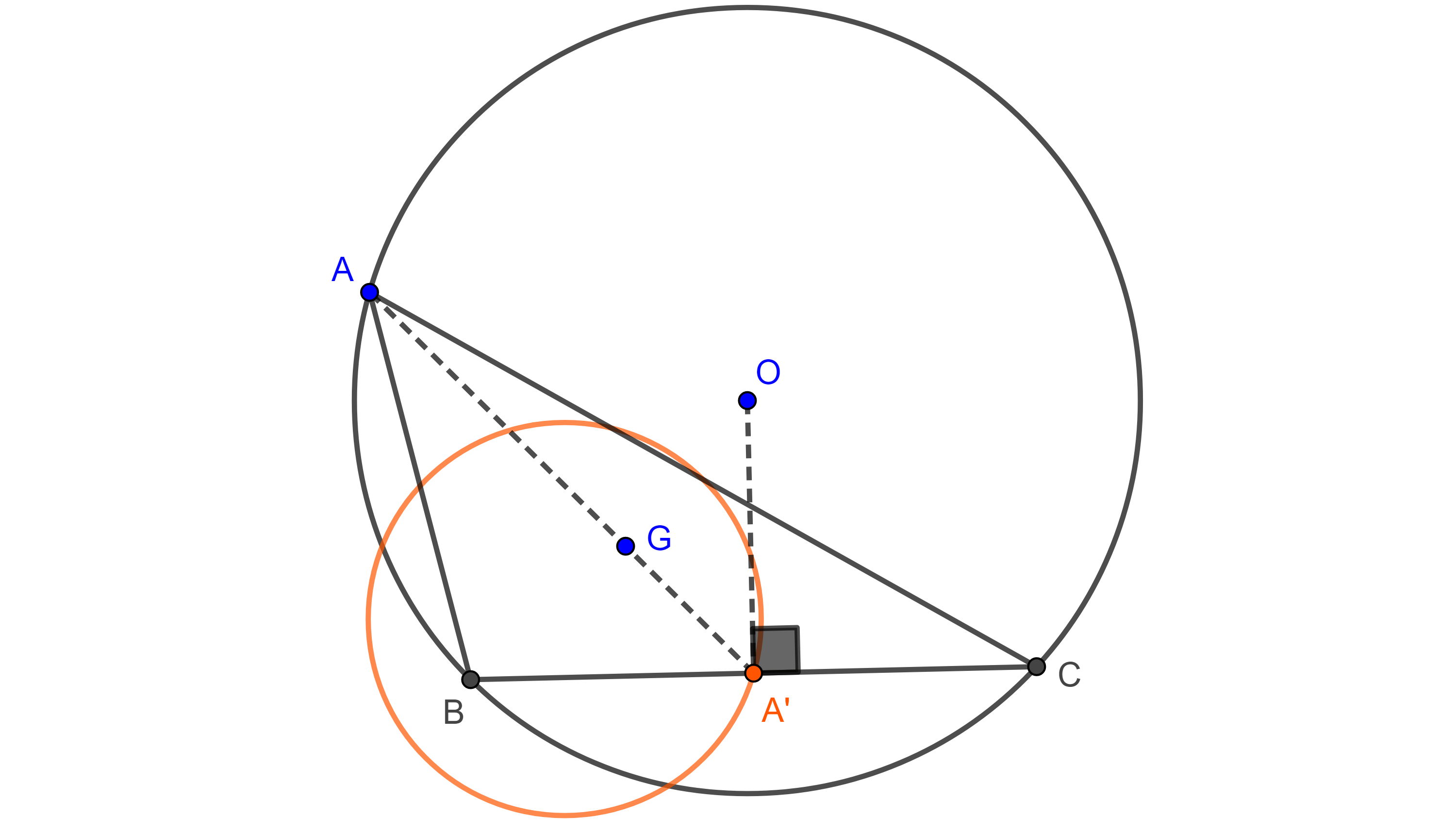
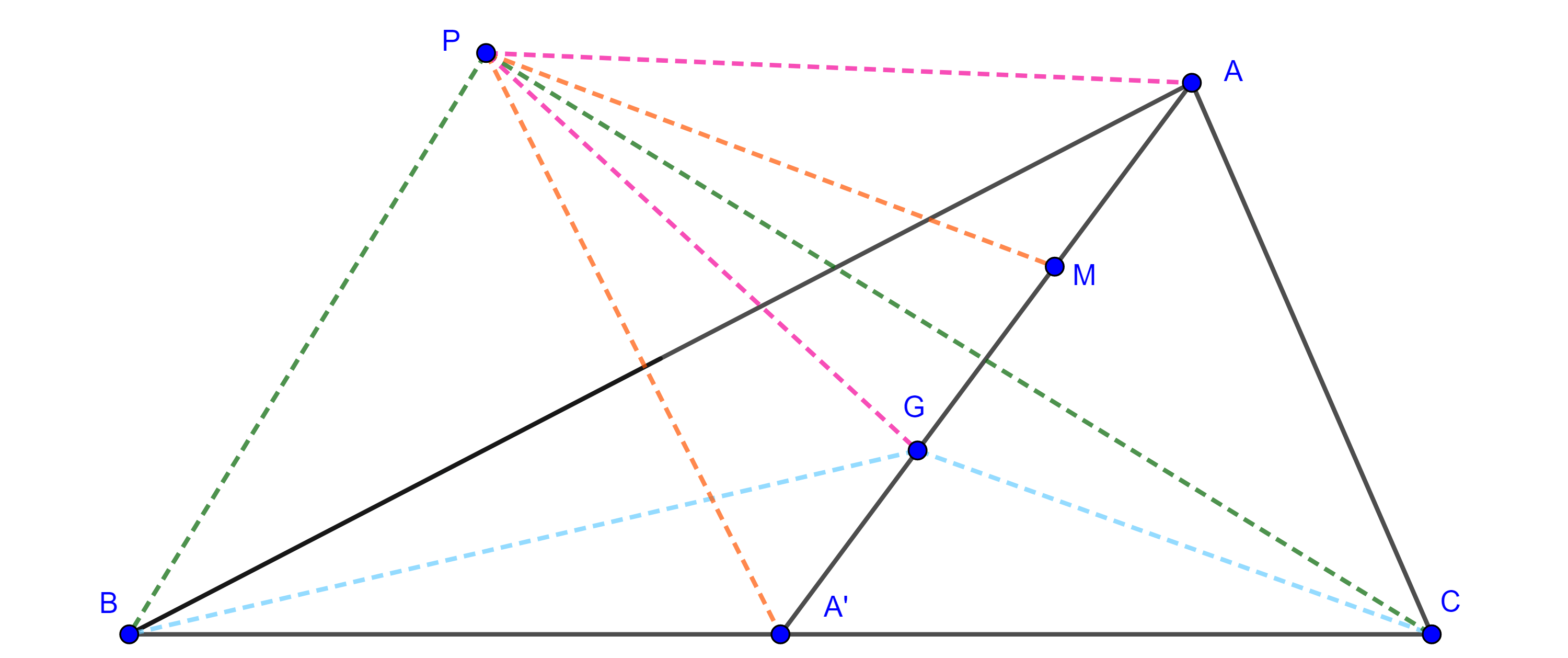
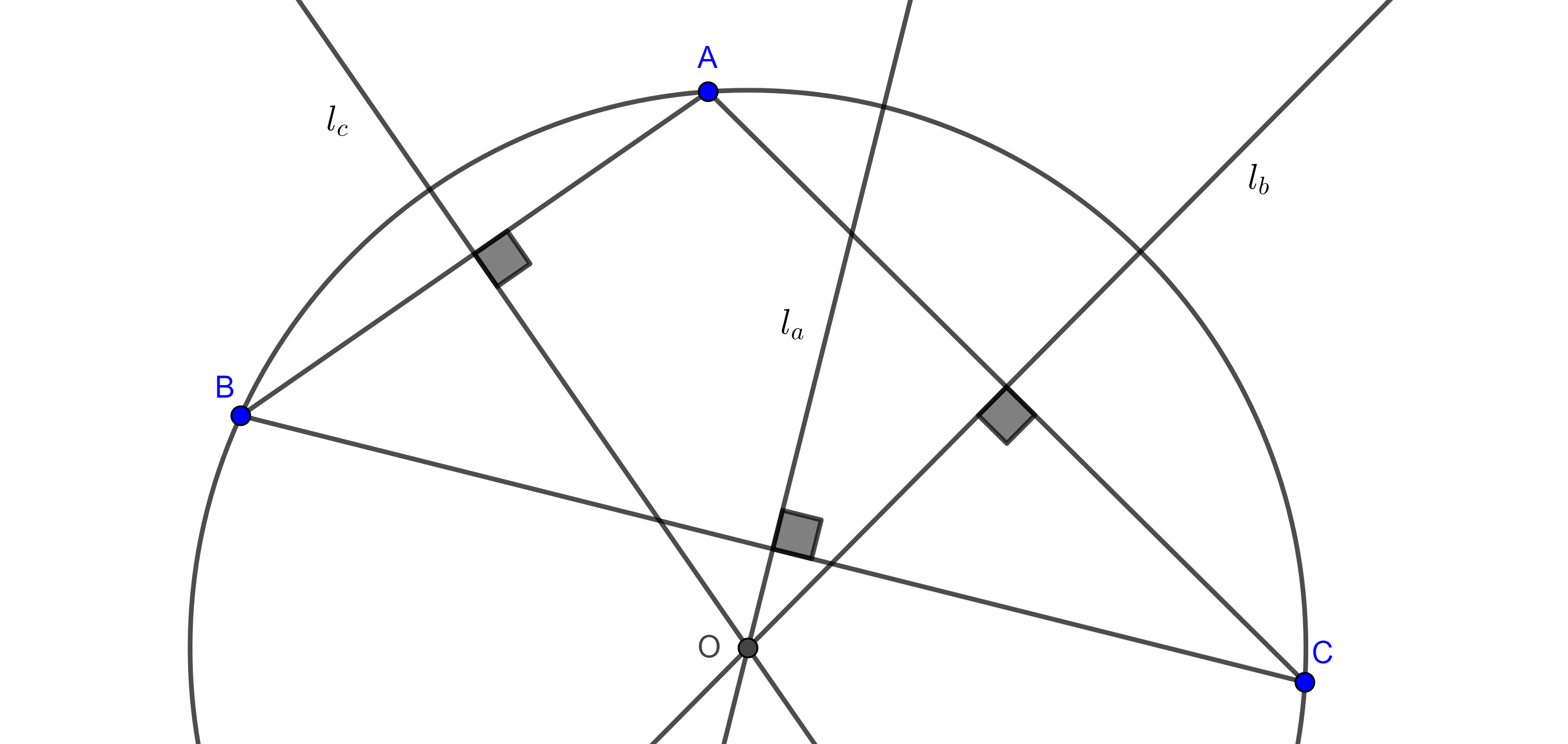
Problema 2. Dados una circunferencia y un punto dentro de esta, es posible inscribir en la circunferencia una infinidad de triángulos que tienen como centroide el punto dado.

Demostración. Sean $Γ (O)$ y $G$ la circunferencia y el punto dado, tomamos $A \in Γ (O)$ , sobre la recta $A G$ construimos $A^{'}$ tal que $G A^{'} = \frac{A G}{2}$ .

Si $A^{'}$ cae dentro de $Γ (O)$ por $A^{'}$ trazamos una perpendicular a $O A^{'}$ que interseca a $Γ (O)$ en $B$ en $C$ , como $△ B O C$ es isósceles y $O A^{'}$ es la altura por $O$ , entonces $A^{'}$ es el punto medio de $B C$ .

En $△ A B C$ se cumple que $A A^{'}$ es mediana y $G$ triseca a $A A^{'}$ , como el centroide de un triángulo es el único que tienen esa propiedad, entonces $G$ es el centroide de $△ A B C$ .

Notemos que $A$ y $A^{'}$ están en homotecia con centro en $G$ y razón $\frac{- 1}{2}$ , como $A$ describe una circunferencia, $A^{'}$ describe una circunferencia.

Entonces hay dos posibilidades, que la homotecia de $Γ (O)$ este totalmente contenida dentro de ella, con lo que con cualquier punto $A$ de $Γ (O)$ será posible hacer la construcción previa, o la homotecia de $Γ (O)$ este parcialmente contenida dentro de $Γ (O)$ y solo con un arco de $Γ (O)$ será posible hacer la construcción.

Finalmente, notemos que no es posible que la homotecia de $Γ$ se encuentre completamente fuera de esta pues $G$ es un punto interior de $Γ$ .

Una propiedad del centroide

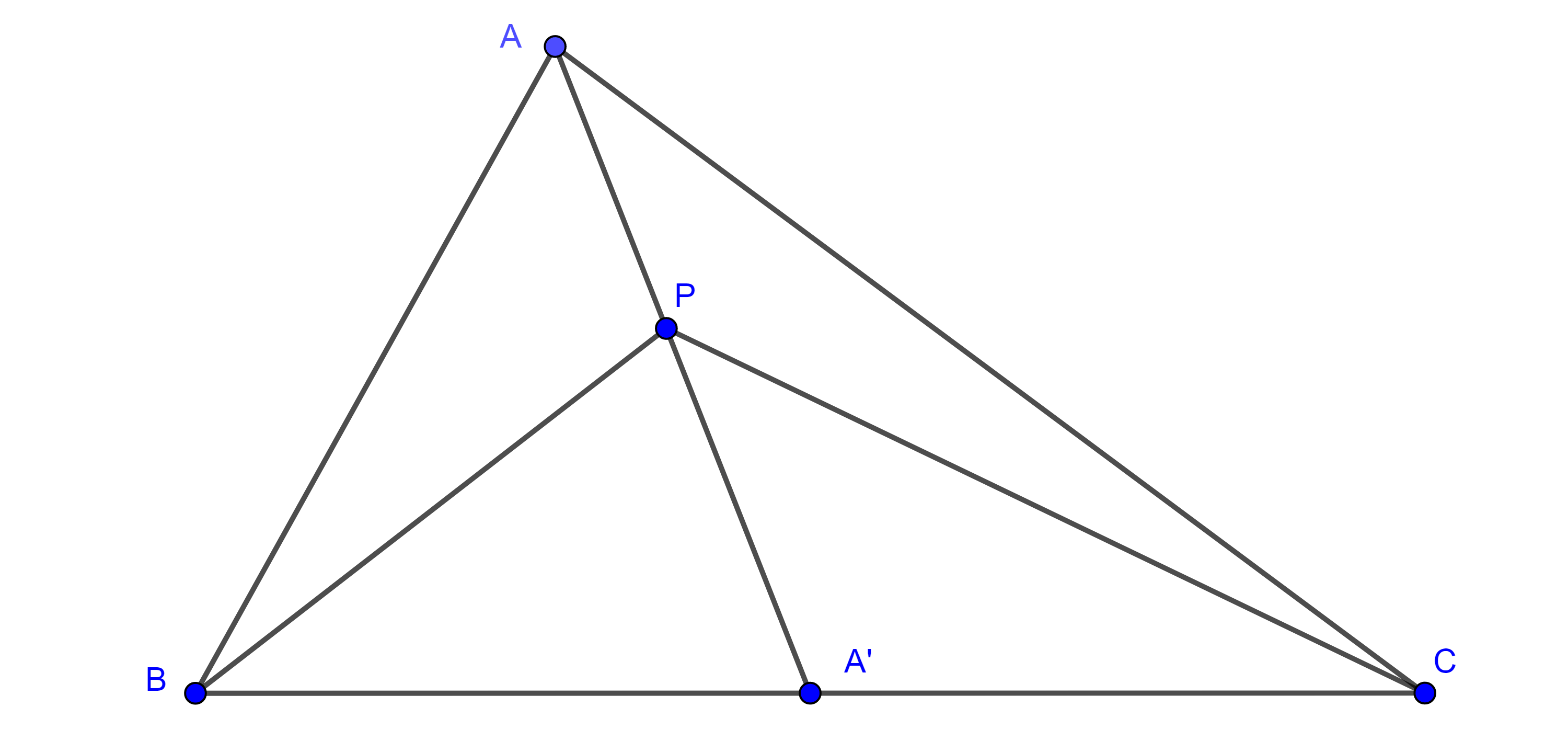
Lema. Sea $P$ un punto dentro de un triángulo $△ A B C$ , entonces las áreas $(△ A P B) = (△ A P C)$ si y solo si $P$ se encuentra en la mediana $A A^{'}$ .

Demostración. Supongamos que $(△ A P B) = (△ A P C)$ . Como $△ A P B$ y $△ A P C$ tienen la misma base $A P$ entonces sus alturas son iguales es decir la distancia de $B$ a $A P$ es igual a la distancia de $C$ a $A P$ .

Ahora consideremos $A^{'} = A P \cap B C$ , los triángulos $△ A^{'} P B$ y $△ A^{'} C P$ tienen la misma base $P A^{'}$ , por lo anterior sus alturas por B y C respectivamente también son iguales y así sus áreas son iguales $(△ A^{'} P B) = (△ A^{'} C P)$ .

Por otro lado, para ambos triángulos, $△ A^{'} P B$ y $△ A^{'} C P$ , la altura trazada por $P$ es la misma, esto implica que las respectivas bases son iguales, es decir $B A^{'} = A^{'} C$ .

Por lo tanto, $P$ está en la mediana trazada por $A$ .

Recíprocamente supongamos que $P$ es un punto en la mediana $A A^{'}$ , como los pares de triángulos $△ B A^{'} A$ , $△ A^{'} C A$ y $△ B A^{'} P$ , $△ A^{'} C P$ tienen la misma altura desde $A$ y $P$ respectivamente, entonces
$(△ B A^{'} A) = (△ A^{'} C A)$ y $(△ B A^{'} P) = (△ A^{'} C P)$ ,

Por lo tanto,
$(△ B A^{'} A) - (△ B A^{'} P) = (△ A^{'} C A) - (△ A^{'} C P)$
$\Rightarrow (△ A P B) = (△ A P C)$ .

Teorema 2. Sea $G$ un punto dentro de un triángulo $△ A B C$ , entonces $(△ A G B) = (△ A G C) = (△ B G C)$ si y solo si $G$ es el centroide de $△ A B C$ .

Demostración. Supongamos que $(△ A G B) = (△ A G C) = (△ B G C)$ , por el teorema anterior esto ocurre si y solo si $G$ está en la intersección de las medianas, si y solo si $G$ es el centroide de $△ A B C$ .

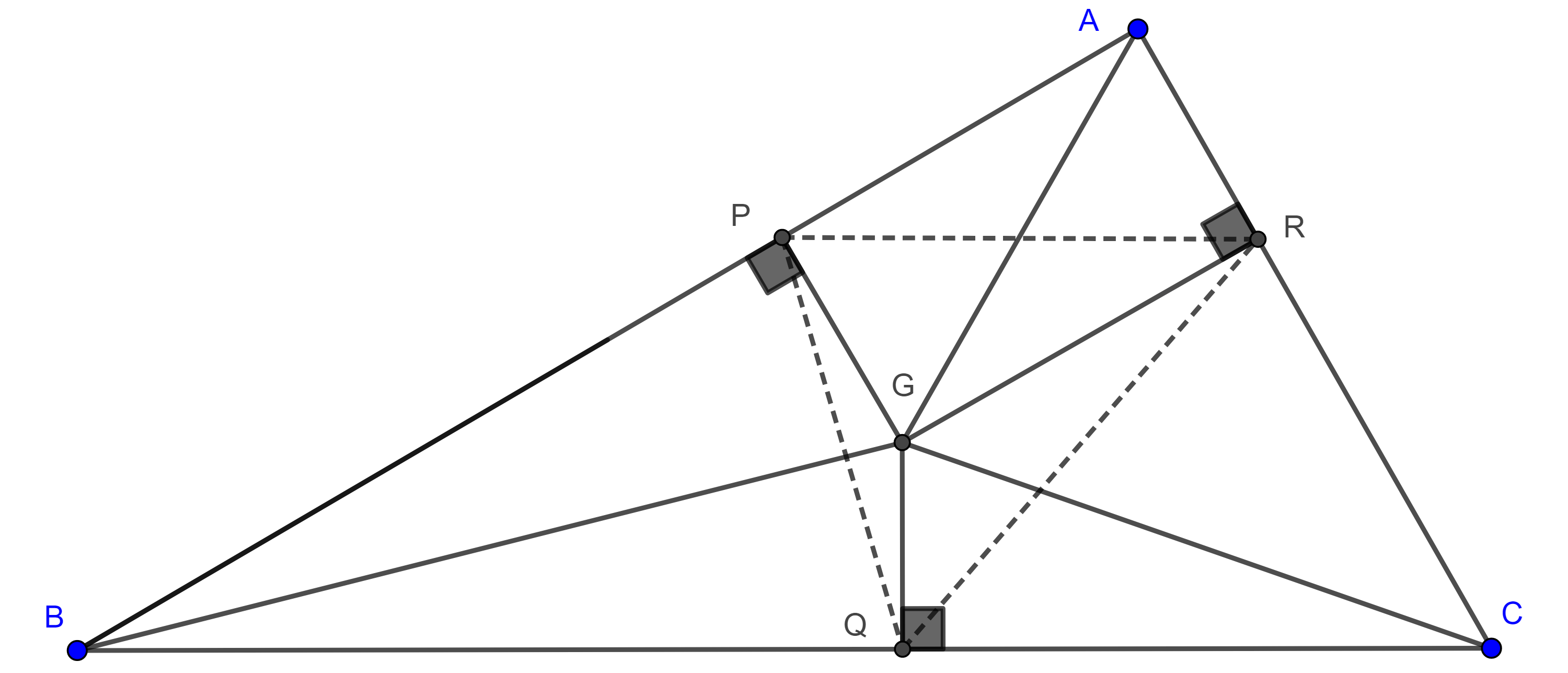
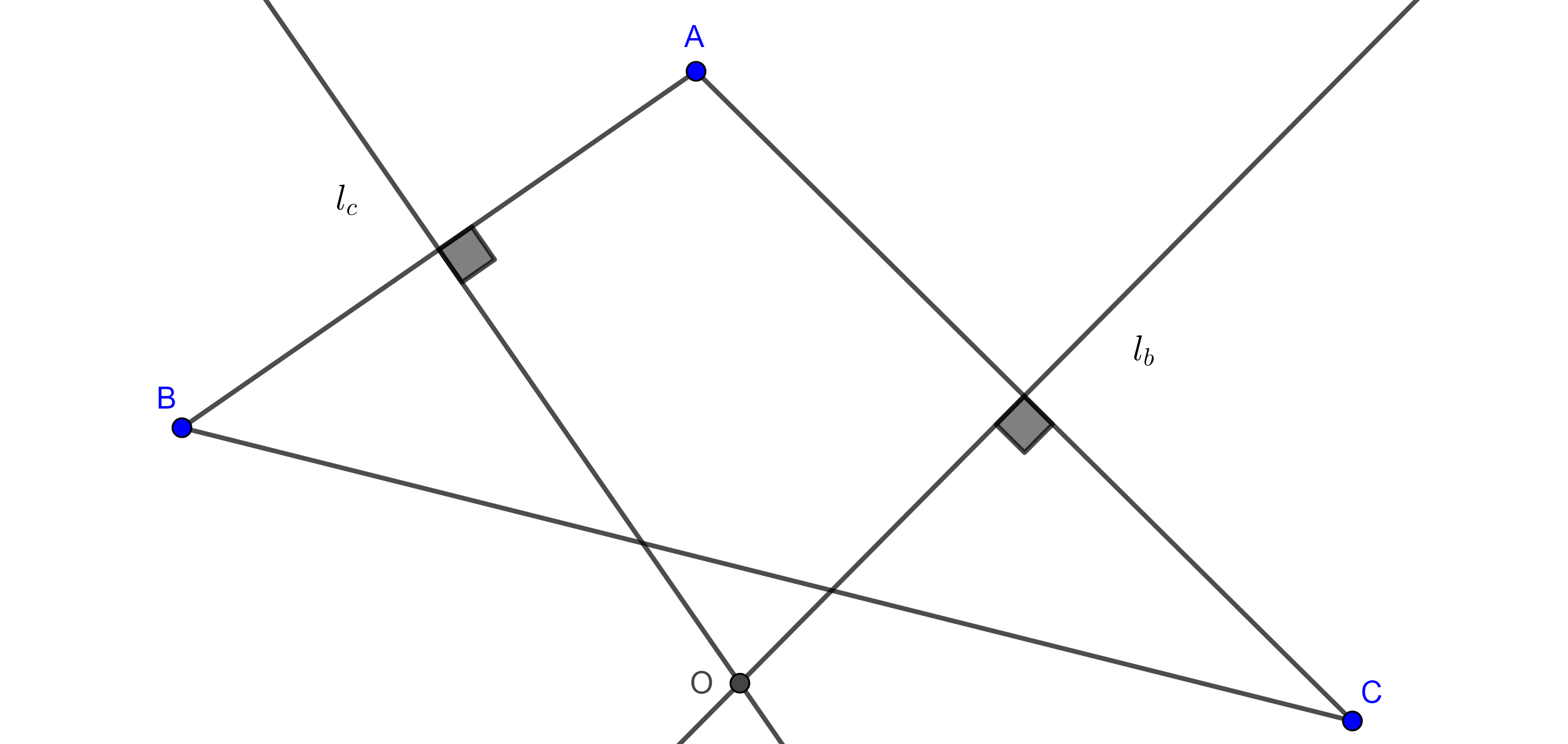
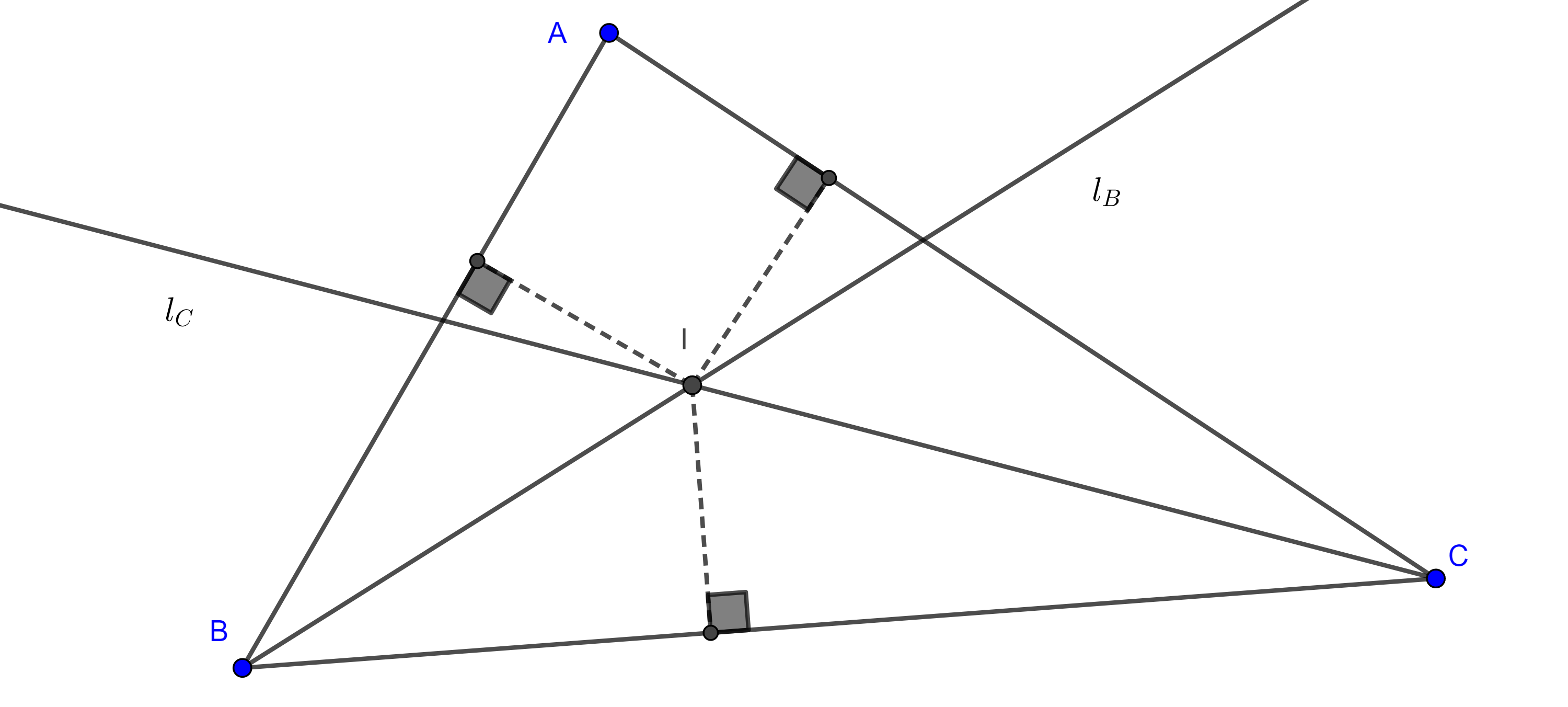
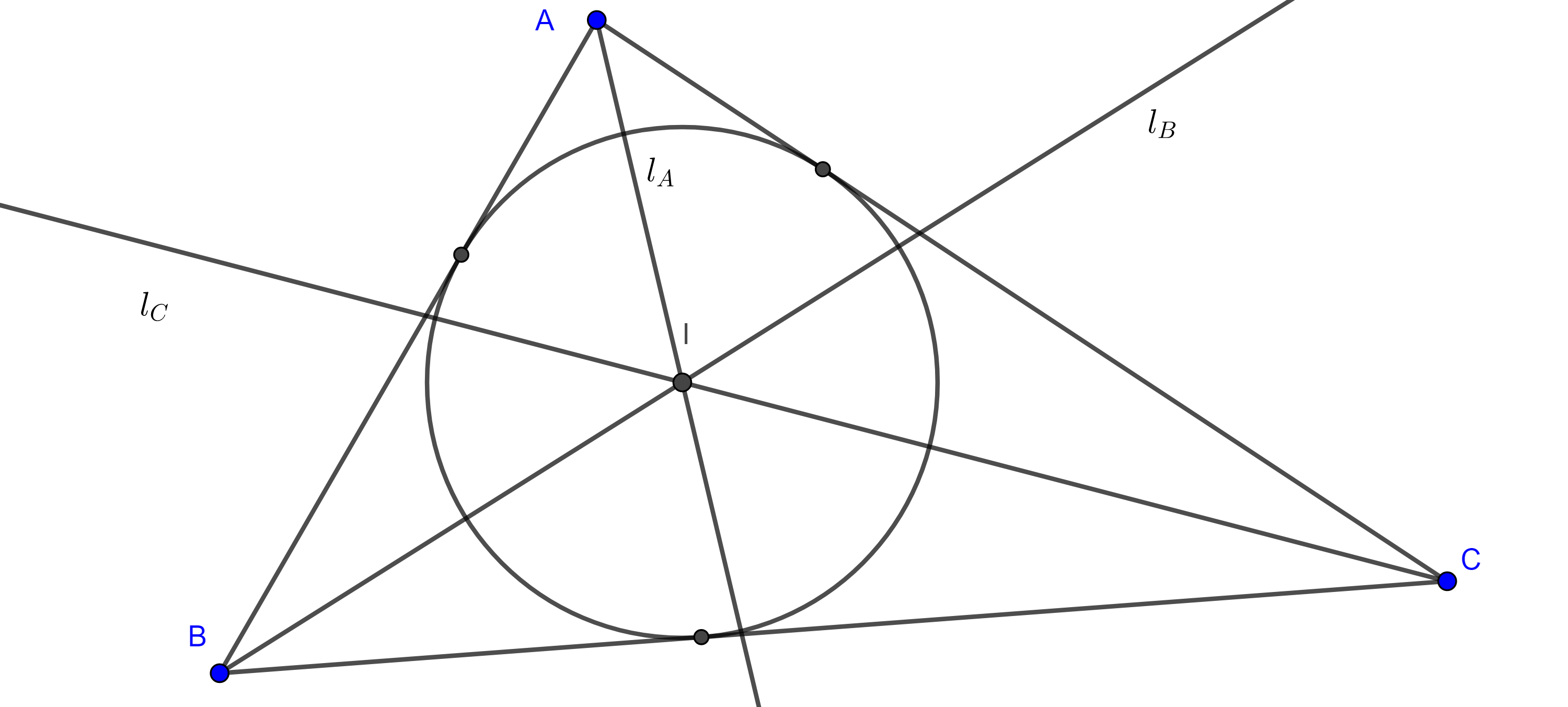
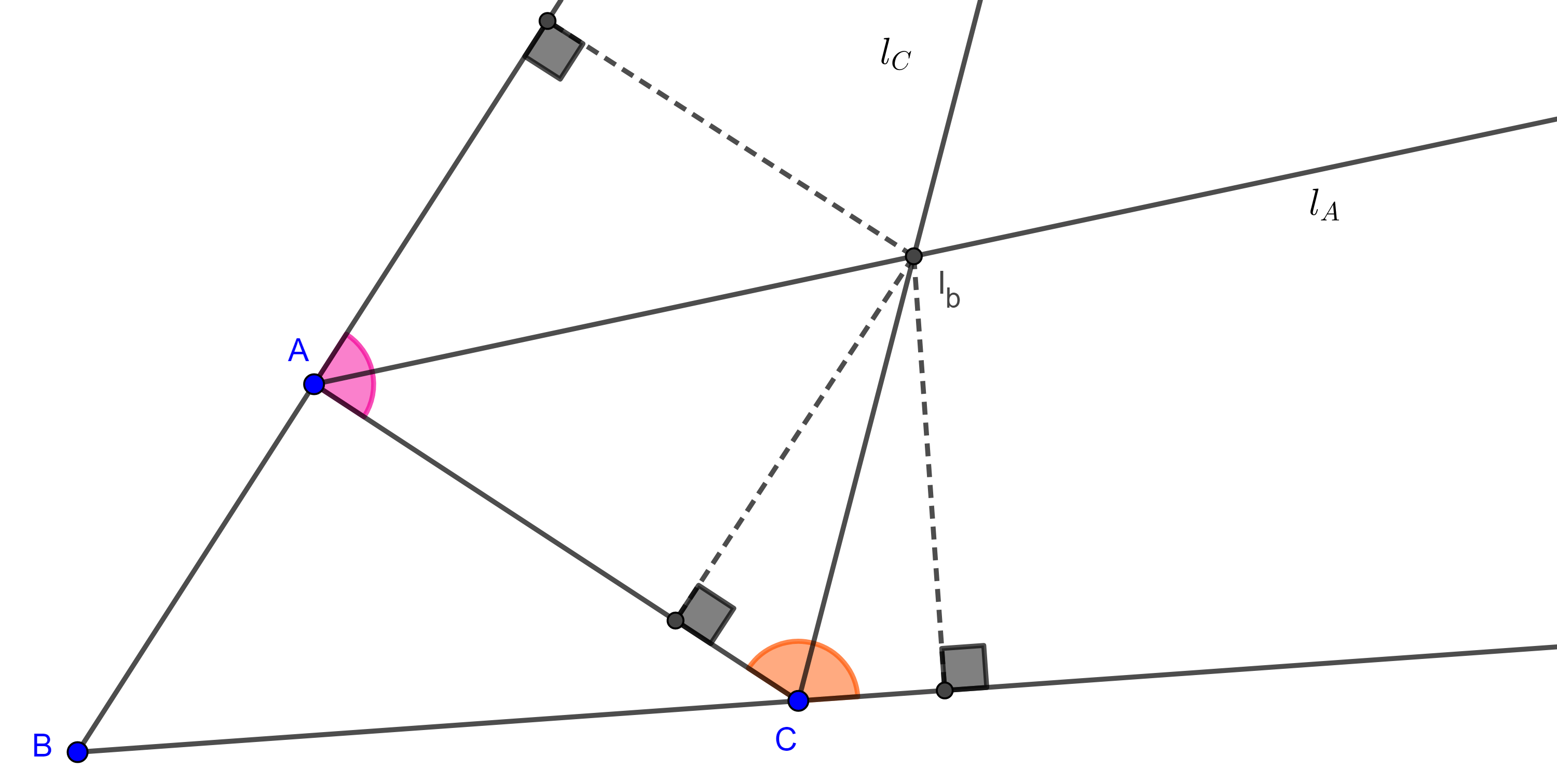
Proposición 1. Sean $△ A B C$ con $B C = a$ , $A C = b$ y $A B = c$ . Sean $G$ el centroide y $P$ , $Q$ , $R$ los pies de las perpendiculares desde $G$ a los lados $A B$ , $B C$ y $A C$ respectivamente, entonces
$(△ P Q R) = \frac{4}{9} (△ A B C)^{3} (\frac{a^{2} + b^{2} + c^{2}}{a^{2} b^{2} c^{2}})$ .

Demostración. Por el teorema 3, $△ A G B$ , $△ A G C$ y $△ B G C$ tienen la misma área, entonces
$(△ B G C) = \frac{B C \times G Q}{2}$
$\Rightarrow G Q = \frac{2 (△ B G C)}{a} = \frac{2 (△ A B C)}{3 a}$ .

De manera análoga tenemos que
$G P = \frac{2 (△ A B C)}{3 c}$ y $G R = \frac{2 (△ A B C)}{3 b}$ .

Notemos que en $P B Q G$ , $∠ P + ∠ Q = π$ , en consecuencia tenemos que
$∠ G + ∠ B = π$
$\Rightarrow \sin ∠ P G Q = \sin ∠ B$

Recordemos que podemos calcular el área de $△ A B C$ con la formula $\frac{a c \sin ∠ B}{2}$ .

Ahora calculamos
$(△ P G Q) = \frac{G P \times G Q \sin ∠ B}{2}$

$= \frac{4 (△ A B C)^{2}}{9 a c} \frac{(△ A B C)}{a c}$

$= \frac{4 (△ A B C)^{3}}{9 a^{2} c^{2}}$ .

De lo anterior se sigue que
$(△ P Q R) = (△ P G Q) + (△ Q G R) + (△ R G P)$

$= \frac{4 (△ A B C)^{3}}{9 a^{2} c^{2}} + \frac{4 (△ A B C)^{3}}{9 a^{2} b^{2}} + \frac{4 (△ A B C)^{3}}{9 b^{2} c^{2}}$

$= \frac{4}{9} (△ A B C)^{3} (\frac{a^{2} + b^{2} + c^{2}}{a^{2} b^{2} c^{2}})$ .

Distancia entre el centroide y el circuncentro

Teorema 3. Sean $△ A B C$ , $G$ su centroide y $P$ un punto en el plano, entonces tenemos la siguiente igualdad
$P A^{2} + P B^{2} + P C^{2} = G A^{2} + G B^{2} + G C^{2} + 3 P G^{2}$ .

Demostración. Consideremos $A^{'}$ y $M$ puntos medios de $B C$ y $A G$ respectivamente, con el teorema de Apolonio podemos calcular las medianas de los triángulos $△ B P C$ , $△ A^{'} P M$ y $△ G P A$ y tomemos en cuenta que $G A = M A^{'}$ .

Por lo tanto,
$P B^{2} + P C^{2} = 2 P A^{' 2} + \frac{B C^{2}}{2}$ ,
$P G^{2} + P A^{2} = 2 P M^{2} + \frac{G A^{2}}{2}$ ,
$P A^{' 2} + P M^{2} = 2 P G^{2} + \frac{M A^{' 2}}{2} = 2 P G^{2} + \frac{G A^{2}}{2}$ .

Sumando las tres expresiones y recordando que $G A = 2 G A^{'}$ , obtenemos
$P A^{2} + P B^{2} + P C^{2} = (P A^{' 2} + P M^{2}) + P G^{2} + G A^{2} + \frac{B C^{2}}{2}$
$= 2 P G^{2} + \frac{G A^{2}}{2} + P G^{2} + G A^{2} + \frac{B C^{2}}{2}$
$= 3 P G^{2} + G A^{2} + 2 G A^{' 2} + \frac{B C^{2}}{2}$ .

Ahora aplicamos el teorema de Apolonio a $△ B G C$ y obtenemos
$G B^{2} + G C^{2} = 2 G A^{' 2} + \frac{B C^{2}}{2}$ .

Por lo tanto,
$P A^{2} + P B^{2} + P C^{2} = 3 P G^{2} + G A^{2} + G B^{2} + G C^{2}$ .

Proposición 2. La suma de los cuadrados de las distancias del centroide de un triángulo a sus vértices es igual a un tercio la suma de los cuadrados de los lados del triángulo.

Demostración. Sea $△ A B C$ con $a = B C$ , $b = A C$ y $c = A B$ , con la formula para las medianas obtenemos:
$G A^{2} = \frac{4}{9} A A^{' 2} = \frac{4}{9} (\frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4})$ ,
$G B^{2} = \frac{4}{9} B B^{' 2} = \frac{4}{9} (\frac{a^{2} + c^{2}}{2} - \frac{b^{2}}{4})$ ,
$G C^{2} = \frac{4}{9} C C^{' 2} = \frac{4}{9} (\frac{a^{2} + b^{2}}{2} - \frac{c^{2}}{4})$ .

Por lo tanto,
$G A^{2} + G B^{2} + G C^{2} = \frac{a^{2} + b^{2} + c^{2}}{3}$ .

Corolario 2. La distancia entre el centroide $G$ y el circuncentro $O$ de un triángulo $△ A B C$ con circunradio $R$ se puede expresar de la siguiente forma:

$O G^{2} = R^{2} - (\frac{a^{2} + b^{2} + c^{2}}{9})$ .

Demostración. Por el teorema 3 y la proposición 2 tenemos lo siguiente
$3 R^{2} = O A^{2} + O B^{2} + O C^{2} = 3 O G^{2} + G A^{2} + G B^{2} + G C^{2}$
$= 3 O G^{2} + \frac{a^{2} + b^{2} + c^{2}}{3}$ .

Despejando $O G^{2}$ obtenemos el resultado
$O G^{2} = R^{2} - (\frac{a^{2} + b^{2} + c^{2}}{9})$ .

Más adelante…

En la siguiente entrada estudiaremos algunas propiedades de un triangulo especial asociado a un triangulo dado, aquel que tiene como vértices los puntos medios del triangulo dado. Esto nos permitirá mostrar que el ortocentro, el centroide y el circuncentro de un triángulo siempre son colineales.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Construye un triángulo dados dos vértices y el centroide.
Prueba que en un triángulo la recta que une el punto medio de una de sus medianas con uno de los vértices del triángulo triseca el lado opuesto al vértice considerado.
Muestra que las medianas de un triángulo dividen al triangulo en seis triángulos que tienen la misma área.
Demuestra que en un triangulo,
$i)$ entre cualesquiera dos de sus medianas la menor de ellas biseca al lado mas grande,
$i i)$ si dos de sus medianas son iguales entonces el triangulo es isósceles.
Sean $△ A B C$ y $A A^{'}$ , $B B^{'}$ , $C C^{'}$ sus medianas, muestra que $\frac{3}{4} (A B^{2} + B C^{2} + A C^{2}) = A A^{' 2} + B B^{' 2} + C C^{' 2}$ .
Sea $△ A B C$ con medianas $A A^{'}$ , $B B^{'}$ y $C C^{'}$ , sean $m = A A^{'} + B B^{'} + C C^{'}$ y $s = A B + B C + C A$ , muestra que $\frac{3}{2} s > m > \frac{3}{4} s$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Desigualdades geométricas.
Siguiente entrada del curco: Triángulo medial y recta de Euler.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-71.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 80-84.
Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 14.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Puntos notables del triángulo

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos la concurrencia de rectas importantes en el triangulo, a saber, las medianas, mediatrices, bisectrices y alturas. Mencionamos también consecuencias inmediatas de los puntos de concurrencia.

Centroide

Teorema 1. Las medianas de todo triángulo concurren en un punto que las triseca.

Demostración. Sean $△ A B C$ , $B^{'}$ y $C^{'}$ los puntos medios de $A C$ y $A B$ respectivamente, por el teorema del segmento medio sabemos que $C^{'} B^{'} = \frac{B C}{2}$ y $C^{'} B^{'} ∥ B C$ .

Sea $G$ la intersección de las medianas $B B^{'}$ y $C C^{'}$ , en $△ G B C$ consideremos $M$ y $N$ los puntos medios de los lados $G B$ y $G C$ respectivamente, entonces
$M N = \frac{B C}{2}$ y $M N ∥ B C$ .

Por transitividad $C^{'} B^{'} = M N$ y $C^{'} B^{'} ∥ M N$ , esto implica que $C^{'} M N B^{'}$ es un paralelogramo y por lo tanto sus diagonales se bisecan, es decir,
$C^{'} G = G N$ y $M G = G B^{'}$ .

Por construcción, $M G = B M$ y $G N = N C$
$\Rightarrow G B^{'} = \frac{B B^{'}}{3}$ y $C^{'} G = \frac{C C^{'}}{3}$ ,
esto es, la medianas $B B^{'}$ y $C C^{'}$ se trisecan

Si repetimos el mismo procedimiento pero ahora con las medianas $A A^{'}$ y $B B^{'}$ encontraremos un punto $G^{'}$ en donde las medianas se trisecaran, $G^{'} B^{'} = \frac{B B^{'}}{3}$ y $G^{'} A^{'} = \frac{A A^{'}}{3}$ .

Como $G B^{'} = \frac{B B^{'}}{3} = G^{'} B^{'}$ , concluimos que $G^{'} = G$ .

Por lo tanto, las medianas de un triángulo concurren en un punto que las triseca.

Definición 1. Decimos que el punto en que concurren las medianas de un triángulo es el gravicentro, baricentro o centroide del triángulo y lo denotamos con la letra $G$ mayúscula.

Circuncentro

Teorema 2. Las mediatrices de los lados de todo triángulo son concurrentes.

Demostración. Sea $△ A B C$ , consideremos las mediatrices $l_{c}$ y $l_{b}$ de $A B$ y $A C$ respectivamente y $O = l_{b} \cap l_{c}$ .

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la mediatriz de un segmento si y solo si equidista a los puntos extremos del segmento.

Ya que $O \in l_{c}$ y $O \in l_{b}$ , entonces $O A = O B$ y $O A = O C$
$\Rightarrow O B = O C$ .

Por el resultado mencionado anteriormente $O B = O C$ implica que $O \in l_{a}$ , la mediatriz de $B C$ .

Por lo tanto, las mediatrices de un triángulo son concurrentes.

Corolario. Tres puntos distintos y no colineales se encuentran en una única circunferencia.

Demostración. Sea $△ A B C$ , por el teorema anterior las mediatrices de los segmentos determinados por los vértices del triángulo concurren en un punto $O$ cuya distancia a cada uno de los vértices es la misma $R = O A = O B = O C$ .

Por definición de circunferencia, $A$ , $B$ y $C$ pertenecen a la circunferencia con centro en $O$ y radio $R$ , $A$ , $B$ , $C \in (O, R) = Γ$ .

Ahora supongamos que existe $Γ^{'} = (O^{'}, R^{'})$ tal que $A$ , $B$ , $C \in Γ^{'}$ , entonces, por definición, $O^{'} A = O^{'} B = O^{'} C = R^{'}$ .

Esto implica que $O^{'} \in l_{a}$ , $O^{'} \in l_{b}$ y $O^{'} \in l_{c}$ , las mediatices de $B C$ , $A C$ y $A B$ respectivamente,
$\Rightarrow O \in l_{a} \cap l_{b} \cap l_{c}$ .

Como ya probamos que las mediatrices son concurrentes entonces $O^{'} = O$ y $R^{'} = R$ , así que $Γ$ es única.

Definición 2. Al punto de concurrencia de las mediatrices de los lados de un triángulo le llamamos circuncentro y lo denotamos como $O$ .

A la distancia constante de $O$ a los vértices del triángulo le llamamos circunradio denotado con la letra $R$ mayúscula.

A la circunferencia única $(O, R)$ determinada por los vértices del triángulo se le conoce como circuncírculo.

Incentro

Teorema 3. Las bisectrices interiores de todo triángulo son concurrentes.

Demostración. Sean $l_{B}$ y $l_{C}$ las bisectrices de los ángulos interiores en $∠ B$ y $∠ C$ respectivamente e $I = l_{B} \cap l_{C}$ .

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la bisectriz de un ángulo si y solo si equidista a los lados que forman el ángulo. Recordemos que la distancia de un punto a una recta es la longitud del punto al pie de la perpendicular a la recta trazada desde el punto.

Denotamos la distancia de un punto $P$ a una recta $l$ como $(P, l)$ .

Como $I \in l_{b}$ e $I \in l_{c}$ , entonces $(I, A B) = (I, B C)$ y $(I, B C) = (I, A C)$ ,
$\Rightarrow (I, A B) = (I, A C)$ .

Por el resultado citado anteriormente, $(I, A B) = (I, A C)$ implica que $I \in l_{A}$ , la bisectriz interior de $∠ A$ .

Por tanto, las bisectrices interiores de un triángulo son concurrentes.

Si consideramos los pies de las perpendiculares a los lados del triángulo trazados desde el punto en que concurren las bisectrices, encontramos tres puntos distintos que equidistan a un punto fijo y por el corolario anterior estos determinan una única circunferencia, esto motiva la siguiente definición.

Definición 3. Al punto de concurrencia de las bisectrices interiores de un triángulo se le conoce como incentro del triángulo y lo denotamos con la letra $I$ mayúscula.

A la distancia de $I$ a los lados del triángulo le llamamos inradio y lo denotamos como $r = (I, A B) = (I, B C) = (I, A C)$ .

La circunferencia con centro en $I$ y radio $r$ , $(I, r)$ , se llama incírculo.

Excentros

Teorema 4. En todo triángulo las bisectrices exteriores de dos ángulos y la bisectriz interior del tercer ángulo son concurrentes.

Demostración. Sea $△ A B C$ , $l_{A}$ y $l_{C}$ las bisectrices exteriores de $∠ A$ y $∠ C$ respectivamente e $I_{b} = l_{A} \cap l_{C}$ .

De manera análoga al caso de las bisectrices internas tenemos que
como $I_{b} \in l_{A}$ e $I_{b} \in l_{C}$ , entonces $(I_{b}, A B) = (I_{b}, A C)$ y $(I_{b}, A C) = (I_{b}, B C)$ ,
$\Rightarrow (I_{b}, A B) = (I_{b}, B C)$ .

Como $I_{b}$ está en la región acotada por el ángulo $∠ C B A$ entonces $I \in l_{B}$ , la bisectriz interior de $∠ B$ .

Por lo tanto, la bisectriz interna de $∠ B$ y las bisectrices externas de $A$ y $C$ son concurrentes.

De manera análoga probamos que las bisectrices externas de $∠ A$ y $∠ B$ concurren con la bisectriz interna de $∠ C$ , y las bisectrices externas de $∠ B$ y $∠ C$ concurren con la bisectriz interna de $∠ A$ .

Similarmente a como lo hicimos con el incentro, notamos que, para cada uno de estos tres puntos de concurrencia, existen tres puntos distintos, uno en cada lado del triángulo que equidistan a un punto fijo y por lo tanto determinan una única circunferencia.

Definición 4. A los puntos en que concurren dos bisectrices externas y una bisectriz interna de un triángulo les llamamos excentros del triángulo y los denotamos como $I_{a}$ , $I_{b}$ e $I_{c}$ de acuerdo a si se encuentran en la bisectriz interna de $∠ A$ , $∠ B$ o $∠ C$ respectivamente y decimos que son opuestos a dichos vértices.

Las distancias de $I_{a}$ , $I_{b}$ e $I_{c}$ a los lados del triángulo son los exradios y se les denota como $r_{a}$ , $r_{b}$ y $r_{c}$ respectivamente.

A las circunferencias $(I_{a}, r_{a})$ , $(I_{b}, r_{b})$ y $(I_{c}, r_{c})$ se les conoce como excírculos del triángulo.

Ortocentro

Teorema 5. Las alturas de todo triángulo son concurrentes.

Demostración. Sea $△ A B C$ , tracemos en cada vértice la paralela al lado opuesto.

Sean $A^{'}$ la intersección de la paralela a $A B$ trazada en $C$ con la paralela a $A C$ trazada en $B$ , de manera análoga definimos $B^{'}$ y $C^{'}$ .

Por construcción, $A B C B^{'}$ es un paralelogramo por lo que $A B^{'} = B C$ , también $C^{'} B C A$ es paralelogramo así que $C^{'} A = B C$ ,
$\Rightarrow A B^{'} = B C = C^{'} A \Rightarrow A$ es el punto medio de $C^{'} B^{'}$ .

De manera similar podemos ver que $B$ es el punto medio de $C^{'} A^{'}$ y $C$ es el punto medio de $A^{'} B^{'}$ .

En consecuencia, las alturas del triángulo $△ A B C$ son las mediatrices del triángulo $△ C^{'} A^{'} B^{'}$ y ya probamos que las mediatrices de los lados de todo triangulo son concurrentes, por lo tanto, las alturas de $△ A B C$ son concurrentes.

Definición 5. Al punto en común en que las tres alturas de un triángulo se intersecan le llamamos ortocentro y lo denotamos con la letra $H$ mayúscula.

Más adelante…

En la siguiente entrada demostraremos algunos teoremas que nos permitirán calcular la magnitud de ángulos relativos a una circunferencia.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

¿Qué puntos notables vistos en esta entrada, caen siempre dentro del triangulo y cuales siempre fuera?
Muestra que una recta paralela a un lado de un triangulo a través del centroide divide el área del triangulo en dos partes tal que la razón de esta áreas es $\frac{4}{5}$ .
Considera un triangulo rectángulo $△ A B C$ con $∠ B = \frac{π}{2}$ , sean $C C^{'}$ la mediana por $C$ y $D$ el pie de la perpendicular a $C C^{'}$ trazada desde $B$ (figura 11), calcula la distancia de $D$ al centroide $G$ del triangulo en términos de los catetos.

Un triángulo rectángulo tiene un ángulo interior de $\frac{π}{3}$ , calcula la distancia del vértice donde se intersecan los catetos al incentro $I$ del triángulo en términos de la hipotenusa.
Sea $△ A B C$ un triángulo tal que la mediana $A D$ es perpendicular a la mediana $B E$ , encuentra $A B$ si $B C = a$ y $A C = b$ .

Entradas relacionadas

Ir a Geometría Moderna I
Entrada anterior del curso: Segmentos dirigidos y teorema de Stewart.
Siguiente entrada del curso: Ángulos en la circunferencia.

Fuentes

Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 29-34.
Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-94.
Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: centroide

Geometría Moderna I: Medianas y centroide

Introducción

Medianas como los lados de un triángulo

Construcciones

Una propiedad del centroide

Distancia entre el centroide y el circuncentro

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Puntos notables del triángulo

Introducción

Centroide

Circuncentro

Incentro

Excentros

Ortocentro

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos