Archivo de la etiqueta: cálculo

Cálculo Diferencial e Integral III: Divergencia, laplaciano y rotacional

Por Alejandro Antonio Estrada Franco

2 respuestas

Introducción

Después de algunas entradas muy técnicas, en las que hemos demostrado dos resultados sumamente importantes (el teorema de la función inversa y el teorema de la función implícita), pasaremos brevemente a una entrada un poco más ligera en términos de teoría, pero también relevante. En esta entrada nos volcaremos a una cara más práctica del cálculo diferencial e integral.

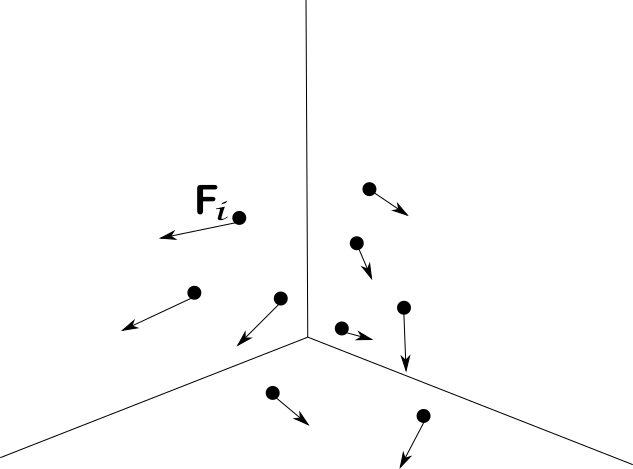
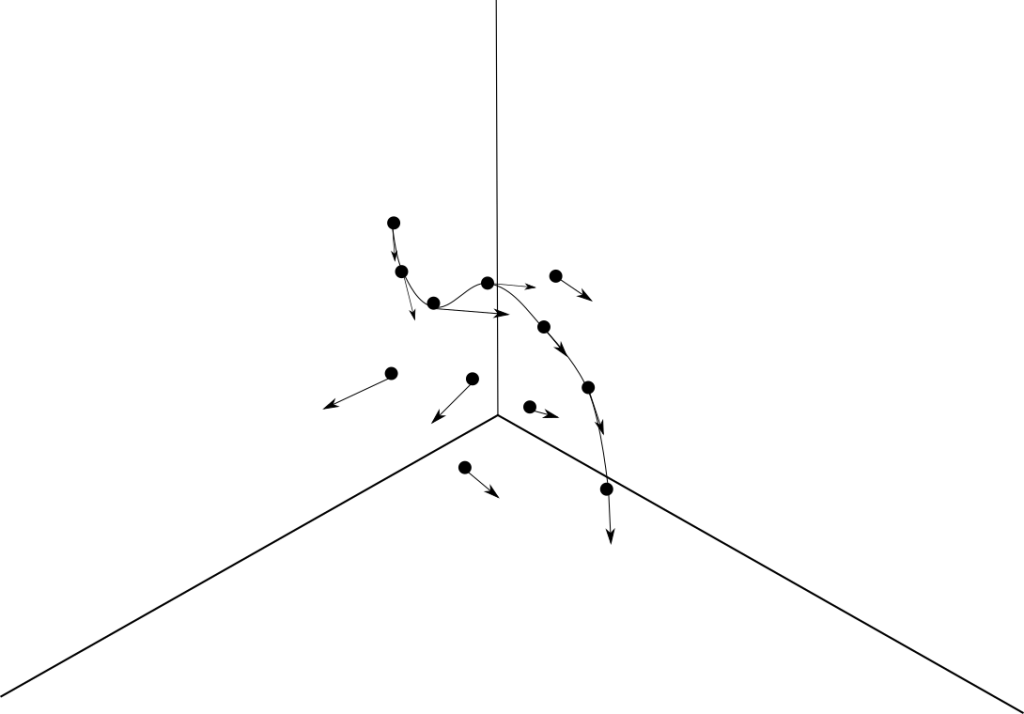
Recordemos que un campo vectorial es una función $F:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$. El nombre de campo vectorial está justificado con que a cada punto de un espacio base $\mathbb{R}^n$, estamos asignando otro vector, en $\mathbb{R}^m$. Si pegamos a cada vector del dominio el vector que le corresponde en a partir de $F$, podemos tener otra intuición geométrica de lo que hacen estas funciones. En la figura 1 apreciamos un ejemplo de esto, donde tenemos un campo vectorial $F$ de $\mathbb{R}^{3}$ en $\mathbb{R}^{3}$ y entonces a cada vector de $\mathbb{R}^3$ le estamos «pegando una flecha».

Figura 1

Esta manera de pensar a los campos vectoriales se presta mucho para entender propiedades físicas de los objetos: flujo eléctrico, flujo de calor, fuerza, trabajo, etc. Si pensamos en esto, otros conceptos que hemos estudiado también comienzan a tener significado. Por ejemplo, el gradiente de un campo escalar está íntimamente relacionado a otras propiedades físicas descritas por el campo escalar. Un ejemplo que hemos discutido es que el gradiente, por ejemplo, nos da la dirección de cambio máximo.

Un ejemplo más concreto sería el siguiente. Pensemos en $\mathbb{R}^{3}$ en un sólido $S$ y un campo escalar $T:S\rightarrow \mathbb{R}$ que da la temperatura de cada punto del sólido. Si consideramos la expresión $\textbf{J}=-k\triangledown T$, obtenemos lo que se conoce como el flujo de calor. Tiene sentido. Por lo que aprendemos en educación elemental, el calor va de los puntos de mayor temperatura a los de menor temperatura. El gradiente $\triangledown T$ da la dirección de máximo crecimiento. Pero entonces $-\triangledown T$ da la dirección de máximo descenso (así como su magnitud). La $k$ que aparece tiene que ver con qué tan bien el material del que hablamos transmite el calor.

Notación tradicional de los campos vectoriales

En el ámbito de las aplicaciones generalmente se usa la notación con gorros. Veamos un ejemplo de cómo escribir con esta notación. En vez de escribir para $\bar{v}\in \mathbb{R}^{3}$ la expresión $\bar{v}=(x,y,z)$, escribimos $$\bar{v}=x\hat{\imath}+y\hat{\jmath}+z\hat{k},$$ es decir, podemos pensar que $\hat{\imath}=(1,0,0)$, $\hat{\jmath}=(0,1,0)$, $\hat{k}=(0,0,1)$.

Si $F:\mathbb{R}^3\to \mathbb{R}^3$ es un campo vectorial, escribimos $$F=P\hat{\imath}+Q\hat{\jmath}+R\hat{k},$$ donde $P$, $Q$ y $R$ son los campos escalares componente, que cada uno de ellos va de $\mathbb{R}^3$ a $\mathbb{R}$.

Generalmente escribimos también $$F(x,y,z)=P(x,y,z)\hat{\imath}+Q(x,y,z)\hat{\jmath}+R(x,y,z)\hat{k}$$ tras evaluar.

Con esta notación también podemos escribir al gradiente y pensarlo como un «operador» que manda campos escalares a campos vectoriales. A este operador se le llama operador nabla. Lo escribimos de la siguiente manera:

\[ \triangledown =\frac{\partial}{\partial x}\hat{\imath}+\frac{\partial}{\partial y}\hat{\jmath}+\frac{\partial}{\partial z}\hat{k}. \]

Si tenemos un campo escalar $\phi:\mathbb{R}^3\to \mathbb{R}$, entonces el operador hace lo siguiente

\[ \triangledown \phi (x,y,z)=\frac{\partial \phi (x,y,z)}{\partial x}\hat{\imath}+\frac{\partial \phi (x,y,z)}{\partial y}\hat{\jmath}+\frac{\partial \phi (x,y,z)}{\partial z}\hat{k}.\]

Es decir, a partir de $\phi$ obtenemos su gradiente.

Líneas de flujo

Ahora introducimos el concepto de línea de flujo el cual es muy usado para campos vectoriales en el modelado fenómenos físicos.

Definición. Si $F:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es un campo vectorial, una línea de flujo para $F$ es una función $\alpha :U\subseteq \mathbb{R}\rightarrow \mathbb{R}^{n}$ tal que $\alpha^{\prime}(t)=F(\alpha(t))$ para todo $t\in U$.

Es decir una línea de flujo es una trayectoria sobre la cual $F$ asigna en cada punto de ella su correspondiente vector tangente. En la Figura 2 tenemos una ilustración de una línea de flujo en un campo vectorial.

Figura 2

Divergencia

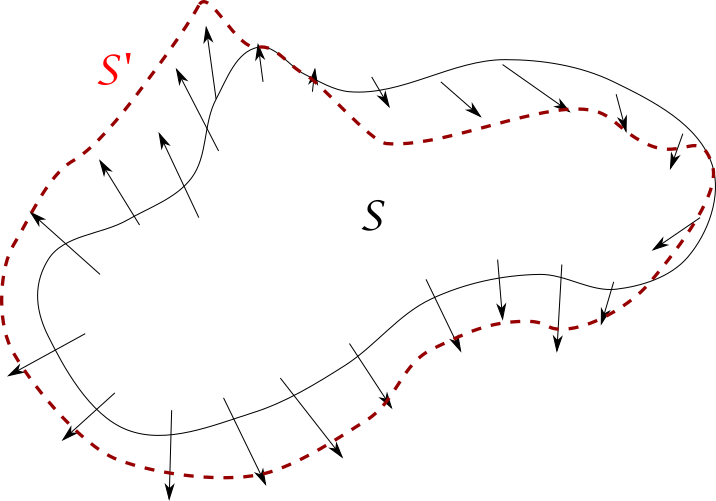
Supongamos que tenemos en el plano (o el espacio) una región $S$. Para cada punto $\bar{x}$ de $S$ sea $\textbf{x}(t)$ una línea de flujo que parte de $\bar{x}$ bajo el campo vectorial $F$. El conjunto de líneas $\textbf{x}(t)$ describe cómo cambia el conjunto $S$ bajo la acción de $F$ a través del tiempo. Formalizando esto un poco, en el caso del plano tomemos $F:S\subseteq \mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$. Para cada $\bar{x}\in S$ podemos considerar $\gamma_x:I_{x}\subset \mathbb{R}\rightarrow \mathbb{R}^{2}$, como la trayectoria $\textbf{x}(t)$ y que es línea de flujo bajo $F$. Estas trayectorias van mostrando «cómo se va deformando $S$ a causa del campo vectorial $F$». También, consideremos al conjunto $S’=\{\bar{x}+F(\bar{x})|\bar{x}\in S \}$, al cual pensaremos como el conjunto resultante de aplicar a $S$ el campo vectorial $F$.

Estas nociones se pueden analizar a través de una herramienta llamada divergencia. La definimos a continuación, pero una demostración formal de que el operador divergencia mide la expansión del efecto de un campo vectorial es un tema que se estudia en un cuarto curso de cálculo diferencial e integral.

Figura 3. Aquí se ilustra el efecto de un campo vectorial sobre una sección $S$ del plano.

Damos la definición en $\mathbb{R}^3$, pero podrías dar una versión análoga para $\mathbb{R}^2$.

Definición. Si $F=P\hat{\imath}+Q\hat{\jmath}+R\hat{k}$ es un campo vectorial definimos la divergencia de $F$ como:

\[ \triangledown \cdot F=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}.\]

En dimensiones más altas, si $F=(F_{1},\dots ,F_{n})$, entonces $\triangledown \cdot F=\sum_{i=1}^{n}\frac{\partial F_{i}}{\partial x_{i}}$.

Rotacional

Figura 4

Pensemos en un fluido que se mueve de acuerdo con el flujo marcado por el campo vectorial $F$. Tenemos una forma de determinar la rotación que el fluido imprimiría sobre un sólido llevado por él. Imaginemos un remolino y una pequeña esfera solida llevada por el remolino. Lo que llamaremos el rotacional del vector nos proporcionará la información sobre las rotaciones sobre su eje que el fluido imprime a la pequeña esfera (Figura 4).

Definición. Sea $$F(x,y,z)=F_{1}(x,y,z)\hat{\imath}+F_{2}(x,y,z)\hat{\jmath}+F_{3}(x,y,z)\hat{k}.$$ Entonces definimos al rotacional de $F$ como el siguiente campo vectorial:

\[ \triangledown \times F(x,y,z)=\left( \frac{\partial F_{3}}{\partial y} – \frac{\partial F_{2}}{\partial z} \right)\hat{\imath}+\left( \frac{\partial F_{1}}{\partial z}-\frac{\partial F_{3}}{\partial x} \right)\hat{\jmath}+\left( \frac{\partial F_{2}}{\partial x}-\frac{\partial F_{1}}{\partial y} \right)\hat{k}.\]

También suele representarse por el siguiente determinante:

\[ \triangledown \times F=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ {\large \frac{\partial}{\partial x}} & {\large \frac{\partial}{\partial y}} & {\large \frac{\partial}{\partial z}} \\ F_{1} & F_{2} & F_{3} \end{vmatrix}. \]

Una visión mas clara de por qué esta expresión calcula lo que queremos se puede aprender en un cuarto curso de cálculo diferencial e integral, o bien en algún curso de aplicaciones del cálculo a la física. Por ahora veremos en los ejemplos solamente la parte operativa.

Laplaciano

Hay un operador más que surge naturalmente en las ecuaciones que involucran al gradiente y a la divergencia.

Definición. Sea $f:\mathbb{R}^3\to \mathbb{R}$ un campo escalar. El operador laplaciano se establece de la siguiente manera:

\[ \triangledown ^{2}f=\frac{\partial ^{2}f}{\partial x^{2}}\hat{\imath}+\frac{ \partial^{2}f}{\partial y^{2}}\hat{\jmath}+\frac{\partial ^{2}f}{\partial z^{2}}\hat{k}. \]

Es decir, el laplaciano consiste en aplicar el operador divergencia al gradiente de un campo escalar.

Ejemplos de problemas de los conceptos anteriores

Revisemos algunos problemas que tienen que ver con estos operadores. Esto nos permitirá ampliar nuestra visión en cuanto a la practicidad de esta herramienta matemática.

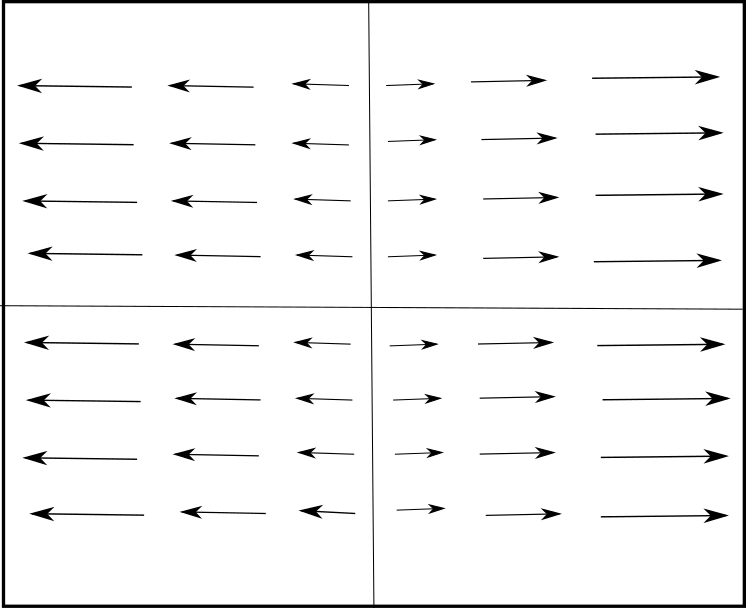
Consideremos el siguiente campo vectorial en el plano $F(x,y)=x\hat{\imath}$. Pensaremos el signo de la divergencia de $F$ como la razón del cambio de áreas bajo este campo. Interpretaremos a $F$ como aquel que asigna a cada punto del plano un vector velocidad de un fluido en el plano.

Para $x>0$ el campo apunta hacia la derecha con vectores paralelos al eje $x$ con tamaño $|x|$, para $x<0$ los vectores apuntan a la izquierda paralelamente al eje $x$ con tamaño $|x|$ (Figura 5). Por ello las longitudes de las flechas de $F$ son mas cortas en torno al origen; así cuando el fluido se mueve, se expande. Y esto coincide con el hecho de que $\triangledown \cdot F=1$.

Figura 5

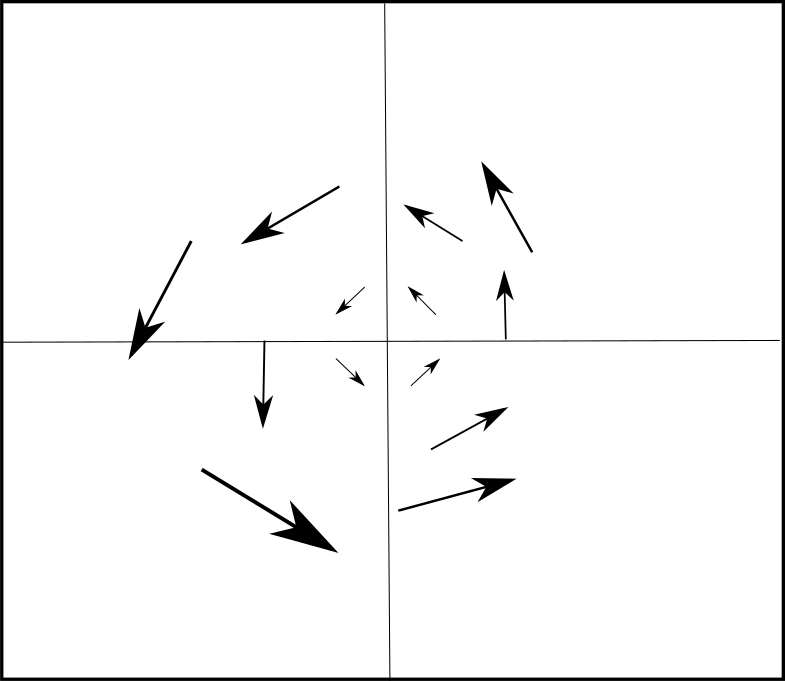
En el siguiente ejemplo consideremos el campo vectorial $F(x,y)=-y\hat{\imath}+x\hat{\jmath}$. Las líneas de flujo de $F$ siguen circunferencias concéntricas centradas al origen en dirección contrarias a las manecillas del reloj. Al calcular la divergencia tenemos lo siguiente:

\[ \triangledown \cdot F=\frac{\partial }{\partial x}(-y)+\frac{\partial}{\partial y}(x)=0. \]

En la figura 6 tenemos la ilustración de cómo se ve el campo de este ejemplo. Suena razonable. En este caso el fluido no se está expandiendo, sino que más bien está rotando.

Figura 6

En el laplaciano aplicamos la divergencia a un gradiente. Pero, ¿qué pasa cuando aplicamos el rotacional a un gradiente? Consideremos una función $f$ con derivadas parciales diferenciables continuas es decir, de clase $C^{2}$. Para una función así tenemos

\[ \triangledown f(x,y,z)=(\partial f/\partial x,\partial f/ \partial y,\partial f/\partial z). \]

De acuerdo con la definición de rotacional, tenemos:

\begin{align*} \triangledown \times (\triangledown f)&= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & \frac{\partial f}{\partial z} \end{vmatrix}\\ &= \left( \frac{\partial ^{2}f}{\partial y\partial z}-\frac{\partial ^{2}f}{\partial z\partial y} \right)\hat{\imath}+\left( \frac{\partial ^{2}f}{\partial z\partial x}-\frac{\partial ^{2}f}{\partial x \partial z} \right)\hat{\jmath}+\left( \frac{\partial ^{2}f}{\partial x\partial y}-\frac{\partial ^{2}f}{\partial y\partial x} \right)\hat{k}\\ &=\bar{0} \end{align*}

por la igualdad de las parciales mixtas. Es decir; si $f$ es un campo escalar cuyas derivadas parciales son diferenciables con derivada continua tenemos $\triangledown \times \triangledown f=0$.

Esto nos puede ayudar a saber si una cierta función puede obtenerse como gradiente de otra. Tomemos $G(x,y,z)= y\hat{\imath}-x\hat{\jmath}$. Notemos que las funciones en $\hat{\imath}$ y en $\hat{\jmath}$ son diferenciables con derivada continua. Entonces nos preguntaremos ¿$G$ es gradiente de un campo escalar? Para ello calculemos $\triangledown \times G$ cuyo resultado en caso afirmativo debería ser igual a cero. Sin embargo,

\[ \triangledown \times G=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ y & -x & 0 \end{vmatrix}=-2\hat{k}\neq 0,\]

por lo tanto $G$ no es un gradiente.

También tenemos que la divergencia de un rotacional es igual a cero, es decir si $F$ es un campo vectorial $\triangledown \cdot (\triangledown \times F)=0$. Queda como tarea moral demostrar este hecho.

Mas adelante…

Con esta entrada terminamos nuestro estudio de conceptos relacionados con campos vectoriales. Sin embargo, aún no los descartaremos por completo. Retomaremos a los campos vectoriales en la última unidad del curso. En ella, retomaremos varias partes de la teoría para establecer resultados de optimización de campos escalares, y de funciones bajo restricciones.

Tarea moral

  1. Para los siguientes campos vectoriales, halla su divergencia
    • $F(x,y)=x^{3}\hat{\imath}+x\hspace{0.1cm}sen\hspace{0.1cm}(xy)\hat{\jmath}$
    • $G(x,y,z)=e^{xy}\hat{\imath}+e^{xy}\hat{\jmath}+e^{yz}\hat{k}$.
  2. Obtén el rotacional de los siguientes campos vectoriales:
    • $F(x,y,z)=(x^{2}+y^{2}+z^{2})(3\hat{\imath}+4\hat{\jmath}+5\hat{k})$
    • $G(x,y,z)=yz\hat{\imath}+xz\hat{\jmath}+xy\hat{k}$.
  3. Dibuja algunas líneas de flujo del campo $F(x,y)=-3x\hat{\imath}-y\hat{\jmath}$. Calcula $\triangledown \cdot F$ y explica el significado del resultado de la divergencia en su relación con las líneas de flujo.
  4. Demuestra que $\triangledown \cdot (\triangledown \times F)=0$
  5. Sean $f$ y $g$ dos campos escalares diferenciables, y $F$, y $G$ dos campos vectoriales diferenciables. Demuestra las siguientes identidades (solo usa la parte operativa, piensa que todos los campos tanto los vectoriales como los escalares tienen el mismo dominio):
    1. $\triangledown \cdot gG =g(\triangledown \cdot G) + G\cdot (\triangledown g)$
    2. $\triangledown (fg)=f(\triangledown g) +g (\triangledown f)$
    3. $\triangledown \cdot (F\times G)= G\cdot (\triangledown \times F)-F\cdot (\triangledown \times G)$

Entradas relacionadas

Cálculo Diferencial e Integral III: Ejemplos e intuición del teorema de la función implícita

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En la entrada anterior revisamos el teorema de la función implícita formalmente enunciado y demostrado. En ésta lo que haremos será reflexionar sobre él y observar con más detalle su propósito y usos.

Dicho de forma simplista pero resaltando su objetivo principal el teorema de la función implícita busca establecer las condiciones bajo las cuales podemos despejar unas variables en término de otras. Da una condición en términos de cierta diferenciabilidad. Como esbozamos en la entrada anterior, lo que el teorema nos dice es cuándo es posible despejar las variables de un sistema de ecuaciones (o funciones coordenadas de un campo vectorial) en función de ciertas las variables libres, y alrededor de una vecindad. Para hacer esto, básicamente hay que resolver un sistema de ecuaciones en donde ciertos coeficientes vienen de ciertas derivadas parciales. El teorema de la función implícita también habla de cómo derivar una función definida implícitamente respecto de cualquiera de sus derivables.

¿Por qué teorema de la función implícita?

¿Por qué este nombre? En numerosos problemas matemáticos derivados de aplicaciones diversas se utilizan modelos geométricos. Estos modelos geométricos usualmente se construyen a partir de restringir ciertas variables con ciertas ecuaciones. Pensemos en objetos geométricos en tres dimensiones. Tenemos variables $x,y,z$. Definamos $G(x,y,z):=x^{2}+y^{2}+z^{2}-1$. Podemos preguntarnos por el objeto geométrico descrito por la ecuación $G(x,y,z)=0.$ Sabemos que las ternas $(x,y,z)$ que satisfacen esto justo conforman una esfera de radio 1 centrada en el origen. Decimos que esta ecuación proporciona una representación implícita de la superficie.

Pero quizás nuestra aplicación nos lleva a preguntarnos si alguna coordenada está en términos de las otras para los puntos que están en dicha esfera. En afortunadas ocasiones es posible despejar en la ecuación $G(x,y,z)$ algunas de las variables en términos de las otras. Esto nos lleva a una o varias ecuaciones de la forma $z=g(x,y)$, en nuestro caso particular tenemos:

\begin{align*}z=\sqrt{1-x^{2}-y^{2}} && \textup{y} && z=-\sqrt{1-x^{2}-y^{2}}.\end{align*}

El teorema de la función inversa nos dice que si ciertas derivadas existen y son invertibles como transformaciones lineales, entonces podemos hacer estos despejes. De hecho, nos dice algo mejor: que podemos hacerlos alrededor de toda una vecindad donde no se anule dicha derivada. De aquí sale la idea de «función implícita». Algunas ecuaciones, aunque no permitan despejar variables, sí lo permiten «localmente» y entonces ahí hay una «función oculta».

En la gran mayoría de los casos es difícil lograr estos despejes mediante expresiones algebraicas sencillas por ejemplo en una superficie representada por la ecuación $y^{3}+z^{2}-xz+e^{zx}-4=0$ suena muy difícil que podamos despejar $z$. Sin embargo el teorema de la función implícita nos garantiza que, aunque no sepamos cómo, la variable $z$ sí se puede poner en función de las variables $x$ y $y$.

La derivada de la función implícita

Otra buena notica es que aunque no conozcamos explícitamente el despeje que nos interesa, con el teorema de la función implícita sí podemos encontrar las derivadas parciales de la función implícita que aparece. Si pensaste los problemas de la tarea moral de la entrada anterior, quizás ya hayas llegado al siguiente resultado.

Corolario. Sea $F:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar diferenciable con $S$ abierto. Supongamos que la ecuación $F(x_{1},\dots ,x_{n})=0$ define implícitamente a $x_{n}$ como función diferenciable de $x_{1},\dots ,x_{n-1}$ como $x_{n}=f(x_{1},\dots ,x_{n-1})$, para todos los puntos $(x_{1},\dots ,x_{n-1})\in S’\subseteq \mathbb{R}^{n-1}$, entonces para cada $k=1,2,\dots ,n-1$ la derivada parcial $\frac{\partial f}{\partial x_{k}}$ está dada por la fórmula:

\[ \begin{equation}\frac{\partial f}{\partial x_{k}}=-\frac{\frac{\partial F}{\partial x_{k}}}{\frac{\partial F}{\partial x_{n}}}\end{equation} \]

en los puntos en los que $\frac{\partial F}{\partial x_{n}}\neq 0$. Las derivadas parciales de $F$ están calculadas en el punto $(x_{1},\dots ,x_{n-1},f(x_{1},\dots ,x_{n}))$.

Demostración. Pensemos $F:\mathbb{R}^{n-1}\times \mathbb{R} \to \mathbb{R}$. Si $(x_{1},\dots x_{n})$ es tal que $F(x_{1},\dots ,x_{n})=0$, por el teorema de la función implícita tenemos a una única función $f:\mathbb{R}^{n-1}\rightarrow \mathbb{R}$ tal que $F(x_{1},\dots ,x_{n-1},f(x_{1},\dots ,x_{n-1}))=0$.

(Nota. En la entrada anterior teníamos entradas de la forma $(y,x)$ y $y$ quedaba en función de $x$. De manera totalmente análoga podemos intercambiar los papeles de $x$ y $y$, pidiendo las hipótesis correctas. De hecho, usualmente se piensa en parejas $(x,y)$ y las variables de $y$ son las que quedan en términos de las variables $x$)

Ahora, pensemos en el campo vectorial $G:S’\subseteq \mathbb{R}^{n-1}\rightarrow \mathbb{R}^{n}$ dado por $G(x_{1},\dots ,x_{n-1})=(x_{1},\dots ,x_{n-1},f(x_{1},\dots ,x_{n-1}))$. Así $(F\circ G)(x_{1},\dots ,x_{n-1})=0$. Por regla de la cadena, $DFDG=0$. Tenemos así $0=\triangledown F\cdot DG$, lo cual explícitamente es:

\[ 0=\begin{bmatrix} \frac{\partial F}{\partial x_{1}} & \dots & \frac{\partial F}{\partial x_{n}} \end{bmatrix} \begin{bmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & 1 \\ \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}} & \dots & \frac{\partial f}{\partial x_{n-1}} \end{bmatrix}= \]

\[ \begin{bmatrix} \frac{\partial F}{\partial x_{1}}+\frac{\partial F}{\partial x_{n}}\frac{\partial f}{\partial x_{1}} & \frac{\partial F}{\partial x_{2}}+\frac{\partial F}{\partial x_{n}}\frac{\partial f}{\partial x_{2}} & \dots & \frac{\partial F}{\partial x_{n-1}}+\frac{\partial F}{\partial x_{n}}\frac{\partial f}{\partial x_{n-1}} \end{bmatrix}.\]

Por ello, para cada $i$ tenemos:

\[ \frac{\partial F}{\partial x_{i}}+\frac{\partial F}{\partial x_{n}}\frac{\partial f}{\partial x_{i}}=0.\]

De esta ecuación se deduce la $(1)$.

$\square$

Un primer ejemplo del teorema de la función inversa

Pasemos ahora a hacer algunas cuentas concretas para entender mejor lo que uno tiene que hacer para aplicar el teorema de la función implícita en funciones particulares.

Ejemplo. Consideremos la ecuación $y^{2}+xz+z^{2}-e^{z}-c=0$. Expresaremos a $z$ en función de $x$ e $y$, es decir, $z=f(x,y)$. Nos gustaría encontrar un valor de la constante $c$ tal que $f(0,e)=2$. Para dicha $c$, queremos calcular las derivadas parciales con respecto a $x$ y $y$ en el punto $(x,y)=(0,e)$.

Para la primera parte sustituimos $x=0$, $y=e$ y $z=2$. Tenemos $$e^{2}+0\cdot 2+2^{2}-e^{2}-c=0,$$ que es lo mismo que $4-c=0$, y esto implica $c=4$. De esta manera, estudiaremos la función $$F(x,y,z)=y^{2}+xz+z^{2}-e^{z}-4.$$

Notemos que

\begin{align*}\frac{\partial F}{\partial z}=x+2z-e^{z},&&\frac{\partial F}{\partial x}=z,&&\frac{\partial F}{\partial y}=2y,\end{align*}

por lo cual

\begin{align*} \frac{\partial f}{\partial x}=-\frac{z}{x+2z-e^{z}},&&\frac{\partial f}{\partial y}=-\frac{2y}{x+2z-e^{z}}.\end{align*}

Así para $x=0$, $y=e$ y $z=2$ al sustituir resulta

\begin{align*} \frac{\partial f}{\partial x}(0,e)=\frac{2}{e^{2}-4}&&\textup{y}&&\frac{\partial f}{\partial y}(0,e)=\frac{2e}{e^{2}-4}. \end{align*}

$\triangle$

En este ejemplo vemos cómo hemos podido calcular las derivadas parciales de $z=f(x,y)$ usando el valor de $f$ en el punto $(0,e)$, sin conocer quién es la función $f(x,y)$.

Un repaso chiquito de la demostación del teorema de la función implícita

Ahora repasaremos la demostración del teorema de la función implícita pero para un caso muy particular: Dos superficies $S_{1}$ y $S_{2}$ en el espacio con las siguientes representaciones implícitas:

$$ \textup{para}\hspace{0.3cm}S_{1}:\Psi (x,y,z)=0\hspace{1cm}\textup{y}\hspace{1cm}\textup{para}\hspace{0.3cm}S_{2}:\Gamma (x,y,z)=0.$$

Supongamos que las superficies se cortan en la curva $\mathfrak{C}$. En otras palabras, $\mathfrak{C}$ es el conjunto solución para el siguiente sistema de ecuaciones:

\[ \left \{\begin{matrix} \Psi (x,y,z)=0 \\ \Gamma (x,y,z)=0. \end{matrix} \right.\]

Supongamos que podemos despejar $x$ y $y$ en estas ecuaciones en términos de $z$ de la siguiente manera:

\[ \begin{equation}x=X(z),\hspace{1cm}y=Y(z)\hspace{0.3cm}\textup{para todo}\hspace{0.1cm}z\in (a,b).\end{equation} \]

Aquí, al reemplazar $x$ y $y$ por $X(z)$ y $Y(z)$ (respectivamente), el sistema $(2)$ se satisface. Por tanto tenemos $\Psi (X(z),Y(z),z)=0$ y $\Gamma (X(z),Y(z),z)=0$ para todo $z\in (a,b)$. Podemos calcular las derivadas $X^{\prime}(z)$, $Y^{\prime}(z)$, sin un conocimiento explícito de $X(z)$ y $Y(z)$.

¿Cómo hacemos esto? Consideramos las siguientes funciones auxiliares:

\begin{align*}
\psi (z)&=\Psi (X(z),Y(z),z),\\
\gamma (z)&=\Gamma (X(z),Y(z),z).
\end{align*}

Tenemos $\psi (z)=\gamma (z)=0$ y en consecuencia $\psi^{\prime}(z)=\gamma^{\prime}(z)=0$.

Derivando con la regla de la cadena tenemos:

\begin{align*}
\psi^{\prime}(z)&=\frac{\partial \Psi}{\partial x}X'(z)+\frac{\partial \Psi}{\partial y}Y'(z)+\frac{\partial \Psi}{\partial z},\\
\gamma^{\prime}(z)&=\frac{\partial \Gamma}{\partial x}X'(z)+\frac{\partial \Gamma}{\partial y}Y'(z)+\frac{\partial \Gamma}{\partial z}
\end{align*}

Dado que $\psi^{\prime} (z)=\gamma^{\prime}(z)=0$ tenemos el siguiente sistema de dos ecuaciones con dos incógnitas $X^{\prime}(z)$, $Y^{\prime}(z)$:

\[ \left \{\begin{matrix}\frac{\partial \Psi}{\partial x}X^{\prime}(z)+\frac{\partial \Psi}{\partial y}Y^{\prime}(z)=-\frac{\partial \Psi}{\partial z}\\ \frac{\partial \Gamma}{\partial x}X^{\prime}(z)+\frac{\partial \Gamma}{\partial y}Y^{\prime}(z)=-\frac{\partial \Gamma}{\partial z} \end{matrix} \right.\]

En los puntos en los cuales el determinante del sistema no es cero, usamos la regla de Cramer para obtener las soluciones como sigue:

\[ X^{\prime}(z)={\Large -\frac{\begin{vmatrix}\frac{\partial \Psi}{\partial z} & \frac{\partial \Psi}{\partial y}\\ \frac{\partial \Gamma}{\partial z} & \frac{\partial \Gamma }{\partial y}\end{vmatrix}}{\begin{vmatrix}\frac{\partial \Psi}{\partial x} & \frac{\partial \Psi}{\partial y} \\ \frac{\partial \Gamma}{\partial x} & \frac{\partial \Gamma}{\partial z} \end{vmatrix}} },\hspace{0.5cm}Y^{\prime}(z)={\Large -\frac{\begin{vmatrix}\frac{\partial \Psi}{\partial x} & \frac{\partial \Psi}{\partial z}\\ \frac{\partial \Gamma}{\partial x} & \frac{\partial \Gamma }{\partial z}\end{vmatrix}}{\begin{vmatrix}\frac{\partial \Psi}{\partial x} & \frac{\partial \Psi}{\partial y} \\ \frac{\partial \Gamma}{\partial x} & \frac{\partial \Gamma}{\partial z} \end{vmatrix}} }.\]

Otro ejemplo para encontrar derivadas de funciones implícitas

Veamos un último ejemplo en donde pondemos usar las ideas anteriores.

Ejemplo. Consideremos las ecuaciones $y=uv^{2}$, y $x=u+v$. Queremos ver que podemos determinar una función $h$ tal que $v=h(x,y)$ y para la cual:

\[ \frac{\partial h}{\partial x}(x,y)= \frac{h(x,y)}{3h(x,y)-2x}.\]

Además, queremos encontrar una fórmula análoga para $\frac{\partial h}{\partial y}$.

Primero, en la ecuación $x=u+v$ despejamos $u$ y sustituimos en $y=uv^{2}$, tenemos $y=(x-v)v^{2}$. De aquí $$xv^{2}-v^{3}-y=0.$$ Esto nos sugiere pensar en la función $$F(x,y,v):=xv^{2}-v^{3}-y,$$ pues nos permite representar nuestra ecuación como $F(x,y,v)=0$. Por el teorema de la función implícita (¡verifica las hipótesis!), esta ecuación define implícitamente a $v$ como función de $x$ e $y$, digamos, como $v=h(x,y)$. Aplicando las fórmulas que conocemos para las derivadas de la función implicita, tenemos lo siguiente:

\[ \frac{\partial h}{\partial x}= -\frac{\partial F /\partial x}{\partial F /\partial v}\hspace{0.5cm}\textup{y}\hspace{0.5cm}\frac{\partial h}{\partial y}=-\frac{\partial F /\partial y}{\partial F /\partial v} \]

Donde $\frac{\partial F}{\partial x}=v^{2}$, $\frac{\partial F}{\partial v}=2xv-3v^{2}$ y $\frac{\partial F}{\partial y}=-1$. Luego tenemos:

\begin{align*} \frac{\partial h}{\partial x}(x,y)&=-\frac{v^{2}}{2xv-3v^{2}}\\ &=-\frac{v}{2x-3v}\\ &=\frac{h(x,y)}{3h(x,y)-2x}.\end{align*}

Esto muestra la primera parte. Para encontra la fórmula análoga, volvemos a usar las fórmulas para derivadas de la función implícita:

\begin{align*}\frac{\partial h}{\partial y}(x,y)&=-\frac{-1}{2xv-3v^{2}}\\ &=\frac{1}{2xh(x,y)-3h^{2}(x,y)}.\end{align*}

$\triangle$

Más adelante…

Hemos cubierto el teorema de la función inversa y el teorema de la función implícita. Estos son temas teóricos profundos e importantes que tienen muchas consecuencias. Tienen también otras versiones en contextos más amplios como variedades, geometría diferencial, etc. Por el momento, dejaremos hasta aquí nuestro estudio de estos temas, pero te recomendamos de vez en cuando repasarlos, pues cada vez entenderás más de sus demostraciones y lo que significan.

Nuestra atención se enfocará ahora en otros conceptos que se pueden definir en términos de funciones de varias variables: la divergencia, el laplaciano y el rotacional. Después, hablaremos un poco de cómo la teoría que hemos desarrollado nos ayudará a encontrar puntos críticos para funciones de varias variables.

Tarea moral

  1. Las ecuaciones $x+y=uv$ y $xy=u-v$ definen $x$ y $y$ como funciones implícitas de $u$ y $v$, sean éstas $x=X(u,v)$ y $y=Y(u,v)$. Demuestra que $\partial X/\partial u=(xv-1)/(x-y)$ si $x\neq y$, y halla las fórmulas para $\partial X/\partial v$, $\partial Y/\partial v$, $\partial Y/\partial u$.
  2. Las tres ecuaciones \[ \left\{\begin{matrix} x^{2}-y\hspace{0.1cm}cos\hspace{0.1cm}(uv)+z^{2}=0, \\ x^{2}+y^{2}-\hspace{0.1cm}sen\hspace{0.1cm}(uv)+2z^{2}=2, \\ xy-\hspace{0.1cm}sen\hspace{0.1cm}u\hspace{0.1cm}cos\hspace{0.1cm}v+z=0 \end{matrix}\right.\] definen $x$, $y$, y $z$ como funciones de $u$ y $v$. Calcula las derivadas parciales $\partial x/\partial u$ y $\partial x/\partial v$ en el punto $x=y=1$, $u=\pi /2$, $v=0$, $z=0$.
  3. Las ecuaciones $x+y=uv$ y $xy=u-v$ definen $x$ y $v$ como funciones de $u$ y $y$, sean éstas $x=X(u,v)$ y $v=V(u,y)$. Demuestra que $\partial X/\partial u=(u+v)/(1+yu)$ si $1+yu\neq 0$ y halla las fórmulas de $\partial X/\partial y$, $\partial V /\partial u$, $\partial V /\partial y$.
  4. Sigue las ideas de los resultados de la entrada anterior para escribir una calca de ella pero ahora para $f:S\subseteq \mathbb{R}^{m} \times \mathbb{R}^{l}$, en donde la función que se busca tiene ahora dominio en $\mathbb{R}^{m}$ que pone a las variables del dominio $\mathbb{R}^l$ en términos de las de $\mathbb{R}^m$.
  5. Haz un esfuerzo extra, y medita nuevamente en el teorema de la función implícita tratando de escribir una demostración de como sería el asunto para $f$ con dominio en $\mathbb{R}^{m}\times \mathbb{R}^{l}\times \mathbb{R}^{k}$. ¿Se podrá hallar la función $h$, pero ahora con dominio en $\mathbb{R}^{l}$?

Entradas relacionadas

Cálculo Diferencial e Integral III: Teorema de la función implícita y demostración

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En esta parte del curso estamos abordando los resultados principales de campos vectoriales y su diferenciabilidad. Hemos hablado de cómo la derivada de una composición se calcula con regla de la cadena. También, enunciamos el teorema de la función inversa, lo demostramos, y vimos un ejemplo de cómo se usa. Ahora pasaremos a otro de los resultados fundamentales en el tema: el teorema de la función implícita. Vamos a motivarlo a partir del problema de resolver sistemas de ecuaciones no lineales. Luego, lo enunciaremos formalmente y lo demostraremos. La discusión y los ejemplos los dejaremos para la siguiente entrada.

Una motivación: resolver sistemas de ecuaciones no lineales

Con lo que repasamos sobre sistemas de ecuaciones lineales, y con lo que se ve en un curso de Álgebra Lineal I, se puede entender completamente cómo resolver sistemas de eccuaciones lineales. Recordemos un poco de esto. Tomemos el siguiente sistema de ecuaciones lineales en las variables $x_1,\ldots,x_n$:

\begin{align*}
\left\{ \begin{matrix}
a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n = b_1\\
a_{21}x_1+a_{22}x_2+\ldots+a_{2n}x_n = b_2\\
\vdots\\
a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n = b_m.\\
\end{matrix} \right.
\end{align*}

Para resolverlo, se podría utilizar el proceso de reducción gaussiana. Tras hacer esto, podíamos clasificar a las variables en libres (que podían valer lo que sea) y pivote (que dependían afinmente de las libres). Esto daba todas las soluciones. Si, por decir algo, las variables pivote son $x_1,x_2,\ldots,x_m$ y las libre son $x_{m+1},\ldots,x_n$, entonces podemos reescribir lo anterior de la siguiente manera: «podemos despejar a las primeras en función de las segundas», algo así como

\begin{align*}
x_1 &= T_1(x_{m+1},\ldots,x_n)\\
x_2 &= T_2(x_{m+1},\ldots,x_n)\\
\vdots \\
x_m&=T_m(x_{m+1},\ldots,x_n).
\end{align*}

Elegimos a $x_{m+1},\ldots,x_n$ como queramos. De ahí $x_1,\ldots,x_m$ quedan definidos afinmente con las $T_1,\ldots,T_m$. Y esto da todas las soluciones. Pero, ¿qué sucedería si tenemos un sistema de ecuaciones mucho más general?

Para plantear esto, imaginemos que ahora tenemos cualesquiera funciones $f_1,\ldots,f_m:\mathbb{R}^n\to \mathbb{R}$ y que queremos encontrar todas las soluciones $x_1,\ldots,x_n$ al siguiente sistema de ecuaciones:

\begin{equation}
\label{eq:sistemadificil}
\left\{ \begin{matrix}
f_{1}(x_{1},\dots ,x_{n})=0 \\
\vdots \\
f_{m}(x_{1},\dots ,x_{n})=0.
\end{matrix}\right.
\end{equation}

Esto es tan general como pudiéramos esperar. A la izquierda hay ceros, pero es porque si hubiera otras cosas, podríamos pasarlas a la izquierda para dejar ceros a la derecha.

Este sistema \eqref{eq:sistemadificil} parece imposible de resolver: no tenemos idea de quiénes son las funciones $f_1,\ldots, f_n$, no hay reducción gaussiana, no hay variables libres, etc. Pero imaginemos que el campo vectorial $(f_1,\ldots,f_m)$ es de clase $C^1$ alrededor de algún punto $\bar{v}_0=(x_{1}^{0},\dots,x_{n}^{0})$ en donde queremos despejar. Esto nos diría que cerca de $\bar{v}_0$ cada expresión $f_i(\bar{v})$ con $\bar{v}=(x_{1},\dots,x_{n})$ se parece muchísimo a su mejor aproximación lineal:

\[f_i(\bar{v}_0)+\triangledown f_i(\bar{v}_0)\bullet (\bar{v}-\bar{v}_0)\]

donde, tenemos:
\begin{align*}
f_i(\bar{v}_0)+\triangledown f_i(\bar{v}_0)\bullet (\bar{v}-\bar{v}_0)
&=f_i(\bar{v}_0)+\left(\frac{\partial f_i}{\partial x_1}(\bar{v}_0),\dots ,\frac{\partial f_i}{\partial x_n}(\bar{v}_0)\right)\bullet\left(x_1 -x_{1}^{0},\dots , x_n -x_{n}^{0}\right)\\ &=f_i(\bar{v}_0)+\sum_{j=1}^n \frac{\partial f_{i}}{\partial x_{j}}(\bar{v}_0)(x_j -x_{j}^{0})\\ &=f_i(\bar{v}_0)+\sum_{j=1}^n \frac{\partial f_{i}}{\partial x_{j}}(\bar{v}_0)x_j -\sum_{j=1}^n \frac{\partial f_{i}}{\partial x_{j}}(\bar{v}_0)x_{j}^{0}\\ &=\triangledown f_i(\bar{v}_0)\bullet (\bar{v})+f_i(\bar{v}_0) -\sum_{j=1}^n \frac{\partial f_{i}}{\partial x_{j}} (\bar{v}_0)x_{j}^{0}\\ &=\triangledown f_i(\bar{v}_0)\bullet (\bar{v}) + \bar{b}_i,
\end{align*}

donde $\bar{b}_i=f_i(\bar{v}_0)-\sum_{j=1}^n \frac{\partial f_{i}}{\partial x_{j}}(\bar{v}_0)x_{j}^0$. Pero entonces el sistema es prácticamente el mismo sistema que

\begin{equation}\label{eq:sistemafacil}\left \{\begin{matrix}\frac{\partial f_{1}}{\partial x_{1}}(\bar{v}_{0})x_{1}\hspace{0.1cm}+ & \dots & +\hspace{0.1cm}\frac{\partial f_{1}}{\partial x_{n}}(\bar{v}_{0})x_{n}\hspace{0.1cm}+\hspace{0.1cm}b_{1}\hspace{0.1cm}=\hspace{0.1cm}0 \\
\frac{\partial f_{2}}{\partial x_{1}}(\bar{v}_{0})x_{1}\hspace{0.1cm}+ & \dots & +\hspace{0.1cm}\frac{\partial f_{2}}{\partial x_{n}}(\bar{v}_{0})x_{n}\hspace{0.1cm}+\hspace{0.1cm}b_{2}\hspace{0.1cm}=\hspace{0.1cm}0 \\ \vdots & \vdots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{v}_{0})x_{1}\hspace{0.1cm}+ & \dots & +\hspace{0.1cm}\frac{\partial f_{m}}{\partial x_{n}}(\bar{v}_{0})x_{n}\hspace{0.1cm}+\hspace{0.1cm}b_{m}\hspace{0.1cm}=\hspace{0.1cm}0 \end{matrix}\right.\end{equation}

Esto se ve un poco complicado, pero cada $\frac{\partial f_{i}}{\partial x_{j}}(\bar{v}_{0})x_{j}$ es simplemente un número real. ¡Cerquita de $\bar{v}_0$ el sistema de ecuaciones \eqref{eq:sistemadificil} es prácticamente un sistema lineal! Sería entonces de esperarse que las soluciones el sistema \eqref{eq:sistemadificil} original sean muy cercanas a las del sistema lineal \eqref{eq:sistemafacil} que sale y de nuevo recuperamos los trucos usuales: reducción gaussiana, variables libres, variables pivote, etc.

Pensando en que en el sistema \eqref{eq:sistemafacil} las variables pivote son $x_1,\ldots, x_m$ y las libres son $x_{m+1},\ldots,x_n$, entonces podemos encontrar transformaciones afines $T_1,\ldots,T_m:\mathbb{R}^n\to \mathbb{R}$ tales que las soluiones de \eqref{eq:sistemafacil} consisten en elegir $x_{m+1},\ldots,x_n$ arbitrariamente, y tomar

\begin{align*}
x_1 &= T_1(x_{m+1},\ldots,x_n)\\
x_2 &= T_2(x_{m+1},\ldots,x_n)\\
\vdots \\
x_m&=T_m(x_{m+1},\ldots,x_n).
\end{align*}

Muy probablemente $(x_1,\ldots,x_n)$ no será una solución de \eqref{eq:sistemadificil}, pues son sistemas diferentes entre sí. Pero suena a que son tan tan cercanos, que con tantita maniobra podremos encontrar funciones $S_1,\ldots, S_m: \mathbb{R}^n\to \mathbb{R}$ tales que cualquier solución a \eqref{eq:sistemadificil} similarmente está dada por elegir $x_{m+1},\ldots, x_n$ arbitrariamente y tomar

\begin{align*}
x_1 &= S_1(x_{m+1},\ldots,x_n)\\
x_2 &= S_2(x_{m+1},\ldots,x_n)\\
\vdots \\
x_m&=S_m(x_{m+1},\ldots,x_n).
\end{align*}

Gracias a que pudimos poner a todos los $x_1,\ldots x_m$ en función de los $x_{m+1},\ldots,x_n$, hemos logrado encontrar todas las soluciones a \eqref{eq:sistemadificil} cerca de $\bar{v}_0$. El teorema de la función inversa nos ayuda a volver precisas muchas de las cosas discutidas en esta sección.

Enunciado del teorema de la función implícita

Pensemos que tenemos algunas restricciones dadas por ecuaciones como las del sistema \eqref{eq:sistemadificil}. Lo que el teorema de la función implícita nos dirá es que bajo suficiente regularidad y algunas condiciones de invertibilidad, en una vecindad de un punto $\bar{v}_{0}$ las incógnitas $x_{1},\dots ,x_{m}$ se pueden poner en función de las incógnitas $x_{m+1},\dots ,x_{n}$, es decir, que se puede despejar como lo mencionamos al final de la sección anterior. El enunciado es el siguiente.

Teorema (de la función implícita). Sea $f:S\subseteq\mathbb{R}^{m}\times \mathbb{R}^{l}\rightarrow \mathbb{R}^m$ un campo vectorial de clase $C^1$ en $S$ con funciones componentes $f_i: S\subseteq\mathbb{R}^{m}\times \mathbb{R}^{l}\rightarrow \mathbb{R}$, para $i=1,\ldots,m$.

Pensemos en el conjunto $A$ de soluciones $(y_1,\ldots,y_m,x_1,\ldots,x_l)$ del siguiente sistema de ecuaciones:

\begin{equation}
\label{eq:sistemaimplicita}
\left\{ \begin{matrix}
f_{1}(y_{1},\dots ,y_m,x_1,\ldots,x_l)=0 \\
\vdots \\
f_{m}(y_{1},\dots ,y_m,x_1,\ldots,x_l)=0.
\end{matrix}\right.
\end{equation}

Supongamos además que para el punto $$(\bar{y}_0,\bar{x}_0)=\left(y_{1}^{0},\dots ,y_{m}^{0},x_{1}^{0},\dots ,x_{l}^{0}\right)\in S\cup A$$ la matriz

\[ \begin{pmatrix} \frac{\partial f_{1}}{\partial y_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{i}}{\partial y_{m}}(\bar{y}_{0},\bar{x}_{0}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial y_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{m}}{\partial y_{m}}(\bar{y}_{0},\bar{x}_{0}) \end{pmatrix} \]

es invertible. Entonces existen abiertos $V\subset \mathbb{R}^{m}$ y $U\subset \mathbb{R}^l$ con $\bar{y}_0\in V$, $\bar{x}_0\in U$, para los cuales hay una única función $h:U\to V$ de clase $C^{1}$ en $V$, tal que $f(\bar{y},\bar{x})=\bar{0}$ si y sólo si $\bar{y}=h(\bar{x})$.

Sólo para aclarar algunas diferencias con lo discutido anteriormente, aquí ya estamos separando en lo que esperaremos que serán las variables libres $x_1,\ldots,x_m$ y las variables pivote $y_1,\ldots,y_l$. Estamos además estudiando el caso en el que tenemos tantas variables libres como ecuaciones, pues este caso es fácil de enunciar en términos de la invertibilidad de una matriz. El caso más general se trata con reducción gaussiana como platicamos en la sección anterior. La igualdad $\bar{y}=h(\bar{x})$ es lo que entendemos como «despejar» a los $y_i$’s en función de los $x_j$’s.

Demostración del teorema de la función implícita

Veamos la demostración del teorema.

Demostración. Definamos $F:S\subset \mathbb{R}^{m}\times \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}\times \mathbb{R}^{l}$ como $F(\bar{y},\bar{x})=(f(\bar{y},\bar{x}),\bar{x})$. Dado que $f$ es de clase $C^1$, se tendrá que $F$ también (explica esto como tarea moral).

Notemos que

\begin{align*}
F(\bar{y}_{0},\bar{x}_{0})&=(f(\bar{y}_{0},\bar{x}_{0}),\bar{x}_{0})=(\bar{0},\bar{x}_0).\end{align*}

Por otro lado, notemos que la matriz jacobiana de $F$ en $(\bar{y}_0,\bar{x}_0)$ es

$$\begin{bmatrix} \frac{\partial f_{1}}{\partial \bar{y}_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{1}}{\partial y_{m}}(\bar{y}_{0},\bar{x}_{0}) & \frac{\partial f_{1}}{\partial x_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{1}}{\partial x_{l}}(\bar{y}_{0},\bar{x}_{0}) \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial y_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{m}}{\partial y_{m}}(\bar{y}_{0},\bar{x}_{0}) & \frac{\partial f_{m}}{\partial x_{1}}(\bar{y}_{0},\bar{x}_{0}) & \dots & \frac{\partial f_{m}}{\partial y_{l}}(\bar{y}_{0},\bar{x}_{0}) \\ 0 & \dots & 0 & 1 & \dots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \dots & 0 & 0 & \dots & 1 \end{bmatrix}$$

esta matriz además es invertible (también tendrás que explicar ambas cosas de tarea moral).

La idea clave es que entonces podemos usar el teorema de la función inversa en $F$. Aplícandolo en este contexto, obtenemos que existe $\delta >0$ tal que $F$ es inyectiva en una bola $B_{\delta}(\bar{y}_{0},\bar{x}_{0})\subset S$. Nos dice también que $F(B_{\delta}(\bar{y}_0,\bar{x}_{0}))$ es un conjunto abierto, y que $F ^{-1}:F(B_{\delta}(\bar{y}_0,\bar{x}_{0}))\subset \mathbb{R}^{m}\times \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}\times \mathbb{R}^{l}$ es de clase $C^{1}$ en $F(B_{\delta}(\bar{y}_{0},\bar{x}_{0}))$. También dice algo de quién es la derivada explícitamente, pero eso no lo necesitaremos por ahora (de tarea moral tendrás que pensar qué nos dice esto).

Como $F$ manda $(\bar{y}_0,\bar{x}_0)$ a $(\bar{0},\bar{x}_0)$ y $F(B_{\delta}(\bar{y}_0,\bar{x}_{0}))$ es un abierto, entonces hay una bola abierta $W$ alrededor de $(\bar{0},\bar{x}_0)$ contenida en $F(B_{\delta}(\bar{y}_0,\bar{x}_{0}))$. El conjunto $U$ que propondremos será el abierto que se obtiene al intersectar $W$ con el espacio en donde la coordenada correspondiente a $f(\bar{y},\bar{x})$ es cero. En otras palabras, $U$ es un abierto y consiste de $\bar{x}$ para los cuales existe un $\bar{y}$ tal que $F(\bar{y},\bar{x})=(\bar{0},\bar{x})$ (es decir, $f(\bar{y},\bar{x})=\bar{0}$).

Tomemos ahora un $\bar{x}\in U$. Afirmamos que hay sólo un $\bar{y}$ tal que $(\bar{y},\bar{x})\in B_{\delta}(\bar{y}_{0},\bar{x}_{0})$ y $f(\bar{y},\bar{x})=\bar{0}$. Si hubiera $\bar{y}$ y $\bar{y}’$ que satisfacen eso, tendríamos

$$F(\bar{y},\bar{x})=(f(\bar{y},\bar{x}),\bar{x})=(\bar{0},\bar{x})=(f(\bar{y}’,\bar{x}),\bar{x})=F(\bar{y}’,\bar{x}),$$

que por la inyectividad de $F$ implica $\bar{y}=\bar{y}’$. De hecho, dicho único $\bar{y}$ está en función de $F^{-1}$, que es de clase $C^1$ de modo que el conjunto de los $\bar{y}$ asignados a los $\bar{x}$ en $U$ es un abierto $V$.

Así, podemos definir $h:U\to V$ de la siguiente manera: $h(\bar{x})=\bar{y}$, donde $\bar{y}$ es el único elemento para el cual $f(\bar{y},\bar{x})=\bar{0}$ y $(\bar{y},\bar{x})\in B_{\delta}(\bar{y}_{0},\bar{x}_{0})$. De la discusión desarrollada, $h$ está bien definida y cumple con las propiedades buscadas.

Por último probemos que $h$ es de clase $C^{1}$ en $U$. Como $F^{-1}$ esta definida y, además es de clase $C^{1}$ sobre el conjunto $F(B_{\delta}(\bar{x}_{0},\bar{y}_{0}))$, si escribimos que $F^{-1}=\left( (F^{-1})_{1},\dots ,(F^{-1})_{m} \right)$, bastaría con demostrar:

\[ h(\bar{x})=\left( (F^{-1})_{1}(\bar{0},\bar{x}),\dots , (F^{-1})_{m}(\bar{0},\bar{x})\right) \]

para cada $\bar{x}\in V$. Esto se hace como sigue:

\begin{align*} (h(\bar{x}),\bar{x})&=F^{-1}(F(h(\bar{x}),\bar{x}))\\ &=F^{-1}(\bar{0},\bar{x}) \\ &=\left( (F^{-1})_{1}(\bar{0},\bar{x}),\dots ,(F^{-1})_{m}(\bar{0},\bar{x}),(F^{-1})_{m+1}(\bar{0},\bar{x}),\dots ,(F^{-1})_{m+l}(\bar{0},\bar{x}) \right). \end{align*}

Así queda terminada de la demostración de este importante teorema.

$\square$

Algunas reflexiones finales

Si quisiéramos usar de manera práctica la demostración para encontrar la función implícita $h$, necesitaríamos calcular la inversa $F^{-1}$. Sin embargo, las técnicas que tenemos hasta ahora no nos permiten hacer eso tan fácilmente. La versión del teorema de la función inversa que tenemos nos dice que hay una inversa, pero no nos dice quién es. La mayoría de las veces dar esta inversa es muy difícil, por no decir imposible.

Aunque esto parezca algo negativo, de cualquier forma tenemos un resultado muy importante. En algunos casos, sí podremos dar la función inversa con relativa facilidad. Y en otros contextos, aunque no podamos dar la inversa explícitamente, sí tendremos una base teórica robusta para demostrar otros resultados. El teorema de la función implícita es una palanca importante para otros resultados que brindan mucha luz acerca del comportamiento de los campos vectoriales.

Mas adelante…

La demostración y el desarrollo teórico tanto del teorema de la función inversa, como el de la función implícita, son muy técnicos. Dejaremos los aspectos técnicos hasta aquí y en la siguiente entrada procesaremos mejor lo que quiere decir este teorema hablando de varios ejemplos, y también de sus consecuencias.

Tarea moral

  1. Considérese la función $T:\mathbb{R}^{3}\rightarrow \mathbb{R}^{2}$ dada por $T(x,y,z)=(x+z,y+x)$ aplica el teorema de la función implícita para obtener una función $h:\mathbb{R}\rightarrow \mathbb{R}^{2}$ tal que $(h(\bar{a}),\bar{a})$ es solución de la ecuación $T(x,y,z)=(0,0)$.
  2. Explica con detalle por qué la función $F$ de la demostración del teorema de la función implícita es de clase $C^1$.
  3. Verifica que en efecto $DF(\bar{y}_0,\bar{x}_0)$ es la expresión dada en la demostración del teorema. Además, justifica por qué es invertible.
  4. Justifica con detalle por qué los conjuntos $U$ y $V$ de la demostración en efecto son conjuntos abiertos.
  5. El teorema de la función inversa también nos dice quién es la derivada de la inversa. ¿Eso qué quiere decir en el contexto del teorema de la función implícita?

Entradas relacionadas

Cálculo Diferencial e Integral III: Derivadas parciales de segundo orden

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En las entradas anteriores definimos qué quiere decir que un campo escalar sea diferenciable. Así mismo, definimos las derivadas parciales y el gradiente. Ya usamos estas herramientas para hablar de dirección de cambio máximo y de puntos críticos. Además demostramos una versión del teorema del valor medio para este caso, lo que nos permitió poner un poco de orden a nuestra teoría: una función es diferenciable en un punto cuando existen sus parciales en ese punto y son continuas. Es momento de hablar de derivadas parciales de segundo orden. Cualquiera de las derivadas parciales es por sí misma un campo escalar, así que podemos preguntarnos si tiene o no sus propias derivadas parciales. Exploraremos esta idea.

Derivadas parciales de segundo orden

Las derivadas parciales de un campo escalar $f$ nos originan nuevos campos escalares. Supongamos que $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ es un campo escalar para el cual existe la $k$-ésima derivada parcial en un conjunto abierto $S’\subseteq S$. Entonces, obtenemos un nuevo campo escalar $\frac{\partial f}{\partial x_{k}}:S’\rightarrow \mathbb{R}$.

Este campo escalar puede o no tener $j$-ésima derivada parcial. Suponiendo que la tiene en algún $U\subseteq S’$ podríamos escribirla como

$$\frac{\partial\left(\frac{\partial f}{\partial x_k}\right)}{\partial x_j}.$$

Sin embargo, esta notación es engorrosa, y por ello optamos o bien por escribir la expresión como sigue

\[ \frac{\partial}{\partial x_{j}}\left( \frac{\partial f}{\partial x_{k}}\right)\]

o todavía más compacto, como

\[ \frac{\partial ^{2}f}{\partial x_{j}\partial x_{k}}.\]

A esto le llamamos una derivada parcial de segundo orden. Si $j=k$, introducimos la notación

\[ \frac{\partial ^{2}f }{\partial x_{k}^{2}}.\]

Las derivadas parciales de segundo orden vuelven a ser, una vez más, cada una de ellas un campo escalar. Esto permite seguir iterando la idea: podríamos hablar de derivadas parciales de segundo, tercero, cuarto, … , $k$-ésimo, … orden. Daremos una definición un poco más formal en una siguente entrada, pero por ahora trabajemos en entender a las derivadas parciales de segundo orden.

Un ejemplo de derivadas parciales de segundo orden

Ejemplo. Consideremos el campo escalar $f(x,y,z)=x^{2}yz$. Para este campo escalar tenemos que sus derivadas parciales con respecto a $x$, $y$ y $z$ son:

\begin{align*}
\frac{\partial f}{\partial x}(x,y,z)&=2xyz,\\
\frac{\partial f}{\partial y}(x,y,z)&=x^{2}z\\
\frac{\partial f}{\partial z}(x,y,z)&=x^{2}y.
\end{align*}

Cada una de estas expresiones es a su vez un campo escalar. Cada una de ellas es derivable con respecto a $x$ en todo $\mathbb{R}^3$. Al derivarlas con respecto a $x$ obtenemos:

\begin{align*}
\frac{\partial ^{2}f}{\partial x^{2}}(x,y,z)&=2yz,\\
\frac{\partial ^{2}f}{\partial x\partial y}(x,y,z)&=2xz,\\
\frac{\partial ^{2}f}{\partial x\partial z}(x,y,z)&=2xy.
\end{align*}

Por otro lado, las derivadas parciales de primer orden también podríamos haberlas derivado con respecto a $y$. En este caso, hubieramos obtenido.

\begin{align*}
\frac{\partial ^{2}f}{\partial y \partial x}(x,y,z)&=2xz,\\
\frac{\partial ^{2}f}{\partial y ^2}(x,y,z)&=0,\\
\frac{\partial ^{2}f}{\partial y\partial z}(x,y,z)&=x^2.
\end{align*}

También podríamos derivar a las derivadas parciales de primer orden con respecto a $z$ para obtener las tres derivadas de orden dos faltantes. En total tenemos tres derivadas parciales de primer orden y nueve derivadas parciales de segundo orden.

$\triangle$

Igualdad de las derivadas parciales de segundo orden mixtas

En numerosos campos escalares de interés tenemos una propiedad muy peculiar: que los operadores «obtener la derivada parcial con respecto a $x$» y «obtener la derivada parcial con respecto a $y$» conmutan. Es decir, varias veces podemos intercambiar el orden de derivación de las parciales y obtener el mismo resultado. En el ejemplo anterior quizás hayas notado que

\[ \frac{\partial ^{2}f}{\partial y\partial x}=2xz=\frac{\partial ^{2}f}{\partial x\partial y}.\]

Esto no siempre pasa, pero hay criterios de suficiencia sencillos de verificar. Por ejemplo, basta que las parciales mixtas existan y sean continuas para que sean iguales. El siguiente teorema formaliza el resultado.

Teorema. Sea $f:S\subseteq \mathbb{R}^{2}\rightarrow \mathbb{R}$ un campo escalar tal que las derivadas parciales $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial^{2} f}{\partial y\partial x}$, $\frac{\partial ^{2}f}{\partial x\partial y}$ existen en un conjunto abierto $U$. Si $(a,b)\in U$ es tal que $\frac{\partial^{2} f}{\partial y\partial x}$, $\frac{\partial ^{2}f}{\partial x\partial y}$ son continuas en $(a,b)$, entonces dichas derivadas mixtas de segundo orden son iguales en $(a,b)$.

Demostración. Sean $h,k\neq 0$ suficientemente chicos para que los puntos en el plano $(a,b)$, $(a,b+k)$, $(a+h,b)$, y $(a+h,b+k)$ estén en $U$.

Definamos la función $\Gamma (x)=f(x,b+k)-f(x,b)$ para $x\in [a,a+h]$ y definamos

\begin{equation} \Delta (h,k)=\Gamma (a+h)-\Gamma (a).\end{equation}

Notemos que $\Gamma$ es una función de $\mathbb{R}$ en $\mathbb{R}$ cuya derivada es $$\Gamma'(x)=\frac{\partial f}{\partial x}(x,b+k)-\frac{\partial f}{\partial x}(x,b).$$ Así, se le puede aplicar el teorema del valor medio con extremos en $a$ y $a+h$ para concluir que existe $\xi _{1}\in [a,a+h]$ que nos permite escribir $\Delta(h,k)$ de la siguiente manera:

\begin{align*}
\Delta(h,k)&=\Gamma (a+h)-\Gamma (a)\\
&= h\Gamma'(\xi _{1})\\
&=h\left[ \frac{\partial f}{\partial x}(\xi _{1},b+k)-\frac{\partial f}{\partial x}(\xi _{1},b) \right]
\end{align*}

Ahora podemos aplicar el teorema del valor medio en la función $y\mapsto \frac{\partial f}{\partial x} (\xi _{1},y)$ con extremos $b$ y $b+k$. Esto nos permite continuar la cadena de igualdades anterior mediante un $\eta _{1}\in [b,b+k]$ que cumple

\begin{equation}\label{eq:primerdelta} \Delta (h,k)=hk\frac{\partial ^{2}f}{\partial y\partial x}(\xi _{1},\eta _{1}).\end{equation}

Como $(\xi _{1},\eta _{1})\in [a,a+h]\times[b,b+k]$, se tiene que $(\xi _{1},\eta _{1})\to (a,b)$ conforme $(h,k)\to \bar{0}$.

Ahora consideremos análogamente a la función $\varLambda (y)=f(a+h,y)-f(a,y)$. Mediante un procedimiento similar al que acabamos de hacer, pero aplicado a $\varLambda$ en vez de a $\Gamma$, se tiene otra forma de expresar a $\Delta(h,k)$:

\begin{equation}\label{eq:segundodelta}\Delta(h,k)=hk\frac{\partial ^{2} f}{\partial x\partial y}(\xi _{2},\eta _{2}),\end{equation} donde $(\xi _{2},\eta _{2})\in [a,a+h]\times[b,b+k]$. Nuevamente, $(\xi _{2},\eta _{2})\to (a,b)$ conforme $(h,k)\to (0,0)$.

Igualando las expresiones en \eqref{eq:primerdelta} y \eqref{eq:segundodelta}, tenemos lo siguiente:

\[ \frac{\partial f}{\partial y\partial x}(\xi _{1},\eta _{1})=\frac{\partial f}{\partial x\partial y}(\xi _{2},\eta _{2}).\]

El resultado se sigue de hacer tender $(h,k)\to (0,0)$, ya que dado que las derivadas parciales les estamos pidiendo que sean continuas, tenemos que:

\begin{align*}
\frac{\partial ^{2} f}{\partial y\partial x}(a,b)&=\lim\limits_{(h,k)\to (0,0)}\frac{\partial ^{2} f}{\partial y\partial x}(\xi _{1},\eta _{1})\\
&=\lim\limits_{(h,k)\to (0,0)}\frac{\partial ^{2}f}{\partial x\partial y}(\xi _{2},\eta _{2})\\
&=\frac{\partial ^{2}f}{\partial x\partial y}(a,b).
\end{align*}

Así concluimos nuestro resultado.

$\square$

Más adelante…

En esta entrada hablamos de las derivadas parciales de segundo orden y vimos que bajo condiciones razonables podemos elegir las variables de derivación en el orden que queramos. Estas ideas son más generales, y a continuación nos llevarán a definir las derivadas parciales de cualquier orden $k$. Después, usaremos estas derivadas parciales para generalizar otro de los teoremas de cálculo unidimensional: el teorema de Taylor.

Tarea moral

  1. Para las siguientes funciones calcula $\frac{\partial ^{2}f}{\partial x^{2}}$:
    • $f(x,y)=x^{2}+y^{2}cos(xy)$
    • $f(x,y)=e^{x}cos(y)$
    • $f(x,y,z)=\textup{log}(x^{2}+2y^{2}-3z^{2})$
  2. En el teorema que afirma que las derivadas parciales mixtas son iguales usamos cuatro veces el teorema del valor medio (¿cuáles 4 son?). Asegúrate de que en verdad lo podamos usar.
  3. Calcula $\frac{\partial ^{2}f}{\partial y^{2}}$, y $\frac{\partial ^{2}f}{\partial x\partial y}$ para las funciones del punto 1. Explica por qué no es necesario calcular de manera separada $\frac{\partial ^{2}f}{\partial y\partial x}$
  4. Investiga de un ejemplo en el que las derivadas parciales $\frac{\partial ^{2}f}{\partial x\partial y}$ y $\frac{\partial ^{2}f}{\partial y\partial x}$ no sean iguales. Realiza las cuentas para verificar que en efecto tienen valores distintos en algún punto.
  5. El teorema que enunciamos está muy limitado. Sólo nos habla de campos escalares de $\mathbb{R}^2$ en $\mathbb{R}$. Sin embargo, debería también funcionar si $f:\mathbb{R}^n\to \mathbb{R}$. Enuncia y demuestra un resultado similar que te permita garantizar que $$\frac{\partial^{2} f}{\partial x_i\partial x_j}=\frac{\partial ^{2}f}{\partial x_j\partial x_i}.$$

Entradas relacionadas

Cálculo Diferencial e Integral III: Teorema del valor medio para campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Ya hemos definido qué es el gradiente $\nabla f$ de un campo escalar $f$. Hemos visto cómo está relacionado con las derivadas direccionales. Así mismo, mostramos que conocer este gradiente nos permite dar información sobre los máximos y mínimos del campo escalar. En esta entrada mostraremos una propiedad más del gradiente: que nos ayuda a dar una generalización del teorema del valor medio de Cálculo I, pero para campos escalares. Este será un resultado fundamental para demostrar otras propiedades de los campos escalares. Como ejemplo, también damos en esta entrada un criterio suficiente para que un campo escalar sea diferenciable.

Teorema del valor medio para funciones de $\mathbb{R}$ en $\mathbb{R}$

Para facilitar la lectura de este material, recordemos lo que nos dice el teorema del valor medio sencillo, es decir, el de $\mathbb{R}$ en $\mathbb{R}$.

Teorema. Sean $a<b$ reales. Sea $f:[a,b]\to\mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe algún punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

Una vez que uno interpreta el teorema gráficamente, se vuelve muy intuitivo. Considera la siguiente figura.

Intuición geométrica del teorema del valor medio

El término $$\frac{f(b)-f(a)}{b-a}$$ es la pendiente del segmento que une los puntos $(a,f(a))$ y $(b,f(b))$ El término $f'(c)$ va marcando la pendiente de la recta tangente a $f$ en cada punto $c$. En términos geométricos, lo que nos dice este teorema es que para algún valor de $c$, la pendiente de la recta tangente en $c$ es la pendiente del segmento entre los extremos.

Lo que haremos a continuación es dar una generalización apropiada para funciones de $\mathbb{R}^n$ a $\mathbb{R}$.

Teorema del valor medio para funciones de $\mathbb{R}^n$ en $\mathbb{R}$

Para generalizar el teorema del valor medio a funciones de $\mathbb{R}^n$ a $\mathbb{R}$, necesitaremos cambiar un poco las hipótesis. El segmento $[a,b]$ que usábamos ahora será un segmento (multidimensional) que conecte a dos vectores $\bar{x}$ y $\bar{y}$ en $\mathbb{R}^n$. La diferenciabilidad la pediremos en todo un abierto que contenga al segmento. El enunciado apropiado se encuentra a continuación.

Teorema (del valor medio para campos escalares). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar diferenciable. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

En este caso no podemos «pasar dividiendo $\bar{y}-\bar{x}$» pues no tiene sentido dividir entre vectores. Pero en el caso $n=1$ sí se puede, y justo obtenemos de vuelta el teorema del valor medio de $\mathbb{R}$ en $\mathbb{R}$. Uno podría pensar que entonces esta es una manera alternativa de demostrar el teorema para funciones de $\mathbb{R}$ en $\mathbb{R}$. Sin embargo, como veremos a continuación, la demostración de la versión para campos escalares usa la versión para funciones reales.

Demostración. Consideremos la función $\gamma:[0,1] \to \mathbb{R}^{n}$ dada $\gamma (t)=(1-t)\bar{x}+t\bar{y}$. Notemos que $\gamma$ es diferenciable, con $\gamma’ (t)=\bar{y}-\bar{x}$. Además, por hipótesis $f$ es diferenciable en $S$. Así, $f\circ \gamma:[0,1]\to \mathbb{R}$ también es diferenciable, y por regla de la cadena

\begin{align*}
(f\circ \gamma)'(t)&=\nabla f(\gamma(t))\cdot \gamma'(t)\\
&=\nabla f(\gamma(t))\cdot (\bar{y}-\bar{x}).
\end{align*}

¡Pero $f\circ \gamma$ ya es una función de $\mathbb{R}$ en $\mathbb{R}$! Así, podemos aplicarle el teorema del valor medio real (verifica las hipótesis como tarea moral). Al hacer esto, obtenemos que existe una $c\in (0,1)$ tal que
\begin{align*}
(f\circ \gamma)'(c) &= \frac{(f\circ \gamma)(1)-(f\circ \gamma)(0)}{1-0}\\
&=f(\bar{y})-f(\bar{x}).
\end{align*}

Usando la fórmula que obtuvimos por regla de la cadena para $(f\circ \gamma)’$ y la definición de $\gamma$ obtenemos que

$$ \nabla f((1-c)\bar{x}+c\bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}),$$

tal y como buscábamos.

$\square$

En el teorema anterior estamos pidiendo que $f$ sea diferenciable. Sin embargo, basta con que exista la derivada de la composición en el segmento que nos interesa y el resultado también se sigue. Es decir, tenemos la siguiente versión con una hipótesis más débil. La enunciamos pues la usaremos en la siguiente sección.

Teorema (del valor medio para campos escalares, hipótesis debilitada). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$ y tales que para toda $c\in[0,1]$ se cumple que la derivada (real) de $f((1-c)\bar{x}+c\bar{y}))$ existe. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

La demostración es exactamente la misma.

Aplicación del teorema del valor medio

Como primera aplicación del teorema del valor medio para campos escalares mostraremos un criterio de diferenciabilidad muy útil, al que llamaremos el teorema de diferenciabilidad y derivadas parciales.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Supongamos que para cierto punto $\bar{a}\in S$ y cierta vecindad $B_r(\bar{a})\subset S$ existen las derivadas parciales $\frac{\partial f}{\partial x_{1}},\dots ,\frac{\partial f}{\partial x_{n}}$ y son continuas en $\bar{a}$. Entonces $f$ es diferenciable en $\bar{a}$.

Demostración. Elijamos un vector $\bar{u}=u_1\hat{e}_1+\dots +u_n\hat{e}_n$ de norma $1$ y tomemos $\bar{v}=\lambda \bar{u}$ con $\lambda$ suficientemente chico como para que $\bar{a}+\bar{v}$ esté en $B_{r}(\bar{a})$. Definamos los siguientes vectores:

\begin{align*}
\bar{v}_0&=\bar{0}\\
\bar{v}_1&=u_1\hat{e}_1\\
\bar{v}_2&=u_1\hat{e}_1+u_2\hat{e}_2\\
&\vdots\\
\bar{v}_n&=u_1\hat{e}_1+u_2\hat{e}_2+\ldots+u_n\hat{e}_n=\bar{u}.
\end{align*}

Con ellos creamos la siguiente suma telescópica para expresar a $f(\bar{a}+\bar{v})-f(\bar{a})$

\begin{align}
f(\bar{a}+\bar{v})-f(\bar{a})&=f(\bar{a}+\lambda \bar{u})-f(\bar{a}) \nonumber\\
&=\sum_{k=1}^{n}[f(\bar{a}+\lambda \bar{v}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1})] \label{eq:telescopica}
\end{align}

Notemos que el $k$-ésimo término de esta suma puede ser escrito como $$f(\bar{a}+\lambda \bar{v}_{k-1}+\lambda u_{k}\hat{e}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1}).$$ Para simplificar, definimos $\bar{b}_{k}=\bar{a}+\lambda \bar{v}_{k-1}$ y reescribiendo el $k$-ésimo término tenemos $$f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k}).$$

Aplicando el teorema del valor medio con hipótesis debilidada para campos escalares a los puntos $\bar{b}_{k}$ y $\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}$ (verifica las hipótesis), tenemos que para cada $k$ existe $\xi_k \in (0,1)$ tal que

\begin{align*}
f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})&=\triangledown f((1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}))\cdot (\lambda u_{k}\hat{e}_{k})\\
&=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}),
\end{align*}

en donde hemos definido $\bar{c}_k:=(1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})$, que es un punto en el segmento que une a $\bar{b}_k$ con $\bar{b}_k+\lambda u_k\hat{e}_k$.

Tenemos pues que podemos escribir al $k$-ésimo término como:

$$f(\hat{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}).$$

Notemos además que si $\lambda \to 0$, entonces $\bar{b}_{k}\to \bar{a}$, $\bar{c}_{k} \to a$ y $\bar{v}\to \bar{0}$.

Escribimos entonces la ecuación \eqref{eq:telescopica} como:

\begin{equation}
\label{eq:resumen}
f(\bar{a}+\bar{v})-f(\bar{a})=\lambda \sum_{k=1}^{n}u_k\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})
\end{equation}

En unos momentos usaremos esta expresión. Antes de ello, estudiemos otro de los términos involucrados en la diferenciabilidad. Tenemos que:

\begin{align}
\triangledown f(\bar{a})\cdot \bar{v}&=\triangledown f(\bar{a})\cdot \lambda u \nonumber\\
&=\lambda \triangledown f(\bar{a})\cdot u \nonumber\\
&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a}) \label{eq:ppunto}.
\end{align}

Empecemos entonces a combinar lo visto hasta ahora para entender los términos en la definición de diferenciabilidad. Tenemos juntando \eqref{eq:resumen} y \eqref{eq:ppunto} que

\begin{align*}
f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot v&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a})\\&=\lambda \sum_{k=1}^{n}u_{k}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right].
\end{align*}

Como mencionamos, si $\lambda \to 0$ entonces $\bar{v}\to \bar{0}$. Además, $||\bar{v}||=|\lambda|$. Así:

\[ \lim\limits_{\bar{v}\to \bar{0}} \frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=\lim\limits_{\lambda \to 0} \left|\sum_{k=1}^{n}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|.\]

Veamos qué más sucede cuando $\lambda \to 0$. Ya notamos que $\bar{c}_k\to \bar{a}$, así que usando la continuidad de las derivadas parciales tenemos:

\[ \lim\limits_{\lambda \to 0}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\lim\limits_{\bar{c}_{k}\to \bar{a}}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\frac{\partial f}{\partial x_{k}}(\bar{a}).\]

Aplicando desigualdad del trángulo en la suma, el límite buscado es menor o igual a

\[ \lim\limits_{\lambda \to 0}\sum_{k=1}^{n}\left|\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|=0.\]

Y aquí cada sumando se va a $0$. La conclusión final es que

\[ \lim\limits_{\bar{v}\to \bar{0}}\frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=0,\]

de modo que $f$ es diferenciable en $\bar{a}$.

$\square$

El regreso del teorema anterior no se vale

El teorema de diferenciabilidad nos dice que si las derivadas parciales existen y son continuas, entonces la función es diferenciable. Sin embargo, el regreso de este teorema no se vale, en el sentido de que existen funciones diferenciables cuyas derivadas parciales no son continuas. En otras palabras, si las derivadas parciales no son continuas, no podemos descartar la diferenciablidad de una función.

A continuación esbozamos un ejemplo que deberás completar como tarea moral.

Ejemplo. Consideremos la función

$$f(x,y)=\begin{cases} (x^2+y^2)\sin\left(\frac{1}{\sqrt{x^2+y^2}}\right) &\text{si $(x,y)\neq (0,0)$}\\ 0 & \text{si $(x,y)=(0,0)$}\end{cases}$$

Se puede demostrar que $f$ es diferenciable en $(0,0)$. De manera intuitiva, la función queda entre las funciones $(x,y)\to x^2+y^2$ y $(x,y)\to -x^2-y^2$. Se puede usar un argumento de acotamiento para mostrar que el plano tangente coincide entonces con el de estas funciones en $(0,0)$ que es el plano $z=0$. Verifica los detalles de tarea moral.

Así mismo, se puede ver que las derivadas parciales en $(0,0)$ existen y que de hecho se satisface $$\frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 0.$$

Finalmente, se puede ver que las derivadas parciales no convergen a $0$. Fuera del $(0,0)$, tenemos por reglas de derivación que

\begin{align*} \frac{\partial f}{\partial x}(x,y) &= 2 x \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{x \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}\\ \frac{\partial f}{\partial y}(x,y) &= 2 y \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{y \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}. \end{align*}

Una manear de ver que estas no son contínuas es aproximándonos por un eje. Por ejemplo, puedes verificar que sobre el eje $x$, conforme $x\to 0$, tenemos que la primera parcial oscila entre $-1$ y $1$.

$\triangle$

Más adelante…

Hemos enunciado y demostrado una versión del teorema del valor medio para campos escalaras. Gracias a ella hemos podido mostrar que si un campo escalar tiene derivadas parciales continuas, entonces es diferenciable. Las aplicaciones del teorema del valor medio para campos escalares van más allá. En la siguiente entrada hablaremos de las derivadas parciales de orden superior. El teorema del valor medio para campos escalares nos permitirá demostrar que bajo ciertas condiciones, en cierto sentido estas derivadas parciales «conmutan».

Tarea moral

  1. ¿Qué dice el teorema del valor medio para campos escalares para la función $f(x,y)=\sin(x)\cos(y)$ tomando como extremos los puntos $\left(0,\frac{\pi}{2}\right)$ y $\left(\frac{\pi}{2},0\right)$? Verifica si puedes aplicar las hipótesis.
  2. En la demostración del teorema del valor medio que dimos, verifica que la función $f\circ \gamma$ dada en efecto satisface las hipótesis del teorema del valor medio real.
  3. Supongamos que $f:\mathbb{R}^n\to \mathbb{R}$ es diferenciable en un abierto $S$ que contiene al segmento cuyos extremos son ciertos vectores $\bar{x}$ y $\bar{y}$ de $\mathbb{R}^n$. Supongamos que $f(\bar{x})=f(\bar{y})$. ¿Será cierto siempre que $\nabla f$ se anula en algún vector del segmento que une $x$ con $y$? Ten cuidado, pues hay un producto escalar involucrado. En caso de que no siempre sea cierto, ¿Qué es lo que sí puedes garantizar?
  4. En la demostración del teorema de diferenciabilidad, verifica que se pueden usar las hipótesis del teorema del valor medio para campos escalares con hipótesis debilitada. Necesitarás ver que la derivada real que tiene que existir es justo una parcial de las que suponemos que existen, completa los detalles. Luego, verifica que en efecto la conclusión que obtuvimos es justo la que se obtiene. Observa además que no podemos usar el teorema del valor medio para campos diferenciables con la hipótesis usual pues necesitaríamos saber que $f$ es diferenciable, lo cual es justo lo que queremos mostrar.
  5. Completa el contraejemplo al regreso del teorema de diferenciabilidad. Entre otras cosas, tienes que hacer lo siguiente:
    • Verificar que en efecto la función es diferenciable en $(0,0)$. Puedes proceder por definición o acotando como se sugiere.
    • Revisar que las parciales en $(0,0)$ en efecto existen y coinciden con lo que sabemos a partir de que el plano tangente en el origen es $(0,0)$.
    • Obtener paso a paso la fórmula que dimos para las parciales, usando lo que sabes de regla de la cadena, derivadas en $\mathbb{R}$, etc.
    • Verificar que ninguna de las dos derivadas parciales es continua, completando el argumento de que al acercarnos por los ejes tenemos oscilaciones.

Entradas relacionadas