(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
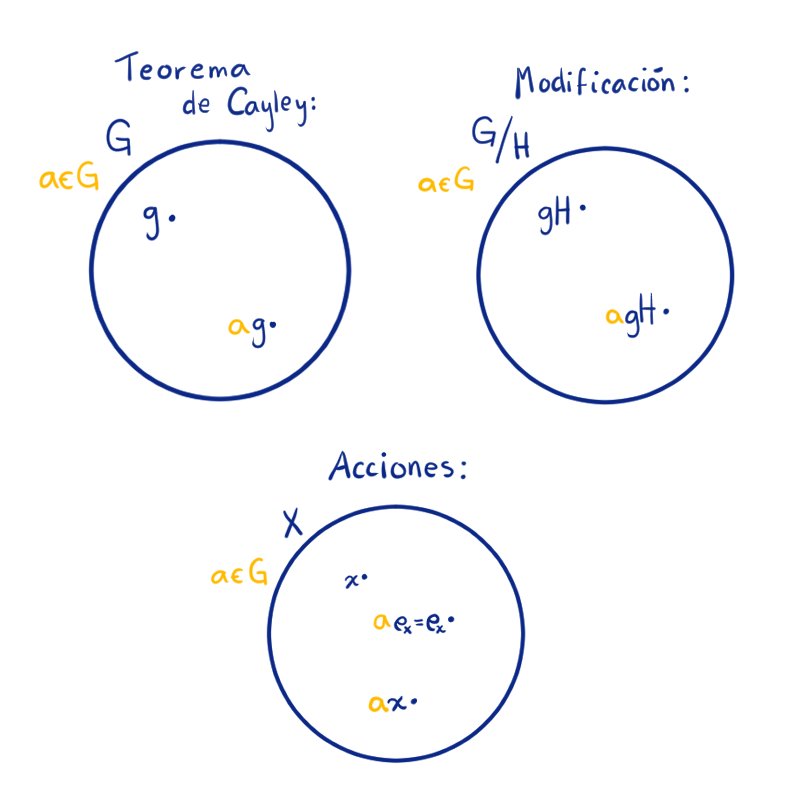
Antes de comenzar con el tema que nos compete, repasemos lo que hemos visto del Teorema de Cayley y su modificación de la entrada anterior. Primero, en el Teorema de Cayley, comenzamos tomando un grupo $G$, un $a$ en el grupo y actuamos con ese $a$ sobre el grupo, es decir multiplicamos los elementos. En resumen, nos permite mover los elementos del mismo grupo.
Con la modificación avanzamos en la abstracción. En el teorema nos tomamos el conjunto de clases laterales y ahora, $G$ actúa sobre las clases laterales. Detente un minuto para pensar, si cada vez somos más generales ¿cuál es el siguiente paso? ¿sobre quién queremos que actúe $G$ ahora?
La respuesta es: sobre un conjunto cualquiera $X$. Ahora queremos pensar que usamos los elementos de $G$ para mover elementos de $X$. Para eso necesitamos una especie de producto, además de algunos matices. Por ejemplo, para un $x\in X$ cuando $a = e$, el elemento $a\cdot x = x$ se quede fijo y que si se multiplica por $a$ y luego por $b$, que sea lo mismo que multiplicar por $ab$, es decir $a\cdot(b\cdot x) = ab\cdot x$. Si se cumplen estas dos condiciones diremos que $a$ es una acción de $G$ en el conjunto $X$.
Luces, cámara, ¡acción!
Como verás, hemos estado usando el verbo actuar para referirnos a esta transformación que sucede al operar un $a\in G$ y otro elemento, sea del mismo $G$ o de las clases laterales. Aunque no hayamos definido formalmente qué es una acción, la realidad es que ya usar actuar da una idea de lo que estamos queriendo decir. Estamos usando un elemento de un grupo para transformar un elemento de otro. A continuación definiremos formalmente a una acción.
Definición. Sea $G$ un grupo, $X$ un conjunto. Si existe una función:
\begin{align*}
G \times X &\to X\\
(a,x) &\mapsto a\cdot x
\end{align*}
para todos $a\in G, x\in X$, tal que:
- $e \cdot x = x$ para toda $x\in X$.
- $a \cdot (b\cdot x) = (ab)\cdot x $ para todas $a,b\in G, x\in X$,
decimos que la función es una acción de $G$ en $X$, y que $G$ actúa en $X$ o que $X$ es un $G$-conjunto.
Ejemplos.
Veamos algunos ejemplos nuevos y retomemos algunos otros, para verificar que esto es una generalización para lo que se hizo en el Teorema de Cayley y en su modificación.
Ejemplo 1. Sean $G$ grupo, $X=G$ definimos $a\cdot x = ax$ para todas $a\in G, x\in X$. Es decir, definimos una acción sobre sí mismo. Probemos las dos condiciones:
\begin{align*}
&e\cdot x = ex = x &\forall x\in X\\
&a\cdot(b\cdot x) = a\cdot(bx) = a(bx) = (ab)x = (ab)\cdot x &\forall a,b\in G,\; x\in X.
\end{align*}
Así, todo grupo $G$ actúa en sí mismo mediante su operación binaria. Como vimos en la entrada del Teorema de Cayley.
Ejemplo 2. Sean $G$ grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH)= agH$ para toda $a,g\in G$. Ahora, probemos las dos condiciones de una acción:
\begin{align*}
&e\cdot(gH) = egH = gH &\forall g\in G
\end{align*}
\begin{align*}
a\cdot(b\cdot(gH)) &= a\cdot(bgH) = a(bg)H = (ab)gH \\
&= ab\cdot (gH) &\forall a,b,g\in G
\end{align*}
Así se tiene una acción de $G$ en las clases laterales de $H$ en $G$. Este ejemplo lo vimos en la entrada de la modificación al Teorema de Cayley.
Por último, podemos ver un ejemplo nuevo.
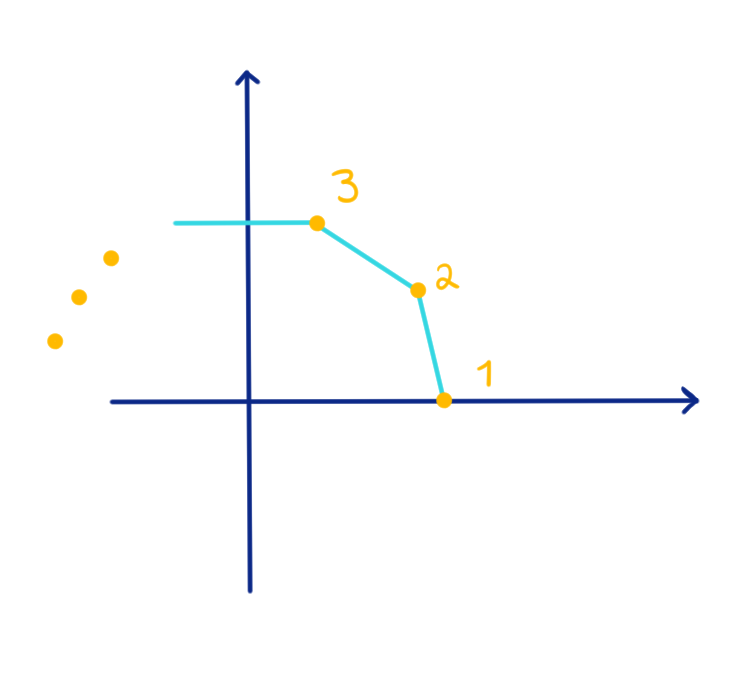
Ejemplo 3. Sea $G = D_{2n}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices de polígono regular de $n$ lados.
Dados $g\in G, i\in X$ definimos $g\cdot i = j$ si $g$ manda el vértice $i$ en el vértice $j$. Recordemos que los elementos de un grupo diédrico son las simetrías del polígono regular de $n$ lados, es decir, son transformaciones lineales del plano que mandan del polígono en sí mismo. En particular, los vértices van a dar a vértices bajo estas transformaciones.
Entonces, como son transformaciones del plano nuestra acción quedaría como una evaluación $g \cdot i = g(i)$. Así, para todos $i\in X, g,h\in G$,
\begin{align*}
\text{id}\cdot i &= \text{id}(i) = i \\
g\cdot (h\cdot i )& = g\cdot (h(i)) = g(h(i)) = (gh) (i) = (gh) \cdot i.
\end{align*}
Así, $D_{2n}$ actúa en el conjunto de vértices.
Recordemos que al escribir $(gh)\cdot i$, la operación que ocurre entre $g$ y $h$ es la composición. En este momento se omitió el símbolo $\circ$ para evitar confusiones con el símbolo $\cdot$ de acción.
Otra definición de Acción
Anteriormente hemos visto la noción de que los elementos de un grupo dan lugar a permutaciones. Usaremos esta idea para dar una definición de acción equivalente a la definición que acabamos de dar.
Teorema. Sean $G$ un grupo, $X$ un conjunto. Toda acción de $G$ en $X$ induce un homomorfismo de $G$ en $S_X$ y viceversa.
Demostración.
Sean $G$ un grupo y $X$ un conjunto.
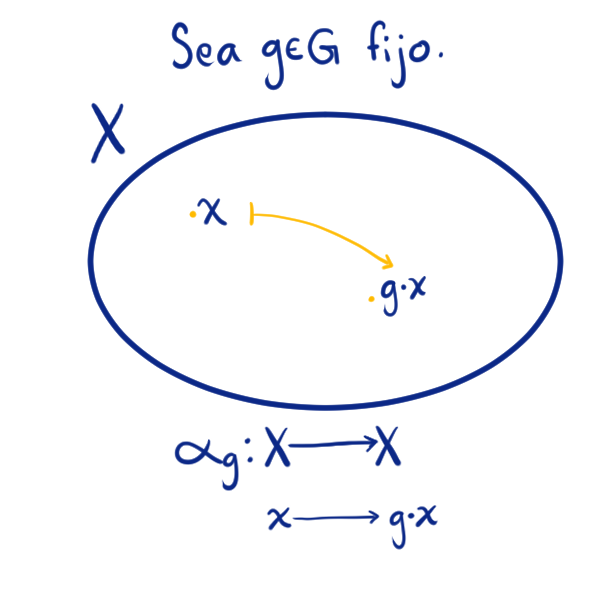
Supongamos que $G\times X \to X$ es una acción de $G$ en $X$ tal que $(g,x)\mapsto g\cdot gx$. Para cada $g\in G$ definimos $\alpha_g : X\to X$ dada por $\alpha_g(x) = g\cdot x$ para toda $x\in X$.
Analicemos las funciones $\alpha_g$, veamos que son biyectivas:
\begin{align*}
\alpha_g\circ\alpha_{g^{-1}}(x) & = \alpha_g(\alpha_{g^{-1}}) = \alpha_g(g^{-1}\cdot x) = g\cdot(g^{-1}\cdot x)\\
&= (gg^{-1})\cdot x &\text{Condición 2 de acción}\\
&= e\cdot x = x &\text{Condición 1 de acción}.
\end{align*}
Entonces $\alpha_g\circ\alpha_{g^{-1}} = \text{id}_X$.
Anáogamente $\alpha_{g^{-1}}\circ \alpha_g = \text{id}_X$, entonces $\alpha_g$ es biyectiva, es decir $\alpha_g \in S_X$.
Definimos $\psi: G \to S_X$ con $\psi (g) = \alpha_g$ para toda $g\in G$.
Veamos que $\psi$ es un homomorfismo. Tomemos $g,h\in G$,
\begin{align*}
\psi(gh)(x) &= \alpha_{gh}(x) = (gh)\cdot x = g\cdot(h\cdot x) = \alpha_g(\alpha_h(x)) & \text{Condición 2}\\
&= \alpha_g \circ \alpha_g(h) = \psi(g) \psi(h)(x) &\forall x\in X.
\end{align*}
Entonces $\psi(gh) = \psi(g)\psi(h)$ para todos $g,h\in G$.
Por lo tanto $\psi$ es un homomorfismo.
Ahora de regreso. Supongamos ahora que se tiene un homomorfismo $\psi: G\to S_X$. Entonces, para cada $g\in G, \psi(g) \in S_x$.
Definimos la función $G\times X \to X$ donde $(g,x)\mapsto g\cdot x$. Entonces $g\cdot x = \psi(g)(x)$ para toda $g\in G, x\in X$. Además, $\psi(g)(x) \in X$.
Ahora veamos que esta función es una acción. La primera condición para ser acción se cumple de la siguiente manera:
Como $\psi$ es un homomorfismo, $\psi(e) = \text{id}_X$. Así,
\begin{align*}
e\cdot x& = \psi(e)(x) = \text{id}_X(x) = x &\forall x\in X
\end{align*}
Probemos la segunda condición de acción:
\begin{align*}
g\cdot (h\cdot x) &= \psi(g) (\psi(h)(x)) = \psi(g)\circ \psi(h)(x) \\
&= \psi(gh)(x) = (gh) \cdot x & \psi\text{ es un homomorfismo}.
\end{align*}
Para todas $g,h\in G, x\in X$. Así $G$ actúa en $X$.
$\blacksquare$
Una relación de equivalencia
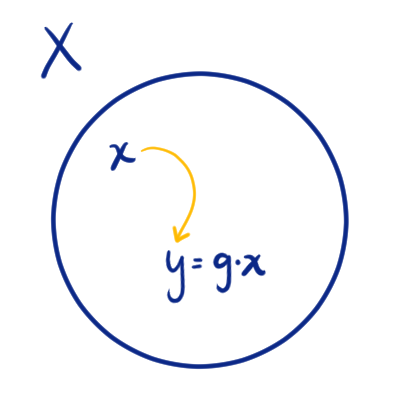
Si tenemos un grupo $G$ actuando sobre un conjunto $X$, entonces podemos considerar $g\in G$ y $x,y\in X$. Con los dos elementos $x,y$ de $X$, podemos preguntarnos ¿es posible llegar de $x$ a $y$ usando a $g$?, algo como $y = g\cdot x$. En realidad esto no es siempre posible, entonces podemos crear una relación de $x$ con $y$ si existe tal $g\in G$. Esto lo veremos en el siguiente resultado.
Lema. Sean $G$ un grupo, $X$ un $G$-conjunto. Para todo $x,y\in X$, la relación en $X$: $x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$ es una relación de equivalencia.
Demostración.
Sean $G$ un grupo, $X$ un $G$-conjunto. Definimos la relación en $X$ donde para todo $x,y\in X$.
\begin{align*}
x\sim y \Leftrightarrow g\cdot x = y \text{ para algún }g\in G.
\end{align*}
Primero, por la condición 1 de acción, $e\cdot x = x$ para toda $x\in X$ con $e\in G$, entonces $x\sim x$ para toda $x\in X$. Por lo que nuestra relación es reflexiva.
Si $x,y\in X$ son tales que $x\sim y$, entonces existe $g\in G$ tal que $g\cdot x = y$. Así,
\begin{align*}
g^{-1} \cdot y &= g^{-1}\cdot (g\cdot x) \\
&= (g^{-1}g)\cdot x & \text{por condición } 2\\
&= (e\cdot x )\\
&= x & \text{por condición } 1
\end{align*}
con $g^{-1} \in G$, entonces $y\sim x$. Por lo que tenemos una relación simétrica.
Si $x,y,z\in X$ son tales que $x\sim y$ y $y\sim z$, entonces existen $g,h\in G$ tales que $g\cdot x = y$, $h\cdot y = z$. Así
\begin{align*}
(hg)\cdot x &= h\cdot (g\cdot x) &\text{condición } 2\\
&= h \cdot y = z
\end{align*}
con $hg\in G$. Entonces $x\sim z$. Así, nuestra relación es transitiva.
Por lo tanto $\sim$ es una relación de equivalencia.
$\blacksquare$
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- En los siguientes incisos determina si la función dad es una acción de $G$ en $X$:
- Considera un campo $K$ y $V$ un $K$-espacio vectorial. Sea $G= K^*$ con el producto y $X= V$. Definimos $\lambda\cdot v = \lambda v$ para cada $\lambda\in K^*$ y $v\in V$. (Nota que $K^*$ es el campo sin el neutro aditivo).
- Sea $G$ un grupo y $X=G$. Definimos $g\cdot x = g^{-1}xg$ para cada $g\in G$ y cada $x\in X$.
- Sea $G$ un grupo y $X = \{H|H\leq G\}$. Definimos $g\cdot H = gHg^{-1}$ para cada $g\in G$ y cada $H\in X$.
- Sea $G$ un grupo y $X=N$ un subgrupo normal de $G$. Definimos $g\cdot n= gng^{-1}$ para cada $g\in G$ y cada $n\in N$.
- Sea $G$ un grupo y $X$ un $G$ conjunto. Considera el homomorfismo $\psi: G\to S_X$ asociado. ¿Es necesariamente $\psi$ un monomorfismo? Si lo es, pruébalo y si no, establece qué condiciones debería cumplir la acción para que lo sea.
- Para repasar lo que hemos visto desde el Teorema de Cayley, puedes consultar el video en inglés de Mathemaniac.
Más adelante…
Hemos expandido la idea de que un grupo puede mover a los elementos de otro hasta llamarlo una acción. Luego, encontramos una relación de equivalencia a partir de la acción. Como es usual en este tipo de cursos, estudiaremos la partición inducida por esta relación de equivalencia y a partir de estos conjuntos, definiremos otros tipos de acciones.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Una modificación al Teorema de Cayley.
- Siguiente entrada del curso: Órbita de $x$ y tipos de acciones.
- Resto de cursos: Cursos.