Introducción

En entradas anteriores hemos estudiado a detalle sistemas de dos ecuaciones lineales homogéneas con coeficientes constantes de la forma $$\dot{\textbf{X}}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}$$. Resolvimos tales sistemas de manera analítica, hallando su solución general, y también estudiamos el comportamiento de las curvas solución en el plano fase. Vimos que los valores propios asociados al sistema determinan la estabilidad de los puntos de equilibrio y la forma del plano fase. Finalmente, en la entrada anterior clasificamos las formas de los planos fase y los puntos de equilibrio, según la traza y el determinante de la matriz asociada al sistema.

Ahora que tenemos esta información a nuestra disposición, podemos estudiar sistemas de ecuaciones no lineales. Como en el caso lineal, nos enfocaremos en sistemas autónomos, donde la variable independiente $t$ no aparece explícitamente en el sistema. Lo primero que haremos será analizar algunos sistemas y sus campos vectoriales asociados, los cuales van a sugerir soluciones que ya no tienen un comportamiento conocido o fácil de interpretar como en los sistemas lineales. Necesitaremos nuevos métodos para conocer el plano fase por completo.

De tu curso de Cálculo de varias variables, sabes que la mejor aproximación lineal a una función $\textbf{F}:\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ en un punto $(x_{0},y_{0})$ está dada por la matriz jacobiana evaluada en dicho punto. En nuestro caso, tenemos que $$\textbf{F}(x,y)=(F_{1}(x,y).F_{2}(x,y))$$ entonces la matriz jacobiana se convierte en $$\textbf{DF}(x_{0},y_{0})= \begin{pmatrix} \frac{\partial{F_{1}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \\ \frac{\partial{F_{2}}}{\partial{x}}(x_{0},y_{0}) & \frac{\partial{F_{1}}}{\partial{y}}(x_{0},y_{0}) \end{pmatrix}.$$ Esta matriz tendrá coeficientes constantes, y al sistema $$\dot{\textbf{X}}=\textbf{DF}(x_{0},y_{0})\textbf{X}$$ ya sabemos analizarlo.

El teorema de Hartman – Grobman nos garantizará que las soluciones al sistema no lineal cercanas al punto de equilibrio se comportarán de una manera similar a las curvas del plano fase del sistema lineal obtenido por la linealización. Con este método, podremos conocer una parte del plano fase.

Sistemas de ecuaciones no lineales. Linealización de puntos de equilibrio

En el primer video revisamos tres ejemplos de sistemas de ecuaciones no lineales, estudiamos sus planos fase a través del campo vectorial asociado y vemos las dificultades que se presentan. Posteriormente linealizamos un sistema de ecuaciones cerca de sus puntos de equilibrio mediante la matriz jacobiana del campo asociado. Finalmente enunciamos el teorema de Hartman – Grobman.

En el segundo video linealizamos dos sistemas de ecuaciones no lineales, y estudiamos el comportamiento de las curvas solución cerca de los puntos de equilibrio.

El péndulo simple

Estudiamos el sistema de ecuaciones asociado al movimiento simple de un péndulo. Linealizamos los puntos de equilibrio, estudiamos el plano fase y por último, interpretamos las curvas solución del plano fase.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

• Construye un sistema de dos ecuaciones no lineal tal que $(0,0)$ sea el único punto de equilibrio, y tal que las soluciones cerca del origen se comporten como espirales. Justifica tu respuesta.
• Prueba que el sistema $$\begin{array}{rcl} \dot{x} & = & x^{2}-xy^{3} \\ \dot{y} & = & x+y^{2} \end{array}$$ tiene dos puntos de equilibrio. Linealiza cerca de los puntos de equilibrio y determina el comportamiento de las soluciones cercanas, siempre y cuando esto sea posible.

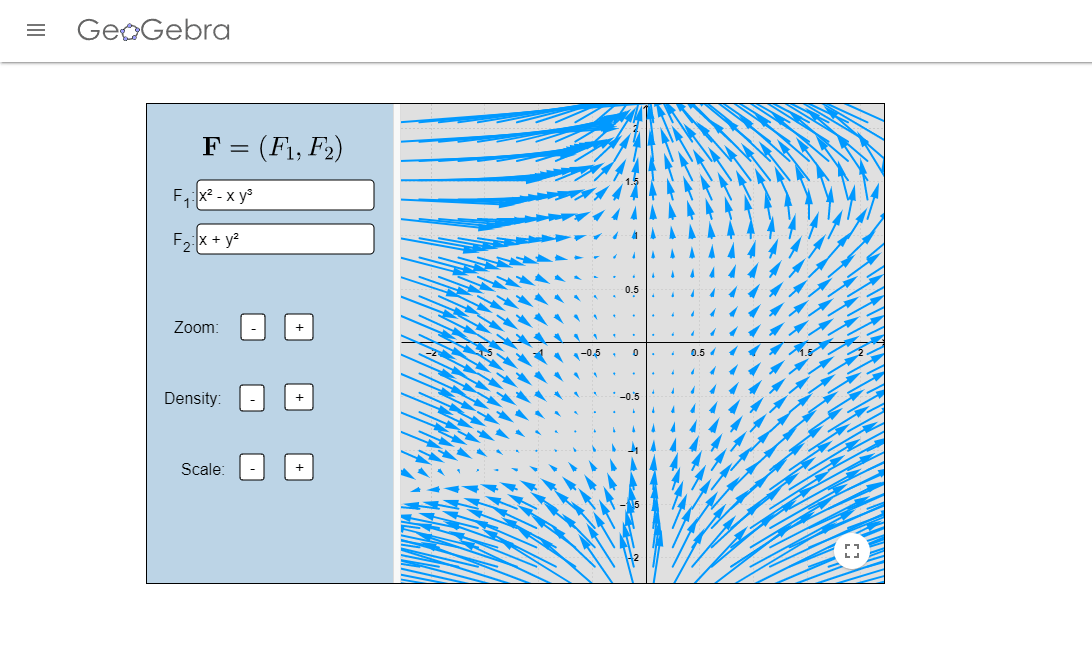
• Determina los puntos de equilibrio y el comportamiento de las soluciones cerca de estos, del sistema $$\begin{array}{rcl} \dot{x} & = & -2x+y \\ \dot{y} & = & x^{2}-y. \end{array}$$

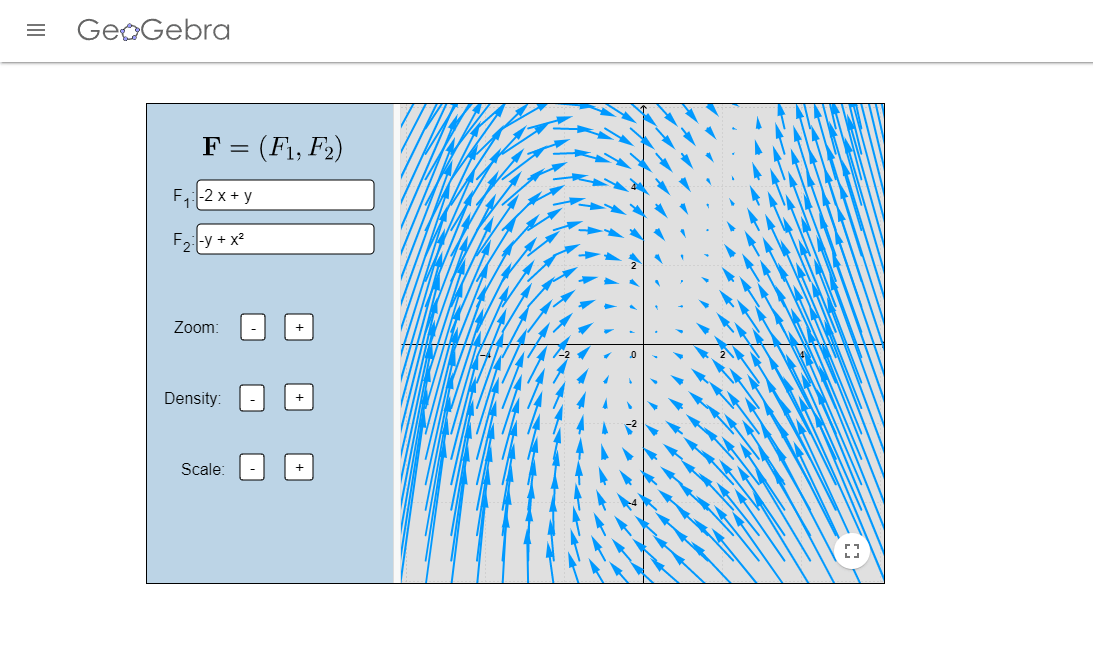
• Calcula los puntos de equilibrio del sistema $$\begin{array}{rcl} \dot{x} & = & x^{2}-y^{2} \\ \dot{y} & = & x^{2}-y. \end{array}$$ Determina el comportamiento de los puntos de equilibrio, cuando esto sea posible.

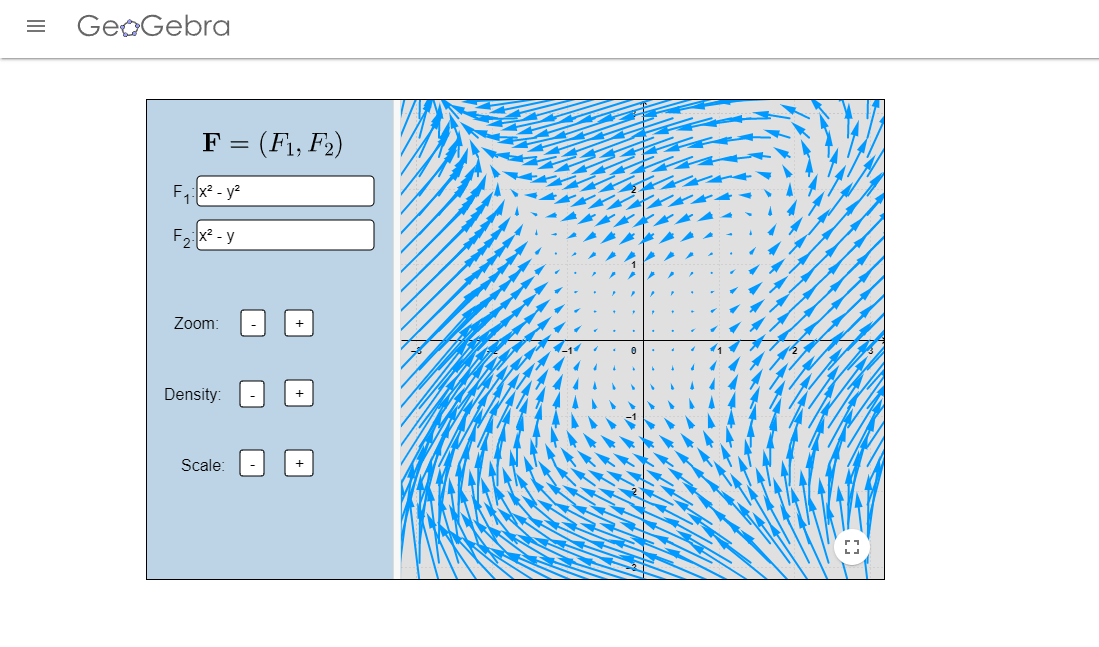
• Encuentra los puntos de equilibrio y el comportamiento de las soluciones cerca de estos, para el sistema $$\begin{array}{rcl} \dot{x} & = & \sin{x} \\ \dot{y} & = & \cos{y} \end{array}$$ cuando sea posible.

Más adelante

Hemos avanzado un poco en nuestro propósito de estudiar el plano fase de sistemas de dos ecuaciones no lineales. Al obtener la linealización de los puntos de equilibrio conocemos, al menos, el comportamiento de las curvas solución cerca de estos.

En la siguiente entrada estudiaremos el método de las nulclinas, que nos permitirá conocer más aspectos del plano fase a un sistema no lineal, no solamente cerca de los puntos de equilibrio, sino que además nos permitirá conocer el comportamiento de soluciones lejanas. Las nulclinas son los conjuntos de puntos donde las funciones coordenadas $\textbf{F}_{i}$ del campo vectorial asociado al sistema se anulan. En el caso de sistemas de dos ecuaciones, las nulclinas dividirán el plano $x(t)-y(t)$ en regiones. Estudiaremos el comportamiento de las soluciones en cada región y podremos tener un mejor conocimiento del plano fase entero.

Entradas relacionadas

• Ir a Ecuaciones Diferenciales I
• Entrada anterior del curso: El plano traza – determinante
• Siguiente entrada del curso: Sistemas de ecuaciones no lineales. Las nulclinas y el plano fase

• Notas escritas relacionadas con el tema: Linealización de los puntos de equilibrio de sistemas no lineales

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»