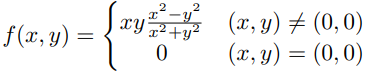Introducción
Extremos Locales parte 2
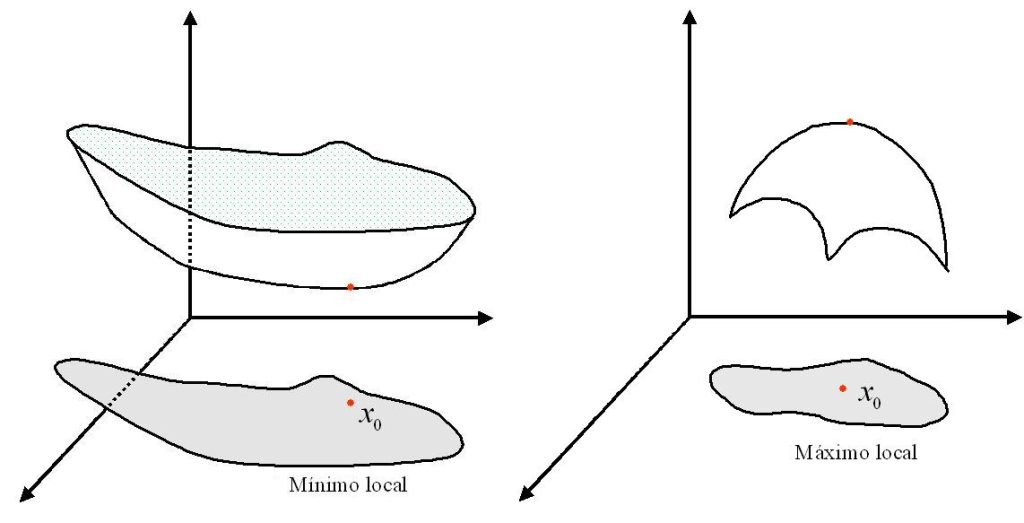
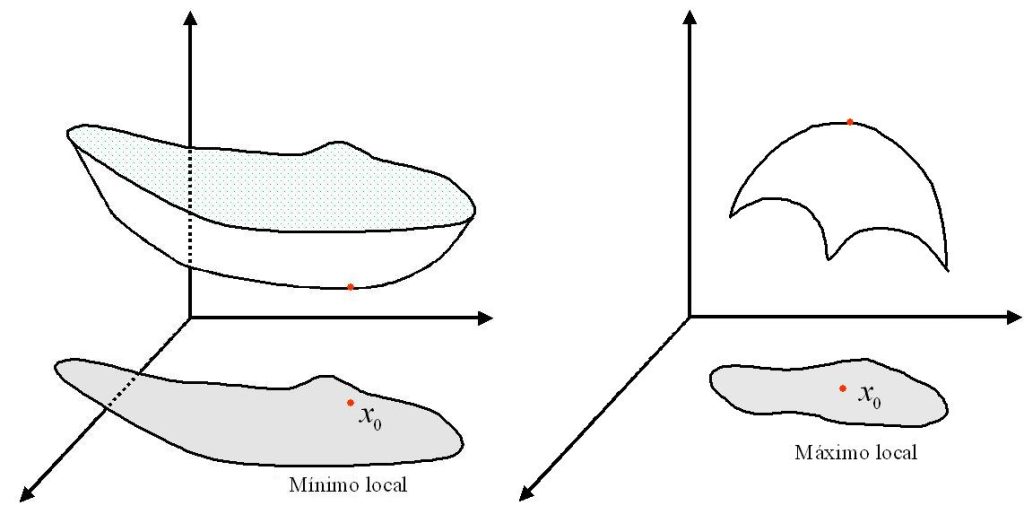
Entre las caracteristicas geometricas básicas de la gráficas de una
función estan sus puntos extremos, en los cuales la función alcanza
sus valores mayor y menor.
Definición 1. Si $f:u\subset \mathbb{R}^n \rightarrow
\mathbb{R}$ es una función escalar, dado un punto $x_0 \in u$
se llama mínimo local de $f$ si existe una vecindad $v$ de $x_0$ tal que $\forall x \in v$ , $f(x)>f(x_0)$. De manera analoga, $x_0 \in u$ es un máximo local si existe una vecindad $v$ de $x_0$ tal que $f(x)< f(x_0)$, $\forall \quad x \in v$. El punto $x_0 \in u$ es un extremo local o relativo, si es un mínimo local o máximo local.
Teorema 1. $\textcolor{Red}{\textbf{Criterio de la primera derivada}}$ Si $u \in \mathbb{R}$ es abierto, la función $f:u\subset \mathbb{R}^n \rightarrow \mathbb{R}$ es diferenciable y $x_0 \in u$ es un extremo local entonces $\nabla f(x_0)=0$, esto es $x_0$ es un punto crítico de $f$.
Demostración. Supongamos que $t$ alcanza su máximo local en $x_0$. Entonces para cualquier $h \in \mathbb{R}^n$ la función $g(t)=f(x_0+th)$ tiene un máximo local en $t=0$. Asi, del cálculo de una variable $g'(0)=0$ ya que como $g(0)$ es máximo local, $g(t)\leq g(0)$ para $t > 0$ pequeño
$$\therefore \quad g'(0)=\displaystyle\lim_{t \rightarrow t_0^+}\frac{g(t)-g(0)}{t}=0$$
Análogamente para $t< 0$ pequeño tomamos
$$g'(0)=\displaystyle\lim_{t \rightarrow t_0^-}\frac{g(t)-g(0)}{t}=0$$
Ahora por regla de la cadena $$g'(0)=\frac{\partial f}{\partial x_{1}}(x_{0})h_{1}+\frac{\partial f}{\partial x_{2}}(x_{0})h_{2}+\cdots+\frac{\partial f}{\partial x_{n}}(x_{0})h_{0}=\nabla f(x_{0})\cdot h$$
Así $\nabla f(x_{0})\cdot h=0 \quad \forall \: h$ de modo que $\nabla f(x_{0})=0$. En resumen si $x_0$ es un extremo local, entonces $\displaystyle\frac{\partial f}{\partial x_i}(x_0)=0 \quad \forall~i=1,\ldots,n$. En otras palabras $\nabla f(x_0)=0$.
Ejemplo. Hallar los máximos y mínimos de la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$, definida por $$f(x,y)=x^2+y^2-2x-6y+14$$
Solución. Debemos identificar los puntos críticos de $f$ resolviendo $\displaystyle{\frac{\partial f}{\partial x}=0}$, $\displaystyle{\frac{\partial f}{\partial y}=0}$ para $x,y$, $$2x-2=0~~~2y-6=0$$ De modo que el punto crítico es $(1,3)$. Como $$f(x,y)=\left(x^{2}-2x+1\right)+\left(y^{2}-6y+9\right)+4=\left(x-1\right)^{2}+\left(y-3\right)^{2}+4$$
tenemos que $f(x,y)\geq 4$ por lo tanto en $(1,3)$ f alcanza un mínimo relativo.
Ejemplo. Considerar la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$,
$f(x,y)=4-x^2-y^2$ entonces $\displaystyle{\frac{\partial f}{\partial x}=-2x}$, $\displaystyle{\frac{\partial f}{\partial y}=-2y}$. $f$ solo tiene un punto crítico en el origen, donde el valor de $f$ es 4. Como $$f(x,y)=4-(x^{2}+y^{2})$$
tenemos que $f(x,y)\leq 4$ por lo tanto en $(0,0)$ f alcanza un máximo relativo.
Ejemplo. En el siguiente ejemplo mostramos que no todo punto critico es un valor extremo\Sea $f(x,y)=x^{2}y+y^{2}x$ tenemos que sus puntos criticos son
$$\frac{\partial f}{\partial x}=2xy+y^{2}~~~\frac{\partial f}{\partial y}=2xy+x^{2}=0$$
por lo tanto
$$\left(\begin{matrix}2xy+y^{2}=0\\2xy+x^{2}=0\end{matrix}\right)\Leftrightarrow\left(\begin{matrix}x=y\\x=-y\end{matrix}\right)$$
tomando $x=-y$ tenemos que
$$2xy+y^{2}=0~\Rightarrow~-2y^{2}+y^{2}=0~\Rightarrow~-y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$
tomando $x=y$ tenemos que
$$2xy+y^{2}=0~\Rightarrow~2y^{2}+y^{2}=0~\Rightarrow~-3y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$
por lo tanto $(0,0)$ es el único punto critico.
Ahora bien para $f(x,y)$ tomamos $x=y$
$$f(x,x)=2x^{3}$$
la cual es ($<0$ si $x<0$) y ($>0$ si $x>0$) por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de $f$
Ahora bien para $f(x,y)$ tomamos $x=-y$
$$f(x,-x)=0~~~\forall x$$
por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de $f$
Para el caso de funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ tenemos que recordando un poco de la expresión de taylor
$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})+$$
$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y_{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}{p}(z-z_{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}{p}(z-z_{0})(y-y_{0})\right)}$$
$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial z^{2}}_{p}(z-z_{0})}$$
Haciendo $x-x_{0}=h_{1},y-y_{0}=h_{2},z-z_{0}=h_{3}$ podemos escribir el término rojo de la siguiente manera
$$\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}\right)$$
y también se puede ver como producto de matrices
$$\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$
Si $(x_{0},y_{0},z_{0})$ es un punto critico de la función entonces en la expresión de Taylor
$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial
x}\right)_{p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right)_{p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})$$
$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}_{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}_{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}_{p}(y-y_{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}_{p}(z-z_{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}_{p}(z-z_{0})(y-y_{0})\right)}$$
$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial
z^{2}}_{p}(z-z_{0})(x-x_{0})}$$
El término
$$\frac{\partial f}{\partial x}{p}(x-x{0})+\frac{\partial f}{\partial y}{p}(y-y{0})+\frac{\partial f}{\partial z}{p}(z-z{0})=0$$
y por lo tanto
$$f(x,y)-f(x_{0},y_{0})=\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$
vamos a determinar el signo de la forma
$$Q(h)=\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$
vamos a trabajar sin el término $\displaystyle{\frac{1}{2!}}$ que no afectara al signo de la expresión, tenemos entonces
$$Q(h)=(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial ^{2}f}{\partial
z\partial y}\\\frac{\partial^{2}f}{\partial
x\partial z}&\frac{\partial^{2}f}{\partial
y\partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)=\textcolor{Red}{\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
$$=\textcolor{Red}{\frac{\partial^{2}f}{\partial x^{2}}\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right)^{2}+\left(\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)h_{2}^{2}}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
hacemos $\displaystyle{b_{1}=\frac{\partial^{2}f}{\partial x^{2}},h_{1}’=\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right),b_{2}=\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}},~~h_{2}’=h_{2}}$ y obtenemos
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
que podemos escribir
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}\left(h_{1}+\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}-\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}\right)h_{3}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}\left(h_{1}’-\frac{\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}h_{2}’\right)h_{3}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{1}’h_{3}+\left(2\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)h_{2}’h_{3}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
hacemos
$$2b_{23}=2\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}$$y obtenemos
$$=b_{1}h_{1}’^{2}+b_{2}h_{2}’^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{1}’h_{3}+2b_{23}h_{2}’h_{3}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
que se puede escribir
$$=b_{1}\left(h_{1}’^{2}+2\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{1}’h_{3}+\left(\frac{\frac{\partial^{2}f}{\partial x\partial z}h_{3}}{b_{1}}\right)^{2}\right)+b_{2}\left(h_{2}’^{2}+2\frac{b_{23}}{b_{2}}h_{2}’h_{3}+\left(\frac{b_{23}}{b_{2}}h_{3}\right)^{2}\right)+\left(\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}\right)h_{3}^{2}$$
hacemos
$$b_{3}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}$$
y obtenemos
$$=b_{1}\left(h_{1}’^{2}+2\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{1}’h_{3}+\left(\frac{\frac{\partial^{2}f}{\partial x\partial z}h_{3}}{b_{1}}\right)^{2}\right)+b_{2}\left(h_{2}’^{2}+2\frac{b_{23}}{b_{2}}h_{2}’h_{3}+\left(\frac{b_{23}}{b_{2}}h_{3}\right)^{2}\right)+b_{3}h_{3}^{2}$$
$$=b_{1}\left(h_{1}’+\frac{\frac{\partial^{2}f}{\partial x\partial z}}{b_{1}}h_{3}\right)^{2}+b_{2}\left(h_{2}’+\frac{b_{23}}{b_{2}}h_{3}\right)^{2}+b_{3}h_{3}^{2}$$
esta última expresión será positiva si y solo si $b_{1}>0~~b_{2}>0$ y $b_{3}>0$ en clases pasadas vimos los dos primeros, veamos ahora que $$b_{3}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}>0$$
tenemos entonces que
$$\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{b_{1}}-\frac{b_{23}^{2}}{b_{2}}=\frac{\partial^{2}f}{\partial z^{2}}-\frac{\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial z^{2}}}-\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}-\frac{2\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}\right)^{2}}{\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}}$$
$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}-\frac{\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\left(\frac{\partial^{2}f}{\partial x^{2}}\right)^{2}}}{\frac{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}}=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}}-\frac{\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)\frac{\partial^{2}f}{\partial x^{2}}}$$
$$=\frac{\left(\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\right)\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)-\left(\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$
$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}+\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\left(\frac{\partial^{2}f}{\partial y\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial x^{2}}\right)^{2}-}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$
$$\frac{2\left(\frac{\partial^{2}f}{\partial x^{2}}\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}\right)-\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}{\frac{\partial^{2}f}{\partial x^{2}}\left(\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}\right)}$$
$$=\frac{\frac{\partial^{2}f}{\partial z^{2}}\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\frac{\partial^{2}f}{\partial z^{2}}\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}-\frac{\partial^{2}f}{\partial y^{2}}\left(\frac{\partial^{2}f}{\partial x\partial z}\right)^{2}-\left(\frac{\partial^{2}f}{\partial y\partial z}\right)^{2}\frac{\partial^{2}f}{\partial x^{2}}+2\frac{\partial^{2}f}{\partial y\partial z}\frac{\partial^{2}f}{\partial x\partial z}\frac{\partial^{2}f}{\partial y\partial x}}{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}$$
$$=\frac{\left|\begin{matrix}\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y\partial x}&\frac{\partial^{2}f}{\partial z\partial x}\\\frac{\partial^{2}f}{\partial x\partial y}&\frac{\partial^{2}f}{\partial y^{2}}&\frac{\partial^{2}f}{\partial z\partial y}\\\frac{\partial^{2}f}{\partial x\partial z}&\frac{\partial^{2}f}{\partial y\partial z}&\frac{\partial^{2}f}{\partial z^{2}}\end{matrix}\right|}{\frac{\partial^{2}f}{\partial y^{2}}\frac{\partial^{2}f}{\partial x^{2}}-\left(\frac{\partial^{2}f}{\partial y\partial x}\right)^{2}}$$
por lo tanto
$$b_{3}>0~\Leftrightarrow~\left|\begin{matrix}\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y\partial x}&\frac{\partial^{2}f}{\partial z\partial x}\\\frac{\partial^{2}f}{\partial x\partial y}&\frac{\partial^{2}f}{\partial y^{2}}&\frac{\partial^{2}f}{\partial z\partial y}\\\frac{\partial^{2}f}{\partial x\partial z}&\frac{\partial^{2}f}{\partial y\partial z}&\frac{\partial^{2}f}{\partial z^{2}}\end{matrix}\right|>0$$
Un poco de Algebra Lineal
Si $A\in M_{n\times n}$ una matriz simétrica entonces existe una $B\in M_{n\times n}$ una matriz ortonormal tal que
$$BAB^{T}$$
es una matriz diagonal, es decir
$$BAB^{T}=\left[\begin{matrix}\lambda_{1}&\cdots&0\\0&\ddots&\vdots\\0&\cdots&\lambda_{n}\end{matrix}\right]$$
Las matrices ortonormales se usan para realizar un cambio de base.
Si $F:\mathbb{R}^{n}\rightarrow\mathbb{R}$ es una forma cuadrática que tiene asociada la matriz simétrica A (en una base ortonormal) es decir
$$F(x_{1},x_{2},…,x_{n})=(x_{1}\cdots x_{n})A(x_{1}\cdots x_{n})^{T}$$
existe entonces una base ortonormal tal que la matriz asociada a $F$ en esta nueva base es una matriz diagonal.
Tenemos que si
$$B=\left[\begin{matrix}b_{11}&\cdots&b_{1n}\\\vdots&\ddots&\vdots\\b_{n1}&\cdots&b_{nn}\end{matrix}\right]$$
es tal que $BAB^{T}$ es diagonal entonces
$$(x_{1}\cdots x_{n})=[x_{1}’\cdots x_{n}’]\left[\begin{matrix} b_{11} & \cdots &b_{1n}\\ \vdots&\ddots&\vdots \\b_{n1}&\cdots&b_{nn}\end{matrix}\right]$$
$$=[x_{1}’\cdots x_{n}’]B$$
Por lo que
$$F(x_{1},x_{2},…,x_{n})=(x_{1}\cdots x_{n})A(x_{1}\cdots x_{n})^{T}$$
$$=F(x_{1},x_{2},…,x_{n})=(x_{1}’\cdots x_{n}’)BA(x_{1}’\cdots x_{n}’B)^{T}$$
$$=(x_{1}’\cdots x_{n}’)BAB^{T}(x_{1}’\cdots x_{n})^{T}$$
$$=(x_{1}’\cdots x_{n}’)\left[\begin{matrix}\lambda_{1}&\cdots&0\\0&\ddots&\vdots\\0&\cdots&\lambda_{n}\end{matrix}\right](x_{1}’\cdots x_{n})^{T}$$
$$=\lambda_{1}x_{1}^{2}+\lambda_{2}x_{2}^{2}+\cdots +\lambda_{n}x_{n}^{2}$$
por lo que $F$ es positiva si $\lambda_{1},\cdots,\lambda_{n}$ son positivos, de igual manera $F$ es negativa si $\lambda_{1},\cdots,\lambda_{n}$ son negativos
Si definimos, para cada $k\in{1,\ldots,n}$
$$D_{k}=\left[\begin{matrix}\lambda_{1}&\cdots&0\\ \vdots&\ddots&\vdots\\0&\cdots&\lambda_{k}\end{matrix}\right]$$
entonces
$$\det (D_{k})=\lambda_{1}\cdot \lambda_{2}\cdots \lambda_{k}$$
de tal forma que podemos decir que F es positiva si $\det (D_{k})>0$ y también $F$ es negativa si $\det (D_{k})< 0$ lo cual ocurre si $\det (D_{k})<0$ si k es impar y $\det (D_{k})>0$ si k es par para cada $k\in \left\{1,..,n\right\}$
Definición 2. La forma $Q(x)=xAx^{t}$, que tiene asociada la matriz $A$ (respecto a la base canónica de $\mathbb{R}^{n}$) se dice:
$\textcolor{Red}{\text{Definida positiva}}$, si $Q(x)>0~\forall x \in~\mathbb{R}^{n}$
La forma $Q(x)=xAx^{t}$, que tiene asociada la matriz $A$ (respecto a la base canónica de $\mathbb{R}^{n}$) se dice:
$\textcolor{Red}{\text{Definida negativa}}$, si $Q(x)<0~\forall x\in~\mathbb{R}^{n}$
Definición 3. Si la forma $Q(x)=xAx^{t}$ es definida positiva, entonces $f$ tiene un mínimo local en en $x$. Si la forma $Q(x)=xAx^{t}$ es definida negativa, entonces $f$ tiene un máximo local en en $x$.
Definición 4. Dada una matriz cuadrada $A=a_{ij}j=1,…,ni=1,…,n$ se consideran las submatrices angulares $A_{k}k=1,…,n$ definidas como $$A_{1}=(a_{11})~A_{2}=\left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}\right)~~A_{3}=\left(\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{matrix}\right),\cdots,A_{n}=A$$
se define $\det A_{k}=\triangle_{k}$
$\textbf{Criterio 1 (a)}$ Se tiene entonces que la forma $Q(x)=xAX^{t}$ es definida positiva si y solo si todos los determinantes $\triangle_{k}~~k=1,…,n$ son números positivos.
$\textbf{Criterio 1 (b)}$ La forma $Q(x)=xAX^{t}$ es definida negativa si y solo si los dterminantes $\triangle_{k}k=1,…,n$ tienen signos alternados comenzando por $\triangle_{1}<0$ $\triangle_{2}>0,…$ respectivamente.
Ejemplo. Consideremos la función $f:\mathbb{R}^3\rightarrow\mathbb{R}$ $f(x,y,z)=\sin x +\sin y + \sin z -\sin(x+y+z)$, el punto $P=\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)$ es
un punto crítico de $f$ y en ese punto la matriz hessiana de
$f$ es $$H(p)=\left[\begin{array}{ccc}
-2 & -1 & -1 \\
-1 & -2 & -1 \\
-1 & -1 & -2 \\
\end{array}
\right]
$$
los determinantes de las submatrices angulares son
$$\Delta_1=det(-2)\qquad \quad $$ $$\Delta_2=det \left[
\begin{array}{cc}
-2 & -1 \\
-1 & -2 \\
\end{array}
\right]$$
$$\Delta_3=det H(p)=-4$$ puesto que son signos alternantes con $\Delta t< 0$ concluimos que la funcion $f$ tiene en $\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)$ un máximo local. Este máximo local vale $f\left(\frac{\pi}{2},\frac{\pi}{2},\frac{\pi}{2}\right)=4$
Más adeante
Tarea moral
1.- Determina qué tipo de punto crítico presenta la función $f(x,y)=ax^n+cy^n$ donde $ac \neq0$
2.- Determina los puntos críticos y determina que tipo de puntos son bajos los criterios mencionados anteriormente :
$f(x,y)= x^3+y^2-6xy+6x+3y$
Demuestra que si dada $f(x)=U \subset \mathbb{R}^n \rightarrow \mathbb{R}$, donde $U$ es un conjunto abierto dos veces diferenciable y $\overline{x}_{0}$ es un punto crítico de $f$ entonces se satisface que:
3.- Si $f$ tiene un mínimo local en $\overline{x}_0$, entonces la hessiana de $f$ en $\overline{x}_0$ es una forma cuadrática semipositiva y
4.- Si $f$ tiene un máximo local en $\overline{x}_0$, entonces la hessiana de $f$ en $\overline{x}_0$ es una forma cuadrática seminegativa.
5.- Sea $f(x,y,z)=ax^2+by^2+cz^2$, donde $abc \neq 0$ Muestra que el $(0,0,0)$ es el único punto crítico de $f$ y determina su tipo en términos de $a, b$ y $c$