Archivo de la categoría: Matemáticas

Posts de matemáticas, la ciencia más cercana a las artes.

Cálculo Diferencial e Integral II: Fuerza y presión hidrostática

Por Miguel Ángel Rodríguez García

Introducción

En esta sección veremos otra aplicación de las integrales en el área de la física y es en la presión hidrostática, que resuelve algunos problemas que requieren determinar fuerzas o presiones que actúan sobre un objeto sumergido en algún fluido estático.

Fuerza y presión hidrostática

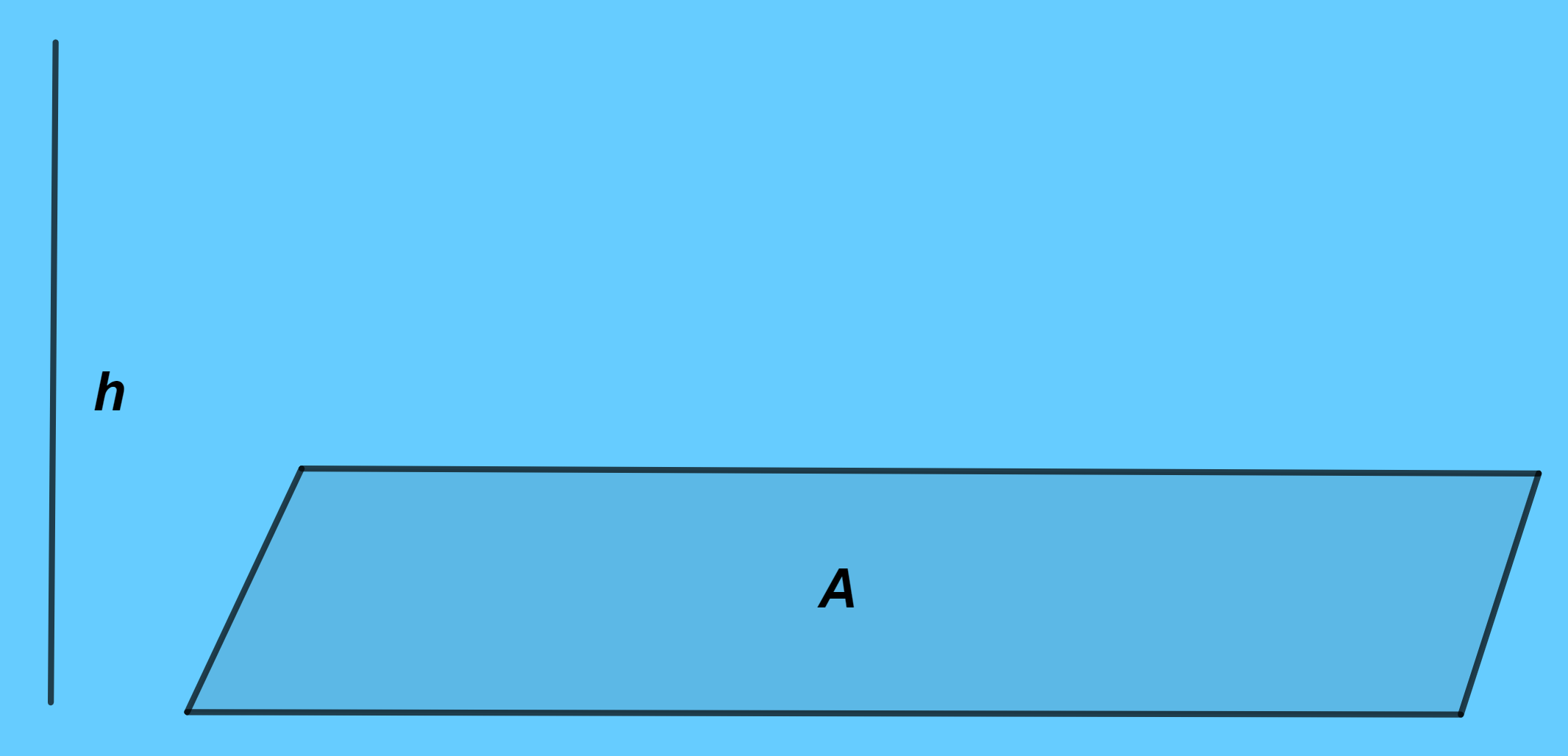
Supongamos que una placa horizontal delgada con área $A$ sumergido en un fluido con densidad constante $ρ$ a una profundidad $h$ debajo de la superficie del fluido como se muestra en la figura $(1)$ .

El volumen del fluido sobre la placa es:

$V = A h$

De modo que su masa es:

$m = ρ V = ρ A h$

Por lo que la fuerza que ejerce la placa sobre el fluido es:

$F = m g = ρ g A h$

Donde $g$ es la aceleración ejercida por la gravedad $(g = 9.81 m / s^{2})$ en la Tierra. Recordemos que la presión $P$ se define como la fuerza por unidad de área:

$P = \frac{F}{A} = ρ g h$

Donde las unidades son Pascales o Newton por metro cuadrado: $1 N / m^{2} = 1 P a$ .

A la cantidad $w = ρ g$ se le conoce como el peso específico, gravedad especifica o densidad de peso.

Veamos un ejemplo:

¿Cuál es la presión y la fuerza sobre la parte superior de un plato plano y circular de 3 metros que está sumergido a 10 metros bajo el agua.

Recordemos que la densidad del agua es: $ρ = 1000 k g / m^{3}$ , entonces podemos calcular la presión como:

$P = ρ g h = (1000 k g / m^{3}) (9.81 m / s^{2}) (10 m) = 98000 P a$ .

Como la fuerza la podemos calcular como: $F = P A$ , entonces:

$F = P π r^{2} = (98000 P a) (π) {(3 m)}^{2} = 2.77 \times 10^{6} N$

Existe un principio importante, a este principio se le denomina el principio de Pascal, el cual nos dice que la presión de un fluido en el que cualquier punto en un líquido, la presión es la misma en todas las direcciones, es decir, un buzo siente la misma presión en la nariz y en ambos oídos. Al tener la presión dependiente de la profundidad, entonces al sumergir un cuerpo más profundo en un fluido, la presión va cambiando, veamos como va cambiando.

Figura 2: Superficie sumergido en un fluido.

Supongamos que una superficie plana se sumerge verticalmente en un fluido con densidad de peso $w$ donde la parte sumergida se extiende sobre el eje $y$ desde $y = a$ hasta $y = b$ . Hacemos una partición de $[a, b]$ cortando la región en delgadas franjas horizontales perpendiculares al eje $y$ por lo que el ancho de estas franjas es $Δ y$ unidades por $L (y)$ unidades de largo (figura $(2)$ ), por lo que la fuerza que ejerce el fluido contra un lado de la franja se aproxima como:

$Δ F \approx w \cdot (p r o f u n d i d a d d e l a f r a n j a) \cdot L (y) \cdot Δ y$

Supongamos que hay $n$ franjas en el intervalo $[a, b]$ , sumamos estas $n$ franjas, por lo que la suma de Riemann es:

$F \approx \sum_{i = 1}^{n} w \cdot (p r o f u n d i d a d d e l a f r a n j a) \cdot L (y_{i}) \cdot Δ y_{i}$

Para una función continua en el intervalo $[a, b]$ y tendiendo a $n \to \infty$ entonces se tiene que:

$F = \int_{a}^{b} w h (y) L (y) d y$

Veamos un ejemplo:

Calcule la fuerza del fluido total que se ejerce sobre una pared vertical en una represa con altura de $100 m$ y ancho $300 m$

Calculemos la densidad de peso como:

$w = ρ g = (1000 k g / m^{3}) (9.81 m / s^{2}) = 9800 N / m^{2}$

Supongamos que la profundidad va variando como $h (y) = y$ y el ancho de la represa es $L = 300 m$ , por lo que la fuerza la podemos calcular como:

$F = \int_{0}^{100} w h (y) L (y) d y = \int_{0}^{100} (9800) (y) (300) d y = 2.94 \times 10^{6} \int_{0}^{100} y d y$

$= 2.94 \times 10^{6} [\frac{y^{2}}{2}] |_{0}^{100} = 1.47 \times 10^{10} N$ .

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

¿Cuál es la presión en el fondo de una alberca a 2 metros?.
Encuentre la fuerza en un lado de un contenedor cubico de $6 c m$ si el recipiente esta lleno de mercurio. La densidad del mercurio es $ρ = 13600 k g / m^{3}$
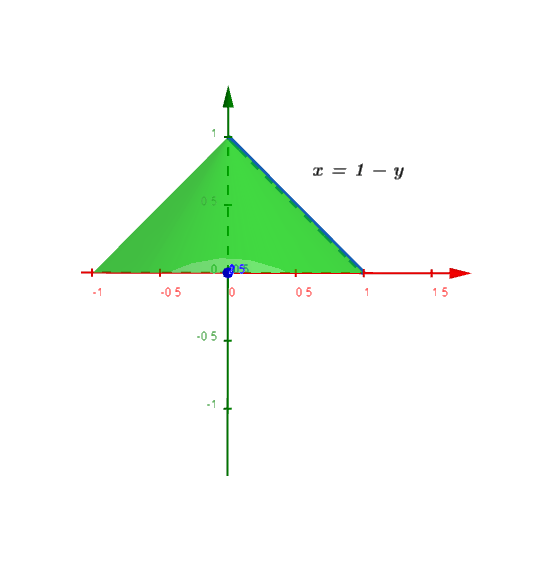
Una placa triangular rectángulo de base $2 m$ altura $1 m$ está sumergida verticalmente en agua, con el vértice superior $3 m$ debajo de la superficie. Encuentra la fuerza en un lado de la placa. Hint: Considere la ecuación de una recta.
Determine la fuerza hidrostática sobre una cara de un cilindro con radio de $3 c m$ si el cilindro esta sumergido a $10 c m$ . Hint: Utilice la ecuación de un circulo y ponga el origen en el centro del cilindro.
Una placa triangular rectángulo de base $2 m$ y altura $1 m$ está sumergida verticalmente en agua, con el vértice superior $3 m$ debajo de la superficie. Encuentra la fuerza en un lado de la placa.

Más adelante…

En esta sección, vimos como resolver algunos problemas de fuerza y presión en algún fluido estático, en la siguiente sección veremos otra aplicación de la integral en el área de la probabilidad.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencia e Integral II: Aplicación de la integración al concepto de trabajo – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencial e Integral II: Probabilidad – El blog de Leo (nekomath.com)

Cálculo Diferencia e Integral II: Aplicación de la integración al concepto de trabajo

Por Miguel Ángel Rodríguez García

4 respuestas

Introducción

En la sección anterior vimos como calcular el momento y el centro de masa con ayuda de la integral, en esta sección revisaremos el concepto de trabajo en el área de la física como una aplicación más de la integración.

Trabajo

Consideremos una partícula $P$ en un plano, que se mueve una distancia $d$ a lo largo de una curva $C$ como resultado de la aplicación de una fuerza externa $F$ , que es función de la posición de la partícula en el espacio, es decir, $F = F (x)$ y sea $d x$ un desplazamiento infinitesimal experimentado por la partícula en un intervalo de tiempo $d t$ , se define el trabajo infinitesimal $d W$ a la fuerza $F$ durante el desplazamiento infinitesimal $d x$ al producto escalar $F \cdot d x$ esto es:

$d W = F \cdot d x$

Ahora, supongamos que la partícula $P$ recorre una trayectoria en el espacio a lo largo del eje $x$ , para determinar el trabajo que se realiza sobre esta partícula en un desplazamiento a lo largo de las posiciones $a$ y $b$ , hacemos una partición en el intervalo $[a, b]$ en $n$ subintervalos con puntos extremos $x_{0}, x_{1}, \dots ., x_{n}$ e igual ancho $Δ x$ . Sea $x_{i^{}}^{*}$ un punto en el subintervalo $[x_{i - 1}, x_{i}]$ , si $F$ es continua en el intervalo $[a, b]$ entonces podemos aproximar el trabajo como una suma dada como:

$T r a b a j o \approx \sum_{i = 1}^{n} F (x_{i^{}}^{*}) Δ x$

Por tanto, se define el trabajo efectuado al mover una partícula u objeto en el intervalo $[a, b]$ como el límite cuando $n \to \infty$ como:

$\begin{matrix} (1) & W = lim_{n \to \infty} \sum_{i = 1}^{n} F (x_{i^{}}^{*}) Δ x = \int_{a}^{b} F (x) d x \end{matrix}$

En el sistema internacional de unidades $(S I)$ , el trabajo se mide en Joules $(J)$ .

Ley de Hooke

La ley de Hooke nos dice que la fuerza necesaria para estirar o comprimir un resorte a una cierta longitud a partir de su estado de equilibrio, es proporcional a $x$ , es decir:

$\begin{matrix} (2) & F = - k x \end{matrix}$

Donde $k$ es la constante del resorte o constante de fuerza del resorte, esta constante $k$ es una característica propia del resorte. Nótese que $k$ es positiva.

Figura 1: Estiramiento del resorte a partir de su estado de equilibrio $o$ .

Ejemplos

Cuando una partícula se ubica una distancia $x$ pies del origen, una fuerza de $x^{2} + 2 x$ libras actúa sobre ella. ¿Cuánto trabajo se efectúa al moverla desde $x = 1$ hasta $x = 3$ ?

De la definición del trabajo $(1)$ , tenemos que:

$W = \int_{1}^{3} (x^{2} + 2 x) d x = [\frac{x^{3}}{3} + x^{2}] |_{1}^{3} = \frac{3^{3}}{3} + 3^{2} - \frac{1}{3} - 1 = \frac{50}{3}$

Por tanto, el trabajo realizado es: $16.6 I b . p i e .$

Una partícula eléctrica $q_{1}$ está en reposo con una carga de $2 C$ efectúa un trabajo sobre otra partícula eléctrica $q_{2}$ a una distancia de $20$ cm. con carga $1 C$ . ¿Cuánto trabajo se efectúa al moverla a $40$ cm.?

En este caso, la fuerza de la particula $q_{1}$ que actua sobre la particula $q_{2}$ es la fuerza de Coulomb, que se define como:

$F = k \frac{q_{1} q_{2}}{r^{2}}$

Donde $k$ es la constante de Coulomb.

Para calcular el trabajo efectuado tenemos que:

$W = \int_{a}^{b} F (x) d x = \int_{0.2}^{0.4} k \frac{q_{1} q_{2}}{r^{2}} d r = \int_{0.2}^{0.4} k \frac{(2 C) (1 C)}{r^{2}} d r = 2 C^{2} k \int_{0.2}^{0.4} \frac{d r}{r^{2}}$

$= 2 C^{2} k [- \frac{1}{r}] |_{0.2}^{0.4} = 2 C^{2} k (2.5 \frac{1}{m})$

Como $k = 9 \cdot 10^{9} \frac{N m^{2}}{C^{2}}$ , entonces:

$W = 4.5 \cdot 10^{10} J$

Una fuerza de $40 N$ se requiere para retener un resorte desde su longitud natural de 10 cm. a una longitud de 15 cm. ¿Cuánto trabajo se hace al estirar el resorte de 15 a 18 cm.?

Tenemos un resorte, de acuerdo con la ley de Hooke $(2)$ que nos dice que $F = - k x$ donde $k$ se denomina constante del resorte, la fuerza que se requiere para mantener el resorte estirado $x$ metros más allá de su longitud natural es $f (x) = - k x$ .

Primero calculamos $k$ , vemos que cuando el resorte se pasa de $10$ a $15$ cm, la cantidad estirada es $5 c m = 0.05 m$ lo que quiere decir que: $f (0.05) = 40$ , de modo que:

$f (0.05) = 0.05 k = 40 \Rightarrow k = \frac{40}{0.05} = 800$

El trabajo hecho para estirar el resorte de 15 a 18 cm es:

$W = \int_{0.05}^{0.08} (800) x d x = 800 [\frac{x^{2}}{2}] |_{0.05}^{0.08} = 400 [(0.08)^{2} - (0.05)^{2}] = 1.56 J$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Un resorte tiene una longitud natural de 1m. una fuerza de 24N lo estira hasta una longitud de 1.8m.
1. a Determinar la constante $k$ del resorte.
2. ¿Cuánto trabajo se requerirá para estirar el resorte hasta 2m mas que su longitud natural?
3. ¿Hasta que longitud se estirara el resorte si le aplicamos una fuerza de 45?
Una cubeta de 5 Ib se eleva desde el piso, jalándola con una cuerda de 20 pies a una velocidad constante. La cuerda pesa 0.08 $i b / p i e$ . ¿Cuánto trabajo se realiza al subir la cubeta y la cuerda?
Una partícula se desplaza a lo largo del eje x impulsada por una fuerza que mide $\frac{10}{(1 + x)^{2}}$ libras en un punto a x pies del origen. Calcule el trabajo realizado al mover la partícula desde el origen a una distancia de 9 pies.
Una fuerza de 2N estirara una banda elástica 2 cm (0.02m. Suponiendo que en este caso se cumple la ley de Hooke, ¿Cuánto se estirara la banda al aplicarle una fuerza de 4N? ¿Cuánto trabajo se realizara para estirar la banda esa longitud?
Cuando una partícula de masa m esta en $(x, 0)$ , es estirada hacia el origen con una fuerza de magnitud $\frac{k}{x^{2}}$ . Si la partícula parte del reposo en $x = b$ y no actúa sobre ella ninguna otra fuerza, determine el trabajo realizado sobre ella cuando llega a $x = a, 0 < a < b$ .

Más adelante…

En esta entrada vimos la aplicación de la integral en el área de la física con ejemplos sencillos, dando la definición de trabajo y la definición de la ley de Hooke, en la siguiente entrada veremos otra aplicación en la física que es la definición de fuerza y presión en la hidrostática.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencial e Integral II: Centro de masa y momentos – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencial e Integral II: Fuerza y presión hidrostática – El blog de Leo (nekomath.com)

Cálculo Diferencial e Integral II: Centro de masa y momentos

Por Miguel Ángel Rodríguez García

1 respuesta

Introducción

En la sección anterior vimos el teorema de Pappus-Guldin el cual nos permite calcular el centroide, área y volumen de un sólido de revolución, en esta sección veremos una aplicación en el área de la física como aplicación de la integración para el cálculo de centro de masas y momentos. Cabe destacar que estudiaremos objetos unidimensionales y bidimensionales, ya que para objetos en el espacio se necesitan integrales múltiples, lo cual, no estudiaremos en este curso.

Centro de masas y momentos (unidimensional)

Figura 1: Varilla con dos pesas en sus extremos.

Comencemos con el caso de una varilla balanceada en un punto sobre el eje $x$ y en sus extremos una masa $m_{1}$ en $x_{1}$ y $m_{2}$ en $x_{2}$ como se muestra en la figura $(1)$ . Sea $\bar{x}$ el centro de masa, la varilla se balanceara si:

$m_{1} d_{1} = m_{2} d_{2}$

Donde $d_{1} = \bar{x} - x_{1}$ y $d_{2} = x_{2} - \bar{x}$ , sustituyendo esto en la ecuación anterior, tenemos que:

$m_{1} (\bar{x} - x_{1}) = m_{2} (x_{2} - \bar{x})$

$\Rightarrow m_{1} \bar{x} - m_{1} x_{1} = m_{2} x_{2} - m_{2} \bar{x}$

$\Rightarrow \bar{x} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}}$

Por lo que, podemos calcular el centro de masa $\bar{x}$ del sistema con la relación anterior.

Se define a $m_{i} x_{i}$ el momento de la masa $m_{i}$ , en este caso, tenemos dos momentos $m_{1}$ y $m_{2}$ con respecto al origen.

En general, si tenemos un sistema de $n$ partículas con sus respectivas masas $m_{1}, m_{2}, \dots ., m_{n}$ respectivamente localizadas en los puntos $x_{1}, x_{2}, \dots ., x_{n}$ sobre el eje $x$ y análogamente al estudio anterior, se puede demostrar que el centro de masa se puede calcular como:

$\bar{x} = \frac{\sum_{i = 1}^{n} m_{i} x_{i}}{\sum_{i = 1}^{n} m_{i}} = \frac{M}{m}$

Donde $m$ es la suma de las $n$ masas y $M$ es la suma de los $n$ momentos.

Centro de masas y momentos (bidimensional)

Consideremos ahora un sistema de $n$ partículas con masas $m_{1}, m_{2}, \dots ., m_{n}$ localizadas en los puntos $(x_{1}, y_{1}), (x_{2}, y_{2}), \dots ., (x_{n}, y_{n})$ en el plano $x y$ como se muestra en la figura $(2)$ .

Figura 2: Sistema de $4$ partículas con masa $m$ .

Análogamente al caso unidimensional, se define el momento del sistema respecto del eje $y$ como:

$\begin{matrix} (1) & M_{y} = \sum_{i = 1}^{n} m_{i} x_{i} \end{matrix}$

Y el momento del sistema respecto del eje $x$ como:

$\begin{matrix} (2) & M_{x} = \sum_{i = 1}^{n} m_{i} y_{i} \end{matrix}$

Por lo que el centro de masa $(\bar{x}, \bar{y})$ está dado como:

$\bar{x} = \frac{M_{y}}{m} \bar{y} = \frac{M_{x}}{m}$

Consideremos una placa con densidad uniforme $ρ$ , se desea localizar su centro de masa, para esto, supongamos que esta región está en el intervalo $[a, b]$ , dividimos este intervalo en $n$ subintervalos con puntos extremos $x_{0}, x_{1}, \dots ., x_{n}$ e igual amplitud $Δ x$ . Sea $\bar{x_{i}}$ el punto medio del intervalo $[x_{i - 1}, x_{i}]$ , por lo que $\bar{x_{i}} = (x_{i - 1} + x_{i}) / 2$ , así, tendremos $n$ polígonos o $R_{i}$ rectángulos, aproximando a la placa como se muestra en la figura $(3)$ .

El área del i-esimo rectángulo es:

$A_{i} = f (\bar{x_{i}}) Δ x_{i}$

Como estamos en el caso bidimensional, recordemos que la densidad es una densidad superficial dada como:

$ρ = \frac{M}{A}$

Por lo que, para la masa:

$M = ρ f (\bar{x_{i}}) Δ x_{i}$

El momento del rectángulo $R_{i}$ respecto del eje $y$ es el producto de su masa y la distancia del centroide del i-esimo rectángulo $R_{i}$ que es $C_{i} (\bar{x_{i}}, \frac{1}{2} f (\bar{x_{i}}))$ como se muestra en la figura $(3)$ , por la definición de $M_{y}$ $(1)$ , se tiene que:

$M_{y} (R_{i}) = (ρ f (\bar{x_{i}}) Δ x_{i}) \bar{x_{i}}$

Al sumar estos momentos y tender $n \to \infty$ tenemos que:

$M_{y} = lim_{n \to \infty} \sum_{i = 1}^{n} (ρ f (\bar{x_{i}}) Δ x_{i}) \bar{x_{i}} = ρ \int_{a}^{b} x f (x) d x$

Del modo similar, el momento del rectángulo $R_{i}$ respecto del eje $x$ está dado como el producto de su masa por la distancia $C_{i} (\bar{x_{i}}, \frac{1}{2} f (\bar{x_{i}}))$ al eje $x$ , por la definición de $M_{x}$ $(2)$ , se tiene que:

$M_{x} (R_{i}) = (ρ f (\bar{x_{i}}) Δ x_{i}) \frac{1}{2} f (\bar{x_{i}}) = ρ \frac{1}{2} [f (\bar{x_{i}}]^{2} Δ x$

Tomando el límite:

$M_{x} = lim_{n \to \infty} \sum_{i = 1}^{n} ρ \frac{1}{2} [f (\bar{x_{i}}]^{2} Δ x = \int_{a}^{b} ρ \frac{1}{2} [f (\bar{x_{i}}]^{2} d x$

El centro de masa de la placa se define análogamente al sistema de $n$ partículas como:

$\bar{x} = \frac{M_{y}}{m}$

$\bar{y} = \frac{M_{x}}{m}$

Pero la masa de la placa es el producto de su densidad y su área, la cual podemos calcularla por medio de una integral:

$m = ρ A = ρ \int_{a}^{b} f (x) d x$

Por tanto, para calcular el centroide $(\bar{x}, \bar{y})$ de esta placa se tiene que:

$\begin{matrix} (3) & \bar{x} = \frac{M_{y}}{m} = \frac{ρ \int_{a}^{b} x f (x) d x}{ρ \int_{a}^{b} f (x) d x} = \frac{\int_{a}^{b} x f (x) d x}{\int_{a}^{b} f (x) d x} = \frac{1}{A} \int_{a}^{b} x f (x) d x \end{matrix}$

$\begin{matrix} (4) & \bar{y} = \frac{M_{x}}{m} = \frac{ρ \int_{a}^{b} \frac{1}{2} [f (x)]^{2} d x}{ρ \int_{a}^{b} f (x) d x} = \frac{\int_{a}^{b} \frac{1}{2} [f (x)]^{2} d x}{\int_{a}^{b} f (x) d x} = \frac{1}{A} \int_{a}^{b} \frac{1}{2} [f (x)]^{2} d x \end{matrix}$

Si la región se encuentra entre dos curvas $y = f (x)$ y $y = g (x)$ donde $f (x) \geq g (x)$ podemos utilizar el mismo método anterior para encontrar el centroide $(\bar{x}, \bar{y})$ como:

$\bar{x} = \frac{\int_{a}^{b} x [f (x) - g (x)] d x}{\int_{a}^{b} (f (x) - g (x)) d x}$

$\bar{y} = \frac{\int_{a}^{b} [f^{2} (x) - g^{2} (x)] d x}{2 \int_{a}^{b} (f (x) - g (x)) d x}$

Veamos los siguientes ejemplos.

Ejemplos

Suponga que se colocan tres masas puntuales en el plano $x y$ de la siguiente manera: $m_{1} = 2 k g$ en la coordenada $(- 1, 3)$ , $m_{2} = 6 k g$ en la coordenada $(1, 1)$ y $m_{3} = 4 k g$ en la coordenada $(2, - 2)$ . Encuentre el centro de masa del sistema.

Calculamos la masa total como:

$m = \sum_{i = 1}^{3} m_{i} = 2 + 6 + 4 = 12 k g$

Ahora, encontrando los momentos respectivos en el eje $x$ y $y$ :

$M_{y} = \sum_{i = 1}^{3} m_{i} x_{i} = - 2 + 6 + 8 = 12$

$M_{x} = \sum_{i = 1}^{3} m_{i} y_{i} = 6 + 6 - 8 = 4$

Calculando el centro de masas:

$\bar{x} = \frac{M_{y}}{m} = \frac{12}{12} = 1$

$\bar{y} = \frac{M_{x}}{m} = \frac{4}{12} = \frac{1}{3}$

Por lo que el centro de masas de este sistema es:

$(\bar{x}, \bar{y}) = (1, \frac{1}{3})$

Encuentre el centroide de la región acotada por las curvas $y = \cos (x)$ , $y = 0$ , $x = 0$ y $x = π / 2$ .

El área de la región es:

$A = \int_{0}^{π / 2} \cos (x) d x = \sin (x) |_{0}^{π / 2} = 1$

Así, calculando el centroide se tiene que, para $\bar{x}$ $(3)$ :

$\bar{x} = \frac{1}{A} \int_{0}^{π / 2} x f (x) d x = \int_{0}^{π / 2} x \cos (x) d x = x \sin (x) |_{0}^{π / 2} - \int_{0}^{π / 2} \sin (x) d x$

$= \frac{π}{2} - 1$

Para $\bar{y}$ $(4)$ :

$\bar{y} = \frac{1}{A} \int_{0}^{π / 2} \frac{1}{2} (f (x))^{2} d x = \frac{1}{2} \int_{0}^{π / 2} \cos^{2} (x) d x$

$= \frac{1}{4} \int_{0}^{π / 2} (1 + \cos (2 x)) d x = \frac{1}{4} [x + \frac{1}{2} \sin (2 x)] |_{0}^{π / 2} = \frac{π}{8}$

Por tanto, el centroide es: $(\bar{x}, \bar{y}) = (\frac{π}{2} - 1, \frac{π}{8})$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Encuentre los momentos del centro de masas cuyas masas son 3, 4 y 8 con coordenadas $(- 1, 1)$ , $(2, - 1)$ y $(3, 2)$ respectivamente.
Demuestre que el centro de masas de una varilla o de una franja recta y delgada de densidad constante se encuentra en su punto medio.
Una varilla de longitud de 10cm. aumenta su grosor de izquierda a derecha en función de $f (x) = 1 + (x / 10) k g / m$ . Determinar el centro de masas de la varilla.
Encuentre el centro de masas de una placa semicircular de radio $r$ .
Encuentre el centroide de la región acotada por la recta $y = x$ y la parábola $y = x^{2}$ .

Más adelante…

En esta sección vimos como calcular el centro de masas y el momento de un sistema, en la siguiente sección veremos otra la aplicación de la integral en el área de la física, y es la aplicación de la integración al concepto de trabajo.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencia e Integral II: Aplicación de la integración al concepto de trabajo – El blog de Leo (nekomath.com)

Cálculo Diferencial e Integral II: Área de una superficie de revolución

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos como calcular el volumen de una superficie de revolución por el método de capas cilíndricas, ahora, en esta entrada veremos como calcular el área de una superficie de revolución.

Área de una superficie de revolución

Consideremos una región delimitada por el eje $x$ , las rectas $x = a$ y $x = b$ y la curva que tiene como función $y = f (x)$ , continua en el intervalo $[a, b]$ , giramos esta región alrededor del eje $x$ obteniendo una superficie de revolución como en la figura $(1)$ .

*Figura 1: Aproximación de un cono al area $Δ S_{i}$*

Dividimos el intervalo $[a, b]$ en $n$ subintervalos en donde el i-ésimo subintervalo es $[x_{i - 1}, x_{i}]$ y sea $Δ S_{i}$ el valor del área superficial del i-ésimo subintervalo $[x_{i - 1}, x_{i}]$ lo podemos calcular viéndolo como un tronco cónico (encerrado en líneas puntuadas, figura $(1)$ ) en donde su área de superficial es:

$\begin{matrix} (1) & S = π (r_{1} + r_{2}) g \end{matrix}$

Donde $g$ es la generatriz del tronco cónico, $r_{1}$ y $r_{2}$ son los radios respecto al eje de rotación.

Para dar correspondencia a la figura $(1)$ , sea $g_{i} = Δ L_{i}$ la generatriz del i-esimo tronco cónico, que se aproxima a la gráfica $y = f (x)$ como se muestra en la figura $(1)$ en el intervalo $[x_{i - 1}, x_{i}]$ , por lo que el área superficial del i-esimo tronco cónico designado como $Δ S_{i}$ , lo podemos aproximar mediante la relación $(1)$ como:

$Δ S_{i} \approx π (f (x_{i - 1}) + f (x_{i})) Δ L_{i}$

Pero $Δ L_{i}$ lo podemos aproximar por la definición de la longitud de arco en el intervalo $[x_{i - 1}, x_{i}]$ , así:

$Δ L_{i} \approx \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x$

Con $Δ x = x_{i} - x_{i - 1}$ , por tanto:

$\begin{matrix} (2) & Δ S_{i} \approx π (f (x_{i - 1}) + f (x_{i})) \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x \end{matrix}$

Por otro lado, en el curso de Cálculo I, se vio el desarrollo de Taylor de una función $f (x)$ , por lo que la definición del desarrollo en Taylor está dado de la forma:

$y (x + h) \approx y (x) + h y^{'} (x) + \frac{h^{2} y^{''} (x)}{2!} + \dots .$

Aplicando lo anterior para $f (x_{i - 1})$ suponiendo que $Δ^{n} x$ es pequeño respecto al término $Δ x$ , se tiene que:

$f (x_{i - 1}) = f (x_{i - 1} + x_{i} - x_{i}) = f (x_{i} - Δ x) \approx f (x_{i}) - f^{'} (x_{i}) Δ x$

Substituyendo en $Δ S_{i}$ $(2)$ , tenemos que:

$Δ S_{i} \approx π \sqrt{1 + (f^{'} (x_{i})^{2})} (f (x_{i - 1}) + f (x_{i})) Δ x = π \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x (f (x_{i}) - f^{'} (x_{i}) Δ x + f (x_{i}))$

$= π \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x (2 f (x_{i}) - f^{'} (x_{i}) Δ x) = π \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x 2 f (x_{i}) - π \sqrt{1 + (f^{'} (x_{i})^{2})} Δ^{2} x f^{'} (x_{i})$

Observemos que cuando $n$ es demasiado grande el termino $Δ^{2} x$ es pequeño respecto al término $Δ x$ , por lo que para $n$ lo suficientemente grande podemos despreciar el termino $Δ^{2} x$ , así:

$Δ S_{i} \approx 2 π f (x_{i}) \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x$

Sumando todas las $n$ áreas superficiales y tendiendo $n \to \infty$ tenemos que el área de superficie $A_{s}$ es:

$A_{s} = lim_{n \to \infty} \sum_{i = 1}^{n} Δ S_{i} = lim_{n \to \infty} \sum_{i = 1}^{n} 2 π f (x_{i}) \sqrt{1 + (f^{'} (x_{i})^{2})} Δ x$

Se define el área superficial de un sólido de revolución si una función $f (x) \geq 0$ es continua en el intervalo $[a, b]$ y gira alrededor del eje $x$ como:

$\begin{matrix} (3) & A_{s} = \int_{a}^{b} 2 π y \sqrt{1 + {(\frac{d y}{d x})}^{2}} d x = \int_{a}^{b} 2 π f (x) \sqrt{1 + (f^{'} (x)^{2})} d x \end{matrix}$

Análogamente, se define el área superficial de un sólido de revolución alrededor del eje $y$ como:

$\begin{matrix} (4) & A_{s} = \int_{c}^{d} 2 π x \sqrt{1 + {(\frac{d x}{d y})}^{2}} d y = \int_{c}^{d} 2 π f (y) \sqrt{1 + (f^{'} (y)^{2})} d y \end{matrix}$

Ejemplos

Determinar el área de la superficie generada al hacer girar la curva $2 \sqrt{x}$ , donde $1 \leq x \leq 2$ alrededor del eje x.

Figura 2: Grafica de la función $f (x) = 2 \sqrt{x}$ y su correspondiente superficie de revolución.

Tenemos que $a = 1$ , $b = 2$ y la curva que tiene como función $f (x) = 2 \sqrt{x}$ , derivando obtenemos:

$\frac{d y}{d x} f (x) = \frac{1}{\sqrt{x}}$

La gráfica la vemos en la figura $(2)$ , así, utilizamos la relación $(3)$ y calculamos el área como:

$S = \int_{1}^{2} 2 π (2 \sqrt{x}) \sqrt{1 + {(\frac{1}{\sqrt{x}})}^{2}} d x$

Vemos que:

$\sqrt{1 + {(\frac{1}{\sqrt{x}})}^{2}} = \sqrt{1 + \frac{1}{x}} = \sqrt{\frac{x + 1}{x}} = \frac{\sqrt{x + 1}}{\sqrt{x}}$

Sustituyendo esta expresión:

$S = \int_{1}^{2} 2 π (2 \sqrt{x}) \frac{\sqrt{x + 1}}{\sqrt{x}} d x = \int_{1}^{2} 4 π \sqrt{x + 1} d x$

Utilizando el método de sustitución tenemos que esta integral nos da por resultado:

$S = 4 π \frac{2}{3} [(x + 1)^{2 / 3}] |_{1}^{2} = \frac{8 π}{3} (3 \sqrt{3} - 2 \sqrt{2})$

El segmento de recta $x = 1 - y$ , $0 \leq y \leq 1$ se hace girar alrededor del eje $y$ para generar el cono de la figura $(3)$ , determinar el área de su superficie lateral (la cual excluye el área de la base).

*Figura 3: Grafica de la recta $x = 1 - y$ y su correspondiente superficie de revolución.*

Tenemos que $c = 0$ , $d = 1$ y la función de la curva:

$x = 1 - y \Rightarrow \frac{d x}{d y} = - 1 \Rightarrow \sqrt{1 + {(\frac{d x}{d y})}^{2}} = \sqrt{1 + (- 1)^{2}} = \sqrt{2}$

Utilizamos la relación $(4)$ y calculamos el área superficial como:

$S = \int_{0}^{1} 2 π f (y) \sqrt{2} d y = \int_{0}^{1} 2 π (1 - y) \sqrt{2} d y = 2 π \sqrt{2} [y - \frac{y^{2}}{2}] |_{0}^{1} = 2 π \sqrt{2} (1 - \frac{1}{2}) = π \sqrt{2}$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

El segmento de recta $y = \frac{x}{2}$ , $0 \leq x \leq 4$ se hace girar alrededor del eje x para generar un cono, determinar el área de su superficie lateral.
Un segmento de recta $y = \sqrt{2}$ , $\frac{3}{4} \leq x \leq \frac{15}{4}$ se hace girar alrededor del eje x determinar el área de su superficie.
El segmento de recta $x = \frac{y^{3}}{3}$ , $0 \leq y \leq 1$ se hace girar alrededor del eje y determinar el área de su superficie.
Un segmento de recta $x = 2 \sqrt{4 - y}$ , $0 \leq y \leq \frac{15}{4}$ se hace girar alrededor del eje y determinar el área de su superficie.
El segmento de recta $y = \sqrt{x + 1}$ , $1 \leq x \leq 5$ se hace girar alrededor del eje x determinar el área de su superficie.

Más adelante…

En esta entrada vimos como calcular el área de superficie de un sólido generado a partir de una curva respecto de un eje. En la siguiente sección trabajaremos con un teorema relacionado con el cálculo de estas áreas llamado el teorema de Pappus-Guldinus.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencial e Integral II: Cálculo de volúmenes por medio de casquillos cilíndricos – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus – El blog de Leo (nekomath.com)

Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En las secciones anteriores vimos como calcular tanto el volumen como el área de un sólido de revolución, en esta entrada veremos un teorema en el que podemos calcular áreas y volúmenes de sólidos de revolución con sus respectivos centroides, es decir, su centro de simetría, a este teorema se le conoce como teorema del centroide de Pappus que se divide a su vez en dos teoremas y aunque no es una aplicación directa de las integrales, podemos calcular el volumen o el área de estos sólidos de una manera más sencilla, veamos el primer teorema.

Teorema de Pappus (Volúmenes)

El volumen $V$ de un sólido de revolución generado mediante la rotación de una curva plana $C$ alrededor de un eje externo, de manera que, esta última no corte el interior de la región, es igual al producto del área $A$ por la distancia $2 π d$ recorrida por su centroide en una rotación completa alrededor del eje:

$V = 2 π A d$

Demostración:

Sea un área $A$ generada mediante la rotación de una curva plana $C$ alrededor del eje $x$ , consideremos un elemento $d A$ de dicha área, el volumen $d V$ generado por el elemento $d A$ es igual a:

$d V = 2 π y d A$

Donde $y$ es la distancia entre el eje $x$ y el elemento $d A$ , por tanto:

$V = \int 2 π y d A = 2 π \bar{y} A$

Con $\bar{y} = d$ y $2 π \bar{y}$ es la distancia recorrida por el centroide de $A$ .

Teorema 2 de Pappus (Áreas)

El área $A$ de una superficie de revolución generada mediante la rotación de una curva plana $C$ alrededor de un eje externo, es igual a su longitud $L$ , multiplicada por la distancia $2 π d$ recorrida por su centroide en una rotación completa alrededor del eje, entonces:

$A = 2 π L d$

Demostración:

Sea $L$ la longitud de una curva plana $C$ que rota alrededor del eje $x$ y consideremos un elemento $d L$ de dicha longitud. El área $d A$ generada por el elemento $d L$ es igual a:

$d A = 2 π y d L$

Donde $y$ es la distancia del elemento $d L$ al eje $x$ , por tanto:

$A = \int 2 π y d L = 2 π \bar{y} L$

Con $\bar{y} = d$ y $2 π \bar{y}$ es la distancia recorrida por el centroide $L$ .

Veamos unos ejemplos de como aplicar el teorema de Pappus-Guldinus.

Ejemplos

Un toroide se forma al hacer girar un círculo de radio $r$ respecto a una recta en el plano del círculo que es la distancia $R > r$ desde el centro del círculo. Encuentre el volumen del toroide.

El círculo tiene área $A = π r^{2}$ , por simetría su centroide es su centro, por tanto, la distancia recorrida por el centroide durante una rotación está dada como $d = 2 π R$ .

Por el teorema de Pappus (volumen), el volumen del toroide es:

$V = A d = (π r^{2}) (2 π R) = 2 π^{2} r^{2} R$

Calcule el área de la superficie del toro del ejercicio anterior.

Del segundo teorema de Pappus (Área) tenemos que:

$A = 2 π L d = 2 π (r) (2 π R) = 4 π^{2} r R$

Calcula el área de la superficie generada por una circunferencia cuyo radio es de $3 m$ , girando $2 π$ alrededor de una recta tangente.

Tenemos que la longitud es $L = 2 π (3) = 6 π$

Por el segundo teorema de Pappus calculamos el área de la superficie como:

$A = 2 π L d = 2 π (6 π) (3) = 36 π^{2}$

Calcula el centroide de un alambre semicircular de radio $R$ , que gira alrededor del eje $x$ .

Para calcular el centroide podemos utilizar cualquiera de los dos teoremas de Pappus, en este caso, es fácil calcular el centroide por el teorema de Pappus de áreas, veamos:

Sabemos que el área generada es:

$A = 4 π R^{2}$

Y la longitud es:

$L = π R$

Por el teorema de Pappus (áreas), tenemos que:

$4 π R^{2} = 2 π \bar{y} (π R) \Rightarrow \bar{y} = \frac{2 R}{π}$

Calcule el volumen del sólido generado por un cuadrado de lado $a = 3$ que gira alrededor del eje $y$ .

Sabemos que el área lo calculamos como:

$A = a^{2} = 3^{2} = 9$

Sabemos que el centroide de un cuadrado está justo en el centro, o a la mitad de cada cara, por lo que:

$\bar{y} = 1.5$

Así, calculando el volumen por el teorema de Pappus para volúmenes, tenemos que:

$V = 2 π A \bar{y} = 2 π (9) (1.5) = 27 π$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Hallar el volumen y el área de la superficie de un solido de una esfera de radio r.
Hallar el volumen de un solido de un cono con altura h y radio r.
Calcule el volumen del solido obtenido al hacer girar el triangulo con vértices $(2, 3)$ , $(2, 5)$ y $(5, 4)$ respecto al eje x.
La región cuadrada con vértices $(0, 2)$ , $(2, 0)$ , $(4, 2)$ y $(2, 4)$ se hace girar alrededor del eje $x$ para generar un solido. Determine el volumen y el área de la superficie del sólido.
Localice el centroide de una región semicircular entre la semicircunferencia $y = \sqrt{a^{2} - x^{2}}$ y el eje x.

Más adelante…

Vimos en esta sección el teorema de Pappus con el que se puede calcular el volumen, centroide y el área de un solio de revolución, en la siguiente sección veremos una aplicación más de la integral, en este caso, en el área de la física, que es cálculo de momentos y centros de masa.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencial e Integral II: Área de una superficie de revolución – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencial e Integral II: Centro de masa y momentos – El blog de Leo (nekomath.com)