Introducción
En esta sección veremos otra aplicación de las integrales en el área de la física y es en la presión hidrostática, que resuelve algunos problemas que requieren determinar fuerzas o presiones que actúan sobre un objeto sumergido en algún fluido estático.
Fuerza y presión hidrostática
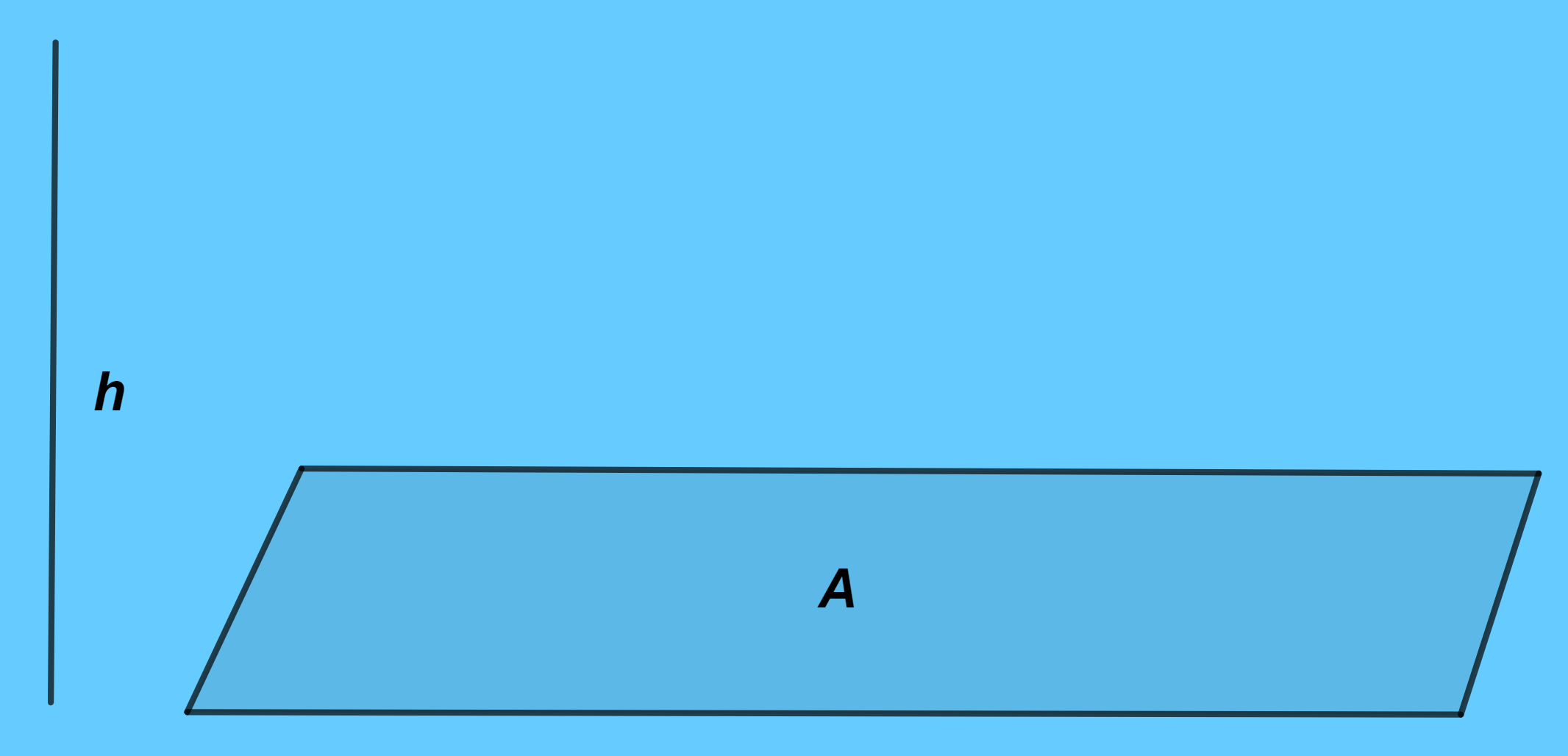
Supongamos que una placa horizontal delgada con área $A$ sumergido en un fluido con densidad constante $\rho$ a una profundidad $h$ debajo de la superficie del fluido como se muestra en la figura $(1)$.
El volumen del fluido sobre la placa es:
$$V=Ah$$
De modo que su masa es:
$$m=\rho V=\rho Ah$$
Por lo que la fuerza que ejerce la placa sobre el fluido es:
$$F=mg=\rho g Ah$$
Donde $g$ es la aceleración ejercida por la gravedad $(g=9.81 \space m/s^{2})$ en la Tierra. Recordemos que la presión $P$ se define como la fuerza por unidad de área:
$$P=\frac{F}{A}=\rho gh$$
Donde las unidades son Pascales o Newton por metro cuadrado: $1 \space N/m^{2}=1 \space Pa$.
A la cantidad $w=\rho g$ se le conoce como el peso específico, gravedad especifica o densidad de peso.
Veamos un ejemplo:
- ¿Cuál es la presión y la fuerza sobre la parte superior de un plato plano y circular de 3 metros que está sumergido a 10 metros bajo el agua.
Recordemos que la densidad del agua es: $\rho=1000 \space kg/m^{3}$, entonces podemos calcular la presión como:
$$P=\rho gh=\left ( 1000 \space kg/m^{3}\right )\left (9.81 \space m/s^{2} \right )\left (10m \right )=98000 \space Pa$$.
Como la fuerza la podemos calcular como: $F=PA$, entonces:
$$F=P \pi r^{2}=\left (98000 \space Pa \right )\left (\pi \right )\left (3m \right )^{2}=2.77×10^{6}N$$
Existe un principio importante, a este principio se le denomina el principio de Pascal, el cual nos dice que la presión de un fluido en el que cualquier punto en un líquido, la presión es la misma en todas las direcciones, es decir, un buzo siente la misma presión en la nariz y en ambos oídos. Al tener la presión dependiente de la profundidad, entonces al sumergir un cuerpo más profundo en un fluido, la presión va cambiando, veamos como va cambiando.
Supongamos que una superficie plana se sumerge verticalmente en un fluido con densidad de peso $w$ donde la parte sumergida se extiende sobre el eje $y$ desde $y=a$ hasta $y=b$. Hacemos una partición de $[a, b]$ cortando la región en delgadas franjas horizontales perpendiculares al eje $y$ por lo que el ancho de estas franjas es $\Delta y$ unidades por $L(y)$ unidades de largo (figura $(2)$), por lo que la fuerza que ejerce el fluido contra un lado de la franja se aproxima como:
$$\Delta F\approx w \space \cdot (profundidad \space de \space la \space franja) \cdot \space L(y)\cdot \Delta y$$
Supongamos que hay $n$ franjas en el intervalo $[a, b]$, sumamos estas $n$ franjas, por lo que la suma de Riemann es:
$$F \approx \sum_{i=1}^{n} w \space \cdot (profundidad \space de \space la \space franja) \cdot \space L(y_{i})\cdot \Delta y_{i}$$
Para una función continua en el intervalo $[a, b]$ y tendiendo a $n \to \infty$ entonces se tiene que:
$$F=\int_{a}^{b} w \space h(y) L(y)dy$$
Veamos un ejemplo:
- Calcule la fuerza del fluido total que se ejerce sobre una pared vertical en una represa con altura de $100m$ y ancho $300m$
Calculemos la densidad de peso como:
$$w=\rho g=\left (1000 \space kg/m^{3} \right )\left (9.81 \space m/s^{2} \right )=9800 \space N/m^{2}$$
Supongamos que la profundidad va variando como $h(y)=y$ y el ancho de la represa es $L=300 \space m$, por lo que la fuerza la podemos calcular como:
$$F=\int_{0}^{100}wh(y)L(y)dy=\int_{0}^{100}\left (9800 \right )\left (y \right )\left (300 \right )dy=2.94×10^{6}\int_{0}^{100}y dy$$
$$=2.94×10^{6}\left [ \frac{y^{2}}{2} \right ]\bigg|_{0}^{100}=1.47×10^{10} \space N$$.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
- ¿Cuál es la presión en el fondo de una alberca a 2 metros?.
- Encuentre la fuerza en un lado de un contenedor cubico de $6 \space cm$ si el recipiente esta lleno de mercurio. La densidad del mercurio es $\rho=13600 \space kg/m^{3}$
- Una placa triangular rectángulo de base $2 \space m$ altura $1 \space m$ está sumergida verticalmente en agua, con el vértice superior $3 \space m$ debajo de la superficie. Encuentra la fuerza en un lado de la placa. Hint: Considere la ecuación de una recta.
- Determine la fuerza hidrostática sobre una cara de un cilindro con radio de $3 \space cm$ si el cilindro esta sumergido a $10 \space cm$. Hint: Utilice la ecuación de un circulo y ponga el origen en el centro del cilindro.
- Una placa triangular rectángulo de base $2 \space m$ y altura $1\space m$ está sumergida verticalmente en agua, con el vértice superior $3\space m$ debajo de la superficie. Encuentra la fuerza en un lado de la placa.
Más adelante…
En esta sección, vimos como resolver algunos problemas de fuerza y presión en algún fluido estático, en la siguiente sección veremos otra aplicación de la integral en el área de la probabilidad.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencia e Integral II: Aplicación de la integración al concepto de trabajo – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Probabilidad – El blog de Leo (nekomath.com)