$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
En otros cursos, donde el conjunto de los números reales es el protagonista, se suele hablar de una propiedad: El conjunto $\mathbb{R}$ es completo. Esto puede concluirse a partir de 3 situaciones que son válidas en $\mathbb{R}:$
- El axioma del supremo o de completitud.
- La intersección de intervalos cerrados encajados cuya longitud tiende a cero es no vacía.
- Las sucesiones de Cauchy son convergentes en $\mathbb{R}.$
En las siguientes entradas veremos cómo las propiedades $2$ y $3$ son generalizadas a los espacios métricos. La primera no es posible, por ejemplo, en conjuntos métricos que no están ordenados. Pero tampoco basta que un conjunto tenga un orden en sus elementos para que todos sus subconjuntos acotados tengan un supremo en el conjunto. Este es el caso de algunos conjuntos acotados en el subespacio $\mathbb{Q}$ que tendrán supremo en $\mathbb{R}$ pero no en $\mathbb{Q}.$ ¿Puedes dar un ejemplo?
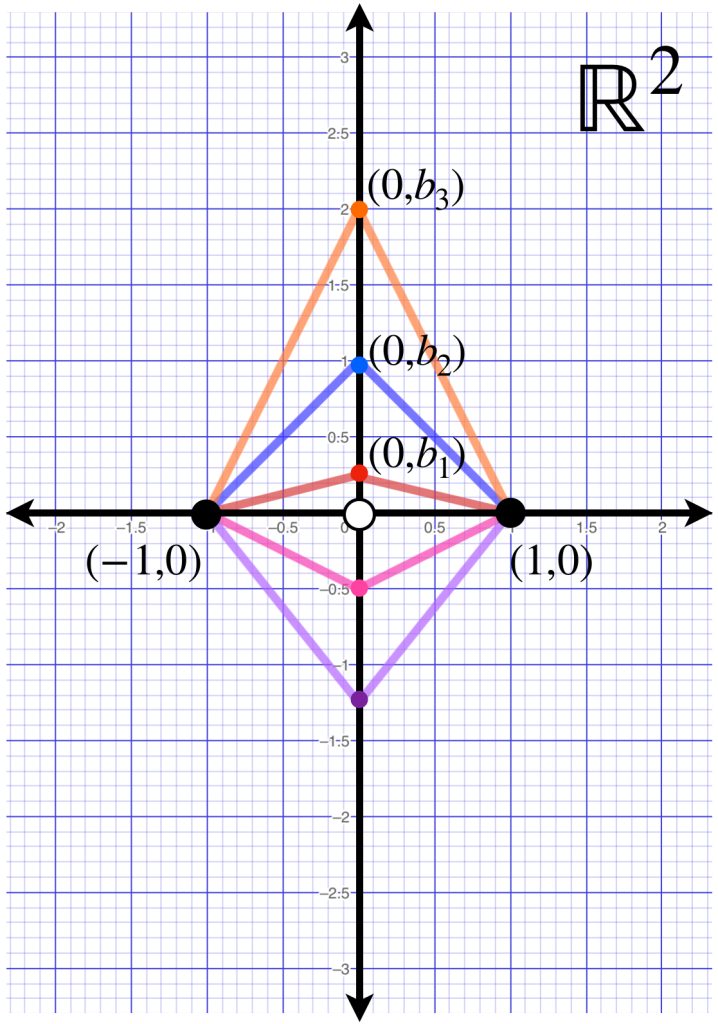
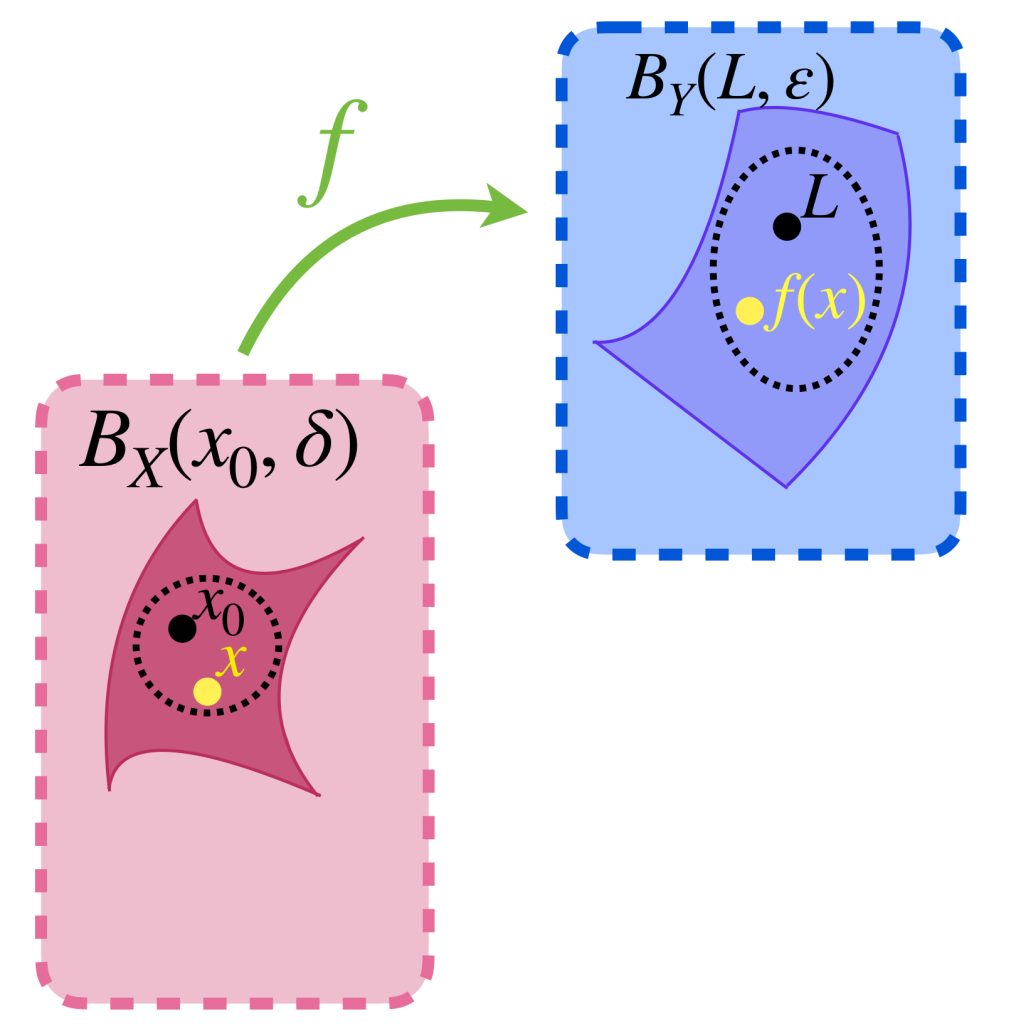
Recordemos que en la entrada de Convergencia vista anteriormente, hablamos de sucesiones $(x_n)_{n \in \mathbb{N}}\,$ que se aproximan a un punto $x$ en un espacio métrico $(X,d).$ Según la definición, $x_n \to x$ significa que dado $\varepsilon >0$ existe $N \in \mathbb{N}$ que cumple para cada $n \geq N, \, d(x_n,x)< \varepsilon.$ Esta definición compara la distancia entre cada punto de la sucesión con un punto fijo $x.$ Sin embargo, ¿qué podemos decir de la distancia entre cualesquiera dos puntos de la sucesión?
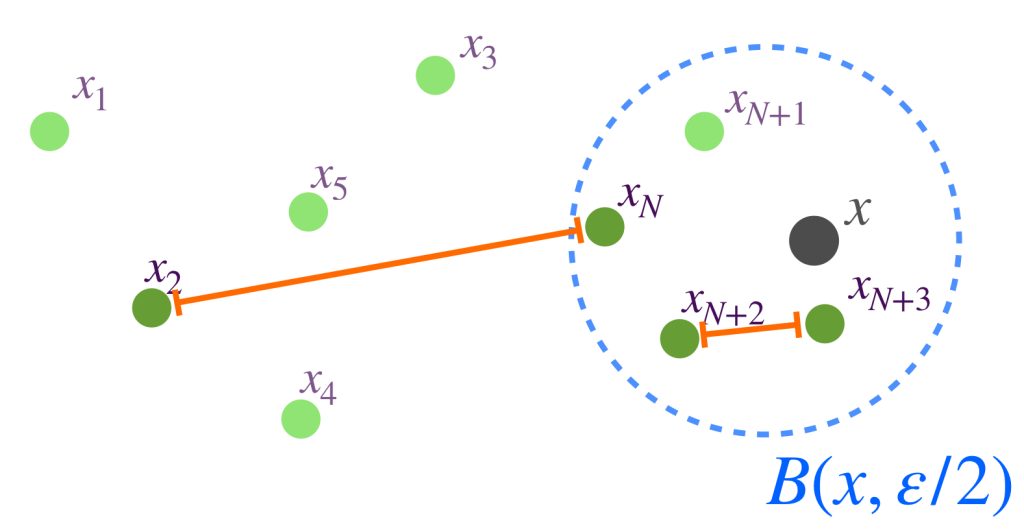
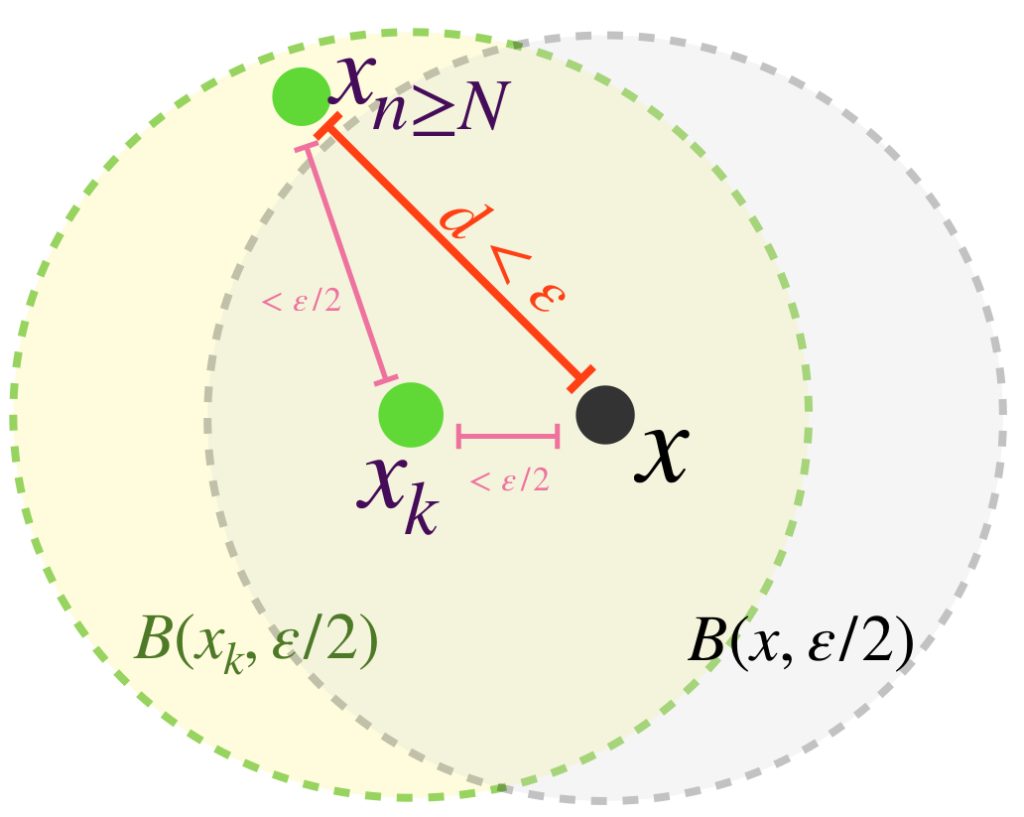
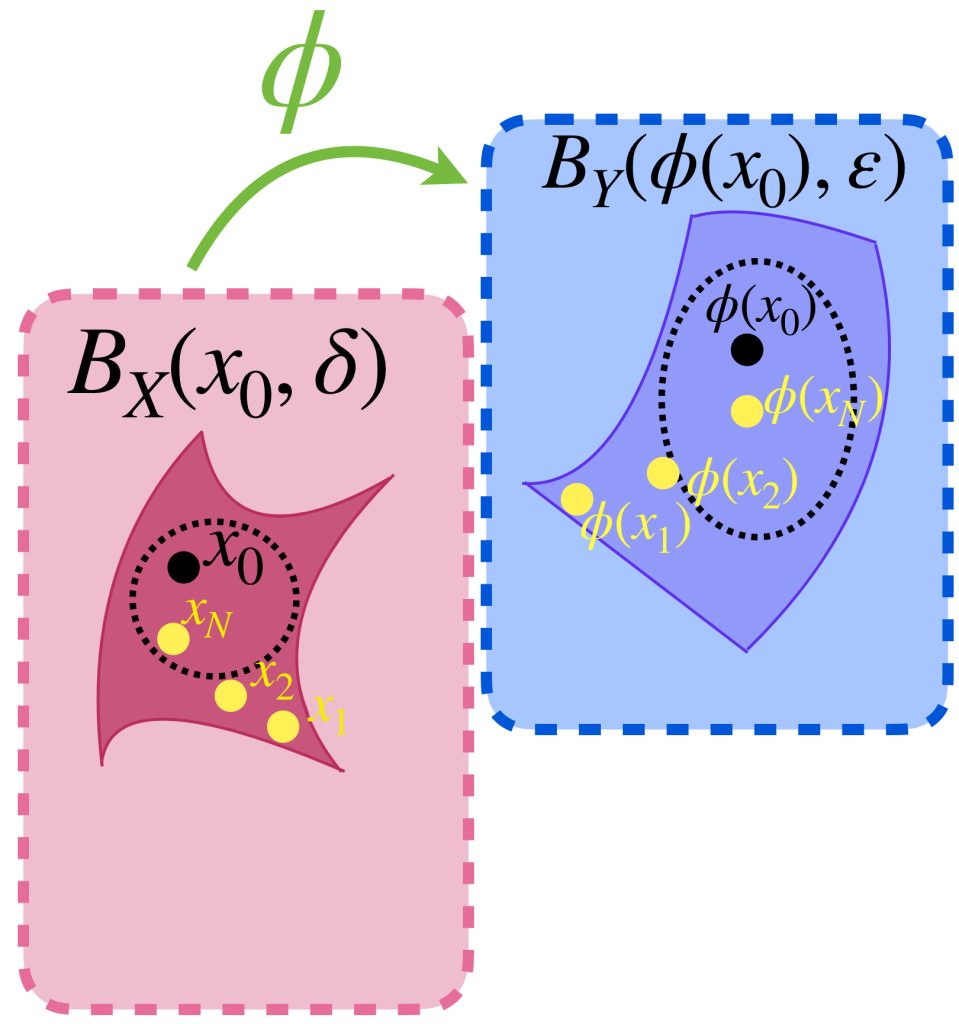
Sea $\varepsilon>0.$ En una sucesión convergente $(x_n)_{n \in \mathbb{N}}\,$ ocurrirá que para algún $N \in \mathbb{N}$ si $n \geq N$ entonces $d(x_n,x)< \frac{\varepsilon}{2}.$
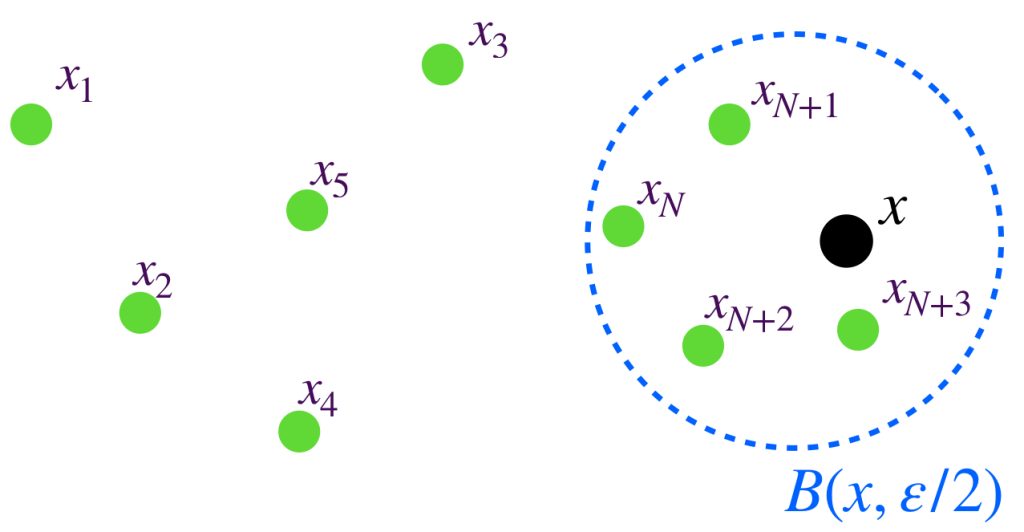
Podemos ver que mientras más se aproximan los puntos de la sucesión al punto de convergencia $x$, los puntos de la sucesión se acercan cada vez más entre ellos también.
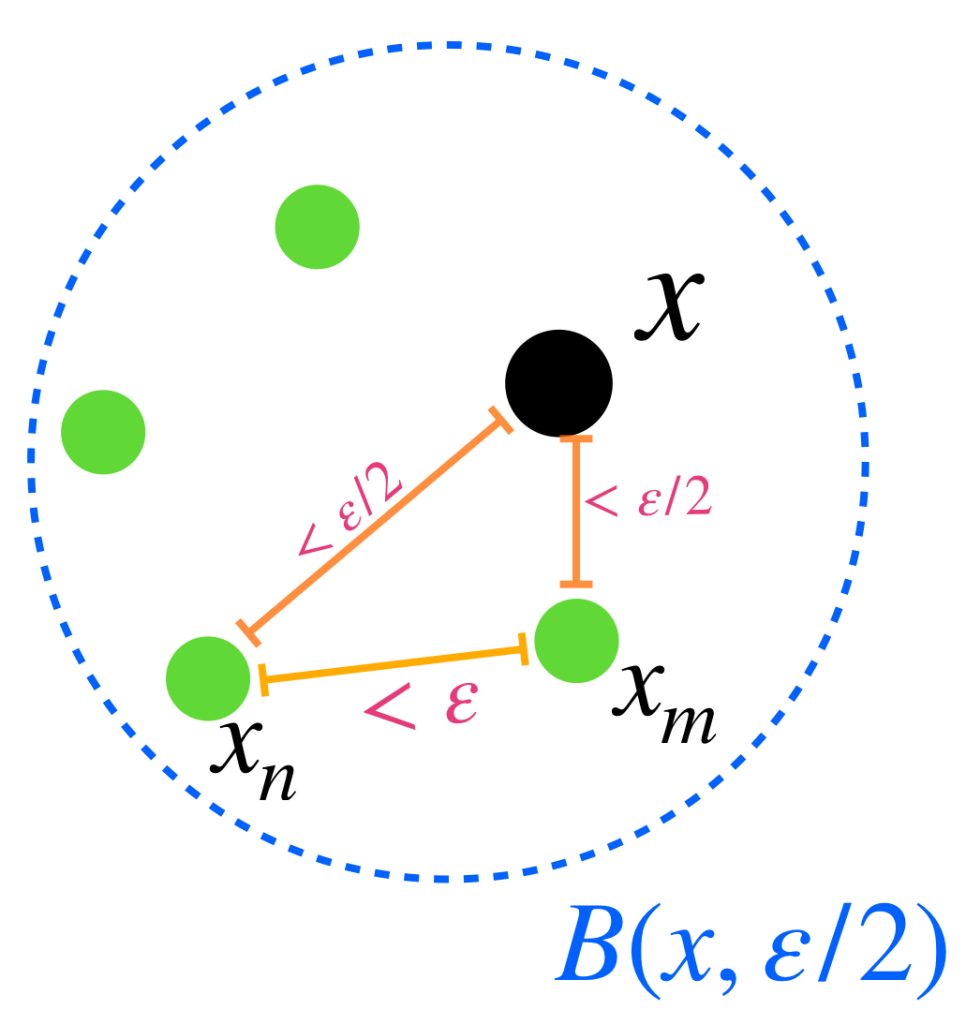
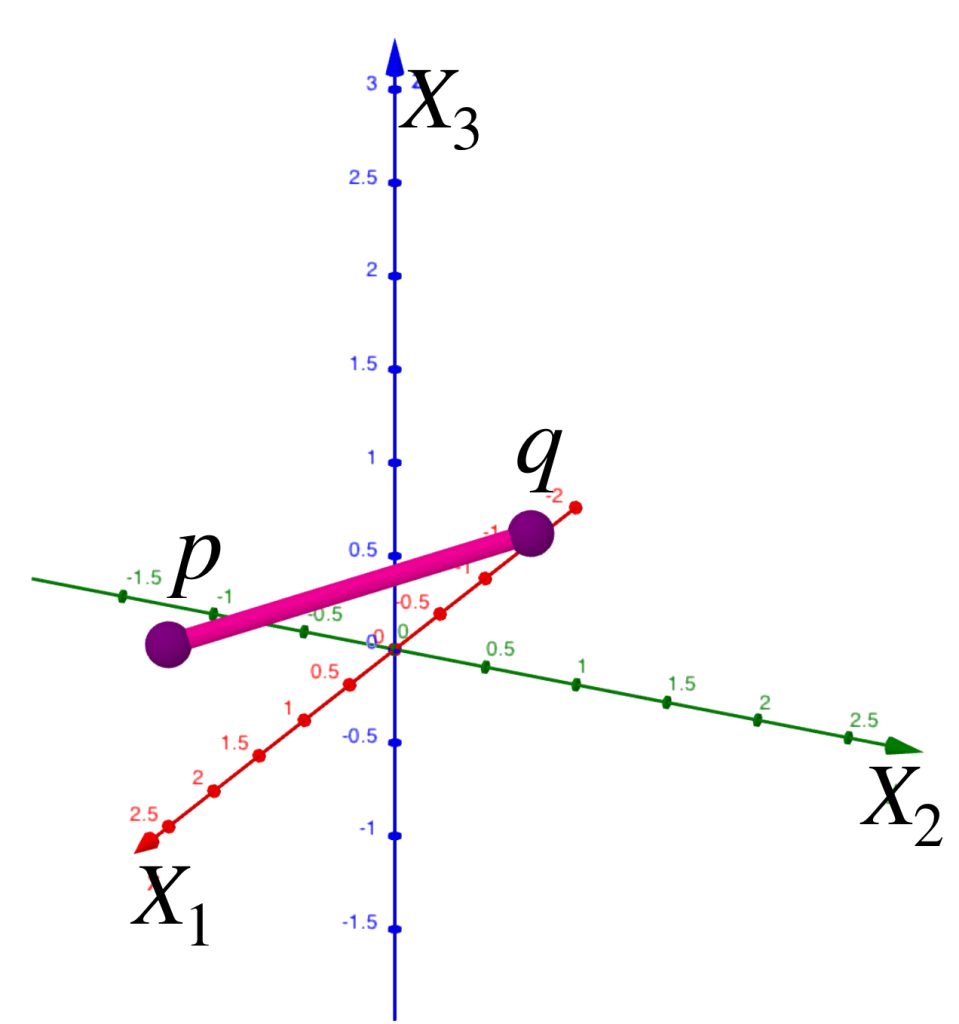
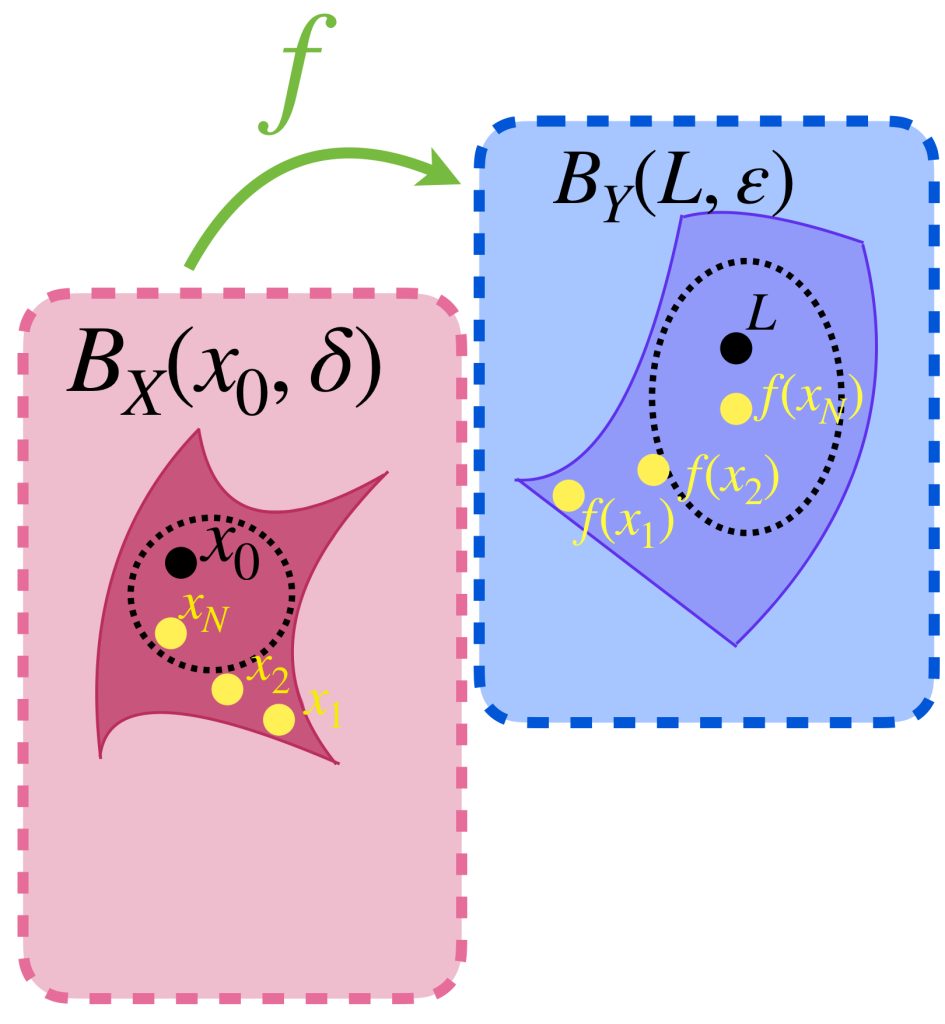
Más aún, la desigualdad del triángulo garantiza que si $n,m \geq N$ entonces:
$$d(x_n,x_m) \leq d(x_n,x) + d(x,x_m) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon.$$ como lo expresa la siguiente imagen:
Esto indica que es posible identificar un término de la sucesión, a partir del cual las distancias entre cualesquiera dos de ellos será arbitrariamente pequeña. Aunque ya vimos que esto pasa en sucesiones convergentes también puede ocurrir en algunas que no lo son. Cuando las sucesiones tienen esta característica son denominadas como sigue:
Definición. Sucesión de Cauchy. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de un espacio métrico $(X,d).$ Decimos que es una sucesión de Cauchy si satisface la condición de Cauchy que es que:
para todo $ \, \varepsilon>0,$ existe $N \in \mathbb{N}$ tal que para todo $ \, n,m \geq N$ ocurre que $d(x_n,x_m)< \varepsilon.$
Proposición. Si una sucesión es de Cauchy entonces es acotada.
Demostración:
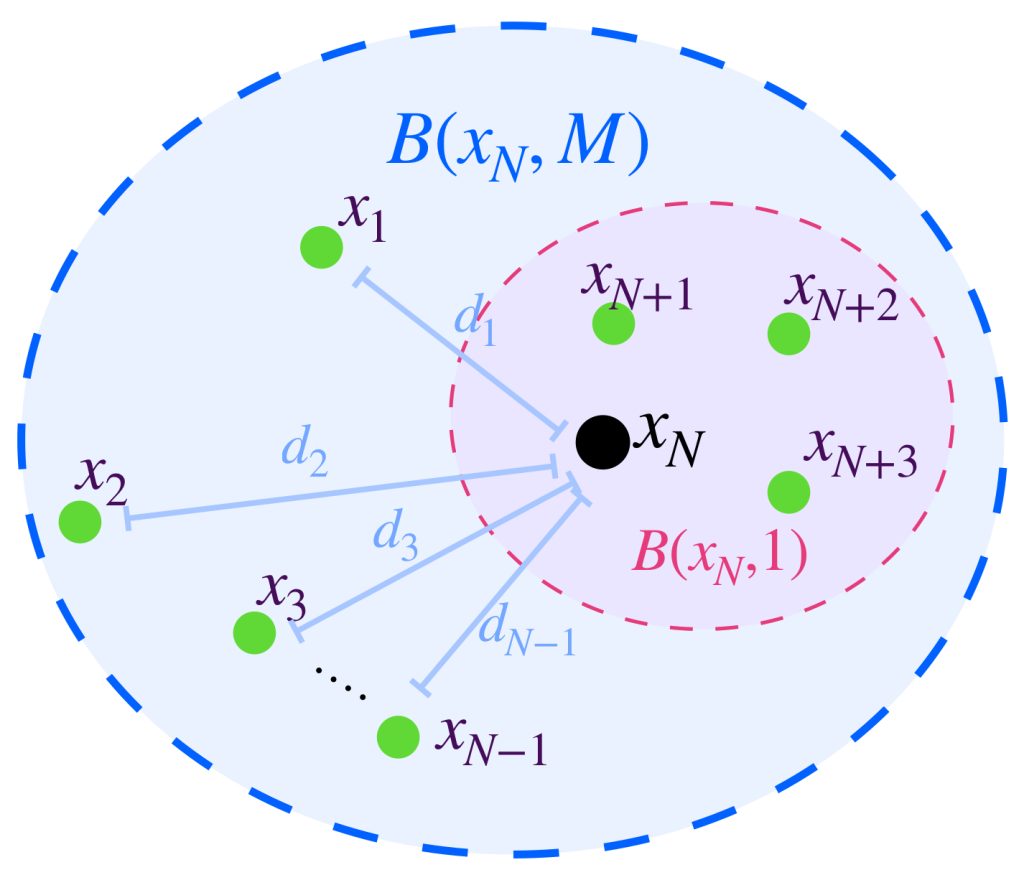
Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy. Entonces para $\varepsilon=1$ existe $N \in \mathbb{N}$ tal que para todo $ \, n,m \geq N$ se cumple que $d(x_n,x_m)<1$ Entonces, para todo $ \, m \geq N, d(x_N,x_m)< 1.$ Si definimos las distancias faltantes en los términos de la sucesión, es decir, las distancias $d_i:= d(x_N,x_i) \, $ con $ \, i=1,…,N-1$ y elegimos $M > max \{ d_1,…,d_{N-1},1 \} , $ se concluye que existe una bola abierta que tiene todos los términos de la sucesión, la bola $B(x_N,M).$
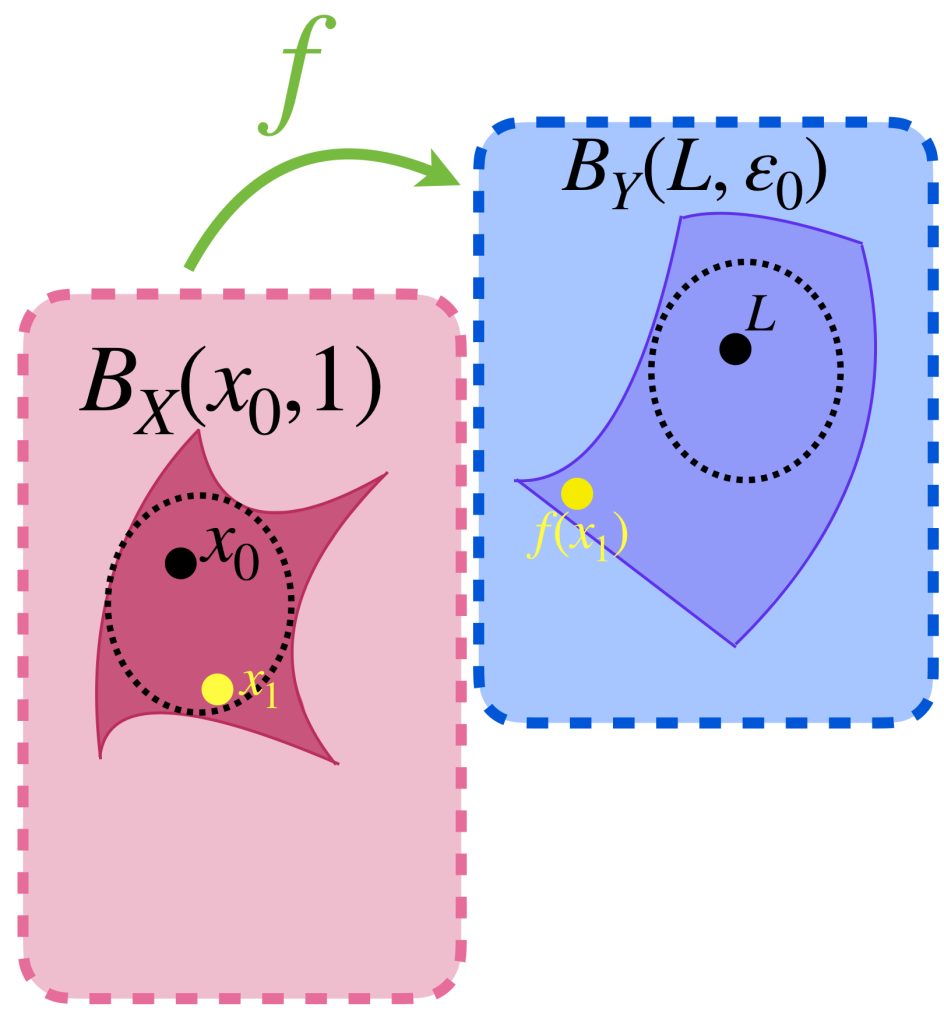
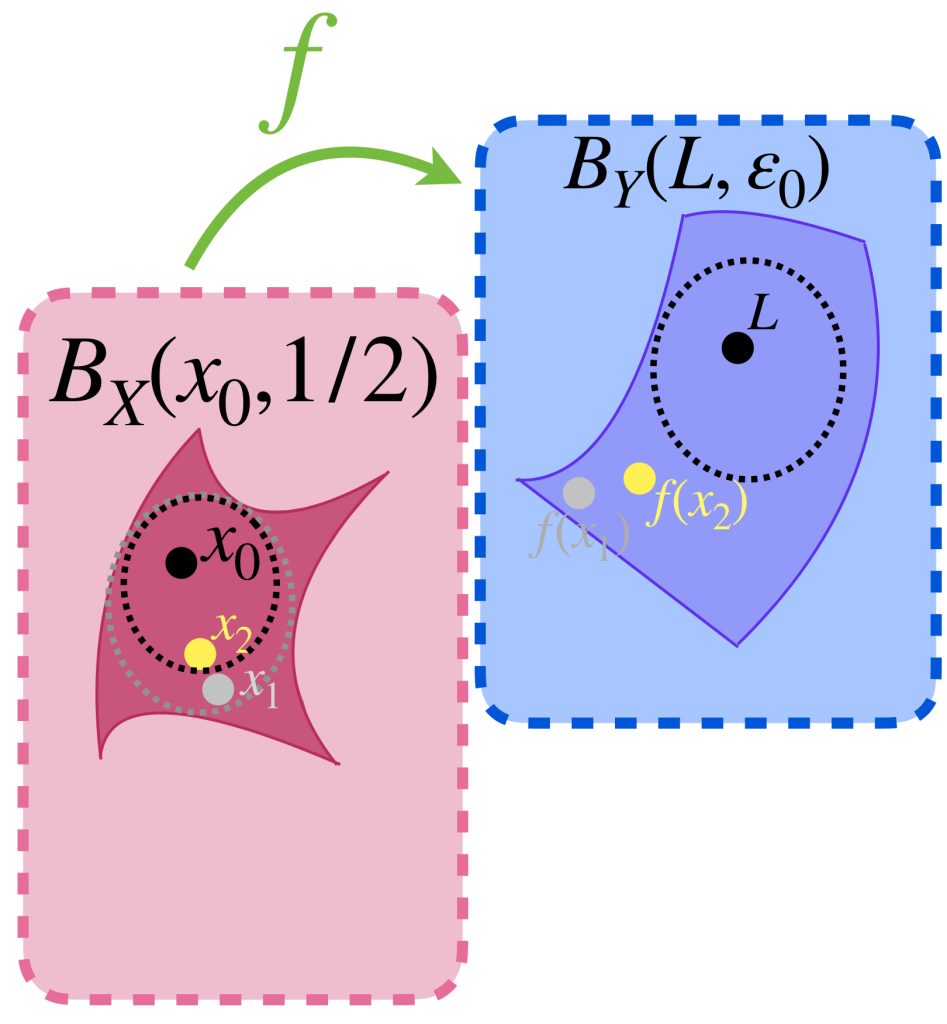
A pesar de que una sucesión convergente es de Cauchy, no toda sucesión de Cauchy es convergente.
Ejemplo: La sucesión $(\frac{1}{n})_{n \in \mathbb{N}} \,$ en el subespacio euclidiano $(0,1]$ es de Cauchy, pero no es convergente en $(0,1].$ La demostración se deja como ejercicio.
No obstante tenemos el siguiente resultado:
Proposición. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy en el espacio euclidiano $\mathbb{R}^n$, entonces la sucesión también es convergente.
Demostración:
Si el conjunto de términos de la sucesión dado por $\{ x_n \} :=\{x_n:n \in \mathbb{N}\} \,$ es finito entonces es convergente. (Ejercicio de la tarea moral de la entrada de Convergencia). Pero si es infinito entonces, al ser también acotado (por la proposición anterior) se sigue que el conjunto de los términos de la sucesión tiene un punto de acumulación $x \in \mathbb{R}^n.$ Esto es resultado del teorema de Bolzano-Weierstrass, que se ve en los cursos de cálculo y dice que todo conjunto infinito acotado en $\mathbb{R}^n$ tiene un punto de acumulación. (La demostración puede consultarse en el libro «Análisis Matemático, Introducción Moderna al Cálculo Superior» de Tom. M. Apóstol. Para una referencia formal y pública, consultar Universidad de Alicante. (s.f.). El espacio euclídeo real n-dimensional [Material de curso]. RUA – Repositorio Institucional de la Universidad de Alicante).
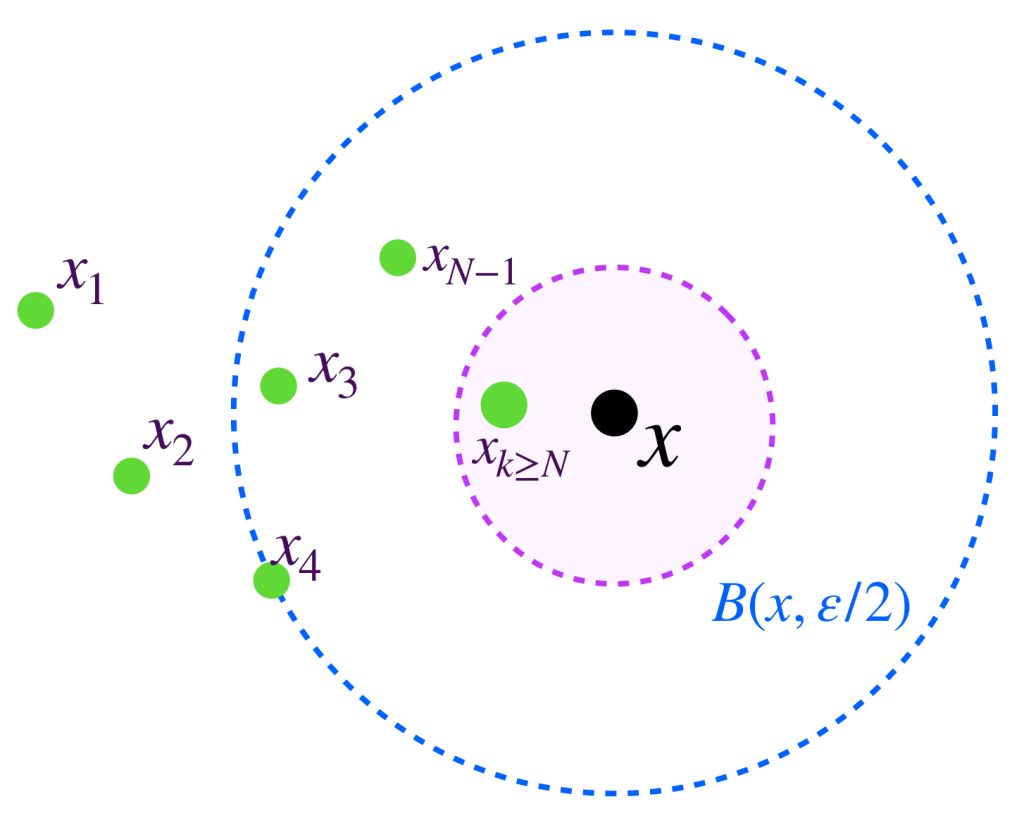
Sea $\varepsilon >0.$ Como $(x_n)$ es de Cauchy entonces existe $N \in \mathbb{N}$ tal que para todo $ \, n,m \geq N$ ocurre que $d(x_n,x_m)<\frac{\varepsilon}{2}.$
Como $x$ es punto de acumulación del conjunto $\{x_n\}$ podemos garantizar que existe un término de la sucesión $x_k \in B(x,\frac{\varepsilon}{2})$ con $k \geq N.$ (Se te pedirá argumentar esto al final de esta sección).
Entonces, para todo $ \, n \geq N$
\begin{align*}
d(x_n,x) &\leq d(x_n,x_k)+d(x_k,x) \\
&\leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2}\\
&= \varepsilon
\end{align*}
Por lo tanto $x_n \to x.$
Finalizamos esta sección con la siguiente:
Proposición. Sea $(X,d)$ un espacio métrico y $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy en $X.$ Entonces $(x_n)$ es convergente si y solo si tiene una subsucesión convergente.
Demostración: Queda como ejercicio.
Más adelante…
Ya que conocemos el concepto de las sucesiones de Cauchy procederemos a explorar espacios donde este tipo de sucesiones sí es convergente. Esto motiva la definición de espacio métrico completo que conoceremos en la siguiente entrada.
Tarea moral
- Demuestra que la sucesión $(\frac{1}{n})_{n \in \mathbb{N}} \,$ en el subespacio euclidiano $(0,1]$ es de Cauchy, pero no es convergente en $(0,1].$
- En la demostración de la proposición anterior, prueba que que existe un término de la sucesión $(x_n)$ de $\mathbb{R}^n$, digamos $x_k$ tal que $x_k \in B(x,\frac{\varepsilon}{2})$ con $k \geq N.$
- Demuestra que si $(x_n)_{n \in \mathbb{N}} \,$ es una sucesión de Cauchy en un espacio $X$, entonces $(x_n)$ es convergente si y solo si tiene una subsucesión convergente.
- Sea $X = [1,\infty)$ y sea $d(x,y):=|\frac{1}{x}-\frac{1}{y}|.$ Demuestra que $d$ es una métrica en $X.$
- Para cada $n \in \mathbb{N}$ definimos $x_n:=n+1.$ Prueba que la sucesión $(x_n)$ es de Cauchy en el espacio métrico del ejercicio anterior.
Bibliografía
- Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 88 y 89.
- Bartle, R.G., The Elements of Real Analysis. New York: J. Wiley, 1964. Págs: 115-119.
- Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 75-77.
- Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Pág: 52.