Introducción

En esta entrada revisaremos el teorema del máximo-mínimo que nos indica que para una función continua en un intervalo $[a, b]$, existe un punto $x_0$ tal que $f(x_0) \geq f(x)$ para todo valor de $x$ en el intervalo. Para llegar a la prueba de tal teorema, revisaremos antes la definición de función acotada y probaremos que toda función continua en un intervalo está acotada en tal intervalo.

Funciones acotadas

Comenzaremos dando la definición de función acotada.

Definición. Decimos que $f$ está acotada superiormente en $A$ si existe $M \in \mathbb{R}$ tal que para todo $x \in A$ se cumple que $f(x) \leq M$. De manera similar, decimos que $f$ está acotada inferiormente en $A$ si existe $m \in \mathbb{R}$ tal que para todo $x \in A$ se tiene que $m \leq f(x)$. Finalmente, diremos que $f$ está acotada si existen $m$, $M \in \mathbb{R}$ tales que para todo $x \in A$ se tiene que $m \leq f(x) \leq M$.

Revisaremos el siguiente ejemplo para aplicar esta nueva definición.

Ejemplo 1. Sea $f: \mathbb{R} \setminus \{0\} \to \mathbb{R}$ definida como $f(x) = \frac{1}{x}.$

Afirmación. $f$ está acotada en el intervalo $A = [1, \infty)$.

Demostración.

Sea $x \in [1, \infty)$. Como $1 \leq x$, entonces $\frac{1}{x} \leq 1$. Se sigue que
\begin{gather*}
& 0 < \frac{1}{x} \leq 1 \quad \forall x \in [1, \infty). \\ \\
& \therefore 0 \leq f(x) \leq 1 \quad \forall x \in [1, \infty).
\end{gather*}

Por tanto, $f$ está acotada en el intervalo $A = [1, \infty)$.

$\square$

Afirmación. $f$ no está acotada superiormente en $B = (0, 1].$

Demostración.

Supongamos que la función $f$ sí está acotada superiormente en $B$, entonces existe $M \in \mathbb{R}$ tal que para todo $x \in B$ se tiene que $f(x) = \frac{1}{x} \leq M$.

Para todo $n \in \mathbb{N}$, se tiene que $n \geq 1$, entonces $0 < \frac{1}{n} \leq 1$ y, por tanto, $\frac{1}{n} \in B$.

\begin{gather*}
& f \left( \frac{1}{n} \right) = \frac{1}{\frac{1}{n}} \leq M. \\ \\
\therefore & n \leq M \quad \forall n \in \mathbb{N}.
\end{gather*}

Lo cual es una contradicción pues el conjunto de los números naturales no está acotado superiormente, por lo tanto $f$ no está acotada superiormente.

De forma análoga, se puede probar que $f$ está acotada en el intervalo $(-\infty, 1]$ y que no está acotada inferiormente en $[-1,0)$.

$\square$

Ahora veremos dos proposiciones respecto a las funciones acotadas. La primera nos indica que si $f$ es una función acotada en $A$ y se tiene un subconjunto $B$ de $A$, entonces $f$ también está acotada en $B$; mientras que la segunda nos indica que si $B$ y $C$ son subconjuntos de $A$, entonces $f$ también estará acotada en la unión de $B$ y $C.$

Proposición. Si $f$ está acotada en $A$ y $B \subset A$, entonces también está acotada en $B.$

Demostración.

Dado que $f$ está acotada en $A$, existen $m$, $M \in \mathbb{R}$ tal que para todo $x \in A$ se tiene que $m \leq f(x) \leq M$. Como $B \subset A$, entonces para todo $x \in B$ se tiene que $x \in A$, así $f$ también está acotada en $B.$

$\square$

Proposición. Si $B \subset A$, $C \subset A$. Si $f$ está acotada en $B$ y en $C$, entonces $f$ está acotada en $B \cup C.$

El razonamiento detrás de la prueba de esta proposición es similar al anterior, por lo que se dejará como tarea moral.

Continuaremos revisando una equivalencia de la definición de función acotada donde, en lugar de tener dos reales $m$, $M$ que acoten inferior y superiormente, solo se considerará un real $T$ que cumpla que $|f(x)| \leq T.$

Proposición. Existen $m$, $M \in \mathbb{R}$ tales que para todo $x \in A$, $m \leq f(x) \leq M$ si y solo si existe $T \in \mathbb{R}$ tal que para todo $x \in A$, $|f(x)| \leq T.$

Demostración.

$\Rightarrow]$ Sabemos que existen $m$, $M$ en $\mathbb{R}$ tales que para todo $x \in A$, $m \leq f(x) \leq M.$

Consideremos $T = max\{ |m|, |M| \}.$

Sea $x \in A$, entonces

\begin{gather*}
& f(x) \leq M \leq |M| \leq T. \\
\Rightarrow & f(x) \leq T. \tag{1}
\end{gather*}

Por otro lado

\begin{gather*}
& m \leq f(x). \\
\Leftrightarrow & – m \geq -f(x).
\end{gather*}

De esta forma, se sigue que
\begin{gather*}
-f(x) \leq -m \leq |m| \leq T.
\end{gather*}

Es decir,
\begin{gather*}
& -f(x) \leq T. \\
\therefore & -T \leq f(x). \tag{2}
\end{gather*}

De $(1)$ y $(2)$ podemos concluir que $|f(x)| \leq T.$

$\Leftarrow]$ Supongamos que existe $T$ tal que para todo $x \in A$, $|f(x)| \leq T.$

Consideremos $m = -T$ y $M = T$, entonces $ m \leq f(x) \leq M.$

$\square$

Teorema de acotabilidad

La siguiente propiedad nos indica que si $f$ es continua en un punto, entonces existe un intervalo alrededor de dicho punto donde la función está acotada. Esta propiedad será ampliamente usada para probar el teorema del máximo-mínimo.

Proposición. Sea $a \in A$, si $f$ es continua en $a$, entonces existe $\delta > 0$ tal que $f$ está acotada en el intervalo $(a-\delta, a+\delta) \cap A.$

Demostración.

Como $f$ es continua en $a$, considerando particularmente $\varepsilon = 1$, existe $\delta > 0$ tal que si $|x-a| < \delta$, $x \in A$, entonces

$$|f(x)-f(a)|<1.$$

Es decir, si $x \in (a – \delta, a + \delta) \cap A$, entonces

\begin{gather*}
& |f(x)|- |f(a)| < |f(x)- f(a)| < 1. \\
\Rightarrow & |f(x)| < 1 + |f(a)|.
\end{gather*}

Por tanto, $f$ está acotada en el intervalo $(a – \delta, a + \delta) \cap A.$

$\square$

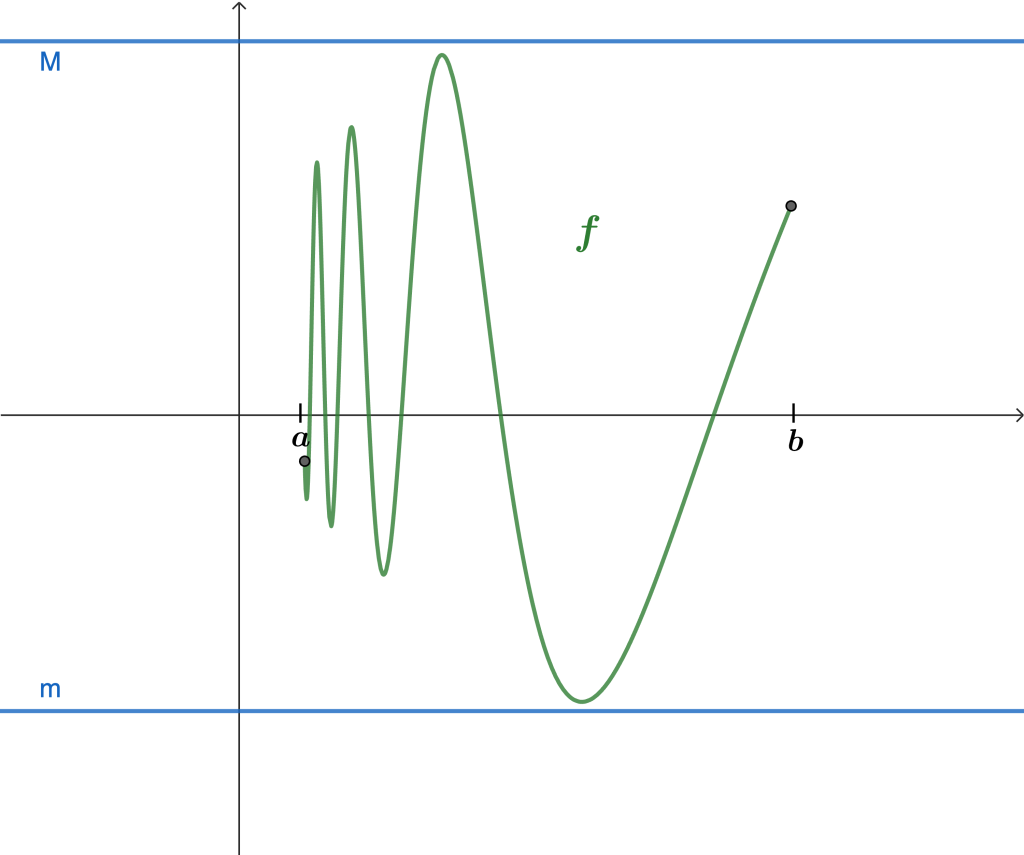
El último teorema que veremos antes del máximo-mínimo nos indica que toda función continua en un intervalo cerrado está acotada en tal intervalo. De forma ilustrativa, podemos observarlo en la siguiente gráfica.

Teorema de acotabilidad. Sea $f: [a,b] \to \mathbb{R}$ tal que $f$ es continua en $[a,b]$. Entonces $f$ está acotada en $[a,b].$

Demostración.

Sea $A = \{ t \in [a, b] \quad | \quad f \text{ sí está acotada en } [a, t] \}$.

Veamos que $A \neq \varnothing$.
Consideremos $a \in [a,b]$. Como $f$ es continua en $[a,b]$ y por la proposición anterior, existe $\delta_1 > 0$ tal que para todo $x \in (a-\delta_1, a+\delta_1) \cap [a, b]$ se tiene que $f$ está acotada.
Por lo tanto, para todo $x \in [a, a+\delta_1)$, $f$ sí está acotada.

Notemos que tenemos dos casos derivados de si $a+ \delta_1$ está o no en el intervalo $[a,b].$

• Si $b > a + \delta_1$, entonces $a+\delta_1 \in A$.
• Si $b \leq a + \delta_1$, entonces $b \in A$.

$$\therefore A \neq \varnothing.$$

Además, $A$ está acotado superiormente pues si $t \in A$, por definición del conjunto, $t \leq b$.

Como $A$ es no vacío y está acotado superiormente, entonces tiene supremo. Sea $\alpha = supA$, notemos que $\alpha \leq b$, pues $\alpha$ es el supremo y $b$ es una cota superior.

Probaremos que $\alpha = b$, es decir, veremos que el supremo del conjunto $A$ es justamente $b$ y, en consecuencia, $f$ está acotada en $[a,b].$

Supongamos que $\alpha \neq b$. Entonces $a < \alpha < b$. Como $f$ es continua en $[a,b]$, entonces $f$ es continua en $\alpha$. Por la proposición anterior, existe $\delta_2$ tal que $f$ está acotada en $(\alpha-\delta_2, \alpha + \delta_2) \cap [a, b].$

Como $\alpha – \delta_2 < \alpha$, existe $t \in A$ tal que $\alpha – \delta_2 \leq t \leq \alpha$. Tomemos $s$ tal que $\alpha < s < \alpha + \delta_2$ y $s < b$. De esta forma se tiene que $[t,s] \subset (a- \delta_2, a + \delta_2) \cap [a, b]$ y $f$ está acotada en $[a, t]$ pues $t \in A$. Por lo tanto $f$ está acotada en $[a,s] = [a,t] \cup [t,s].$

Así $s \in A$ y $\alpha < s$, lo cual es una contradicción al hecho de que $\alpha$ es el supremo del conjunto $A.$

Por tanto, concluimos que $\alpha = b$. Ahora solo falta probar que $b \in A$ y, en consecuencia, $f$ está acotada en $[a,b].$

Dado que $b \in [a, b]$, f es continua en b, entonces existe $\delta_3 > 0$ tal que $f$ está acotada en $(b- \delta_3, b + \delta_3) \cap [a,b] = (b- \delta_3, b]$. Como $b = supA$ y $b-\delta_3 < b$, entonces existe $t \in A$ tal que $b-\delta_3 < t \leq b$, entonces $f$ está acotada en $[a,t]$. Como $[t, b] \subset (b – \delta_3, b]$ entonces $f$ está acotada en $[a,b] = [a,t] \cup [t, b].$

$\square$

Teorema del máximo-mínimo

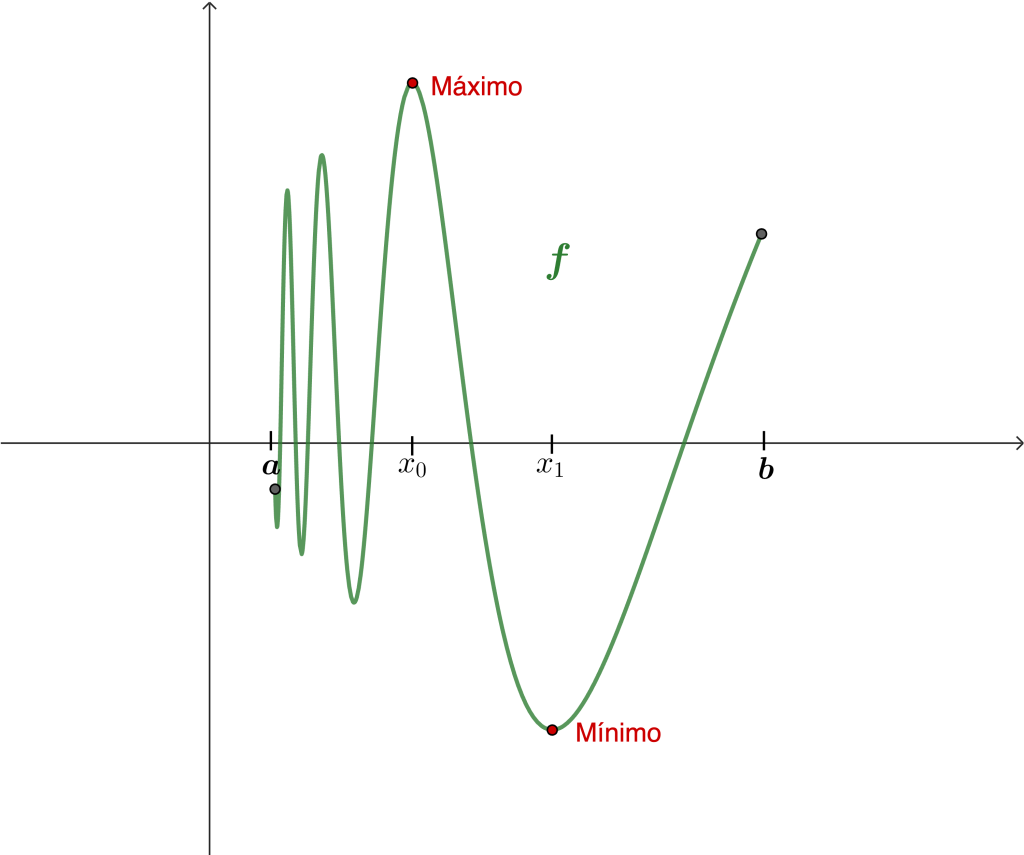
Estamos listos para demostrar que para toda función continua en un intervalo $[a,b]$ existen $x_0, x_1 \in [a,b]$ donde la función alcanza su máximo y su mínimo respectivamente.

Teorema. Sea $f: [a,b] \to \mathbb{R}$ y continua en $[a,b]$, entonces existe $x_0 \in [a,b]$ tal que para todo $x \in [a,b]$ se tiene que $f(x) \leq f(x_0).$

Demostración.

Sea $B = \{ y = f(x) | x \in [a,b] \}.$

Por el teorema anterior, sabemos que existe $M \in \mathbb{R}$ tal que para todo $x \in [a,b]$ se tiene que $y = f(x) \leq M$. Por lo tanto $B$ está acotado.

Además $a \in [a,b]$, entonces $f(a) \in B$, así $B \neq \varnothing$. Por tanto, sabemos que existe $\alpha \in \mathbb{R}$ tal que $\alpha = supB$. Notemos que para todo $y \in B$, $y \leq \alpha$. Es decir, para todo $x \in [a,b]$, se tiene que $f(x) \leq \alpha.$

Ahora probaremos que existe $x_0 \in [a,b]$ tal que $f(x_0) = \alpha$ y, por tanto, para todo $x \in [a,b]$, $f(x) \leq f(x_0).$

Supongamos que para todo $x \in [a, b]$, $f(x) \neq \alpha.$
Entonces para todo $x \in [a,b]$, se tiene que $f(x) < \alpha.$ Es decir,

$$0 < \alpha – f(x).$$

Consideremos la siguiente función auxiliar $g(x) = \frac{1}{\alpha – f(x)}$. Se tiene que

$$g(x) = \frac{1}{\alpha – f(x)} > 0 \quad \forall x \in [a,b]. \tag{1}$$

Además, $g$ es la división de dos funciones continuas y el denominador no se hace cero en $[a,b]$, entonces $g$ es continua en $[a,b]$, por lo tanto $g$ está acotada en $[a,b]$. Es decir, existe $T \in \mathbb{R}$ tal que para todo $x \in [a,b]$ se tiene

\begin{gather*}
&|g(x)|\leq T. \\
\Rightarrow & 0 < \frac{1}{\alpha – f(x)} \leq T \text{, por }(1).
\end{gather*}

Se sigue que
\begin{gather*}
& \alpha – f(x) \geq \frac{1}{T} \quad \forall x \in [a,b]. \\
\therefore & \alpha – \frac{1}{T} \geq f(x) \quad \forall x \in [a,b]. \\
\end{gather*}

Entonces se tiene que $\alpha – \frac{1}{T}$ es cota superior de $B$, pero como $\frac{1}{T} > 0$, entonces $\alpha – \frac{1}{T} < \alpha$ y esto es una contradicción al hecho de que $\alpha$ es el supremo.

Por lo tanto, podemos concluir que sí existe $x_0 \in [a,b]$ tal que $f(x_0) = \alpha.$
$$\therefore f(x) \leq f(x_0) \quad \forall x \in [a,b].$$

$\square$

Corolario. Sea $f: [a,b] \to \mathbb{R}$ continua en $[a,b]$. Entonces existe $x_1 \in [a,b]$ tal que para todo $x \in [a,b]$ se tiene que $f(x_1) \leq f(x)$.

Demostración.

Consideremos la función $g: [a,b] \to \mathbb{R}$, $g(x) = -f(x)$ continua en $[a,b]$.

Por el teorema anterior existe $x_1 \in [a,b]$ tal que

\begin{gather*}
& g(x) \leq g(x_1) \quad \forall x \in [a,b]. \\
\Rightarrow & -f(x) \leq -f(x_1) \quad \forall x \in [a,b]. \\
\end{gather*}

$$\therefore f(x_1) \leq f(x) \quad \forall x \in [a,b].$$

$\square$

Más adelante…

En la siguiente entrada estudiaremos resultados derivados del teorema del valor intermedio y del teorema del máximo-mínimo, razón por la cual será fundamental tenerlos presentes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• Sean $f$, $g: \mathbb{R} \to \mathbb{R}$. Prueba que si $f$ y $g$ están acotadas en $\mathbb{R}$, entonces la suma $f+g$ también está acotada en $\mathbb{R}$.
• Si $B \subset A$, $C \subset A$. Si $f$ está acotada en $B$ y en $C$, entonces $f$ está acotada en $B \cup C$.
• Prueba que si $f : \mathbb{R} \to \mathbb{R}$ está acotada en $\mathbb{R}$ y definimos $g: \mathbb{R} \to \mathbb{R}$ tal que $g(x)=xf(x)$, entonces $g$ es continua en $x_0=0.$
• Si $f$ es una función continua en $[0,1]$, sea $||f||$ el valor máximo de $|f|$ en $[0,1]$. Prueba que $||c \cdot f|| = |c|\cdot||f||$.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I
• Entrada anterior del curso: Teorema del valor intermedio
• Siguiente entrada del curso: Resultados derivados de los teoremas del valor intermedio y del máximo-mínimo
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»