Introducción
En la unidad anterior desarrollamos todo lo concerniente a los números reales, ahora comenzaremos a ver funciones. Para ello recordemos de nuestros cursos de álgebra cómo se define el producto cartesiano de un par de conjuntos $A$ y $B$:
$$ A\times B := \left\{ (a,b) : a \in A, b \in B \right\},$$
así vemos que sus elementos son pares ordenados.
Por lo que decimos que cualquier subconjunto $R \subseteq A\times B$, es llamado una relación entre $A$ y $B$.
Basándonos en este par de conceptos daremos la definición formal de función entre un par de conjuntos.
Definición de función
Definición (función): Una función $f$ entre los conjuntos $A$ y $B$ es una relación tal que:
- Para todo $a \in A$ existe $b \in B$ donde $(a,b) \in f$.
- Si $(a, b_{1}), (a, b_{2})$ entonces $b_{1}= b_{2}$.
Notación:
- $f : A \rightarrow B$ es una función con dominio $A$ y codominio $B$.
- $f(a)=b$ es llamada la regla de correspondencia de f.
En resumen, a una función $f : A \rightarrow B$ la conforman tres cosas:
- Su dominio.
- Su codominio.
- Su regla de correspondencia.
El conjunto imagen de una función
Definición (Conjunto imagen): Sea $f : A \rightarrow B$ una función. La imagen de f se define como:
$$Im_{f}:= \left\{ b \in B : \exists a \in A (f(a) =b) \right\}.$$
Simplificado sería:
$$Im_{f}:= \left\{ f(a) \in B : a \in A \right\}.$$
Ejemplo: Sea $f: \r \rightarrow \r$. Si $f(x)=|x|$ entonces $Im_{f}=[0, \infty)$.
Demostración:
$\subseteq )$ Sea $x \in \r$. Vemos que $f(x)= |x|\geq 0$ por lo que $f(x) \in [0, \infty)$.
$\supseteq )$ Tomemos $y \in [0, \infty)$. Debemos probar que existe $x \in \r$ tal que $f(x)= y$.
Sea $x=y \in \r$ con $y \geq 0$. Así se sigue que $f(y)= |y|=y$ por lo que $f(y)=x$.
$\square$
Ejemplo
Encuentra el dominio y la imagen de la siguiente función:
$$f(x)= \sqrt{1-x^{2}}\quad \text{.}$$
Dominio:
Vemos que $y=\sqrt{1-x^{2}}$ está bien definido
\begin{align*}
&\Leftrightarrow 1-x^{2} \geq 0\\
&\Leftrightarrow 1 \geq x^{2}\\
&\Leftrightarrow 1 \geq |x|\\
\end{align*}
Así concluimos que el dominio es el conjunto:
$$D_{f}= [-1,1]\quad \text{.}$$
Imagen:
Como $x \in [-1,1]$ entonces
\begin{align*}
-1 \leq x \leq 1 &\Leftrightarrow 0 \leq x^{2} \leq 1\\
&\Leftrightarrow 0 \geq -x^{2} \geq -1\\
&\Leftrightarrow 1\geq 1-x^{2} \geq 1-1\\
&\Leftrightarrow 1\geq 1-x^{2} \geq 0\\
&\Leftrightarrow 1\geq \sqrt{1-x^{2}} \geq 0\\
\end{align*}
Por lo anterior tenemos:
$$Im_{f} = [0,1]\quad \text{.}$$
Ejercicio 1
Encuentra el dominio de la siguiente función:
\begin{equation*} f(x)= \frac{1}{4-x^{2}} \end{equation*}
Vemos que la función está bien definido si y sólo si:
\begin{align*}
4-x^{2} \neq 0 &\Leftrightarrow (2-x)(2+x) \neq 0\\
&\Leftrightarrow x \neq 2 \quad \text{y} \quad x\neq -2
\end{align*}
Por lo que su dominio sería:
$$D_{f}= \r – \left\{-2,2 \right\}\quad \text{.}$$
es decir, todos los reales quitando el $-2$ y el $2$.
Ejercicio 2
Encuentra el dominio de la siguiente función:
$$f(x)= \sqrt{x-x^{3}}\quad \text{.}$$
Dominio:
Vemos ahora que para $y=\sqrt{x-x^{3}}$ está bien definido
\begin{align*}
&\Leftrightarrow x-x^{3} \geq 0\\
&\Leftrightarrow x(1-x^{2}) \geq 0\\
&\Leftrightarrow x(1-x)(1+x) \geq 0\\
&\Leftrightarrow x \geq 0,\quad x\leq 1, \quad x \geq -1
\end{align*}
De las condiciones anteriores vemos que tenemos los siguientes posibles intervalos que cumplen la desigualdad inicial:
- $(-\infty, -1]$
Vemos que al sustituir $x= -1 \in (-\infty,-1]$ tenemos que:
$$-1-(-1)^{3} = -1-(-1)= 0 \geq 0$$
por lo que se cumple la desigualdad $x-x^{3} \geq 0$. - $(-1,0)$
Tomando $x=-\frac{1}{2}$ vemos que:
$$-\frac{1}{2} -\left(-\frac{1}{2} \right) ^{3} = -\frac{1}{2} + \frac{1}{8} = -\frac{3}{8}$$
Por lo que no se cumple ser mayor o igual que cero. - $[1,0]$
Ahora si tomamos $x=1$ observamos:
$$1- 1^{3} =1-1 =0$$
por lo que cumple la desigualdad. - $(1,\infty)$
Por último si consideramos $x= 2$ ocurre que:
$$2- (2)^{3} =2-8 =-6$$
que no cumple la desigualdad.
Del análisis anterior vemos que los intervalos que cumplen con $x-x^{3} \geq 0$ son:
$$(-\infty, -1] \cup [1,0]\quad \text{.}$$
Por lo que el dominio de la función sería:
$$D_{f}=(-\infty, -1] \cup [1,0]\quad \text{.}$$
Gráfica de una función
Definición (gráfica): Sea $f:D_{f} \subseteq \r \rightarrow \r$ Definimos a la gráfica de f como el conjunto:
$$ Graf(f)= \left\{ (x,y)\in {\mathbb{R}}^2: x \in D_{f}, \quad y=f(x) \right\},$$
que es equivalente a decir:
$$Graf(f)= \left\{(x, f(x)): x \in D_{f} \right\}\quad \text{.}$$
Ejemplos
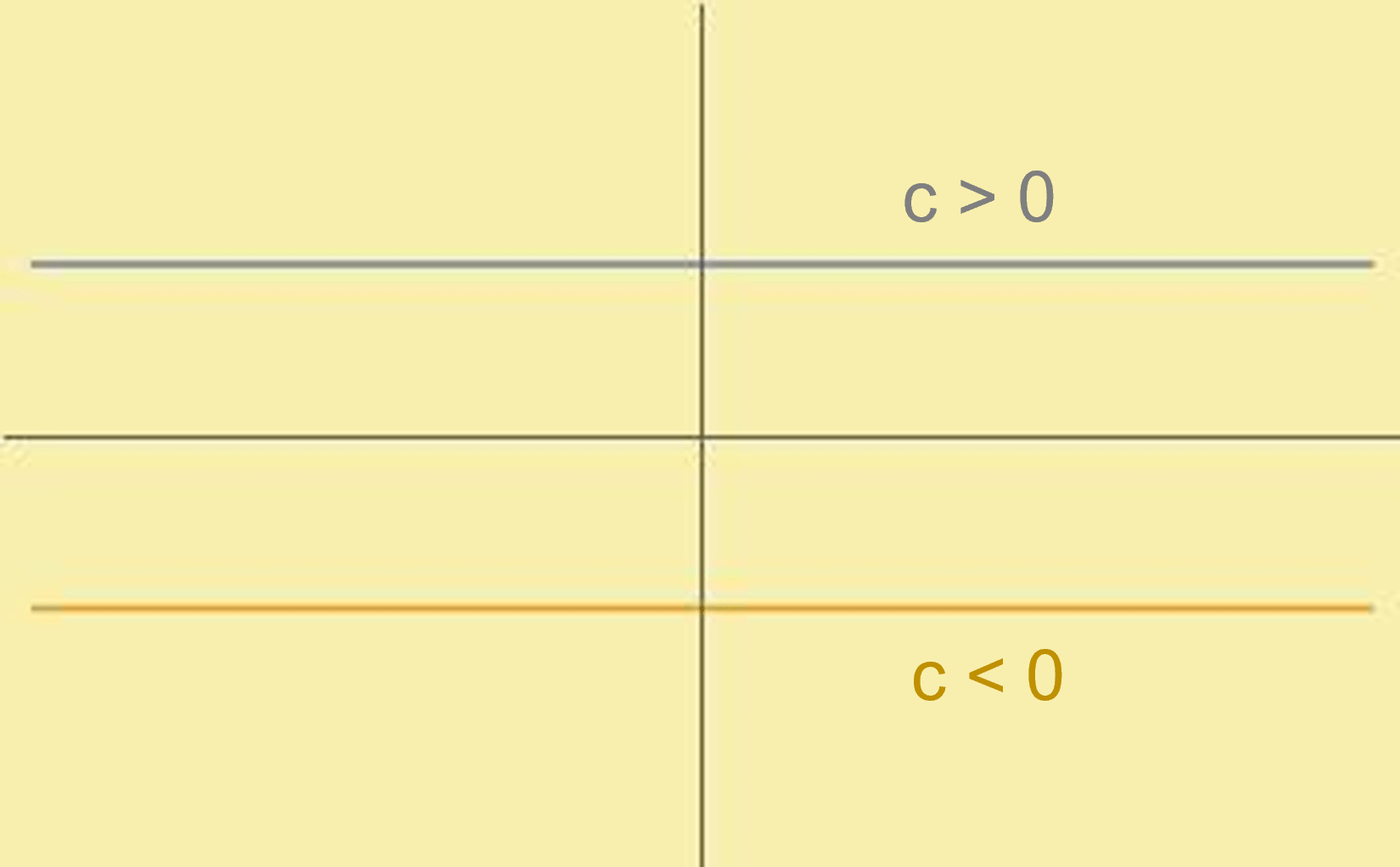
- Para la función constante tenemos:
$$f(x)=c ,$$
donde $D_{f}= \r$ y $Im_{f}= {c}$.
Por lo que su gráfica se vería como:
- Para la función identidad tenemos:
$$Id(x)=x ,$$
donde $D_{f}= \r$ y $Im_{f}= \r$.
Así su gráfica se vería:
Más adelante
En la próxima entrada veremos las definiciones relacionadas con las operaciones entre funciones: suma, producto, cociente y composición.
Tarea moral
A continuación encontrarás una serie de ejercicios que te ayudarán a repasar los conceptos antes vistos:
- Sea $f: \r \rightarrow \r$. Demuestra que si $f(x)=x^{2}$ entonces $Im_{f}=[0, \infty).$
- Encuentra el dominio de las siguientes funciones:
- $\begin{multline*} f(x)= \sqrt{x+1} \end{multline*}$
- $\begin{multline*} f(x)= x \sqrt{x^{2}-2} \end{multline*}$
- $\begin{multline*} f(x)= \sqrt{-x}+ \frac{1}{\sqrt{x+2}} \end{multline*}$
- $\begin{multline*} f(x)= \sqrt{2+x-x^{2}} \end{multline*}$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Conjuntos Infinitos (Adicional).
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Suma, producto, cociente y composición de funciones.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»