Archivo del Autor: Lizbeth Fernández Villegas

Convergencia puntual y convergencia uniforme

Por Lizbeth Fernández Villegas

Deja un comentario

Introducción

En entradas anteriores trabajamos ideas de convergencia de sucesiones. En ellas se observa una secuencia de puntos de un espacio métrico y se analiza si se pueden acercar mucho entre ellos o si se acercan a algún otro punto. En esta entrada, y otras correspondientes a la sección, observaremos sucesiones originadas por puntos obtenidos al evaluar funciones. Al comparar distancias entre puntos de la imagen de esas funciones podemos pensar ahora en cercanía de funciones, más aún, en si se aproximan a alguna función específica. ¡Comenzamos!

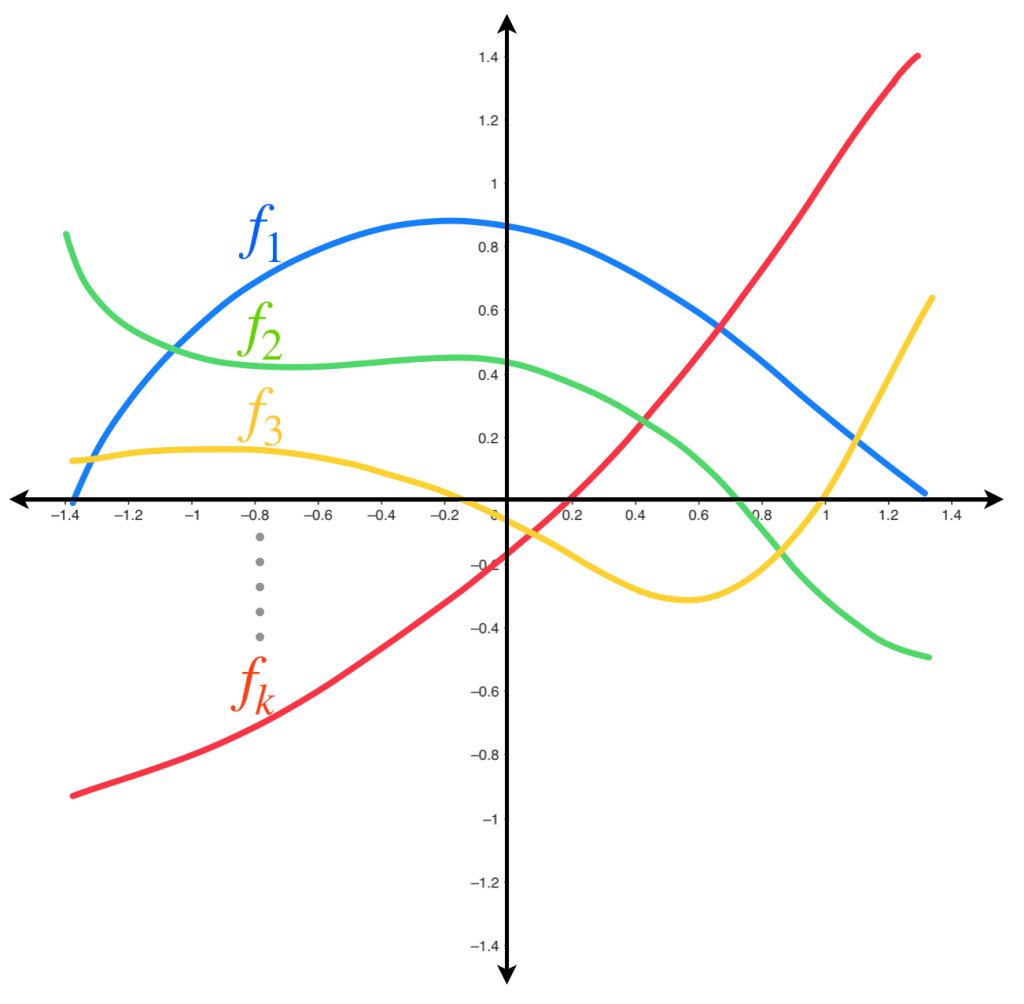
Sea $A$ un conjunto y $(X,d)$ un espacio métrico. Para cada $n \in \mathbb{N}$ considera una función $f_n:A \to X.$ Esto define una sucesión de funciones $(f_n)_{n \in \mathbb{N}}.$

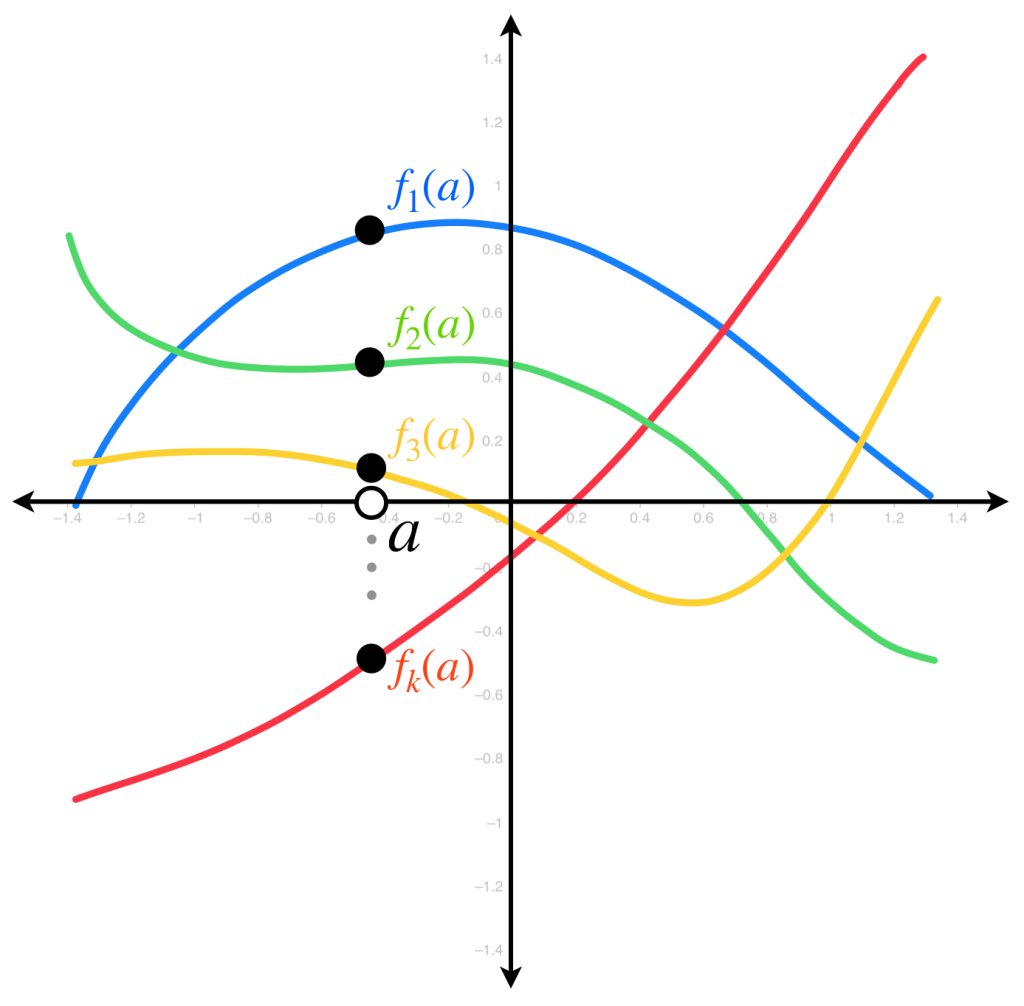
Representación de una sucesión de funciones

A partir de un punto $a \in A$ (fijo) podemos definir otra sucesión con los valores que cada una de las funciones anteriores asignan a ese punto. Es decir, con los términos $f_1(a), f_2(a), f_3(a), …$ definimos la sucesión $(f_n(a))_{n \in \mathbb{N}}.$

Representación de una sucesión $(f_n(a))_{n \in \mathbb{N}}.$

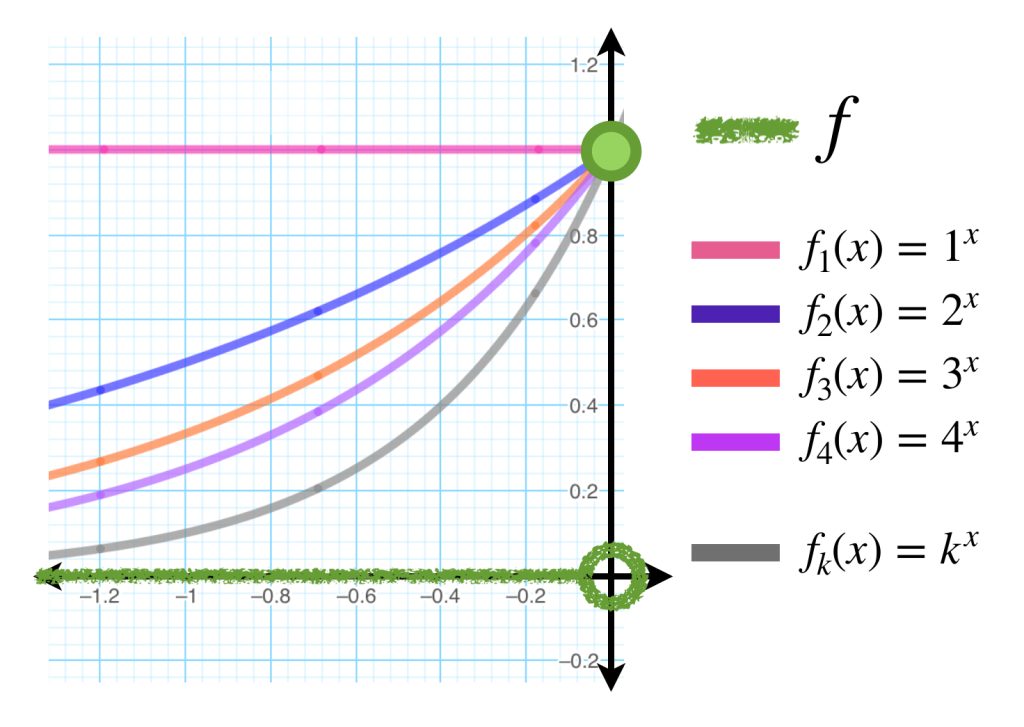
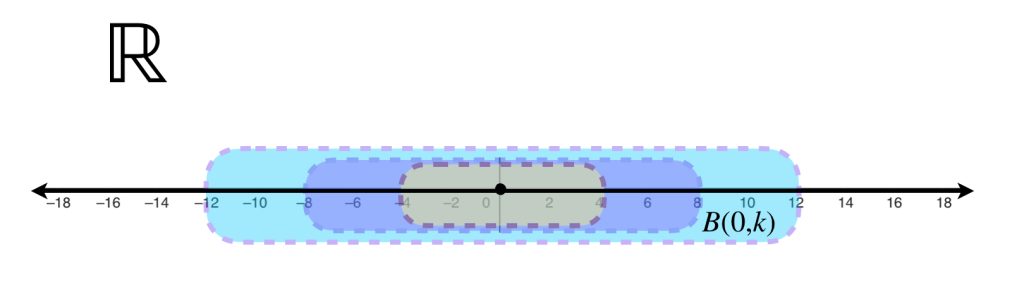
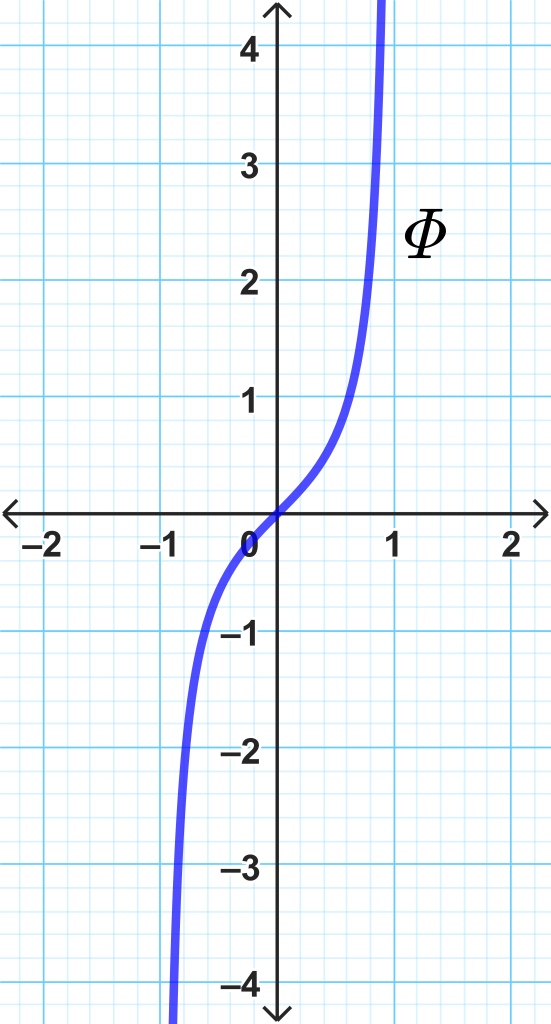
Es natural preguntarse si esa sucesión de puntos es convergente. Gráficamente podemos observar que esto depende de cómo están definidas las funciones y también del valor $a$ elegido en el dominio $A.$ Por ejemplo, en el siguiente dibujo, la sucesión generada con las funciones evaluadas en $a_1$ es convergente, pues los puntos se van aproximando al eje horizontal. Por otro lado, la generada a partir del punto $a_2$ no lo es; sus puntos tienden a infinito.

Sucesiones $(f_n(a_1))_{n \in \mathbb{N}} \,$ y $(f_n(a_2))_{n \in \mathbb{N}},$

Para formalizar estas ideas, al final de esta sección se te pedirá demostrar que la sucesión de funciones del ejemplo anterior evaluadas en $a_1$ (un punto menor que cero), es convergente. ¿Cuál es el límite? Por el contrario, para un punto mayor que cero la sucesión tiende a infinito. ¿Qué pasa al evaluar las funciones en cero?

Pero en un conjunto donde todos los puntos $a$ forman sucesiones convergentes $(f_n(a))_{n \in \mathbb{N}},$ podemos pensar en cada límite de esas sucesiones como el valor que otra función $f$ asigna en cada punto $a.$ Eso inspira la siguiente:

Definición. Convergencia puntual: Si $(f_n)_{n \in \mathbb{N}} \,$ es una sucesión de funciones donde para cada $n \in \mathbb{N}$ se tiene $f_n: A \to X,$ decimos que $(f_n)_{n \in \mathbb{N}} \,$ converge puntualmente en $A$ a una función $f:A \to X$ si para cada punto $a \in A$ se cumple que $\underset {n \to \infty}{lim} \, f_n(a) = f(a).$

Aunque la sucesión de funciones del ejemplo anterior no converge puntualmente en $\mathbb{R},$ sí lo hace en el intervalo $(- \infty , 0].$ Converge puntualmente a la función dada por:

\begin{equation*}
f(x) = \begin{cases}
0 & \text{si $x < 0$} \\
1 & \text{si $x = 0$}
\end{cases}
\end{equation*}

La sucesión de funciones converge puntualmente a la función $f.$

La función $f$ recibe el nombre de límite puntual de la sucesión de funciones $(f_n)_{n \in \mathbb{N}}.$

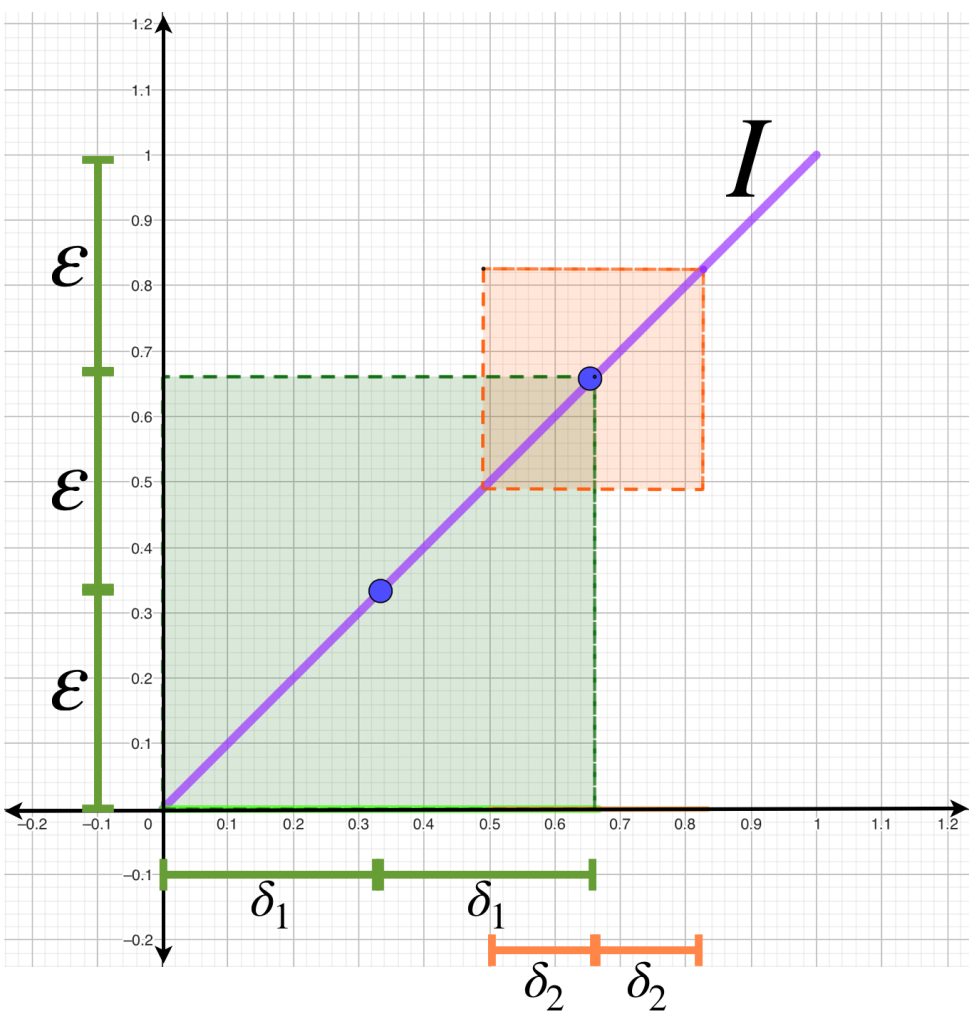
De acuerdo con la definición de convergencia puntual, para cada $\varepsilon >0$ y cada $a \in A$ se requiere de la existencia de un número $N_a \in \mathbb{N}$ tal que $\forall \, n\geq N_a, \, d(f_n(a),f(a)) < \varepsilon.$

Es importante notar que, incluso cuando todas las sucesiones $(f_n(a))_{n \in \mathbb{N}} \,$ son convergentes, posiblemente el natural $N_a \,$ que satisface la definición de convergencia será diferente al variar el punto $a$ en el dominio, de ahí que lo indiquemos con un subíndice.

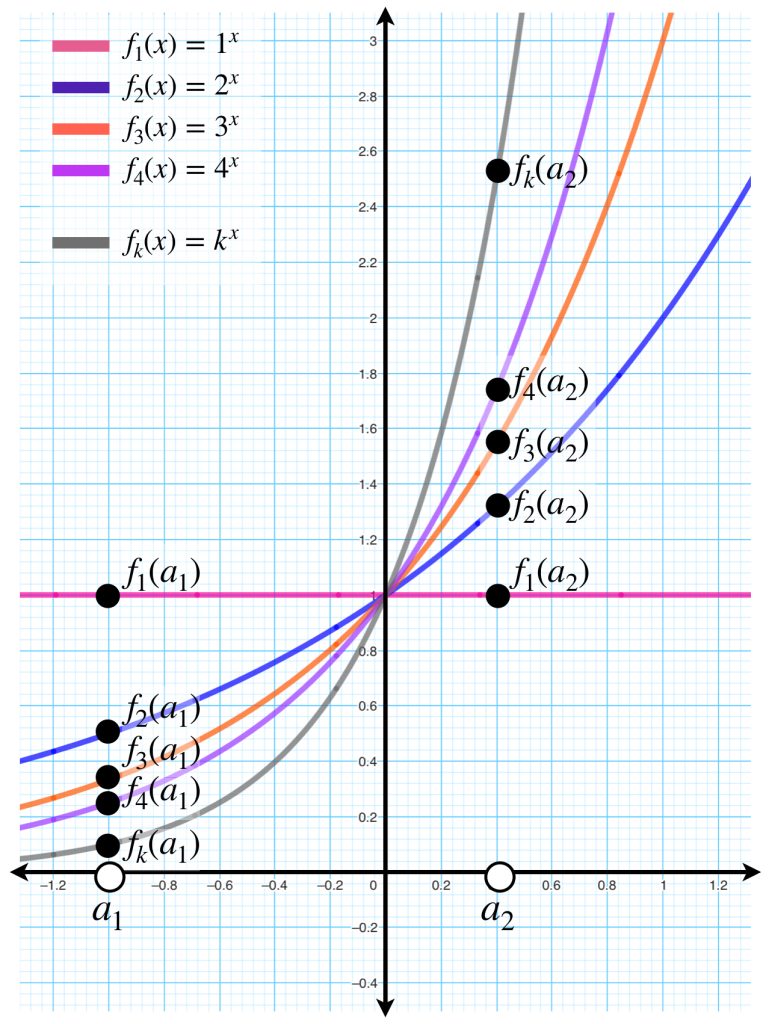
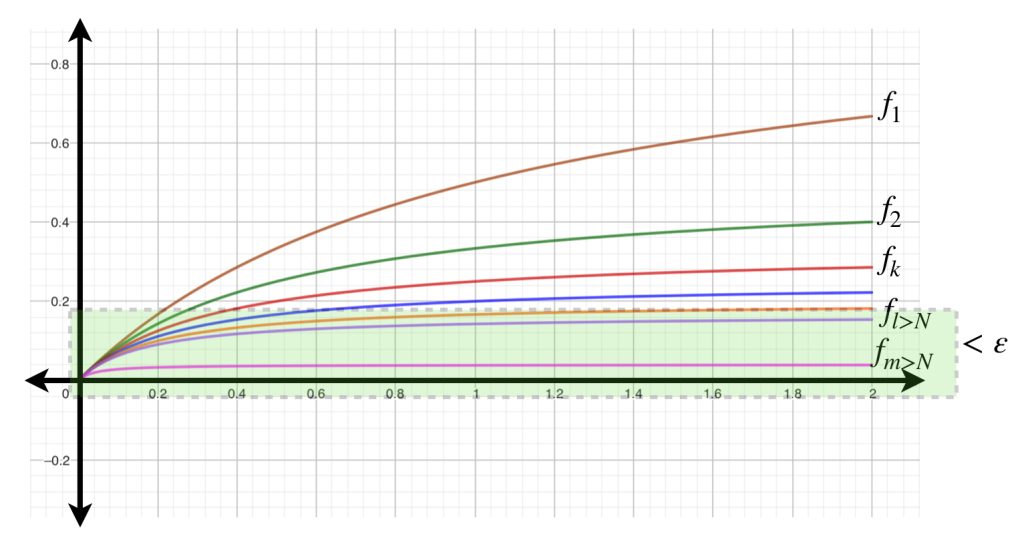
Tomemos nuevamente el ejemplo anterior en el intervalo $(- \infty, 0]$ donde la sucesión de funciones converge puntualmente. Partiendo de un $\varepsilon_0 >0$ fijo, observemos las siguientes sucesiones, en distintos valores del intervalo.

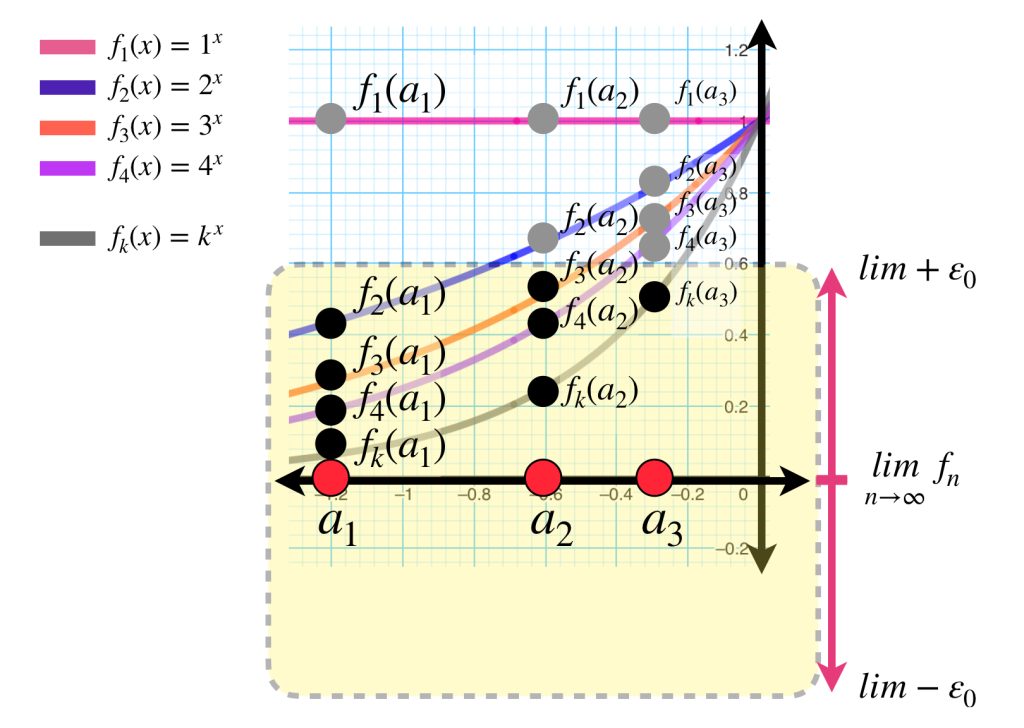
Puntos dentro del radio $\varepsilon_0$

Mientras que para el punto $a_1$ la sucesión se acerca al punto de convergencia $f(a_1) = 0$ en distancias menores que $\varepsilon _0$ a partir del punto evaluado en $f_2,$ para el punto $a_2$ no se acerca lo suficiente sino hasta $f_3.$ Por otra parte, los puntos de las funciones evaluadas en $a_3$ del dibujo, no se acercan en menos que $\varepsilon _0$ a su respectivo punto de convergencia sino hasta a partir de $f_k.$ Entonces, los naturales que satisfacen la condición pueden proponerse como:
$$N_{a_1} = 2; \, N_{a_2}=3; \, N_{a_3} = k$$
¿Es posible reasignar un mismo natural a los puntos $a_1, \, a_2, \, a_3$ y satisfacer también la definición de convergencia?
¿Será posible hacerlo en todos los puntos de $(- \infty ,0]$

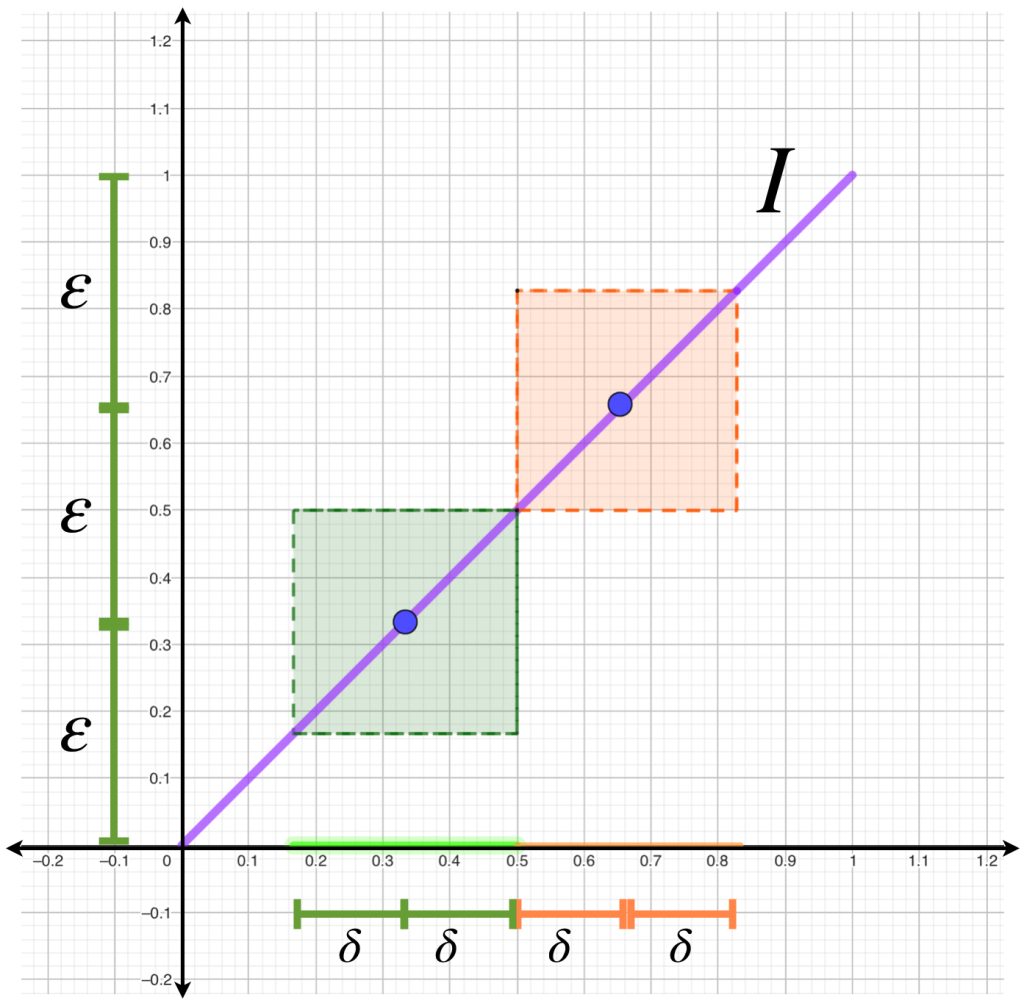
Cuando para todo $\varepsilon>0$ sí sea posible asegurar la existencia de un mismo valor natural $N$ que afirme la convergencia de todas las sucesiones $(f_n(a))_{a \in A} \,$ hablaremos de que la sucesión de funciones converge uniformemente:

Definición. Convergencia uniforme: Considera una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ donde para cada $n \in \mathbb{N}, \, f_n:A \to X \, $ con $A$ un conjunto y $(X,d)$ un espacio métrico. Decimos que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente a una función $f:A \to X$ si para toda $\varepsilon >0$ existe $N \in \mathbb{N}$ tal que para toda $n \geq N$ y para toda $a \in A$ se cumple que $d(f_n(a),f(a))< \varepsilon.$

En este caso nos referiremos a $f$ como el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$

Ejemplo
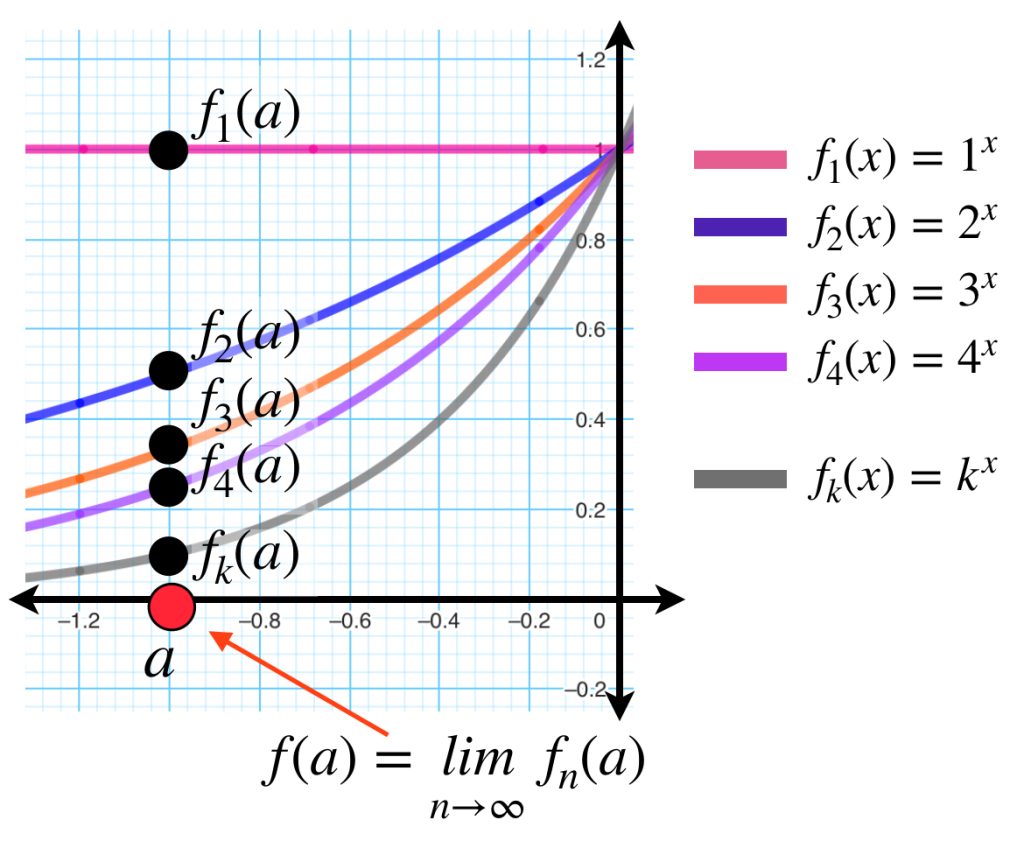
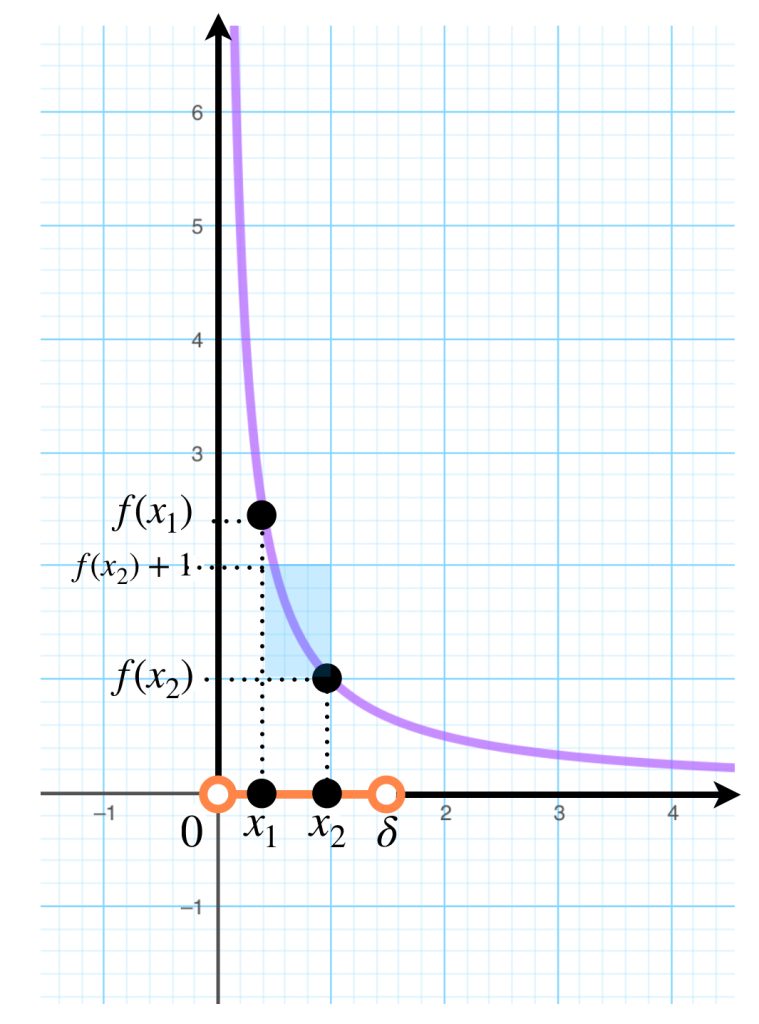
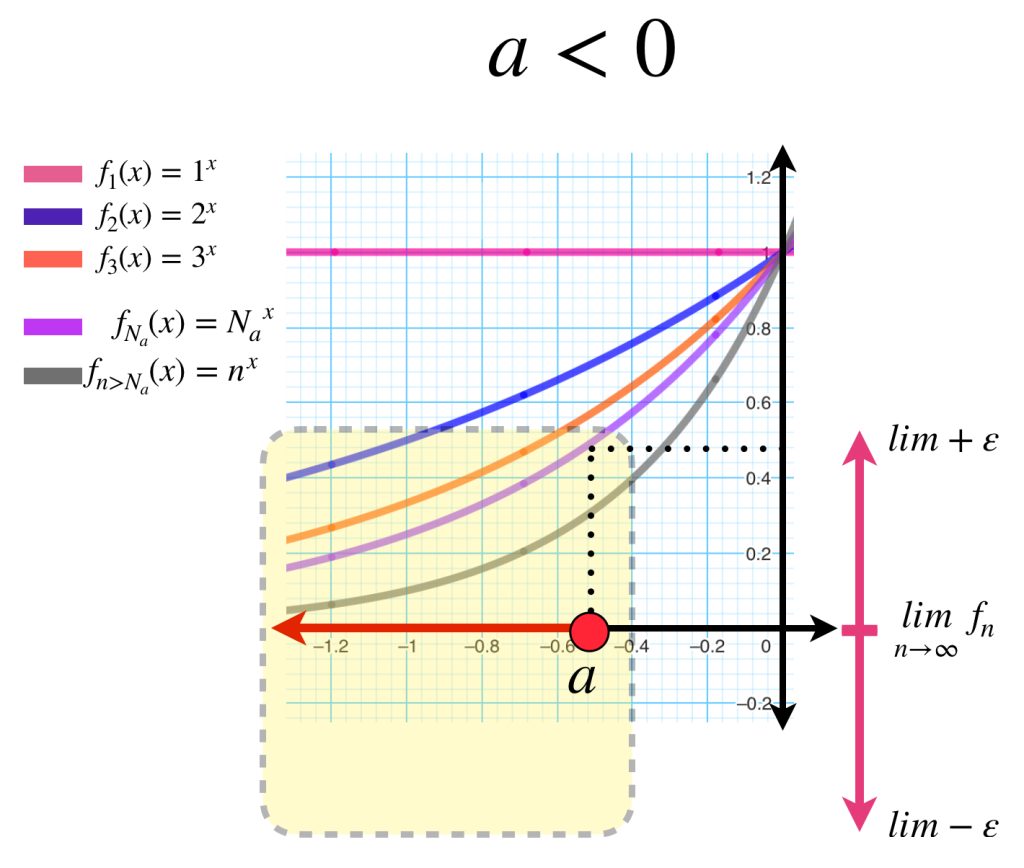
Consideremos la misma sucesión de funciones $(n^x)_{n \in \mathbb{N}} \,$ pero ahora con dominio $(- \infty, a]$ con $a < 0.$

Sea $\varepsilon >0$. Toma el $N_a \in \mathbb{N}$ que satisface que $\forall n\geq N_a, \, d(f_n(a),0) < \varepsilon$ el cual existe, pues $f_n(a) \to 0.$ Nota que este mismo natural funciona para probar la convergencia de la sucesión de puntos de funciones evaluadas en cualquier otro punto de $(- \infty,a].$ La demostración de este hecho quedará como ejercicio.

A partir de la función morada, todas las siguientes están dentro de la región de $\varepsilon$ en el dominio.

Nota que si una sucesión $(f_n)$ converge uniformemente a $f$ entonces también converge puntualmente a $f.$ Por el contrario, podemos tener sucesiones que convergen puntualmente pero no uniformemente:

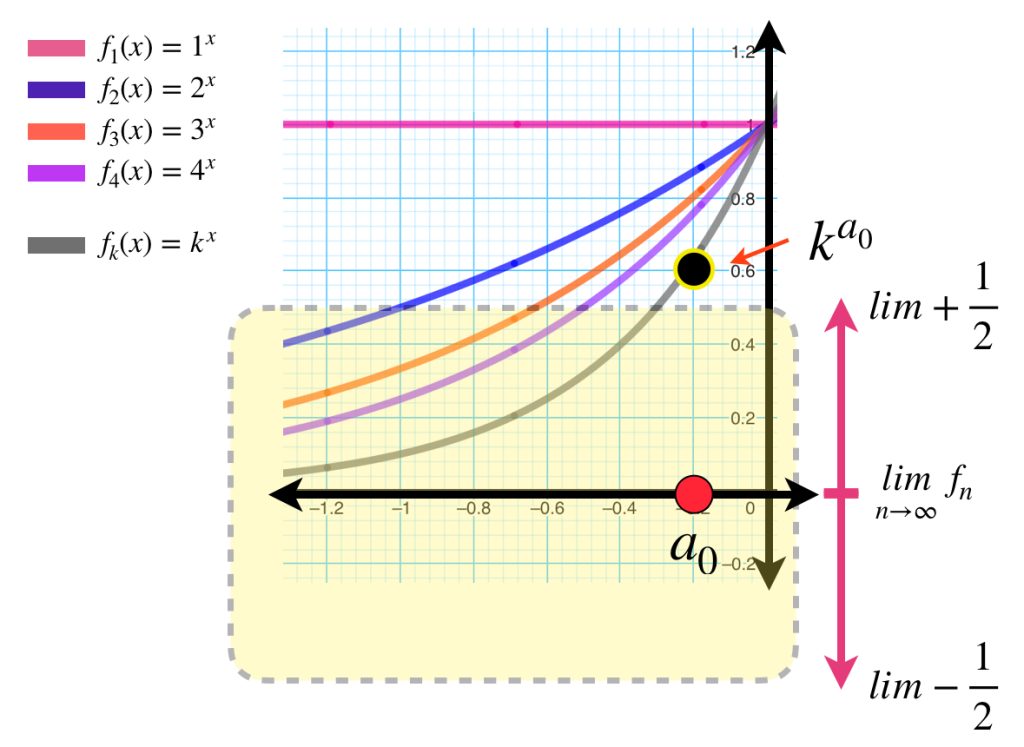
Ejemplo: Aunque la sucesión $(n^x)_{n \in \mathbb{N}} \,$ converge puntualmente en $(- \infty , 0]$ no converge uniformemente en el mismo dominio. Sea $\varepsilon = \frac{1}{2}$ y $k \in \mathbb{N}.$ Como la imagen de $k^x$ es $(0,1]$ entonces existe $a_0 \in (- \infty , 0)$ (donde $(n^{a_0})_{n \in \mathbb{N}} \to 0$) tal que $k^{a_0}> \varepsilon .$ Por lo tanto, el límite no es uniforme.

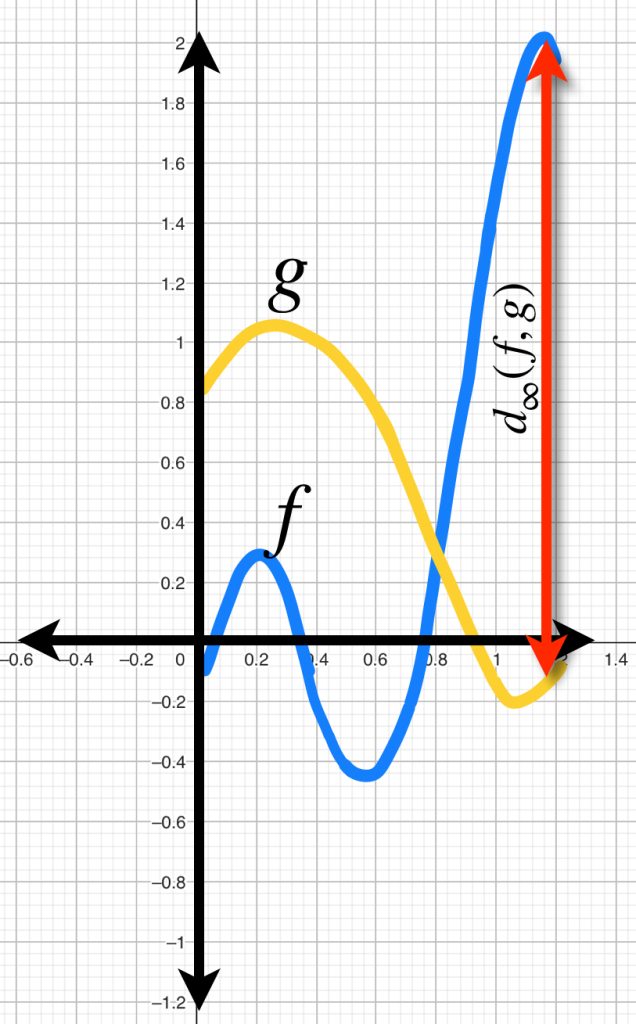
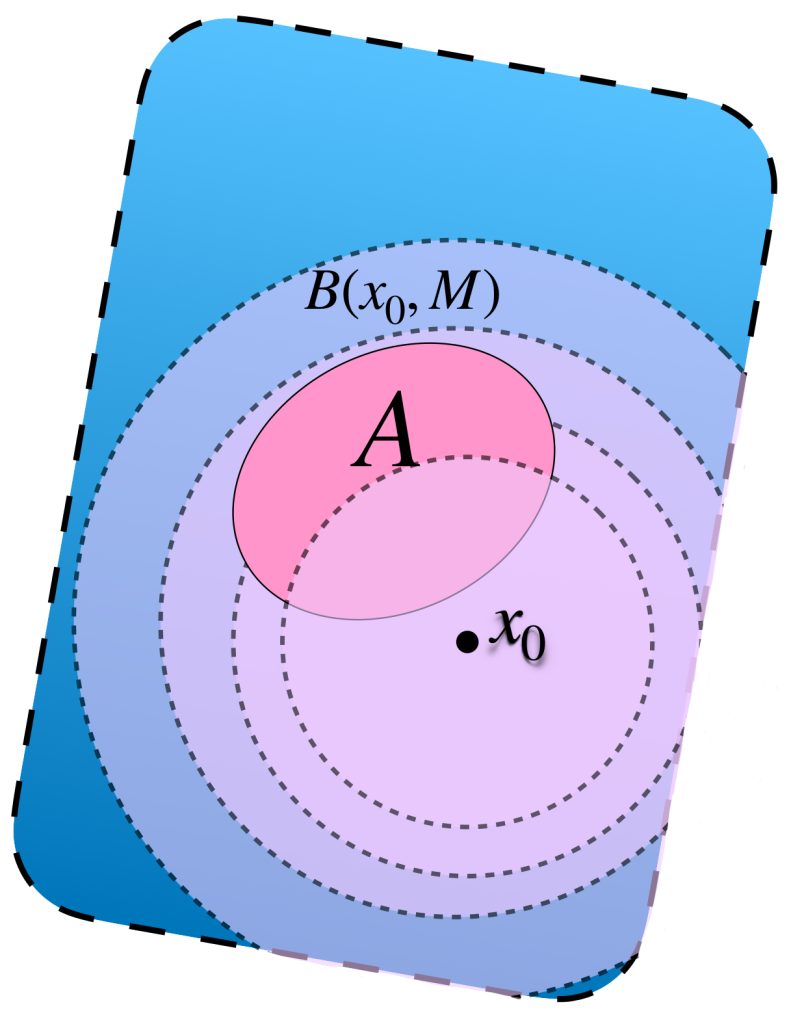
Esta no es la primera vez que hablamos de identificar distancias entre una función y otra. En la entrada Espacios de funciones definimos el espacio $\mathcal{B}(A,X)$ cuyos elementos son funciones acotadas de un conjunto $A$ en un espacio $X$ y la métrica está dada por:
$$d_\infty(f,g)= \underset{a \in A}{sup \,} \, d(f(a),g(a)), \, f,g \in \mathcal{B}(A,X)$$

Representación distancia entre funciones acotadas

La convergencia uniforme de una sucesión de funciones acotadas es equivalente a la convergencia como elementos del espacio métrico de funciones $\mathcal{B}(A,X),$ es decir:

Proposición: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión en $\mathcal{B}(A,X).$ Entonces, $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$

Demostración (ida):
Sea $\varepsilon >0.$ Como $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A,$ existe $N \in \mathbb{N} \,$ tal que para cada $k \geq N$ se cumple que para cada $a \in A, \, d(f_k(a),f(a)) < \frac{\varepsilon}{2} .$

1. $f$ está en el espacio $\mathcal{B}(A,X):$
Como $f_N$ es acotada, existen $x_0 \in X$ y $M \in \mathbb{R}$ tales que para toda $a \in A,$
$d(f_N(a),x_0) \leq M$
En consecuencia $d(f(a),x_0) \leq d(f(a),f_N(a))+d(f_N(a),x_0) < \frac{\varepsilon}{2} + M < \varepsilon + M$
Y como esto es posible $\forall \varepsilon >0$ concluimos que $f$ es acotada.

2. $(f_n)_{n \in \mathbb{N}} \to f$ en $\mathcal{B}(A,X):$
Teniendo a $\varepsilon$ como cota superior del conjunto $\{ d(f_k(a),f(a)) : a \in A \}$ se sigue que $d_\infty(f_k,f)= \underset{a \in A}{sup \,} \, d(f_k(a),f(a)) \leq \frac{\varepsilon}{2} < \varepsilon ,$ lo cual demuestra que $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$

El regreso es análogo y se propone como ejercicio.

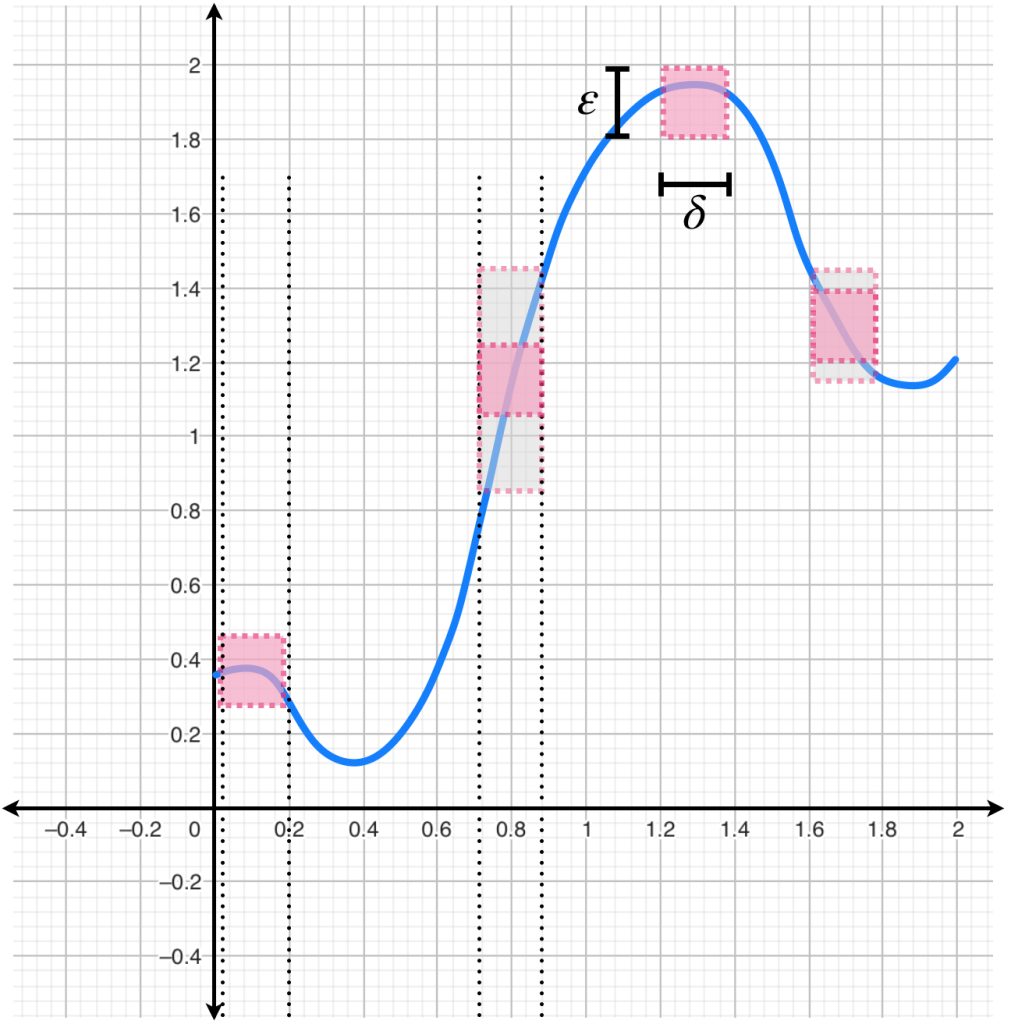
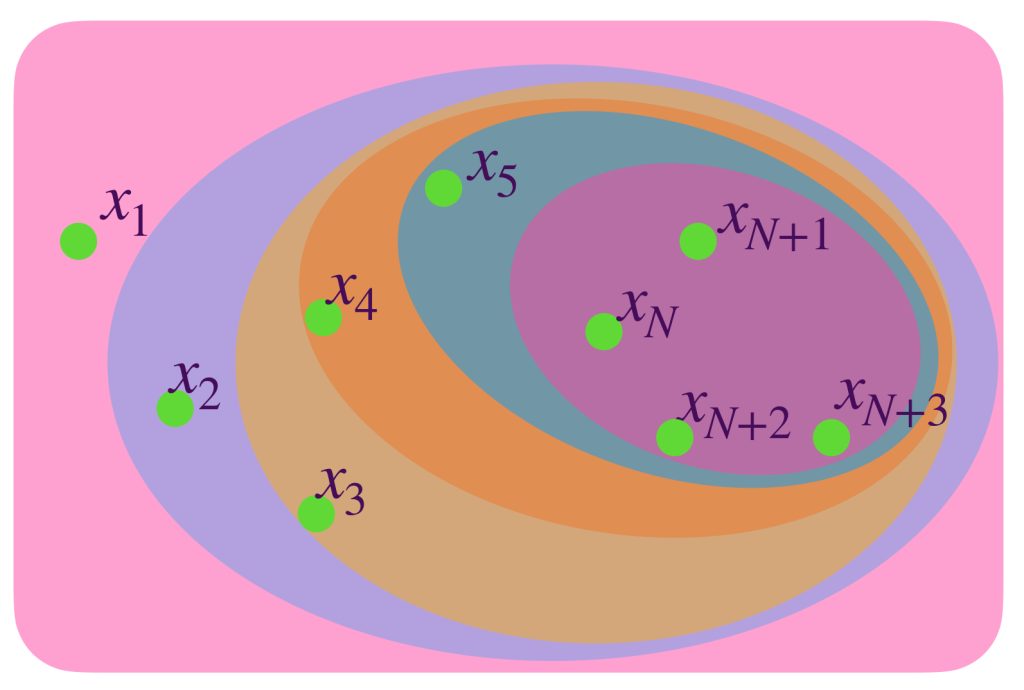
Definición. Sucesión uniformemente de Cauchy: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones con $f_n:A \to X, \, n \in \mathbb{N}.$ Decimos que $(f_n)$ es uniformemente de Cauchy en $A,$ si para todo $\, \varepsilon >0$ existe $N \in \mathbb{N}$ tal que para todo $\, l,m \geq N$ y para todo $ \, a \in A,$
$$d(f_l(a),f_m(a))< \varepsilon .$$

Nota que en la definición solo se menciona que las funciones de la sucesión se vuelven arbitrariamente cercanas dos a dos (en cualquier punto del dominio), a partir de alguna función.

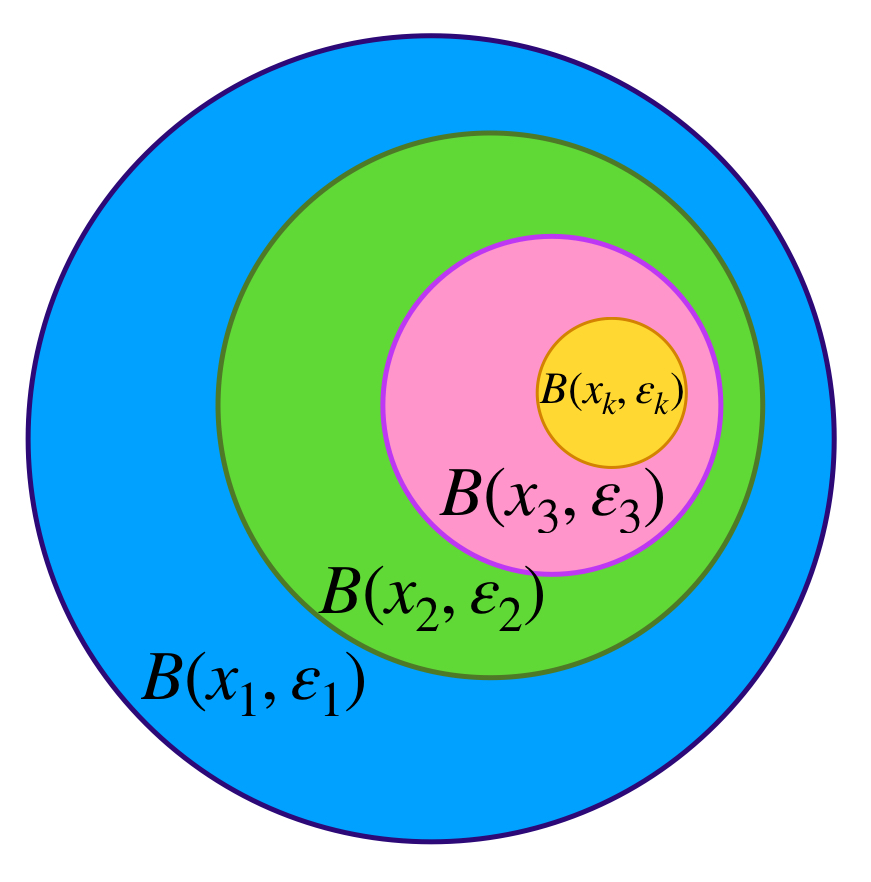
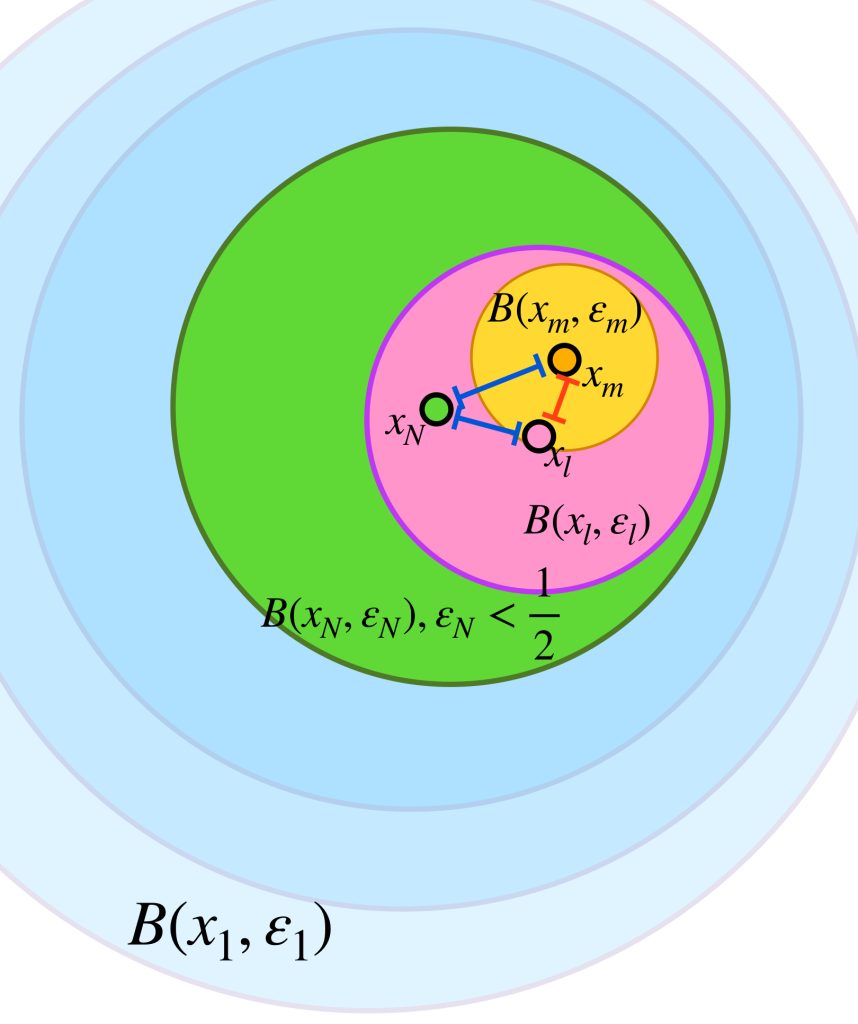
La siguiente imagen muestra una sucesión uniformemente de Cauchy.

$f_k:[0,2] \to \mathbb{R}, \, f_k=\frac{x}{kx+1}, \, k \in \mathbb{N}$

¿Cuándo podremos decir que una sucesión de funciones con esta propiedad converge de manera uniforme?

Para finalizar, veamos el siguiente resultado en espacios donde toda sucesión de Cauchy es convergente.

Teorema. Criterio de convergencia uniforme de Cauchy. Sea $(X,d)$ un espacio métrico completo. Una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ con $f_n:A \to X, \, n \in \mathbb{N}$ converge uniformemente en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ es uniformemente de Cauchy en $A.$

Demostración:
Partamos de suponer que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $A$ a alguna función $f:A \to X.$ Sea $\varepsilon >0.$ Existe $N \in \mathbb{N}$ tal que para cada $l, m \geq N$ se cumple que para cada $a \in A$:
$$d(f_l(a),f_m(a)) \leq d(f_l(a),f_N(a))+d(f_N(a),f_m(a)) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon.$$
Por lo tanto $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente de Cauchy en $A.$

Ahora supón que $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente de Cauchy en $A.$ Sea $\varepsilon>0.$ Existe $N \in \mathbb{N}$ tal que para cada $l, m \geq N$ se cumple que para cada $a \in A, \, d(f_l(a),f_m(a))< \varepsilon.$ Esto significa que la sucesión $(f_n(a))_{n \in \mathbb{N}}$ (formada por los puntos de las funciones evaluadas en un $a \in A$ fijo) es de Cauchy. Como $X$ es completo, se sigue que $(f_n(a))_{n \in \mathbb{N}} \to L_a$ para algún $L_a \in X.$
Sea $f:A \to X$ tal que para cada $a \in A, \, f(a) = L_a.$ Queda como ejercicio al lector demostrar que $f$ es el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$

Más adelante…

Observaremos sucesiones de funciones continuas que convergen. ¿Será continua la función límite? ¿Dependerá de si la convergencia es puntual o uniforme?

Tarea moral

  1. Para cada $n \in \mathbb{N}$ considera la función $n^x: \mathbb{R} \to \mathbb{R}.$ Donde tanto en el dominio como en el contradominio, $\mathbb{R}$ tiene la métrica euclidiana. Sea $a \in \mathbb{R}.$ Demuestra que:
    a) Si $a<0$ entonces $(n^a)_{n \in \mathbb{N}}$ es convergente. ¿Cuál es el límite?
    b) Si $a >0$ entonces $(n^a)_{n \in \mathbb{N}}$ tiende a infinito.
    c) ¿Qué ocurre con la sucesión cuando $a=0?$
  2. Consideremos la misma sucesión de funciones $(n^x)_{n \in \mathbb{N}} \,$ pero ahora con dominio $(- \infty, a]$ con $a < 0.$ Sea $\varepsilon >0$. Toma el $N_a \in \mathbb{N}$ que satisface que $\forall n\geq N_a, \, d(f_n(a),0) < \varepsilon$ el cual existe, pues $f_n(a) \to 0.$ Demuestra que para todo $a^*<a$ también se cumple que $\forall n\geq N_a, \, d(f_n(a^*),0) < \varepsilon$ y por tanto la convergencia en $(- \infty,a]$ es uniforme.
  3. Demuestra el regreso de la siguiente proposición:
    Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión en $\mathcal{B}(A,X).$ Entonces, $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$
  4. En la demostración del criterio de convergencia uniforme de Cauchy, demuestra que $f$ como fue definida, es el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$
  5. Supón que para cada $x \in A$ se cumple que $\underset{n \in \mathbb{N}}{lim} \, f_n(x) =f(x).$ Si definimos $M_n$ como $M_n=\underset{n \in \mathbb{N}}{sup} \, \, d(f_n(x),f(x))$ entonces $f_n \to f$ de manera uniforme si y solo si $M_n \to 0$ en $\mathbb{R}.$

Enlaces:

Continuidad uniforme

Por Lizbeth Fernández Villegas

Deja un comentario

Introducción

Hasta este punto, ya hemos visto varias propiedades que las funciones continuas tienen entre espacios métricos. De acuerdo a la definición, la continuidad en un punto se da cuando los puntos cercanos a él, son enviados a puntos cercanos en el otro espacio métrico.

Dado $\varepsilon >0$, incluso cuando la función $\phi :X \to Y$ es continua en todos los puntos $x_0$ de $X$, el valor de una $\delta_{x_0}$ que cumple que $\phi (B_X(x_0,\delta_{x_0})) \subset B_Y(\phi(x_0), \varepsilon)$ podría ser diferente para cada punto.

Por ejemplo, sabemos que la función identidad $I:[0,1] \to [0,1]$ es continua en $[0,1]$. Si suponemos $\varepsilon = \frac{1}{3}$ podemos hablar más explícitamente de la continuidad en los puntos $\frac{1}{3}$ y $\frac{2}{3}$ asignando $\delta_1 = \frac{1}{3}$ y $\delta_2 = \frac{1}{6}$, respectivamente.

Podemos comprobar que ambas deltas satisfacen la definición de continuidad y sin embargo son diferentes. No obstante, eligiendo $\delta$ como la mínima entre las dos, podemos argumentar también la continuidad en ambos puntos con la misma $\delta.$

En general, en una cantidad finita de puntos donde la función es continua, también es posible elegir el valor de $\delta$ mínimo y este funciona para demostrar la continuidad en cada punto, pero si la continuidad es en un conjunto infinito no siempre existe una delta general .

En los ejemplos de continuidad que hemos visto, fijamos un punto en el espacio del dominio $X$ y observamos un conjunto en torno a él (la bola de radio $\delta$).

¿Qué pasa si nos fijamos en bolas de radio $\delta$ de manera arbitraria en el dominio? ¿Serán enviados a puntos cercanos en el espacio métrico $Y$?

Esta discusión incentiva la siguiente:

Definición. Función uniformemente continua: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Decimos que una función $\phi :X \to Y$ es uniformemente continua en $X$ si dada $\varepsilon >0$ existe $\delta >0$ tal que para cualesquiera $x_1, x_2 \, \in \, X$, si satisfacen que $d_X(x_1,x_2)< \delta$, entonces $d_Y(\phi(x_1), \phi(x_2)) < \varepsilon$.

Al final de esta sección se propone demostrar que toda función uniformemente continua es continua. No obstante, hay funciones continuas que no son uniformemente continuas.

Ejemplo: La función $f:(0,\infty) \to \mathbb{R}, \, f(x)= \frac{1}{x}$ es continua en $(0,\infty)$ pero no es uniformemente continua, pues si consideramos $\varepsilon=1$ y cualquier $\delta>0$ todos los pares de puntos en el intervalo $(0,\delta)$ tienen distancia menor que $\delta.$ Sea $x_1 \in (0,\delta).$ Como $f$ es decreciente y tiende a $\infty$ en cero por la derecha entonces existe $x_2 < x_1$ tal que $f(x_2)>1+f(x_1)$ por lo tanto, aunque $|x_2-x_1|< \delta$ se tiene que $|f(x_2)-f(x_1)|>1= \varepsilon$ y en consecuencia, la función no es uniformemente continua.

$f$ no es uniformemente continua

Pero hay una propiedad que hace equivalentes ambos tipos de funciones:

Proposición: Sea $A$ un espacio métrico compacto. Si $\phi : A \to Y$ es una función continua, entonces $\phi$ es uniformemente continua.
Demostración:
Supón por el contrario que $\phi:A \to Y$ no es uniformemente continua. Entonces existe $\varepsilon >0$ tal que $\forall \, \delta>0$ existen $a_1,a_2$ con distancia menor que $\delta$ pero cuya distancia correspondiente en $Y$ para $\phi(a_1)$ y $\phi(a_2)$ es mayor igual que \varepsilon.

Particularmente, para cada $n \in \mathbb{N}$ existen $x_n,x’_n \in A$ tales que $d_A(x_n,x’_n)<\frac{1}{n}$ y $d_Y(\phi(x_n),\phi(x’_n)) \geq \varepsilon.$

Entonces la sucesión $(x_n)_{n \in \mathbb{N}}$ que está en $A$ compacto, tiene una subsuseción $(x_{k_j})$ que converge en algún $x \in A.$ La sucesión correspondiente $(x’_{k_j})$ también converge en $x,$ pues:

$$d_A(x,x’_{k_j}) \leq d_A(x,x_{k_j})+d_A(x_{k_j},x’_{k_j}) \to 0$$

Entonces, como $\phi$ es continua se cumple que $\phi(x_{k_j}) \to \phi(x)$ y $\phi(x’_{k_j}) \to \phi(x)$ de modo que existe $J \in \mathbb{N}$ tal que.

$d_Y(\phi(x_{k_j}),\phi(x’_{k_j})) \leq d_Y(\phi(x_{k_j}),\phi(x))+d_Y(\phi(x),\phi(x’_{k_j})) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon.$

Pero esto es una contradicción, pues al principio se seleccionaron términos que satisfacen que $d_Y(\phi(x_{k_j}),\phi(x’_{k_j})) \geq \varepsilon.$ Por lo tanto la función sí es uniformemente continua.

Más adelante…

Ya que conocemos algunos resultados de la compacidad en los conjuntos, mostraremos una herramienta para identificarla en espacios de funciones: el teorema de Arzelá-Azcoli. En la siguiente sección veremos las definiciones que nos llevarán a ella.

Tarea moral

  1. Demuestra que toda función uniformemente continua es continua.
  2. ¿Es cierto que toda función Lipschitz continua es uniformemente continua?
  3. ¿Es cierto que toda función uniformemente continua es Lipschitz continua?
  4. ¿Es la función $f:[a,\infty) \to \mathbb{R}, \, f(x)= \frac{1}{x}, \, a>0,$ uniformemente continua?

Enlaces

Compacidad en espacios métricos

Por Lizbeth Fernández Villegas

Deja un comentario

Introducción

En esta sección mostraremos los fundamentos de uno de los términos más importantes de las matemáticas. Una descripción histórica la presenta Yanina del Carmen Rodríguez Reyes, en la tesis «Desarrollo histórico-pedagógico del concepto de compacidad» en la Universidad de Panamá, República de Panamá 2018.

«La compacidad surgió de uno de los periodos más productivos de la actividad matemática. En la segunda mitad del siglo XIX en Europa las matemáticas avanzadas comenzaron a tomar la forma que conocemos actualmente. Muchos matemáticos, incluyendo Weierstrass, Hausdorff y Dedekind estaban preocupados por los fundamentos de las matemáticas y comenzaron a hacer muchas rigurosidades de las ideas que durante siglos habían sido dadas por sentado. Mientras que algunos de los trabajos del siglo XIX se pueden remontar a las preocupaciones matemáticas de los antiguos griegos, el nivel de rigor y la abstracción refleja una revolución en el pensamiento matemático. Fréchet fue influenciado por muchos contemporáneos y predecesores pero parece que merece el crédito como el padre de la compacidad. Fue Fréchet quien dio el nombre al concepto en un documento que conduce a su tesis doctoral de 1906. Fréchet también define por primera vez espacios métricos aunque no usando ese término y de hecho incursiona en el análisis funcional proporcionando así un contexto para el cual la importancia de la compacidad se hizo indiscutible”. (Rodríguez, 2018).

Conjuntos compactos

Sea $(X,d)$ un espacio métrico y $A \subset X$. Podemos pensar en «cubrir» este subconjunto a través de otros a modo de la siguiente imagen, es decir, conjuntos cuya unión logre contener a $A.$

$A$ cubierto por conjuntos

La cantidad de subconjuntos que forman parte de la cubierta elegida puede ser finita, numerable o no numerable, entonces, para ser formales, cada subconjunto se puede indexar con los elementos de algún conjunto $\mathcal{I}$. Así tenemos la siguiente:

Definición cubierta de un conjunto: Sea $A \subset X$. Decimos que una familia de subconjuntos $\mathcal{C} = \{A_{i} \subset X : i \in \mathcal{I} \}$ es una cubierta de $A$ en $X$ si
$$A \subset \underset{i \in \mathcal{I}}{\cup} \, A_{i} \,$$

Cubierta de $A$

Definición. Cubierta abierta: Si para toda $i \in \mathcal{I}$ se cumple que el conjunto $A_i$ es abierto, diremos que $\mathcal{C}$ es una cubierta abierta de $A$ en $X$.

Cubierta abierta de $A$

Definición. Subcubierta: Si tomamos conjuntos de una cubierta $\mathcal{C}$, digamos, una familia $\mathcal{C’} \subset \mathcal{C} \, $ y $\, \mathcal{C’}$ es también una cubierta de $A$ diremos que $\mathcal{C’}$ es una subcubierta de $\mathcal{C}$.

Los conjuntos en rosa son una subcubierta de $\mathcal{C}$

Definición. Conjunto compacto: Sea $A$ un conjunto de un espacio métrico $(X,d)$. Decimos que $A$ es un conjunto compacto si dada cualquier cubierta abierta $\mathcal{C}$ de $A$, existe una subcubierta finita de $\mathcal{C}.$

El concepto de compacidad suele tomar mayor relevancia cuando en un espacio topológico se considera el subespacio generado por el conjunto compacto. En estos casos se le denomina espacio topológico compacto.

Subcubierta abierta finita

Según la definición, para demostrar que un conjunto $A$ no es compacto, bastará con identificar una cubierta de la cual no sea posible extraer una subcubierta finita (conjuntos cuya unión logre contener el conjunto $A$).

Ejemplos

El conjunto $\mathbb{R}$ con la métrica euclidiana no es compacto.

Demostración:
El conjunto de intervalos abiertos con centro en $0$ y radio $n, \, n \in \mathbb{N}$ es decir, $\mathcal{C}=\{(-n,n):n \in \mathbb{N}\}$ es una cubierta abierta de $\mathbb{R}.$ Pero si consideramos un subconjunto finito $\mathcal{C’} \subset \mathcal{C}$ entonces $\mathcal{C’} = \{(-k_1,k_1),(-k_2,k_2),…,(-k_m,k_m)\}$ con $k_1,k_2,…,k_m \in \mathbb{N}.$ Sea $k=máx\{k_1,k_2,…,k_m\}$ podemos ver que la unión de los elementos en $\mathcal{C’}$ es el intervalo $(-k,k)$ que claramente, no contiene a $\mathbb{R}$, por lo tanto $\mathbb{R}$ no es compacto.

Representación de intervalos de la subcubierta finita

Un espacio discreto es compacto si y solo si es finito

Considera un conjunto $X$ con la métrica discreta. Entonces, para cada $x \in X$ el conjunto $\{ x \}$ es abierto, así $\mathcal{C}=\{\{x\}:x \in X\}$ es una cubierta abierta de $X.$ Un subconjunto finito de esta cubierta estaría dada por $\mathcal{C’}=\{\{x_1\},\{x_2\},…,\{x_k\}\}, \, k \in \mathbb{N}$ cuya unión de conjuntos contiene $k$ elementos. Por lo tanto, si $X$ es infinito no es compacto con la métrica discreta. La prueba de que si $X$ es finito entonces es compacto se deja como ejercicio al final de esta sección.

Si $(X,d_{disc})$ es infinito no hay subcubierta finita

Proposición. Si $A$ es un conjunto compacto en $(X,d)$, entonces toda sucesión en $A$ tiene una subsucesión que converge en $A$.

Demostración:
Sea $A \subset X$ compacto y $(x_n)_{n \in \mathbb{N}} \,$ una sucesión en $A$. Demostraremos primero que existe un punto $x \in A$ tal que toda bola abierta con centro en $x$ tiene una subsucesión de $(x_n)$. Supón por el contrario que no es así, es decir, para todo punto $x \in A$ existe $\varepsilon_x >0$ y existe $k_x \in \mathbb{N}$ tal que para toda $k \geq k_x, \, x_k \, \notin \, B(x,\varepsilon_x).$

No hay subsucesión dentro de la bola abierta pues todos los últimos términos de la sucesión están fuera de ella.


El conjunto de todas estas bolas abiertas, $\{B(x, \varepsilon_x): x \in A\}$ es una cubierta abierta del conjunto $A$. Como $A$ es compacto, existe $\{B(x_1, \varepsilon_{x_1}),B(x_2, \varepsilon_{x_2}),…,B(x_m, \varepsilon_{x_m})\}$ subcubierta finita. Sea $l =: máx \{k_{x_1},k_{x_2},…,k_{x_3}$ entonces para toda $k \geq l,$ el término $x_k \notin \underset{1\leq i \leq m}{\cup} \, B(x_i, \varepsilon_{x_i}) \supset A,$ en consecuencia $x _k \notin A$ lo cual es una contradicción, pues todos los términos de la sucesión están en $A$, por lo tanto existe un punto $x \in A$ tal que toda bola abierta con centro en $x$ tiene una subsucesión de $(x_n)$.

Cubierta finita

Sea $x \in A$ dicho punto. Por la propiedad mencionada es posible seleccionar un punto $x_{k_j}$ de la sucesión que esté en cada bola $B(x,\frac{1}{j}), \, j \in \mathbb{N}$ tal que no se repita con los anteriores y conserven el orden de la sucesión original. Por lo tanto $(x_{k_j})$ es subsucesión de $(x_n)$ y $x_{k_{j}} \to x$.
Así probamos que toda sucesión de un conjunto compacto tiene una subsucesión que converge en él.


Proposición: Si $A \subset X$ es compacto entonces es cerrado y acotado.

Demostración:
Recordemos que un conjunto es cerrado si y solo si es igual a su cerradura. Como $A \subset \overline{A}$ basta demostrar que $\overline{A} \subset A$. Sea $x \in \overline{A}$ entonces existe una sucesión $(x_n)_{n \in \mathbb{N}}$ en $A$ que converge en $x$ (Visto en Convergencia). Pero por la proposición que acabamos de ver, $(x_n)$ tiene una subsucesión que converge en $A$. Por la unicidad del límite, ese punto de convergencia es $x$, por lo tanto $x \in A$.

La subsucesión converge en $x$. Por lo tanto $x \in A$

Para probar que $A$ es acotado notemos lo siguiente. Si fijamos un punto $x_0 \in X$, podemos poner cada $x \in A$ en una bola abierta con centro en $x_0$ y radio mayor a la distancia $d(x,x_0).$ Elegimos el radio como un número natural $k \,$ suficientemente grande, tal que $d(x,x_0)<k.$ Entonces $x \in B(x_0,k).$

Cada punto de $A$ está en una bola abierta de $x_0$

En consecuencia el conjunto de bolas abiertas $\{B(x_0,n):n \in \mathbb{N}\}$ es una cubierta abierta del conjunto $A$ que, como es compacto, tiene una subcubierta finita $\{B(x_0,n_1), B(x_0,n_2),…,B(x_0,n_m)\}$. Sea $M =: máx \{n_1,n_2,…,n_m\}$ entonces $A \subset B(x_0,M)$ por lo tanto $A$ es acotado.

$A \subset B(x_0,M)$

Ejemplos

A continuación recordamos un resultado conocido de los cursos de cálculo:

Teorema de Heine Borel: Considera $\mathbb{R}^n$ con la métrica euclidiana y $A \subset \mathbb{R}^n.$ Entonces $A$ es un conjunto compacto si y solo si es cerrado y acotado.

Conjuntos compactos en $\mathbb{R}^3$

No obstante, hay espacios métricos en los que no es suficiente que un conjunto sea cerrado y acotado para que sea compacto:

Ejercicio: Considera el conjunto $\mathbb{R}$ y $d$ definida como $d(x,y)=min\{1, |x-y|\}, \, x,y \in \mathbb{R}$ entonces tenemos lo siguiente:

  1. $d$ es una métrica en $\mathbb{R}.$
  2. $d$ induce en $\mathbb{R}$ los mismos conjuntos abiertos que la métrica usual. Entonces un conjunto es compacto en $(\mathbb{R},d)$ si y solo si lo es en $(\mathbb{R},d_2).$
  3. El conjunto $[0,\infty)$ es cerrado y acotado en $(\mathbb{R},d),$ pero no es compacto, pues no lo es en $(\mathbb{R},d_2).$

Veamos una propiedad que hereda la compacidad a un subconjunto de un conjunto compacto:

Proposición: Un subconjunto cerrado $B$ de un conjunto compacto $A$ también es compacto.

Demostración:

Sea $B \subset A$ con $B$ cerrado y $A$ compacto. Considera $\mathcal{C} = \{B_{i} \subset X : i \in \mathcal{I} \}$ una cubierta abierta de $B$.

Representación de una cubierta abierta de $B$

Como $B$ es cerrado, entonces el conjunto $X \setminus B$ es abierto.

$X \setminus B$ es abierto

Dado que $B \subset A,$ si agregamos $X \setminus B$ a la cubierta de $B$ tenemos que $\mathcal{C} \cup \{X \setminus B\}$ es una cubierta abierta de $A.$

$\mathcal{C} \cup \{X \setminus B\}$ es una cubierta abierta de $A$


Al ser el conjunto $A$ compacto, se sigue que esta cubierta tiene una subcubierta finita que satisface:
$$B \subset A \subset B_{i_1} \cup…\cup B_{i_n} \cup (X \setminus A).$$ con $n \in \mathbb{N}.$

Por lo tanto $\mathcal{C’}=B_{i_1},…,B_{i_n}$ es una subcubierta finita de $\mathcal{C}$ lo cual concluye que $B$ es compacto.

La cubierta abierta de $B$ tiene una subcubierta finita

Finalizamos esta sección con los siguientes resultados para así cumplir con una deuda pendiente.

Teorema: Considera $ \{ A_{\alpha} : \alpha \in \mathcal{A} \}$ una colección de subconjuntos compactos de un espacio métrico $(X,d).$ Si ocurre que cualquier intersección finita de elementos de $\{A_{\alpha}\}$ es no vacía, entonces la intersección de todos los elementos también es no vacía. Es decir:
$$\underset{\alpha \in \mathcal{A}}{\bigcap} \, A_{\alpha} \, \neq \emptyset$$

Demostración:
Supón por el contrario que la intersección es vacía. Sea $A_1 \in \{A_{\alpha}\}$ entonces no existe punto de $A_1$ que pertenezca al mismo tiempo, a todos los elementos de $\{A_{\alpha}\}$
Sea $C_{\alpha} := X \setminus A_{\alpha}.$ Entonces $ \{ C_{\alpha} : \alpha \in \mathcal{A} \}$ es una cubierta abierta de $A_1$ que, por ser compacto, tiene una subcubierta finita, así:
$A_1 \subset (C_{\alpha_1} \cup … \cup C_{\alpha_n})$ p.a. ${\alpha_1},…{\alpha_n}, \in \mathcal{A}$
En consecuencia $A_{\alpha_1} \cap … \cap A_{\alpha_n} = \emptyset$ lo cual no es cierto, por lo tanto
$$\underset{\alpha \in \mathcal{A}}{\bigcap} \, A_{\alpha} \, \neq \emptyset$$

Corolario: Si $ \{ A_{n} : n \in \mathbb{N} \}$ es una colección de subconjuntos compactos no vacíos de un espacio métrico $(X,d)$ tales que para cada $n \in \mathbb{N} , \, A_n \supset A_{n+1}$ se cumple que $\underset{n \in \mathbb{N}}{\bigcap} \, A_n \neq \emptyset .$

En la entrada Convergencia uniforme y continuidad se enunció el siguiente resultado. Vamos a retomarla ahora con demostración.

Proposición: Sea $A$ un espacio métrico compacto, $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones continuas con $f_n:A \to \mathbb{R}, n \in \mathbb{N}$ tal que $(f_n)$ converge puntualmente a una función continua $f$. Si para cada $x \in A$ y $n \in \mathbb{N} \, f_n(x) \geq f_{n+1}(x),$ entonces $(f_n)$ converge a $f$ uniformemente en $A.$

Demostración:
Para cada $n \in \mathbb{N}$ definimos $g_n := f_n – f.$ Entonces $(g_n)_{n \in \mathbb{N}} \,$ es una sucesión de funciones continuas en $A.$ Es sencillo probar que $(g_n)_{n \in \mathbb{N}} \,$ converge puntualmente a $0.$

Sea $\varepsilon >0.$ Ahora, para cada $n \in \mathbb{N}$ definimos un conjunto con los puntos de $A$ que bajo la función $g_n \,$ quedan fuera de la bola de radio $\varepsilon$ con centro en $0.$ Formalmente:

$A_n:= \{a \in A: g_n(a) \notin \, B(0,\varepsilon)\}$

Nota que este conjunto es complemento de la imagen inversa de la función continua $g_n \,$ en la bola abierta $B(0,\varepsilon).$ Por lo tanto $A_n$ es cerrado en $A.$ Esa propiedad se vio en Funciones continuas en espacios métricos. Arriba vimos que cada conjunto cerrado de un compacto hereda la compacidad, en consecuencia cada $A_n$ es compacto.

Nota además que para cada $n \in \mathbb{N}, \, A_{n+1} \subset A_n.$ La intersección de todos estos conjuntos es vacía, pues si existe $x_0 \in \underset{\n \in \mathbb{N}}{\cap} \, A_n$ entonces para toda $n \in \mathbb{N}, \, g_n(a) \notin \, B(0,\varepsilon)$ lo cual no puede ser, pues $g_n(x_0) \to 0.$ A partir del corolario visto un par de lineas arriba se sigue que existe $N \in \mathbb{N}$ tal que $A_N$ es vacío. Entonces, para todo $k \geq N, \, A_k = \emptyset.$ Así para cada $a \in A$ se cumple que $0 \leq g_n(a) < \varepsilon.$ Por lo tanto $(f_n)$ converge a $f$ uniformemente en $A.$

Más adelante…

Conoceremos los efectos que producen algunas funciones al ser aplicadas en conjuntos compactos. ¿Será posible conservar la compacidad al enviar conjuntos de un espacio métrico a otro? ¿Qué propiedades tendrá la imagen de una función continua?

Tarea moral

  1. Resuelve el ejercicio planteado arriba.
  2. Prueba que un espacio discreto finito es compacto. ¿Es necesario que tenga asociada la métrica discreta?
  3. Demuestra que cada subconjunto infinito de un conjunto compacto posee un punto de acumulación en el conjunto compacto.
  4. Da un ejemplo de un conjunto $A$ que sea cerrado pero no acotado y una cubierta abierta y numerable de $A$ que no tenga una subcubierta finita.
  5. Prueba que si $A$ es cerrado y $B$ es compacto, entonces $A \cap B$ es compacto.
  6. Prueba que la intersección arbitraria de conjuntos compactos es compacta.
  7. Demuestra que una sucesión de Cauchy en un conjunto compacto es convergente.
  8. Sea $(X,d)$ un espacio métrico y $A \subset X$ un conjunto compacto. Demuestra que el subespacio $(A,d)$ es completo.

Enlaces

Conjuntos anidados

Por Lizbeth Fernández Villegas

Deja un comentario

Introducción:

En esta ocasión nos vamos a fijar en colecciones de conjuntos que están contenidos unos en otros. Vamos a suponer que es una cantidad numerable de conjuntos. El primer conjunto contiene al segundo, que a su vez contiene a un tercero y así, sucesivamente.

Ahora pensemos en la intersección de todos esos conjuntos. Intuitivamente podemos visualizar que se tratará de un conjunto muy pequeño, que estará contenido en todos los demás.

Aquí tenemos un ejemplo de una sucesión de conjuntos donde los últimos términos corresponden al mismo conjunto. La intersección de todos los conjuntos es, evidentemente, ese último conjunto

Observemos la sucesión de intervalos $[-\frac{1}{n},\frac{1}{n}]_{n \in \mathbb{N}}.$

Nota que todos tienen como elemento al cero. Además es el único elemento que pertenece a la intersección de todos los intervalos, pues si suponemos que hay otro más, dado que $\frac{1}{n} \to 0$ es posible encontrar un intervalo suficientemente pequeño, que deje fuera este elemento.

Con un radio menor a la distancia entre $0$ y el punto rojo, este último queda fuera.

Ahora consideremos el subespacio $\mathbb{Q}$ con la métrica usual. En esta ocasión los intervalos serán $(\sqrt{2}-\frac{1}{n},\sqrt{2}+\frac{1}{n}), \, n \in \mathbb{N}.$ Queda como ejercicio al lector demostrar que la intersección de estos conjuntos es vacía en $\mathbb{Q}$.

Entonces, ¿bajo qué condiciones podremos asegurar que la intersección no es vacía pese a que los conjuntos se hagan «cada vez más pequeños» y estén contenidos unos en otros? Veamos la siguiente definición:

Definición bolas encajadas: Sea $(X,d)$ un espacio métrico y $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ una sucesión de bolas cerradas en $X$. Si $\forall n \in \mathbb{N}$ se cumple que $\overline{B}(x_{n+1},\varepsilon_{n+1}) \subset \overline{B}(x_{n},\varepsilon_{n})$ diremos que la sucesión $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}}$ es de bolas encajadas.

Sucesión de bolas cerradas encajadas

Proposición principio de bolas encajadas: $(X,d)$ es un espacio métrico completo si y solo si para cualquier sucesión de bolas cerradas encajadas $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}}$ cuyos radios tienden a cero, es decir $\varepsilon_n \to 0,$ se cumple que la intersección de todas las bolas cerradas es no vacía. Además $\underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n) = \{x\}$ para algún $x \in X.$

Demostración:
Supongamos que $(X,d)$ es completo. Sea $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ una sucesión de bolas encajadas. Vamos a probar primero que la sucesión de los centros de las bolas cerradas $(x_n)_{n \in \mathbb{N}} \,$ es de Cauchy. Sea $\varepsilon > 0,$ como $\varepsilon_n \to 0,$ existe $N \in \mathbb{N}$ tal que $\forall \, n \geq N, \, \varepsilon_n < \frac{\varepsilon}{2}.$ Como la sucesión es de bolas encajadas, tenemos que $\forall \, l,m \geq N, \, \overline{B}(x_l,\varepsilon_l) \subset \overline{B}(x_N,\varepsilon_N)$ y $\overline{B}(x_m,\varepsilon_m) \subset \overline{B}(x_N,\varepsilon_N)$ entonces $d(x_l,x_m) \leq d(x_l,x_N) + d(x_N,x_m) \leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon.$ Por lo tanto $(x_n)$ es de Cauchy. Como $X$ es completo, se sigue que $x_n \to x$ para algún $x \in X$


Vamos a demostrar que $x \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n).$ Sea $n \in \mathbb{N}.$ Como las bolas son encajadas, tenemos que $\forall k \geq n, \, B(x_k,\varepsilon_k) \subset B(x_n,\varepsilon_n)$ en consecuencia $\forall k \geq n,$ el término de la sucesión $x_k$ es elemento de $B(x_n,\varepsilon_n),$ que es un conjunto cerrado. Ya que la subsucesión formada por estos últimos términos converge en $x$ se sigue de lo que vimos en Convergencia que $x \in B(x_n,\varepsilon_n).$ Como esto ocurre $\forall n \in \mathbb{N},$ concluimos que $x \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n).$

Además $x$ es el único punto en la intersección, pues si existe otro punto $x’ \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n)$ existen también bolas cerradas suficientemente pequeñas que no contienen a ambos puntos. La demostración de este hecho se deja como ejercicio.

Para el regreso buscamos demostrar que $(X,d)$ es completo. Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy.

Vamos a construir una sucesión de bolas encajadas de la siguiente forma:
Ya que la sucesión $(x_n)$ es de Cauchy, podemos afirmar que existe $N_1 \in \mathbb{N}$ tal que $\forall \, n,m \geq N_1, \, d(x_n,x_m)\leq \frac{1}{2}.$ Entonces $\forall \, n \geq N_1, \, x_n \in B(x_{N_1}, \frac{1}{2}) \subset B(x_{N_1},1).$

Nuevamente, como $(x_n)$ es de Cauchy, existe $N_2 \in \mathbb{N}$ tal que $\forall \, n,m \geq N_2, \, d(x_n,x_m)\leq \frac{1}{2^2}.$ Entonces $\forall \, n \geq N_2, \, x_n \in B(x_{N_2}, \frac{1}{2^2}) \subset B(x_{N_2},\frac{1}{2}).$ Nota que esta bola está contenida en la anterior.

Continuando recursivamente, la bola $k$ de la sucesión en construcción estará dada por el centro $x_{N_k}$ donde $N_k$ es tal que $\forall \, n,m \geq N_k, \, d(x_n,x_m)\leq \frac{1}{2^k}.$ Entonces $\forall \, n \geq N_k, \, x_n \in B(x_{N_k}, \frac{1}{2^k}) \subset B(x_{N_k},\frac{1}{2^{k-1}}).$

Así, la sucesión $(B(x_{N_n},\frac{1}{2^{n-1}}))_{n \in \mathbb{N}}$ es de bolas encajadas y sus radios tienden a cero. Por hipótesis sabemos que la intersección de estos conjuntos es $\{x\},$ para algún $x \in X.$ Es sencillo probar que la sucesión de centros $(x_{N_n})_{n \in \mathbb{N}}$ converge en $x$ (se dejará como ejercicio). Entonces tenemos una subsucesión de la sucesión de Cauchy $(x_n)$ que es convergente y, como vimos en entrada anterior, esto demuestra que $(x_n) \to x$ por lo que $X$ es completo.

Notemos que para asegurar la contención de un conjunto en otro, necesitamos obtener información acerca de las distancias entre sus elementos. Esto motiva una definición para conjuntos más generales que una bola cerrada:

Definición diámetro de un conjunto: Sea $A \subset X$. Entonces el diámetro de $A$ se define como:
$$diam(A) = sup\{d(x_1,x_2): x_1,x_2 \in A \}$$.

Cuando el conjunto $\{d(x_1,x_2): x_1,x_2 \in A \}$ no es acotado, diremos que el diámetro es $\infty.$

Proposición: Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión en $(X,d)$ y para cada $N \in \mathbb{N}, \, X_N=\{x_k:k\geq N\}$ el conjunto de los términos de la sucesión que van a partir de $x_N.$ Entonces $(x_n)$ es una sucesión de Cauchy si y solo si
$$\underset{N \to \infty}{lim}\, diam \, (X_N)=0$$

Demostración:
Supón que $(x_n)$ es una sucesión de Cauchy en $X$ y sea $\varepsilon>0$. Entonces existe $K \in \mathbb{N}$ tal que $\forall \, l,m \geq K, \, d(x_l,x_m)<\varepsilon$. En consecuencia $diam\,(X_K) \leq \varepsilon.$ Como para todo $L \geq K, \, (X_L) \subset (X_K)$ se sigue que para todo $L \geq K, \, diam(X_L) \leq diam(X_K) \leq \varepsilon.$ Por lo tanto $\underset{N \to \infty}{lim}\, diam \, (X_N)=0$

Ahora supongamos que $\underset{N \to \infty}{lim}\, diam \, (X_N)=0.$ Buscamos demostrar que $(x_n)$ es de Cauchy. Sea $\varepsilon >0$, como los diámetros tienden a cero, existe $K \in \mathbb{N}$ tal que en particular $(X_K)$ satisface que $diam \, (X_K) < \varepsilon.$ Entonces $\forall \, l,m \geq K, \, d(x_l,x_m) < \varepsilon$ lo cual demuestra que $(x_n)$ es de Cauchy.

Terminemos con la siguiente:

Proposición: Sean $(A_n)_{n \in \mathbb{N}}\,$ una sucesión de subconjuntos cerrados de un espacio métrico completo $(X,d)$ tales que para todo $n \in \mathbb{N}, \, A_{n+1} \subset A_{n}$ y además $\underset{n \to \infty}{lim} \, diam(A_n) \to 0.$ Entonces $\underset{n \in \mathbb{N}}{\cap}A_n=\{x\}$ para algún $x \in X$).

Demostración:
Para cada $n \in \mathbb{N}$ elegimos $x_n \in A_n.$ Entonces para cada $N \in \mathbb{N}$ el conjunto $X_N$ definido en la proposición anterior está contenido en $A_N$, pues los conjuntos están anidados. En consecuencia, $diam(X_N) \leq diam(A_n) \to 0.$ La proposición anterior nos permite concluir que $(x_n)$ es una sucesión de Cauchy. Como $X$ es completo, se sigue que $(x_n) \to x$ para algún $x \in X.$ Dejamos como ejercicio demostrar que $\underset{n \in \mathbb{N}}{\cap}A_n=\{x\}$.

¿Recuerdas la distancia de Hausdorff vista en La métrica de Hausdorff? Nota que si $A$ y $B$ son subconjuntos de $X$ entonces $d_H(A,B)\leq diam(A \cup B).$ En esa misma entrada vimos que conjuntos anidados convergen a la intersección de todos ellos, y que este conjunto está formado por los puntos de convergencia de sucesiones que tienen elementos en los conjuntos anidados. En entradas futuras veremos que los espacios compactos son cerrados. ¿Cómo justificarías las proposiciones vistas en esta entrada a partir de los resultados presentados en la métrica de Hausdorff?

Más adelante…

Veremos los conceptos de conjunto denso y conjunto nunca denso. Descubriremos un resultado que ha sido muy importante en el estudio de los espacios métricos completos: El teorema de Baire.

Tarea moral

  1. Sea $\mathbb{Q}$ el subespacio de $\mathbb{R}$ con la métrica usual. Demuestra que la intersección de los intervalos $[\sqrt{2}-\frac{1}{n},\sqrt{2}+\frac{1}{n}], \, n \in \mathbb{N}$ es vacía.
  2. Demuestra que si $x$ está en la intersección de bolas encajadas $\underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n)$ entonces es único.
  3. Demuestra que la sucesión de centros $(x_{N_n})_{n \in \mathbb{N}}$ de la proposición converge en $x$.
  4. Sea $A \subset X.$ Demuestra que $diam(A)=diam(\overline{A}).$
  5. Da un ejemplo de un espacio métrico completo y de una sucesión de bolas cerradas en este espacio, encajadas unas en otras que tenga intersección vacía.

Enlaces

Espacios métricos completos

Por Lizbeth Fernández Villegas

Deja un comentario

Introducción

En la entrada anterior vimos que no es suficiente que una sucesión sea de Cauchy para asegurar que sea convergente. Hay espacios donde sí lo es y serán llamados «completos». Contar con este recurso nos permite solo tener que justificar que una sucesión satisface la condición de Cauchy cuando esto resulte ser más sencillo que demostrar su convergencia en un punto. Comencemos con la definición:

Definición espacio métrico completo y espacio de Banach: Sea $(X,d)$ un espacio métrico. Decimos que $X$ es un espacio métrico completo si toda sucesión de Cauchy $(x_n)_{n \in \mathbb{N}}$ es convergente en $X$.
A un espacio normado que es completo con la métrica inducida por su norma le llamaremos espacio de Banach.

Ejemplos:

  1. El espacio métrico euclideano $\mathbb{R}^n$ es completo. La demostración la vimos en la sección anterior. (Sucesiones de Cauchy).
  2. Sea $X$ un conjunto no vacío con la métrica discreta. Entonces $X$ es completo. La demostración se propondrá como ejercicio.
  3. $\mathbb{R}^n$ con la métrica $d_\infty(x,y)=máx \{ |x_1-y_1|,…,|x_n-y_n| \}$ donde $x=(x_1,…,x_n)$ y $y=(y_1,…,y_n)$ es completo.

Demostración:
Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $\mathbb{R}^n$. En la sección anterior vimos que $(x_n)$ converge en la métrica euclidiana $d_2$. Sea $x$ el punto de convergencia. En la entrada Más conceptos de continuidad vimos que $d_\infty$ y $d_2$ son métricas equivalentes, entonces para todo $\varepsilon >0$ existe $N \in \mathbb{N}$ y $c>0$ tales que para todo $n \geq N$:
$d_\infty(x_n,x)\leq c\,d_{2}(x_n,x) \leq c \frac{\varepsilon}{c}=\varepsilon$
Por lo tanto $x_n \to x$ en $(\mathbb{R}^n, d_\infty),$ lo cual demuestra que es un espacio métrico completo.

En general, la completitud no es una propiedad invariante bajo homeomorfismos. Esto es, un espacio completo puede ser homeomorfo a otro que no lo sea.

Ejemplo: El espacio euclidiano $\mathbb{R}$ es homeomorfo al subespacio $(-1,1).$

En efecto:

$$ \phi: (-1,1) \longrightarrow \mathbb R, \qquad \phi(x) = \frac{x}{1-x^2} $$

Es un homeomorfismo entre ambos espacios. No obstante la sucesión $(1- \frac{1}{n})_{n \in \mathbb{N}} \,$ tiene sus elementos en $(-1,1)$ y es de Cauchy pero no converge en el subespacio. Por lo tanto $(-1,1)$ no es completo pese a que $\mathbb{R}$ sí lo es.

$(-1,1)$ es homeomorfo a $\mathbb{R}$

Por otro lado, la completitud sí se conserva bajo equivalencias. (Concepto visto en Más conceptos de continuidad):

Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $\phi: X \to Y$ una equivalencia entre ellos. Entonces $X$ es completo si y solo si $Y$ lo es.

Demostración:
Supongamos que $X$ es completo. Buscamos demostrar que $Y$ también lo es. Sea $(y_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $Y$. Como $\phi$ es equivalencia entonces $\phi^{-1}$ es lipschitz continua. Considera la sucesión $\phi^{-1}(y_n)_{n \in \mathbb{N}}$ en $X$. Dadas las hipótesis, para toda $\varepsilon >0$ existe $N \in \mathbb{N}$ y $c>0$ tales que si $n,m \geq N$ entonces:
$d_X(\phi^{-1}(y_n),\phi^{-1}(y_m))\leq c\, d_Y(y_n,y_m) \leq c \, \frac{\varepsilon}{c} = \varepsilon$ lo cual prueba que la sucesión $\phi^{-1}(y_n)_{n \in \mathbb{N}}$ es de Cauchy en $X$, espacio que es completo, en consecuencia $\phi^{-1}(y_n) \to x$ en $X$ para algún $x \in X.$

Finalizamos aplicando $\phi$ a la última sucesión. En la entrada de Funciones continuas en espacios métricos vimos que podemos concluir que $\phi(\phi^{-1}(y_n)) \to \phi(x)$ en $Y$. Por lo tanto $(y_n)$ es una sucesión convergente lo cual demuestra que $Y$ es un espacio métrico completo.
El regreso es análogo y se propondrá como ejercicio al final de esta sección.

Proposición: Todo espacio normado de dimensión finita es de Banach.

Demostración:
Sea $V$ un espacio con norma asociada $\norm{\cdot}_V$ con dimensión finita $n$. En la entrada anterior probamos que el espacio euclideano $\mathbb{R}^n$ es de Banach. En la entrada Más conceptos de continuidad probamos que la norma $\norm{\cdot}_2$ es equivalente a $\norm{\cdot}_1$. De acuerdo a la proposición anterior, bastará con encontrar una equivalencia entre $(\mathbb{R}^n,\norm{\cdot}_1)$ y $(V, \norm{\cdot}_V)$.
Sea $\{e_1,…,e_n\}$ la base canónica de $\mathbb{R}^n,$ $\{v_1,…,v_n\},$ una base ordenada de $V$ y $\mathcal{L}: \mathbb{R}^n \to V$ tal que para cada $i=1,…,n, \, \mathcal{L}(e_i)=v_i.$ Es sencillo demostrar que $\mathcal{L}$ es una transformación lineal y que es también una función biyectiva. Esta afirmación se propondrá como ejercicio.
Sean $a,b \in \mathbb{R}^n$ tales que $a=\sum_{i=1}^{n}a_i e_i$ y $b=\sum_{i=1}^{n}b_i e_i$ con $a_i,b_i \in \mathbb{R}, 1\leq i\leq n.$ Sea $c=\underset{1 \leq i \leq n}{máx} \, \{ \norm{v_i}_V\},$ entonces:

\begin{align*}
\norm{\mathcal{L}(\sum_{i=1}^{n}a_i e_i) -\mathcal{L}(\sum_{i=1}^{n}b_i e_i)}_V&=\norm{\sum_{i=1}^{n}a_i \mathcal{L}(e_i)-\sum_{i=1}^{n}b_i \mathcal{L}(e_i)}_V\\
&=\norm{\sum_{i=1}^{n}a_i v_i-\sum_{i=1}^{n}b_i v_i}_V\\
&=\norm{\sum_{i=1}^{n}(a_i-b_i) v_i}_V \\
&\leq \sum_{i=1}^{n}|a_i-b_i| \norm{v_i}_V \\
&\leq \underset{1 \leq i \leq n}{máx} \, \{ \norm{v_i}_V\}\sum_{i=1}^{n}|a_i-b_i|\\
&=c \sum_{i=1}^{n}|a_i-b_i| \\
&=c \norm{a-b}_1
\end{align*}

Entonces $\mathcal{L}$ es una función Lipschitz continua. La prueba de que la inversa es Lipschitz continua se deja como ejercicio. Esto demostraría que $V$ también es un espacio de Banach.

La completitud no siempre se hereda a los subespacios de un espacio métrico completo. La siguiente proposición nos muestra las condiciones requeridas para que esto ocurra:

Proposición: Sea $(X,d)$ un espacio métrico completo y $A \subset X.$ Entonces el subespacio $(A,d)$ es completo si solo si $A$ es cerrado en $X.$

Demostración:

Supón que $(A,d)$ es completo. Buscamos demostrar que $\overline{A} \subset A.$ Sea $x \in \overline{A}.$ En la entrada de Convergencia concluimos que existe una sucesión $(x_n)_{n \in \mathbb{N}}$ de términos en $A$ tal que $x_n \to x.$ Como converge, se concluye que es de Cauchy. Como todos los términos están en $A$, que es completo, se concluye que es convergente en $A.$ Como el límite es único, concluimos que el punto de convergencia $x \in A.$ Por lo tanto $\overline{A} \subset A,$ probando así que $A$ es cerrado.

Ahora partamos de suponer que $A \subset X$ es cerrado. Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $A.$ Como $X$ es completo, se sigue que $x_n \to x$ en $X$ para algún $x \in X.$ Por el mismo resultado de la entrada de Convergencia concluimos que $x \in A.$ por lo tanto $x_n \to x$ en $A$ lo cual demuestra que $A$ es completo.

Ya que sabemos que un espacio normado de dimensión finita es de Banach, es natural preguntarse qué ocurre con los de dimensión infinita. Como ejemplo tenemos al espacio de los polinomios $\mathcal{P}[0,1].$ Visto como subespacio del espacio de funciones continuas $C^0[0,1]$ es de dimensión infinita pero no es cerrado. La proposición anterior nos permite concluir que $\mathcal{P}[0,1]$ no es completo. La demostración del ejemplo se puede consultar en las notas de Luis O. Manuel. El documento se encuentra en este link.

Más adelante…

Buscaremos aplicar estos resultados en conjuntos anidados, unos dentro de otros. Partir de una sucesión de Cauchy nos permitirá asegurar la existencia de un punto de convergencia, cuando estemos en un espacio completo. Conoceremos condiciones en las que dicho punto existe y pertenece a la intersección de los conjuntos anidados.

Tarea moral

  1. Demuestra que si $X$ es un conjunto no vacío con la métrica discreta entonces $X$ es completo.
  2. Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $\phi: X \to Y$ una equivalencia entre ellos. Prueba que si $Y$ es completo entonces $X$ lo es.
  3. Sea $V$ un espacio con norma asociada $\norm{\cdot}_V$ con dimensión finita $n$ y $\{v_1,…,v_n\},$ una base ordenada de $V.$ Sea $\{e_1,…,e_n\}$ la base canónica de $\mathbb{R}^n,$ y $\mathcal{L}: \mathbb{R}^n \to V$ tal que para cada $i=1,…,n, \, \mathcal{L}(e_i)=v_i.$ Demuestra que $\mathcal{L}$ es una transformación lineal y que es también una función biyectiva.
  4. Prueba que la función inversa de la función del ejercicio anterior es Lipschitz continua.
  5. Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión creciente y acotada en $\mathbb{R}.$ Concluye que $(x_n)$ es convergente en $\mathbb{R}$ demostrando que es de Cauchy.

Enlaces