(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción.

En este capítulo veremos las leyes de De Morgan, que nos hablan de cómo es el complemento de una unión o de una intersección de conjuntos. Para ello usaremos los resultados adquiridos en notas anteriores, observando que cuando un elemento del conjunto universo no es parte de un conjunto, es por que no cumple con la propiedad que caracteriza sus elementos, y por tanto cumple la negación de esa propiedad.

Una vez que tengamos las leyes de De Morgan en nuestro repertorio de proposiciones adquiridas, junto con algunas propiedades de la diferencia de conjuntos, definiremos la diferencia simétrica y usaremos los resultados previos para obtener algunas de sus propiedades.

Teorema. Leyes de De Morgan.

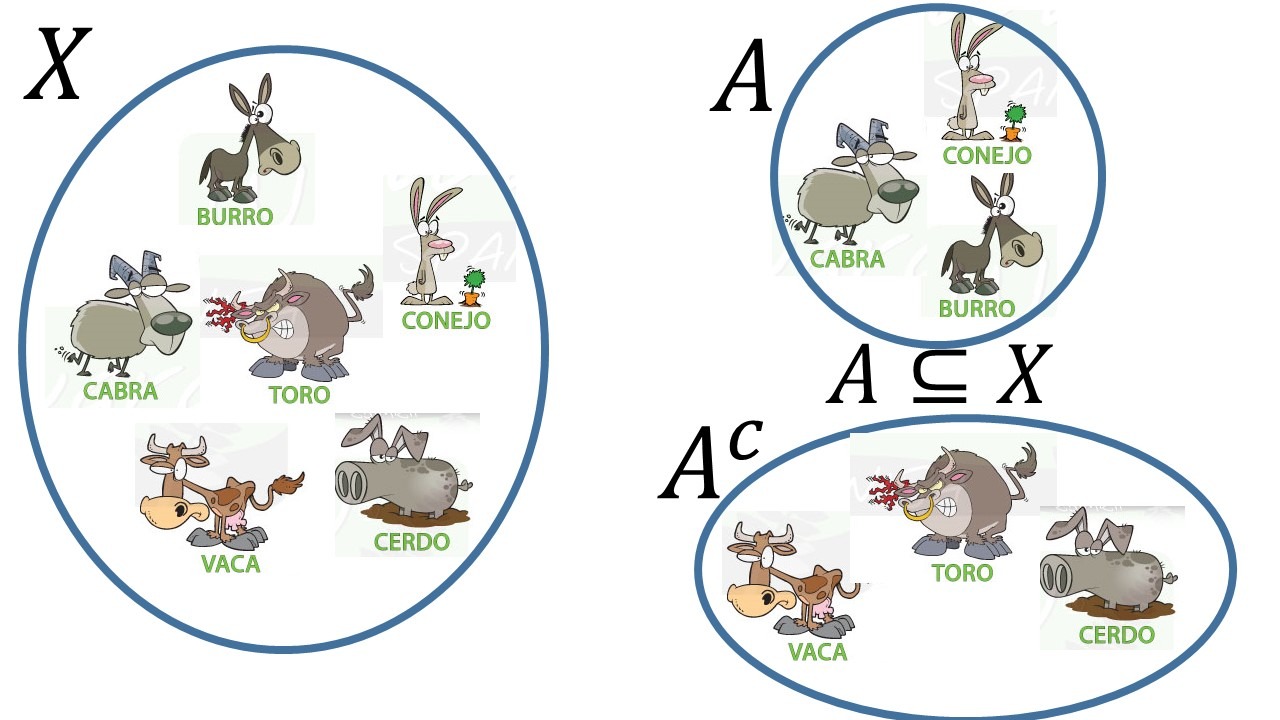
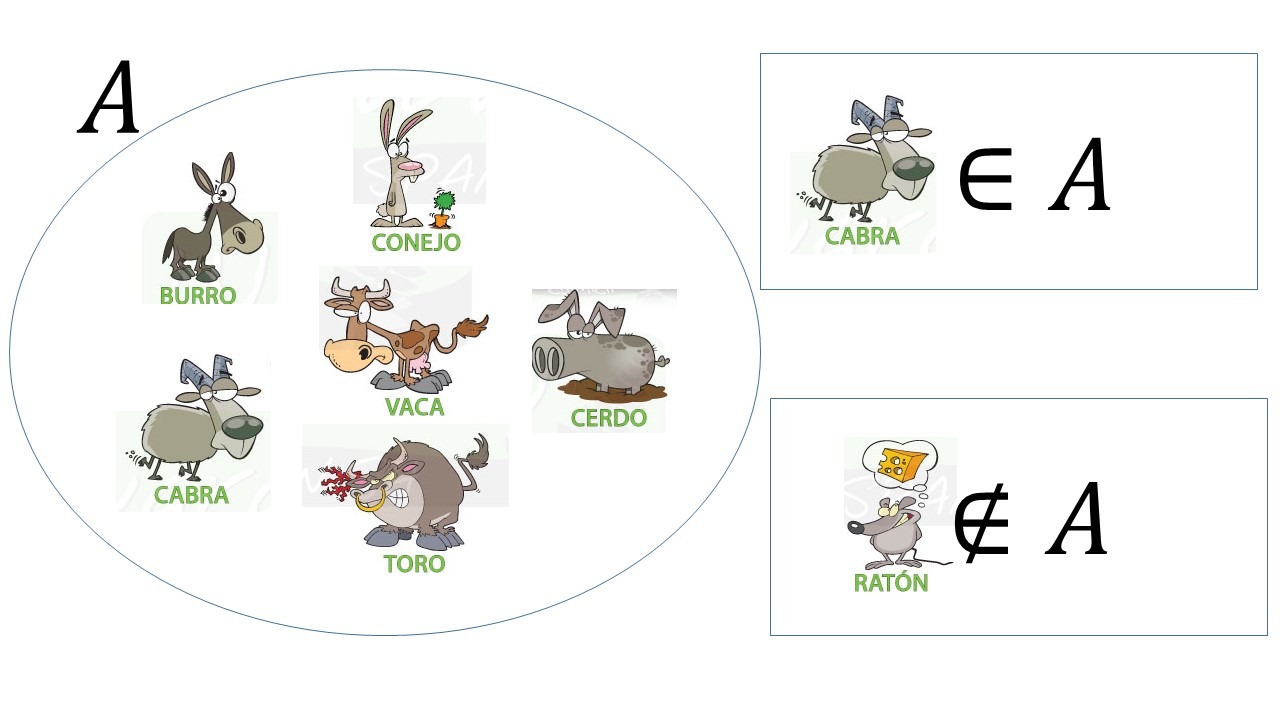
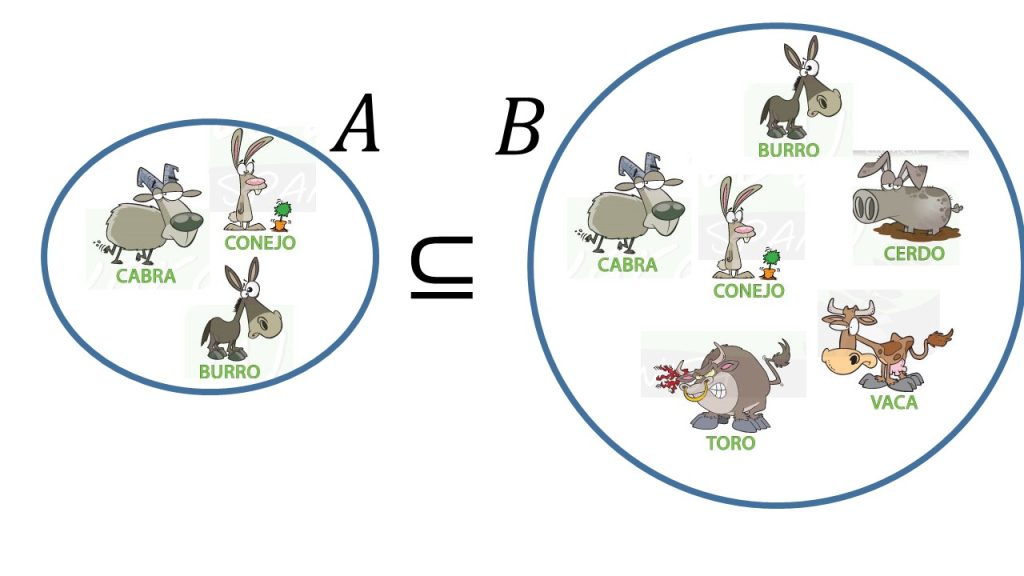
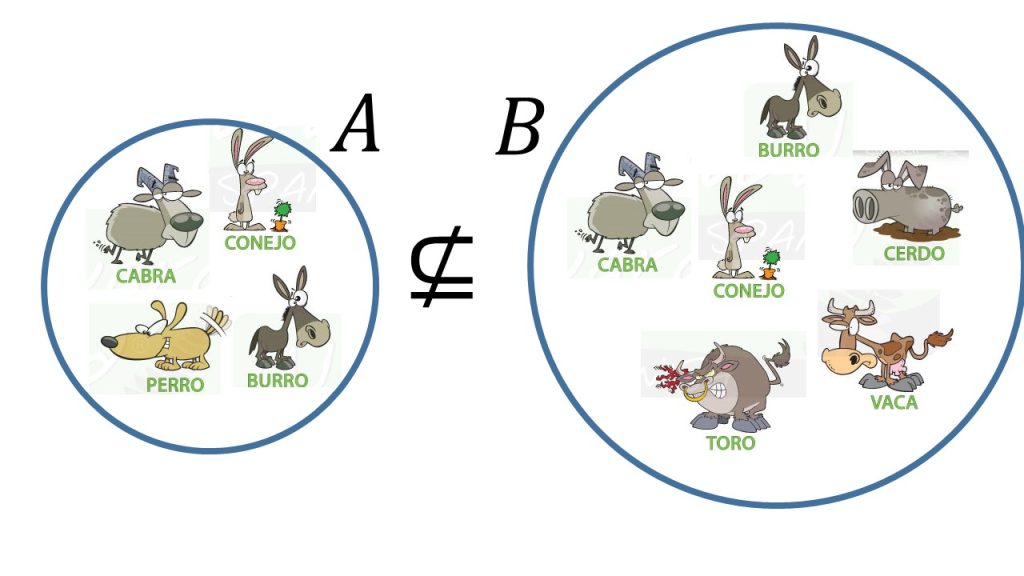
Sea $X$ el conjunto universo, $A$ y $B$ subconjuntos de $X$.

1. $(A\cup B)^c=A^c\cap B^c$
2. $(A\cap B)^c=A^c\cup B^c$

Demostración

Demostración de la propiedad 1.

Por demostrar que $(A\cup B)^c=A^c\cap B^c$.

Esta prueba la haremos por doble contención, la cadena de implicaciones de ida y regreso nos dará la prueba por doble contención.

Prueba condensada.	Explicación de las implicaciones de ida que probarán la primera contención $(A\cup B)^c\subseteq A^c\cap B^c$	Explicación de las implicaciones de regreso que probarán la segunda contención $(A\cup B)^c\supseteq A^c\cap B^c$
$z\in (A\cup B)^c$	Empezamos la prueba tomándonos un elemento en el conjunto $(A\cup B)^c$ , con la intención de mostrar que también está en $A^c\cap B^c$	Por definición de complemento.
$\Longleftrightarrow$ $z\notin A\cup B$	Esto es por la definición de complemento.	Los elementos que no están ni en $A$ ni en $B$ son precisamente los que no están en la unión.
$\Longleftrightarrow$ $z\notin A$ y $z\notin B$ $\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $	Si $z$ no está en la unión, no cumple con la propiedad que caracteriza a los elementos de la unión, es decir $z$ no cumple que $z\in A$ o $z\in B$, por lo que $z$ no puede estar ni en $A$ ni en $B$, es decir $z\notin A$ y $z\notin B$. Nota cómo la negación de la disyunción es la conjunción.	Por definición de complemento.
$\Longleftrightarrow$ $z\in A^c$ y $z\in B^c$	Si $z$ no está en $A$, está en su complemento, y lo mismo pasa con $B$.	Por definición de intersección.
$\Longleftrightarrow$ $z\in A^c\cap B^c$	Por definición de intersección.	Empezamos la prueba tomándonos un elemento en el conjunto $A^c\cap B^c$, con la intención de mostrar que también está en $(A\cup B)^c$.

Las explicaciones de la prueba en la tabla se leen de arriba a abajo para la primera contención y de abajo a arriba en el caso de la segunda contención, para saber cómo cambiamos de paso, o empezamos la prueba, atendemos a la explicación, cada columna nos da una contención, la primera nos muestra que $(A\cup B)^c\subseteq A^c\cap B^c$, y la segunda nos muestra que $A^c\cap B^c\subseteq (A\cup B)^c$, lo que nos garantiza según el axioma de extensionalidad lo que queríamos probar: $(A\cup B)^c=A^c\cap B^c$. De esta manera, al hacer la equivalencia en cada paso no es necesario escribir por separado la prueba de cada contención. Sin embargo, debes tener cuidado porque no siempre es posible realizar este proceso y hay igualdades de conjuntos en las que sí es necesario desarrollar por separado cada contención.

En muchas ocasiones y sobre todo cuando se adquiere más habilidad haciendo demostraciones se puede dar la demostración condensada sin escribir todas las explicaciones de las equivalencias:

$z\in (A\cup B)^c \Longleftrightarrow z\notin A\cup B \Longleftrightarrow z\notin A\,\, y \,\,z\notin B \Longleftrightarrow z\in A^c\,\, y \,\, z\in B^c \Longleftrightarrow z\in A^c\cap B^c$

$\square$

Demostración de la propiedad 2.

Por demostrar que $(A\cap B)^c=A^c\cup B^c$

Prueba condensada.	Explicación de las implicaciones de ida que probarán la primera contención $(A\cap B)^c\subseteq A^c\cup B^c$	Explicación de las implicaciones de regreso que probarán la segunda contención $(A\cap B)^c\supseteq A^c\cup B^c$
$z\in (A\cap B)^c$	Empezamos la prueba tomándonos un elemento en el conjunto $(A\cap B)^c$, con la intención de mostrar que también está en $A^c\cup B^c.$	Por definición de complemento.
$\Longleftrightarrow$ $z\notin A\cap B$	Por definición de complemento.	Si el elemento cumple con no estar en $A$ o en $B$ entonces no está en la intersección.
$\Longleftrightarrow$ $z\notin A$ o $z\notin B$ $\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $	Si $z$ no está en la intersección, no cumple con la propiedad que cumplen los elementos de la intersección, es decir $z$ no cumple que $z\in A$ y $z\in B$, por lo que debe fallar al menos una de ambas condiciones, es decir $z\notin A$ o $z\notin B$. Nota cómo la negación de la conjunción $y$ es la disyunción $o$.	Por definición de complemento.
$\Longleftrightarrow$ $z\in A^c$ o $z\in B^c$	Si no está en $A$, está en su complemento, y lo mismo pasa con $B$.	Por definición de unión.
$\Longleftrightarrow$ $z\in A^c\cup B^c$	Por definición de unión.	Empezamos la prueba tomándonos un elemento en el conjunto $A^c\cup B^c$, con la intención de mostrar que también está en $(A\cap B)^c$

Igual que en la primera demostración las dos contenciones nos dan la igualdad y así:

$(A\cap B)^c=A^c\cup B^c$, que es lo queríamos demostrar.

$\square$

Hay que estar atentos pues usaremos el resultado anterior para probar algunas propiedades de una operación destacable, la diferencia simétrica, pero antes de llegar a ello, definamos una operación más.

Definición

Sea $X$ el conjunto universo, $A$,$B$, subconjuntos de $X$.

La diferencia de $A$ con $B$ es el conjunto de los elementos que están en $A$, pero no están en $B$.

$A \setminus B = \set{x\in A\mid x\notin B}$

Proposición

Sea $X$ el conjunto universo, $A$,$B$, subconjuntos de $X$.

1. $A\setminus B=A\cap B^c$
2. $A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$
3. $A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$

Demostración

Demostración de 1

Tenemos que:

$z\in A\setminus B = \set{x\in A\mid x\notin B}$ $\Longleftrightarrow$ $z\in A$ y $z\notin B$ $\Longleftrightarrow$ $z\in A$ y $z\in B^c$ $\Longleftrightarrow$ $z\in A\cap B^c$.

Nota que ésta es una prueba por doble contención, la cadena de si y sólo si ($\Longleftrightarrow$) nos da las dos contenciones.

$\square$

Demostración de 2

De nuevo recurriremos a una tabla para ir mostrando los pasos, esta vez entre igualdades.

Prueba condensada	Explicación
$A\setminus (B\cap C)=$	Empezamos considerando este conjunto.
$A\cap (B\cap C)^c=$	Por lo mostrado en la proposición anterior $A\setminus B=A\cap B^c$.
$A\cap (B^c\cup C^c)=$	Observa que en este paso nos valimos de las leyes de De Morgan y utilizamos que $(B\cap C)^c= B^c\cup C^c $.
$(A\cap B^c)\cup (A\cap C^c)=$	Esta igualdad es por la propiedad distributiva de la intersección.
$(A\setminus B)\cup (A\setminus C)$	Por lo mostrado en la proposición anterior $A\setminus B=A\cap B^c$ y $A\setminus C=A\cap C^c$.

Por lo tanto $A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$.

$\square$

Demostración de 3

Prueba condensada	Explicación
$A\setminus (B\cup C)=$	Empezamos considerando este conjunto.
$A\cap (B\cup C)^c=$	Por lo mostrado en la propiedad 1 $A\setminus B=A\cap B^c$.
$A\cap (B^c\cap C^c)=$	Observa que en este paso nos valimos de las leyes de De Morgan y utilizamos que $(B\cup C)^c= B^c\cap C^c $.
$A\cap A\cap B^c \cap C^c=$	Como $ A\cap A=A$, simplente reescribimos a $A$ de esta forma.
$(A\cap B^c)\cap (A \cap C^c)=$	Por las propiedades de asociatividad y conmutatividad de la intersección.
$(A\setminus B)\cap (A\setminus C)$	Por lo mostrado en la propiedad 1 $A\setminus B=A\cap B^c$.

Por lo tanto $A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$.

$\square$

Con estas herramientas estamos listos para dar la definición de diferencia simétrica.

Definición

Sea $X$ el conjunto universo, $A$, $B$, subconjuntos de $X$, la diferencia simétrica de $A$ con $B$ es la diferencia de la unión de los dos conjuntos con su intersección:

$A\vartriangle B=(A\cup B)\setminus (A\cap B).$

Proposición

Sea $X$ el conjunto universo, $A$,$B$, subconjuntos de $X$.

1. $A\vartriangle B=B\vartriangle A$
2. $A\vartriangle B=(A\setminus B)\cup (B\setminus A)$

Demostración de 1

$A\vartriangle B= (A\cup B)\setminus (A\cap B) = (B\cup A)\setminus (B\cap A) =B\vartriangle A$, nota que en la prueba se está usando la conmutatividad de la unión y de la intersección.

$\square$

Demostración de 2

Prueba condensada	Explicación
$A\vartriangle B=$	Empezamos con este conjunto.
$(A\cup B)\setminus (A\cap B)=$	Por definición de diferencia simétrica.
$(A\cup B)\cap (A\cap B)^c=$	Por lo mostrado en la propiedad 1 $A\setminus B=A\cap B^c$.
$(A\cup B)\cap (A^c\cup B^c)=$	Por las leyes de De Morgan.
$[(A\cup B)\cap A^c]\cup [(A\cup B) \cap B^c]=$	Por la propiedad distributiva de la intersección sobre la unión.
$[(A\cap A^c)\cup (B\cap A^c)]\cup [(A\cap B^c)\cup (B\cap B^c)]=$	Por la propiedad distributiva de la intersección sobre la unión.
$[\emptyset\cup (B\cap A^c)]\cup [(A\cap B^c)\cup \emptyset ]=$	La intersección de un conjunto con su complemento es el vacío.
$(B\cap A^c)\cup (A\cap B^c)=$	El vacío unión cualquier conjunto nos deja el mismo conjunto.
$(B\setminus A)\cup (A\setminus B)$	Por lo mostrado en la proposición anterior $A\setminus B=A\cap B^c$.

Esto muestra que $A\vartriangle B=(A\setminus B)\cup (B\setminus A)$.

$\square$

Tarea Moral

En los siguientes incisos el conjunto universo es $X$, $A\subseteq X$, $B\subseteq X$.

i) Encuentra: $A^c$, $B^c$, $A^c\cup B^c$, $A^c\cap B^c$, $(A\cup B)^c$, $(A\cap B)^c$.

1. $X=\mathbb{N}$
   $A=\set{x\in \mathbb{N}\mid x\,\,es\,\,un\,\,primo}$
   $B=\set{x\in \mathbb{N}\mid x\,\,es\,\,un\,\,impar}$
2. $X=\mathbb{Z}$
   $A=\set{x\in \mathbb{Z}\mid x=4k+1,para\,\,alguna\,\,k\in \mathbb{Z}}$
   $B=\set{x\in \mathbb{N}\mid x\,\,es\,\,negativo}$
3. $X=\mathbb{N}$
   $A=\set{x\in \mathbb{N}\mid x\,\,es\,\,un\,\,irracional}$
   $B=\set{x\in \mathbb{N}\mid x>3}$
4. $X=\mathbb{N}$
   $A=\set{x\in \mathbb{N}\mid x\leq 5 }$
   $B=\set{x\in \mathbb{N}\mid 1\leq x<11}$

ii) Sean $A$ y $B$ conjuntos, demuestra las siguientes igualdades entre conjuntos.

• $A\cup (B\setminus A)=A\cup B$
• $A\cap (B\setminus A)=\emptyset$
• $(B\setminus A)\cup (A\cap B)=B$
• $(B\setminus A)\cap (A\cap B)=\emptyset$

iii) Prueba que $A\vartriangle B\subseteq (A\vartriangle C)\cup (C\vartriangle B)$. Encuentra un ejemplo donde la contención sea propia y otro donde se dé la igualdad.

Más adelante

En la siguiente nota definiremos una manera de crear un nuevo subconjunto, estableceremos como un axioma que el conjunto de los subconjuntos de un conjunto dado $A$ también es un subconjunto y lo llamaremos el conjunto potencia. Iremos encaminando nuestros esfuerzos a definir una de las mas útiles maneras de estudiar los distintos conjuntos, el concepto de función, pero para ello hablaremos de algo más primitivo, las relaciones entre conjuntos, que caracterizaremos y para las cuales deduciremos propiedades.

Entradas Relacionadas

Página principal del curso.

Nota Anterior del curso. Nota 4. Unión e intersección de conjuntos.

Nota siguiente del curso. Nota 6. Conjunto potencia y el producto cartesiano.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Dado un conjunto podemos considerar colecciones formadas por algunos de sus elementos. Estudiaremos estas colecciones que como veremos son también conjuntos y por ende objetos de estudio de la teoría de conjuntos. En esta nota estudiaremos el concepto de subconjunto y a partir de ello estableceremos cuándo dos conjuntos se considerarán iguales. Se desarrollarán pruebas matemáticas intentando explicar a detalle cómo se realizan. Es conveniente que prestes mucha atención a estas demostraciones ya que a lo largo de tus estudios requerirás realizar y entender muchas pruebas y éstas son una parte esencial en las matemáticas.

Definición.

Dados $A$,$B$ conjuntos, decimos que $A$ es un subconjunto de $B$ si todo elemento de $A$ es un elemento de $B$, es decir si para toda $z$, $z\in A$ implica que $z\in B$.

En este caso decimos que $A$ está contenido en $B$ o que $B$ contiene al conjunto $A$.

Nota que $A$ no está contenido en $B$, si existe al menos un $z$, tal que $z\in A$, pero $z\notin B$.

Notación:

Se escribe: $A\subseteq B$ si $A$ está contenido en $B$.

Se escribe: $A\nsubseteq B$ si $A$ no está contenido en $B$.

Si $A$ está contenido en $B$, pero $B$ no está contenido en $A$, decimos que la contención es propia o que $A$ es un subconjunto propio de $B$ y se denota por $A\subsetneq B$ (en este caso si $z\in A$, entonces $z\in B$, pero existe al menos un $z\in B$ tal que $z\notin A$).

Como se mencionó en la nota previa, los números naturales serán conjuntos y resultarán ser distintos como conjuntos cuando sean distintos como números, ver la sección 5.1, página 207, del libro de Avella y Campero que se menciona en la bibliografía de este curso. Para el siguiente ejemplo consideraremos, como usualmente lo hacemos, que los números $1,2,3$ y $4$ son distintos entre sí.

Ejemplo 1

$\set{1,2,3}\subseteq \set{1,2,3}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3}$.

$\set{1,2,3}\subseteq \set{1,2,3,4}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3,4}$.

$\set{1,2,3, 4}\nsubseteq \set{1,2,3}$ ya que $4\in \set{1,2,3, 4}$ pero $4\notin \set{1,2,3}$ pues $4$ es distinto de $1,2$ y $3$.

$\set{1,2,3}\subsetneq \set{1,2,3,4}$ ya que $\set{1,2,3}\subseteq \set{1,2,3,4}$ pero $\set{1,2,3, 4}\nsubseteq \set{1,2,3}$.

Así, es correcto decir que $\set{1,2,3}$ es un subconjunto de $\set{1,2,3,4}$, pero también que $\set{1,2,3}$ es un subconjunto propio de $\set{1,2,3,4}$, simplemente en el segundo enunciado estamos siendo un poco más precisos.

Proposición

Sean $A$, $B$, $C$ conjuntos.

1. $A\subseteq A$, es decir, cada conjunto se contiene a sí mismo.
2. Si $A\subseteq B$ y $B\subseteq C$, se tiene que $A\subseteq C$. Este hecho se conoce como la propiedad transitiva de la contención de conjuntos.
3. $\emptyset\subseteq A$, es decir, el conjunto vacío es subconjunto de cualquier conjunto.
   

Fíjate muy bien cómo se hace una prueba. Vamos a partir de una afirmación que consideraremos válida, a la que llamaremos hipótesis, y probaremos su consecuencia mediante razonamientos lógicos usando las definiciones o resultados previos.

Demostración de 1
En este primer caso:
La hipótesis es que $A$ es un conjunto cualquiera.
la consecuencia o lo que queremos demostrar es que $A\subseteq A$.
Demostración:
Como queremos probar que un conjunto es subconjunto de otro, entonces tenemos que verificar que la definición de subconjunto se satisface, recuerda que

$A\subseteq B$ si y sólo si para toda $z$, $z\in A$ implica que $z\in B$,

pero en nuestro caso $B=A$. Así, sea $z\in A$, entonces tenemos que $z\in A$. Por lo tanto tenemos que $A\subseteq A$.

$\square$

Demostración de 2

La hipótesis ahora es que $A,B$ y $C$ son conjuntos, con $A\subseteq B$ y $B\subseteq C$
y lo que se tiene que demostrar es que $A\subseteq C$
Demostración:
Dado que queremos probar que $A\subseteq C$, debemos ver que cualquier elemento en $A$ es también un elemento de $C$. Así, consideremos $z\in A$ y verifiquemos que $z\in C$. Como $A\subseteq B$ y $z\in A$, entonces por la definición de subconjunto $z\in B$, y como $B\subseteq C$, nuevamente por la definición de subconjunto $z\in C$. Con ello hemos verificado que para toda $z$, $z\in A$ implica $z\in C$ lo cual es la definición de que $A\subseteq C$, que es exactamente lo que queríamos demostrar.

$\square$

Demostración de 3

De nuevo la hipótesis es que $A$ es un conjunto cualquiera.
lo que queremos demostrar es que el conjunto vacío es un subconjunto de $A$, i.e. $\emptyset\subseteq A$.
Demostración:
Esta prueba la haremos por un método llamado contradicción, el cual consiste en negar la conclusión a la que queremos llegar, manteniendo las mismas hipótesis, y llegar a una contradicción de los teoremas o axiomas de la teoría que se está construyendo.
Primero neguemos la conclusión:

Existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$.

Después se procede a encontrar la contradicción:

Si esto sucediera, es decir si $\emptyset\nsubseteq A$, entonces existiría al menos un elemento en el conjunto $\emptyset$, que no sería elemento del conjunto $A$, pero eso es dar por hecho que el conjunto $\emptyset$ tiene elementos lo cual está en contradicción con el axioma de conjunto vacío visto en la nota anterior.

La contradicción viene de suponer que existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$, por lo tanto no puede existir dicho subconjunto probando así que $\emptyset\subseteq A$ para todo conjunto $A$.

$\square$

Ahora procederemos a dar dos axiomas más, el primero establece cuándo dos conjuntos serán considerados iguales.

Axioma de extensionalidad

Dos conjuntos son iguales cuando tienen exactamente los mismos elementos. Es decir, si $A$ y $B$ son conjuntos:

• $A=B$ significa que $A\subseteq B$ y $B\subseteq A$.
• $A\neq B$ significa que $A\nsubseteq B$ o $B\nsubseteq A$.

Ejemplos

2. Veamos que $\emptyset\neq \{\emptyset\}$.

Notemos que $\emptyset\subseteq \{\emptyset\}$ (ya que por la proposición anterior $\emptyset\subseteq A$ para todo conjunto $A$). Por otro lado recordemos que el conjunto vacío no tiene elementos, así que $A\notin \emptyset$ para todo conjunto $A$, en particular $\emptyset\notin \emptyset$. Tenemos entonces que $\{\emptyset\}\nsubseteq \emptyset$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, no es un elemento del conjunto $\emptyset$.

Así, $\emptyset\subseteq \{\emptyset\}$ pero $\{\emptyset\}\nsubseteq \emptyset$, por lo tanto $\emptyset\neq \{\emptyset\}$. (Intuitivamente podemos imaginar a los conjuntos como cajas y de esa forma $\emptyset$ sería una caja vacía, mientras que $ \{\emptyset\}$ sería una caja que tiene dentro una caja vacía, por lo que tiene sentido considerarlos distintos, ya que la primera caja no tiene nada, mientras que la segunda sí, tiene dentro una caja vacía).

3. Veamos que que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

$\{\emptyset\}\nsubseteq\{\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, el conjunto $\emptyset$, no es un elemento de $\{\{\emptyset\}\}$, pues el único elemento de $\{\{\emptyset\}\}$ es $\{\emptyset\}$ y como se vio en el ejemplo previo $\emptyset\neq \{\emptyset\}$.

Así, podemos concluir que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

4. Consideremos el conjunto $C$ cuyos elementos son el conjunto vacío, $\emptyset$ y el unitario del vacío, $\{\emptyset\}$, es decir $C=\{\emptyset,\{\emptyset\}\}$. Observamos que:

$\emptyset\in \{\emptyset,\{\emptyset\}\}$ y $\{\emptyset\}\in \{\emptyset,\{\emptyset\}\}$ ya que por construcción $\emptyset$ y $\{\emptyset\}$ son los elementos de $C$.

$\emptyset\subseteq \{\emptyset,\{\emptyset\}\}$ ya que por la proposición previa $\emptyset\subseteq A$ para todo conjunto $A$, en particular $\emptyset\subseteq C$.

$\{\emptyset\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

$\{\emptyset,\{\emptyset\}\}\nsubseteq \{\emptyset\}$ ya que existe un elemento en $\{\emptyset,\{\emptyset\}\}$, el elemento $\{\emptyset\}$, que no es un elemento de $\{\emptyset\}$ (ya que el único elemento en $\{\emptyset\}$ es $\emptyset$ y por el ejemplo anterior $\{\emptyset\}\neq \emptyset$).

$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

Notemos que $\{\{\emptyset\}\}\neq\emptyset$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, no es un elemento de $\emptyset$ pues el conjunto vacío no tiene elementos. Por otro lado sabemos por el ejemplo 3 que $\{\{\emptyset\}\}\neq\{\emptyset\}$. Así,

$\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$.

En este último ejemplo notamos que$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ pero $\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$, haciéndonos ver que las relaciones de pertenencia y de contención no son iguales por lo que debemos ser muy cuidadosos al usar una u otra.

El siguiente nos permite elegir elementos de un conjunto dado que tienen cierta característica en común para formar nuevos conjuntos.

Axioma de separación o de comprensión

Dado $A$ un conjunto y $P$ una propiedad, $\set{\,x\in A\mid\,x\,cumple\,P\,}$ es un conjunto.

Notemos que a diferencia de la colección considerada en la paradoja de Russell dada en la nota anterior, en este caso se considera, no a cualquier objeto con la propiedad $P$, sino a los objetos de algún conjunto que cumplen con la propiedad $P$, es decir partimos de un conjunto y tomamos ahí algunos de sus elementos.

Tarea Moral

1. Considera los conjuntos $B=\{x\in\mathbb{N}\,|\,x \text{ es un número primo}\}$, $C=\{x\in\mathbb{N}\,|\,x \text{ es un número primo y } x>2\}$ y $D=\{x\in\mathbb{N}\,|x\, \text{ es un número impar}\}$.

Determina si las siguientes afirmaciones son verdaderas o falsas:

$i)\,\, B \subseteq D$	$iv)\,\, C \subsetneq B$.
$i)\,\, B \subsetneq D$	$v) \,\, C \subseteq D$.
$iii)\,\, C \subseteq B$.	$vi) \,\, C \subsetneq D$.

2. Considera el conjunto $E=\{\emptyset,\{\{\emptyset\}\}\}$, determina si los siguientes objetos son elementos o subconjuntos de $E$:

$i)\,\, \emptyset\in E$.	$vii)\,\, \{\{\emptyset\}\}\subseteq E$.
$ii)\,\, \emptyset\subseteq E$.	$vii)\,\, \{\{\{\emptyset\}\}\}\in E$.
$iii)\,\, \{\emptyset\}\in E$.	$viii)\,\, \{\{\{\emptyset\}\}\}\subseteq E$.
$iv)\,\, \{\emptyset\}\subseteq E$.	$ix)\,\, \{\{\{\{\emptyset\}\}\}\}\in E$.
$v)\,\, \{\{\emptyset\}\}\in E$.	$x)\,\, \{\{\{\{\emptyset\}\}\}\}\subseteq E$.

3. Intenta hacer las pruebas de las proposiciones tú solo.

Más adelante

En la siguiente nota hablaremos del complemento de un conjunto y deduciremos propiedades básicas pero muy importantes asociadas a este concepto.

Entradas Relacionadas

Página principal del curso.

Nota anterior del curso. Nota 1 Noción de conjunto.

Nota siguiente del curso: Nota 3 El complemento de un conjunto.

Nota. Las imágenes mostradas para ilustrar los conjuntos no fueron de diseño propio, y se da las gracias a: https://www.spanish.cl/ por sus divertidos dibujos. Se deja el link de donde se obtuvieron: https://www.spanish.cl/vocabulario/animales-de-la-granja.htm.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta nota iniciaremos el estudio de los números naturales. Hasta ahora sabemos trabajar con conjuntos, podemos considerar su complemento, unirlos, intersecarlos, considerar subconjuntos de ellos, considerar particiones y relaciones de equivalencia, etc. Con estas herramientas vamos a dar una definición de los números naturales basada en el sucesor, esta definición implicará los llamados axiomas de Peano, en honor al matemático Giuseppe Peano quien en el siglo XIX, los estableció para definir los números naturales. Así nuestro primer objetivo es dar una definición conjuntista de los números naturales y ver que implica los axiomas de Peano. Puedes consultar el siguiente enlace para conocer más a profundidad la historia de cómo se formalizó la aritmética: Los axiomas de Peano.

Empecemos definiendo lo que es el sucesor de un conjunto $x.$

Definición

Sea $x$ un conjunto, el sucesor de $x$ es:

$x^+=x\cup\set{x}.$

Observa que si definimos al cero como el conjunto vacío tenemos que:

$0=\emptyset$

y entonces su sucesor $0^+$ es:

$0^+=\emptyset^+ =\emptyset\cup \set{ \emptyset}= \set{ \emptyset} =\set{ 0}$

Ese sucesor $0^+$ será por definición el $1$, entonces:

$1^+=1\cup\set{1}=\set{0}\cup \set{1}=\set{0,1}$

que es por definición el número 2, y así sucesivamente:

$2^+=2\cup \set{2}= \set{0,1}\cup \set{2}=\set{0,1,2}=3$

$3^+=3\cup \set{3}= \set{0,1,2}\cup \set{3}=\set{0,1,2,3}=4$

$\vdots$

$n^+=n\cup \set{n}= \set{0,\dotsc,n-1}\cup \set{n}=\set{0,\dotsc,n}=n+1$

Aceptaremos que esta construcción puede ser llevada a infinito, y lo postularemos como un axioma.

Axioma del infinito

Existe un conjunto que tiene al cero y al sucesor de cada uno de sus elementos.

Démosle ahora nombre a este tipo especial de conjuntos, aquellos que tienen al cero y todos sus sucesores.

Definición

Sea $A$ un conjunto. Decimos que $A$ es un conjunto de sucesores si tiene como elemento al cero y al sucesor de cada uno de sus elementos.

Observemos que el Axioma del infinito asegura la existencia de al menos un conjunto de sucesores. Tiene sentido entonces considerar la intersección de cualquier familia no vacía de conjuntos sucesores y veremos que la intersección también es un conjunto de sucesores.

Lema

Si $\mathscr F$ una colección no vacía formada por conjuntos de sucesores. Entonces $\bigcap\mathscr F$ es un conjunto de sucesores.

Demostración

Sea $\mathscr F$ una colección no vacía formada por conjuntos de sucesores. Como $\mathscr F$ es no vacía sabemos por la nota nota 14 que podemos considerar el conjunto $\bigcap \mathscr F$ que es la intersección de la colección $\mathscr F$.

Como $A$ es un conjunto de sucesores $\forall A\in \mathscr F$, entonces $0\in A\,\,\forall A\in \mathscr F$, así $0\in \bigcap \mathscr F$.

Veamos ahora que $\bigcap \mathscr F$ tiene al sucesor de cada uno de sus elementos.

Sea $x\in \bigcap \mathscr F$ entonces $x\in A$ $\forall A\in \mathscr F$. Como cada $A$ es un conjunto de sucesores, se tiene que $x^+\in A$ $\forall A\in \mathscr F$, así $x^+\in \bigcap \mathscr F$.

Concluimos finalmente que $\bigcap \mathscr F$ es un conjunto de sucesores.

$\square$

Con esta definición de conjunto de sucesores y el lema anterior vamos a definir a los números naturales siguiendo las ideas del libro de José Alfredo Amor mencionado en la bibliografía. Por el lema anterior, existe un conjunto de sucesores, por lo que la colección de todos los conjuntos de sucesores es no vacía y, de acuerdo a la definición de la nota 14, podemos considerar su intersección. Así, definiremos a los números naturales como la intersección de todos los conjuntos de sucesores.

Definición

Sea $\mathscr{F}=\{S|S\text{ es un conjunto de sucesores}\}$ la colección formada por todos los conjuntos de sucesores. Los números naturales, denotados por $\mathbb N$ son:

$\mathbb N= \mathop{\displaystyle \bigcap}\mathscr{F}$.

Observación 1

Por el lema anterior, $\mathbb N$ es un conjunto de sucesores, así $0\in \mathbb N$ y si $x\in \mathbb N$, entonces $x^+\in \mathbb N$.

Observación 2

Sea $A$ un conjunto de sucesores cualquiera, entonces si $x\in \bigcap \mathscr{F}$ tenemos que $x\in S$ para toda $S \in \mathscr F$, es decir, $x\in S$ para toda $S$ un conjunto de sucesores, por lo que en particular $x\in A$. Así,

$\mathop{\displaystyle \bigcap} \mathscr{F}\subseteq A$

Esto nos dice que $\mathbb N$ está contenido en cada conjunto de sucesores. Es decir $\mathbb N$ es el conjunto de sucesores «más pequeño» posible.

Proposición

Si $A\subseteq \mathbb N$ es tal que:

$i)$ $0\in A$

$ii)$ $\forall n$, si $n\in A$ entonces $n^+\in A$

se tiene que $\mathbb N\subseteq A$ y así $A=\mathbb N$.

Demostración

Sea $A\subseteq \mathbb N$ que cumple las condiciones $i$ y $ii$, entonces por definición $A$ es un conjunto de sucesores y de acuerdo a la observación previa sabemos que $\mathbb N$ está contenido en cada conjunto de sucesores, en particular $\mathbb N$ está contenido en $A$, es decir $ \mathbb N\subseteq A$. Así, $A\subseteq \mathbb N$ y $ \mathbb N\subseteq A$ , por lo tanto $A=\mathbb N$.

$\square$

Veremos que la definición que dimos de los números naturales anteriormente implica los axiomas de Peano. Enunciemos dichos axiomas y notemos cómo se derivan de nuestra definición.

Axiomas de Peano

1. $0\in \mathbb N$.

2. Si $n\in \mathbb N$, entonces $n^+\in \mathbb N$.

3. $\forall n\in \mathbb N$, $n^+\neq 0$.

4. $\forall n,m\in \mathbb N$ si $n^+=m^+$, entonces $n=m$.

5. Si $A\subseteq \mathbb N$ es tal que:

$i)$ $0\in A$

$ii)$ $\forall n$, si $n\in A$, entonces $n^+\in A$

se tiene que $\mathbb N\subseteq A$ y así $A=\mathbb N$.

El quinto axioma de Peano se conoce como el Principio de inducción, lo estudiaremos con detalle ya que se usa mucho para hacer pruebas referentes a afirmaciones de los números naturales.

Observa que en nuestro caso los axiomas de Peano no se usarán como axiomas, es decir no partiremos de que se cumplen pues hemos construido los números naturales a partir de conjuntos, así que se tomarán como una proposición y se demostrará que con esta construcción de los naturales se cumplen las condiciones enunciadas. Sin embargo, les llamaremos axiomas de Peano porque inicialmente se establecieron como axiomas que describían a la colección de los números naturales.

Demostración

Observa que $1$ y $2$ se cumplen ya que por la observación 1, consecuencia del lema $\mathbb N$, es un conjunto de sucesores, $5$ se cumple por la proposición antes demostrada.

Demostración de 3

Queremos demostrar que: $\forall n\in \mathbb N$, $n^+\neq 0$.

Sea $n\in \mathbb N$, por definición $n^+=n\cup\set{n}$. Como $n\in\{n\}$ tenemos que , $n\in n\cup\set{n}$. Así, $n\in n^+$ y entonces $n^+\neq \emptyset=0$.

Para probar $4$ requerimos un resultado.

Lema

Todo elemento de un número natural es también subconjunto de éste.

Demostración

Esta prueba se hará usando el quinto axioma de Peano, ya demostrado.

Sea $A=\set{n\in \mathbb N\mid si\,\,x\in n \,\, entonces \,\, x\subseteq n}\subseteq \mathbb N$. Probaremos que $A$ cumple $i$ y $ii$ del inciso 5 de la proposición anterior y concluiremos con ello que $A=\mathbb N.$

Primero vamos a probar que el $0\in A$. Como $0=\emptyset$, $0$ no tiene elementos y por vacuidad se cumple entonces que si $x\in 0$, entonces $x\subseteq 0$ (ya que no existen elementos de $0$ y por lo tanto no podríamos exhibir ninguno que no sea subconjunto de $0$). Así, $0\in A$ y se cumple $i$.

Ahora, veamos que si $n\in A$, entonces $n^+\in A$. Sea $n\in A$, observa que al estar $n$ en $A$, $n$ cumple la propiedad que caracteriza a los elementos de $A$, es decir, si $x\in n, \,\, entonces \,\, x\subseteq n$. Demostremos con ello que $n^+\in A,$ es decir que todo elemento de $n^+$ es un subconjunto de $n^+$. Consideremos $x\in n^+=n\cup \set{n}$ y verifiquemos que $x\subseteq n^+$.

Caso $1$, $x\in n$

Como $n\in A$ y $x\in n$, entonces $x\subseteq n$, además $n\subseteq n\cup \set{n}= n^+$. Así, $x\subseteq n$ y $n\subseteq n^+$, entonces $x\subseteq n^+$.

Caso $2$, $x\in \set{n}$

En este caso $x=n$ y como $x=n\subseteq n\cup \set{n}=n^+$ tenemos que $x\subseteq n^+.$

En ambos casos, suponiendo que $n\in A$, se tiene que $x\in n^+\,\, implica\,\, que \,\,x\subseteq n^+,$ probando así que $n^+$ es un elemento de $A$.

El conjunto $A$ cumple entonces las condiciones del quinto axioma de Peano (que ya hemos demostrado), y por lo tanto $A=\mathbb N$.

$\square$

Demostración de 4

Sea $n,m\in \mathbb N$ tales que $n^+=m^+$, entonces $n\cup \set{n}= m\cup \set{m}$. Así, $n\in n\cup \set{n}= m\cup \set{m}$, lo que implica que $n\in m$ o $n=m$. Por otro lado $m\in m\cup \set{m}= n\cup \set{n}$, entonces $m\in n$ o $m=n$.

Supongamos por reducción al absurdo que $n\neq m$, entonces se concluye de lo anterior que $n\in m$ y $m\in n$. Por el lema previo $n\subseteq m$ y $m\subseteq n$, así $n=m$, lo cual es una contradicción y por lo tanto $n=m$.

Hemos verificado que la construcción que dimos de los números naturales cumple los axiomas de Peano.

$\square$

Para concluir esta nota, mencionaremos las definiciones y propiedades de la suma y el producto de los números naturales que acabamos de definir. Aunque se presentan las definiciones y se enuncian las propiedades, cabe destacar que las pruebas de las mismas, realizadas por inducción, se desarrollarán en la nota 18b con el fin de estudiar primero la inducción matemática en casos menos abstractos.

Definición. Suma en $\mathbb N$

Dado $n\in \mathbb N$ definimos:

$n+0=n$

$n+m^+=(n+m)^+$ $\forall m\in \mathbb N$

Propiedades de la suma

Sean $n,m,l\in \mathbb N.$

1. $n+0=n$. Neutro aditivo.
2. $(n+m)+l=n+(m+l)$. Asociatividad.
3. Si $n+l=m+l$, entonces $n=m$. Cancelación.
4. $n+m=m+n$. Conmutatividad.
5. Si $n\neq 0$ o $m\neq 0$, entonces $n+m\neq 0$

Obsevración 3

Hay que observar que una vez se tiene definida la suma en $\mathbb N$ se puede ver que $n^+=n+1$, donde $1$ es el sucesor de $0$.

Demostración

Sea $m=0$, por definición de la suma en $\mathbb N$ se tiene que $n+0^+=(n+0)^+$. Pero $0^+=1$ y por la definición de suma se tiene que $n+0=n$, por lo que sustituyendo tenemos que $n+1=n^+$.

Definición. Producto en $\mathbb N$

Dado $n\in \mathbb N$ definimos:

$n\cdot 0=0$

$n\cdot m^+=n \cdot m+n$ $\forall m\in\mathbb N$

Propiedades del producto

Sean $n,m,l\in \mathbb N.$

1. $1\cdot n=n$. Neutro multiplicativo.
2. $(n+m)\cdot l=n\cdot l+m\cdot l$. Distributividad.
3. $n\cdot m=m\cdot n$. Conmutatividad.
4. $(n\cdot m)\cdot l=n\cdot (m\cdot l)$. Asociatividad.
5. Si $n\neq 0$ y $m\neq 0$, entonces $n\cdot m\neq 0$
6. Si $l\neq 0$ y $n\cdot l=m\cdot l$ entonces $n=m$. Cancelación.

Tarea Moral

1. Describe a los números naturales $3$, $5$ y $7$ como conjuntos, usando la definición conjuntista.

2. Determina si las siguientes afirmaciones se cumplen o no.

• $3\subseteq 5$
• $7\subseteq 5$
• $3\in 5$
• $7\in 3$

3. Prueba que si $n\in \mathbb N$, entonces $n=0$ o $n=m^+$ con $m\in \mathbb N$. Sugerencia: define $A=\{0\}\cup\{m^+|m\in\mathbb{N}\}$ y usa el principio de inducción para demostrar que $A=\mathbb{N}$.

Más adelante

En la siguiente nota definiremos el orden en los números naturales y veremos distintos ejemplos donde aplicaremos el principio de inducción matemática para hacer demostraciones.

Enlaces relacionados

Página principal del curso.

Nota anterior. Nota 15. Relaciones de equivalencia y particiones.

Nota siguiente. Nota 17. El orden en los números naturales.