(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción.

En notas anteriores dimos una definición de lo que es un conjunto, vimos entre otras cosas que dada una propiedad $P$, no todos los elementos que cumplan la propiedad van a ser un conjunto, si consideramos por ejemplo $\set{x\mid x=x}$, la colección de todos los objetos de la teoría de conjuntos, resultaba no ser un conjunto ya que de considerarlo como tal teníamos paradojas, conjeturas que son al mismo tiempo verdaderas y falsas. Por otro lado si ya tenemos un conjunto $X$ y consideramos los elementos en él que cumplan una propiedad $\set{x\in X\mid x\,cumple\,la\,propiedad\,}$, ese sí es un conjunto y establecemos ese hecho como un axioma de la teoría llamado de compresión o separación.

Por otra parte definimos lo que es un subconjunto de un conjunto dado como:

$A\subseteq B \Longleftrightarrow$ para toda $z$, $z\in A$ implica que $z\in B.$

Dedujimos propiedades de la contención haciendo énfasis en la manera en la que se hace una prueba. Ver la nota 2.

En esta tercera nota definiremos el complemento de un conjunto y deduciremos algunas propiedades básicas pero muy importantes, que nos servirán para analizar distintos tipos de conjuntos, como los sistemas numéricos.

Como mencionamos la colección $\set{x\mid x=x}$, que consiste de todos los objetos, es demasiado grande para poder ser considerada un conjunto ya que nos lleva a contradicciones, pero no debemos preocuparnos, ya que usualmente trabajaremos en algún contexto específico, por ejemplo con los números racionales, o con los puntos del plano cartesiano, o con la colección de todas las funciones de los reales en sí mismos. A este conjunto dentro del cual se encuentran todos los objetos que trabajaremos en algún momento dado, le llamaremos el conjunto universo y lo denotaremos usualmente por $X$.

Definición

Sea $X$ el conjunto universo, $A$ un subconjunto de $X$. El complemento de $A$ respecto a $X$ es:

$X\setminus A =A^c=\set{x\in X\mid x\notin A}.$

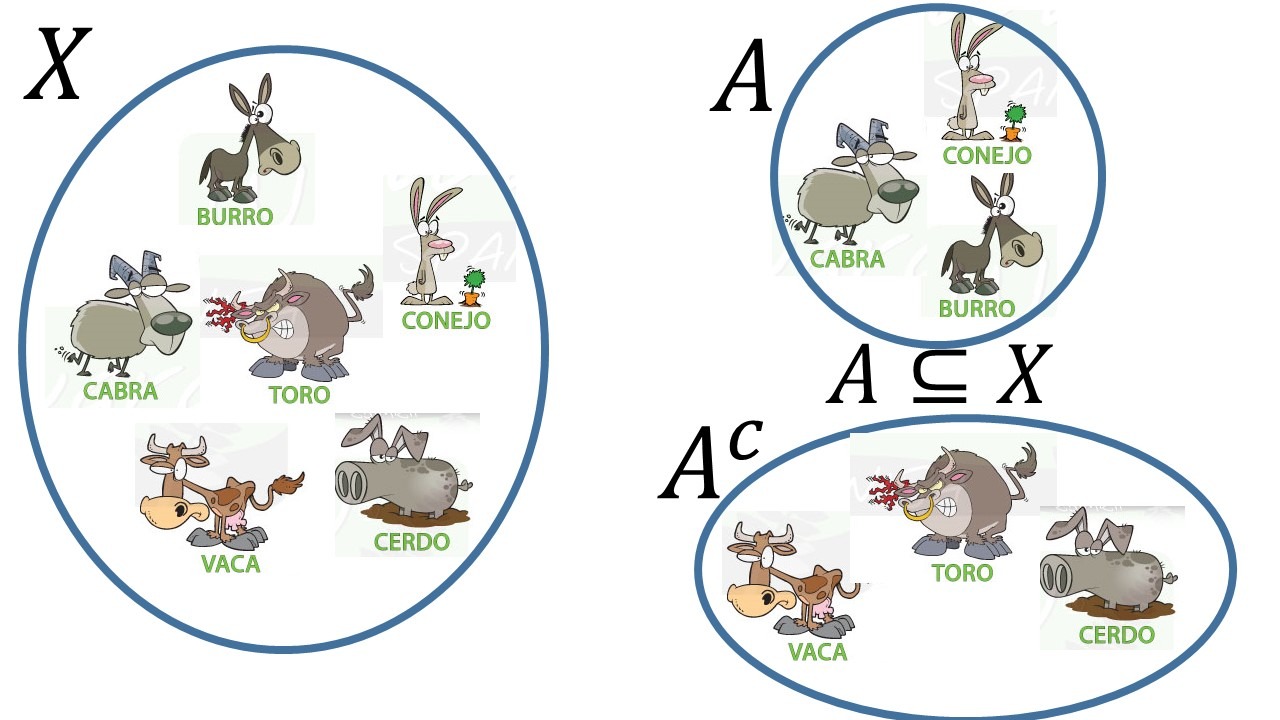
Ejemplos:

1. Si $X=\set{1,2,3,4,5}$ y $A=\set{1,3,5}$
   $X\setminus A =A^c=\set{ 2,4}$.
2. Si $X=\mathbb N$ y $A=\set{x\in \mathbb N\mid 5\leq x}=\set{5,6,7,…}$
   $ \mathbb N \setminus A =A^c=\set{x\in \mathbb N \mid x\notin A}$ = $\set{x\in \mathbb N \mid x< 5}=\{0,1,2,3,4\}.$
3. Si $X=\mathbb Z$ y $A=\set{x\in \mathbb N\mid 5\leq x}=\set{5,6,7,…}\phantom{zzzzzzz}$ $\mathbb Z \setminus A =A^c=\set{x\in \mathbb Z \mid x\notin A}$ = $\set{x\in \mathbb Z \mid x< 5}=\{\dots, -2,-1,0,1,2,3,4\}.$

De acuerdo a los ejemplos 2 y 3 nota que siempre tienes que delimitar el conjunto universo $X$ para hablar del complemento de un conjunto. La notación $A^c$ es bastante útil pero debemos tener claro quién es el conjunto $X$ con respecto al cual estamos calculando el complemento del conjunto $A$.

En el siguiente recurso de Geogebra, mueve los deslizadores para construir el conjunto $A$ y obtener su complemento.

Vamos a revisar algunas propiedades del complemento.

Propiedades

Sean $X$ el conjunto universo y $A$ un subconjunto de $X$.

1. $(A^c)^c=A.$
2. $A\subseteq B \Longleftrightarrow B^c\subseteq A^c.$
3. $A=B \Longleftrightarrow B^c=A^c.$
4. $\emptyset^c=X.$
5. $X^c=\emptyset .$

Demostración de 1.

Según el axioma de extensionalidad $A=B$ es equivalente a $A\subseteq B$ y $B\subseteq A$.

Estas pruebas de igualdad entre conjuntos se realizan usando el axioma de extensionalidad y se dice entonces que se trata de una prueba por doble contención.

Así para demostrar que:

$(A^c)^c=A$

Mostraremos que $(A^c)^c\subseteq A$ y que $A\subseteq (A^c)^c$.

Primero probemos que $(A^c)^c\subseteq A$.

Sea $z\in (A^c)^c$, por definición de complemento tenemos que $ (A^c)^c=\set{x\in X \mid x\notin A^c}$, así:

$z\in \set{x\in X \mid x\notin A^c}$

por lo que $z$ cumple la propiedad que define al conjunto, es decir $z\in X$ pero $z\notin A^c$. Como $ A^c=\set{x\in X \mid x\notin A}$, se deduce que $z\in A$ (pues en caso contrario $z$ sería un elemento de $A^c$), y de esta manera tenemos lo que queríamos demostrar pues cada vez que $z\in (A^c)^c$ también $z\in A$. Por lo tanto $(A^c)^c\subseteq A$.

Procedamos a probar la segunda contención $A\subseteq (A^c)^c$.

Sea $z\in A$, entonces $z\notin \set{x\in X \mid x\notin A}= A^c$ (debido a que no cumple la segunda condición que se pide para que un elemento pertenezca a este conjunto, el hecho de no ser elemento de $A$). Por otro lado, como $z\in A$ y $A\subseteq X$ (ya que $X$ es el conjunto universo), se tiene que $z\in X$. Así, $z$ cumple la propiedad que define al siguiente conjunto:

$\set{x\in X\mid x\notin A^c}$

que son los elementos que cumplen con la propiedad de no pertenecer al complemento de $A$, pero por definición ese conjunto es $(A^c)^c$, y por lo tanto $z\in (A^c)^c$. Así $A\subseteq (A^c)^c$.

Como hemos probado las dos contenciones, $(A^c)^c\subseteq A$ y que $A\subseteq (A^c)^c$, por el axioma de extensionalidad podemos afirmar que $A=(A^c)^c$.

Demostración de 2.

Por demostrar que $A\subseteq B \Longleftrightarrow B^c\subseteq A^c$.

Esta es una implicación de ida y vuelta, bicondicional o si y sólo si.

Procederemos a mostrar las dos implicaciones en este orden:

• $A\subseteq B \Longrightarrow B^c\subseteq A^c.$
• $B^c\subseteq A^c \Longrightarrow A\subseteq B.$

Por demostrar que $A\subseteq B \Longrightarrow B^c\subseteq A^c$.

Como queremos mostrar que $ B^c\subseteq A^c$, sea $z\in B^c$ y veamos que $z\in A^c$. Como $z\in B^c=\set{x\in X\mid x\notin B}$ tenemos que $z\in X$ y $z\notin B$. Sabemos que hay dos opciones, que $z\in A$ o que $z\notin A$. Pero si $z\in A$, dado que por hipótesis $A\subseteq B$, tendríamos que $z\in B,$ lo que contradice el hecho de que $z\notin B$. Concluimos entonces que $z\notin A$, lo que muestra que $z$ es elemento del conjunto $\set{x\in X \mid x\notin A}=A^c$, que es lo que queríamos demostrar y por tanto: $A\subseteq B \Longrightarrow B^c\subseteq A^c$.

Por demostrar que $B^c\subseteq A^c \Longrightarrow A\subseteq B$.

Por la implicación que acabamos de probar podemos afirmar que si:

$B^c\subseteq A^c$

entonces:

$(A^c)^c\subseteq (B^c)^c.$

Y por lo demostrado en 1:

$(A^c)^c=A$ y $(B^c)^c=B.$

Así:

$A\subseteq B$, que es lo que queríamos probar.

Demostración 3.

Por demostrar que $A=B \Longleftrightarrow B^c=A^c$.

Nota cómo esta cadena de implicaciones son derivadas de los axiomas o de las propiedades ya demostradas.

Demostración 4.

Por demostrar que $\emptyset^c=X$

La prueba se hará por doble contención.

Así, primero mostremos que $\emptyset^c\subseteq X$.

Sea $z\in \emptyset^c=\set{x\in X\mid x\notin \emptyset}.$

En particular $z\in X$, y por lo tanto $\emptyset^c\subseteq X$, lo que nos da la primera contención.

Ahora mostremos que $X\subseteq \emptyset^c$

Sea $z\in X$. Sabemos que el vacío no tiene elementos así que ningún objeto puede ser elemento del vacío, en particular $z\notin\emptyset$. Entonces, por definición de complemento:

$z\in \set{x\in X \mid z\notin \emptyset}=\emptyset^c.$

Y así, $X\subseteq \emptyset^c$, lo que nos da la segunda contención.

Finalmente como $\emptyset^c\subseteq X$ y $X\subseteq \emptyset^c$ por el axioma de extensionalidad tenemos que $X= \emptyset^c$, que es lo que queríamos demostrar.

Demostración 5.

Por demostrar que $X^c=\emptyset.$

De la propiedad 4 sabemos que: $\emptyset^c=X$, y por la propiedad 3 esto implica que $(\emptyset^c)^c=X^c$. Pero $(\emptyset^c)^c=\emptyset$ por la propiedad 1, así $\emptyset=X^c$, que es lo que queríamos demostrar.

Esto concluye la demostración de las 5 propiedades mencionadas, en la tarea moral hay ejercicios que te permitirán aplicar los nuevos teoremas que hemos estudiado.

$\square$

Tarea Moral.

1. Considera los siguientes conjuntos:

• $C=\set{t\in \mathbb Z\mid\,t=9k+3\,para\,alguna\,k\in \mathbb Z}.$
• $D=\set{t\in \mathbb Z\mid\,t\,es\,un\,múltiplo\,de\,3}. $

2. Prueba lo siguiente:

• Prueba que $C\subseteq D$.
• Encuentra $C^c$.
• Encuentra $D^c$
• Verifica que $D^c\subseteq C^c$ a partir de cómo están definidos los conjuntos $C^c$ y $D^c$ .

3. Sea $X=\mathbb R$ el conjunto universo. Encuentra el complemento de los siguientes conjuntos:

• $\set{x\in \mathbb R \mid x<2}.$
• $\set{x\in \mathbb R \mid -3\leq x< 2}.$
• $\set{x\in \mathbb R \mid\,x\,es\,un\,número\,racional\, }.$
• $\set{x\in \mathbb R \mid \,x\,es\,irracional\,y\,x\leq0\,}.$

Más adelante

En la siguiente sección definiremos dos operaciones con conjuntos, la unión e intersección de conjuntos. Además demostraremos propiedades bastante útiles para el desarrollo de muchas áreas de la matemática como la topología y el análisis.

Entradas relacionadas

Página principal del curso.

• Entrada anterior del curso. Nota 2. Subconjuntos
• Entrada siguiente del curso. Nota 4. Unión e intersección de conjuntos

Nota. Las imágenes mostradas para ilustrar los conjuntos no fueron de diseño propio, y se da las gracias a: https://www.spanish.cl/ por sus divertidos dibujos. Se deja el link de donde se obtuvieron: https://www.spanish.cl/vocabulario/animales-de-la-granja.htm.