Archivo del Autor: Cecilia del Carmen Villatoro Ramos

Álgebra Moderna I: Lemas previos al teorema fundamental de los grupos abelianos finitos.

Por Cecilia del Carmen Villatoro Ramos

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Como dijimos en la primera entrada de esta unidad, uno de los temas a los que queremos llegar es el Teorema fundamental de los grupos abelianos finitos. Para ello seguiremos el desarrollo hecho por Judson, T.W. en el libro Abstract Algebra: Theory and Applications, Department of Mathematics and Statistics Stephen F. Austin State University que aparece en la bibliografía y que puede revisarse en http://abstract.ups.edu/aata/struct-section-finite-abelian-groups.html. Así, en esta entrada presentaremos tres lemas para que sea más sencillo identificarlos y que serán útiles en la demostración del Teorema fundamental de los grupos abelianos finitos en la siguiente entrada. En los tres lemas se considerará $G$ un $p$ -grupo abeliano y se hablará de elementos de orden máximo (o mínimo) en algún grupo refiriéndose a elementos cuyo orden es mayor (o menor) o igual que el orden de los demás elementos del grupo en cuestión.

El primer lema nos dice que si tomamos un elemento de orden máximo $g$ en $G$ y un $p$ -subgrupo, tal que $⟨ g ⟩$ no es todo $G$ y luego tomamos un elemento de orden mínimo $h$ en $G ∖ ⟨ g ⟩$ , entonces el orden de $h$ es $p$ .

El segundo lema nos dice que si tenemos un elemento de orden máximo $g$ en $G$ , podemos ver a $G$ como el producto directo interno del generado de $g$ y un $H$ subgrupo de $G$ .

El tercer lema nos dice que cualquier $p$ -subgrupo abeliano es producto directo interno de grupos cíclicos.

En esta entrada enunciamos y probamos los primeros dos lemas, el tercero está en la siguiente entrada.

El orden de un elemento mínimo

Lema 1. Sean $p \in Z^{+}$ un primo y $G$ un $p$ -grupo abeliano. Sea $g \in G$ un elemento de orden máximo. Si $⟨ g ⟩ ⪇ G$ ( $⟨ g ⟩$ es subgrupo propio de $G$ ) y $h$ es un elemento de orden mínimo en $G ∖ ⟨ g ⟩$ , entonces $o (h) = p$ y $⟨ g ⟩ \cap ⟨ h ⟩ = {e}$ .

Demostración.
Sean $p \in Z^{+}$ un primo y $G$ un $p$ -grupo abeliano.

Por la definición de $p$ -grupo $| G | = p^{n}$ para algún $n \in N$ .

Sea $g \in G$ de orden máximo. Como $| G | = p^{n}$ , sabemos que $o (g)$ divide a $| G | = p^{n}$ y así $o (g) = p^{m}$ con $m \leq n$ .

Observemos que
$\begin{array}{r} (1) & a^{p^{m}} = e para toda a \in G, \end{array}$
ya que para toda $a \in G$ , $o (a) = p^{l}$ con $l \leq m$ (debido a que $o (g) = p^{m}$ es máximo).

Supongamos que $⟨ g ⟩ ⪇ G$ . Consideremos un elemento $h$ de orden mínimo en $G ∖ ⟨ g ⟩$ .

Veamos primero que $o (h) = p$ .

Sabemos que $o (h) = p^{t}$ para alguna $t \leq n$ .

Sabemos que $o (h^{p}) = p^{t - 1} < p^{t} = o (h)$ . Así, por la elección de $h$ , $h^{p} \in ⟨ g ⟩$ y en consecuencia tenemos que
$\begin{array}{r} (2) & h^{p} = g^{s} para algún s \in N . \end{array}$

Entonces $(g^{s})^{p^{m - 1}} = (h^{p})^{p^{m - 1}} = h^{p^{m}} = e$ por ( $1$ ). Así,
$\begin{array}{r} (3) & o (g^{s}) < p^{m} y g^{s} no genera a ⟨ g ⟩ . \end{array}$

Sabemos que $o (g^{s}) = \frac{o (g)}{(s, o (g))}$ . Si $p$ no divide a $s$ , como $o (g)$ es una potencia de $p$ tendríamos que $(s, o (g)) = 1$ y así $o (g^{s}) = o (g) = p^{m}$ contradiciendo ( $3$ ). Concluimos entonces que $p | s$ es decir $s = p q$ para algún $q \in Z$ .

Consideremos $a = g^{- q} h$ . Tenemos que
$\begin{aligned} a^{p} = g^{- p q} h^{p} = g^{- s} h^{p} & = g^{- s} g^{s} & por (2) \\ = e . \end{aligned}$

Además, si $a \in ⟨ g ⟩$ tendríamos que $h = a g^{q} \in ⟨ g ⟩$ lo cual contradice la elección de $h$ .

Hemos encontrado entonces un elemento $a \notin ⟨ g ⟩$ con $a^{p} = e$ . Notamos que $a \neq e$ ya que $a \notin ⟨ g ⟩$ , entonces $a$ debe ser un elemento de orden $p$ . Pero $h$ es un elemento de orden mínimo en $G ∖ ⟨ g ⟩$ y $a \in G ∖ ⟨ g ⟩$ con $o (a) = p$ . Así, $h$ debe ser también de orden $p$ .

Veamos ahora que $⟨ g ⟩ \cap ⟨ h ⟩ = {e}$ .

Sabemos que $⟨ g ⟩ \cap ⟨ h ⟩$ es un subgrupo de $⟨ h ⟩$ y $⟨ h ⟩$ es de orden $p$ , entonces $⟨ g ⟩ \cap ⟨ h ⟩$ es de orden $1$ o $p$ . Si $| ⟨ g ⟩ \cap ⟨ h ⟩ | = p$ tendríamos que $⟨ g ⟩ \cap ⟨ h ⟩ \leq ⟨ h ⟩$ con $| ⟨ g ⟩ \cap ⟨ h ⟩ | = p = | ⟨ h ⟩ |$ , entonces $⟨ g ⟩ \cap ⟨ h ⟩ = ⟨ h ⟩$ lo que implica que $⟨ h ⟩ \subseteq ⟨ g ⟩$ . En consecuencia tendríamos que $h \in ⟨ g ⟩$ , lo que contradice la elección de $h$ .

Concluimos que $⟨ g ⟩ \cap ⟨ h ⟩ = {e}$ .

$G$ como producto de $⟨ g ⟩$ y un subgrupo cualquiera

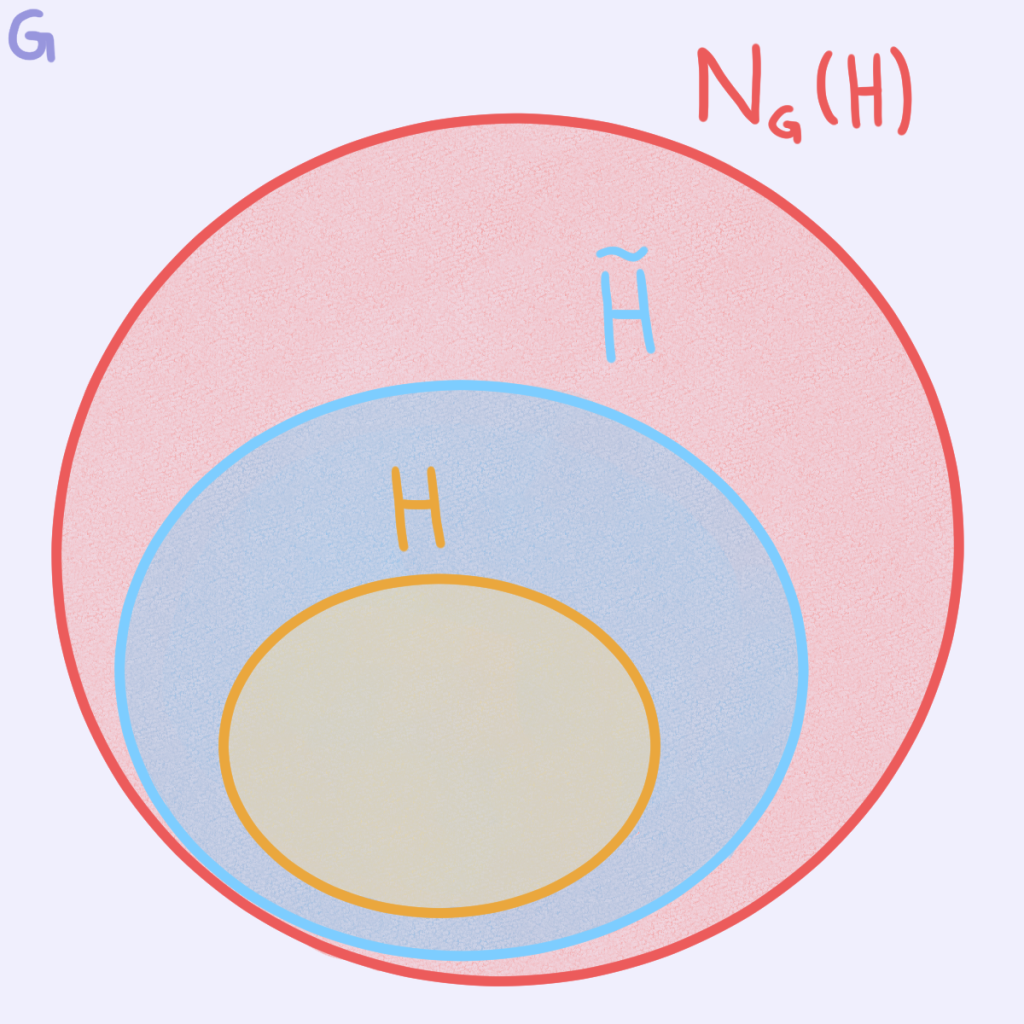
Lema 2. Sean $p \in Z^{+}$ un primo y $G$ un $p$ -grupo abeliano. Supongamos que $g \in G$ es un elemento de orden máximo. Entonces $G$ es el producto directo interno de $⟨ g ⟩$ y un subgrupo $H$ de $G$ .

Demostración.
Sean $p \in Z^{+}$ primo.

Realizaremos la demostración por el segundo principio de inducción.

H.I. Supongamos que para todo grupo abeliano $\tilde{G}$ con $| \tilde{G} | = p^{k}$ y $0 \leq k < n$ se tiene que si $\tilde{g} \in \tilde{G}$ es de orden máximo, entonces $\tilde{G}$ es el producto directo interno de $⟨ \tilde{g} ⟩$ y un subgrupo $\tilde{H}$ de $\tilde{G}$ .

Sea $G$ un $p$ -grupo abeliano con $| G | = p^{n}$ para algún $n \in N$ .

Sea $g \in G$ de orden máximo. Como $| G | = p^{n}$ , sabemos que $o (g)$ divide a $| G | = p^{n}$ y así $o (g) = p^{m}$ con $m \leq n$ .

Si $G = ⟨ g ⟩$ el resultado se cumple considerando $H = {e}$ .

Si $⟨ g ⟩ ⪇ G$ consideremos un elemento $h$ de orden mínimo en $G ∖ ⟨ g ⟩ .$

Por el lema 1, sabemos que $o (h) = p$ y que $⟨ g ⟩ \cap ⟨ h ⟩ = {e}$ . Sea $H = ⟨ h ⟩ .$

Observemos que $g H$ es un elemento de orden máximo en $G / H$ ya que por ( $1$ ), $(a H)^{p^{m}} = a^{p^{m}} H = H$ para todo $a \in G$ . Además $(g H)^{o (g)} = g^{o (g)} H = H$ por lo que $o (g H) \leq o (g) = p^{m}$ , y si $o (g H) < p^{m}$ tendríamos que
$\begin{array}{r} H = (g H)^{p^{m - 1}} = g^{p^{m - 1}} H \end{array}$
y así $g^{p^{m - 1}} \in ⟨ g ⟩ \cap H = {e}$ , es decir $g^{p^{m - 1}} = e$ contradiciendo que $o (g) = p^{m}$ .

Concluimos así que $g H$ es un elemento de orden máximo en $G / H$ , con $G / H$ un $p$ -grupo abeliano de orden $| G / H | = | G | / | H | = \frac{p^{n}}{p} = p^{n - 1}$ que es menor que el orden de $G$ .

Por H.I. sabemos que $G / H$ es el producto directo interno de $⟨ g H ⟩$ y un subgrupo $\tilde{H}$ de $G / H$ .

Por el teorema de la correspondencia $\tilde{H} = K / H$ para algún $H \leq K \leq G$ .

Veamos que $G$ es el producto directo interno de $⟨ g ⟩$ y $K$ .

Veamos primero que $⟨ g ⟩ \cap K = {e}$ .

Si $x \in ⟨ g ⟩ \cap K$ , entonces $x H \in ⟨ g H ⟩ \cap K / H = ⟨ g H ⟩ \cap \tilde{H}$ y como $G / H$ es el producto directo de $⟨ g H ⟩$ y $\tilde{H}$ , entonces $⟨ g H ⟩ \cap \tilde{H} = {H}$ . Así, $x H \in {H}$ , entonces $x H = H$ lo que implica que $x \in H$ .

Tenemos que $x \in ⟨ g ⟩ \cap H = {e}$ probando que $x = e$ . Así, $⟨ g ⟩ \cap K = {e}$ .

Veamos ahora que $G = ⟨ g ⟩ K$ .

Sea $y \in G$ , sabemos que $y H \in G / H = ⟨ g H ⟩ \tilde{H} = ⟨ g H ⟩ K / H$ . Esto implica que
$\begin{aligned} y H & = (g H)^{t} k H para algunos t \in Z, k \in K \\ = g^{t} k H . \end{aligned}$

Entonces $(g^{t} k)^{- 1} y = \hat{h}$ con $\hat{h} \in H$ . Así $y = g^{t} k \hat{h}$ . Como $H \leq K$ tenemos que $k \hat{h} \in K$ , entonces $y \in ⟨ g ⟩ K$ .

Concluimos que $⟨ g ⟩ \cap K = {e}$ y $⟨ g ⟩ K = G$ .

Así, $G$ es el producto directo interno de $⟨ g ⟩$ y $K$ .

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Considera los siguientes grupos y realiza para cada uno los ejercicios descritos a continuación:

$S_{4} .$
$Z_{11} .$
$A_{5} .$
$Q_{8} = {\pm 1, \pm i, \pm j, \pm k} .$

Determina si los grupos anteriores son $p$ -grupos abelianos. De no serlo, considera un $p$ -subgrupo abeliano de ellos.
Busca (en el grupo o en el $p$ -subgrupo abeliano) un elemento $g$ de orden máximo tal que $⟨ g ⟩$ sea un subgrupo propio y encuentra $h$ elemento de orden mínimo en el complemento de $⟨ g ⟩$ tal que su orden sea $p$ .
Describe al grupo o al $p$ -subgrupo abeliano como el producto directo interno $⟨ g ⟩$ y un subgrupo $H$ .

Más adelante…

Aunque estos lemas pueden parecer muy técnicos, su función es clara y se verá en la siguiente entrada. Como estos lemas ya están demostrados, la prueba del Teorema fundamental de los grupos abelianos finitos es bastante directa. En la siguiente entrada enunciaremos y demostraremos el tercer lema que se requiere y por fin podremos enfrentarnos al Teorema fundamental de los grupos abelianos finitos.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Producto directo interno.
Siguiente entrada del curso: Teorema fundamental de los grupos abelianos finitos.

Resto de cursos: Cursos.

Álgebra Moderna I: Producto directo interno

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Continuamos con el estudio del producto de grupos siguiendo el desarrollo de la sección 4.3 del libro de Grupos I de Avella, Mendoza, Sáenz y Souto que se encuentra en la bibliografía del curso. En la entrada anterior definimos el producto directo externo de grupos, luego vimos unas funciones naturales y definimos los subgrupos $G_{i}^{*}$ . Demostramos que para un grupo $G = G_{1} \times \dots \times G_{n}$ se cumple que:

$G_{i}^{*} ⊴ G \forall i \in {1, \dots, n}$ .
$G_{i}^{*} \cap (\prod_{j \neq i} G_{j}^{*}) = {e_{G}} para toda i \in {1, \dots, n}$ .
$G = \prod_{i = 1}^{n} G_{i}^{*}$ .

En resumen, esta proposición nos dice que si $G$ es el producto directo externo de varios grupos, también lo podemos ver como producto de subgrupos normales que cumplen el inciso 2.

En esta entrada queremos generalizar esta idea: ahora $G$ será un grupo cualquiera, tomaremos subgrupos normales $H_{i}$ , con $i \in {1, \dots, n}$ de $G$ que cumplan estas propiedades y probaremos que $G$ se puede ver como el producto directo externo de estos subgrupos.

En el producto directo externo, construíamos $G$ a partir de otros grupos que pudieran incluso no estar relacionados entre sí. Ahora intentaremos describir a un grupo $G$ como producto de algunos de sus subgrupos normales, por eso llamaremos a este concepto el producto directo interno.

Producto directo interno de subgrupos

Comencemos definiendo nuestro nuevo producto entre subgrupos normales de $G$ .

Definición. Sean $G$ un grupo, $H_{1}, \dots, H_{n}$ subgrupos de $G$ . Decimos que $G$ es el producto directo interno de $H_{1}, \dots, H_{n}$ si

$H_{i} ⊴ G$ para toda $i \in {1, \dots, n}$ .
$H_{i} \cap (\prod_{j \neq i} H_{j}) = {e}$ para toda $i \in {1, \dots, n}$ .
$G = \prod_{i = 1}^{n} H_{i}$ .

Observación 5. $G_{1} \times \dots \times G_{n}$ es el producto directo interno de los $G_{i}^{*}$ .

Observación 6. Si $G$ es el producto directo interno de $H_{1}, \dots, H_{n}$ , entonces $x y = y x$ para toda $x \in H_{i}, y \in H_{j}$ con $i \neq j$ .

Demostración.
Sea $G$ producto directo de $H_{1}, \dots, H_{n}$ , sean $x \in H_{i}, y \in H_{j}$ , con $j \neq i$ , entonces
$\begin{array}{r} x y x^{- 1} y^{- 1} = x (y x^{- 1} y^{- 1}) \in H_{i}, \end{array}$
porque $x \in H_{i}$ y $y x^{- 1} y^{- 1} \in H_{i}$ pues $H_{i} ⊴ G$ .

Por otro lado,
$\begin{array}{r} x y x^{- 1} y^{- 1} = (x y x^{- 1}) y^{- 1} \in H_{j}, \end{array}$
ya que, análogamente, $x y x^{- 1} \in H_{j}$ debido a que $H_{j} ⊴ G$ y $y^{- 1} \in H_{j} .$

Así, $x y x^{- 1} y^{- 1} \in H_{i} \cap H_{j} \subseteq H_{i} \cap \prod_{k \neq i} H_{k} = {e}$ . Entonces $x y x^{- 1} y^{- 1} = e$ .

Por lo tanto $x y = y x$ .

Ejemplo. Sea $G = ⟨ a ⟩$ con $o (a) = 12$ . Busquemos subgrupos $H_{1}, \dots, H_{n}$ para alguna $n \in N$ tales que $G$ sea el producto directo interno de estos subgrupos.

Sean $H_{1} = ⟨ a^{3} ⟩, H_{2} = ⟨ a^{4} ⟩$ . Como $G$ es abeliano, $H_{1} ⊴ G, H_{2} ⊴ G$ . Además
$\begin{array}{r} H_{1} \cap H_{2} = {e, a^{3}, a^{6}, a^{9}} \cap {e, a^{4}, a^{8}} = {e} . \end{array}$

Como
$\begin{array}{r} a = a e = a a^{12} = a^{13} = a^{9} a^{4} \in H_{1} H_{2} \end{array}$
tenemos que $G = ⟨ a ⟩ \subseteq H_{1} H_{2}$ . Por la cerradura del producto en $G$ se tiene además que $H_{1} H_{2} \subseteq G$ , entonces $G = H_{1} H_{2}$ .

Por lo tanto $G$ es el producto directo interno de $H_{1}$ y $H_{2}$ .

Observación 7. Sean $G$ un grupo, $H_{1}, \dots, H_{n}$ subgrupos de $G$ . Si $G$ es el producto directo interno de $H_{1}, \dots, H_{n}$ , entonces
$\begin{array}{r} φ : H_{1} \times \dots \times H_{n} \to G \end{array}$
con $φ (h_{1}, \dots, h_{n}) = h_{1} \dots h_{n}$ para toda $(h_{1}, \dots, h_{n}) \in H_{1} \times \dots \times H_{n}$ es un isomorfismo.

Es consecuencia, si $G$ es finito tenemos que $| G | = | H_{1} | \dots | H_{n} |$ .

Descomposición de $G$ en $p$ -subgrupos

Algunos subgrupos importantes que vimos son los $p$ -subgrupos de Sylow, para $p$ primo. Ahora los usaremos junto con el producto directo interno para describir a $G$ como el producto de sus $p$ -subgrupos de Sylow, esto nos recuerda mucho al Teorema Fundamental de la Aritmética. Siguiendo el desarrollo de la página 193 del libro de Dummit, D. S. y Foote R. M. que aparece en la bibliografía tenemos:

Teorema. Sea $G$ un grupo finito con $p_{1}, \dots, p_{t}$ los distintos factores primos del orden de $G$ y $P_{1}, \dots, P_{t}$ subgrupos de Sylow de $G$ asociados a $p_{1}, \dots, p_{t}$ respectivamente. Si $P_{i} ⊴ G$ para toda $i \in {1, \dots, t}$ , entonces $G$ es el producto directo interno de $P_{1}, \dots, P_{t}$ .

Demostración.
Sea $G$ un grupo finito de orden $n$ . Sean $p_{1}, \dots, p_{t}$ los distintos factores primos de $n$ con $n = p_{1}^{α_{1}} p_{2}^{α_{2}} \dots p_{t}^{α_{t}}$ . Sean $P_{1}, \dots, P_{t}$ subgrupos de $G$ con $P_{i}$ un $p_{i}$ -subgrupo de Sylow de $G$ y $P_{i} ⊴ G$ para toda $i \in {1, \dots, t}$ .

Veamos que para todo $S \subseteq {1, \dots, t}$ , $\prod_{j \in S} P_{j}$ es un producto directo interno por inducción sobre $# S$ .

Caso Base. Supongamos que $# S = 1$ ,
$S = {i} \subseteq {1, \dots, t}$ y $P_{i}$ es el producto directo interno de $P_{i}$ .

H.I. Supongamos que si $T \subseteq {1, \dots, t}$ con $# T < # S$ , entonces $\prod_{j \in T} P_{j}$ es un producto directo interno.

Sea $H = \prod_{j \in S} P_{j}$ . Veamos que $H$ es el producto directo interno de los $P_{j}$ con $j \in S$ .

Por hipótesis se cumplen las condiciones $1$ y $3$ de la definición de producto directo interno. Veamos que se cumple $2$ .

Sean $i \in S$ , $x \in P_{i} \cap \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} P_{j}$ .

Como $x \in P_{i}$ , entonces $o (x)$ divide a $| P_{i} |$ .

Como $x \in \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} P_{j}$ , entonces el orden de $x$ divide al orden del producto: $o (x) | | \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} P_{j} | = \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} | P_{j} |$ donde la última igualdad se debe a que $\prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} P_{j}$ es un producto directo interno por H.I. y por la observación 7.

Pero $| P_{i} | = p_{i}^{α_{i}}$ y $\prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} | P_{j} | = \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} p_{j}^{α_{j}}$ con $α_{j} \in N^{+}$ para toda $j \in S$ , entonces $| P_{i} |$ y $\prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} | P_{j} |$ son primos relativos. Así, $o (x) = 1$ . Por lo que $P_{i} \cap \prod_{\begin{matrix} j \in S \\ j \neq i \end{matrix}} P_{j} = {e}$ .

Hemos probado entonces que $\prod_{\begin{matrix} j \in S \end{matrix}} P_{j}$ es un producto directo interno para toda $S \subseteq {1, \dots, t}$ . En particular para $S = {1, \dots, t}$ tenemos que $\prod_{j = 1}^{t} P_{j}$ es un producto directo interno. Por la observación 7,
$\begin{array}{r} | \prod_{j = 1}^{t} P_{j} | = \prod_{j = 1}^{t} | P_{j} | = n = | G | \end{array}$
ya que $P_{1}, \dots, P_{t}$ son subgrupos de Sylow asociados a los distintos factores primos de $G$ .

Como $\prod_{j = 1}^{t} P_{j}$ es un subgrupo de $G$ de orden $| G |$ tenemos que $G = \prod_{j = 1}^{t} P_{j}$ .

Por lo tanto $G$ es el producto directo interno de $P_{1}, \dots, P_{t}$ .

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra las observaciones 5 y 7.
- $G_{1} \times \dots \times G_{n}$ es el producto directo interno de los $G_{i}^{*}$ .
- Sean $G$ un grupo, $H_{1}, \dots, H_{n}$ subgrupos de $G$ . Si $G$ es el producto directo interno de $H_{1}, \dots, H_{n}$ , entonces
  $\begin{array}{r} φ : H_{1} \times \dots \times H_{n} \to G \end{array}$
  con $φ (h_{1}, \dots, h_{n}) = h_{1} \dots h_{n}$ para toda $(h_{1}, \dots, h_{n}) \in H_{1} \times \dots \times H_{n}$ es un isomorfismo.
Regresa a la entrada de Ejemplo de Sylow y considera $S_{4}$ .
- De existir, busca $H_{1}, \dots, H_{n}$ tal que $S_{4}$ sea producto directo de $H_{1}, \dots, H_{n} .$
- Usando los $p$ -subgrupos de Sylow que encontramos, describe a $S_{4}$ como producto directo interno de ellos. Aplica el último teorema visto.
Aplica el último teorema visto a los grupos $Z_{6}$ y $T = S_{3} \times Z_{4}$ . Para cada uno encuentra los primos $p_{1}, \dots, p_{n}$ que conforman al orden del grupo y los $P_{1}, \dots, P_{n}$ subgrupos de Sylow que corresponden a estos primos. Al final, representa a cada grupo como producto directo interno de estos $p$ -subgrupos de Sylow.

Más adelante…

La descomposición de un grupo en $p$ -subgrupos que vimos es una probada de lo que veremos en el Teorema fundamental de grupos abelianos finitos, la relación de los primos que componen al orden del grupo con los $p$ -subgrupos del mismo grupo. Pero antes de poder enunciarlo, necesitamos enunciar algunos teoremas que nos ayudarán y que se sirven de los productos directos interno y externo que hemos estado viendo.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Producto directo externo.
Siguiente entrada del curso: Lemas previos al teorema fundamental de los grupos abelianos finitos.
Resto de cursos: Cursos.

Álgebra Moderna I: Producto directo externo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Esta entrada es el inicio de la última unidad del curso de Álgebra Moderna I, uno de los temas centrales que estudiaremos en esta unidad es el Teorema Fundamental de los Grupos Abelianos Finitos. Como es costumbre, para poder sumergirnos en el teorema, primero tenemos que construir algunos cimientos.

Seguramente a lo largo de tu estudio de las matemáticas te has encontrado con la notación $R^{2} = R \times R$ y otras similares. $R^{2}$ se usa para denotar al plano cartesiano y rápidamente entendemos que sus elementos tienen la forma de pares ordenados $(x, y)$ donde $x, y \in R$ . Esto mismo sucede con potencias mayores, como por ejemplo $(x, y, z) \in R^{3} = R \times R \times R$ y $(x_{1}, \dots, x_{n}) \in R^{n} = R \times \dots \times R$ ( $n$ veces).

De la misma manera, podríamos hacer $Z \times R$ y obtener objetos de la forma $(z, r)$ donde $z$ es un entero y $r$ un real. Es decir, podemos usar a la operación $\times$ entre dos grupos completamente distintos. Pero más allá de poder, ¿esto es algo que podamos estudiar? En pocas palabras, sí, resulta que la operación $\times$ es una manera práctica de construir grupos más grandes a partir de otros grupos.

En esta entrada y la próxima seguiremos el desarrollo de la sección 4.3 del libro de Grupos I de Avella, Mendoza, Sáenz y Souto que se encuentra en la bibliografía del curso.

Hablemos del producto de grupos

Comencemos definiendo formalmente al producto de grupos.

Definición. Sean $(G_{1}, *_{1}), \dots, (G_{n}, *_{n})$ grupos. El producto directo externo de $G_{1}, \dots, G_{n}$ es
$\begin{array}{r} G_{1} \times \dots \times G_{n} = {(g_{1}, \dots, g_{n}) | g_{i} \in G \forall i \in {1, \dots, n}} \end{array}$
con la operación
$\begin{array}{r} (g_{1}, \dots, g_{n}) * (h_{1}, \dots, h_{n}) = (g_{1} *_{1} h_{1}, \dots, g_{n} *_{n} h_{n}) . \end{array}$

Observación. $G_{1} \times \dots \times G_{n}$ es un grupo con neutro $(e_{G_{1}}, \dots, e_{G_{n}})$ y $(g_{1}^{- 1}, \dots, g_{n}^{- 1})$ es el inverso de cada $(g_{1}, \dots, g_{n}) \in G_{1} \times \dots \times G_{n}$ .

Ejemplo 1. Consideremos $G = S_{3} \times Z_{2} \times D_{2 (4)} .$
Un elemento es $((1 2 3), \bar{1}, a^{2} b)$ .
Dados $(α, \bar{a}, f), (β, \bar{b}, g) \in G$ se tiene que
$\begin{array}{r} (α, \bar{a}, f) * (β, \bar{b}, g) = (α \circ β, \bar{a} + \bar{b}, f \circ g) . \end{array}$

Ejemplo 2. Tomemos el producto $Z_{2} \times Z_{2} = {(\bar{0}, \bar{0}), (\bar{0}, \bar{1}), (\bar{1}, \bar{0}), (\bar{1}, \bar{1})}$ .
Observemos que $o (\bar{0}, \bar{0}) = 1$ , $o (\bar{0}, \bar{1}) = o (\bar{1}, \bar{0}) = o (\bar{1}, \bar{1}) = 2.$
La suma de dos elementos en ${(\bar{0}, \bar{1}), (\bar{1}, \bar{0}), (\bar{1}, \bar{1})}$ nos da el tercero. Entonces, $Z_{2} \times Z_{2}$ es isomorfo al grupo de Klein.

Ejemplo 3. Por último, tomemos $Z_{2} \times Z_{3} = {(\bar{0}, \bar{0}), (\bar{0}, \bar{1}), (\bar{0}, \bar{2}), (\bar{1}, \bar{0}), (\bar{1}, \bar{1}), (\bar{1}, \bar{2})}$ .
Observemos que $o (\bar{1}, \bar{1}) = 6.$
Tenemos que $Z_{2} \times Z_{3} = ⟨ (\bar{1}, \bar{1}) ⟩$ y así $Z_{2} \times Z_{3} ≅ Z_{6}$ .

Dos funciones naturales

Definición. Sean $G_{1}, \dots, G_{n}$ grupos, $G = G_{1} \times \dots \times G_{n}$ . Para cada $i \in {1, \dots, n}$ definimos la inclusión natural
$\begin{array}{r} {inc}_{i} : G_{i} \to G como {inc}_{i} (g_{i}) = (e_{G_{1}}, \dots, g_{i}, \dots, e_{G_{n}}), \end{array}$
donde $g_{i}$ está en la $i$ -ésima posición.

Definición. Sean $G_{1}, \dots, G_{n}$ grupos, $G = G_{1} \times \dots \times G_{n}$ . Para cada $i \in {1, \dots, n}$ definimos la proyección natural
$\begin{array}{r} π_{i} : G \to G_{i} con π_{i} (g_{1}, \dots, g_{n}) = g_{i} . \end{array}$

Observación 1 . ${inc}_{i}$ es un monomorfismo.

Observación 2 . $π_{i}$ es un epimorfismo.

Notación. $G_{i}^{*} = {inc}_{i} ⌈ G_{i} ⌉ = {e_{G_{1}}} \times \dots \times G_{i} \times \dots {e_{G_{n}}} .$

Observación 3. Para $G = G_{1} \times \dots \times G_{n}$ , los siguientes incisos son ciertos:

$G_{i} ≅ G_{i}^{*}$ ,
$G_{i}^{*} ⊴ G$ y
$G / G_{i}^{*} ≅ G_{1} \times \dots \times G_{i - 1} \times G_{i + 1} \times \dots G_{n} .$

Demostración.
${inc}_{i}$ es un monomorfismo y si restringimos a su imagen $G_{i}^{*}$ obtenemos un epimorfismo, dando un isomorfismo de $G_{i}$ a $G_{i}^{*}$ .

Ahora $φ : G \to G_{1} \times \dots \times G_{i - 1} \times G_{i + 1} \times \dots \times G_{n}$ con $φ (g_{1}, \dots, g_{n}) = (g_{1}, \dots, g_{i - 1}, g_{i + 1}, \dots, g_{n})$ es un epimorfismo y $Núc φ = G_{i}^{*}$ , probando con ello que $G_{i}^{*} ⊴ G$ . Además, por el 1er teorema de isomorfía
$\begin{array}{r} G / G_{i}^{*} ≅ G_{1} \times \dots \times G_{i - 1} \times G_{i + 1} \times \dots G_{n} . \end{array}$

Observación 4. Sean $i \neq j$ , $x \in G_{i}^{*}$ , $y \in G_{j}^{*}$ . Entonces $x *_{n} y = y *_{n} x$ .

¿Y si ahora recuperamos $G$ a partir de los $G_{i}^{*}$ ?

En la entrada Producto de subgrupos y clases laterales, definimos el producto de dos subgrupos. Generalicemos esta idea para una cantidad finita de subgrupos:

Definición. Sea $G$ un grupo. Dados $H_{1}, \dots, H_{n}$ subgrupos de $G$ , el producto de $H_{1}, \dots, H_{n}$ es
$\begin{array}{r} \prod_{i = i}^{n} H_{i} = H_{1} \dots H_{n} = {h_{1} h_{2} \dots h_{n} | h_{i} \in H_{i}; \forall i \in {1, \dots, n}} . \end{array}$

Observemos que para realizar el producto de $h_{1} h_{2} \dots h_{n}$ sólo usamos la operación del grupo $G$ porque todas las $H_{i}$ son subgrupos de $G$ . Sin embargo, como estudiamos en la entrada Producto de subgrupos y clases laterales, el conjunto $H_{1} \dots H_{n}$ no necesariamente es un subgrupo ya que la operación no siempre es cerrada. En la siguiente entrada agregaremos condiciones a los subgrupos $H_{i}$ para que $H_{1} \dots H_{n}$ sí sea un subgrupo de $G$ .

Relacionemos ahora el producto directo externo con el producto de los subgrupos $G_{i}^{*}$ antes definidos:

Proposición. Sean $G_{1}, \dots, G_{n}$ grupos, $G = G_{1} \times \dots \times G_{n} .$

$G_{i}^{*} ⊴ G \forall i \in {1, \dots, n}$ .
$G_{i}^{*} \cap (\prod_{j \neq i} G_{j}^{*}) = {e_{G}} para toda i \in {1, \dots, n}$ .
$G = \prod_{i = 1}^{n} G_{i}^{*}$ .

Demostración.
Sean $G_{1}, \dots, G_{n}$ grupos, $G = G_{1} \times \dots \times G_{n}$ .

Por la observación 3: $G_{i}^{*} ⊴ G$ , para toda $i \in {1, \dots, n}$ .
La contención ${e_{G}} \subseteq G_{i}^{*} \cap (\prod_{j \neq i} G_{j}^{*})$ , donde $e_{G} = (e_{G_{1}}, \dots, e_{G_{n}})$ , es clara. Así que probaremos la otra.
Sea $g = (g_{1}, \dots, g_{n}) \in G_{i}^{*} \cap (\prod_{j \neq i} G_{j}^{*})$ .
Como $g \in G_{i}^{*} = {e_{G_{1}}} \times \dots \times G_{i} \times \dots \times {e_{G_{n}}}$ , entonces la $j$ -ésima entrada de $g$ es $g_{j} = e_{G_{j}}$ para toda $j \neq i$ .
Como $g \in \prod_{j \neq i} G_{j}^{*}$ , $g = h_{1} \dots h_{i - 1} h_{i + 1} \dots h_{n}$ con $h_{j} \in G_{j}^{*}$ para toda $j \neq i$ .
Dado que cada $h_{j} \in G_{j}^{*}$ y $j \neq i$ , la entrada $i$ de cada $h_{j}$ es $e_{G_{i}}$ , por lo tanto la entrada $i$ de $g$ es $e_{G_{i}}$ .
Por lo tanto $g = (e_{G_{1}}, \dots, e_{G_{n}}) = e_{G}$ .
Como $G_{i}^{*} \subseteq G$ para toda $i \in {1, \dots, n}$ , entonces $\prod_{i = 1}^{n} G_{i} \subseteq G .$
Ahora, si $g \in G$ ,
$\begin{array}{r} g = (g_{1}, \dots, g_{n}) = (g_{1}, e_{G_{2}}, \dots, e_{G_{n}}) (e_{G_{1}}, g_{2}, e_{G_{3}}, \dots, e_{G_{n}}) \dots (e_{G 1}, \dots, e_{G_{n - 1}}, g_{n}) . \end{array}$
Entonces $g \in \prod_{i = 1}^{n} G_{i}^{*} .$
Por lo tanto $G = \prod_{i = 1}^{n} G_{i}^{*}$ .

Lo anterior muestra que un producto directo externo es un producto de subgrupos normales que cumple el inciso 2 de la proposición.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra las observaciones 1, 2 y 4:
- ${inc}_{i}$ es un monomorfismo.
- $π_{i}$ es un epimorfismo.
- Sean $i \neq j$ , $x \in G_{i}^{*}$ , $y \in G_{j}^{*}$ . Entonces $x *_{n} y = y *_{n} x$ .
Sean $G_{1}, \dots, G_{n}$ grupos finitos, demuestra que el orden de su producto directo externo es $| G_{1} | | G_{2} | \dots | G_{n} | .$
Prueba que el centro de un producto externo es el producto externo de los centros, esto es: $Z (G_{1} \times G_{2} \times \dots \times G_{n}) = Z (G_{1}) \times Z (G_{2}) \times \dots \times Z (G_{n}) .$ Deduce que el producto directo externo de grupos abelianos es abeliano.
Sea $G = A_{1} \times A_{2} \dots \times A_{n}$ y para cada $i \in {1, \dots, n}$ sea $B_{i} ⊴ A_{i}$ . Prueba que $B_{1} \times B_{2} \times \dots \times B_{n} ⊴ G$ y que $(A_{1} \times A_{2} \dots \times A_{n}) / (B_{1} \times B_{2} \times \dots \times B_{n}) ≅ (A_{1} / B_{1}) \times (A_{2} / B_{2}) \times \dots \times (A_{n} / B_{n}) .$
Sean $A$ y $B$ dos grupos finitos y sea $p$ un primo.
- Prueba que cualquier $p$ -subgrupo de Sylow de $A \times B$ es de la forma $P \times Q$ , donde $P$ es un $p$ -subgrupo de Sylow de $A$ y $Q$ es un $p$ -subgrupo de Sylow de $B$ .
- Prueba que además, la cantidad de $p$ -subgrupos de Sylow de $A \times B$ es igual a la cantidad de $p$ -subgrupos de Sylow de $A$ por la cantidad de $p$ -subgrupos de Sylow de $B$ , es decir: $r_{p} (A \times B) = r_{p} (A) r_{p} (B) .$
- Generaliza este resultado para el producto directo externo de una cantidad finita de grupos, es decir, para $A_{1} \times A_{2} \times \dots \times A_{n}$ determina que sus $p$ -subgrupos de Sylow son el producto directo externo de $p$ -subgrupos de Sylow de sus factores.

Más adelante…

La última proposición es prácticamente la conclusión de esta entrada, porque iniciamos definiendo a $G$ como el producto de grupos externos a él y terminamos describiendo a $G$ como producto de subgrupos específicos de él mismo. ¿Habrá alguna manera de generalizar esto, es decir, cuándo un grupo $G$ se podrá expresar como un producto de subgrupos específicos de él mismo? Esta pregunta nos lleva a la definición del producto directo interno que se dará en la siguiente entrada.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Ejemplos de Sylow.
Siguiente entrada del curso: Producto directo interno.
Resto de cursos: Cursos.

Álgebra Moderna I: Ejemplo de Sylow

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Siendo la última entrada de la Unidad 4, está dedicada a un ejemplo que se justifica usando el Tercer Teorema de Sylow que vimos en la entrada anterior. Por lo mismo, es mucho más corta de lo que estamos acostumbrados, pero es importante para reforzar el conocimiento antes aprendido.

Ilustrando el TTS

Veamos un ejemplo del Tercer Teorema de Sylow.

Ejemplo.

Tomemos $G = S_{4}$ y veamos la factorización en primos del orden de $G$ , $| G | = 24 = 2^{3} \cdot 3$ .

Primero, consideremos al $3$ . Notamos que $⟨ (1 2 3) ⟩$ es un $3$ -subgrupo de Sylow ya que tiene $3$ elementos y no podemos encontrar subgrupos de Sylow de $9, 27$ u otra potencia de $3$ , porque esta no dividiría al orden de $G$ .

Ahora nos preguntamos ¿cuál es la cantidad de $3$ -subgrupos de Sylow, denotada por $r_{3}$ ? Bueno, por el Tercer Teorema de Sylow sabemos que se cumple:

$\begin{array}{r} r_{3} | 2^{3} \cdot 3 y r_{3} \equiv 1 (mód 3) . \end{array}$

Como $3 \equiv 0 (mód 3)$ , entonces $r_{3}$ no es un múltiplo de $3$ , así que $r_{3}$ tiene que ser un divisor de $2^{3} = 8$ congruente con uno módulo $3$ , por lo que $r_{3} \in {1, 4}$ .

Pero podemos encontrar $⟨ (2 3 4) ⟩$ , otro $3$ -subgrupo de Sylow diferente al anterior, así que $r_{3} = 4$ . Los otros $3$ -subgrupos de Sylow son $⟨ (1 3 4) ⟩$ y $⟨ (1 2 4) ⟩$ .

Ahora nos fijamos en el primo $2$ . Por el TTS, la cantidad de $2$ -subgrupos de Sylow ( $r_{2}$ ) tiene que cumplir,
$\begin{array}{r} r_{2} | 2^{3} \cdot 3 y r_{2} \equiv 1 (mód 2) . \end{array}$

La condición del módulo nos indica que $r_{2}$ es impar, por lo que tiene que ser divisor de $3$ para además se cumpla la primera condición, esto nos deja con $r_{2} \in {1, 3} .$

Busquemos estos $2$ -subgrupos de Sylow. Sabemos que cada $2$ -subgrupo de Sylow tiene orden igual a la máxima potencia de $2$ que divide a $| G |$ , esto es 8. Sabemos que si tenemos un cuadrado y numeramos los vértices, podemos codificar cada simetría del cuadrado con una permutación de $S_{4}$ . Recordemos que no toda permutación de $S_{4}$ es una simetría, pero sí al revés.

Las simetrías de un cuadrado son $8$ en total y estas simetrías pueden ser generadas por la combinación de una rotación y la reflexión con respecto al eje $x$ . Como hay $8$ simetrías del cuadrado y éstas pueden ser codificadas en permutaciones de $S_{4}$ , tendremos un subgrupo de $S_{4}$ de orden $8$ , es decir, un $2$ -subgrupo de Sylow.

Supongamos que numeramos los vértices de un cuadrado $1, 2, 3, 4$ como en la imagen, entonces la rotación estará dada por $(1 2 3 4)$ y la reflexión con respecto al eje $x$ sería $(2 4)$ . Así, el $2$ -subgrupo de Sylow que obtenemos es $⟨ (1 2 3 4), (2 4) ⟩$ .

Simetrías del cuadrado $1, 2, 3, 4$ usando $⟨ (1 2 3 4), (2 4) ⟩ .$

Estamos buscando todos los $2$ -subgrupos de Sylow posibles, como $r_{2} \in {1, 3}$ bien podíamos pensar que $⟨ (1 2 3 4), (2 4) ⟩$ es el único. Pero podemos nombrar los vértices del cuadrado de manera distinta para que las simetrías de $S_{4}$ que le correspondan cambien y encontremos otro $2$ -subgrupo de Sylow.

Numerando los vértices del cuadrado $2, 1, 3, 4$ como en la imagen, encontramos que la simetrías están generadas por la rotación $(2 1 3 4)$ y la reflexión $(1 4)$ . Así $⟨ (2 1 3 4), (1 4) ⟩$ es otro $2$ -subgrupo de Sylow.

Si nos damos cuenta, lo único que hicimos en este cuadrado fue intercambiar los vértices $1$ y $2$ del cuadrado. Esto nos da un subgrupo diferente al anterior porque ese cambio no es una simetría del cuadrado.

Simetrías del cuadrado $2, 1, 3, 4$ usando $⟨ (2 1 3 4), (1 4) ⟩ .$

Pero $r_{2} = 1$ o $r_{2} = 3$ , así que no puede haber sólo dos $2$ -subgrupos de Sylow, deben ser $3$ . Nos queda entonces otro $2$ -subgrupo de Sylow por encontrar. Análogamente, tomamos el cuadrado numerando los vértices $1, 3, 2, 4$ , donde sólo intercambiamos los vértices $3$ y $4$ del cuadrado original. En este caso nos encontramos que sus simetrías son generadas por $⟨ (1 3 2 4), (3 4) ⟩$ y este es el último $2$ -subgrupo de Sylow que nos faltaba.

Simetrías del cuadrado $1, 3, 2, 4$ usando $⟨ (1 3 2 4), (3 4) ⟩ .$

Así, encontramos todos los subgrupos de Sylow de $S_{4}$ .

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Considera el grupo de los cuaternios $Q_{8}$ , ¿cuántos y cuáles son sus $2$ -subgrupos de Sylow?
Busca los $2$ y $3$ -subgrupos de Sylow de $Z_{6} .$
Sean $a, b \in G := S_{3} \times Z_{4}$ , donde $a = ((1 2 3), [2])$ y $b = ((1 3), [1]) .$ Considere el subgrupo $T := ⟨ a, b ⟩ \leq G .$ Prueba que $T = ⟨ a, b : a^{6} = 1_{G}, b^{2} = a^{3} = (a b)^{2} ⟩$ y que $T$ es un grupo no abeliano con $12$ elementos.
La notación anterior se lee como $T$ es el generado por los elementos $a$ y $b$ tales que $a^{6} = 1_{G}, b^{2} = a^{3} = (a b)^{2}$ .

Más adelante…

Con esta entrada no sólo concluimos en tema de los Teoremas de Sylow, si no también la unidad 4 del curso. ¡Felicidades! Sigue avanzando, ya casi acabamos.

En la siguiente unidad planeamos estudiar el Teorema Fundamental de los Grupos abelianos finitos. Pero para ello comenzaremos viendo una forma sencilla de construir nuevos grupos a partir de una cantidad finita de grupos previos.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Teoremas de Sylow.
Siguiente entrada del curso: Producto directo externo.
Resto de cursos: Cursos.

Álgebra Moderna I: Teoremas de Sylow

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior definimos a los $p$ -subgrupos de Sylow de un grupo $G$ como un $p$ -subgrupo de $G$ tal que no estuviera contenido en otro $p$ -subgrupo de $G$ . En esta entrada estudiaremos los Teoremas de Sylow que hablan, como su nombre nos indica, de los $p$ -subgrupos de Sylow que definimos antes.

El primero trata sobre del orden de los $p$ -subgrupos de Sylow, que es la máxima potencia de $p$ que divide al orden del grupo $G$ . El segundo habla de la relación entre los $p$ -subgrupos de Sylow y establece que todo par de $p$ -subgrupos son conjugados. El tercero describe de modo aproximado la cantidad de $p$ -subgrupos de Sylow que hay en un grupo $G$ . No nos da un número exacto, pero nos da alguna información al respecto.

Ahora, prepárate para leer el nombre de Sylow aún más veces.

Primer Teorema de Sylow

Teorema (1er Teorema de Sylow). Sea $p \in Z^{+}$ un primo, $G$ un grupo finito con $| G | = p^{t} m$ , $t \in N^{+}, m \in N^{+}, p ⧸ | m .$ Entonces

para cada $i \in {1, \dots, t}$ , $G$ contiene un subgrupo de orden $p^{i}$ .
Todo subgrupo de $G$ de orden $p^{i}$ con $i \in {1, \dots, t - 1}$ es un subgrupo normal de algún subgrupo de $G$ de orden $p^{i + 1}$ .

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un grupo finito con $| G | = p^{t} m$ , $t, m \in N^{+}$ , $p ⧸ | m$ .

P.D. Para toda $i \in {1, \dots, t}$ existe $P_{i} \leq G$ con $| P_{i} | = p^{i}$ y de forma que $P_{i} ⊴ P_{i + 1}$ para toda $i \in {1, \dots, t - 1}$ .
De hecho, con esto quedarían probados los dos incisos del PTS (Primer Teorema de Syow).

Primero necesitamos un subgrupo de orden $p$ . Éste se tiene gracias al Teorema de Cauchy. Así, podemos afirmar que $G$ tiene un subgrupo de orden $p$ .
Ahora, si $i \in {1, \dots, t - 1}$ y $H$ es un subgrupo de orden $p^{i}$ veamos que podemos construir un subgrupo de $G$ de orden $p^{i + 1}$ tal que $H$ sea normal a él:

Sabemos que $p$ divide a $[G : H]$ y como $[G : H] \equiv [N_{G} (H) : H] (mód p)$ entonces
$\begin{array}{r} p divide a [N_{G} (H) : H] = | N_{G} (H) / H | . \end{array}$

Entonces por Cauchy, el grupo cociente $N_{G} (H) / H$ tiene un subgrupo de orden $p$ , y por el teorema de la correspondencia es de la forma $\tilde{H} / H$ con $H \leq \tilde{H} \leq N_{G} (H)$ . Así,

$\begin{aligned} p = | \tilde{H} / H | = \frac{| \tilde{H} |}{| H |} = \frac{\tilde{H}}{p^{i}} \\ \Rightarrow \frac{| \tilde{H} |}{p^{i}} = p \\ \Rightarrow | \tilde{H} | = p^{i + 1} \end{aligned}$
pero $H ⊴ N_{G} (H)$ por construcción del normalizador y $\tilde{H} \leq N_{G} (H)$ , entonces $H ⊴ \tilde{H} .$

Ilustración de por qué $H ⊴ \tilde{H}$ .

De esta manera, dado un subgrupo de orden $p^{i}$ podemos encontrar un subgrupo de orden $p^{i + 1}$ tal que el primero sea normal en el segundo. Entonces, considerando $P_{1}$ un subgrupo de $G$ de orden $p$ , existe $P_{2}$ un subgrupo de $G$ de orden $p^{2}$ tal que $P_{1} ⊴ P_{2}$ y a partir de $P_{2}$ podemos hallar $P_{3}$ un subgrupo de $G$ de orden $p^{3}$ tal que $P_{2} ⊴ P_{3}$ y así sucesivamente.

Concluimos entonces que existen $P_{1}, \dots, P_{t}$ subgrupos de $G$ con $| P_{i} | = p^{i}$ para toda $i \in {1, \dots, t}$ tales que $P_{1} ⊴ P_{2} ⊴ \dots ⊴ P_{t}$ .

En consecuencia, el PTS nos dice qué tamaño tienen los $p$ -subgrupos de Sylow, una incógnita que no habíamos resuelto. Esto se ilustra en el siguiente corolario.

Corolario. Sea $p \in Z^{+}$ un primo, $G$ un grupo finito con $| G | = p^{t} m$ , $t, m, \in N^{+}$ y $p ⧸ | m$ . Los $p$ -subgrupos de Sylow de $G$ tienen orden $p^{t}$ .

Segundo Teorema de Sylow

Antes de enunciar y probar el STS (Segundo Teorema de Sylow) vamos a dar una observación.

Observación. Los conjugados de un $p$ -subgrupo de Sylow son también $p$ -subgrupos de Sylow.

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un grupo finito, $| G | = p^{t} m$ con $t, m \in N^{+}$ , $p ⧸ | m .$

Al tomar $P$ un $p$ -subgrupo de Sylow de $G$ , por el corolario del PTS sabemos que $| P | = p^{t}$ .

Ahora, al conjugarlo mediante $g \in G$ se tiene que $g P g^{- 1} \leq G$ con $| g P g^{- 1} | = | P | = p^{t}$ . Así, $g P g^{- 1}$ es un $p$ -grupo y debido a que su orden es la máxima potencia de $p$ que divide a $| G |$ se tiene que es un $p$ -subgrupo de Sylow.

Esta observación nos dice que todos los conjugados de un $p$ -subgrupo de Sylow son igual un $p$ -subgrupo de Sylow, pero el STS va más allá y nos dice que conjugando $p$ -subgrupos de Sylow podemos encontrar todos los $p$ -subgrupos de Sylow de un grupo $G$ .

Teorema (2do Teorema de Sylow). Sean $p \in Z^{+}$ un primo, $G$ un grupo finito. Todos los $p$ -subgrupos de Sylow de $G$ son conjugados en $G$ .

Demostración.

Sea $p \in Z^{+}$ un primo, $G$ un grupo finito, $P$ y $Q p$ -subgrupos de Sylow de $G$ .

Sea $X = {g P | g \in G}$ . Para comenzar definimos $q \cdot (g P) = q g P$ para todas $q \in Q, g \in G .$ Ésta es una acción de $Q$ en $X$ . Como $Q$ es un $p$ -grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$ , Ecuación de Clase y $p$ -Grupo sabemos que
$\begin{array}{r} # X \equiv # X_{Q} (mód p) . \end{array}$

Como $p$ no divide a $[G : P]$ y $[G : P] = # X$ , entonces $p$ tampoco divide a $# X_{Q}$ . En particular $# X_{Q} \neq 0$ y así $X_{Q} \neq \emptyset$ .

Pero
$\begin{aligned} X_{Q} & = {g P | q \cdot (g P) = g P \forall q \in Q} \\ = {g P | q g P = g P \forall q \in Q} \\ = {g P | g^{- 1} q g \in P \forall q \in Q} \\ = {g P | g^{- 1} Q g \subseteq P} & porque es para toda q \in Q \\ = {g P | g^{- 1} Q g = P} . \end{aligned}$

donde la última igualdad se da porque $g^{- 1} Q g$ y $P$ son $p$ -subgrupos de Sylow y entonces tienen el mismo orden, la máxima potencia de $p$ que divide al orden de $G$ .

Así, ${g P | g^{- 1} Q g = P} \neq \emptyset$ y en consecuencia existe $g \in G$ tal que $g^{- 1} Q g = P$ .

Por lo tanto $P$ y $Q$ son conjugados en $G$ .

Tercer Teorema de Sylow

Teorema (3er Teorema de Sylow). Sea $p \in Z^{+}$ un primo, $G$ un grupo finito y $r_{p}$ el número de $p$ -subgrupos de Sylow de $G$ . Entonces

$r_{p} \equiv 1 (mód p)$ .
$r_{p}$ divide a $| G |$ .

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un grupo finito y $r_{p}$ el número de $p$ -subgrupos de Sylow de $G$ .

Sea $X = {P_{1}, \dots, P_{r_{p}}}$ la colección de todos los $p$ -subgrupos de Sylow de $G$ . Definimos $g \cdot P_{i} = g P_{i} g^{- 1}$ para todas $g \in P_{1}$ e $i \in {1, \dots, r_{p}}$ , que es una acción de $P_{1}$ en $X$ ya que $g P_{i} g^{- 1}$ es nuevamente un $p$ -subgrupo de Sylow por la observación previa. Como $P_{1}$ es un $p$ -grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$ , Ecuación de Clase y $p$ -Grupo sabemos que
$\begin{array}{r} # X \equiv # X_{P_{1}} (mód p) . \end{array}$
Pero por la construcción de $X$ , tenemos que $r_{p} = # X \equiv # X_{P_{1}} (mód p) .$
Ahora, veamos que $# X_{P_{1}} = 1$ y para ello analicemos quién es $X_{P_{1}}$
$\begin{aligned} X_{P_{1}} & = {P_{i} \in X | g \cdot P_{i} = P_{i} \forall g \in P_{1}} \\ = {P_{i} \in X | g P_{i} g^{- 1} = P_{i} \forall g \in P_{1}} . \end{aligned}$
Así, para toda $P_{i} \in X_{P_{1}}$ se tiene que $P_{1} \leq N_{G} (P_{i})$ y también $P_{i} \leq N_{G} (P_{i})$ .
Entonces $P_{1}$ y $P_{i}$ son $p$ -subgrupos de Sylow de $N_{G} (P_{i}) .$
Por el 2do Teorema de Sylow, $P_{1}$ y $P_{i}$ son conjugados en $N_{G} (P_{i})$ , es decir existe $g \in N_{G} (P_{i})$ tal que
$\begin{aligned} P_{1} & = g P_{i} g^{- 1} \\ = P_{i} & pues g \in N_{G} (P_{i}) . \end{aligned}$
Concluimos entonces que $P_{1}$ es el único elemento en $X_{P_{1}}$ y así $# X_{P_{1}} = 1$ . Por lo tanto $r_{p} \equiv 1 (mód p)$ .
Sea $X = {P_{1}, \dots, P_{r_{p}}}$ la colección de todos los $p$ -subgrupos de Sylow de $G$ .
Definimos $g \cdot P_{i} = g P_{i} g^{- 1}$ para todas $g \in G$ e $i \in {1, \dots, r_{p}}$ , que es una acción de $G$ en $X$ .
Por el segundo teorema de Sylow sabemos que $P_{1}, \dots, P_{r_{p}}$ son conjugados de $P_{1}$ , entonces $O (P_{1}) = {g \cdot P_{1} | g \in g} = {g P_{1} g^{- 1} | g \in g} = {P_{1}, \dots, P_{r_{p}}} = X$ es decir, la acción es transitiva.
Entonces obtenemos que $r_{p} = # O (P_{1})$ . Pero, sabemos que $# O (P_{1}) = [G : G_{P_{i}}] = \frac{| G |}{| G_{P_{i}} |}$
que es un divisor de $| G |$ . Por lo tanto $r_{p}$ es un divisor de $| G |$ .

Tarea moral

Demuestra el corolario del PTS: Sea $p \in Z^{+}$ un primo, $G$ un grupo finito con $| G | = p^{t} m$ con $t, m, \in N^{+}$ y $p ⧸ | m$ . Los $p$ -subgrupos de Sylow de $G$ tienen orden $p^{t}$ .
Sean $p \in Z^{+}$ un número primo, $G$ un grupo y $P$ un $p$ -subgrupo de Sylow de $G$ . Demuestra que $P$ es el único $p$ -subgrupo de Sylow de $G$ si y sólo si $P ⊴ G .$
Sea $p \in Z^{+}$ un número primo. Da un ejemplo de un grupo finito $G$ que tenga tres $p$ -subgrupos de Sylow $P$ , $Q$ y $R$ tales que $P \cap Q = {1}$ y $P \cap R \neq {1} .$
(Sugerencia: Considera $S_{3} \times S_{3} .$ )
Sean $p \in Z^{+}$ un número primo y $G$ un grupo finito. Considera $Q$ un $p$ -subgrupo de $G$ tal que $Q ⊴ G$ . Prueba que $Q \leq P$ para cada $p$ -sugrupo de Sylow $P$ de $G$ .
(Sugerencia: Usa el hecho de que cualquier otro $p$ -subgrupo de Sylow de $G$ es conjugado de $P$ .)
Sean $p \in Z^{+}$ un número primo y $G$ un grupo finito. Para cada primo $p$ divisor del orden de un grupo finito $G$ , escoge un $p$ -subgrupo de Sylow $Q_{p}$ . Prueba que $G = ⟨ ⋃_{p} Q_{p} ⟩ .$ (Sugerencia: Usa el orden de los subgrupos generados por los subgrupos de Sylow.)

Más adelante…

En esta entrada abarcamos los tres Teoremas de Sylow, se colocaron los tres en esta entrada para que fuera más fácil consultarlos. Sin embargo, esto hace a la entrada un poco larga, así que la siguiente estará dedicada a algunos ejemplos de la aplicación de estos teoremas.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: $p$ -Subgrupo de Sylow y el Normalizador de $H$ en $G$ .
Siguiente entrada del curso: Ejemplos de Sylow.
Resto de cursos: Cursos.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo del Autor: Cecilia del Carmen Villatoro Ramos

Álgebra Moderna I: Lemas previos al teorema fundamental de los grupos abelianos finitos.

Introducción

El orden de un elemento mínimo

$G$ como producto de $⟨ g ⟩$ y un subgrupo cualquiera

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Producto directo interno

Introducción

Producto directo interno de subgrupos

Descomposición de $G$ en $p$ -subgrupos

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Producto directo externo

Introducción

Hablemos del producto de grupos

Dos funciones naturales

¿Y si ahora recuperamos $G$ a partir de los $G_{i}^{*}$ ?

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Ejemplo de Sylow

Introducción

Ilustrando el TTS

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Teoremas de Sylow

Introducción

Primer Teorema de Sylow

Segundo Teorema de Sylow

Tercer Teorema de Sylow

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

El orden de un elemento mínimo

G como producto de ⟨g⟩ y un subgrupo cualquiera

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Producto directo interno de subgrupos

Descomposición de G en p-subgrupos

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Hablemos del producto de grupos

Dos funciones naturales

¿Y si ahora recuperamos G a partir de los Gi∗?

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Ilustrando el TTS

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Primer Teorema de Sylow

Segundo Teorema de Sylow

Tercer Teorema de Sylow

Tarea moral

Más adelante…

Entradas relacionadas

$G$ como producto de $⟨ g ⟩$ y un subgrupo cualquiera

Descomposición de $G$ en $p$ -subgrupos

¿Y si ahora recuperamos $G$ a partir de los $G_{i}^{*}$ ?