Archivo del Autor: Cecilia del Carmen Villatoro Ramos

Álgebra Moderna I: Definición de Grupos

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Ahora sí, comenzaremos con el tema de este curso. Después de estudiar las operaciones binarias por fin veremos para qué nos sirven. Los grupos son una estructura algebraica. Están constituidos por dos partes, un conjunto y una operación ¿Puedes imaginarte de qué tipo de operación estamos hablando?

Para motivarlo, veamos cómo resolvemos esta ecuación:

\begin{align*}
x+8 & = 5\\
(x + 8) + (-8) &= 5 + (-8)\\
x + 0 &= -3\\
x &= -3
\end{align*}

Al resolver la ecuación, formalmente estamos usando las siguientes propiedades:

  • Asociatividad
  • Inverso aditivo
  • Neutro

En ese mismo orden.

En esta entrada definiremos formalmente a los grupos y daremos muchos ejemplos para que te empapes de la definición. Revisaremos los ejemplos que vimos en entradas anteriores y determinaremos cuáles son un grupo y cuáles no.

¿Qué es un grupo?

Definición. Sea $G$ un conjunto con una operación binaria $*$. Decimos que $(G,*)$ es un grupo si

  1. La operación $*$ es asociativa, es decir, $(a * b)*c = a*(b*c) \quad \forall a,b,c \in G$
  2. Existe $e \in G$ tal que $e*a = a*e = a \quad \forall a \in G$.
    A $e$ se le llama neutro en $G$.
  3. Para toda $a \in G$ existe $\tilde{a} \in G$ tal que $a*\tilde{a} = \tilde{a}*a=e$.
    En este caso, $\tilde{a}$ se llama inverso de a.

Si además * es conmutativa, es decir $a*b = b*a \quad \forall a,b \in G$, decimos que $(G,*)$ es un grupo abeliano.

Nota. Sea $G$ conjunto con una operación binaria $*$:

  • Si $G \neq \emptyset$, $(G,*)$ se llama magma.
  • Si $G\neq \emptyset$ y se cumple 1, $(G,*)$ se llama semigrupo.
  • Si se cumplen 1 y 2, $(G,*)$ se llama monoide.

Repaso de ejemplos anteriores

Veamos de nuevo algunos ejemplos de las entradas anteriores y comprobemos si cumplen con la definición de grupo.

  • $G : = \z^+$, $a*b = \text{máx}\{a,b\}$.
    • En la entrada anterior vimos que $*$ es asociativa y conmutativa.
    • $1$ es el neutro.
      Demostración. $1*a = a*1 = \text{máx}\{1,a\} = a \quad \forall a \in \z^+$. $\blacksquare$
    • $2$ no tiene inverso.
      Demostración. $2*a = \text{máx}\{2,a\} \geq 2 \quad \forall a \in \z^+$, por lo que $2 * a \neq 1 \quad a \in \z^+$.

$\therefore (\z^+,*)$ NO es un grupo. $\blacksquare$

  • $G:= \z^+$, $a*b = a$.
    • No tiene neutro, si existiera $e \in \z^+$ neutro, entonces para toda $a\in\z^+$, por la definción de la operación $e*a = e$, pero la definición de neutro requiere que $e*a = a$. Entonces, esto implica que $e = a$ y como esto no es necesariamente cierto, pues $a$ es un entero positivo cualquiera, obtenemos una contradicción.

$\therefore (\z^+,*)$ NO es un grupo. $\blacksquare$

  • $(\cM_{2\times 2}(\z), +)$ es un grupo abeliano, la demostración queda como ejercicio.
  • $(\{ f \; | \; f:\r \to \r\}, \circ)$ no es un grupo, pues aunque $\mathrm{id}_{\r}$ es neutro, no todo elemento tiene inverso, como se ve en Álgebra Superior I.
  • $(S_3, \circ)$ es un grupo no abeliano. Generalizaremos este ejemplo más adelante y le llameremos grupo simétrico.
  • $\cS = \{2,4,6\}$ con la operación
$*$$2$$4$$6$
$2$$2$$4$$6$
$4$$4$$4$$6$
$6$$6$$6$$6$

Si observamos la tabla, podemos concluir que:

  • $2$ es neutro.
  • $4$ y $6$ no tienen inversos.

Por lo tanto, NO es un grupo.

$\blacksquare$

  • $\cS = \{2,4,6\}$ con la operación
$*$$2$$4$$6$
$2$$2$$2$$2$
$4$$4$$4$$4$
$6$$6$$6$$6$
  • No hay un neutro.

Como no hay neutro, ni siquiera tiene sentido pensar en la existencia de inversos. Por lo tanto, NO es un grupo.

$\blacksquare$

  • $\cS = \{1,-1\}$
$*$$1$$-1$
$1$$1$$-1$
$-1$$-1$$1$
  • El $1$ es el neutro.
  • La operación es asociativa.
  • $1$, $-1$ son sus propios inversos.
  • Además, la operación conmuta, porque la operación es el producto usual.

Por lo tanto es un grupo abeliano.

$\blacksquare$

  • $(\z, +)$ es un grupo.
  • Sea $K$ un campo y $K^* = K \setminus \{0_K\}$. Si consideramos $(K^*, \cdot)$ tenemos un grupo abeliano. Le quitamos el $0_K$ pues es el único número que no tiene inverso multiplicativo.
  • $\mathbb{S}’ = \{z \in \mathbb{C} \; |\; |z|= 1\}$. Es decir, los complejos con norma igual a $1$. Es un grupo abeliano con el producto.
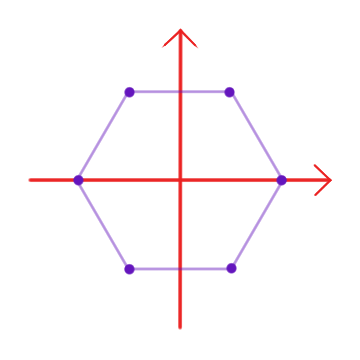
Representación geométrica del conjunto.
  • Dentro de los complejos podemos considerar $$\Gamma_n = \left\{ \xi^k \; | \; 0 \leq k < n \right\},$$ con $\xi = e^{\frac{2\pi i}{n}}$. Geométricamente corresponden a los vértices de un polígono regular de $n$ lados y algebraicamente son las raíces $n$-ésimas de la unidad. Forman un grupo abeliano con el producto.
Representación geográfica del conjunto cuando $n= 6$.

Ejemplos importantes de matrices

Los siguientes son ejemplos de algunos grupos importantes. Recuérdalos porque son ejemplos que serán recurrentes en futuras entradas. Recuerda que no todas las matrices tienen inverso multiplicativo y que el producto de matrices no es conmutativo. Para refrescar tu memoria, puedes consultar las entradas de matrices inversas y operación de matrices.

  1. $$GL(n,\r) = \{A \in \cM_{n\times n}(\r) \;|\; \det A \neq 0\},$$ con el producto usual es un grupo no abeliano. Este par ordenado $(GL(n,r), \cdot)$ es conocido como el grupo lineal general.
  2. $$SL(n,\r) = \{A \in \cM_{n\times n}(\r) \;|\; \det A = 1\},$$ con el producto usual es un grupo no abeliano. Este es el grupo lineal especial.
  3. $$SO(n,\r) = \{A \in \cM_{n\times n}(\r) \; | \; AA^t = I_n, \; \det A = 1\},$$ con el producto usual es un grupo no abeliano. A éste se le conoce como grupo ortogonal especial.
  4. $$O(n, \r) = \{A \in \cM_{n\times n}(\r) \; |\; AA^t = I_n\},$$ con el producto usual es un grupo no abeliano. Este es conocido como el grupo ortogonal.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Determina, en cada uno de los siguientes casos, si el sistema descrito es grupo o no. En caso negativo, señala cuál o cuáles de los axiomas de grupo no se verifican. En caso afirmativo demuestra que es un grupo:
    • $G = \r \setminus \{-1\}$, $a*b := a+b+ab$.
    • $G = \r^*$, $a*b = |a|b$.
    • $G = \{r \in \mathbb{Q} \;|r\text{ se puede expresar como }\; r = \frac{p}{q} \text{ con } (p,q)= 1 \text{ y } q \text{ impar}\}$, $a*b = a+b$ (la adición usual).
    • Sea $X$ un conjunto. Considera $G = \mathcal{P}(X)$ el conjunto potencia de $X$ con la operación binaria $A \triangle B = (A \cup B)\setminus (A \cap B)$ para todo $A,B \in \mathcal{P}(X)$.
  2. Demuestra la siguientes afirmaciones referentes a grupos, dadas en los ejemplos anteriores:
    • $(\cM_{2\times 2}(\z), +)$ es un grupo abeliano.
    • $(S_3, \circ)$ es un grupo no abeliano.
    • $(\z, +)$ es un grupo.
    • $(K^*, \cdot)$ con $K$ un campo, es un grupo abeliano.
    • $(\Gamma_n, \cdot)$ es un grupo abeliano, con $\cdot$ el producto.
  3. Demuestrá por qué los ejemplos importantes de matrices son grupos no abelianos.

Más adelante…

Después de tantas definiciones y ejemplos, comenzaremos a ver más teoremas y demostraciones. En la siguiente entrada profundizaremos en las propiedades de grupos derivadas de su definición. Además, veremos un teorema conocido como la «Definición débil de Grupo».

Entradas relacionadas

Álgebra Moderna I: Operación binaria asociativa y conmutativa

Por Cecilia del Carmen Villatoro Ramos

3 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior definimos el concepto de operación binaria, en esta entrada veremos dos tipos más específicos de operaciones binarias: las operaciones binarias asociativas y las operaciones conmutativas. Éstas nos interesan ya que hacen que las operaciones sean más sencillas de manejar.

Nuevas definiciones

Definición. Una operación binaria $*$ en un conjunto $\mathcal{S}$ es asociativa si, para todos $a, b, c \in \mathcal{S}$

$(a*b)*c = a*(b*c)$.

Definición. Una operación binaria $*$ en un conjunto $\mathcal{S}$ es conmutativa si, para todos $a,b \in \mathcal{S}$

$a*b=b*a$.

Ejemplos de operaciones binarias asociativas y conmutativas

Repasemos los ejemplos vistos en la entrada anterior. Ahora los analizaremos con mayor profundidad.

  • Consideremos $\mathcal{S} := \mathbb{R}$ con la operación $a*b=ab-2$. Entonces $*$ no es asociativa.

Demostración. Sean $a,b,c \in \mathbb{R}$.

Si sustituimos los valores de acuerdo a la forma en que está definida $*$, por un lado obtenemos

$\begin{align}(a * b)*c = (ab-2)c -2 = (ab)c -2c-2\end{align}$

y por otro,

$\begin{align}a*(b*c) = a*(bc -2) = a(bc-2)-2 = a(bc)-2a-2. \end{align}$

Observamos que $(1)$ y $(2)$ en general son distintos. Por lo tanto $*$ no es asociativa.

Ejemplo. Si hacemos la operación con $1, 2, 3$ obtenemos:

$(1*2)*3 = 0 * 3 = -2$

$1*(2*3)= 1 *4 = +2$

Así, claramente no es asociativa.

$\blacksquare$

Sin embargo, sí es conmutativa.

Demostración. Por la conmutatividad de la multiplicación de reales,

$a*b = ab-2 = ba-2 = b*a \qquad \forall a,b \in \mathbb{R}$.

$\blacksquare$

  • Consideremos ahora el conjunto $\mathcal{S} := \mathbb{R}^+$ (los reales positivos), con la operación $a*b=\frac{a}{b}$. Entonces $*$ no es asociativa.

Demostración. Sean $a,b,c \in \mathbb{R}^+$.

Si sustituimos de acuerdo a la definición de nuestra operación binaria, obtenemos

$(a*b)*c = \frac{a}{b}*c =\frac{\frac{a}{b}}{c} = \frac{a}{bc}$

por otro lado,

$a*(b*c)= a* \frac{b}{c} = \frac{a}{\frac{b}{c}} = \frac{ac}{b}$.

En general, $(a*b)*c \neq a*(b*c)$, por lo que esta operación binaria no es asociativa.

$\blacksquare$

Ejemplo. Tomemos $3,4$ y $5$:

$(3*4)*5 = \frac{3}{4} * 5 = \frac{\frac{3}{4}}{5} = \frac{3}{20}$.

$3*(4*5) = 3* \frac{4}{5} = \frac{3}{\frac{4}{5}} = \frac{15}{4}$.

Claramente, $$\frac{3}{20} \neq \frac{15}{4}.$$

$\blacksquare$

Esta operación tampoco es conmutativa.

Demostración. Sean $a,b \in \mathbb{R}^+$.

Sustituyendo nuestra definición, en general tenemos que,

$a*b = \frac{a}{b} \neq \frac{b}{a} = b*a$.

Por lo tanto, nuestra operación binaria no es conmutativa.

$\blacksquare$

Ejemplo. Un ejemplo sencillo y claro,

$1*2 = \frac{1}{2} \neq 2 = 2*1$.

$\blacksquare$

  • En $\mathcal{S} := \mathbb{Z}^+$, $a*b = \text{máx} \{a,b\}$ es asociativa y conmutativa.
  • En $\mathcal{S} := \mathbb{Z}^+$, $a*b = a$ es asociativa y no conmutativa.
  • En $\mathcal{S} := \mathcal{M}_{2\times 2}(\mathbb{Z})$, $A*B = A + B$ es asociativa y conmutativa.
  • En $\mathcal{S}:= \{f \; | \; f: \mathbb{R} \to \mathbb{R} \}$, $f*g := f\circ g$ es asociativa pero no conmutativa.
  • En $\mathcal{S}:= S_3$, $f*g = f\circ g$. Es asociativa pero no conmutativa.

Ejemplo con tablas

En esta sección analizaremos algunas operaciones binarias definidas con tablas. El hecho de que una función sea conmutativa se ve reflejado en la tabla. Cuando la operación es conmutativa, si nos fijamos en la línea diagonal que divide a la tabla (la diagonal principal), podemos observar que la tabla es simétrica con respecto a la diagonal.

Demostrar la asociatividad a partir de la tabla es un poco más complicado. Se tendrían que escoger todas las distintas combinaciones de tres elementos del conjunto, lo que lo haría muy largo, incluso para conjuntos pequeños. Por eso conviene definir la operación de otra manera. En los siguientes ejemplos encontrarás la función definida de ambas maneras, con la tabla y con una regla de correspondencia.

  • En $\mathcal{S} = \{2,4,6\}$, la operación $a*b = \text{máx}\{a,b\}$ se vería como
$*$$2$$4$$6$
$2$$2$$4$$6$
$4$$4$$4$$6$
$6$$6$$6$$6$

La tabla es simétrica con respecto a la diagonal principal, por lo tanto esta operación sí es conmutativa. Queda como ejercicio demostrar que es asociativa.

  • En $\mathcal{S} = \{2,4,6\}$, la operación $a*b = a$ se vería como
$*$$2$$4$$6$
$2$$2$$2$$2$
$4$$4$$4$$4$
$6$$6$$6$$6$

De la misma manera, si nos fijamos en la diagonal principal, observamos que esta operación no es conmutativa. Pero, será tu trabajo demostrar que sí es asociativa.

  • En $\mathcal{S} = \{1, -1\}$, la operación $a*b = ab$ se vería como
$*$$1$$-1$
$1$$1$$-1$
$-1$$-1$$1$

A diferencia de los anteriores dos ejemplos, esta operación sí es conmutativa y también asociativa.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra o da contraejemplos de las propiedades (conmutatividad y asociatividad) que quedaron pendientes en los ejemplos.
  2. Con ayuda de las tablas, verifica las propiedades de conmutatividad y asociatividad que quedaron pendientes en los ejemplos correspondientes.
  3. Para el conjunto $\mathcal{S}:= \{\bigstar, \blacktriangledown, \blacklozenge, \clubsuit \}$, define
    • una operacion binaria conmutativa (pero no asociativa),
    • una operación asociativa (pero no conmutativa),
    • una operación asociativa y conmutativa,
    • una operación que no sea ni asociativa ni conmutativa.
  4. De los ejemplos que hiciste en la tarea moral anterior, determina si son conmutativas, asociativas o ambas.
  5. Del ejercicio 5 de la tarea moral anterior, determina si las operaciones binarias son conmutativas, asociativas, ambas o ninguna de las dos.

Más adelante…

Ahora sí, ya estás listo para que comencemos con los grupos. En la siguiente entrada comenzaremos a definirlos y a dar algunos ejemplos. Verás que las operaciones binarias tienen un papel importante a la hora de definir esta estructura algebraica.

Entradas relacionadas

Álgebra Moderna I: Operación binaria

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Bienvenido al curso de Álgebra Moderna I. Antes de comenzar de lleno con el tema principal del curso, los grupos, es necesario sentar ciertas bases, así que en esta primera entrada comenzaremos con la definición de una operación binaria.

El objetivo de una operación binaria, como dice su nombre, es tomar dos elementos de un conjunto, operarlos y obtener un resultado que también pertenezca al mismo. La suma (+) y la multiplicación (•) de números reales son operaciones binarias que conocemos desde hace tiempo. Además de ellas, veremos ejemplos de varias operaciones binarias definidas en diversos conjuntos, no sólo en los reales.

¿Qué es una Operación Binaria?

Como mencionamos en la introducción, la operación binaria es una función que toma dos elementos de un conjunto y devuelve un elemento del mismo. Formalmente escrito, quedaría de la siguiente manera:

Definición. Una operación binaria en un conjunto $\mathcal{S}$ es una función $\mu : \mathcal{S} \times \mathcal{S} \to \mathcal{S}$, es decir una forma de asignar a cada par ordenado $(a,b) \in \mathcal{S} \times \mathcal{S}$ un elemento $\mu (a,b) \in \mathcal{S}$.

Sin embargo, normalmente no trabajamos la notación de función. Así que hacemos la siguiente aclaración:

Notación. Nuestra operación binaria $\mu$ será denotada por $*$ y al elemento asignado a la pareja $(a,b)$. En lugar de ser denotado por $\mu (a,b)$ será denotado por $a*b$, más adelante será denotada simplemente por $ab$ o por $a+b$.

Además, necesitamos las siguientes observaciones para que nuestra función sea una operación binaria:

Observación 1. A cada par de elementos en $\mathcal{S}$ se le asigna exactamente un elemento de $\mathcal{S}$, es decir, $*$ es una función bien definida.

Observación 2. Para cada par de elementos en $\mathcal{S}$ el elemento debe estar en $\mathcal{S}$, es decir, $*$ es una operación cerrada en $\mathcal{S}$.

Ejemplos de operaciones binarias

Para ilustrar los ejemplos, tomaremos el símbolo $:=$ como una asignación de valor, y lo usaremos para definir y al símbolo $=$ como la igualdad usual, que indica eso, una igualdad entre dos valores.

  1. En $\mathcal{S} := \mathbb{R}$, podemos definir la siguiente operación binaria, $a*b := ab – 2$, es decir, la multiplicación de ambos números, menos dos unidades.
  2. En $\mathcal{S} := \mathbb{R}^+$, observemos que es posible tomar la operación $a*b := \frac{a}{b}$ como la división usual. Es importante considerar el conjunto $\mathcal{S}$ en el que estamos trabajando. Por ejemplo, esta operación no se podría considerar en $\mathbb{Z}^+$ porque no podemos asegurar que siempre nos dé un entero, por lo tanto no sería una operación binaria.
  3. Ahora, si tomamos $\mathcal{S} := \mathbb{Z}^+$ y definimos $a*b := \text{máx}{\{a,b\}}$, es decir, una operación binaria no tiene que ser siempre aritmética.
  4. En $\mathcal{S} := \mathbb{Z}^+$, podemos definir $a*b = a$, es decir, la operación asigna a cada par de números el primero de los dos.
  5. También podemos trabajar con matrices, por ejemplo $\mathcal{S} := \mathcal{M}_{2\times2}(\mathbb{Z})$ (el conjunto de matrices $2\times 2$ con entradas enteras), definida como $A*B := A + B$, es decir, la suma de matrices.
  6. Si pensamos en funciones, podemos considerar $\mathcal{S}:=\{f \;| f:\mathbb{R} \to \mathbb{R}\}$ y definir la composición de funciones, $f*g:= f\circ g$. Como todas las funciones comparten dominio y codominio, tiene sentido componer. Recordemos que esa notación se lee de derecha a izquierda, es decir, primero se aplica $g$ y luego $f$.
  7. En $\mathcal{S}:= S_3$, con $S_3 := \{f | f: \{1,2,3\} \to \{1,2,3\}, f \text{ es biyectiva}\}$, también podemos considerar $f*g := f\circ g$ y sería una operación binaria en el conjunto.

Para este último ejemplo, recordemos que como el dominio de $f$ es finito podemos denotar a $f$ como una matriz de la forma,

$f = \begin{pmatrix} 1 & 2 & 3\\ f(1) & f(2) & f(3) \end{pmatrix}.$

Ejemplo:

Si $f = \begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}$ y $g = \begin{pmatrix} 1 & 2 & 3\\ 3 & 1 & 2 \end{pmatrix}$, entonces la composición $f \circ g = \begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}$. Puesto que $g$ manda el $1$ al $3$ y $f$ manda el $3$ al $1$, $g$ manda el $2$ al $1$ y $f$ manda el $1$ al $2$ y $g$ manda el $3$ al $2$ y $f$ manda el $2$ al $3$.

$\blacksquare$

De modo más general, si $f$ es una función cuyo dominio es un conjunto finito con $n$ elementos $a_1,a_2,\dots, a_n,$ la regla de correspondencia de $f$ se puede describir con el arreglo

$f = \begin{pmatrix} a_1 & a_2 & \dots & a_n\\ f(a_1) & f(a_2)&\dots & f(a_n) \end{pmatrix}.$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Como calentamiento, piensa por qué ocurren las dos observaciones dadas.
  2. Investiga cómo se pueden definir operaciones binarias con tablas.
  3. De los ejemplos dados, busca conjuntos en donde la operación binaria deje de serlo por no cumplir con la cerradura.
  4. Da cinco ejemplos de conjuntos y operaciones binarias sobre ellos.
  5. Determina si las siguientes operaciones son binarias o no y en caso de no serlo, ¿qué le cambiarías al conjunto para que lo sea?
    • En $\mathcal{S} = \mathbb{R}^+$, $a*b = ab-2$.
    • En $\mathcal{S} = \mathcal{M}_{2\times2}(\mathbb{Z})$, $A*B = A^{-1}B$.
    • En $\mathcal{S} = \mathbb{Z}\setminus \{-1\}$, $a*b = 1 + ab$.
    • En $\mathcal{S} = \mathbb{Z}_5$, $a*b = ab(\text{mód } 7)$.

Más adelante…

Con el fin de trabajar con operaciones que sean más manejables, continuaremos expandiendo nuestro concepto de operación binaria agregándole las propiedades de conmutatividad y asociatividad.

Entradas relacionadas