Introducción
En la entrada anterior, nos dedicamos a buscar una definición apropiada para la suma de números naturales, y después nos dedicamos a probar las propiedades más elementales que esta operación satisface.
Ahora es el turno de la multiplicación o producto, que se definirá de forma similar a la suma, ya que ocuparemos el teorema de Recursión Débil, y para probar sus propiedades ocuparemos el principio de Inducción.
Te motivamos a releer la entrada anterior y pensar unos momentos en el ejercicio 5 de la entrada anterior.
Definición del producto
Así como con la suma, recurriremos a una definición recursiva, la cual existe en virtud del teorema de Recursión.
Definición. Sea $m\in\mathbb{N}$, defnimos la función $p_{m}:\mathbb{N}\longrightarrow\mathbb{N}$, como la función que satisface las propiedades siguientes:
- $p_{m}(0)=0$.
- $p_{m}(\sigma(n))=s_{m}((p_{m}(n))$.
Denotaremos a $p_{m}(n)$ como $m\cdot n$, o simplemente como $mn$
Ejemplo. Para aclarar la definición anterior, consideremos $p_{7}$ y realicemos el diagrama conmutativo correspondiente a su definición recursiva.
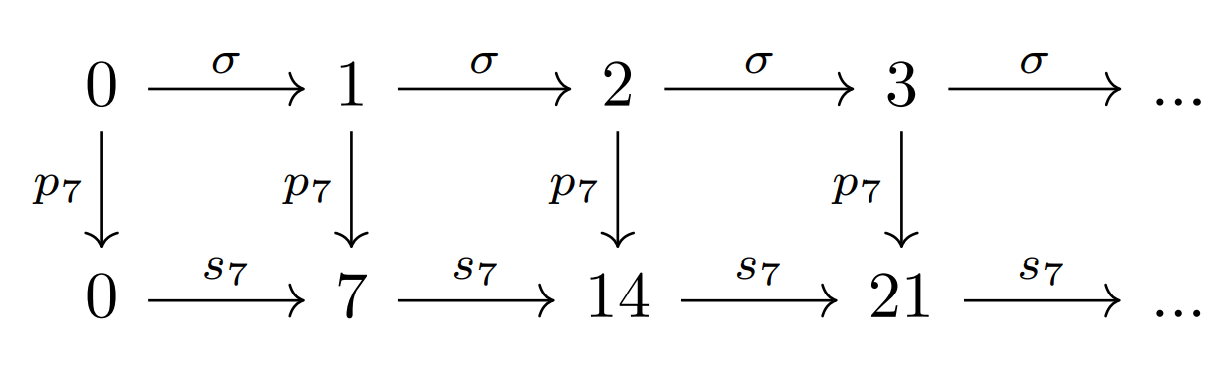
Recordemos que las flechas indican a donde es mandado cada elemento bajo cada función, entonces las flechas verticales, justamente son las que nos indican los valores de $p_{7}$ en cada número natural, observemos que estos valores coinciden con la conocida tabla del $7$.
$\triangle$
Aprendiendo a multiplicar por uno
En este momento, demostraremos las propiedades más importantes del producto. Tenemos la fortuna de que contamos con una buena cantidad de propiedades de las funciones $s_{n}$, las cuales ya podremos usar sin ningún problema, más aún, para simplificar la notación haremos uso de la notación $m+n$, en vez de la notación $s_{m}(n)$, cada vez que se pueda.
Siguiendo la idea anterior, mencionamos la siguiente identidad, que es solo una reformulación del punto (2) de la definición del producto, pero que nos servirá para esclarecer la mayor parte de las pruebas.
Observación. $a\cdot\sigma(n)=a+(a\cdot n)$.
Para referir a esta observación en una demostración ocuparemos el símbolo $\overset{*}{=}$.
Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{1}(n)=n$, es decir, $1\cdot n=n$
Demostración. Como se esperaba, la prueba es por inducción sobre $n$.
Base inductiva: Por la definición de $p_{1}$, tenemos que $p_{1}(0)=0$.
Hipótesis de inducción: Supongamos que para algún $n$, se tiene que $p_{1}(n)=n$
Paso inductivo: Debemos demostrar que $p_{1}(\sigma(n))=\sigma(n)$, esto se sigue por las siguientes igualdades
\begin{align*}
p_{1}(\sigma(n))&\overset{*}{=}1+(p_{1}(n))\\ &\overset{\text{H.I.}}{=}1+n=\sigma(n).
\end{align*}
Donde la última igualdad se da recordando que en la entrada anterior probamos que $s_{1}(n)=\sigma(n)$.
$\square$
Con esto hemos aprendido a multiplicar por $1$.
Aprendiendo a multiplicar por cero
Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{0}(n)=0$.
Demostración. Procedamos por inducción sobre $n$, la base inductiva es directa de la definición, ya que $p_{0}(0)=0$.
Nuestra hipótesis de inducción consiste en suponer que para alguna $n$ se tiene que $p_{0}(n)=0$. Entonces queda demostrar que $p_{0}(\sigma(n))=0$. Esto se sigue de las siguientes igualdades.
\begin{align*}
p_{0}(\sigma(n))&\overset{*}{=}0+p_{0}(n)\\ &\overset{\text{H.I.}}{=}0+0=0
\end{align*}
$\square$
La propiedad distributiva izquierda
La siguiente propiedad es una de las más famosas, ya que nos permitirá relacionar la suma y el producto, además jugará un papel importante en la demostración de las siguientes propiedades.
Proposición (propiedad distributiva izquierda). Si $a,b,n$ son números naturales, entonces $p_{s_{a}(b)}(n)=s_{p_{a}(n)}(p_{b}(n))$, u ocupando la notación familiar $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.
Demostración. Procedamos por inducción, como podrás notar con todas estas demostraciones, la inducción será sobre la variable que aparezca más a la derecha de nuestras expresiones, es decir, la inducción será sobre $n$.
Base inductiva: Por la definición del producto tenemos que, $(a+b)\cdot 0=0$, y por las propiedades que demostramos para la suma, concluimos que $0=0+0$, sin embargo; de nuevo por la definición del producto, $0=(a\cdot n)$ y $0=(b\cdot n)$, uniendo todas estas igualdades concluimos que $(a+b)\cdot 0=(a\cdot n)+(b\cdot n)$, justo como queremos.
Hipótesis de inducción: Supongamos que para algún $n$ se tiene que $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.
Paso inductivo: Debemos probar que $(a+b)\cdot\sigma(n)=(a\cdot\sigma(n))+(b\cdot\sigma(n))$. Por la observación que hicimos, tenemos
\begin{align*}
(a+b)\cdot\sigma(n)&\overset{*}{=}(a+b)+((a+b)\cdot n)\\ &\overset{\text{H.I.}}{=}(a+b)+((a\cdot n)+(b\cdot n))
\end{align*}
A partir de aquí, el resultado se seguirá usando la asociatividad y la conmutatividad de la suma, en la siguiente cadena de igualades detallamos la demostración paso a paso ¿Puedes identificar cómo ocupamos las propiedades de la suma?.
\begin{align*}
(a+b)+((a\cdot n)+(b\cdot n))&=a+(b+((a\cdot n)+(b\cdot n)))\\
&=a+((b+(a\cdot n))+(b\cdot n))\\
&=a+(((a\cdot n)+b)+(b\cdot n))\\
&=a+((a\cdot n)+(b+(b\cdot n)))\\
&=(a+(a\cdot n))+(b+(b\cdot n))\\
&\overset{*}{=}(a\cdot \sigma (n))+(b\cdot \sigma (n))
\end{align*}
$\square$
Aunque la prueba anterior fue un poco más confusa que las anteriores, las consecuencias que tendrá esta proposición serán sumamente importantes.
El producto es conmutativo
Como mencionamos, la asociatividad y la conmutatividad, serán una consecuencia de las propiedades distributivas, por el momento veamos que en efecto el producto conmuta.
Proposición (conmutatividad). Si $m,n\in \mathbb{N}$, entonces $m\cdot n=n\cdot m$.
Demostración. Una vez más hagamos la prueba por inducción sobre $n$
Base inductiva: Por definición tenemos que $m\cdot 0 =0$, además $p_{0}(m)=0$ por lo demostrado antes, es decir que $m\cdot 0=0=0\cdot m$
Hipótesis de inducción: Supongamos que para alguna $n$, se tiene que $m\cdot n=n\cdot m$.
Paso inductivo: Debemos probar que $m\cdot\sigma(n)=\sigma(n)\cdot m$. Esto se sigue ya que
\begin{align*}
m\cdot\sigma(n)&\overset{*}{=}m+(m\cdot n)\\
&\overset{\text{H.I.}}{=}m+(n\cdot m)
\end{align*}
Pero ya demostramos que $m=1\cdot m$, usando esto y la propiedad ditributiva, podemos concluir que
\begin{align*}
m+(n\cdot m)&=(1\cdot m )+(n\cdot m)\\
&=(1+n)\cdot m=\sigma(n)\cdot m
\end{align*}
$\square$
Con la conmutatividad, podemos probar de manera inmediata el siguiente resultado
Corolario (propiedad distributiva derecha). Si $a,b,n$ son números naturales, entonces $a\cdot(b+ n)=(a\cdot b)+(a\cdot n)$.
La prueba queda como un ejercicio moral, en parte porque su prueba no requiere Inducción. Con este resultado, podemos probar la propiedad asociativa del producto.
El producto es asociativo
Con la propiedad distributiva derecha , podemos dar la demostración de la propiedad asociativa del producto.
Proposición (asociatividad). Si $a,b,n$ son números naturales, se tiene que $a\cdot(b\cdot n)=(a\cdot b)\cdot n$.
Demostración. De nuevo procedamos por inducción sobre $n$
Base inductiva: Notemos que por definición, para cualquier número natural $m$ se tiene que $0=p_{m}(0)=m\cdot 0$. Con esto en mente tenemos que, $(a\cdot b)\cdot(0)=0=a\cdot 0=a\cdot(b\cdot 0)$ que es justo la base de inducción.
Hipótesis de Inducción: Supongamos que para alguna $n\in \mathbb{N}$, tenemos que $(a\cdot b)\cdot n=a\cdot(b\cdot n)$
Paso Inductivo: Demostremos que $(a\cdot b)\cdot\sigma(n)=a\cdot(b\cdot \sigma(n))$. Como
\begin{align*}
(a\cdot b)\cdot\sigma(n)&\overset{*}{=}(a\cdot b)+(a\cdot b)\cdot n\\
&\overset{\text{H.I.}}{=}(a\cdot{b})+a\cdot(b\cdot n)\\
&=a\cdot (b+b\cdot n)\\
&\overset{*}{=}a\cdot(b\cdot \sigma (n))
\end{align*}
la igualdad que no está justificada es la aplicación de la propiedad distributiva.
$\square$
Ley de la cancelación
Para concluir con las propiedades del producto, enunciamos la propiedad de la cancelación del producto, recordemos que esta propiedad también es válida para la suma. Para hacer esta prueba necesitamos trabajar un poco.
Recordemos el ejercicio 2 de la Tarea moral de la entrada Principio de inducción y teoremas de recursión, el cual ya hemos ocupado anteriormente:
Si $n\neq0$, entonces existe $a\in \mathbb{N}$ tal que $n=\sigma(a)$
De la misma forma, el ejercicio 1 de la Tarea moral de la entrada pasada dice que:
Si $a,b\in\mathbb{N}$ son tales que $a+b=0$, entonces $a=b=0$
Con estos resultados en mente probamos el siguiente lema.
Lema. Si $n\neq 0$ y $m\in \mathbb{N}$ es tal que $m\cdot n=0$, entonces $m=0$.
Demostración. Como $n\neq0$, entonces existe $a\in \mathbb{N}$, tal que $n=\sigma(a)$, entonces tenemos que
\begin{align*}
0&=m\cdot n\\
&=m\cdot\sigma(a)\\
\overset{*}{=}m+(m\cdot a).
\end{align*}
Entonces tenemos que $m\cdot a=0$ y que $m=0$ que es lo que debíamos probar.
$\square$
Es común usar una equivalencia lógica del enunciado anterior, la cual dice:
Si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$
Proposición (ley de cancelación). Si $m,n$ son números naturales y $a\neq0$ y cumplen que $a\cdot n=a\cdot m$, entonces, $n=m$
Demostración. De nuevo, procedamos por inducción sobre $n$
Base inductiva: Supongamos que $n=0$ y $a\neq0$, entonces $a\cdot m=a\cdot n=a\cdot0 =0,$ por el Lema tenemos que $m=0=n$.
Hipótesis de inducción: Supongamos que para algún $n$, tenemos que si $a\neq0$ y $a\cdot n=a\cdot m$, entonces $n=m$.
Paso inductivo: Probemos para $\sigma(n)$, sea $a\neq 0$ y supongamos que $a\cdot\sigma(n)=a\cdot m$.
Como $\sigma(n)\neq 0$, y por hipótesis, $a\neq0$, entonces por la equivalencia del lema, concluimos que $a\cdot\sigma(n)\neq 0$, de donde $a\cdot m\neq 0$, esto implica que $m\neq 0$, por lo que existe $b$ tal que $m=\sigma(b)$, entonces podemos escribir
\begin{align*}
a+a\cdot n& \overset{*}{=}a\cdot\sigma(n)\\
&=a\cdot m\\
&=a\cdot\sigma(b)\\
&\overset{*}{=}a+a\cdot b
\end{align*}
Ocupando la ley de cancelación de la suma, tenemos que $a\cdot n=a\cdot b$.
Pero por hipótesis de inducción debemos de tener que $n=b$, esto quiere decir que $\sigma(n)=\sigma(b)=m$, justo como debíamos probar.
$\square$
Con esta prueba concluimos las propiedades más fundamentales del producto.
Resumen de las propiedades del producto
Para finalizar con la entrada, haremos un compendio de las propiedades que demostramos
- Para todo $n$ natural, se tiene que $1\cdot n=n=n \cdot 1$
- Para todo $n$ natural, se tiene que $0\cdot n=0=n \cdot 0$
- Para $l,m,n$ naturales cualesquiera se tiene que $(l+m)\cdot n=(l\cdot n)+(m\cdot n)$
- Para $m,n$ naturales se tiene que $m\cdot n=n\cdot m$
- Para $l,m,n$ naturales cualesquiera se tiene que $l\cdot(m+n)=(l\cdot m)+(l\cdot n)$
- Para $l,m,n$ naturales cualesquiera se tiene que $(l\cdot m)\cdot n=l\cdot(m\cdot n)$
- Para $m,n$ naturales con $m\neq 0$, si $m\cdot n=0$, entonces $n=0$
- Para $l,m,n$ naturales con $l\neq 0$, si $l\cdot n=l\cdot m$, entonces $n=m$
Más adelante…
Con las propiedades de la suma y del producto en nuestra bolsa de herramientas, tenemos ya una rica teoría que desarrollar; nos falta aún definir una relación muy familiar en el conjunto $\mathbb{N}$, el orden, al cual ya hemos apelado en la demostración del teorema de la Recursión Débil.
Por el momento estudiaremos con mayor detalle los conjuntos infinitos, donde veremos la importancia de los naturales dentro de esta clase de conjuntos.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba la Propiedad distributiva derecha.
- Usando únicamente la ley de cancelación el producto, demuestra el Lema previo a la demostración de la ley de cancelación.
- ¿Qué pasa si en el enunciado de la ley de la cancelación, no asumimos que $a\neq 0$?
- Demuestra usando el Lema previo a la demostración de la ley de cancelación que si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$.
- Da una definición recursiva de las funciones $\eta_{m} (n)=m^n$ y prueba las leyes de los exponentes.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Definición de la suma y sus propiedades básicas
- Entrada siguiente del curso: Otras definiciones recursivas
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
