Introducción

Habiendo hablado del producto cartesiano, ya tenemos los ingredientes para irnos acercando a la definición de función, pero antes de hablar de ellas, tenemos que hablar de relaciones y de algunos de sus conceptos. En esta entrada introduciremos el concepto de relación, dominio, codominio y composición entre relaciones.

Relaciones

Cuando estamos hablando de el producto cartesiano, estamos juntando las parejas posibles de elementos entre dos conjuntos. Pero quizá no nos interesen todas las parejas posibles, quizá a veces solo nos interesaría hablar de algún subconjunto de estas parejas. Por ejemplo, si tenemos los conjuntos de zapatos izquierdos y derechos denotados por $I,D$ entonces no siempre nos interesan todas las parejas posibles de zapatos, quizá solo nos interese combinar cada zapato izquierda con su par correspondiente. Para dar un ejemplo, imagina que hay tres zapatos $A,B,C$ y los conjuntos $I$ y $D$ contienen tres zapatos de cada uno de los zapatos que hay:

$I = \{I_A, I_B, I_C\} $

$D = \{D_A, D_B, D_C\} $

Si quisieramos unir cada zapato con su par, nos podemos fijar en su producto cartesiano $I \times D$, sin embargo hay elementos que sí nos van a interesar y otros que no. Por ejemplo, la pareja $(I_A,D_A)$ sí nos interesa, pues es el zapato izquierdo y derecho del zapato $A$. Por otro lado, la pareja $(I_A,D_C)$ no nos interesa, pues estamos juntando dos zapatos pero de modelos distintos. En particular, el subconjunto de $I \times D$ que describe a los tres zapatos es: $$R = \{(I_A,D_A),(I_B,D_B),(I_C,D_C)\}.$$ Este conjunto es una relación entre los conjuntos $I$ y $D$. Como podrás notar, $R \subset I \times D$, y para la definición de relación, basta con que el conjunto esté contenido en el producto cartesiano para que cumpla la definicón.

Definición. Sean $X$ y $Y$ dos conjuntos, una relación entre los conjuntos $X$ y $Y$ es un subconjunto $R$ del producto cartesiano $X \times Y$: $$R \subset X \times Y $$

Definición. Si $R$ es una relación de $X$ en $Y$, diremos que $x$ está relacionado con $y$ bajo la relación $R$ si la pareja $(x,y) \in X \times Y$ y $(x,y) \in R$.

Con esta última definición, podemos notar que el zapato izquierdo $A$ ($I_A$) está relacionado con el zapato derecho $A$ ($D_A$) bajo la relación $R$, pues la pareja $(I_A,D_A)$ pertenece a la relación $R$.

En nuestro ejemplo anterior, mostramos una relación entre $I$ y $D$. Otros ejemplos de relaciones entre $I$ y $D$ son los siguientes:

$\{(I_B,D_A),(I_C,D_B),(I_C,D_A)\},$
$\{(I_C,D_B)\}$
$\{(I_A,D_A),(I_C,D_B)\}$
$\emptyset$
$I \times D$

Dominio y codominio de relaciones

Vamos ahora a trabajar con el conjunto de los números enteros $\mathbb{Z}$. Y trabajaremos con el producto cartesiano $\mathbb{Z} \times \mathbb{Z}$. Llamemos a este producto cartesiano $\mathbb{Z}^2$ que es la forma en que comúnmente se le denota al producto cartesiano entre el mismo conjunto (en este caso $\mathbb{Z}$) en la literatura.

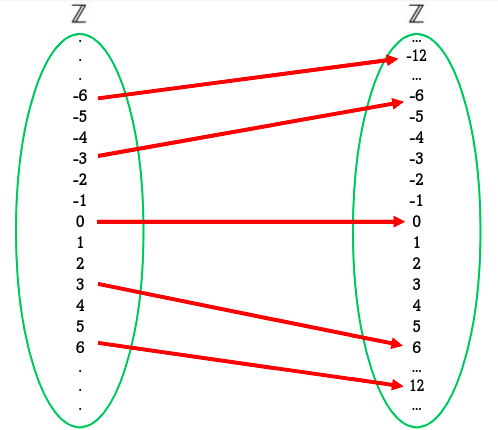
Ahora, consideremos la siguiente relación entre los conjuntos: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$

Y notemos que algunos ejemplos de elementos de esta relación son: $\{ (3,6),(0,0),(-3,-6),(3^{10},2*3^{10}) ,(-300,-600)\} \subset R$. Gráficamente, podemos ver la relación en la siguiente imagen:

Del lado izquierdo corresponden los elementos $x$ de las parejas $(x,y) \in R$ y del lado derecho los elementos $y$. Notemos que del lado izquierdo (los elementos $x$), no consideramos todos los elementos. Por ejemplo, los números $\{-5,-4,-2,-1,1,2,4,5\}$ no forman ninguna pareja, pues en la definición de nuestro conjunto, solo estamos considerando los múltiplos de $3$ del lado izquierdo de la relación. A estos números que sí forman parejas del lado izquierdo, les llamamos dominio.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El dominio de la relación $R$ es $$Dom(R) = \{x \in X: \exists y \in Y \text{ tal que } (x,y) \in R\}$$

Notemos que siempre pasará que $Dom(R)\subset X$, otra definición que no hay que confundir con la de dominio es la de contradominio, al que nos referimos como el conjunto $Y$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El contradominio de $R$ es el conjunto $Y$.

En nuestro ejemplo anterior, $$Dom(R)=\{x \in X: x \text{ es múltiplo de 3}\}$$.

Esto es cierto, pues las parejas de la relación $R$ son aquellas parejas de la forma $(3n,6n)$, pues pedimos que del lado izquierdo estén los múltiplos de $3$ (todo múltiplo de $3$ puede escribirse como algún número entero $n$ multiplicado por $3$), y del lado izquierdo el doble del número que escribimos del otro lado (si del lado izquierdo está $3n$ entonces del derecho estará $2*3n=6n$). Así que el dominio son aquellos números que forman alguna pareja, es decir, los múltiplos de $3$.

Por otro lado, el contradominio es $\mathbb{Z}$. Ahora, podemos preguntarnos en un concepto análogo a la idea de los elementos $y$ para los cuales existe un elemento $x$ de forma que $(x,y)$ pertenezca a la relación, para eso, podemos observar que los únicos elementos de $Z$ que pertenecen a alguna pareja del lado derecho son $\{\dots,-12,-6,0,6,12,\dots\}$, es decir, los múltiplos de $6$, de manera que podríamos hablar de que este conjunto es la imagen de la relación $R$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. La imagen de $R$ es: $$Im(R) = \{y \in Y: \exists x \in X \text{ tal que } (x,y) \in R\}$$

Imagen Directa e Imagen Inversa

Ahora, tomemos a los conjuntos $A=\{0,2,3,5,6,7,8,9\}$ y $B=\{-6,-1,2,3,4,6,7,12,21\}$ veamos que $A \times B \subset \mathbb{Z}^2$ pues ambos son subconjuntos de números enteros. El siguiente concepto que vamos a presentar, va a ser la imagen directa e inversa. Para esto, consideremos nuevamente nuestra relación $R$ de la sección anterior. Veamos que los elementos de $A$ que pertenecen al dominio de $R$ son $\{0,3,6,9\}$ esto pues $\{(0,0),(3,6),(6,12),(9,18)\} \subset R$. Definamos la imagen directa de $A$ como los elementos en la imagen de $R$ con la restricción de que únicamente consideremos elementos de $A$ del lado izquierdo.

Definición. Sean $X,Y$ dos conjuntos, $A \subset X$ y $R$ una relación de $X$ en $Y$. La imagen directa de $A$ es el conjunto: $$Im[A]=\{y \in Y: \exists x \in A \text{ tal que }(x,y) \in R\}$$

Compara esta definición con la definición de imagen, lo único que estamos cambiando es el conjunto al que pertencen las $x$.

De manera similar, tenemos un concepto similar para $B$, en donde restringiremos ahora el dominio. Para esto, nota que las parejas de $R$ que tienen su imagen en $B$ son $\{(-3,-6),(3,6),(6,12)\}$. Y el concepto de imagen inversa, serán aquellos elementos del dominio de $R$ los cuales están relacionados con algún elemento de $B$.

Definición. Sean $X,Y$ dos conjuntos, $B\subset Y$ y $R$ una relación de $X$ en $Y$. La imagen inversa de $B$ es el conjunto: $$Im^{-1}[B]=\{x \in X: \exists y \in B \text{ tal que }(x,y) \in R\}$$

De esta, manera:

$$Im[A]=\{0,6,12,18\},$$ $$ Im^{-1}[B]=\{-3,3,6\}.$$

A continuación, vamos a introducir una última definición de esta entrada, que da la idea intuitiva de juntar distintas relaciones.

Composición de funciones

Ahora, veremos la siguiente relación entre el conjunto de zapatos izquierdos $I$ y conjunto de zapatos derechos $D$:

$$R = \{(x,y) \in I \times D: x \text{ es del mismo color que }y\} $$

Y la relación entre zapatos derechos y el conjunto $P$ de pantalones:

$$ T = \{(x,y) \in D \times P:x \text{ es del mismo color que }y\} $$

Estas relaciones solo nos están juntando colores de prendas, la primera nos junta zapatos del mismo color y la tercera relaciones el color de los zapatos derechos con el del pantalón.

Así que por si ejemplol tuvieramos los colores rojo, amarillo y azul entre zapatos izquierdos, derechos y pantalones, entonces la primera relación tendría al zapato izquierdo rojo $I_R$, el zapato derecho rojo $D_R$ y el pantalón rojo $P_R$, de manera que $(I_R,D_R) \in R \land (D_R,P_R) \in T$. ¿Podemos establecer la conexión entre los zapatos izquierdos y los pantalones? Pues con esta pareja, resulta que de alguna manera el zapato $D_R$ une a los dos elementos mediante dos relaciones distintas. La primera relación tiene como contradominio el conjunto $D$ mientras que la segunda lo tiene como dominio.

De la misma manera, podemos conectar el zapato izquierdo azul $I_A$ con algún pantalón de la siguiente manera:

1. Notamos que $I_A$ está relacionado con el zapato derecho azul $D_A$ mediante la relación $R$.
2. Observamos que a su vez el zapato $D_A$ está relacionado con el pantalón azul $P_A$ mediante $T$.

De esta manera, podemos encontrar alguna conexión del zapato $I_A$ al pantalón $P_A$ viendo que hay una relación entre $I_A$ con $D_A$ y de $D_A$ con $P_A$. Así que podríamos definir una relación entre los zapatos izquierdos y los pantalones a través de las relaciones $R$ y $T$. Definamos esta relación como $R \circ T$ de la siguiente manera:

$$T \circ R = \{(x,y) \in I \times P: \exists z \in D \text{ tal que }\big( (x,z) \in R \land (z,y) \in T\big) \} $$

Lo que queremos decir con esta expresión, es que los elementos de la relación $T \circ R$ son los elementos $(x,y)$ de tal forma que existe una forma de conectar $(x,y)$ mediante un elemento $z$ de tal forma que $x$ está relacionado con $y$ mediante la relación $T \circ R$ si existe un elemento $z$ que los conecta, es decir, si existe $z$ en $Im(R) \cap Dom(T)$ de tal forma que $(x,z) \in R$ y $(z,y) \in T$.

Definición. Sean $X,Z,Y$ tres conjuntos, $R$ una relación de $X$ en $Z$ y $T$ una relación de $Z$ en $Y$. La relación composición de $R$ con $T$ es la relación:
$$T \circ R = \{ (x,y) \in X \times Y: \exists z \in Z\big( (x,z) \in R \land (z,y) \in T\big)$$

Veamos ahora un ejemplo de nuevo con los número enteros. Considera la relación que ya habíamos visto anteriormente, dada por: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$ Nota ahora, que como dijimos anteriormente, estos son las parejas de la forma $(3n,6n)$ de manera que otra forma de escribir el conjunto es $$R = \{(3n,6n): n \in \mathbb{Z} \} $$.

Ahora considera la siguiente relación $T$:$$T = \{(x,y) \in \mathbb{Z}^2: x = y+1\}$$

Algunos elementos de esta relación son: $\{(3,2),(7,6),(1,0),(-9,-10)\}$. Gráficamente se ve de la siguiente manera:

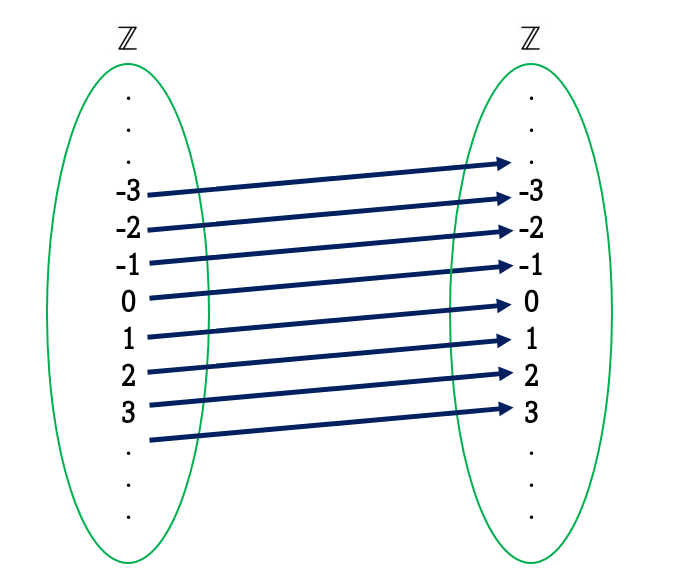
Y si te das cuenta, únicamente son los números de la forma $(n+1,n)$. Por lo que podríamos escribir esta relación como $$T = \{(n+1,n): n \in \mathbb{Z} \} $$.

Ahora veamos cómo se ve la composición $T \circ R$. Para ello, tomemos un elemento de la relación $R$. Por ejemplo, $(3,6) \in R$. Ahora notemos que de igual forma, $(6,5)$ pertenece a la relación $T$. De manera que $(3,5) \in T \circ R$. En general, un elemento de la relación $R$ se escribe como $(3n,6n)$, y un elemento de la relación $T$, como dijimos al principio del párrafo, es de la forma $(n+1,n)$ o lo que es lo mismo, $(n,n-1)$. Y enseguida nota que si tomamos un número entero $n$, entonces $(3n,6n) \in R$ y $(6n,6n-1) \in T$. De esta manera, podemos escribir a la composición de $R$ con $T$ como el conjunto: $$ T \circ R = \{(3n,6n-1): n \in \mathbb{Z}\}$$

Más adelante…

En la siguiente entrada seguiremos hablando de las relaciones entre conjuntos y veremos algunos tipos de relaciones especiales que tendrán algunas propiedades interesantes. También hablaremos un poco más de relaciones de un conjunto en sí mismo, este tipo de relaciones ya las hemos visto, sin embargo, veremos más propiedades que pueden cumplir estas. Esto nos servirá para hablar después de órdenes entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sea $$R=\{(x,y) \in \mathbb{Z}^2: x+y=0\}$$ y la relación$$T=\{(x,y) \in \mathbb{Z}^2: x-y=0\}.$$Encuentra:
   • $Dom(R)$
   • $Im(R)$
   • Escribe todos los elementos de $T \circ R$
   • Encuentra $Im[\{1,2,3,4,5\}]$ sobre la relación $R$
   • Encuentra $Im^{-1}[\{-1,-2,-3,-4,-5\}]$ sobre la relación $T$
2. Demuestra que si $R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $, entonces $$R = \{(3n,6n): n \in \mathbb{Z} \} $$
3. La recta $\mathcal{L}$ con pendiente $m$ e intersección $b$ con el eje $y$ en los números enteros es el conjunto: $$\mathcal{L}=\{(x,y) \in \mathbb{Z}^2: mx+b=y\} $$ Encuentra $\mathcal{L_1}\cap \mathcal{L_2}$ donde $\mathcal{L_1}$ es la recta con $m=1,b=0$ y $\mathcal{L_2}$ es la recta con $m=-1,b=2$.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Problemas de producto cartesiano
• Siguiente entrada del curso: Tipos de relaciones en conjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»