(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
Como pudiste darte cuenta por el título, en esta entrada definiremos una relación de equivalencia en un grupo. Permítenos dar una motivación usando un grupo que tal vez ya hayas estudiado en cursos anteriores como el de Álgebra Superior II.
Dicho grupo tan importante, es el de los enteros con la suma $(\z, +)$. Para $a,b\in \z$ y $n \in \z^+$ es posible establecer una relación $\thicksim$ dentro de los enteros como sigue
\begin{align*}
a \thicksim b \Leftrightarrow b-a \text{ es múltiplo de } n.
\end{align*}
Esta relación de equivalencia induce una partición de $\z$, con exactamente $n$ conjuntos. Donde cada conjunto es una de las clases módulo $n$. En esta entrada queremos introducir una relación parecida, pero generalizada a cualquier grupo.
Comencemos modificando este ejemplo un poco. Primero, llamemos $H$ al conjunto de todos los enteros múltiplos de $n$. Así nuestra relación quedaría, para $a,b\in \z$,
\begin{align*}
a \thicksim b \Leftrightarrow b-a \in H.
\end{align*}
Luego, notemos que a pesar de que la operación que usamos para definir el grupo es la suma usual, nuestra relación está definida usando la resta. En realidad, lo que está pasando es que estamos sumando $b$ con el inverso aditivo de $a$, es decir $-a$. Entonces $b -a = b + (-a)$. Además, $(\z,+)$ es un grupo abeliano, por lo que $b + (-a) \in H \Leftrightarrow (-a) + b \in H$. Para nuestra generalización usaremos el segundo caso.
Así, tenemos que comenzar tomando un subgrupo cualquiera de $G$, es decir, nos tomamos $H\leq G.$ Entonces nuestra relación debe quedar, dados $a,b\in G$,
\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b\in H.
\end{align*}
Ya al tener esa relación y demostrar que es una relación de equivalencia, usaremos las propiedades de grupo para descubrir que las clases de equivalencia son las clases laterales vistas en la entrada anterior.
Relación Generalizada
Lo anterior queda formalizado en la siguiente definición.
Definición. Sean $G$ un grupo y $H$ un subgrupo de $G$. Definimos una relación en $G$ del siguiente modo: dados $a,b \in G$,
\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b \in H.
\end{align*}
Ahora, demostraremos que esa relación, así como la de la introducción, es una relación de equivalencia.
Proposición. La definición anterior es una relación de equivalencia.
Demostración.
Sean $G$ un grupo y $H\leq G$.
Primero, tomamos $a \in G$.
También podemos tomar $a^{-1}$ . Así $a^{-1}a = e \in H$. Por lo tanto $a \thicksim a$ y nuestra relación es reflexiva.
Ahora tomamos $a,b \in G$. Si $a \thicksim b$, entonces $a^{-1} b\in H$.
\begin{align*}
\Rightarrow b^{-1}a = (a^{-1}b)^{-1} \in H \Rightarrow b \thicksim a
\end{align*}
Por lo que nuestra relación es simétrica.
Sean $a,b,c \in G$. Si $a \thicksim b$ y $b \thicksim c$. Luego, $a^{-1}b \in H$ y $b^{-1}c \in H$, entonces usando la cerradura de $H$ y asociando, obtenemos
\begin{align*}
a^{-1}c = (a^{-1}b)(b^{-1}c) \in H \Rightarrow a \thicksim c.
\end{align*}
Así, nuestra relación es transitiva.
Por lo tanto, nuestra relación es una relación de equivalencia.
$\square$
Nótese que para probar las tres propiedades de una relación de equivalencia (reflexividad, simetría y transitividad) usamos las tres condiciones de un subgrupo (la existencia del neutro, la cerradura de los inversos y la cerradura del producto).
A continuación, veamos cómo son las clases de equivalencia:
Sea $a \in H$.
\begin{align*}
\bar{a} &= \{b \in G | a \thicksim b\} = \{b \in G | a^{-1}b \in H\} \\
&= \{b \in G | a^{-1}b = h, h \in H\} = \{b \in G | b = ah, h \in H\} \\
&= \{ah | h \in H\} = a H.
\end{align*}
Ahora veremos algunas observaciones de lo anterior.
Observación. Sean $G$ un grupo, $H\leq G$ y $a,b\in G$, entonces
\begin{align*}
a H = bH & \Leftrightarrow a^{-1}b \in H.
\end{align*}
En particular,
\begin{align*}
H = bH & \Leftrightarrow b \in H.
\end{align*}
Nota. Análogamente se puede trabajar con clases laterales derechas. Es decir, $$Ha = Hb \Leftrightarrow ba^{-1}\in H.$$
Como $\thicksim$ es una relación de equivalencia, esta induce una partición y, como sus clases de equivalencia son las clases laterales, tenemos el siguiente teorema.
Teorema. Sean $G$ un grupo y $H$ subgrupo de $G$.
- $aH \neq \emptyset \quad \forall a \in G$ .
- Si $a,b \in G$ son tales que $aH \cap bH \neq \emptyset$, entonces $aH = bH$.
- $\displaystyle \bigcup_{a\in G} aH = G.$
Claramente el teorema anterior enuncia las características de una partición, por lo que no hay nada que probar.
Ejemplos
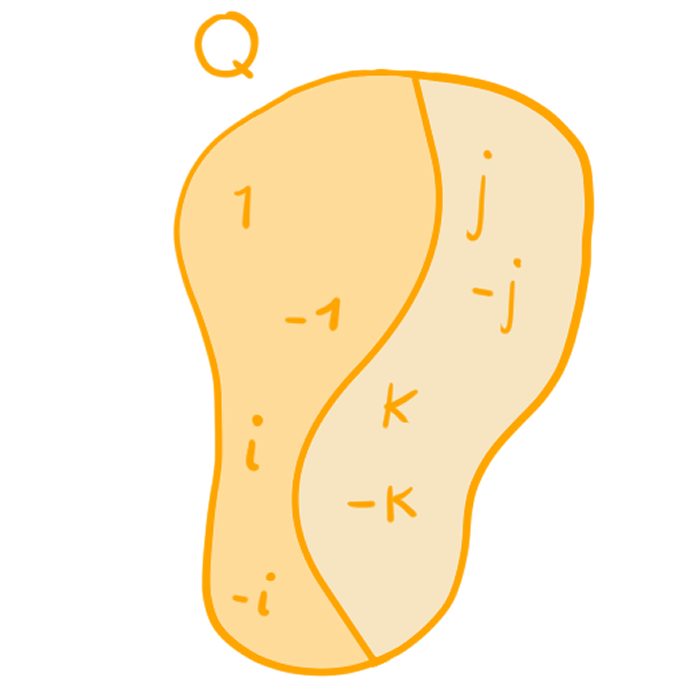
Ejemplo 1. Consideremos al grupo de los cuaternios $Q$ y tomemos el subgrupo $H = \left< i \right> = \{\pm 1 , \pm i\}$. Veamos qué sucede con sus clases laterales.
\begin{align*}
jH &= \{j(+1), j(-1), j(+i), j(-i)\}\\
&= \{j, -j, -k k\} \\
&= Hj.
\end{align*}
La última igualdad la puedes comprobar tú, multiplicando los mismos elementos por $j$, pero ahora del lado izquierdo.
Así, las clases laterales son:
- Clases laterales izquierdas: $H, jH$.
- Clases laterales derechas: $H, Hj$.
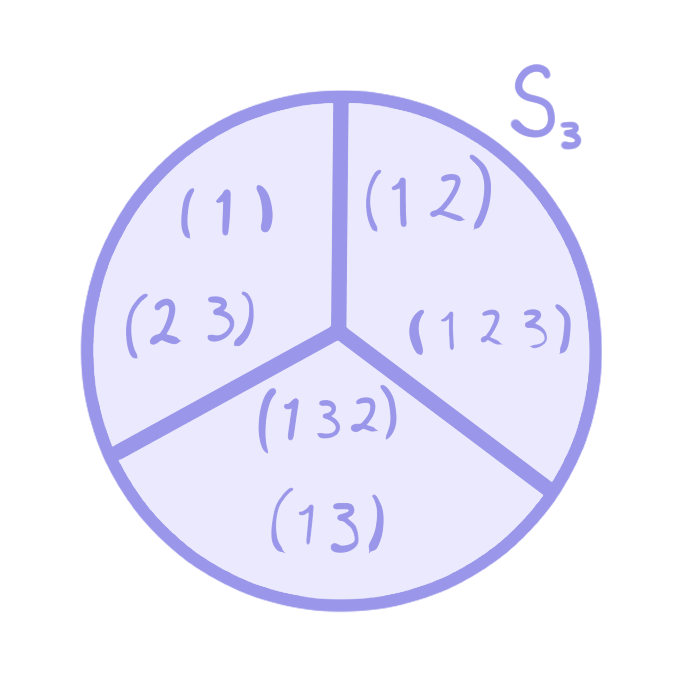
Ejemplo 2. Tomemos $S_3$ y $H = \{(1), (32)\}$.
Primero, veamos cómo se ven las clases laterales izquierdas.
Primero, tenemos la clase del neutro, es decir $(1) H = H$. Luego, tenemos que tomarnos un elemento de $S_3$ que no esté en $H$, digamos $(1\;2\;3)$, entonces,
\begin{align*}
(1\;2\;3)H &= \{(1\;2\;3)(1), (1\;2\;3)(3\;2)\}\\
&= \{(1\;2\;3), (1\;2)\}.
\end{align*}
Repetimos lo anterior, tomamos un elemento de $S_3$ que no esté en $H$ y sea distinto al que ya nos tomamos para obtener una clase distinta. Esto nos da
\begin{align*}
(1\;3\;2)H &= \{(1\;3\;2)(1), (1\;3\;2)(3\;2)\} \\
& = \{(1\;3\;2)(1\;3)\}.\\
\end{align*}
Por lo que las clases laterales izquierdas son:
\begin{align*}
(1)H &= H\\
(1\;2\;3)H &= \{(1\;2\;3), (1\;2)\}\\
(1\;3\;2)H &= \{(1\;3\;2)(1\;3)\}.\\
\end{align*}
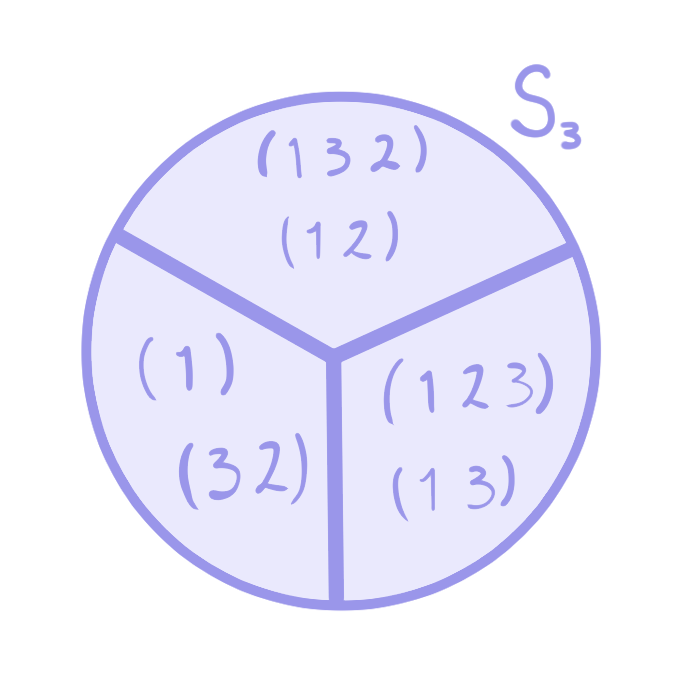
De la misma manera obtenemos las clases laterales derechas:
\begin{align*}
H(1) &= H \\
H(1\;2\;3) &= \{(1)(1\;2\;3), (3\;2)(1\;2\;3)\} = \{(1\;2\;3), (1\;3)\} \\
H(1\;3\;2) &= \{(1)(1\;3\;2), (3\;2)(1\;3\;2)\} = \{(1\;3\;2), (1\;2)\}.\\
\end{align*}
Este ejemplo nos permite ver que las clases laterales izquierdas y las clases laterales derechas no siempre coinciden.
Número de elementos en las clases laterales
El último ejemplo nos dice que las clases laterales derechas e izquierdas no siempre coinciden, sin embargo probaremos que siempre hay la misma cantidad de ambas.
Teorema. Sean $G$ un grupo y $H$ un subgrupo de $G$. Entonces
\begin{align*}
\#\{a H | a \in G\} = \#\{Ha | a \in G\}.
\end{align*}
Demostración.
Sea $\psi: \{a H | a \in G\} \to \{Ha | a \in G\}$, definida como $\psi(aH) = Ha^{-1} \quad \forall a \in G$. Probaremos que esta función es biyectiva.
Pequeño paréntensis:
Antes de comenzar con la demostración, pongamos atención a la definición de $\psi$. En un inicio podríamos pensar ¿por qué no hacemos $\psi(aH) = Ha$? La respuesta es simple, porque esto no funcionaría. Definamos una nueva función para ejemplificar, sea $\phi: \{a H | a \in G\} \to \{Ha | a \in G\} $ tal que $\phi(aH ) = Ha$.
Tomemos $b\in G$ tal que $aH = bH$, para que $\phi$ esté bien definida, necesitaríamos que $\phi(aH) = \phi(bH)$, es decir $Ha = Hb$. Por la relación que definimos, esto implica que si $a^{-1}b \in H$, entonces $ba^{-1} \in H$, pero esto no necesariamente es cierto porque el grupo puede no ser abeliano. Lo que sí sabemos es que si $a^{-1}b\in H$, entonces $Ha^{-1}b = H$, y así $Ha^{-1} = Hb^{-1}$.
Por esto es que escogimos a $\psi$ de esa manera.
Termina paréntesis. Ahora sí comencemos con la demostración.
Sean $a,b \in G$. Entonces,
\begin{align*}
aH = bH & \Leftrightarrow a^{-1}b \in H \\
&\Leftrightarrow Ha^{-1}b = H \\
& \Leftrightarrow Ha^{-1} = Hb ^{-1} \\
& \Leftrightarrow \psi (aH) = \psi (bH).
\end{align*}
Por tanto, $\psi$ está bien definida y es inyectiva.
Además, dada $Ha, con a \in G$.
\begin{align*}
Ha = H(a^{–1})^{-1} = \psi(a^{-1} H)
\end{align*}
así $\psi$ es suprayectiva.
Por lo tanto $\# \{aH | a \in G\} = \# \{Ha|a\in G\}.$
$\square$
Ahora, ya sabemos que la cantidad de clases laterales izquierdas es la misma que la de clases laterales derechas. Entonces podemos nombrar esto como el índice.
Definición. Sean $G$ un grupo y $H$ un subgrupo de $G$. El índice de $H$ en $G$ es
\begin{align*}
[G:H ] = \# \{aH | a\in G\}.
\end{align*}
Ejemplos
Retomemos los ejemplos que ya hemos visto.
- Tomemos a $Q$ como los cuaternios, $H= \left< i \right> = \{\pm 1, \pm i\}$, entonces, $$[Q:H]= 2.$$
- Ahora, tomemos $S_3$, $H = \{(1), (3 2)\}$. Como ya vimos, entonces, $$[S_3:H]= 3.$$
- Consideremos el grupo $(\z, +)$ y $H = \{6m | m \in \z\}$.
Hay 6 clases laterales: $H, 1+H, 2+H, 3+H, 4+H, 5+H$. Que serían los múltiplos de $6$, $6+1$, $6+2$, $\dots$ respectivamente.
Así, $[\z, H ]= 6$.
Tarea moral
- Analizando los ejemplos que tienes hasta ahora observa si existe alguna relación entre el orden de un grupo $G$, el orden del subgrupo $H$ y la cantidad de clases laterales de $H$ en $G$.
- Considera $\{\pm 1\} \leq \left< i \right> \leq Q$. Describe las clases laterales izquierdas de $\{\pm 1\}$ en $\left< i \right>$, las clases laterales izquierdas de $\left< i \right>$ en $Q$, y las clases laterales izquierdas de $\{\pm 1\}$ en $Q$. Encuentra $[Q: \{\pm 1\}]$, $[Q:\left< i \right>]$ y $[\left< i \right>: \{\pm 1\}]$.
- Considera $\left< (1\;2\;3) \right> \leq A_4 \leq S_4$. Describe las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $A_4$, las clases laterales izquierdas de $A_4$ en $S_4$, y las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $S_4$. Encuentra $[S_4:\left< (1\;2\;3) \right>]$, $[S_4: A_4]$ y $[A_4: \left< (1\;2\;3) \right>]$.
- Puedes checar el video de Mathologer.
Más adelante…
Ahora conoces el índice de $H$ en $G$. Recúerdalo para la siguiente entrada, porque intentaremos describir el orden de $G$ en términos del orden de $H$ y del índice. Sin hacer trampa, ¿cómo crees que se puede relacionar el orden de $G$ y el índice?
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Producto de subconjuntos y Clases Laterales.
- Siguiente entrada del curso: Teorema de Lagrange.
- Resto de cursos: Cursos.