(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta entrada veremos el Cuarto Teorema de Isomorfía, para entenderlo mejor es necesario ilustrarlo con diagramas de retícula.
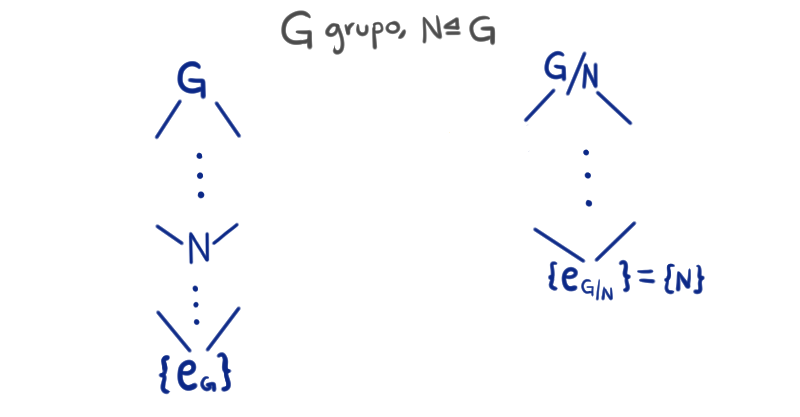
Sean $G$ un grupo y $N$ un subgrupo normal de $G$. Recordemos que podemos escribir todos los subgrupos de $G$ en una retícula. Como estamos considerando a todos los subgruposde $G$, el subgrupo más pequeño es el conjunto que contiene sólo al neutro $\{e_G\}$. Así, $G$ va hasta arriba del diagrama y $\{e_G\}$ al final.
Por otro lado, como $H\unlhd G$, tiene sentido considerar otro diagrama, el del grupo $G/N$. De la misma manera que en el anterior, hasta abajo colocaríamos $\{e_{G/N}\}$ que es el conjunto unitario de $\{N\}$.
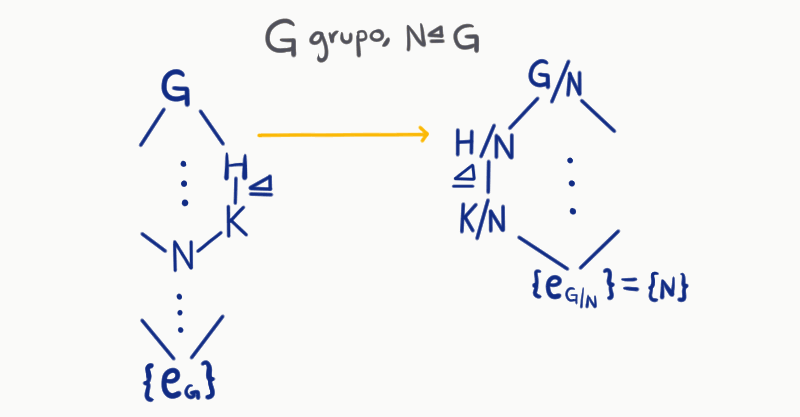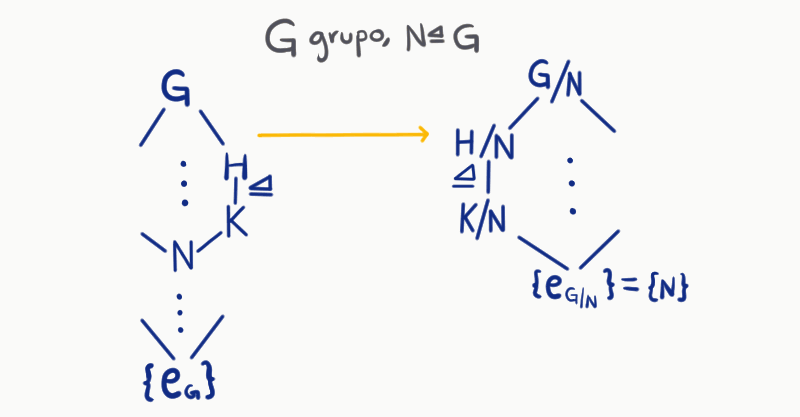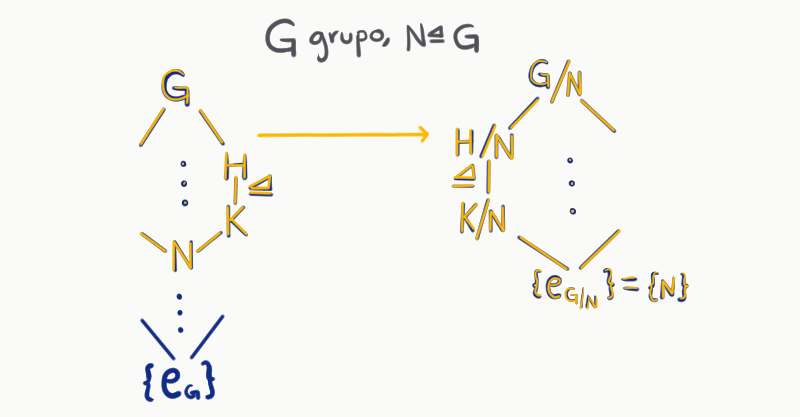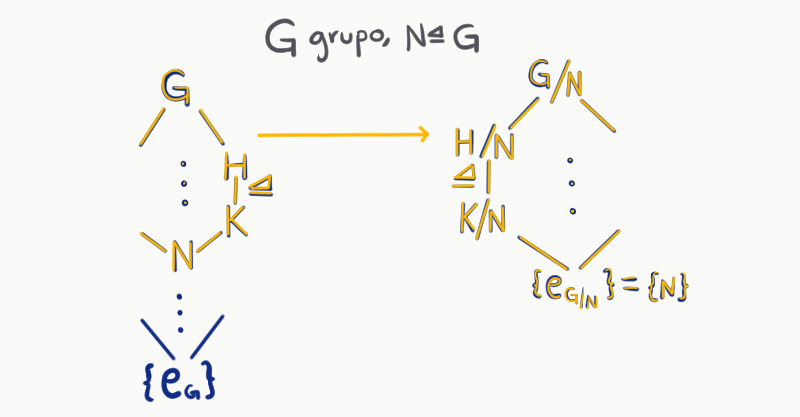
Luego, como $N \unlhd G$. Podemos tomar un subgrupo $H$ de $G$ que contenga $N$ y colocarlos en el diagrama. Además, esto nos daría la existencia de $H/N \leq G/N$, entonces podríamos dar una correspondencia de $H \mapsto H/N$. Esto nos da una relación entre ambas retículas (la de $G$ y la de $G/N$):
\begin{align*}
G &\longmapsto G/N\\
H &\longmapsto H/N\\
N &\longmapsto \{e_G\} = \{N\}.
\end{align*}
La relación que existe entre la retícula desde $N$ a $G$ y la retícula de $G/N$ además de ser biyectica tiene otras propiedades, por ejemplo, si existe $N\leq K \unlhd H$, entonces $K/N \unlhd H/N$. Estas propiedades son las que veremos en el teorema que nos compete.
Enunciado y demostración del Teorema
A continuación veremos el Cuarto Teorema de Isomorfía (CTI), también conocido como Teorema de la Correspondencia.
Teorema. (Cuarto Teorema de Isomorfía)
Sea $G$ un grupo, $N$ subgrupo normal de $G$, $\pi: G \to G/N$ con $\pi(a) = aN$ (la proyección canónica) para toda $a\in G$. Consideremos
\begin{align*}
\text{Sub}_N^G &= \{H| N\leq H \leq G \}, \\
\text{Sub}_{ G/N} &= \{\mathcal{H} | \mathcal{H} \leq G/N\}.
\end{align*}
Entonces $\pi$ define una correspondencia biyectiva
\begin{align*}
F: \text{Sub}_N^G \to \text{Sub}_{ G/N}
\end{align*}
con $F(H) = \pi [H] = H/N$ para todo $H \in \text{Sub}_H^G$.
Además, si $H,K\in \text{Sub}_N^G$:
- $K\leq H$ si y sólo si $K/N \leq H/N$ y en este caso $[ H:K] = [H/N : K/N]$.
- $K \unlhd H$ si y sólo si $K/N \unlhd H/N$.
- $\left< H\cup K \right> / N = \left< H/N \cup K/N \right>$.
- $(H\cap K) / N = (H/ N) \cap (K/N)$.
Demostración.
Sean $G$ un grupo, $N\unlhd G$, $\pi:G\to G/N$ con $\pi(a) = aN$ para toda $a\in G$.
Sean
\begin{align*}
\text{Sub}_N^G &= \{H\,|\, N\leq H \leq G \}, \quad
\text{Sub}_{ G/N} = \{\mathcal{H} | \mathcal{H} \leq G/N\}.
\end{align*}
Definimos
\begin{align*}
F: \text{Sub}_N^G \to \text{Sub}_{ G/N}
\end{align*}
con $F(H) = \pi[ H] = H/N$ para todo $H \in \text{Sub}_H^G$. Donde $\pi[H]$ es la imagen directa de $H$ bajo $\pi$.
Como $\pi$ es un homomorfismo y $H\leq G$ entonces $\pi[H]\leq \pi[G ]$, es decir $H/N\leq G/N$, entonces $F$ está bien definida.
Veamos que $G$ es inyectiva, para ello probemos la primera parte del inciso 1.
Sean $H, K \in \text{Sub}_N^G$.
P.D. $K \leq H \Leftrightarrow K/N \leq H/N$.
$|\Rightarrow]$ Supongamos que $K \leq H$. Sea $x \in K/N, x = kN$ con $k\in K.$
Como $K\subseteq H$, $k\in H$ y así $x = kN \in H/N$. Por lo tanto $K/N \leq H/N$.
$[\Leftarrow|$ Supongamos que $K/N \leq H/N.$ Sea $k\in K$, tenemos las siguientes implicaciones:
\begin{align*}
k N \in K/N &\Rightarrow kN \in H/N &\text{pues } K/N \leq H/N \\
&\Rightarrow kN = hN \;\text{con } h\in H \\
& \Rightarrow k = hn\; \text{con } h\in H, n\in N &\text{por } k \in kN = hN\\
& \Rightarrow k \in H & \text{ya que } N \subseteq H.
\end{align*}
Por lo tanto $K \leq H$.
De este modo, si $H,K \in \text{Sub}_N^G $ son tales que $F(H) = F(K)$, entonces $H/N = K/N$, así
\begin{align*}
H/N \leq K/N &\Rightarrow H \leq K \\
K/N \leq H/N &\Rightarrow K \leq H,
\end{align*}
ambas implicaciones son consecuencia de lo que acabamos de probar del inciso 1 de CTI. Así, $H=K$.
Veamos que $F$ es suprayectiva. Se $\mathcal{H} \in \text{Sub}_{G/N}$, es decir $\mathcal{H} \leq G/N$. Como $\pi: G \to G/N$ es un homomorfismo y $\{N\}\leq \mathcal{H} \leq G/N$, entonces $N \leq \pi^{-1}[\mathcal{H}] \leq G$.
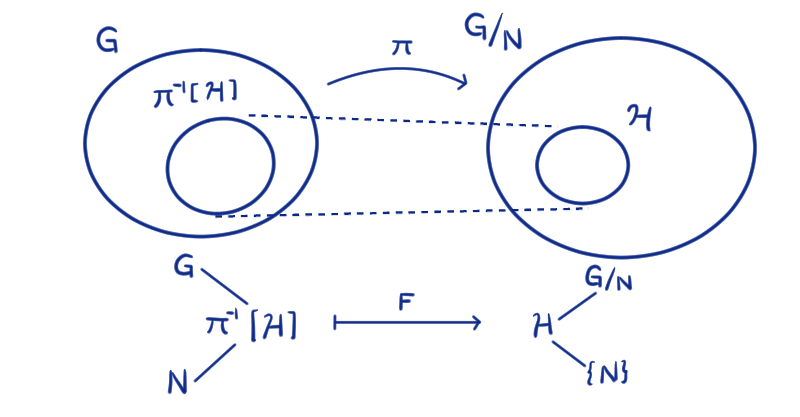
Nos vamos a fijar en el subgrupo $\pi^{-1} [\mathcal{H}]$, porque nos va a servir para probar la suprayectividad que buscamos.
Entonces apliquemos $F$: $$F(\pi^{-1} [\mathcal{H} ]) = \pi [\pi^{-1}[\mathcal{H}]]= \mathcal{H}$$ pues $\pi$ es suprayectiva. Así, $F$ es suprayectiva.
Probaremos ahora la segunda parte del inciso 1).
Sean $H,K\in \text{Sub}_N^G$, con $K\leq H$.
P.D. $[H: K ] = [H/N: K/N]$.
Recordemos que $[H/N : K/N]$ es la cardinalidad de $\{(hN)K/N \,|\, hN \in H/N\}$.
Para simplificar, denotaremos a $K/N$ por $K^*$ y como $\pi (h) = hN$, entonces $[H/N : K/N ]$ es la cardinalidad de $\{\pi(h)K^* | h\in H\}.$
P.D. $\{hK | h \in H \}$ y $\{\pi(h)K^*|h\in H\}$ tienen la misma cardinalidad.
Sea $f: \{hK | h \in H\} \to \{\pi(h)K^*| h\in H\}$ definida por $f(hK) = \pi(h)K^*$ para toda $h\in H$. Demostraremos que es una función biyectiva.
Primero, veamos que $f$ está bien definida. Tomemos $h, \tilde{h} \in H$. Tenemos las siguientes implicaciones:
\begin{align*}
hK = \tilde{h}K &\Rightarrow h^{-1}\tilde{h} \in K \\
&\Rightarrow h^{-1}\tilde{h} N \in K/N = K^*\\
&\Rightarrow \pi(h^{–1}\tilde{h}) \in K^* & \text{definición de }\pi\\
&\Rightarrow \pi(h)^{-1} \pi(\tilde{h}) \in K^* & \pi\text{ es homomorfismo}\\
&\Rightarrow \pi(h)K^* = \pi(\tilde{h})K^*.
\end{align*}
Por lo tanto, $f$ está bien definida.
Ahora veamos que $f$ es inyectiva. Sean $hK,\tilde{h}K$ con $h,\tilde{h}\in H$, tales que $f(hK) = f(\tilde{h}K)$. Seguiremos las siguientes implicaciones,
\begin{align*}
f(hk) = f(\tilde{h}K) & \Rightarrow \pi(h)K^* = \pi(\tilde{h})K^* &\text{definición de }f \\
&\Rightarrow \pi(h)^{-1}\pi(\tilde{h}) \in K^* \\
&\Rightarrow \pi(h^{–1}\tilde{h}) \in K^* &\pi\text{ es homomorfismo}\\
&\Rightarrow h^{–1}\tilde{h}N\in K^*&\text{definición de }\pi\\
&\Rightarrow h^{-1}\tilde{h}N = kN \text{ con } k \in K & \text{porque }K^* = K/N\\
&\Rightarrow h^{-1}\tilde{h} = kn, k\in K, n\in N &\text{porque } h^{-1}\tilde{h}\in h^{-1}\tilde{h}N \\
&\Rightarrow h^{-1}\tilde{h}\in K &\text{pues } N\subseteq K \\
&\Rightarrow hK = \tilde{h}K.
\end{align*}
Por lo tanto $f$ es inyectiva.
Además, si tenemos $\pi(h)K^*$ con $h\in H$, entonces $\pi(h)K^* = f(hK) \in \text{Im}f$. Por lo tanto $f$ es suprayectiva.
Así,
\begin{align*}
[H:K] &= \# \{hK | h \in H\} \\
&= \#\{\pi(h)K^* | h \in H\} = [H/N:K/N].
\end{align*}
Ahora, demostraremos el inciso 2.
Sean $H,K\in \text{Sub}_N^G$.
P.D. $K \unlhd H \Leftrightarrow K/N \unlhd H/N.$
El inciso 1 (que acabamos de probar) ya nos da que $K \leq H \Leftrightarrow K/N \leq H/N.$ Entonces lo que nos resta probar es que son subgrupos normales.
$|\Rightarrow]$ Supongamos que $K\unlhd H$. Sean $x\in H/N, y \in K/N$, entonces $x = hN, y = kN$ con $h\in H, k\in K$.
Lo que queremos es considerar el conjugado $xyx^{-1}$, es decir, ver que si tomamos un elemento de $K$ módulo $N$ (al que llamamos $y$) y lo conjugamos con cualquier elemento de $H$ módulo $N$ (en este caso $x$), vuelvo a tener un elemento en $K$ módulo $N$. Esto se ve de la siguiente manera:
\begin{align*}
x y x^{-1} = (hN)(kN)(hN)^{-1} = (hN)(kN)(h^{-1}N) = hkh^{-1}N.
\end{align*}
Como $k \in K, h \in H$ y $K\unlhd H$, se tiene que $hkh^{-1} \in K$.
Así, $xyx^{-1} = hkh^{-1} N \in K/N$. Por lo que $K/N \unlhd H/N$.
$[\Leftarrow|$ Supongamos que $K/N \unlhd H/N$. Sean $k\in K, h\in H$.
Veamos qué sucede con la clase $hkh^{-1}N$:
\begin{align*}
hkh^{-1} N = (hN)(kN)(h^{-1}N) = (hN)(kN)(hN)^{-1}
\end{align*}
Es otras palabras, estamos conjugando un elemento de $kN\in K/N$ con un elemento de $kN\in K/N$. Luego, como sabemos que $K/N \unlhd H/N$ obtenemos que esta conjugación sigue estando en $K/N$. Es decir, $hkn^{-1}N\in K/N$.
Podríamos reescribir $hkh^{-1}N = \tilde{k}N$ con $\tilde{k} \in K$. Así,
\begin{align*}
hkh^{-1}N &= \tilde{k}N & \text{con }\tilde{k} \in K\\
\Rightarrow hkh^{-1} &= \tilde{k}n, \tilde{k}\in K, n\in N & \text{por } hkh^{-1} \in hkh^{-1}N = \tilde{k}N \\
\Rightarrow hkh^{-1}&\in K &\text{pues } N\subseteq K.
\end{align*}
Por lo tanto $K\unlhd H$.
$\blacksquare$
Ejemplo de CTI
Ejemplo. Tomemos el grupo diédrico (todas las simetrías de un cuadrado) $D_{2(4)} = \left<a,b \right>$, donde $a$ la rotación de $\frac{\pi}{2}$ y $b$ es la reflexión respecto al eje $x$.
Construyamos la retícula de $D_{2(4)}$: comenzamos con $D_{2(4)}$ hasta arriba, este tiene orden de 8. En el siguiente nivel colocamos los subgrupos:
\begin{align*}
\left<a^2,b\right> &= \{\text{id}, a^2, b, a^2b\}\\
\left<a\right> &= \{\text{id}, a, a^2, a^3\} \\
\left<a^2,ab\right> &= \{\text{id}, a^2, ab, a^3b\}.
\end{align*}
Cada uno de esos subgrupos tiene orden 4, en realidad esos son los únicos subgrupos de $D_{2(4)}$ que tienen orden 4. Siéntete libre de confirmar las cuentas.
Luego podemos colocar en el tercer nivel los subgrupos de orden 2:
\begin{align*}
\left< b\right> &= \{\text{id}, b\}\\
\left< a^2b\right> &= \{\text{id}, a^2b\}\\
\left< a^2\right> &= \{\text{id}, a^2\}\\
\left< ab\right> &= \{\text{id}, ab\}\\
\left< a^3b\right> &= \{\text{id}, a^3b\}.
\end{align*}
Por último, hasta abajo tenemos al unitario de la identidad $\{\text{id}\}$. Si verificamos las operaciones, nos daremos cuenta que hemos construido todo el diagrama de retícula de $D_{2(4)}$.
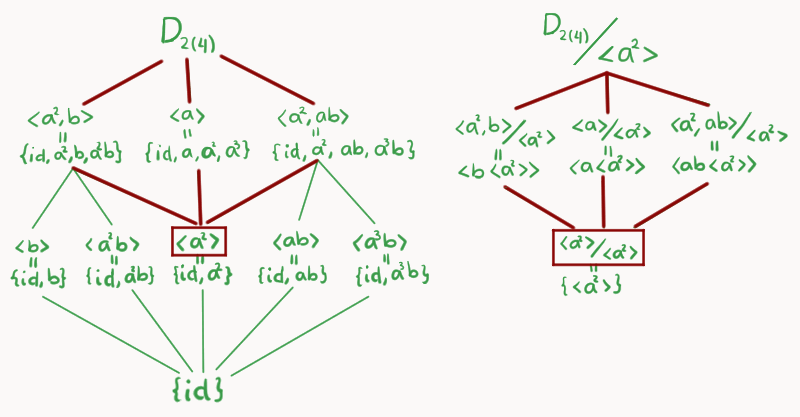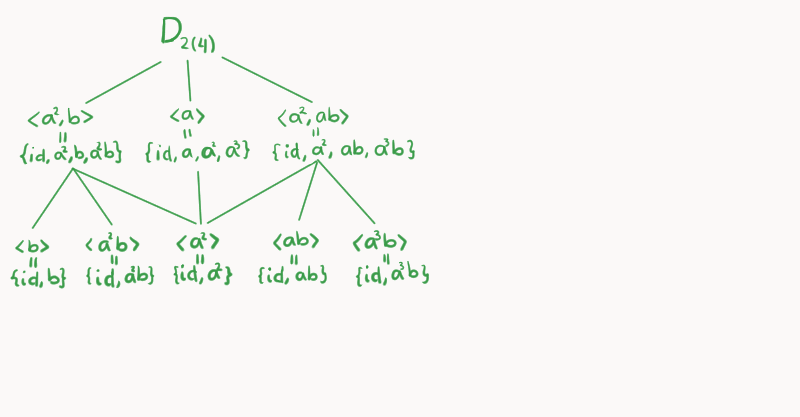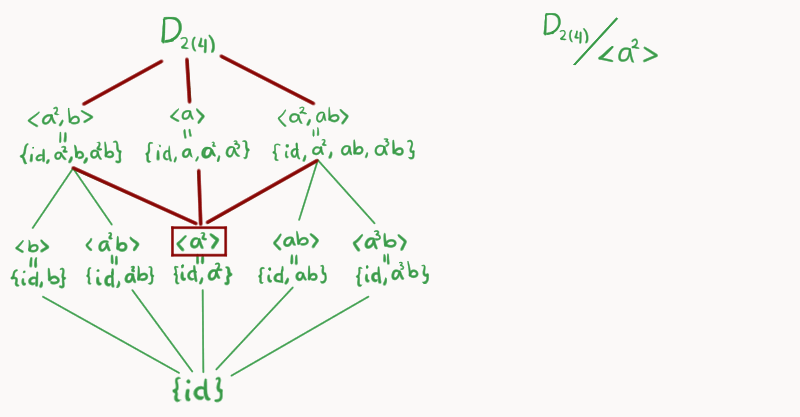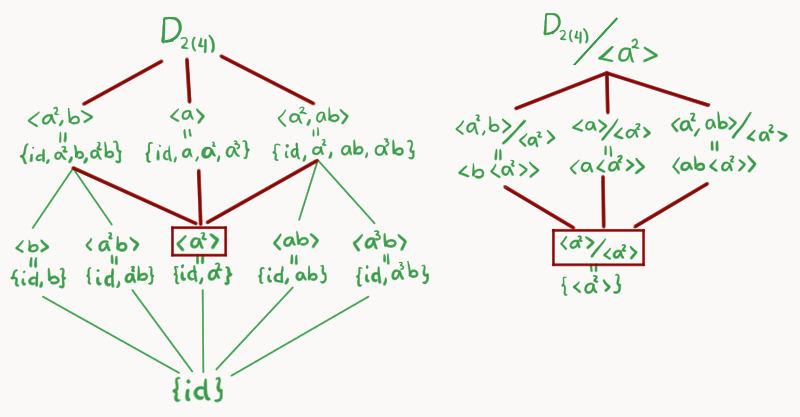
Para poder usar el CTI, consideremos $\left<a^2\right> \unlhd D_{2(4)}$ y concentremos nuestra atención en la parte de la retícula que se encuentra entre esos dos (marcada con rojo en la imagen).
Ahora, dibujaremos el diagrama de retícula de $D_{2(4)}/\left<a^2\right>$, éste va hasta arriba. Colocamos los cocientes respectivos en el siguiente nivel, siguiendo esta correspondencia:
\begin{align*}
\left<a^2,b\right> &\longmapsto \left<a^2,b\right> / \left<a^2\right>\\
\left<a\right> &\longmapsto \left<a\right>/ \left<a^2\right>\\
\left<a^2,ab\right> &\longmapsto \left<a^2,ab\right>/ \left<a^2\right>.
\end{align*}
Haciendo las cuentas veremos que:
\begin{align*}
\left<a^2,b\right> / \left<a^2\right> = \left<b \left<a^2\right>\right>\\
\left<a\right>/ \left<a^2\right> = \left<a \left<a^2\right>\right>\\
\left<a^2,ab\right>/ \left<a^2\right> = \left<ab \left<a^2\right>\right>.
\end{align*}
Por último, haremos una observación. Si tomamos el subgrupos $\left< a^3b\right>$ de orden 2 igual podríamos aplicarle la regla de correspondencia de $F$ y seguirían cayendo en elementos de la retícula de $D_{2(4)}/\left<a^2\right>$ es decir:
\begin{align*}
F(\left< a^3b\right>)=\pi[\left< a^3b\right>] = \{\text{id}\left<a^2\right>, a^3b\left<a^2\right>\} = \left<ab\left<a^2\right>\right>.
\end{align*}
En ese contexto la función con la regla de correspondencia de $F$ no sería biyectiva ya que $F(\left< a^3b\right>)=F(\left< ab\right>)$, pero esto no contradice el Teorema de la Correspondencia porque en realidad $\left< a^3b\right>$ ni siquiera está contemplado en el dominio de $F$ porque no forma parte de la retícula entre $D_{2(4)}$ y $\left<a^2\right>$.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba los incisos 3 y 4 del Teorema de la correspondencia (Cuarto Teorema de Isomorfía).
- Encuentra la retícula de sugrupos de $\z$ que contienen a $24\z$.
- Encuentra la retícula de subgrupos de $\z/24\z$.
- Compara ambas retículas.
- Usando el diagrama reticular de subgrupos de $\z_{36}$ encuentra el de $\z_{36}/N$ donde $N = \{\bar{0}, \overline{12}, \overline{24}\}$.
Más adelante…
Con esta entrada concluimos la Unidad 3. En la siguiente unidad comenzaremos a ver cómo es posible ver a cualquier grupo como un subgrupo de permutaciones. ¿Puedes imaginártelo?
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Tercer Teorema de Isomorfía.
- Siguiente entrada del curso: Teorema de Cayley.
- Resto de cursos: Cursos.