Introducción:
En la primera unidad del curso, hemos definido la integral mediante las sumas de Riemann considerando los distintos comportamiento que estas pueden tener.
Vimos que hacer en los casos sencillos donde se tienen funciones bien portadas como las continuas, acotadas, monótonas, etc. Pero también se vieron casos más interesantes, por ejemplo, como cuando son continuas en subintervalos, y estos podían ser finitos o infinitos, como las funciones escalonadas o la función de Dirichlet.
En estos ejemplos se mostraba la integrabilidad o la no integrabilidad de la función. Pero a pesar de que los ejemplos podían ser contrastantes entre sí, todos compartían una característica y era que se encontraban definidos dentro de un intervalo cerrado.
Esto era, que la función se encontraba dentro de un segmento del eje de las abscisas el cual tenía un inicio y un fin bien determinado.
En esta nueva unidad se tendrá una generalización de este proceso. Ya no se considerarán intervalos con un inicio y fin, ahora trabajaremos la integral en un intervalo que el inicio o el fin (o ambos) dependerán de una variable, por lo que será un intervalo no definido.
A este nuevo fenómeno de generar la integral en un intervalo no definido se le conocerá como integral indefinida.
Integral Indefinida
En la unidad anterior se determinó que el valor de la integral depende del intervalo de integración o de los límites de integración donde teníamos la siguiente representación $[a,b]$.
Y se decía que el límite inferior era el punto $a$ y el límite superior era el punto $b$ y entre esos dos puntos se tenía la curva de la función y la integral era el área contenida bajo esa curva.
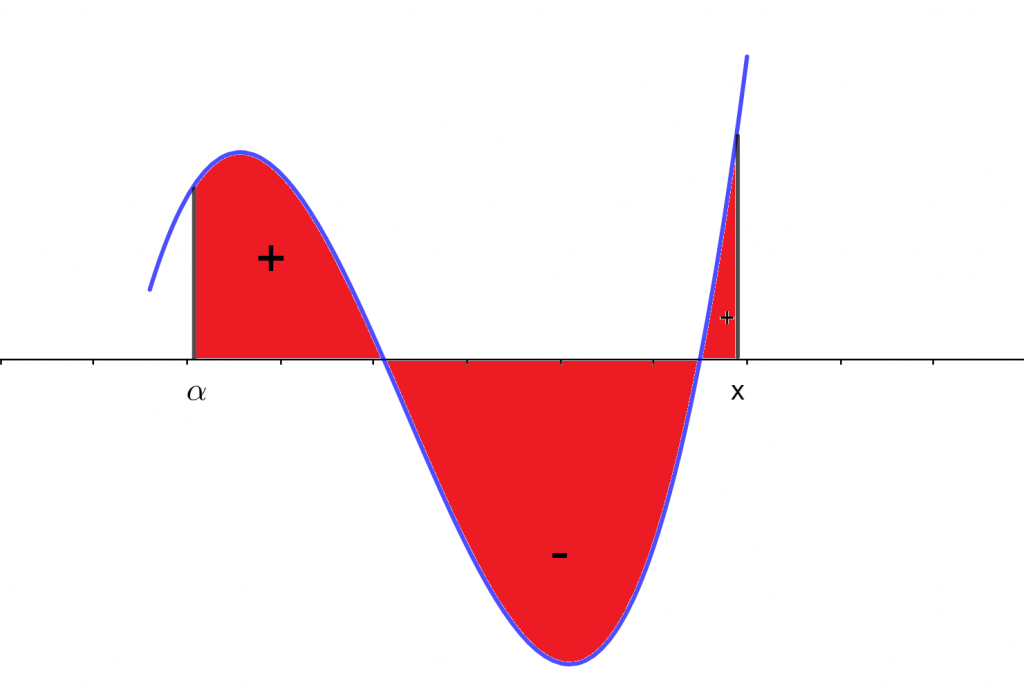
Ahora, consideremos el límite inferior como un número fijo $\alpha$, que no es un número particular, es decir, que puede ser cualquiera. Y el límite superior será una variable denotada con $x$. Teniendo la siguiente notación.
$$ \phi (x) =\int \limits_{\alpha}^{x} f(u) \ du.$$
Así que la función $\phi(x)$ se denomina como la integral indefinida de la función $f(x)$.
De forma que la función $\phi(x)$, es una función que depende de $x$.
Esto cambia la percepción de la integral ya que, anteriormente, solo se concebía la integral como un número (que era el área bajo la curva). Pero ahora la integral ya no solo es un escalar, a partir de este momento, podemos mostrar que la integral también es una función que puede depender de una variable independiente.
De manera análoga, se puede hacer que el límite inferior sea variable y, por lo tanto, que ambos límites puedan variables o dependan de otra función.
De una forma geométrica, se puede ver de la siguiente manera.
Así que la integral indefinida $ \phi (x) $ está dada por el área sombreada en rojo, que se encuentra delimitada por la curva en azul $y=f(u)$ dentro del intervalo $[\alpha , x]$.
Entonces, hasta que no se determine un valor para $x$, el valor de la integral irá cambiando.
Se debe recordar que el signo del área se determina por el cuadrante en el que se encuentra, como se vio en la Unidad 1.
Observación: Cualquier integral definida es un caso particular de una integral indefinida $\phi(x)$.
En el momento en que se define el valor de $\alpha$ y de $x$, recuperamos un intervalo definido y tenemos una integral definida.
Las reglas básicas para la integral que se vieron, tienen su generalización con integrales indefinidas, por ejemplo, la suma:
\begin{align*}
\int \limits_a^b f(u) \ du & = \int \limits_a^\alpha f(u) \ du + \int \limits_\alpha^b f(u) \ du \\ &= – \int \limits_\alpha^a f(u) \ du + \int \limits_\alpha^b f(u) \ du \\ & = \phi(b) \ – \ \phi(a) .
\end{align*}
De esta forma queda una integral definida en términos de integrales indefinidas.
Así, se puede expresar cualquier integral indefinida con límite inferior $\alpha’$ en términos de $\phi(x)$:
$$ \int \limits_{\alpha’}^x f(u) \ du = \phi(x) \ – \ \phi({\alpha’}) . $$
En donde $\phi({\alpha’}) $ es una constante, así que, sin pérdida de generalidad, se puede concluir que cualquier integral definida difiere de la integral indefinida $\phi(x)$ por una constante.
$$ \int \limits^x f(u) \ du = \phi(x) + C.$$
Donde a $C$ se le conoce como la constante de integración.
Continuidad de la integral indefinida
En la unidad anterior, al momento de trabajar con funciones continuas nos era sencillo generar las sumas de Riemann ya que se encontraba la función dentro del intervalo bien definida en todo momento. No presentaba saltos extraños o, como era continua, no presentaba discontinuidades en ningún tramo del intervalo o de cualquier partición de este.
En este caso, hemos dicho que la integral indefinida también es una función. Entonces, es importante conocer cuales son las características de esta nueva función.
En este caso, vamos a mostrar que la integral de una función continua, también es continua, entonces:
Sea $f(x)$ función continua en el intervalo $[a,b]$ y sea $\alpha$ un punto dentro del intervalo, i.e. $\alpha \in [a,b]$. Se define la integral indefinida como:
$$\phi(x) = \int \limits_\alpha^x f(u) \ du.$$
Teorema: La integral indefinida $\phi(x)$ de una función $f(x)$ continua, es asimismo, continua.
Demostración:
Sea $x, y$ dos valores dentro del intervalo donde la función es continua.
Por el teorema del valor medio se tiene que:
\begin{align*}
\phi(y) \ – \ \phi(x) & = \int \limits_x^y f(u) \ du \\ &
= f(\xi) (y \ – \ x).
\end{align*}
Donde $\xi$ es algún valor en el intervalo con puntos extremos $x$ y $y$.
Ahora, por la continuidad de $f$, obtenemos lo siguiente:
\begin{align*}
\lim_{y \rightarrow x} \phi(y) & = \lim_{y \rightarrow x} [\phi(x) + f(\xi) (y \ – \ x) ] \\&
= \ \lim_{y \rightarrow x} \phi(x) + \lim_{y \rightarrow x} f(\xi) (y \ – \ x) \\ &
= \ \phi(x) \ + \ f(\xi) \ \lim_{y \rightarrow x} (y \ – \ x) \\ &
= \ \phi(x) + f(\xi) \cdot 0
\end{align*}
$$\therefore \lim_{y \rightarrow x} \phi(y) = \phi(x).$$
Lo que muestra que $\phi$ es continua.
Adicionalmente, si lo vemos dentro de cualquier intervalo cerrado, obtenemos lo siguiente:
$$|\phi(y) \ – \ \phi(x)| \leq M \ |y \ – \ x|.$$
donde $M$ es el máximo de $|f|$ en el intervalo, de modo que $\phi$ es aún Lipschitz-continua.
Si quieres recordar continuidad, sigue este link.
$\square$
Durante la demostración se recordó el teorema del valor medio, mostrando la siguiente ecuación:
\begin{align*}
\phi(y) \ – \ \phi(x) & = \int \limits_x^y f(u) \ du \\ &
= f(\xi) (y \ – \ x).
\end{align*}
Observación: Si $f(x)$ es una función positiva en todo el intervalo $[x,y]$, se obtiene que $\phi(x)$ es una función creciente.
$$\phi(y) = f(\xi) (y \ – \ x) > \phi(x).$$
Más adelante…
Teniendo definidas las integrales indefinidas, podremos revisar las propiedades que estas integrales tienen y teoremas que son de alta importancia, tanto en cálculo como en las demás asignaturas.
Este paso de trabajar con integrales indefinidas nos da una mayor libertad al momento de trabajar con funciones. Anteriormente, al trabajar con integrales definidas, teníamos plena conciencia de que punto a que punto se necesitaba integrar, lo que, al momento de evaluar o de integral solo encontramos un número; pero ahora que trabajamos con integrales indefinidas.
Y como estamos ampliando la definición de la integral, es necesario mostrar las propiedades que esta extensión genera ya que, si consideramos estas propiedades se nos podrá facilitar el manejo de de esta transformación de funciones.
Estas propiedades las veremos en la siguiente entrada.
Tarea moral
- Escribe las siguientes integrales definidas como integrales indefinidas.
- $ \int \limits_3^{12} x^3 \ dx $
- $ \int \limits_1^5 ln(t) \ dt $
- $ \int \limits_{-\pi}^{\pi} sin(\theta) \ d \theta $
- Sea $f(x)$ una función continua y se cumple que $f(x) = \int \limits_0^x f(t) \ dt$.
Demuestra que $f(x)$ es idénticamente 0.
Entradas relacionadas
- Página del curso: Cálculo Diferencial e Integral II
- Entrada anterior: Funciones que no son Riemann integrables
- Entrada siguiente: Propiedades de la integral indefinida