Introducción

Al momento se trabajó con el concepto general de anualidad, anualidad vencida, anticipada y diferida, así como algunas de sus combinaciones entre ellas, ejemplos de cómo se presentan en la vida cotidiana, y la forma en que resultan muy útiles, para poder encontrar una solución. Sin embargo, aún falta considerar el caso en el que los pagos pueden ser de forma ininterrumpida, por decirlo así: los pagos serían un tiempo «infinito», lo anterior, tiene efecto sobre el capital, el cual, bajo estas condiciones, provoca que nunca se acabe.

Definición del concepto de perpetuidad, descripción y valor presente

Éste concepto, se parece mucho a las anualidades, desde el punto de vista que consisten en una serie de pagos iguales, en los que, en teoría el tiempo tiende al infinito, esto es, la duración del plazo esta continua siempre, en otras palabras, no está definido el término del plazo, mientras la causa subsista, mientras alguna empresa continúe operando, dicha operación continuará existiendo. Un ejemplo de éste tipo de casos se da cuando quieren constituir un fondo, un premio como lo es el premio nobel, o podría ser el caso de los dividendos que otorgan las empresas cuya operación es indefinida, la asignación de becas, en todos esos casos la característica en las que coinciden es, que siempre haya recursos de los cuales disponer, para que nunca se quede en cero los fondos.

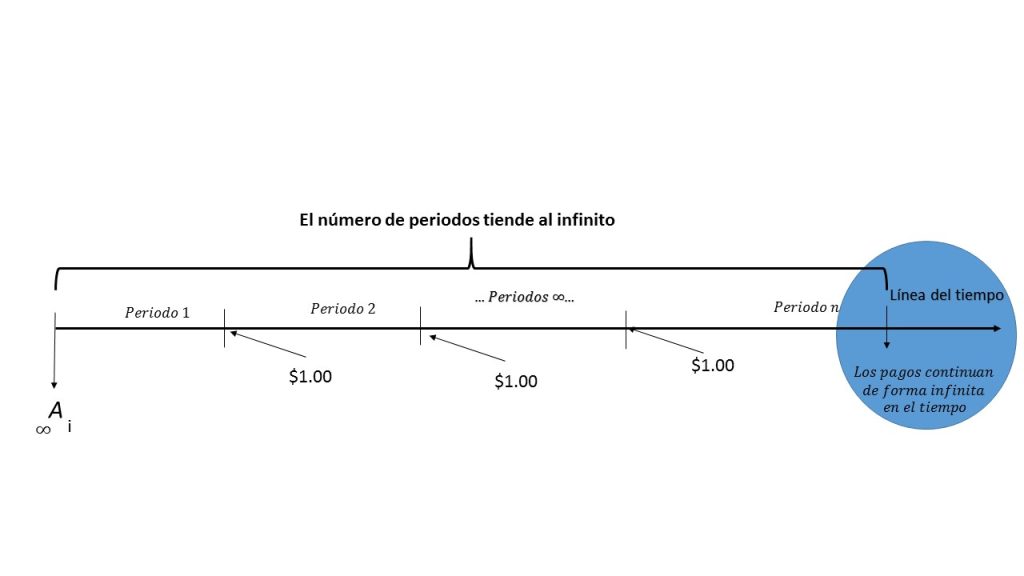
La forma en que será denotada una perpetuidad está dada por la expresión:

$$\prescript{}{\infty}{\mathbf{A}}_i.$$

Por otra parte, la notación usada para los conceptos de las anualidades anticipadas, vencidas, y diferidas será el mismo con el cual se han venido representando cada una respectivamente, sin embargo; para fines prácticos de éste concepto, será incluido el símbolo $\infty$ como subíndice, que como ya se mencionó hace corresponde al uso de una perpetuidad. En lo que respecta a las demás variables permanecerán con la misma denotación. Es importante hacer mención que el concepto de perpetuidad, se puede combinar con los conceptos que ya se han estado trabajando, y que se desarrollarán más adelante, recordemos algunos conceptos que serán utilizados para su construcción.

El valor presente de una anualidad vencida se calcula con la siguiente expresión:

$$\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$$

nos vamos a enfocar en la parte derecha de la igual, específicamente al que contiene a la $n$, el cual corresponde al $v^n$, analizando lo que le ocurre cuando se hace tender a $n$ a infinito. Partiendo de que:

$$v^n=\frac{1}{(1+i)^n}.$$

Cuando $(1+i)^n$, si se hace tender $n$ a infinito, el comportamiento dicha expresión es de una progresión geométrica, por lo que el cociente que allí se expresa, al tener que el denominador se hace tender a infinito, entre algo pequeño, el resultado será cero. Esto hace transformar dicha expresión en:

$$\prescript{}{\infty}{\mathbf{A}}_i=\frac{1-v^{\infty}}{i}=\frac{1-0}{i}=\frac{1}{i}.$$

Ahora, si en vez de un peso, se cambia dicha cantidad por $X$, la expresión queda:

$$\prescript{}{\infty}{\mathbf{A}}_i=\frac{X}{i}$$

dicha ecuación representa el valor presente de una perpetuidad vencida.

De ésa ecuación que se acaba de obtener, se despeja $X$, se obtiene la expresión para calcular el capital inicial, la cual queda denotada por:

$$X=\prescript{}{\infty}{\mathbf{A}}_i i.$$

Monto

De acuerdo con las características que tiene el concepto de perpetuidad, el monto de éste tiende a ser infinito, ya que realizando el siguiente proceso se tiene:

$$\prescript{}{\infty}{\mathbf{S}}_{i}=\frac{(1+i)^{\infty}-1}{i}=\frac{\infty-1}{i}=\infty$$

esto ocurre toda vez que $(1+i)$ resulta ser siempre mayor que $1$, para cualquier $i$ positiva, además de que está elevada a una potencia $\infty$ lo que hace que el resultado sea infinito. Aunado a lo anterior está el hecho de que cualquier cifra infinita, dividida entre cualquier número, el resultado continúa siendo infinito.

Ejercicios resueltos

Ejercicio. Una fundación desea crear un fondo que cuente con recursos suficientes para solventar los gastos de 3 becas que serán asignadas a 3 estudiantes, de manera tal que cuando ellos terminen sus estudios, siga habiendo fondos, para seguir beneficiando a otros 3 estudiantes más. La beca consiste en una cantidad \$2,000 mensuales para cada uno. Se desea saber de ¿cuánto debe ser el capital que se requiere aportar para, si están considerando una cantidad de 8% efectiva anual?

Ejercicio. La familia Godínez, quiere generar un fondo de un millón de pesos, que garantice la educación de su hijo, si al día que se decide crearlo, tiene una edad de 20 años, necesita saber ¿cuánto debería ahorrar semanalmente para asegurar el dinero suficiente para que garantice los gastos cuando su hijo ingrese a la universidad, él señor Godínez calcula hacer dicho ahorro por unos 20 años. La tasa que se estará invirtiendo dichas aportaciones será del 8% efectiva anual.

Más adelante…

Se continuará estudiando las variantes de las anualidades que aún faltan por ver, como lo son las anualidades crecientes, éstas son utilizadas cuando las empresas, deciden ir incrementando el capital que se va abonando para liquidar una deuda, con la finalidad de pagar menos intereses, por ejemplo.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior.
• Entrada siguiente.