Introducción:
Integral Indefinida
En la unidad anterior, el valor de la integral depende del intervalo de integración o, de forma análoga, de los límites de integración $[a,b]$.
Ahora, consideremos el límite inferior como un número fijo $\alpha$, que no es un número particular, es decir, que puede ser cualquiera. Y el límite superior será una variable denotada con $x$. Teniendo la siguiente notación.
$$ \phi (x) =\int \limits_{\alpha}^{x} f(u) ~ du.$$
Así que la función $\phi(x)$ se denomina como una la integral indefinida de la función $f(x)$.
De forma que la función $\phi(x)$, es una función que depende de $x$.
Anteriormente solo se concebía la integral como un número. Ahora podemos mostrar que la integral, es una función que depende de una variable independiente.
De manera análoga, se puede hacer que el límite inferior sea variable y, por lo tanto, que ambos límites puedan variables o dependan de otra función.
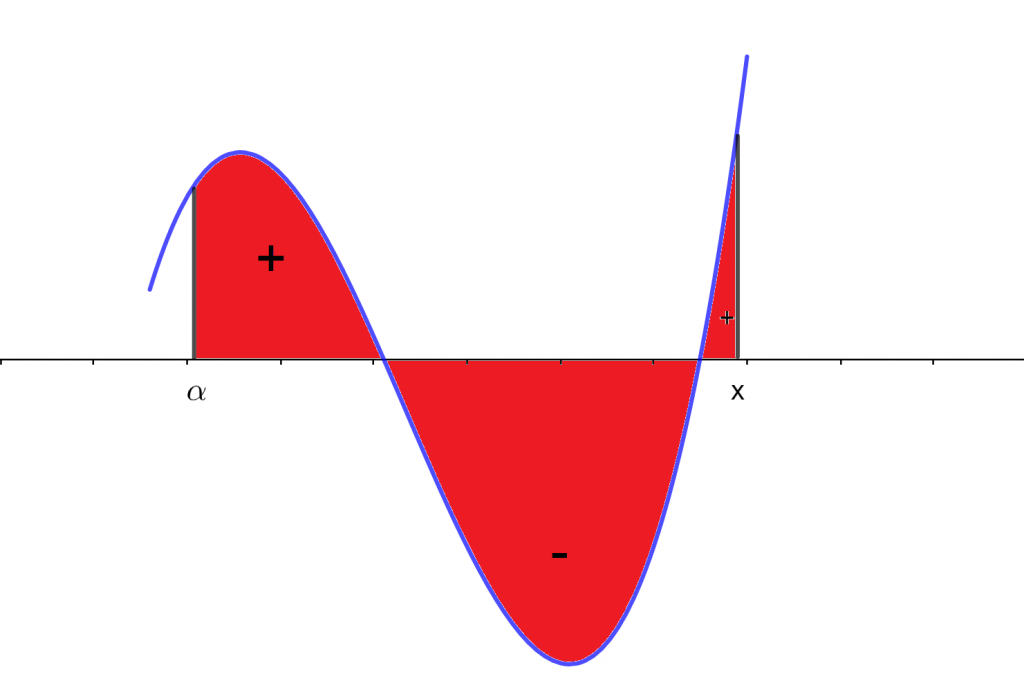
De una forma geométrica, se puede ver de la siguiente manera.
Así que la integral indefinida $ \phi (x) $ está dada por el área sombreada en rojo, que se encuentra delimitada por la curva en azul $y=f(u)$ dentro del intervalo $[\alpha , x]$.
Entonces, hasta que no se determine un valor para $x$, el valor de la integral irá cambiando.
Se debe recordar que el signo del área se determina por el cuadrante en el que se encuentra, como se vio en la Unidad 1.
Observación: Cualquier integral definida es un caso particular de una integral indefinida $\phi(x)$.
Las reglas básicas para la integral que se vieron, tienen su generalización con integrales indefinidas, por ejemplo, la suma:
$$\int \limits_a^b f(u) \ du = \int \limits_a^\alpha f(u) \ du + \int \limits_\alpha^b f(u) \ du. $$
$$= – \int \limits_\alpha^a f(u) \ du + \int \limits_\alpha^b f(u) \ du = \phi(b) \ – \ \phi(a) . $$
De esta forma queda una integral definida en términos de integrales indefinidas.
Así, se puede expresar cualquier integral indefinida con límite inferior $\alpha’$ en términos de $\phi(x)$:
$$ \int \limits_{\alpha’}^x f(u) \ du = \phi(x) \ – \ \phi({\alpha’}) . $$
En donde $\phi({\alpha’}) $ es una constante.
Por lo que se puede concluir que cualquier integral definida difiere de la integral indefinida $\phi(x)$ por una constante.
$$ \int \limits^x f(u) \ du = \phi(x) + C.$$
Donde a $C$ se le conoce como la constante de integración.
Continuidad de la integral indefinida
Sea $f(x)$ función continua en el intervalo $[a,b]$ y sea $\alpha$ un punto dentro del intervalo, i.e. $\alpha \in [a,b]$. Entonces, la integral indefinida:
$$\phi(x) = \int \limits_\alpha^x f(u) ~ du.$$
Es una función que depende de la variable $x$, la cual está definida en el intervalo.
Teorema: La integral indefinida $\phi(x)$ de una función $f(x)$ continua, es asimismo, continua.
Demostración:
Sea $x, y$ dos valores dentro del intervalo donde la función es continua.
Por el teorema del valor medio se tiene que:
$$\phi(y) \ – \ \phi(x) = \int \limits_x^y f(u) \ du = f(\xi) (y \ – \ x).$$
Donde $\xi$ es algún valor en el intervalo con puntos extremos $x$ & $y$.
Ahora, por la continuidad de $f$, obtenemos lo siguiente:
$$\lim_{y \rightarrow x} \phi(y) = \lim_{y \rightarrow x} [\phi(x) + f(\xi) (y \ – \ x) ]. $$
Separamos en límites.
$$ = \ \lim_{y \rightarrow x} \phi(x) + \lim_{y \rightarrow x} f(\xi) (y \ – \ x) . $$
Sacamos los factores que no dependen del límite.
$$ \Rightarrow = \ \phi(x) \ + \ f(\xi) ~\\ \lim_{y \rightarrow x} (y \ – \ x) . $$
$$ = \ \phi(x) + f(\xi) \cdot 0.$$
$$\therefore \lim_{y \rightarrow x} \phi(y) = \phi(x).$$
Lo que muestra que $\phi$ es continua.
$\square$
Si lo vemos dentro de cualquier intervalo cerrado, obtenemos lo siguiente.
$$|\phi(y) \ – \ \phi(x)| \leq M \ |y \ – \ x|.$$
donde $M$ es el máximo de $|f|$ en el intervalo, de modo que $\phi$ es aún Lipschitz-continua.
Si quieres recordar continuidad, sigue este link.
$\square$
Anteriormente se mencionó la siguiente ecuación.
$\phi(y) \ – \ \phi(x) = \int \limits_x^y f(u) \ du = f(\xi) (y \ – \ x).$
Observación: Si $f(x)$ es una función positiva en todo el intervalo $[x,y]$, se obtiene que $\phi(x)$ es una función creciente.
$$\phi(y) = f(\xi) (y \ – \ x) > \phi(x).$$
Más adelante…
Teniendo definidas las integrales indefinidas, podremos revisar las propiedades que estas integrales tienen y teoremas que son de alta importancia, tanto en cálculo como en las demás asignaturas.
Este paso de trabajar con integrales indefinidas nos da una mayor libertad al momento de trabajar con funciones. Anteriormente, al trabajar con integrales definidas, teníamos plena conciencia de que punto a que punto se necesitaba integrar, lo que, al momento de evaluar o de integral solo encontramos un número; pero ahora que trabajamos con integrales indefinidas.
Tarea moral
- P1
- P2
- P3
- P4
- P5
Entradas relacionadas
- Página del curso: Cálculo Diferencial e Integral II
- Entrada anterior: Introducción al curso
- Entrada siguiente: Definición de la integral definida