Introducción

En esta entrada platicaré de un lema muy útil en álgebra lineal, sobre todo cuando se están definiendo las nociones de base y de dimensión para espacios vectoriales de dimensión finita. Se trata del lema de intercambio de Steinitz.

Supondré que el lector ya sabe un poco de álgebra lineal, pero muy poquito. Basta con saber la definición de espacio vectorial. Lo demás lo definiremos sobre el camino.

El nombre del lema es en honor al matemático alemán Ernst Steinitz. Sin embargo, personalmente a mi me gusta pensarlo como el lema del «regalo de vectores», por razones que ahorita platicaremos. El enunciado es el siguiente:

Teorema (Lema de intercambio de Steinitz). Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

• $m\le n$
• Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

En pocas palabras, «cualquier conjunto linealmente independiente tiene a lo mucho tantos elementos como cualquier conjunto generador y, además, cualquier generador le puede regalar vectores al linealmente independiente para volverlo generador».

De manera esquemática, está pasando lo siguiente:

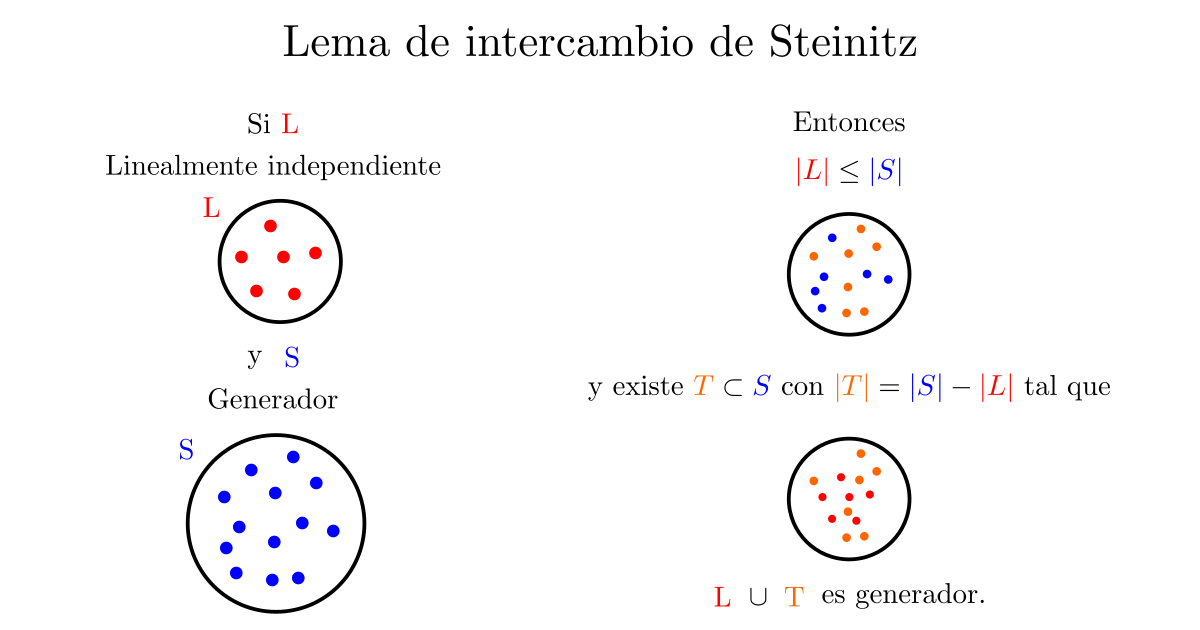
Lo que haremos es hablar de las definiciones necesarias para entender el lema, hablar de la intuición detrás, dar un par de ejemplos y luego dar la demostración. La presentación está ligeramente basada en el libro de álgebra lineal de Titu Andreescu.

Definiciones e intuición

Sea $V$ un espacio vectorial sobre un campo $F$.

Si tenemos vectores $v_1,\dots ,v_n$ de $V$ y escalares $a_1,\dots ,a_n$ en $F$, podemos considerar al vector formado por multiplicar los vectores por los escalares correspondientes y sumarlos todos, es decir al vector $v$ dado por la expresión $a_1{v}_1+\cdots +a_n{v}_n$ . En este caso, decimos que $v$ es una combinación lineal de $v_1,\dots ,v_n$, o a veces que $v_1,\dots ,v_n$ generan a $v$.

Un conjunto $S=\{v_1,v_2,\dots ,v_n\}$ de vectores de $V$ es generador si para cualquier $v$ de $V$ existen escalares $a_1,\dots ,a_n$ en $F$ para los cuales $v=a_1{v}_1+\cdots +a_n{v}_n$. Dicho de otra forma, «$S$ es generador si cualquier vector del espacio vectorial es combinación lineal de vectores de $S$».

De esta definición es fácil ver que si $S$ es un conjunto generador y $T$ es un conjunto que contiene a $S$ (es decir, $T\supset S$), entonces $T$ también es generador: simplemente para cualquier $v$ usamos la combinación lineal que tenemos en $S$ y al resto de los vectores (los de $T\setminus S$) les ponemos coeficientes cero.

Un conjunto $L=\{w_1,w_2,\dots ,w_m\}$ de vectores de $V$ es linealmente independiente si la única combinación lineal de vectores de $L$ que da $0$ es aquella en la que todos los escalares son $0$. Dicho de otra forma, «$L$ es linealmente independiente si $a_1{w}_1+\dots +a_m{w}_m=0$ implica que $a_1=a_2=\dots =a_m=0$.»

Con los conjuntos linealmente independientes pasa lo contrario a lo de los generadores. Si $L$ es un conjunto linealmente independiente y $M$ está contenido en $L$ (es decir, ahora $M\subset L$), entonces $M$ es linealmente independiente. Esto sucede pues cualquier combinación lineal de $M$ también es una combinación lineal de $L$. Como no hay ninguna combinación lineal no trivial de elementos de $L$ que sea igual a cero, entonces tampoco la hay para $M$.

Los párrafos anteriores dejan la idea de que «los conjuntos generadores tienen que ser grandes» y que «los conjuntos linealmente independientes tienen que ser chiquitos». El lema de intercambio de Steinitz es una manera en la que podemos formalizar esta intuición.

Como los conjuntos generadores son «grandes», entonces son bien buena onda y bien generosos. Tienen muchos elementos. Como los conjuntos linealmente independientes son «chiquitos», entonces necesitan elementos. Lo que dice el lema de intercambio de Steinitz es que si tenemos a un generador $S$ y a un linealmente independiente $L$, entonces $S$ tiene más elementos y que puede regalar al linealmente independiente $L$ algunos elementos $T$ para que ahora $L\cup T$ tenga tantos elementos como tenía $S$ y además se vuelva generador. Una cosa importante es que no cualquier subconjunto $T$ funciona. Este tiene que estar bien elegido.

Ejemplo concreto del lema de intercamio de Steinitz

Veamos un ejemplo muy concreto. Supongamos que nuestro espacio vectorial es ${\mathbb{R}}^3$, osea, los vectores con $3$ entradas reales. Tomemos a los siguientes conjuntos de vectores:

• $L=\{(1,2,3),(0,3,0)\}$
• $S=\{(0,1,0),(1,0,0),(0,0,-1),(2,4,6)\}$

Por un lado, el conjunto $L$ es linealmente idependiente. Una combinación lineal $a(1,2,3)+b(0,3,0)=(0,0,0)$ implica de manera directa que $a=0$ (por la primer o tercer coordenadas) y de ahí $b=0$ (por la segunda coordenada).

Por otro lado, el conjunto $S$ es generador, pues con $(0,0,-1)$ podemos obtener a $(0,0,1)$ como combinación lineal, de modo que $S$ genera a los tres de la base canónica y por tanto genera a todo ${\mathbb{R}}^3$.

Notemos que en efecto $L$ tiene menos elementos que $S$. Además, el lema de intercambio de Steinitz garantiza que $S$ puede pasarle $|S|-|L|=4-2=2$ elementos a $L$ para volverlo generador. Pero hay que ser cuidadosos. Si le regala los elementos $(0,1,0)$ y $(2,4,6)$, entonces no funciona (se puede verificar que este conjunto no genera a ${\mathbb{R}}^3$). Pero si le regala, por ejemplo, los elementos $(1,0,0)$ y $(0,0,-1)$ entonces ahora sí generará (se puede argumentar viendo que entonces ahora genera a los tres de la base canónica).

Demostración del lema de intercambio de Steinitz

Pasemos ahora a la demostración del lema de Steinitz. Lo demostraremos por inducción en la cantidad de elementos que tiene $L$, el linealmente independiente. Si $|L|=m=0$, entonces claramente $m=0\le n$, y además $S$ le puede pasar $n-0=n$ elementos (todos) a $L$ y volverlo generador.

Supongamos entonces que es cierta la siguiente afirmación.

Hipótesis inductiva Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

• $m\le n$
• Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

Para el paso inductivo, tomemos $L=\{w_1,w_2,\dots ,w_m,w_{m+1}\}$ un linealmente independiente de $V$ y $S=\{v_1,v_2,\dots ,v_n\}$ un generador de $V$. Aplicándole la hipótesis inductiva al linealmente independiente $L^{\prime }=L\setminus \{w_{m+1}\}=\{w_1,\dots ,w_m\}$ y al generador $S$, tenemos que:

• $m\le n$
• Se puede tomar un subconjunto $T^{\prime }=\{s_1,s_2,\dots ,s_{n-m}\}$ de $S$ tal que $L^{\prime }\cup T^{\prime }=\{w_1,w_2,\dots ,w_m,s_1,\dots ,s_{n-m}\}$ sea generador de $V$.

Como $L^{\prime }\cup T^{\prime }$ es generador, entonces podemos poner a $w_{m+1}$ como combinación lineal de elementos de $L^{\prime }\cup T^{\prime }$, es decir, existen $a_1,\dots ,a_m,b_1,\dots ,b_{n-m}$ tales que $$w_{m+1}=a_1{w}_1+\dots +a_m{w}_m+b_1{s}_1+\dots +b_{n-m}{s}_{n-m}.$$

Ya sabemos que $m\le n$. Si $m=n$, la combinación lineal anterior no tendría ningún $s_i$, y entonces sería una combinación lineal no trivial para los elementos de $L$, lo cual es una contradicción pues $L$ es linealmente independiente. Entonces $m\ne n$ y $m\le n$, así que $m+1\le n$, que era el primer punto que queríamos probar.

También, como $L$ es linealmente independiente, no se vale que todos los $b_i$ sean iguales a cero. Sin perder generalidad, podemos suponer que $b_1\ne 0$. Así, $s_1$ se puede despejar como combinación lineal en términos de $w_1,\dots ,w_n,w_{n+1},s_2,\dots ,s_{n-m}$ y por lo tanto $L\cup (T^{\prime }\setminus \{s_1\})$ genera lo mismo que $L^{\prime }\cup T^{\prime }$, que era todo $V$. Así, $T:=T^{\prime }\setminus \{s_1\}$ es el subconjunto de $S$ de tamaño $n-(m+1)$ tal que $L\cup T$ es generador. Esto termina la prueba del lema.

Algunas aplicaciones

El lema de intercambio de Steinitz se puede utilizar para probar varias afirmaciones con respecto a bases de un espacio vectorial de dimensión finita.

Un espacio vectorial es de dimensión finita si tiene un conjunto generador con una cantidad finita de elementos. Una base de un espacio vectorial es un conjunto que sea simultáneamente generador y linealmente independiente.

Las siguientes afirmaciones se siguen directamente del lema de Steinitz.

1. Todas las bases de un espacio vectorial finito tienen la misma cantidad de elementos.
2. En un espacio vectorial de dimensión $d$:
   • Todo conjunto linealmente independiente tiene a lo más $d$ elementos.
   • Todo conjunto generador tiene al menos $d$ elementos.
3. Si $S$ es un conjunto con $n$ vectores de un espacio vectorial de dimensión $n$, entonces las siguientes tres afirmaciones son equivalentes:
   • El conjunto $S$ es base.
   • $S$ es linealmente independiente.
   • $S$ es generador.

Como primer ejemplo, haremos (1). Tomemos $B_1$ y $B_2$ bases de un espacio vectorial de dimensión finita $B$. Pensando a $B_1$ como linealmente independiente y a $B_2$ como generador, tenemos $|B_1|\le |B_2|$. Pensando a $B_2$ como linealmente independiente y a $B_1$ como generador, tenemos $|B_2|\le |B_1|$. Así, $|B_1|=|B_2|$.

Como segundo ejemplo, haremos una parte de (3). Suponiendo que $S$ es un conjunto de $n$ vectores de un espacio vectorial de dimensión $n$, veremos que su independencia lineal implica $S$ es base. Sea $B$ una base de $V$. Por el lema de Steinitz, podemos pasar $|B|-|S|=n-n=0$ elementos de $B$ a $S$ para volverlo generador. Es decir, $S$ ya es generador. Como además es linealmente independiente, entonces es base.

El resto de las demostraciones son igual de sencillas, como puedes verificar.

Más adelante…

El lema de Steinitz es la herramienta clave para definir dar la definición de dimensión de espacios vectoriales en el caso de dimensión finita. Lo usaremos una y otra vez. Por esta razón, es muy recomendable repasar su demostración y entender a profundidad qué dice.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• Replica por tu cuenta la demostración del lema de Steinitz hasta que te sientas cómodo con los argumentos.
• En el ejemplo que se dio de la aplicación del lema de Steinitz, ¿cuáles son todas las posibilidades de $2$ elementos que se pueden pasar para que $L$ se convierta en generador?
• Usa el lema de Steinitz para demostrar el resto de consecuencias que mencionamos.
• ¿Qué te dice el lema de Steinitz cuando $L$ y $S$ son inicialmente del mismo tamaño?
• Muestra que en el lema de Steinitz la hipótesis de que $L$ sea finito no es necesaria, es decir, que incluso sin esta hipótesis se pueden mostrar todas las conclusiones.

Entradas relacionadas

• Ir a Álgebra Lineal I
• Entrada anterior del curso: Problemas de combinaciones lineales, generadores e independientes
• Siguiente entrada del curso: Bases y dimensión de espacios vectoriales

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

• Mariposa de 7 equivalencias de matrices invertibles
• Una demostración del teorema de la función inversa
• Un ejemplo de aplicación del teorema de la función inversa
• Los teoremas fundamentales de los cuadraditos, o bien, una introducción amigable a los teoremas fundamentales del cálculo
• Un problema de probabilidad y escuchar música
• Mariposa de siete equivalencias de invertibilidad de matrices

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»