Introducción
Decimos que un cuadrilátero convexo es bicéntrico si es circunscrito y cíclico al mismo tiempo. Ahora que hemos estudiado a los cuadriláteros cíclicos y cuadriláteros circunscritos por separado, nos podemos preguntar cuando un cuadrilátero cumple con ambas definiciones y que propiedades tiene, en esta entrada abordaremos este tema.
Dos caracterizaciones para el cuadrilátero bicéntrico
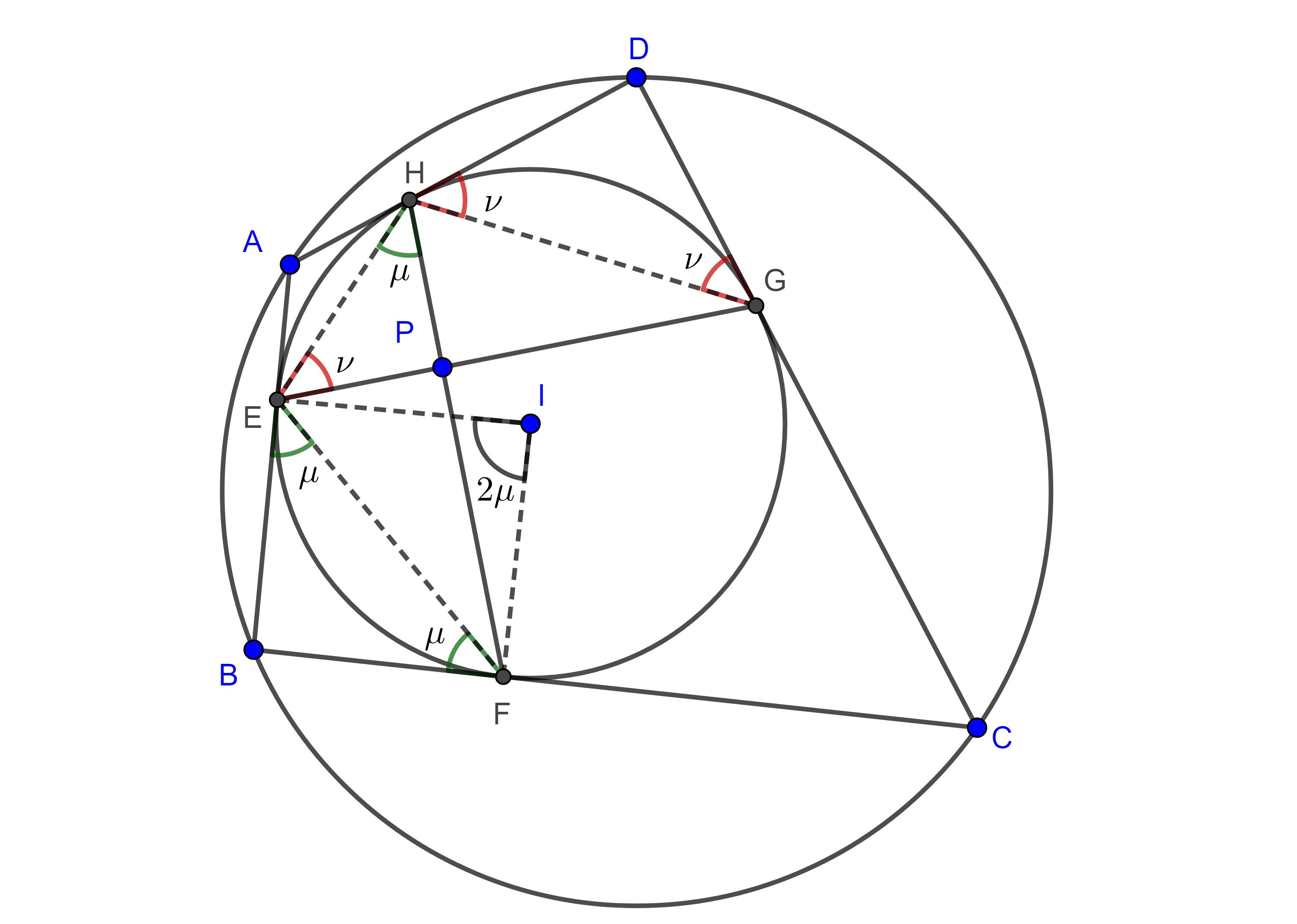
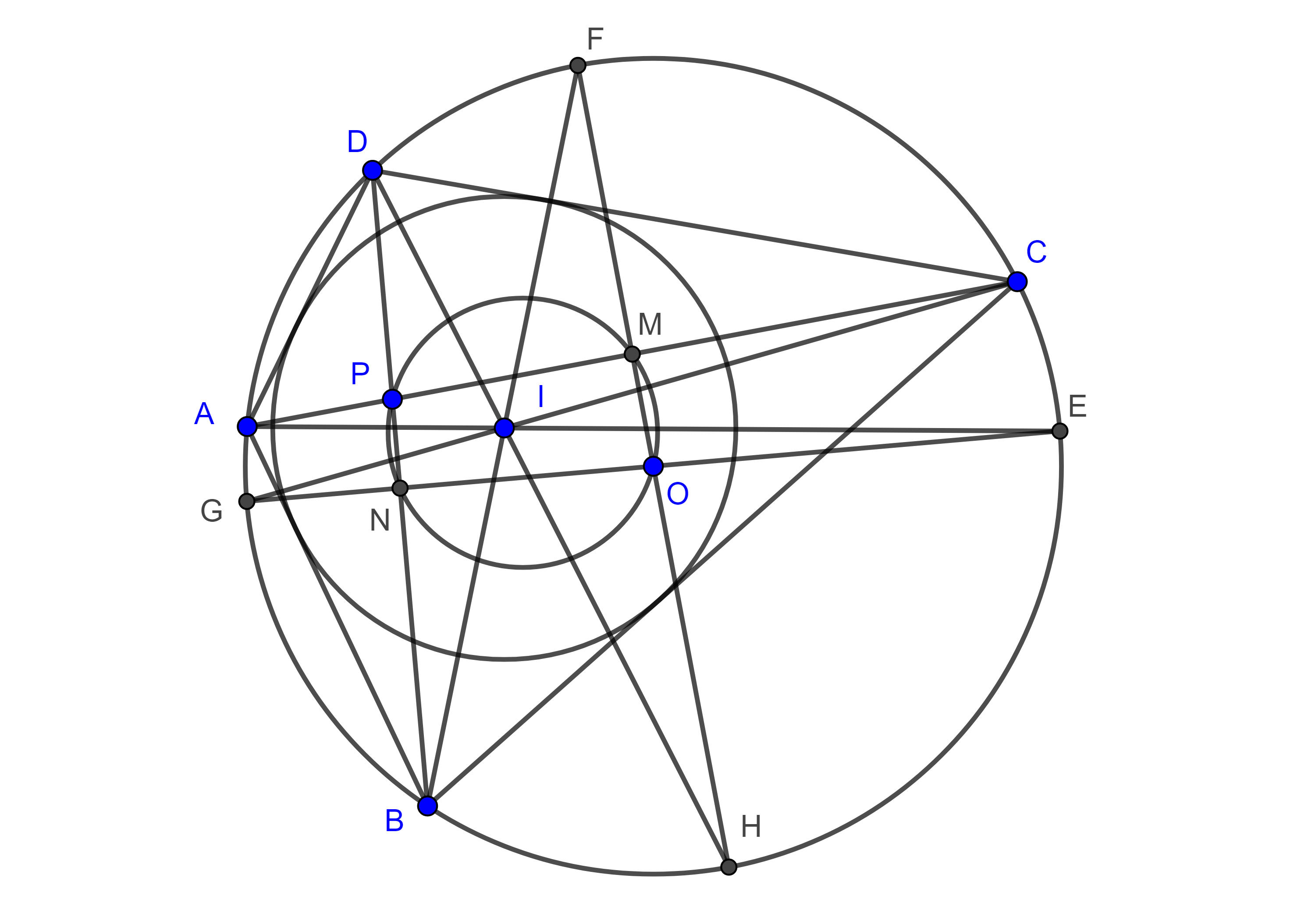
Teorema 1. Sea $\square ABCD$ un cuadrilátero circunscrito y sean $E$, $F$, $G$ y $H$ los puntos de tangencia del incírculo a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, entonces $\square ABCD$ es bicéntrico si y solo si $EG \perp FH$.
Demostración. $\angle BEF$ y $\angle EFB$ son ángulos semiinscritos que abarcan el mismo arco, $\overset{\LARGE{\frown}}{EF}$, por lo tanto, son iguales $\angle BEF = \angle EFB = \mu$.
De manera análoga tenemos que, $\angle DGH = \angle GHD = \nu$.
Así que en los triángulos $\triangle BEF$ y $\triangle DHG$ se tiene $\pi = \angle B + 2 \mu = \angle D + 2 \nu$ por lo que
$\begin{equation} 2\pi = \angle B + \angle D + 2(\mu + \nu). \end{equation}$
Ahora supongamos que $EG$ y $FH$ son perpendiculares, y sea $P = EG \cap FH$, entonces $\angle HPE =\dfrac{\pi}{2}$, así que en $\triangle HPE$, $\dfrac{\pi}{2} = \angle PEH + \angle EHP$.
Pero $\angle EHF$ y $\angle BEF$ abren el mismo arco, por lo tanto, $\angle EHF = \mu$, de manera similar $\angle GEH = \nu$, por lo tanto $\mu + \nu = \dfrac{\pi}{2}$.
Sustituyendo la ultima igualdad en $(1)$ tenemos
$2\pi = \angle B + \angle D + \pi$
$\Leftrightarrow \angle B + \angle D = \pi$
$\Leftrightarrow \square ABCD$ es cíclico.
La proposición reciproca se muestra tomando en sentido contrario la prueba.
$\blacksquare$
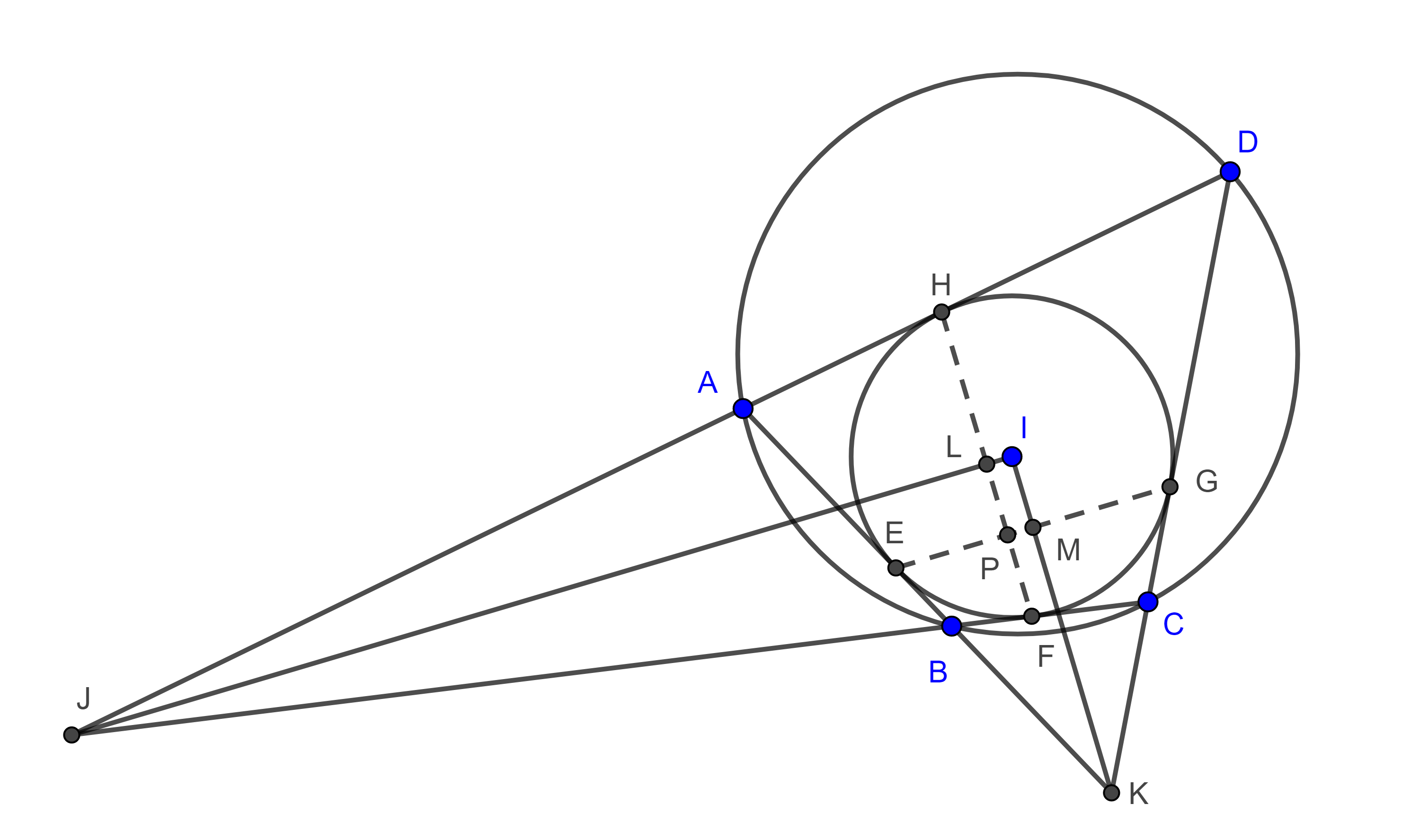
Teorema 2. Sea $\square ABCD$ circunscrito, $I$ su incentro, $K$ y $J$ las intersecciones de los lados $AB$ con $DC$ y $AD$ con $BC$ respectivamente entonces $\square ABCD$ es bicéntrico si y solo si $IK \perp IJ$.
Demostración. Notemos que el incírculo de $\square ABCD$ es al mismo tiempo el excentro de $\triangle AJB$ y $\triangle BKC$ opuesto a los vértices $J$ y $K$ respectivamente.
Esto implica que $IJ$ e $IK$ son las bisectrices internas de $\angle J$ y $\angle K$ respectivamente.
Sean $E$, $F$, $G$ y $H$ los puntos de contacto del incírculo con $AB$, $BC$, $CD$ y $DA$ respectivamente, en la prueba del teorema anterior vimos que $\angle JHF = \angle HFJ$ y $\angle EGK = \angle KEG$.
Por lo tanto, $\triangle JHF$ y $\triangle KEG$ son isósceles.
Entonces las bisectrices de $\angle J$ y $\angle K$ son mediatrices de $FH$ y $EG$ respectivamente.
En consecuencia, $JL \perp FH$ y $KM \perp EG$, donde $L$ y $M$ son los puntos medios de $FH$ y $EG$ respectivamente.
De esto último se sigue que en el cuadrilátero $\square LPMI$, $\angle LIM + \angle MPL =\pi$.
Por lo tanto, $IJ \perp IK \Leftrightarrow FH \perp EG \Leftrightarrow \square ABCD$ es bicéntrico.
La última doble implicación se da por el teorema 1.
$\blacksquare$
Teorema de Fuss
Teorema 3, de Fuss. En un cuadrilátero bicéntrico el circunradio $R$, el inradio $r$ y la distancia $d$ entre el circuncentro y el incentro se relacionan mediante la siguiente expresión:
$\dfrac{1}{(R + d)^2} + \dfrac{1}{(R – d)^2} = \dfrac{1}{r^2}$.
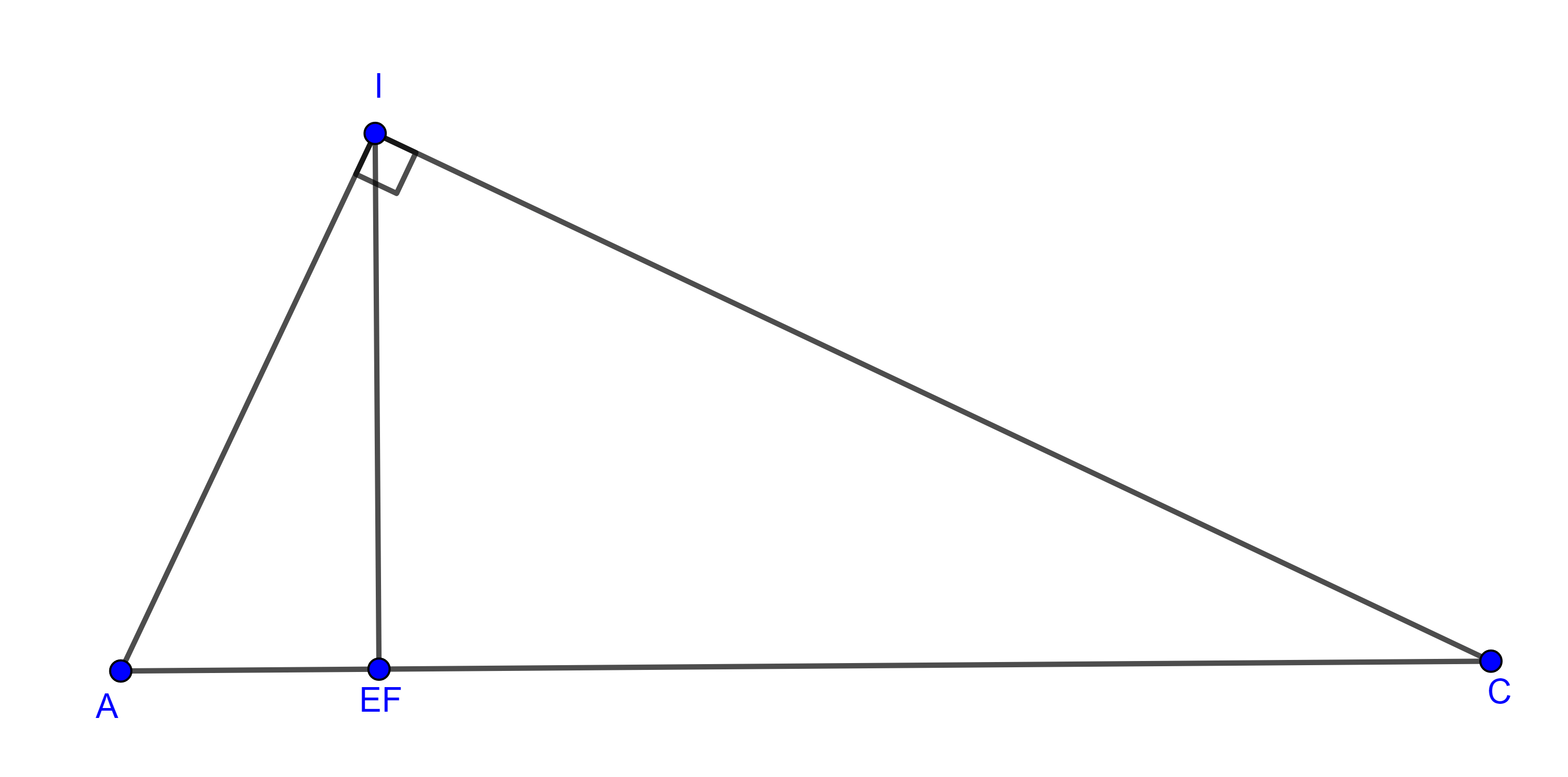
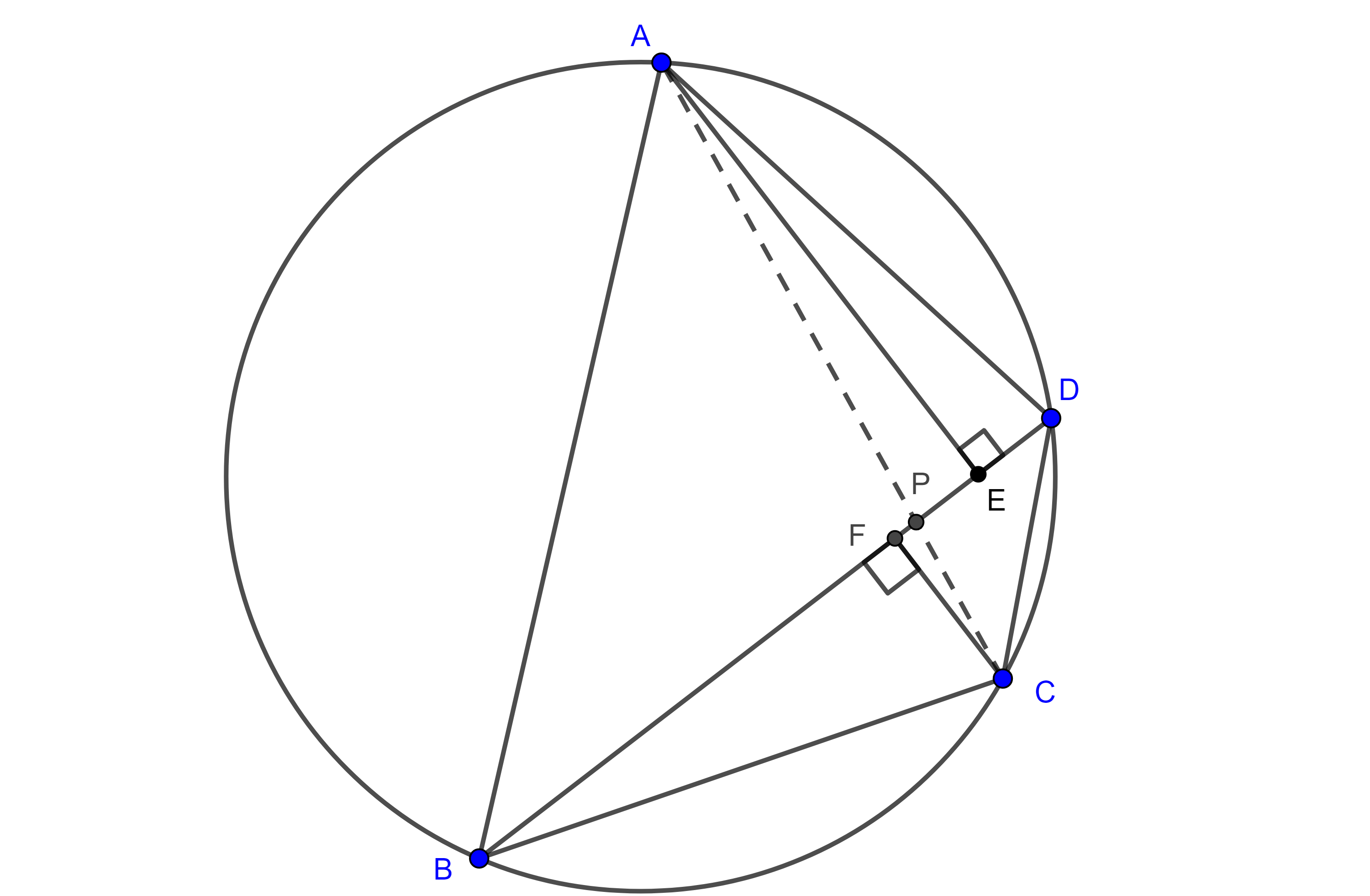
Demostración. Sean $\square ABCD$ bicéntrico, $(O, R)$, $(I, r)$ el circuncírculo y el incírculo respectivamente, $E$ y $F$ los puntos de tangencia de los lados $AB$ y $BC$ respectivamente con $(I, r)$.
Dado que $\square ABCD$ es cíclico, entonces $\angle A + \angle C = \pi$ y como $I$ es la intersección de las bisectrices internas de $\square ABCD$ tenemos lo siguiente:
$\begin{equation} \angle EAI + \angle ICF = \dfrac{\pi}{2}. \end{equation}$
Como $\triangle AEI$ y $\triangle CFI$ son triángulos rectángulos y tienen la misma altura desde $I$.
Al “pegar” los triángulos $\triangle AEI$ y $\triangle CFI$ por la altura formamos un triángulo rectángulo $\triangle ACI$ cuya área es :
$(\triangle ACI) = \dfrac{(AE + FC)r}{2} = \dfrac{AI \times CI}{2}$
$\Leftrightarrow (AE + FC)^2r^2 = AI^2 \times CI^2$.
Podemos calcular $AC$ aplicando el teorema de Pitágoras
$AI^2 + CI^2 = AC^2 = (AE + FC)^2$.
De las últimas dos expresiones obtenemos $(AI^2 + CI^2)r^2 = AI^2 \times CI^2 \Leftrightarrow$
$\begin{equation} \dfrac{1}{AI^2} + \dfrac{1}{CI^2} = \dfrac{1}{r^2}. \end{equation}$
Consideremos $G$ y $H$ los puntos donde $AI$ y $CI$ intersecan a $(O, R)$.
$\angle HAB = \angle HCB = \angle ICF$ pues son subtendidos por el mismo arco.
Por la ecuación $(2)$,
$\angle HAG = \angle HAB + \angle BAG = \angle ICF + \angle EAI = \dfrac{\pi}{2}$,
por lo tanto, $HG$ es diámetro.
Con el teorema de Apolonio calculamos la mediana $IO$ en $\triangle IHG$
$\begin{equation} IH^2 + IG^2 = 2IO^2 + \dfrac{HG^2}{2} = 2d^2 + \dfrac{(2R)^2}{2} = 2(d^2 + R^2). \end{equation}$
Como $\square AHGC$ es cíclico, entonces
$\begin{equation} AI \times GI = HI \times CI = d^2 – R^2. \end{equation}$
Donde la última igualdad se debe a la potencia de $I$ respecto de $(O, R)$.
De $(4)$ y $(5)$ obtenemos
$\dfrac{1}{AI^2} + \dfrac{1}{CI^2} = \dfrac{GI^2}{(R^2 – d^2)^2} + \dfrac{HI^2}{(R^2 – d^2)^2}$
$= \dfrac{GI^2 + HI^2}{(R^2 – d^2)^2} = \dfrac{2(d^2 + R^2)}{(R^2 – d^2)^2} = \dfrac{(R + d)^2 + (R – d)^2}{(R^2 – d^2)^2}$
$\begin{equation} = \dfrac{1}{(R + d)^2} + \dfrac{1}{(R – d)^2}. \end{equation}$
De $(3)$ y $(6)$ obtenemos la relación buscada
$\dfrac{1}{r^2} = \dfrac{1}{(R + d)^2} + \dfrac{1}{(R – d)^2}$.
$\blacksquare$
Puntos colineales en el cuadrilátero bicéntrico
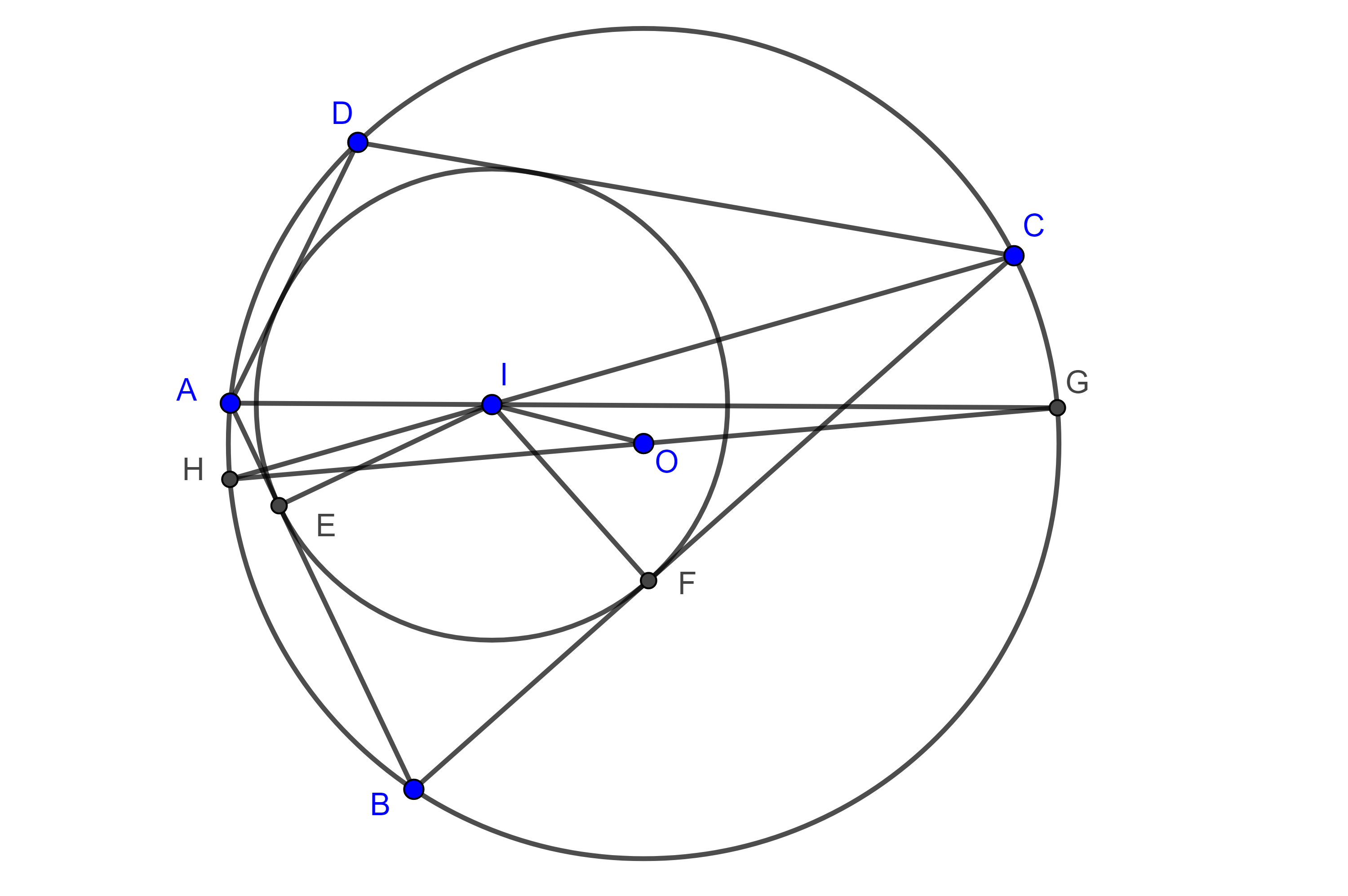
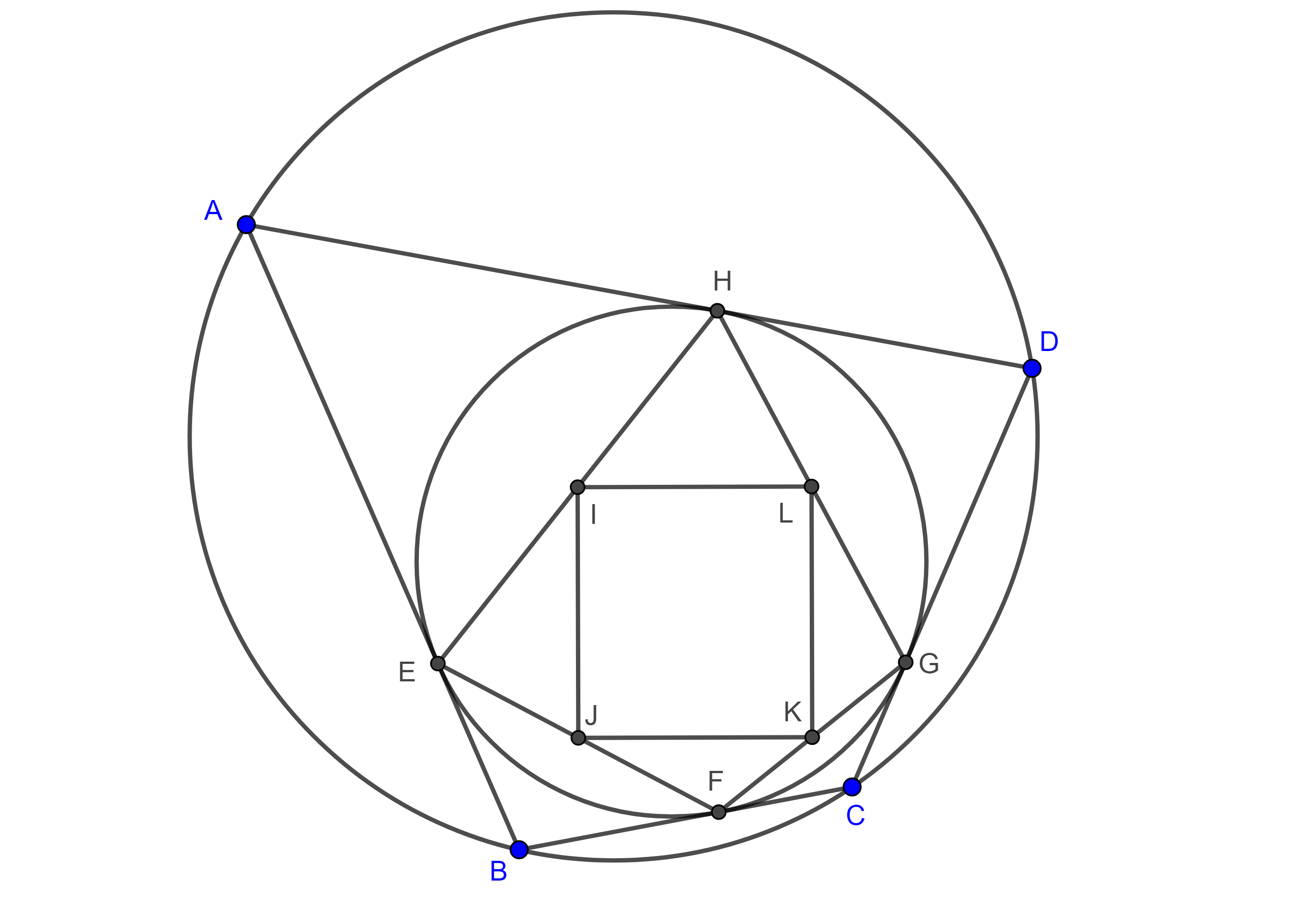
Teorema 4. En un cuadrilátero bicéntrico el incentro, el circuncentro y la intersección de las diagonales son colineales.
Demostración. Sean $\square ABCD$ bicéntrico, $I$, $O$, su incentro y circuncentro respectivamente y consideremos $E$, $F$, $G$ y $H$ las intersecciones de $AI$, $BI$, $CI$ y $DI$ con $(O, R)$, el circuncírculo de $\square ABCD$, respectivamente.
En $\triangle GDB$ la mediatriz de $BD$ pasa por $N$ el punto medio de $BD$ y $O$, y la mediana por $G$ pasa por $G$ y $N$.
Como $CG$ es bisectriz de $\angle DCB$, entonces $\angle DBG = \angle DCG = \angle GCB = \angle GDB$, por tanto, $\triangle GBD$ es isósceles y así la mediatriz de $BD$ y la mediana por $G$ coinciden, por lo que $G$, $N$ y $O$ son colineales, al mismo tiempo que esta recta es diámetro pues pasa por $O$.
En la prueba del teorema de Fuss vimos que $GE$ es diámetro por lo tanto $G$, $N$, $O$ y $E$ son colineales además $\angle ONP = \dfrac{\pi}{2}$ donde $P$ es la intersección de las diagonales $AC$ y $BD$.
De manera análoga $F$, $M$, $O$ y $H$ son colineales donde $M$ es el punto medio de $AC$ y $\angle PMO = \dfrac{\pi}{2}$.
Se sigue que $\square PNOM$ es cíclico, por lo tanto
$\begin{equation} \angle MNP = \angle MOP. \end{equation}$
Por otro lado, como $\square DBHF$ es cíclico e $I$ es la intersección de las diagonales, por construcción, se sigue que $\triangle IBD \sim \triangle IHF$, son semejantes.
$\Rightarrow \dfrac{IB}{IH} = \dfrac{BD}{FH} = \dfrac{\dfrac{1}{2}BD}{\dfrac{1}{2}FH} = \dfrac{BN}{OH}$ y como $\angle IBN = \angle OHI$, por criterio de semejanza LAL, $\triangle IBN \sim \triangle IHO$.
Por lo tanto, $\angle BNI = \angle IOH$ y así
$\begin{equation} \angle INP = \angle MOI. \end{equation}$
Por el teorema de Newton, sabemos que $N$, $I$ y $M$ son colineales, además $I$ se encuentra entre $N$ y $M$.
Por las ecuaciones $(7)$ y $(8)$ tenemos
$\angle MOI = \angle INP = \angle MNP = \angle MOP$.
Es decir, el ángulo que forman las rectas $IO$ y $MO$ es el mismo ángulo que forman las rectas $PO$ y $MO$, por lo tanto $IO$ y $PO$ son la misma recta, y así los puntos $I$, $O$ y $P$ son colineales.
$\blacksquare$
Acotando el área del cuadrilátero bicéntrico
Teorema 5. El área de un cuadrilátero bicéntrico $\square ABCD$ con inradio $r$ y circunradio $R$ cumple la siguiente desigualdad:
$4r^2 \leq (\square ABCD) \leq 2R^2$.
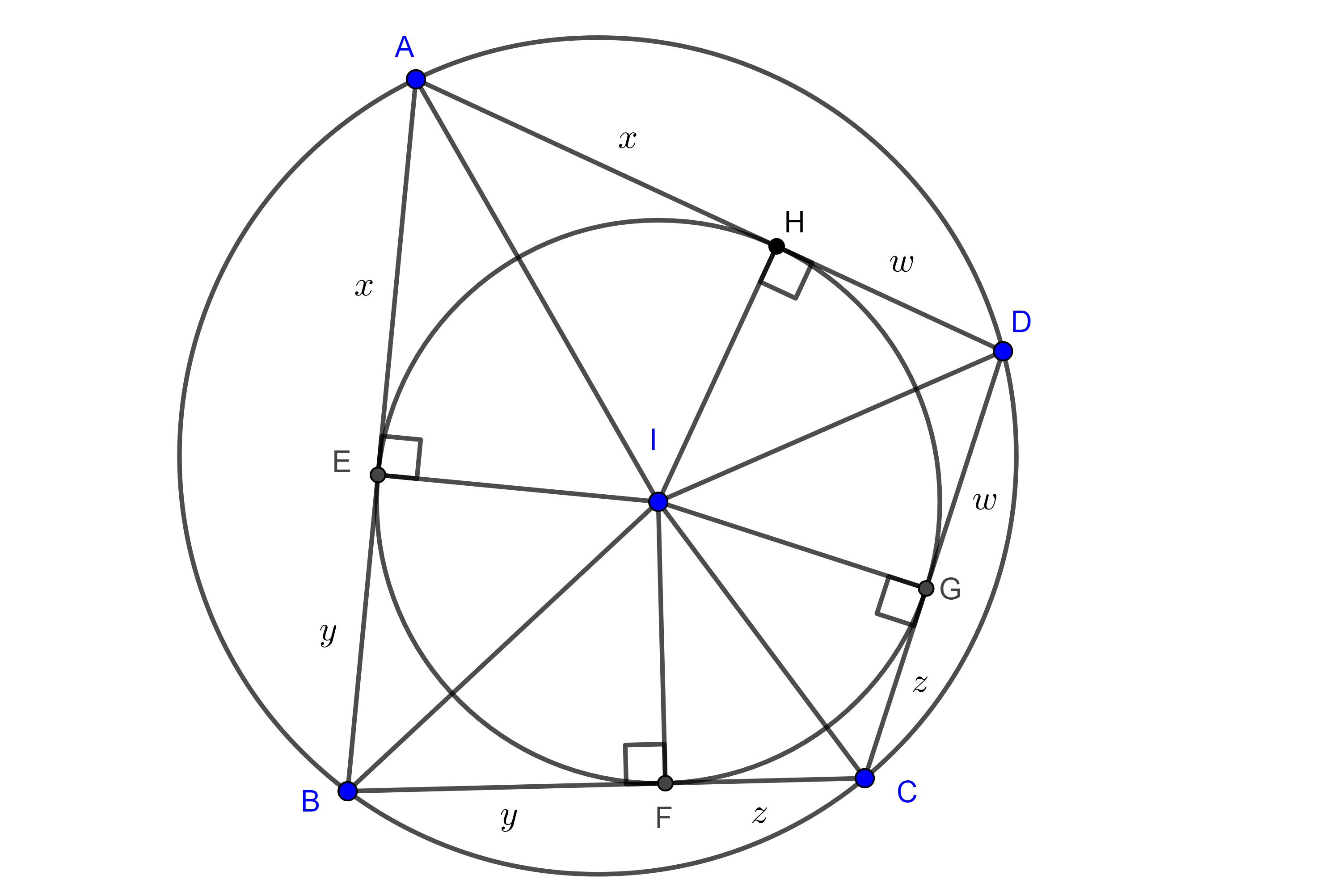
Demostración. Primero veamos que $4r^2 \leq (\square ABCD)$, sean $E$, $F$, $G$ y $H$ los puntos de tangencia del incírculo con los lados $AB$, $BC$, $CD$ y $AD$ respectivamente.
Como las tangentes desde un punto a una circunferencia son iguales tenemos
$AE = AH = x$, $BE = BF = y$, $CF = CG = z$ y $DG = DH = w$.
En la demostración del teorema de Fuss vimos que $\angle IAH + \angle GCI = \dfrac{\pi}{2}$ de esto se sigue que $\triangle IHA$ y $\triangle CGI$ son semejantes
$\Rightarrow \dfrac{r}{z} = \dfrac{x}{r} \Leftrightarrow r^2 = xz$.
De manera análoga vemos que $r^2 = yw$.
Aplicando la desigualdad entre la media aritmética y la media geométrica obtenemos
$(\square ABCD) = 2((\triangle IAE) + (\triangle IBF) + (\triangle ICG) + (\triangle IDH))$
$= r(x + y + z + w)$
$ = 2r (\dfrac{x + z}{2} + \dfrac{y + w}{2}) \geq 2r(\sqrt{xz} + \sqrt{yw})$
$ = (2r)(2r) = 4r^2$.
Donde la igualdad se da si y solo si $x = y = z = w = r$, si esto es así entonces $\triangle ADC$ es isósceles, entonces, $\angle IAH = \angle GCI = \dfrac{\pi}{4}$.
Por lo tanto, $\angle A= \angle C = \dfrac{\pi}{2}$.
Del mismo modo vemos que $\angle B = \angle C = \dfrac{\pi}{2}$, y así, $\square ABCD$ es un cuadrado.
$\blacksquare$
Ahora veamos que $(\square ABCD) \leq 2R^2$, tracemos la diagonal $BD$ y sean $E$ y $F$ los pies de las perpendiculares a $BD$ trazadas desde $A$ y $C$ respectivamente y $P$ la intersección de las diagonales.
Por el teorema de Pitágoras, $AE \leq AP$ y $CF \leq CP \Rightarrow AE + CF \leq AC$
y se tiene la igualdad si y solo si las diagonales son perpendiculares.
Luego,
$(\square ABCD) = (\triangle ABD) + (\triangle CBD) $
$= \dfrac{BD}{2}(AE + CF) \leq \dfrac{AC \times BD}{2}$.
Como $\square ABCD$ es cíclico entonces cada diagonal es menor o igual que el diámetro $2R$ del circuncírculo.
Por lo tanto $(\square ABCD) \leq 2R^2$, donde la igualdad se da si y solo si las diagonales son perpendiculares y son diámetros del circuncírculo, es decir, $\square ABCD$ es un cuadrado.
$\blacksquare$
Más adelante…
En la siguiente entrada veremos una generalización del teorema de Ptolomeo, el teorema de Casey.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Muestra que para un cuadrilátero bicéntrico $\square ABCD$ de lados $a$, $b$, $c$ y $d$, diagonales $p$ y $q$, inradio $r$ y circunradio $R$ se tiene:
$i)$ $(\square ABCD) = \sqrt{abcd}$,
$ii)$ $8pq \leq (a + b + c + d)^2$,
$iii)$ $\sqrt{2}r \leq R$. - Sea $\square ABCD$ un cuadrilátero circunscrito y sean $E$, $F$, $G$ y $H$ los puntos de tangencia del incírculo a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, considera los puntos medios $I$, $J$, $K$ y $L$ de los segmentos $HE$, $EF$, $FG$ y $GH$ respectivamente muestra que $\square ABCD$ es cíclico si y solo si $\square IJKL$ es un rectángulo.
- Sea $\square ABCD$ bicéntrico, $(I, r)$ el incírculo y $P$ la intersección de las diagonales, muestra que:
$i)$ $\dfrac{1}{AI^2} + \dfrac{1}{CI^2} = \dfrac{1}{BI^2} + \dfrac{1}{DI^2} = \dfrac{1}{r^2}$,
$ii)$ $\dfrac{AP}{CP} = \dfrac{AI^2}{CI^2}$ , $Wikipedia\dfrac{BP}{DP} = \dfrac{BI^2}{DI^2}$. - Construye un cuadrilátero bicéntrico.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Cuadrilátero circunscrito.
- Siguiente entrada del curso: Teorema de Casey.
- Otros cursos.
Fuentes
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 38-42.
- Alsina, C. y Nelsen, R., When less is more: visualizing basic inequalities. Mathematical Association of America. 2009, pp 64–66.
- Josefsson, M., Characterizations of Bicentric Quadrilaterals. Forum Geometricorum. 2010, vol 10, pp 165–173.
- Cut the Knot
- Wikipedia
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»