(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
La entrada de Relación de equivalencia dada por un subgrupo e índice de H en G la comenzamos usando a los enteros como motivación. Aquí haremos lo mismo.
Sabemos que $(\z, +_\z)$ es un grupo y que el conjunto $n\z$ es un subgrupo de $\z$ formado por los múltiplos de $n$. Ahora, recordemos lo que son los enteros módulo $n$ denotados por $\z_n$. Supongamos que tenemos $a,b\in \z$, las clases de equivalencia de $a$ y $b$ módulo $n$ se definen de la siguiente manera:
\begin{align*}
\bar{a} = a + n\z, \quad \bar{b} = b + n\z.
\end{align*}
La notación $a + n\z$ y $b + n\z$ se puede entender como clases laterales izquierdas de $n\z$. Pero en lugar de usar la notación multiplicativa que hemos estado usando, en esta ocasión usamos una notación aditiva para representarlas. Es decir, si consideramos $G = \z$ un grupo y $H = n\z$ un subgrupo de $G$, la clase de equivalencia $aH$ sería $a + n\z$.
Cuando queremos sumar dos clases de equivalencia, usamos la suma usual en $\z$. Digamos
\begin{align*}
\bar{a} + \bar{b} = \overline{a+b}.
\end{align*}
Aunque lo escribamos así, en realidad lo que estamos haciendo, es definir la suma $$+_n: \z_n \times \z_n \to \z_n$$ usando $+_\z$ que es la suma del grupo $(\z,+_\z)$. Entonces lo anterior quedaría:
\begin{align*}
\bar{a} +_n \bar{b} = \overline{a+_\z b}.
\end{align*}
Resulta que $+_n$ es una operación bien definida y $(\z_n,+_n)$ es un grupo.
Otra manera de escribirlo sería:
\begin{align*}
(a+n\z) +_n (b+n\z) = (a+_\z b) + n\z.
\end{align*}
Lo que nos da una suma de dos clases laterales izquierdas (con notación aditiva) de $n\z$.
Ahora nos preguntamos, ¿cómo podemos generalizar esta propiedad?
Tomemos $G$ un grupo y $H$ un subgrupo y consideremos dos clases laterales izquierdas de $H$, digamos $aH$ y $bH$. En caso de ser posible, lo que queremos es definir un producto entre clases del siguiente modo:
\begin{align*}
aH \cdot_H bH = ab H.
\end{align*}
Donde $\cdot_H$ es el nuevo producto entre clases y $ab$ se hace con el producto en $G$.
Sin embargo, debemos verificar que este producto $\cdot_H$ esté bien definido. Para ello tenemos que ver que no depende de los representantes elegidos. Tomemos entonces otros representantes de las clases, para simplificarlo, cambiemos sólo el representante de una de las dos clases, digamos $\tilde{a}\in G$ tal que $\tilde{a}H = aH$.
Entonces, quisiéramos que $abH = \tilde{a}bH$, pero esto sucedería sólo de la siguiente manera,
\begin{align*}
abH = \tilde{a}b H \Leftrightarrow\;& (ab)^{-1} \tilde{a}b\in H\\
\Leftrightarrow\;& b^{-1}a^{-1}\tilde{a}b\in H.
\end{align*}
Entonces, ¿cómo sabemos que $b^{-1}a^{-1}\tilde{a}b\in H$? Lo que sí sabemos es que $a^{-1}\tilde{a} \in H$, pues $\tilde{a}H= aH$. Entonces, bastaría pedir que si $h\in H$, al multiplicar a $h$ a un lado por un elemento de $G$, y al otro por su inverso, sigamos obteniendo elementos en $H$.
En esta entrada usaremos la idea anterior para definir un producto entre dos clases izquierdas usando el producto en $G$.
Subgrupos normales
Primero necesitamos definir formalmente qué es un conjugado.
Definición. Sean $G$ un grupo y $b,c \in G$. Decimos que $b$ es conjugado de $c$ si $b = aca^{-1}$ para alguna $a\in G$.
Dado $a\in G$ y $H$ un subgrupo de $G$,el conjugado de $H$ por el elemento $a$ es
$$aHa^{-1} = \{aha^{-1}|h\in H\}.$$
Observación. $aHa^{-1}$ es un subgrupo de $G$, para toda $a \in G$.
La demostración de esta observación queda de tarea moral.
Definición. Sean $G$ un grupo y $N$ subgrupo de $G$. Decimos que $N$ es normal en $G$ si $ana^{-1} \in N$ para todas $a\in G$, $n\in N$.
Notación. $N\unlhd G$.
Ahora, veamos una proposición. Recordemos que en una entrada pasada vimos que las clases laterales izquierdas no siempre coinciden con las clases laterales derechas y dimos algunos ejemplos. La siguiente proposición nos dirá que con subgrupos normales, la igualdad de clases derechas e izquierdas siempre se da.
Proposición. Sean $G$ un grupo y $N$ subgrupo de $G$. Las siguientes condiciones son equivalentes:
- $N\unlhd G$.
- $a N a^{-1} = N$ para todo $a\in G$.
- Para toda $a \in G$, $aN = Na$.
Demostración.
Sean $G$ un grupo y $N \leq G$.
$|1) \Rightarrow 2)]$ Supongamos que $N \unlhd G$. Sea $a\in G$.
P.D. $aNa^{-1} = N$.
Probaremos esto por doble contención.
$\subseteq]$ Como $N\unlhd G$, $ana^{-1} \in N$ para toda $n\in N$. Entonces el conjunto $aNa^{-1} = \{ana^{-1}|n\in N\}$ está contenido en $N$.
$\supseteq]$ Sea $n\in N$, como $N\unlhd G$, $a^{-1}na = a^{-1}n(a^{-1})^{-1} \in N$. Entonces $n = a(a^{-1}n a)a^{-1} \in a N a^{-1}$.
Por lo tanto $aNa^{-1} = N$.
$|2) \Rightarrow 3)]$ Supongamos que para todo $a \in G$, entonces $aNa^{-1} = N$. Sea $a\in G$.
P.D. $aN = Na$.
De nuevo, probaremos esto por doble contención.
$\subseteq]$ Tomemos $an \in aN$ con $n\in N$, como $ana^{-1} \in aNa^{-1}$, y $ aNa^{-1}= N$ por hipótesis, entonces $an = (ana^{-1}) a \in Na$.
$\supseteq]$ Tomemos $na \in Na$ con $n\in N$, como $a^{-1}na \in a^{-1}Na$, y $a^{-1}Na = N$ por hipótesis, entonces $na = a(a^{-1}na) \in aN$.
Por lo tanto $aN = Na$.
$|3)\Rightarrow 1)]$ Supongamos que para todo $a\in G$, existe $b\in G$ tal que $aN = Nb$. Sean $a \in G$ y $n \in N$.
P.D. $ana^{-1} \in N$.
Por hipótesis $aN = Nb$ para alguna $b\in G$. Pero $a \in aN = Nb$, entonces $a\in Nb$, por lo que $a$ es otro representante de la clase lateral $Nb$, y en consecuencia $Na = Nb$. Tenemos entonces que $aN = Nb=Na.$
Así, $an\in aN = Na$ y entonces $an = \tilde{n}a$ para alguna $\tilde{n}\in N$. Entonces
\begin{align*}
ana^{-1} = (an)a^{-1} = (\tilde{n}a)a^{-1} = \tilde{n} \in N.
\end{align*}
Por lo tanto $N \unlhd G$.
Así 1), 2) y 3) son equivalentes.
$\blacksquare$
Observación. (Conmutatividad parcial)
Si $N\unlhd G$, dados $n\in N$ y $a\in G$, tenemos que $an = \tilde{n}a$ para alguna $\tilde{n}\in N$, también $na = a \hat{n}$ para alguna $\hat{n} \in N$.
Ejemplos
- $A_n \unlhd S_n$ ya que si $\beta \in A_n$ y $\alpha\in S_n$.
\begin{align*}
sgn \,(\alpha\beta\alpha^{-1}) &= sgn \,\alpha \; sgn \,\beta \:sgn \,\alpha^{-1}\\
& = sgn \,\alpha \;(+1) \;sgn \, \alpha \\
& = +1.
\end{align*}
Por lo tanto $\alpha\beta\alpha^{-1}\in A_n$. - Consideremos
\begin{align*}
Q &= \{\pm 1, \pm i, \pm j, \pm k\}\\
H &= \{\pm 1, \pm i\}.
\end{align*}
Las clases laterales izquierdas de $H$ en $Q$ son: $H$ y $jH$.
Las clases laterales derechas de $H$ en $Q$ son: $H$ y $Hj$.
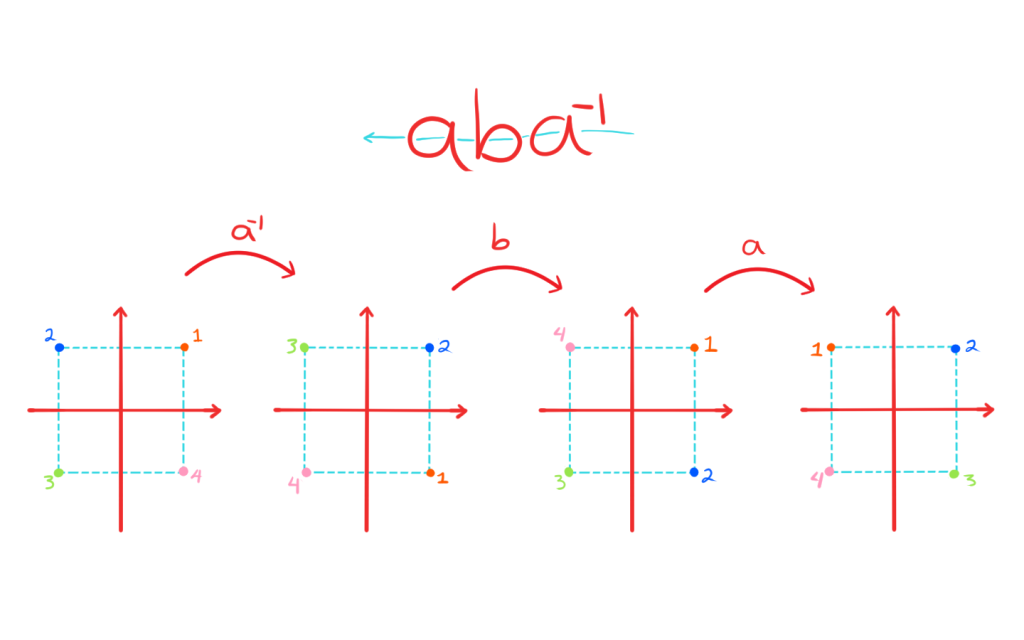
Además $jH = \{\pm j, \pm k\} = Hj$. Por lo tanto $H \unlhd Q$. - Consideremos $D_{2(4)}$ las simetrías del cuadrado. Sean $a$ la rotación $\displaystyle\frac{\pi}{2}$ y $b$ la reflexión con respecto al eje $x$.
Sea $H = \{e, b\}$.
Si tomamos la transformación $aba^{-1}$ podemos desarrollarla algebraicamente y geométricamente. Primero lo haremos de manera algebraica y la interpretación geométrica la podrás encontrar en una imagen más abajo.
Así, como vimos cuando trabajamos con el grupo diédrico:
$$aba^{-1} = aab = a^2b \not\in H$$
con $a^2b$ la reflexión con respecto al eje $y$.
Por lo tanto $H \not\unlhd D_{2(4)}$.
Tarea moral
- Sean $W = \left< (1\;2)(3\;4)\right>$, $V = \{(1), (1\;2)(3\;4),(1\;3)(2\;4),(1\;4)(2\;3)\}\leq S_4$. Verifica si $W$ es normal en $V$, si $V$ es normal en $S_4$ y si $W$ es normal en $S_4$ ¿qué puedes concluir con ello?
- Sea $G$ un grupo, $H$ y $N$ subgrupos de $G$ con $N$ normal en $G$, prueba o da un contraejemplo:
- $N\cap H$ es normal en $H$.
- $N\cap H$ es normal en $G$.
- Demuestra o da un contraejemplo: Si $G$ es un grupo tal que cada subgrupo de él es normal, entonces $G$ es abeliano.
- Sea $G$ un grupo finito con un único subgrupo $H$ de orden $|H|$. ¿Podemos concluir que $H$ es normal en $G$?
Más adelante…
Como ya es costumbre, después de dar las definiciones y de practicarlas un poco con ejemplos, toca profundizar y hablar más sobre las proposiciones y teoremas que involucran a los subgrupos normales. En la siguiente entrada veremos esto.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Caracterización de grupos cíclicos.
- Siguiente entrada del curso: Teoremas y Proposiciones relacionadas con subgrupos Normal y Alternante.
- Resto de cursos: Cursos.
