Introducción
En la entrada anterior construimos un puente entre la intuición que tenemos de las circunferencias y el estudio formal que podemos hacer de ellas utilizando las herramientas de la geometría analítica. Ahora queremos ir más allá de las propiedades básicas del círculo, como lo son su centro y su radio, para abordar propiedades un poco más avanzadas; sus rectas tangentes y polares.
Veremos a lo largo de esta entrada cómo la ecuación vectorial de la circunferencia nos prueba su utilidad al abordar problemas geométricos tales como encontrar puntos de tangencia sobre una circunferencia, hacer demostraciones que involucren las secantes de un círculo, entre otros.
Líneas tangentes a un círculo
Antes de abordar el tema de las líneas tangentes a un círculo, mencionaremos brevemente un problema físico que nos puede motivar a estudiarlo. El problema de la polea consiste en encontrar la longitud de un cable que conecta a dos circunferencias de radio $r_1$ y $r_2$ que no se cruzan; cuyos centros están separados por una distancia $P$. Aunque sea un problema en apariencia sencillo su solución requiere de herramientas como líneas bitangentes, ángulos verticales y congruencia. Pese a que la su solución no es trivial, es un problema de ingeniería bastante importante, pues se usa en el diseño de aeroplanos, bicicletas, autos, etc. No escribiremos explícitamente la solución a este problema, por el momento sólo diremos que para resolverlo es fundamental utilizar el concepto de línea tangente.

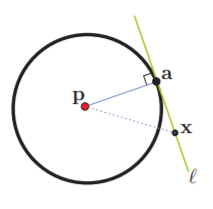
Ahora que comentamos una motivación, empezaremos a discutir el concepto de línea tangente. Intuitivamente podemos pensar que las líneas tangentes son las que tocan a una circunferencia en uno solo de sus puntos. Esto tiene varias implicaciones; la primera de ellas es que podemos pensar en las tangentes como las normales a los radios (los segmentos del centro a sus puntos). Empezaremos proponiendo la definición de las líneas tangentes y haremos una discusión detallada de cada uno de los elementos de esta definición.
Definición. Si $\mathbf{a}$ es un punto del círculo $\mathcal{C}$ dado por la ecuación vectorial
\begin{equation}
(\boldsymbol{x}-\mathbf{p}) \cdot(\boldsymbol{x}-\mathbf{p})=\mathrm{r}^{2}
\end{equation}
entonces su línea tangente es la recta $\ell$ normal a $(\mathbf{a} – \mathbf{p})$ y que pasa por $\mathbf{a}$.
Esta definición tiene algunas implicaciones interesantes que para los elementos que la constituyen que vale la pena observar con detalle. La primera es que, puesto que $\mathbf{a}$ es el punto más cercano a $\mathbf{p}$ en esta recta, para cualquier otro punto $x \in \ell$ se tiene que $\mathrm{d}(\boldsymbol{x}, \mathbf{p})>\mathrm{r}$. Dicho de una forma más sencilla: cualquier otro punto que no sea el punto de tangencia estará alejado del centro del círculo una distancia mayor que el radio. Puedes observar la figura para convencerte de este hecho.
Continuando nuestra exploración de los elementos de la definición que acabamos de presentar, observa que el círculo $\mathcal{C}$ parte el plano en dos pedazos; el interior donde $\mathrm{d}(\boldsymbol{x}, \mathbf{p})<\mathrm{r}$, y el exterior donde $\mathrm{d}(\boldsymbol{x}, \mathbf{p})>\mathrm{r}$, de esta forma $\ell$ está contenida en el exterior salvo por el punto $a \in \mathcal{C}$.
Para obtener una expresión analítica de las líneas tangentes conviene recordar las herramientas vectoriales que fueron presentadas durante la primera unidad, te podrás dar cuenta que si utilizamos la forma de la ecuación normal de recta con los elementos de nuestra definición, podemos ver que la recta $\ell$ está dada por la ecuación
\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\boldsymbol{a} \cdot(\boldsymbol{a}-\mathbf{p}),
\end{equation}
esta ecuación tiene una manera más interesante de escribirse; si restamos $\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})$ a ambos lados, se obtiene:
$$
\mathbf{x} \cdot(\mathbf{a}-\mathbf{p})-\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})=\mathbf{a} \cdot(\mathbf{a}-\mathbf{p})-\mathbf{p} \cdot(\mathbf{a}-\mathbf{p})
$$
$$
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=(\mathbf{a}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})
$$
$$
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=r^{2}
$$
Esta forma de escribir la ecuación será importante en la siguiente sección cuando abordemos las rectas polares, sin embargo, antes de pasar a la siguiente sección hagamos un ejemplo sobre cómo encontrar la tangente de una circunferencia.
Ejemplo. Supongamos que tenemos un círculo con centro en $(4,-3)$ y radio $5$. Encuentre la línea de tangencia que pasa por el punto $(4,2)$.
Primero tenemos que verificar que el punto está dentro de la circunferencia. Si escribimos la ecuación cartesiana de nuestro círculo
\begin{equation}
(x-4)^{2} + (x+3)^{2}=25
\end{equation}
y sustituimos el punto $(4,2)$. Podemos darnos cuenta que el punto sí está en la circunferencia. Como ya vimos que está sobre el círculo, sólo tenemos que sustituir en la expresión analítica de la línea tangente
\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\boldsymbol{a} \cdot(\boldsymbol{a}-\mathbf{p})
\end{equation}
los valores del punto de tangencia y el centro de la circunferencia. Haciendo esto tenemos que:
\begin{equation}
\boldsymbol{x} \cdot ((4,2)-(4,-3)) =\boldsymbol{a} \cdot ((4,2)-(4,-3))
\end{equation}
Por lo tanto, la ecuación de la línea tangente será:
\begin{equation}
\boldsymbol{x} \cdot (0,5) =\boldsymbol{a} \cdot (0,5)
\end{equation}
Escrito en forma cartesiana, tenemos que la recta tangente a nuestra circunferencia a través de ese punto es $y=2$.
Como vimos en nuestro ejemplo, obtener la expresión analítica de la línea tangente a través de un punto es muy fácil si recordamos la definición vectorial. Para terminar esta sección utiliza el siguiente recuadro interactivo para explorar diferentes líneas tangentes de una circunferencia. Nota cómo el punto de tangencia siempre se encuentra en los «bordes» del círculo. ¿Podríamos generalizar vectorialmente el concepto de tangencia para puntos que no se encuentran sobre la circunferencia?
Líneas polares de un círculo
Para empezar nuestro estudio de las líneas polares de un círculo, recuerda el último desarrollo algebraico que hicimos en la sección anterior: ese en el cual sustituimos $\mathbf{a}$ en una de las instancias de $\mathbf{x}$ en la ecuación vectorial. Recuerda cómo en el caso de la línea tangente, consideramos que el punto $\mathbf{a}$ estaba sobre la circunferencia. Con esto en mente, estamos listos para dar una definición de línea polar.
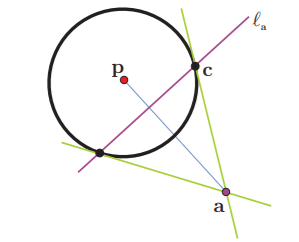
Definición. Consideremos un punto $\mathbf{a}$ en el plano, diferente del centro $(\mathbf{a} \neq \mathbf{p})$, diremos que $\ell_{a}$ es la recta polar de $\mathbf{a}$ respecto al círculo $\mathcal{C}$ y definiremos $\ell_{a}$ como
\begin{equation}
\ell_{\mathbf{a}}: \quad(\boldsymbol{x}-\mathbf{p}) \cdot(\boldsymbol{a}-\mathbf{p})=\mathrm{r}^{2}
\end{equation}
De la definición, se sigue que cuando $\boldsymbol{a} \in \mathcal{C}$ su polar $\ell_{\mathbf{a}}$ es su tangente. Como te puedes dar cuenta, las líneas polares son algo así como una generalización de las líneas tangentes; estamos repitiendo los desarrollos algebraicos que utilizamos en la primera sección sin restringirnos a los puntos que están sobre la circunferencia. Nuestra definición de líneas polares tiene varias consecuencias interesantes; una de ellas es que si el punto $\mathbf{a}$ está en el interior del círculo, entonces $\ell_{a}$ no lo intersecta (está totalmente contenida en el exterior), y que si está en el exterior (el punto $\mathbf{b}$ en la siguiente figura), entonces lo corta, y además lo corta en los dos puntos de $\mathcal{C}$ a los cuales se pueden trazar tangentes.
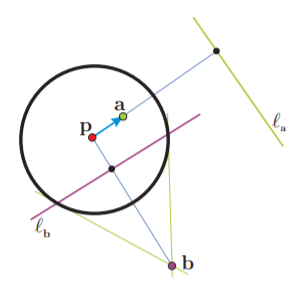
Vamos a demostrar los enunciados que presentamos en el párrafo anterior. Para esto, expresemos las ecuación $\ell_{a}$ en su forma normal; desarrollando [numero de ecuación de la definición] se obtiene:
\begin{equation}
\boldsymbol{x} \cdot(\boldsymbol{a}-\mathbf{p})=\mathrm{r}^{2}+\mathbf{p} \cdot(\boldsymbol{a}-\mathbf{p})
\end{equation}
Esto indica que $\ell_{a}$ es perpendicular al vector que va de $\mathbf{p}$ a $\mathbf{a}$. Ahora veamos cuál es su punto de intersección con la recta que pasa por $\mathbf{p}$ y $\mathbf{a}$. Parametricemos esta última recta con $\mathbf{p}$ de cero y $\mathbf{a}$ de uno (es decir como $\mathbf{p}+\mathbf{t}(\mathbf{a}-\mathbf{p})$) y podemos despejar $t$ al sustituir en la variable $\mathbf{x}$ de la ecuación anterior (o bien, esto se ve más directo al sustituir en la [numero de ecuación de la definición] ), para obtener
\begin{equation}
t=\frac{r^{2}}{(\mathbf{a}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})}=\frac{r^{2}}{d(\mathbf{p}, \mathbf{a})^{2}} .
\end{equation}
Entonces la distancia de $\mathbf{p}$ a $\ell_{a}$ es
\begin{equation}
\mathrm{d}\left(\mathbf{p}, \ell_{a}\right)=\mathrm{t} \mathrm{d}(\mathbf{p}, \mathbf{a})=\frac{\mathrm{r}^{2}}{\mathrm{~d}(\mathbf{p}, \mathbf{a})}=\left(\frac{\mathrm{r}}{\mathrm{d}(\mathbf{p}, \mathbf{a})}\right) \mathrm{r}
\end{equation}
y tenemos lo primero que queríamos probar: si $\mathrm{d}(\mathbf{p}, \boldsymbol{a})<\mathrm{r}$ entonces $\mathrm{d}\left(\mathbf{p}, \ell_{\mathbf{a}}\right)>\mathrm{r}$; y al revés, si $\mathrm{d}(\mathbf{p}, \mathbf{a})>\mathrm{r}$ entonces $\mathrm{d}\left(\mathbf{p}, \ell_{\mathbf{a}}\right)<\mathrm{r}$. Dicho de otra manera, si el punto $\mathbf{a}$ está muy cerca de $\mathbf{p}$, su polar está muy lejos, y al revés, sus distancias al centro $\mathbf{p}$ se comportan como inversos «alrededor de r».
Para demostrar la segunda de nuestras afirmaciones, supongamos ahora que $\mathrm{d}(\mathbf{p}, \mathbf{a})>\mathrm{r}$, y sea $\mathbf{c}$ un punto en $\ell_{a} \cap \mathcal{C}$ (que sabemos que existe pues $\ell_{a}$ pasa por el interior de $\mathcal{C}$). Puesto que $\mathbf{c} \in \ell_{\mathrm{a}}$, se cumple la ecuación
\begin{equation}
(\mathbf{c}-\mathbf{p}) \cdot(\mathbf{a}-\mathbf{p})=\mathbf{r}^{2}
\end{equation}
Pero entonces $\mathbf{a}$ cumple la ecuación de $\ell_{c}$ que es la tangente a $\mathcal{C}$ en $\mathbf{c}$; es decir, la línea de $\mathbf{a}$ a $\mathbf{c}$ es tangente al círculo. Este argumento, visto de una forma todavía más general nos dice que para cualesquiera dos puntos $\mathbf{a}$ y $\mathbf{b}$ (distintos de $\mathbf{p}$) se tiene que
\begin{equation}
a \in \ell_{b} \Leftrightarrow \mathbf{b} \in \ell_{a}
\end{equation}
Y los puntos del círculo son los únicos para los cuales se cumple que $\mathbf{a} \in \ell_{a}$. Puedes apoyarte en la siguiente figura para seguir el desarrollo anterior.
Date cuenta cómo a lo largo de este procedimiento sin querer aprendimos a calcular los puntos de tangencia a un círculo desde un punto exterior $\mathbf{a}$. A saber, de la ecuación lineal de su polar, $\ell_{a}$, se despeja alguna de las dos variables y se sustituye en la ecuación del círculo. Esto nos da una ecuación de segundo grado en la otra variable que se puede resolver, y nos da dos raíces. Sustituyéndolas de nuevo en la ecuación de la polar se obtiene el otro par de coordenadas.
Para dejar bien claro este procedimiento, hagamos un ejercicio sobre cómo encontrar los puntos de tangencia desde un punto fuera de la circunferencia.
Ejemplo. Supongamos que tenemos un círculo con centro en $(3,-1)$ y radio $2$, encontraremos los puntos de tangencia desde el punto $\mathbf{a}=(1,3)$.
Podemos iniciar de dos maneras diferentes: la primera es utilizando lo que aprendimos en la entrada anterior, escribiendo directamente la ecuación vectorial de la circunferencia. Si hacemos esto, encontraremos que la circunferencia tiene la siguiente expresión vectorial
\begin{equation}
((x, y)-(3,-1)) \cdot((x, y)-(3,-1))=4 .
\end{equation}
Otra alternativa sería primero escribir la ecuación cartesiana y luego desarrollarla para pasarla a su forma vectorial; de ambas maneras, lo importante es escribir a la circunferencia en su forma vectorial. Ahora, para conocer los puntos de tangencia desde $\mathbf{a}=(1,3)$ sustituimos en la forma alternativa de la ecuación de la tangente:
$$((x, y)-(3,-1)) \cdot((1,3)-(3,-1))=4$$
$$(x-3, y+1) \cdot(-2,4)=4$$
$$-2 x+4 y+10=4$$
$$x-2 y=3 .$$
De aquí, para encontrar $\ell_{a} \cap \mathcal{C}$, conviene sustituir $x=3+2 y$ en la ecuación original del círculo para obtener
\begin{equation}
\begin{aligned}
(3+2 y)^{2}+y^{2}-6(3+2 y)+2 y &=-6 \
5 y^{2}+2 y-3 &=0
\end{aligned}
\end{equation}
Las raíces de esta ecuación cuadrática se pueden obtener utilizando la fórmula general:
\begin{equation}
y=\frac{-2 \pm \sqrt{4+60}}{10}=\frac{-2 \pm 8}{10}
\end{equation}
que nos da los valores $y_{0}=-1$ y $y_{1}=\frac{3}{5}$. Y estos, al sustituir de nuevo la ecuación de la polar nos dan los puntos de tangencia de $\mathbf{a}$; que son $(1,-1)$ y $\frac{1}{5}(21,3)$. Puedes verificar que satisfacen la ecuación del círculo sustituyendo en la ecuación lineal de la polar, y que efectivamente sus tangentes pasan por $\mathbf{a}$.
Para finalizar esta entrada te invito a que experimentes un momento con el recuadro interactivo. Nota cómo las líneas polares se convierten en las líneas tangentes cuando haces que el punto $\mathbf{a}$ esté sobre la circunferencia.
Más adelante…
En esta entrada finalizamos nuestra discusión de las circunferencias; la primera de las secciones cónicas que abordamos en nuestro curso. En la siguiente entrada podrás ver una serie de ejercicios para familiarizarte con la manipulación algébrica o vectorial de los conceptos que hemos introducido hasta ahora. En las siguientes entradas continuaremos nuestro estudio de las secciones cónicas hablando de parábolas, hipérbolas y elipses. Veremos cómo no es tan fácil dar una ecuación vectorial para el resto de las secciones cónicas; esto lo entenderemos tan pronto como empecemos a hablar de parábolas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Encuentra los puntos de tangencia: al círculo $x^{2}-2 x+y^{2}-4 y=-3$ desde el punto $(-1,2)$. Sugerencia: puedes consultar el segundo ejercicio realizado en esta entrada.
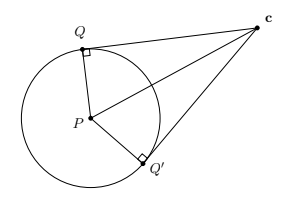
- Demuestra que si $\mathbf{c}$ es un punto exterior (al círculo $\mathcal{C}$ con centro $P$ ) entonces su recta a $P$ biseca sus dos tangentes a $\mathcal{C}$. Y además que las distancias a sus pies en $\mathcal{C}$ (es decir, a los puntos de tangencia) son iguales. Sugerencia: Puedes utilizar la siguiente figura para tu demostración y pensar en el teorema de Pitágoras y en el criterio de congruencia LLL.
Entradas relacionadas
- Ir a Geometría Analítica I
- Entrada anterior del curso: Círculos
- Siguiente entrada del curso: Problemas con círculos