Introducción

En nuestra vida cotidiana podemos encontrar muchos ejemplos de circunferencias. Desde la forma de una rueda, hasta el contorno de una taza y por supuesto en muchos fenómenos físicos como la trayectoria de una partícula en un campo magnético o el movimiento de un satélite alrededor de un planeta. Esta familiaridad que tenemos con las circunferencias, hacen que ésta sea la sección cónica más fácil de reconocer, pues incluso sin estudios formales en geometría estamos familiarizados con sus propiedades.

En esta entrada del blog propondremos una definición formal para la circunferencia; partiendo de la definición de la circunferencia como lugar geométrico, llegaremos a la ecuación cartesiana con la que probablemente ya estés familiarizado. Abordaremos la ecuación vectorial del círculo y vamos a ver qué ventajas tiene sobre la ecuación cartesiana.

Ecuación cartesiana de circunferencia

Probablemente en algún curso previo de álgebra o de geometría te hayas encontrado con el círculo unitario $\mathbb{S}^{1}$, definido por la ecuación

\begin{equation}
x^{2}+y^{2}=1
\end{equation}

Para generalizar las nociones que tenemos del círculo unitario a una circunferencia arbitraria, consideremos ahora a cualquier otro círculo $\mathcal{C}$. Tiene un centro $\mathbf{p}=(h, k)$, un radio $r>0$ y es el lugar geométrico de los puntos cuya distancia a $\mathbf{p}$ es $r$. Es decir, $\mathcal{C}=\left\lbrace\mathbf{x} \in \mathbb{R}^{2} \mid d(\mathbf{x}, \mathbf{p})=r\right\rbrace$; o bien, $\mathcal{C}$ está definido por la ecuación

\begin{equation}
d(\mathbf{x}, \mathbf{p})=r.
\end{equation}

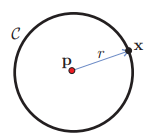
Puesto que ambos lados de esta ecuación son positivos, es equivalente a la igualdad de sus cuadrados que en coordenadas cartesianas toma la forma

\begin{equation}
(x-h)^{2}+(y-k)^{2}=r^{2}
\end{equation}

Así, todos los círculos de $\mathbb{R}^{2}$ están determinados por una ecuación cuadrática en las variables $x$ y $y$. Cuando la ecuación tiene la forma anterior, podemos leer inmediatamente toda la información geométrica (el centro y el radio). Lamentable, la mayoría de las veces que nos encontremos con ecuaciones de circunferencias las encontraremos «disfrazadas» como

\begin{equation}
x^{2}+y^{2}-2 h x-2 k y=\left(r^{2}-h^{2}-k^{2}\right)
\end{equation}

Es fácil ver que esta forma de escribir la circunferencia se obtiene al desarrollar la primera expresión. Veamos un ejemplo de cómo pasar una ecuación de circunferencia a su forma reducida.

Ejemplo. Consideremos la ecuación

\begin{equation}
x^{2}+y^{2}-6 x+2 y=-6 \text { . }
\end{equation}

Tenemos que determinar si la ecuación anterior define un círculo, y en caso de que así sea, qué características tiene. Lo primero que tenemos que hacer es completar los cuadrados, sumando en ambos lados las constantes que faltan

\begin{equation}
(x^{2}-6 x+9)+(y^{2}+2 y+1) =-6+9+1 \rightarrow (x-3)^{2}+(y+1)^{2} =4
\end{equation}

Claramente si desarrollamos esta última ecuación obtenemos la original. Así, podemos concluir que la ecuación define al círculo con centro en $(3,-1)$ y radio $2$.

Para terminar esta sección, puedes utilizar la ventana interactiva de GeoGebra para familiarizarte con la ecuación cartesiana de la circunferencia. Varía el radio y el centro del círculo y observa cómo cambia la ecuación. Intenta hacer una circunferencia por cada uno de los cuadrantes del plano poniendo mucha atención cómo cambian los signos dentro de los sumandos. Prueba casos límite ¿qué pasa si el radio el cero? ¿Un punto es una circunferencia?

Ecuación vectorial de circunferencia

Si nuestra ecuación cartesiana de circunferencia ya nos permitía «leer» toda la información geométrica de un círculo completando cuadrados, te puede parecer superfluo proponer una definición vectorial de la circunferencia. La motivación que tenemos para hacer esto es que una definición vectorial, al no hacer referencia a las coordenadas, tiene sentido en cualquier dimensión. Esto quiere decir que a diferencia de la ecuación cartesiana que sólo nos sirve para $\mathbb{R}^{2}$, una ecuación vectorial nos permitirá definir esferas en $\mathbb{R}^{3}$ y en dimensiones mayores.

Sin más preámbulo, diremos que el círculo $C$ con centro $\mathbf{p}$ y radio $r$ está definido por la ecuación

\begin{equation}
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{x}-\mathbf{p})=r^{2}
\end{equation}

Si tienes dificultades entendiendo por qué se utilizó el producto punto, te ayudará recordar que en la primera unidad de nuestro curso definimos la distancia euclidiana entre dos vectores (o norma) como el producto punto (o producto interior) del vector consigo mismo. En nuestro caso, sólo partimos de la definición de circunferencia como el lugar geométrico de todos los puntos que equidistan de un mismo punto y aplicamos la definición vectorial de distancia.

La ecuación, que llamaremos ecuación vectorial del círculo, se puede también reescribir como

\begin{equation}
\mathbf{x} \cdot \mathbf{x}-2 \mathbf{p} \cdot \mathbf{x}+\mathbf{p} \cdot \mathbf{p}=r^{2}
\end{equation}

Veamos un ejemplo de la ecuación vectorial del círculo para familiarizarnos con ella.

Ejemplo. Considere la circunferencia con centro en $(3,1)$ y radio $2$. Encuentre su ecuación vectorial y su ecuación cartesiana. Demuestre que ambas ecuaciones son equivalentes.

Lo primero que tenemos que hacer es obtener la ecuación vectorial de la circunferencia. Utilizando la definición que acabamos de escribir en esta entrada, podemos ver que la ecuación que buscamos es

\begin{equation}
(\mathbf{x}-(3,1)) \cdot(\mathbf{x}-(3,1))= 4
\end{equation}

También utilizando la definición para la ecuación cartesiana

\begin{equation}
(x-3)^{2}+(y-1)^{2}=4
\end{equation}

Estas dos expresiones, son las ecuaciones que buscamos. Sólo nos falta demostrar su equivalencia. Recordando las propiedades del producto punto que introducimos en la unidad anterior

\begin{equation}
\begin{array}{l}
(\mathbf{x}-(3,1)) \cdot (\mathbf{x}-(3,1)) = 4 \\
((x,y)-(3,1)) \cdot ((x,y)-(3,1)) = 4 \\
(x-3,y-1) \cdot (x-3,y-1) = 4 \\
(x-3)^{2}+(y-1)^{2}=4
\end{array}
\end{equation}

¡Listo! Ya nos convencimos que la ecuación cartesiana y la ecuación vectorial son equivalentes cuando estamos trabajando en $\mathbb{R}^{2}$. Por el momento, conservemos la idea de que la ecuación vectorial es un poco más general y de ella se puede extraer mucha información geométrica interesante.

Para finalizar esta sección, utiliza el siguiente recuadro interactivo para familiarizarte con la ecuación vectorial del círculo. Manipula el centro y el radio para ver cómo se reescribe la ecuación y entiende muy bien cómo el producto punto es la operación clave de la definición. ¿Puedes encontrar los parámetros adecuados para hacer que en ambos interactivos tengamos círculos equivalentes con diferentes formas de escribir la ecuación?

Más adelante…

En esta entrada discutimos detalladamente las definiciones cartesianas y vectorial de la circunferencia, propusimos algunos ejemplos para familiarizarnos con estas expresiones y aprendimos a «leer» la información geométrica que guardan. Sin embargo, no hemos acabado nuestro estudio de las circunferencias. En las siguientes entradas abordaremos el tema de las rectas tangentes y polares y resolveremos algunos ejercicios relacionados a estas secciones cónicas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• ¿Cuáles de las siguientes ecuaciones son ecuaciones de un círculo? Y en su caso, ¿de cuál?

\begin{equation}
\begin{array}{l}
x^{2}-6 x+y^{2}-4 y=12 \\
x^{2}+4 x+y^{2}+2 y=11 \\
2 x^{2}+8 x+2 y^{2}-4 y=-8 \\
x^{2}-4 x+y^{2}-2 y=-6 \\
4 x^{2}+4 x+y^{2}-2 y=4
\end{array}
\end{equation}

• ¿Cuál es el lugar geométrico de los centros de los círculos que pasan por dos puntos (distintos) $a$ y $b$? Sugerencia: considera la definición geométrica de la circunferencia como el conjunto de puntos que equidistan de un centro y ten en cuenta la definición vectorial de la mediatriz.
• Sean $p$ y $q$ dos puntos distintos en el plano. ¿Para cuáles números reales $c$, se tiene que la siguiente ecuación define un círculo? En su caso, ¿cuál es el radio y dónde está su centro?

\begin{equation}
(\mathbf{x}-\mathbf{p}) \cdot(\mathbf{x}-\mathbf{q})=c
\end{equation}

• Determinar la ecuación, centro y radio de la circunferencia que pasa por los tres puntos $A(-1,1)$, $B(3,5)$ y $C(5,-3)$. Sugerencia: considera que la ecuación buscada tiene la forma $x^2 + y^2 + Dx+ Ey + F= 0$, luego sustituye la información que te ofrece el problema para llegar a un sistema de ecuaciones y resuelvelo.

Entradas relacionadas

• Ir a Geometría Analítica I
• Entrada anterior del curso: Introducción a cónicas
• Siguiente entrada del curso: Propiedades de círculos