Archivo de la etiqueta: producto cartesiano

Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Habiendo hablado del producto cartesiano, ya tenemos los ingredientes para irnos acercando a la definición de función, pero antes de hablar de ellas, tenemos que hablar de relaciones y de algunos de sus conceptos. En esta entrada introduciremos el concepto de relación, dominio, codominio y composición entre relaciones.

Relaciones

Cuando estamos hablando de el producto cartesiano, estamos juntando las parejas posibles de elementos entre dos conjuntos. Pero quizá no nos interesen todas las parejas posibles, quizá a veces solo nos interesaría hablar de algún subconjunto de estas parejas. Por ejemplo, si tenemos los conjuntos de zapatos izquierdos y derechos denotados por $I,D$ entonces no siempre nos interesan todas las parejas posibles de zapatos, quizá solo nos interese combinar cada zapato izquierda con su par correspondiente. Para dar un ejemplo, imagina que hay tres zapatos $A,B,C$ y los conjuntos $I$ y $D$ contienen tres zapatos de cada uno de los zapatos que hay:

$I = \{A_I,B_I,C_I\} $

$D = \{A_D,B_D,C_D\} $

Si quisieramos unir cada zapato con su par, nos podemos fijar en su producto cartesiano $I \times D$, sin embargo hay elementos que sí nos van a interesar y otros que no. Por ejemplo, la pareja $(I_A,D_A)$ sí nos interesa, pues es el zapato izquierdo y derecho del zapato $A$. Por otro lado, la pareja $(I_A,D_C)$ no nos interesa, pues estamos juntando dos zapatos pero de modelos distintos. En particular, el subconjunto de $I \times D$ que describe a los tres zapatos es: $$R = \{(I_A,D_A),(I_B,D_B),(I_C,D_C)\}.$$ Este conjunto es una relación entre los conjuntos $I$ y $D$. Como podrás notar, $R \subset I \times D$, y para la definición de relación, basta con que el conjunto esté contenido en el producto cartesiano para que cumpla la definicón.

Definición. Sean $X$ y $Y$ dos conjuntos, una relación entre los conjuntos $X$ y $Y$ es un subconjunto $R$ del producto cartesiano $X \times Y$: $$R \subset X \times Y $$

Definición. Si $R$ es una relación de $X$ en $Y$, diremos que $x$ está relacionado con $y$ bajo la relación $R$ si la pareja $(x,y) \in X \times Y$ y $(x,y) \in R$.

Con esta última definición, podemos notar que el zapato izquierdo $A$ ($I_A$) está relacionado con el zapato derecho $A$ ($D_A$) bajo la relación $R$, pues la pareja $(I_A,D_A)$ pertenece a la relación $R$.

En nuestro ejemplo anterior, mostramos una relación entre $I$ y $D$. Otros ejemplos de relaciones entre $I$ y $D$ son los siguientes:

$\{(I_B,D_A),(I_C,D_B),(I_C,D_A)\},$
$\{(I_C,D_B)\}$
$\{(I_A,D_A),(I_C,D_B)\}$
$\emptyset$
$I \times D$

Dominio y codominio de relaciones

Vamos ahora a trabajar con el conjunto de los números enteros $\mathbb{Z}$. Y trabajaremos con el producto cartesiano $\mathbb{Z} \times \mathbb{Z}$. Llamemos a este producto cartesiano $\mathbb{Z}^2$ que es la forma en que comúnmente se le denota al producto cartesiano entre el mismo conjunto (en este caso $\mathbb{Z}$) en la literatura.

Ahora, consideremos la siguiente relación entre los conjuntos: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$

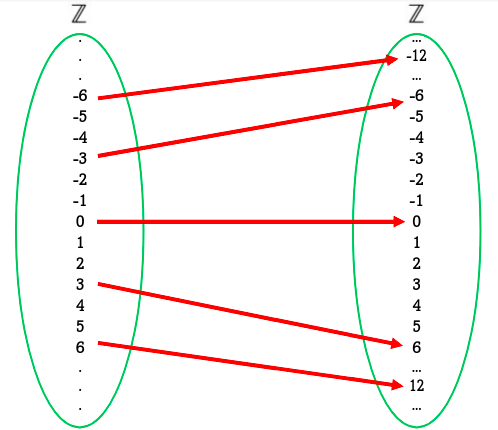
Y notemos que algunos ejemplos de elementos de esta relación son: $\{ (3,6),(0,0),(-3,-6),(3^{10},2*3^{10}) ,(-300,-600)\} \subset R$. Gráficamente, podemos ver la relación en la siguiente imagen:

Del lado izquierdo corresponden los elementos $x$ de las parejas $(x,y) \in R$ y del lado derecho los elementos $y$. Notemos que del lado izquierdo (los elementos $x$), no consideramos todos los elementos. Por ejemplo, los números $\{-5,-4,-2,-1,1,2,4,5\}$ no forman ninguna pareja, pues en la definición de nuestro conjunto, solo estamos considerando los múltiplos de $3$ del lado izquierdo de la relación. A estos números que sí forman parejas del lado izquierdo, les llamamos dominio.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El dominio de la relación $R$ es $$Dom(R) = \{x \in X: \exists y \in Y \text{ tal que } (x,y) \in R\}$$

Notemos que siempre pasará que $Dom(R)\subset X$, otra definición que no hay que confundir con la de dominio es la de contradominio, al que nos referimos como el conjunto $Y$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El contradominio de $R$ es el conjunto $Y$.

En nuestro ejemplo anterior, $$Dom(R)=\{x \in X: x \text{ es múltiplo de 3}\}$$.

Esto es cierto, pues las parejas de la relación $R$ son aquellas parejas de la forma $(3n,6n)$, pues pedimos que del lado izquierdo estén los múltiplos de $3$ (todo múltiplo de $3$ puede escribirse como algún número entero $n$ multiplicado por $3$), y del lado izquierdo el doble del número que escribimos del otro lado (si del lado izquierdo está $3n$ entonces del derecho estará $2*3n=6n$). Así que el dominio son aquellos números que forman alguna pareja, es decir, los múltiplos de $3$.

Por otro lado, el contradominio es $\mathbb{Z}$. Ahora, podemos preguntarnos en un concepto análogo a la idea de los elementos $y$ para los cuales existe un elemento $x$ de forma que $(x,y)$ pertenezca a la relación, para eso, podemos observar que los únicos elementos de $Z$ que pertenecen a alguna pareja del lado derecho son $\{\dots,-12,-6,0,6,12,\dots\}$, es decir, los múltiplos de $6$, de manera que podríamos hablar de que este conjunto es la imagen de la relación $R$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. La imagen de $R$ es: $$Im(R) = \{y \in Y: \exists x \in X \text{ tal que } (x,y) \in R\}$$

Imagen Directa e Imagen Inversa

Ahora, tomemos a los conjuntos $A=\{0,2,3,5,7,8,9\}$ y $B=\{-6,-1,2,3,4,6,7,12,21\}$ veamos que $A \times B \subset \mathbb{Z}^2$ pues ambos son subconjuntos de números enteros. El siguiente concepto que vamos a presentar, va a ser la imagen directa e inversa. Para esto, consideremos nuevamente nuestra relación $R$ de la sección anterior. Veamos que los elementos de $A$ que pertenecen al dominio de $R$ son $\{0,3,6,9\}$ esto pues $\{(0,0),(3,6),(6,12),(9,18)\} \subset R$. Definamos la imagen directa de $A$ como los elementos en la imagen de $R$ con la restricción de que únicamente consideremos elementos de $A$ del lado izquierdo.

Definición. Sean $X,Y$ dos conjuntos, $A \subset X$ y $R$ una relación de $X$ en $Y$. La imagen directa de $A$ es el conjunto: $$Im[A]=\{y \in Y: \exists x \in A \text{ tal que }(x,y) \in R\}$$

Compara esta definición con la definición de imagen, lo único que estamos cambiando es el conjunto al que pertencen las $x$.

De manera similar, tenemos un concepto similar para $B$, en donde restringiremos ahora el dominio. Para esto, nota que las parejas de $R$ que tienen su imagen en $B$ son $\{(-6,-3),(3,6),(6,12)\}$. Y el concepto de imagen inversa, serán aquellos elementos del dominio de $R$ los cuales están relacionados con algún elemento de $B$.

Definición. Sean $X,Y$ dos conjuntos, $B\subset Y$ y $R$ una relación de $X$ en $Y$. La imagen inversa de $B$ es el conjunto: $$Im^{-1}[B]=\{y \in Y: \exists x \in A \text{ tal que }(x,y) \in R\}$$

De esta, manera:

$$Im[A]=\{0,6,12,18\},$$ $$ Im^{-1}[B]=\{-6,3,6\}.$$

A continuación, vamos a introducir una última definición de esta entrada, que da la idea intuitiva de juntar distintas relaciones.

Composición de funciones

Ahora, veremos la siguiente relación entre el conjunto de zapatos izquierdos $I$ y conjunto de zapatos derechos $D$:

$$R = \{(x,y) \in I \times D: x \text{ es del mismo color que }y\} $$

Y la relación entre zapatos derechos y el conjunto $P$ de pantalones:

$$ T = \{(x,y) \in D \times P:x \text{ es del mismo color que }y\} $$

Estas relaciones solo nos están juntando colores de prendas, la primera nos junta zapatos del mismo color y la tercera relaciones el color de los zapatos derechos con el del pantalón.

Así que por si ejemplol tuvieramos los colores rojo, amarillo y azul entre zapatos izquierdos, derechos y pantalones, entonces la primera relación tendría al zapato izquierdo rojo $I_R$, el zapato derecho rojo $D_R$ y el pantalón rojo $P_R$, de manera que $(I_R,D_R) \in R \land (D_R,P_R) \in T$. ¿Podemos establecer la conexión entre los zapatos izquierdos y los pantalones? Pues con esta pareja, resulta que de alguna manera el zapato $D_R$ une a los dos elementos mediante dos relaciones distintas. La primera relación tiene como contradominio el conjunto $D$ mientras que la segunda lo tiene como dominio.

De la misma manera, podemos conectar el zapato izquierdo azul $I_A$ con algún pantalón de la siguiente manera:

  1. Notamos que $I_A$ está relacionado con el zapato derecho azul $D_A$ mediante la relación $R$.
  2. Observamos que a su vez el zapato $D_A$ está relacionado con el pantalón azul $P_A$ mediante $T$.

De esta manera, podemos encontrar alguna conexión del zapato $I_A$ al pantalón $P_A$ viendo que hay una relación entre $I_A$ con $D_A$ y de $D_A$ con $P_A$. Así que podríamos definir una relación entre los zapatos izquierdos y los pantalones a través de las relaciones $R$ y $T$. Definamos esta relación como $R \circ T$ de la siguiente manera:

$$T \circ R = \{(x,y) \in I \times P: \exists z \in D \text{ tal que }\big( (x,z) \in R \land (z,y) \in T\big) \} $$

Lo que queremos decir con esta expresión, es que los elementos de la relación $T \circ R$ son los elementos $(x,y)$ de tal forma que existe una forma de conectar $(x,y)$ mediante un elemento $z$ de tal forma que $x$ está relacionado con $y$ mediante la relación $T \circ R$ si existe un elemento $z$ que los conecta, es decir, si existe $z$ en $Im(R) \cap Dom(T)$ de tal forma que $(x,z) \in R$ y $(z,y) \in T$.

Definición. Sean $X,Z,Y$ tres conjuntos, $R$ una relación de $X$ en $Z$ y $T$ una relación de $Z$ en $Y$. La relación composición de $R$ con $T$ es la relación:
$$T \circ R = \{ (x,y) \in X \times Y: \exists z \in Z\big( (x,z) \in R \land (z,y) \in T\big)$$

Veamos ahora un ejemplo de nuevo con los número enteros. Considera la relación que ya habíamos visto anteriormente, dada por: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$ Nota ahora, que como dijimos anteriormente, estos son las parejas de la forma $(3n,6n)$ de manera que otra forma de escribir el conjunto es $$R = \{(3n,6n): n \in \mathbb{Z} \} $$.

Ahora considera la siguiente relación $T$:$$T = \{(x,y) \in \mathbb{Z}^2: x = y+1\}$$

Algunos elementos de esta relación son: $\{(3,2),(7,6),(1,0),(-9,-10)\}$. Gráficamente se ve de la siguiente manera:

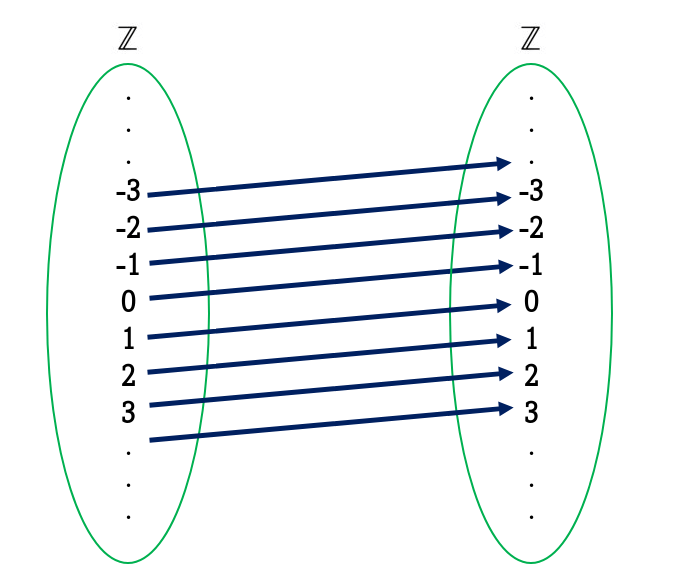
Y si te das cuenta, únicamente son los números de la forma $(n+1,n)$. Por lo que podríamos escribir esta relación como $$T = \{(n+1,n): n \in \mathbb{Z} \} $$.

Ahora veamos cómo se ve la composición $T \circ R$. Para ello, tomemos un elemento de la relación $R$. Por ejemplo, $(3,6) \in R$. Ahora notemos que de igual forma, $(6,5)$ pertenece a la relación $T$. De manera que $(3,5) \in T \circ R$. En general, un elemento de la relación $R$ se escribe como $(3n,6n)$, y un elemento de la relación $T$, como dijimos al principio del párrafo, es de la forma $(n+1,n)$ o lo que es lo mismo, $(n,n-1)$. Y enseguida nota que si tomamos un número entero $n$, entonces $(3n,6n) \in R$ y $(6n,6n-1) \in T$. De esta manera, podemos escribir a la composición de $R$ con $T$ como el conjunto: $$ T \circ R = \{(3n,6n-1): n \in \mathbb{Z}\}$$

Más adelante…

En la siguiente entrada seguiremos hablando de las relaciones entre conjuntos y veremos algunos tipos de relaciones especiales que tendrán algunas propiedades interesantes. También hablaremos un poco más de relaciones de un conjunto en sí mismo, este tipo de relaciones ya las hemos visto, sin embargo, veremos más propiedades que pueden cumplir estas. Esto nos servirá para hablar después de órdenes entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $$R=\{(x,y) \in \mathbb{Z}^2: x+y=0\}$$ y la relación$$T=\{(x,y) \in \mathbb{Z}^2: x-y=0\}.$$Encuentra:
    • $Dom(R)$
    • $Im(R)$
    • Escribe todos los elementos de $T \circ R$
    • Encuentra $Im[\{1,2,3,4,5\}]$ sobre la relación $R$
    • Encuentra $Im^{-1}[\{-1,-2,-3,-4,-5\}]$ sobre la relación $T$
  2. Demuestra que si $R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $, entonces $$R = \{(3n,6n): n \in \mathbb{Z} \} $$
  3. La recta $\mathcal{L}$ con pendiente $m$ e intersección $b$ con el eje $y$ en los números enteros es el conjunto: $$\mathcal{L}=\{(x,y) \in \mathbb{Z}^2: mx+b=y\} $$ Encuentra $\mathcal{L_1}\cap \mathcal{L_2}$ donde $\mathcal{L_1}$ es la recta con $m=1,b=0$ y $\mathcal{L_2}$ es la recta con $m=-1,b=2$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Propiedades del producto cartesiano

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

La vez pasada dimos la definición de parejas ordenadas y el producto cartesiano. Estas ideas tenían que ver con «relacionar» dos conjuntos mediante las parejas ordenadas, ahora exploraremos más sobre el producto cartesiano. En esta entrada revisaremos algunas propiedades interesantes e importantes sobre el producto cartesiano entre dos conjuntos, viendo cómo se comporta con el conjunto vacío y algunos operadores de conjuntos.

Propiedades del producto cartesiano

Algunas de las preguntas que nos pueden surgir al momento de trabajar con los productos cartesianos es cómo estos se comportan con algunos operadores. Por ejemplo la unión y la intersección o la relación de contención. En esta entrada revisaremos algunos resultados útiles a la hora de trabajar con el producto cartesiano.

Trabajando con el vacío

Considera a un conjunto $X$. ¿Cómo será su producto cartesiano con el conjunto vacío?. Pues recuerda que:

$$ X \times \emptyset = \{(x,y): x\in X \land y \in \emptyset\}$$

Pareciera ser que este conjunto no tendría ningún elemento, ¿no? Pues al observar alguna pareja ordenada $(x,y)$ de este conjunto, resultaría que $y \in \emptyset$. Lo cuál es una contradicción, pues recordemos que el conjunto vacío no tiene elementos.

Proposición. Sea $X$ un conjunto, entonces $X \times \emptyset = \emptyset$.

Demostración. Para demostrar la igualdad de conjuntos, deberíamos demostrar que el conjunto de la izquierda está contenido en la derecha, pero notemos que el conjunto de la derecha es el conjunto vacío, y como recordarás, el conjunto vacío, siempre será subconjunto de cualquier conjunto. Esto nos ahorra una contención, y solo habrá que demostrar la contención que falta.

$\subset$. Para demostrar que cada elemento $(x,y) \in X \times \emptyset$ está contenido en el conjunto vacío, será suficiente demostrar que no podemos tomar ningún elemento de dicho conjunto, pues no tiene elementos, ya que ningún elemento cumplirá la definición del conjunto: $x\in X \land y \in \emptyset$. Cuando queremos demostrar que un conjunto es vacío, lo que haremos es hacerlo por reducción al absurdo, suponiendo que sí tiene elementos para llegar a una contradicción.

Para ello, supón $(x,y) \in X \times \emptyset$ (existe algún elemento en el conjunto). Entonces $x \in X$ y $y \in \emptyset$, pero esto es una contradicción, pues el conjunto vacío no tiene elementos por definición. Así, concluímos que $X \times \emptyset \subset \emptyset$.

Más aún, hemos demostrado la igualdad entre conjuntos, pues como dijimos al principio, todo conjunto tiene como subconjunto al vacío. De esta manera $X \times \emptyset = \emptyset$.

$\square$

El mismo argumento puede ser usado para demostrar que $\emptyset \times X = \emptyset$, pues no existen elementos que cumplan la definición de pertenencia del lado derecho.

Contención entre productos cartesianos

Para la siguiente propiedad, veremos cómo es que se comporta el producto cartesiano con la contención de conjuntos. Consideraremos ahora dos conjuntos $X,Y$. Notemos que un elemento del producto cartesiano de $X \times Y$ es de la forma $(x,y)$ donde $x \in X \land y \in Y$. Ahora nota que si $X \subset W \land Y \subset Z$, entonces $(x,y)$ también serán parte del producto cartesiano entre $W$ y $Z$, pues $x \in W \land y \in Z$. Esto es lo que nos dice la siguiente proposición:

Proposición. Sean $W,Z$ dos conjuntos y $X \subset W$, $Y \subset Z$. Entonces: $$X \times Y \subset W \times Z$$

Demostración. Para la demostración, consideremos $(x,y) \in X \times Y$. Lo que habrá que demostrar es que $(x,y) \in W \times Z$. Para ello, nota que si $(x,y) \in X \times Y$ entonces $x \in X$ y al tener la hipótesis $X \subset W$, concluímos que $x \in W$. De manera análoga, $y \in Z$. de esta manera $(x,y) \in W \times Z$

$\square$

Corolario. Sean $X,Y$ dos conjuntos, entonces $X \times X = Y \times Y$ si y solo si $X=Y$.

Esta última demostración no se va a resolver aquí, pero es sencillo notar que la igualdad entre productos cartesianos implica que $X \times X$ es subconjunto de $Y \times Y$ y viceversa, lo cual se puede utilizar para demostrar la contención entre conjuntos.

Propiedades con la unión e intersección

Las siguientes propiedades que vamos a probar serán las referentes a la unión y a la intersección. Para la primera idea de la unión, consideremos al conjunto $$X = \{1,2\}$$ y a los conjuntos $$Y_1 = \{a\}, Y_2 = \{b\}. $$

Entonces el conjunto $$X \times Y_1 = \{(1,a),(2,a)\}.$$ Y el conjunto $$X \times Y_2 = \{(1,b),(2,b)\}. $$De tal manera que si juntamos estos productos cartesianos, nos queda el siguiente conjunto:

$$X \times Y_1 \cup X \times Y_2 = \{(1,a),(2,a),(1,b),(2,b)\}.$$

Nota ahora que si hacemos el producto cartesiano de $X$ con $Y_1 \cup Y_2$, resulta que:

$$X \times (Y_1 \cup Y_2) = \{1,2\} \times \{a,b\}= \{(1,a),(2,a),(1,b),(2,b)\}.$$

De esta manera, $$X \times (Y_1 \cup Y_2)= X \times Y_1 \cup X \times Y_2 .$$

Esto es lo que nos dice la siguiente proposición:

Proposción. Sean $X,Y,Z$ tres conjuntos, entonces $$X \times (Y \cup Z) = X \times Y \cup X \times Z.$$

Demostración.

$\subset.$ Considera $(x,y) \in X \times (Y \cup Z)$. Entonces $x \in X$ y $y \in Y \cup Z$. Nota entonces que tenemos dos casos para $y$.

Caso 1. $y \in Y$

En este caso, $(x,y) \in X \times Y \subset X \times Y \cup X \times Z$, al tener esta última contención, concluimos que se cumple que $X \times (Y \cup Z) \subset X \times Y \cup X \times Z.$

Caso 2. $y \in Z$

Esta demostración es análoga al caso anterior, esto quiere decir que seguimos un razonamiento muy similar que no requiere de pasos muy distintos a los que hicimos. Podemos dejarlo así, pero pondremos el razonamiento análogo para que veas por qué decimos que es análogo.
En este caso, $(x,y) \in X \times Z \subset X \times Y \cup X \times Z$, al tener esta última contención, concluimos que se cumple que $X \times (Y \cup Z) \subset X \times Y \cup X \times Z.$

En cualquiera de los casos, es cierto que $X \times (Y \cup Z) \subset X \times Y \cup X \times Z.$

$\supset.$ Para demostrar la otra contención, simplemente notemos que tanto $X \times Y$ como $X \times Z$ están contenidos en $X \times (Y \cup Z)$. (Recuerda que si dos conjuntos están contenidos en otro conjunto, entonces su unión queda contenida en el conjunto). Para ello, nota que:

$$\begin{align*}
X \times Y &= \{(x,y):x \in X \land y \in Y\}\\
&\subset\{(x,y):x \in X \land y \in (Y \cup Z)\}\\
&= X \times (Y \cup Z)
\end{align*} $$

De igual manera:

$$\begin{align*}
X \times Z &= \{(x,y):x \in X \land y \in Z\}\\
&\subset\{(x,y):x \in X \land y \in (Z \cup Y)\}\\
&=\{(x,y):x \in X \land y \in (Y \cup Z)\}\\
&= X \times (Y \cup Z)
\end{align*} $$

De esta manera $X \times Y \subset X \times (Y \cup Z)$ y $X \times Z \subset X \times (Y \cup Z)$ de manera que $X \times Y \cup X \times Z\subset X \times (Y \cup Z)$

Por lo tanto $X \times Y \cup X \times Z = X \times (Y \cup Z)$

$\square$

Otra propiedad interesante es con la intersección, pues de manera similar si $$X = \{1,2\}$$ y los conjuntos $$Y_1 = \{a,b,c,d,e,1,f\}, Y_2 = \{1,2,3,4,5,a,6\} $$ entonces se cumple que $$X \times Y_1 \cap X \times Y_2 = \{(1,a),(2,a),(1,1),(2,1)\}.$$
Y $$X \times (Y_1 \cap Y_2) = \{(1,a),(2,a),(1,1),(2,1)\}.$$ De esta manera, $X \times Y_1 \cap X \times Y_2 = X \times (Y_1 \cap Y_2)$. Esto es otra proposición:

Proposición. Sean $X,Y,Z$ tres conjuntos, entonces $$X \times Y \cap X \times Z = X \times (Y \cap Z)$$

Demostración. Podemos hacer la demostración como en la proposición anterior, pero vamos a demostrarlo ahora por la definición de los conjuntos. Para esto, nota que:

$$\begin{align*}
X \times (Y \cap Z) &= \{(x,y):x \in X \land y \in (Y \cap Z)\} \\
&= \{(x,y):(x \in X \land y \in Y) \land (x \in X \land y \in Z)\}\\
&= \{(x,y):x \in X \land y \in Y\} \cap \{(x,y):x \in X \land y \in Z\}\\
&= X \times Y \cap X \times Z
\end{align*}$$

$\square$

Es con esto que tenemos algunas de las propiedades del producto cartesiano. Más aún, también hemos continuado con algunas distintas formas de demostrar conjuntos. Ambas formas de demostración de las proposiciones son válidas y son diferentes formas de demostrar.

Como pudiste observar, en general el producto cartesiano se comporta bien con los operadores entre conjuntos, siendo el producto cartesiano de la intersección, la intersección de los productos cartesianos y lo mismo sucede con la unión.

Más adelante…

Ahora que hemos visto algunas propiedades del producto cartesiano, procederemos a definir el siguiente concepto: las relaciones binarias entre conjuntos. Como pudiste observar con el producto cartesiano, este nos permite «unir» elementos de un conjunto con otro. Pues las relaciones serán un subconjunto del producto cartesiano y estudiaremos las distintas formas de relaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que si $X$ es un conjunto, entonces $\emptyset \times X = \emptyset$.
  2. Demuestra que si $X,Y$ son dos conjuntos, entonces $X \times X = Y \times Y$ si y solo si $X=Y.$
  3. Sean $X,Y,Z$ tres conjuntos. Demuestra que:
    • $(X \cup Y) \times Z = X \times Z \cup Y \times Z$
    • $(X \cap Y) \times Z = X \times Z \cap Y \times Z$
  4. Demuestra que si $X,Y,Z$ son tres conjuntos, entonces:
    • $X \times (Y \triangle Z) = X \times Y \triangle X \times Z$
    • $(X \triangle Y) \times Z = X \times Z \triangle Y \times Z$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Parejas ordenadas y producto cartesiano de conjuntos

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En la primera unidad revisamos los conceptos básicos de la teoría de conjuntos. Estos nos permitirán a partir de ahora manejar conjuntos con los operadores que vimos y nos permitirán armar nueva teoría a partir de ellos. En esta unidad nos enfocaremos en las relaciones y funciones. Estas son maneras de «agrupar» unos conjuntos con otros y serán útiles no solo en este curso, sino que en muchos otros que se basan en la idea de las funciones entre conjuntos.

Agrupando zapatos

Empecemos considerando una tienda de zapatos muy disfuncional, pues no se preocupa por hacer coincidir sus zapatos derechos con los izquierdos. Describimos al conjunto $D = \{d_1,d_2, \dots, d_n\}$ como los $n$ zapatos derechos que tiene la tienda, y por $I = \{ i_1, i_2, \dots i_m\}$ como los $m$ zapatos izquierdos. Nota que al ser una tienda poco organizada, puede ser que haya distinto número de zapatos derechos que de izquierdos (puede pasar que $m \neq n$). Cuando un cliente llega a la tienda, el mismo cliente tiene la posibilidad de elegir su par de zapatos. El primer cliente llega y elige el zapato derecho $d_3$ con el zapato izquierdo $i_2$, y eso está permitido, pues la tienda deja que los clientes eligan sus pares como quieran. Llamemos a este par de zapatos, el par $(d_3,i_2)$. Esto es lo que nos va a dar una idea intuitiva de lo que llamaremos parejas ordenadas, que en términos simples es considerar elementos de dos conjuntos y agruparlos en una misma expresión. A continuación damos su definición conjuntista.

Definición. Sean $X$ y $Y$ dos conjuntos. Una pareja ordenada de $X$ y $Y$ es una pareja de dos términos $x \in X$ y $y \in Y$ escrita mediante la expresión $(x,y)$. En términos de conjuntos se define como: $$(x,y) = \{ \{ x\}, \{x,y \} \} $$

El nombre de pareja ordenada viene del hecho de que los dos elementos a considerar respetan un orden de conjuntos, esto quiere decir a que si nos referimos a la pareja ordenada $(x,y)$ de $X$ con $Y$, eso significa que $x \in X \land y \in Y$. Por lo que la pareja $(y,x)$ no es la misma, puesto que esta es una pareja de $Y$ con $X$. Además nota que hay un «orden», pues en su expresión conjuntista, el término $x$ aparece en los dos conjuntos que conforman $(x,y)$, mientras que $y$ solo aparece una vez.

Digamos ahora que $n=4$ y $m=2$, de manera que los zapatos derechos son $D = \{ d_1,d_2,d_3,d_4 \}$ y los izquierdos son $I = \{ i_1,i_2 \}$. Entonces los zapatos que se pueden formar de estos conjuntos son:

$$\{ (d_1,i_1), (d_1,i_2), (d_2,i_1), (d_2,i_2), (d_3,i_1), (d_3,i_2), (d_4,i_1), (d_4,i_2) \} $$

Y como posiblemente te habrás imaginado, los distintos zapatos que se pueden formar con esos conjuntos, corresponden a las distintas parejas ordenadas entre $X$ y $Y$.

Igualdad entre parejas ordenadas

Ahora vamos a definir cuándo diremos que dos pares de parejas ordenadas (zapatos) son el mismo. Para esto observa que en la vida cotidiana, diríamos que dos pares son iguales si el zapato derecho de un par es exactamente el mismo que el zapato derecho del otro par, de la misma manera que el izquierdo de uno será el mismo izquierdo del otro. Anotemos eso como una proposición que habrá que demostrar.

Proposición. Sean $X$ y $Y$ dos conjuntos y $(x,y),(x’, y’)$ dos parejas ordenadas de $X$ con $Y$. Entonces las parejas son la misma ($(x,y)=(x’,y’)$) si y solo si $(x=x’) \land (y=y’)$.

Demostración. $\Rightarrow)$ Para demostrar la primera implicación, notemos que por hipótesis $(x,y)=(x’,y’)$. Esto quiere decir que $$\{\{ x\} ,\{x,y \} \} = \{\{ x’\} ,\{x’,y’ \} \} $$. Para $x$ tenemos dos casos:

Caso 1. $x =y$

En este caso, notemos que $\{\{ x\} ,\{x,y \} \} = \{\{x\}\}$. Al tener este conjunto un único elemento, entonces $\{\{ x’\} ,\{x’,y’ \} \}$ también tiene un único elemento, ya que de otra manera no serían el mismo conjunto. Enseguida, se sigue que $\{\{x\}\} = \{\{x’\}\}$. Donde se tiene que $x=x’$. Ahora notemos que al ser $x=y$, entonces $x’=y’$ y puesto que $\{\{x’\}\} = \{\{ x’\} ,\{x’,y’ \} \}$ entonces $x’=y’$.

Caso 2. $x \neq y$

Ahora, si son distintos, tenemos que $$(x,y) = \{ \{x\}, \{ x,y\} \}$$. Notemos ahora que $\{ \{x\}, \{ x,y\} \} = \{ \{x’\}, \{ x’,y’\} \}$ son conjuntos con ambos dos elementos. Al ser estos conjuntos iguales, entonces cada elemento de un conjunto está en el otro, es decir $\{x\} \in \{ \{x’\}, \{ x’,y’\} \}$ y $\{x,y\} \in \{ \{x’\}, \{ x’,y’\} \}$. Ahora, como $\{x\} \in \{ \{x’\}, \{ x’,y’\} \}$ entonces $(\{x\} = \{x’\} ) \lor (\{x\} = \{x’,y’\})$, al ser $\{x’\}$ el único elemento con un elemento, entonces deducimos que $\{x\} = \{x’\}$. De manera análoga $\{x,y\} = \{x’,y’\}$.

Ahora, como $\{x\} = \{x’\}$ entonces $x=x’$. Y después como $\{x,y\} = \{x’,y’\}$, podemos sustituir $x$ por $x’$, pues son el mismo elemento. Así, $\{x’,y\} = \{x’,y’\}$. Y nota que esto significa que $y=y’$, pues tenemos la igualdad de conjuntos. De esta manera $x=x’$ y $y=y’$ como se quería demostrar.

$\Leftarrow)$. Ahora supongamos que $x=x’$ y $y=y’$. Al tener esta igualdad, entonces $\{x\}=\{x’\}$ y además $\{x,y\} = \{ x’,y’\}$ pues tienen los mismos elementos. De esta forma, los siguientes conjuntos son iguales:$$ \{\{ x\} ,\{x,y \} \} = \{\{ x’\} ,\{x’,y’ \} \}.$$ Por lo tanto $(x,y)=(x’,y’)$

$\square$

Algunos ejemplos de parejas ordenadas que sí son la misma:

  • $(1,4) = (1,4) $
  • $(\frac{1}{2}, 0) = (1- \frac{1}{2}, 9 -9) $
  • $(\{x:P(x)\}, \{x: R(x) \land \neg R(x) \}) = (\{x: P(x) \land P(x) \}, \emptyset) $

Algunos ejemplos de parejas ordenadas que no son la misma:

  • $(1,4) \neq (4,1)$
  • $(1,0) \neq (1, \{0\})$
  • $(\{x: P(x)\}, \{x: P(x) \}) \neq (\{x: P(x) \land R(x)\}, \{x: \neg P(x) \})$

Producto Cartesiano

Hemos hablado ya de las parejas ordenadas particulares entre dos conjuntos. Sin embargo, al estar hablando de parejas ordenadas entre dos conjuntos, realmente el término que usaremos de ahora en adelante será el de producto cartesiano.

Definición. Sean $X$ y $Y$ dos conjuntos. El producto cartesiano $X \times Y$ entre $X$ y $Y$ es el conjunto: $$X \times Y = \{(x,y): (x \in X) \land (y \in Y) \}. $$

De esta manera, volviendo al ejemplo de los zapatos, en párrafos anteriores mencionamos un caso particular en donde $D = \{ d_1,d_2,d_3,d_4 \}$ y $I = \{ i_1,i_2 \}$, entonces:

$$D \times I = \{ (d_1,i_1), (d_1,i_2), (d_2,i_1), (d_2,i_2), (d_3,i_1), (d_3,i_2), (d_4,i_1), (d_4,i_2) \}. $$

Otro ejemplo, podríamos considerarlo tomando $X = \{1, \{1,2\} \}, Y = \{\emptyset, \text{perro}, 1\}$. Entonces:

\begin{align*}
&X \times Y = \{ (1,\emptyset), (1,\text{perro}),(1,1),(\{1,2\},\emptyset),(\{1,2\},\text{perro}), (\{1,2\},1)\} \\
&Y \times X = \{ (\emptyset,1), (\text{perro},1),(1,1),(\emptyset,\{1,2\}),(\text{perro},\{1,2\}), (1,\{1,2\}) \} \\
\end{align*}

Como puedes observar, aquí vemos que no es lo mismo $X \times Y$ que $Y \times X$, de hecho no coinciden en casi ningún elemento, salvo uno:

$(X \times Y) \cap (Y \times X) = \{ (1,1)\}.$

Así que hay que tener cuidado en el orden del producto cartesiano, pues como pudiste ver, no conmutan.

Otra cosa que podemos observar es que tampoco es asociativo el producto cartesiano. Esto quiere decir que no es lo mismo por ejemplo $\mathbb{Z} \times (\mathbb{Z} \times \mathbb{Z})$ que $(\mathbb{Z} \times \mathbb{Z}) \times \mathbb{Z}$. Para convencerte de esto, observa cómo son los elementos del primer conjunto y del segundo conjunto. Para empezar, un elemento de $\mathbb{Z} \times (\mathbb{Z} \times \mathbb{Z})$ es $(1,(1,1))$ mientras que un elemento del segundo es $((1,1),1)$, que no son el mismo elemento. Y de manera general, no es lo mismo para $a,b,c \in \mathbb{Z}$ la pareja $(a,(b,c))$ que la pareja $((a,b),c)$ pues siempre la primera componente de la primera pareja es un número, mientras que de la segunda, es una pareja ordenada.

Más adelante…

En la siguiente entrada, vamos a ver algunas propiedades del producto cartesiano. Algunas de las cuales ya hemos revisado en esta entrada, añadiendo otras sobre cómo se comportan con los conectores entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Cuántas parejas ordenadas hay en el producto cartesiano de $X \times Y$ si $X$ y $Y$ tienen un número finito de elementos?
  2. Demuestra que si $X,Y$ son dos conjuntos no vacíos, entonces $X \times Y = Y \times X$ si y solo si $X=Y$
  3. ¿Cómo es $ \emptyset \times Y$? ¿Cuántos elementos tiene?
  4. Encuentra el producto cartesiano $X \times X$ donde $X = \{x \in \mathbb{Z} : (x \leq 20)\land (x \ \text{es un número primo)} \}$
  5. Encuentra el producto cartesiano de $X \times Y$ donde $X= \{1, 5, 10 \}$ y $Y = X \times X$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»