Archivo de la etiqueta: funciones inyectivas

Teoría de los Conjuntos I: Funciones inyectivas

Por Gabriela Hernández Aguilar

2 respuestas

Introducción

En esta entrada abordaremos el concepto de función inyectiva. Una función inyectiva será aquella que relacione elementos distintos del dominio con elementos distintos del codominio.

Función inyectiva

Definición. Sea $f: X \to Y$. Decimos que $f$ es una función inyectiva si para cualesquiera $x_1$, $x_2 \in X$ tales que $x_1\not=x_2$, se tiene que $f(x_1)\not= f(x_2)$.

Ejemplo.

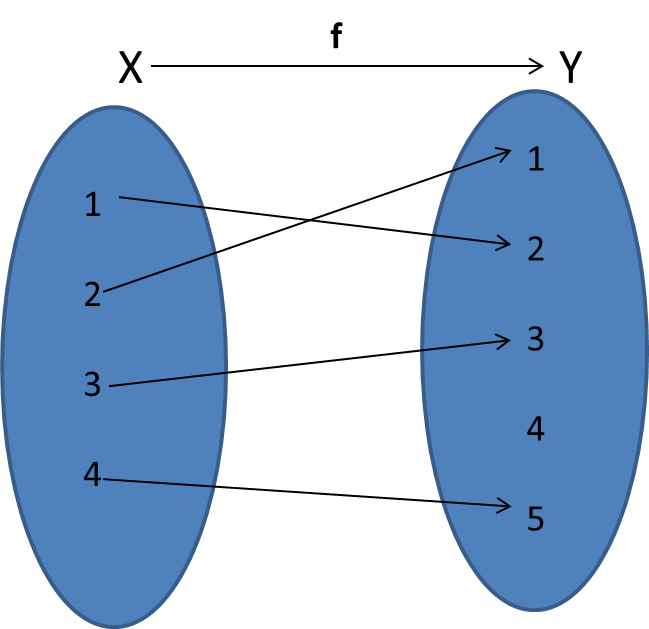
Sean $X=\set{1,2,3,4}$ y $Y=\set{1,2,3,4,5}$ y sea $f:X\to Y$ una función dada por $f=\set{(1,2), (2,1), (3,3), (4,5)}$. Decimos que $f$ es inyectiva pues cada elemento de $X$ bajo la función va a dar a un elemento distinto de $Y$, como se muestra en la siguiente imagen:

Ejemplo.

La función identidad es una función inyectiva.

En efecto, dado que $Id_X:X\to X$ esta dada por $Id_X(x)=x$, entonces si $x_1,x_2\in X$ son tales que $Id_X(x_1)=Id_X(x_2)$, entonces tendríamos $x_1=Id_X(x_1)=Id_X(x_2)=x_2$. Así, $x_1=x_2$ y por lo tanto $Id_X$ es inyectiva.

$\square$

Ejemplo.

La función constante no es inyectiva.

Consideremos $X=\set{1,2,3}$ y $Y=\set{1}$. Sea $f:X\to Y$ la función dada por $f(x)=1$ para toda $x\in X$. Consideremos $x_1=1$ y $x_2=2$ elementos de $X$. Sabemos que $1\not=2$ por lo que para que nuestra función sea inyectiva esperamos que $f(x_1)\not=f(x_2)$, sin embargo, $f(1)=1=f(2)$. Esto demuestra que, en general, las funciones constantes no son inyectivas.

$\square$

Equivalencias de inyectividad

Aunque la definición de inyectividad es muy intuitiva («mandar elementos distintos a elementos distintos»), en la práctica nos conviene tener una serie de equivalencias de esta definición que podamos usar en situaciones variadas.

Teorema.1 Sea $f:X\to Y$ una función tal que $X\not=\emptyset$. Entonces los siguientes enunciados son equivalentes:

  1. $f$ es inyectiva.
  2. Para cualesquiera $x_1,x_2\in X$ si $f(x_1)=f(x_2)$, entonces $x_1=x_2$.
  3. Para cualesquiera $h,k:Z\to X$ si $f\circ h= f\circ k$, entonces $h=k$.
  4. Para cualesquiera $A,B$ subconjuntos de $X$, se cumple que $f[B\setminus A]= f[B]\setminus f[A]$.
  5. Para cualesquiera $A,B$ subconjuntos de $X$ se cumple que $f[A\cap B]= f[A]\cap f[B]$.

Demostración.

$1)\rightarrow 2)$
Supongamos que $f$ es inyectiva, esto es, para cualesquiera $x_1, x_2\in X$ tales que $x_1\not=x_2$ se tiene que $f(x_1)\not=f(x_2)$. Luego, sabemos que la implicación es equivalente a la contrapositiva por lo que podemos concluir que para cualesquiera $x_1, x_2\in X$, si $f(x_1)=f(x_2)$ entonces $x_1=x_2$.

$2)\rightarrow 3)$
Supongamos que para cualesquiera $x_1, x_2\in X$ si $f(x_1)=f(x_2)$, entonces $x_1= x_2$ y supongamos que $h,k:Z\to X$ son funciones tales que $f\circ h= f\circ k$ y veamos que $h=k$.

Sea $z\in Z$, entonces $h(z)\in X$ y $k(z)\in X$, luego como $f\circ h=f\circ k$ tenemos que $(f\circ h)(z)= (f\circ k)(z)$, de donde $f(h(z))= f(k(z))$ y como $f$ es inyectiva entonces $h(z)=k(z)$. Por lo tanto, $h(z)=k(z)$ para todo $z\in Z$. Para concluir que $h=k$ notemos lo siguiente: $(z,y)\in h$ si y sólo si $h(z)=y$, lo cual ocurre si y sólo si $k(z)=y$, es decir, si y sólo si $(z,y)\in k$.

$3)\rightarrow 4)$

Supongamos que para cualesquiera $h,k:Z\to X$ se cumple que si $f\circ h= f\circ k$, entonces $h=k$. Sean $A,B$ conjuntos tales que $A\subseteq B\subseteq X$ y veamos que $f[B\setminus A]= f[B]\setminus f[A]$.

En la entrada de funciones vimos que siempre ocurre que $f[B]\setminus f[A]\subseteq f[B\setminus A]$ por lo que basta ver la otra contención.

Sea $y\in f[B\setminus A]$, entonces existe $x\in B\setminus A$ tal que $f(x)=y$. Tenemos que $x\in B$ y $x\notin A$, de modo que $f(x)\in f[B]$. Resta ver que $f(x)\notin f[A]$. Supongamos que sí ocurre, es decir que $f(x)\in f[A]$. Entonces existe $z\in A$ tal que $f(z)=f(x)$.

Definamos $h:X\to X$ dada por $h(a)=x$ para todo $a\in X$ y $k:X\to X$ dada por $k(a)=z$ para todo $a\in X$. Notemos que $h\not=k$ pues $z\not=x$ ya que $z\in A$ y $x\notin A$. Luego, $(f\circ h)(a)=f(h(a))= f(x)$ y $(f\circ k)(a)= f(k(a))= f(z)=f(x)$ para cada $a\in A$, por lo que $f\circ h=f\circ k$. Así, por hipótesis se sigue que $h=k$ lo cuál es una contradicción, por lo tanto, no debe ocurrir que $f(x)\in f[A]$. Así, $f(x)\in f[B]\setminus f[A]$.

$4)\rightarrow 5)$

Supongamos que para cualesquiera $A, B$ subconjuntos de $X$, se cumple que $f[B\setminus A]=f[B]\setminus f[A]$. Veamos que $f[A\cap B]= f[A]\cap f[B]$.

En la entrada de funciones probamos que $f[A\cap B]\subseteq f[A]\cap f[B]$, por lo que basta ver que $f[A]\cap f[B]\subseteq f[A\cap B]$.

Sea $y\in f[A]\cap f[B]$, entonces $y\in f[A]$ y $y\in f[B]$, así existe $x\in A$ tal que $f(x)=y$. Queremos demostrar que $x\in B$. Supongamos que no es así, es decir $x\notin B$. Por lo tanto, $x\in A\setminus B$ y $y=f(x)\in f[A\setminus B]= f[A]\setminus f[B]$.

Se sigue que $y\in f[A]$ y $y\notin f[B]$ lo cual es una contradicción. Por lo tanto, debe ocurrir que $x\in B$, así existe $x\in A\cap B$ tal que $f(x)=y$.

Por lo tanto, $f[A]\cap f[B]= f[A\cap B]$.

$5)\rightarrow 1)$

Supongamos que para cualesquiera $A, B\subseteq X$ se cumple que $f[A]\cap f[B]= f[A\cap B]$.

Sean $x_1, x_2\in X$ tales que $x_1\not= x_2$, veamos que $f(x_1)\not= f(x_2)$.

Consideremos $\set{x_1}$ y $\set{x_2}$ subconjuntos de $X$. Luego,

\begin{align*}
\emptyset&=f[\emptyset]\\
&=f[\set{x_1}\cap \set{x_2}]\\
&=f[\set{x_1}]\cap f[\set{x_2}]\ \text{por hipótesis}\\
&=\set{f(x_1)}\cap \set{f(x_2)}.
\end{align*}

Luego, como $\set{f(x_1)}\cap \set{f(x_2)}=\emptyset$, se tiene $\set{f(x_1)}\not=\set{f(x_2)}$ y por lo tanto, $f(x_1)\not=f(x_2)$.

Por lo tanto, $f$ es inyectiva.

Por lo tanto, todos los enunciados anteriores son equivalentes.

$\square$

Aunque existen muchas equivalencias de función inyectiva, para estas notas usaremos con mayor frecuencia la equivalencia dos del resultado anterior.

¿Qué pasa con la composición y la inyectividad?

Anteriormente vimos que la composición de funciones (pensándolas como relaciones) resulta ser una función. Podemos preguntarnos qué ocurre si las funciones que conforman a la composición son inyectivas. ¿Será que eso implica que la composición es inyectiva? Esto lo responde el siguiente teorema.

Teorema. Sean $f:X\to Y$ y $g:Y\to Z$ funciones inyectivas. Se cumple que $g\circ f$ es inyectiva.

Demostración.

Sean $f$ y $g$ funciones inyectivas y sean $x_1, x_2\in X$ tales que $(g\circ f)(x_1)= g(f(x_1))=g(f(x_2))= (g\circ f)(x_2)$. Dado que $f(x_1), f(x_2)\in Y$ y $g$ es inyectiva, entonces $ g(f(x_1))=g(f(x_2)) $ implica que $f(x_1)=f(x_2)$. Por la inyectividad de $f$ podemos concluir que $x_1=x_2$. Por lo tanto, $g\circ f$ es una función inyectiva.

$\square$

Tarea moral

La siguiente lista de ejercicios te permitirá reforzar el tema de funciones inyectivas.

  • Demuestra que la función inclusión es inyectiva.
  • Sean $A=\set{1,2,3}$, $B=\set{1,2}$ y $C=\set{1,2}$ conjuntos. Sean $f:A\to B$ y $g:B\to C$ funciones dadas por $f=\set{(1,1), (2,1), (3,2)}$ y $g=\set{(1,2), (2,1)}$ respectivamente. Escribe al conjunto $g\circ f$ y ve si la función correspondiente es inyectiva. Argumenta tu respuesta.
  • Si $f\circ g$ es inyectiva, ¿es cierto que $f$ y $g$ son inyectivas? ¿Será cierto que por lo menos una de ellas siempre es inyectiva?
  • Demuestra que la función $\emptyset$ es inyectiva.
  • Demuestra que $f:X\to Y$ una función constante es inyectiva si y sólo si $X=\set{x}$ para algún conjunto $x$.

Más adelante…

En la siguiente entrada abordaremos el tema de funciones suprayectivas. Con este tema tendremos los conceptos necesarios para comenzar a hablar acerca de funciones biyectivas e invertibles.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

  1. También puedes consultar la prueba de este teorema en: Hernández, F., Teoría de Conjuntos, México: Aportaciones Matemáticas No.13,
    SMM, 1998, p. 51-52 ↩︎