Archivo de la etiqueta: función analítica

Variable Compleja I: Series de Taylor y series de Laurent

Por Pedro Rivera Herrera

Introducción

En la entrada anterior cerramos la cuarta unidad del curso y vimos algunos técnicas para construir funciones analíticas. Por otra parte, en la entrada 39 de la unidad anterior vimos algunos resultados que establecen la relación que existe entre las sucesiones y series de funciones convergentes y la integración compleja, los cuales nos serán de mucha utilidad en esta entrada.

Considerando los resultados de la tercera unidad y el teorema 39.1 vimos que toda serie de potencias define a una función analítica en su disco de convergencia, corolario 39.1. En esta entrada demostraremos un recíproco de este resultado, conocido como el teorema de Taylor de una función analítica, es decir, veremos que cada función analítica en un dominio puede expandirse en series de potencias sobre cada punto del dominio. Más aún, veremos que en una región anular es posible expandir a una función analítica, en dicho dominio, en una serie doblemente infinita llamada serie de Laurent.

Definición 42.1. (Serie de Taylor.)
Sean $D \subset C$ y $f : D \to C$ una función. Si $f$ es analítica en $z_{0} \in D$ , entonces la serie:
$\sum_{n = 0}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n} = f (z_{0}) + f^{'} (z_{0}) (z - z_{0}) + \frac{f^{(2)} (z_{0})}{2!} (z - z_{0})^{2} + \frac{f^{(3)} (z_{0})}{3!} (z - z_{0})^{3} + \dots,$ es llamada la serie de Taylor de $f$ alrededor de $z_{0}$ . Si $z_{0} = 0$ , entonces la serie es llamada la serie de Maclaurin de $f$ .

Observación 42.1.
Claramente una serie de Taylor es una serie de potencias centrada en $z_{0}$ cuyos coeficientes $c_{n}$ , para toda $n \geq 1$ , son las derivadas de la función $f$ .

Teorema 42.1. (Teorema de Taylor.)
Sean $D \subset C$ un dominio, $z_{0} \in D$ , $f : D \to C$ una función analítica en $D$ y $B (z_{0}, R)$ un disco abierto contenido en $D$ . Entonces $f$ tiene una expansión en serie de Taylor alrededor de $z_{0}$ , es decir:
$f (z) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n}, \forall z \in B (z_{0}, R) .$

En particular, dicha convergencia de la serie de Taylor a la función $f (z)$ es única y se mantiene si $B (z_{0}, R)$ es el mayor disco abierto contenido en $D$ . Más aún, la convergencia es uniforme en todo subdisco cerrado $\overset{―}{B} (z_{0}, r)$ , con $0 < r < R$ .

Demostración. Dadas las hipótesis, basta probar que la serie de Taylor converge a la función $f (z)$ para todo $z \in B (z_{0}, R)$ , pues la unicidad se sigue del corolario 30.2 y la convergencia uniforme de la proposición 29.2.

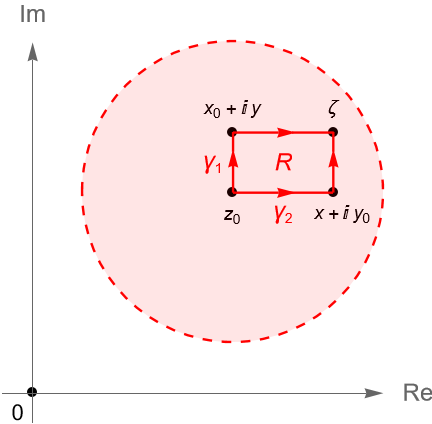
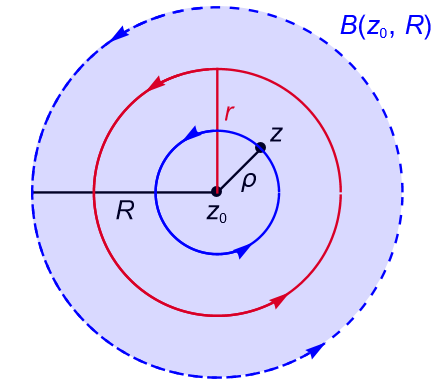
Sea $z \in B (z_{0}, R)$ . Definimos a $ρ := | z - z_{0} |$ , entonces $0 \leq ρ < R$ . Tomamos a $r$ tal que $0 \leq ρ < r < R$ y consideremos a la circunferencia $C (z_{0}, r)$ con centro en $z_{0}$ y radio $r$ , orientada positivamente, figura 147.

Como $f$ es analítica en $D$ y por construcción $C (z_{0}, r)$ está completamente contenido en $D$ , por la fórmula integral de Cauchy, proposición 36.3, tenemos que:
$f (z) = \frac{1}{2 π i} \int_{C (z_{0}, r)} \frac{f (ζ)}{ζ - z} d ζ, \forall z \in B (z_{0}, r) .$

Figura 147: Circunferencia $C (z_{0}, r)$ orientada positivamente contenida en el disco abierto $B (z_{0}, R)$ .

Dado que $ρ = | z - z_{0} | < | ζ - z_{0} | = r$ , tenemos que:
$| \frac{z - z_{0}}{ζ - z_{0}} | < 1,$ por lo que la siguiente serie geométrica es convergente:
$\sum_{n = 0}^{\infty} {(\frac{z - z_{0}}{ζ - z_{0}})}^{n} = \frac{1}{1 - \frac{z - z_{0}}{ζ - z_{0}}} .$

Entonces, para $| z - z_{0} | < | ζ - z_{0} |$ se cumple que:
$\begin{aligned} \frac{1}{ζ - z} & = \frac{1}{(ζ - z_{0}) - (z - z_{0})} \\ = (\frac{1}{ζ - z_{0}}) \frac{1}{1 - \frac{z - z_{0}}{ζ - z_{0}}} \\ = (\frac{1}{ζ - z_{0}}) \sum_{n = 0}^{\infty} {(\frac{z - z_{0}}{ζ - z_{0}})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{{(ζ - z_{0})}^{n + 1}} . \end{aligned}$

Es claro que $f$ es una función continua y acotada en $C (z_{0}, r)$ , por lo que existe $M > 0$ tal que $| f (ζ) | \leq M$ para todo $ζ \in C (z_{0}, r)$ . Entonces:
$| \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) | \leq M \frac{ρ^{n}}{r^{n + 1}} = \frac{M}{r} {(\frac{ρ}{r})}^{n} := M_{n},$ para todo $ζ \in C (z_{0}, r)$ .

Como $ρ < r$ , tenemos que la serie $\sum_{n = 0}^{\infty} M_{n}$ converge para todo $n \in N$ , entonces, del criterio $M$ de Weierstrass, proposición 28.3, se sigue que la serie:
$\sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) = \frac{f (ζ)}{ζ - z},$ converge uniformemente para todo $ζ \in C (z_{0}, r)$ .

Entonces, por el teorema de Weierstrass sobre integración término a término de una serie de funciones uniformemente convergente, proposición 39.1, y la fórmula integral de Cauchy para derivadas, proposición 36.5, tenemos que:
$\begin{aligned} f (z) & = \frac{1}{2 π i} \int_{C (z_{0}, r)} \frac{f (ζ)}{ζ - z} d ζ \\ = \frac{1}{2 π i} \int_{C (z_{0}, r)} \sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) d ζ \\ = \sum_{n = 0}^{\infty} (z - z_{0})^{n} \frac{1}{2 π i} \int_{C (z_{0}, r)} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ \\ = \sum_{n = 0}^{\infty} (z - z_{0})^{n} \frac{f^{(n)} (z_{0})}{n!} \\ = \sum_{n = 0}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n} . \end{aligned}$

Dado que $C (z_{0}, r)$ y $C (z_{0}, R)$ son dos contornos cerrados homotópicos en $D$ , del teorema integral de Cauchy, versión homotópica (teorema 38.3), se tiene que:
$\int_{C (z_{0}, r)} \frac{f (ζ)}{ζ - z} d ζ = \int_{C (z_{0}, R)} \frac{f (ζ)}{ζ - z} d ζ,$ de donde se sigue el resultado.

Observación 42.2.
De acuerdo con la proposición 30.2 y el corolario 30.1, es claro que la serie de Taylor de $f$ , alrededor de un punto $z_{0}$ , puede ser diferenciada término a término dentro de su disco de convergencia, es decir:
$f^{(n)} (z) = \sum_{k = n}^{\infty} \frac{f^{(k)} (z_{0})}{(k - n)!} (z - z_{0})^{k - n}, \forall z \in B (z_{0}, R) .$

Ejemplo 42.1.
Determinemos a la función analítica $f$ tal que satisface la ecuación diferencial:
$\begin{matrix} (42.1) & \frac{d f (z)}{d z} = 3 i f (z) \end{matrix}$ en el disco abierto $B (0, r)$ , para algún $r > 0$ y cumple que $f (0) = 1$ .

Solución. Dado que $f$ es analítica en $z = 0$ , entonces $f$ tine expansión en serie de Maclaurin. De acuerdo con (42.1) y $f (0) = 1$ tenemos que:
$\begin{aligned} f^{'} (0) & = 3 i (1) = 3 i, \\ f^{(2)} (0) & = 3 i f^{'} (0) = (3 i)^{2}, \\ f^{(3)} (0) & = 3 i f^{(2)} (0) = (3 i)^{3}, \end{aligned}$ en general:
$f^{(n)} (0) = 3 i f^{(n - 1)} (0) = (3 i)^{2} f^{(n - 2)} (0) = \dots = (3 i)^{n} .$

Por lo tanto, podemos escribir la solución de la ecuación diferencial como:
$f (z) = 1 + 3 i z + \frac{(3 i)^{2} z^{2}}{2!} + \dots = \sum_{n = 0}^{\infty} \frac{(3 i z)^{n}}{n!} .$

Sabemos que:
$e^{w} = \sum_{n = 0}^{\infty} \frac{w^{n}}{n!},$ por lo que:
$f (z) = e^{i 3 z},$ es la función analítica buscada.

Ejemplo 42.2.
Determinemos la exapansión en serie de Taylor de la función $Log (1 + z)$ alrededor de $z_{0} = 0$ y obtengamos la región de convergencia de la serie resultante.

Solución. Sea $f (z) = Log (1 + z)$ . Por el ejercicio 10 de la entrada 21 sabemos que $f$ es analítica en $C ∖ (- \infty, - 1]$ .

Tenemos que $f^{(0)} (z) = f (z)$ y:
$f^{'} (z) = \frac{1}{1 + z}, f^{(2)} (z) = - \frac{1}{(1 + z)^{2}}, f^{(3)} (z) = \frac{2!}{(1 + z)^{3}}, f^{(4)} (z) = - \frac{3!}{(1 + z)^{4}},$ en general:
$f^{(n)} (z) = \frac{(- 1)^{n - 1} (n - 1)!}{(1 + z)^{n}}, n \geq 1.$

Entonces, del teorema de Taylor, para $z_{0} = 0$ tenemos que:
$\begin{aligned} f (z) = Log (1 + z) & = Log (1 + 0) + \sum_{n = 1}^{\infty} \frac{f^{(n)} (0)}{n!} (z - 0)^{n} \\ = 0 + \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1} (n - 1)!}{(1 + 0)^{n} n!} z^{n} \\ = \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1}}{n} z^{n} . \end{aligned}$

Sea:
$c_{n} = \frac{(- 1)^{n - 1}}{n} z^{n},$ entonces, del criterio del cociente tenemos que:
$lim_{n \to \infty} | \frac{c_{n + 1}}{c_{n}} | = lim_{n \to \infty} | - \frac{n z}{(n + 1)} | = | z | < 1,$ es decir, la serie que define a $f$ converge para $| z | < 1$ . No es difícil verificar que la serie anterior también converge para los $z \in C$ tales que $| z | = 1$ y $z \neq - 1$ , por lo que se deja como ejercicio al lector.

Ejemplo 42.3.
Encontremos la expansión en serie de Taylor de la función $f (z) = (1 - z)^{- 1}$ alrededor del punto $z_{0} = i$ y determinemos su radio de convergencia.

Solución. Primeramente, es claro que la función racional $f$ es analítica en $D = C ∖ {1}$ . De acuerdo con el teorema de Taylor, la expansión en serie de potencias de $f$ es válida en el mayor disco abierto, contenido en $D$ , donde $f$ es analítica, por lo que, podemos determinar el radio de convergencia del desarrollo en serie de Taylor de $f$ considerando la distancia que hay de $z_{0} = i$ a la singularidad $z = 1$ , es decir:
$R = | i - 1 | = \sqrt{2} .$

Por otra parte, notemos que para $z \in B (i, \sqrt{2})$ se cumple que $| z - i | < \sqrt{2} = | 1 - i |$ , entonces:
$| \frac{z - i}{1 - i} | < 1$ por lo que:
$\begin{aligned} f (z) & = \frac{1}{1 - z} \\ = \frac{1}{1 - i - (z - i)} \\ = (\frac{1}{1 - i}) \frac{1}{1 - \frac{z - i}{1 - i}} \\ = (\frac{1}{1 - i}) \sum_{n = 0}^{\infty} {(\frac{z - i}{1 - i})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{(z - i)^{n}}{{(1 - i)}^{n + 1}} . \end{aligned}$

Ejemplo 42.4.
Dado que las funciones complejas $f (z) = e^{z}$ , $g (z) = \cos (z)$ y $h (z) = sen (z)$ son enteras, entonces tienen una expansión como serie de Maclaurin, la cual converge para todo $z \in C$ , es decir, $R = \infty$ para las tres funciones.

Es claro que:
$f^{(n)} (z) = f (z), ⟹ f^{(n)} (0) = e^{0} = 1.$

Mientras que:
$\begin{aligned} g (z) & = \cos (z), ⟹ g (0) = \cos (1) = 1, \\ g^{'} (z) & = - sen (z), ⟹ g^{'} (0) = - sen (0) = 0, \\ g^{(2)} (z) & = - \cos (z), ⟹ g^{(2)} (0) = - \cos (0) = 1, \\ g^{(3)} (z) & = sen (z), ⟹ g^{(3)} (0) = sen (0) = 0, \\ g^{(4)} (z) & = \cos (z), ⟹ g^{(4)} (0) = \cos (0) = 1. \end{aligned}$

Entonces, para todo $z \in C$ se cumple que:
$e^{z} = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} (z - 0)^{n} = \sum_{n = 0}^{\infty} \frac{z^{n}}{n!} .$
$\begin{aligned} \cos (z) & = g (0) + \frac{g^{'} (0)}{1!} (z - 0) + \frac{g^{(2)} (0)}{2!} (z - 0)^{2} + \frac{g^{(3)} (0)}{3!} (z - 0)^{3} + \frac{g^{(4)} (0)}{4!} (z - 0)^{4} + \dots \\ = 1 - \frac{z^{2}}{2!} + \frac{z^{4}}{4!} + \dots \\ = \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n}}{(2 n)!} . \end{aligned}$

Dado que $g^{'} (z) = - sen (z) = - h (z)$ , entonces, por la proposición 30.2, tenemos que:
$\begin{aligned} sen (z) & = - g^{'} (z) \\ = - \frac{d}{d z} \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n}}{(2 n)!} \\ = - \sum_{n = 1}^{\infty} \frac{(- 1)^{n} 2 n z^{2 n - 1}}{(2 n)!} \\ = \sum_{n = 1}^{\infty} \frac{(- 1)^{n + 1} z^{2 n - 1}}{(2 n - 1)!} \\ = \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n + 1}}{(2 n + 1)!} . \end{aligned}$

Proposición 42.1.
Sean $D \subset C$ un dominio, $z_{0} \in D$ y $f : D \to C$ una función analítica en $D$ . Sea $g : D \to C$ dada por:
$g (z) = {\begin{array}{lcc} \frac{f (z) - f (z_{0})}{z - z_{0}} & si & z \neq z_{0}, \\ f^{'} (z_{0}) & si & z = z_{0} . \end{array}$ Entonces $g$ es analítica en $D$ .

Demostración. Dadas las hipótesis, es claro que $g$ es analítica en $D ∖ {z_{0}}$ . Veamos que $g$ es analítica en $z_{0}$ . Como $D$ es abierto, entonces existe $R > 0$ tal que $B (z_{0}, R) \subset D$ . Por el teorema de Taylor, sabemos que en el disco abierto $B (z_{0}, R)$ la función $f$ tiene una expansión en serie de Taylor alrededor de $z_{0}$ , es decir:
$f (z) = f (z_{0}) + \sum_{n = 1}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n}, \forall z \in B (z_{0}, R) .$

Por lo que, para todo $z \in B (z_{0}, R)$ se cumple que:
$\begin{aligned} f (z) - f (z_{0}) & = \sum_{n = 1}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n} \\ = (z - z_{0}) \sum_{n = 1}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n - 1} \\ = (z - z_{0}) g (z), \end{aligned}$ de donde:
$g (z) = \sum_{n = 1}^{\infty} \frac{f^{(n)} (z_{0})}{n!} (z - z_{0})^{n - 1}, \forall z \in B (z_{0}, R) .$

Entonces, del corolario 39.1 se sigue que $g$ es analítica en $B (z_{0}, R)$ y por tanto analítica en $z_{0}$ , además $g$ es la función dada en (42.1).

Ejemplo 42.5.
Veamos que la función:
$g (z) = {\begin{array}{lcc} \frac{sen (z)}{z} & si & z \neq 0, \\ 1 & si & z = 0, \end{array}$ es entera.

Solución. Del ejemplo 42.4 tenemos que:
$sen (z) = \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n + 1}}{(2 n + 1)!} = z \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n}}{(2 n + 1)!} = z h (z),$ donde:
$h (z) := \sum_{n = 0}^{\infty} \frac{(- 1)^{n} z^{2 n}}{(2 n + 1)!},$ es una función entera, corolario 39.1, ya que la serie que la define converge para todo $z \in C$ . Notemos que para $z \neq 0$ se cumple que:
$h (z) = \frac{sen (z)}{z},$ mientras que $h (0) = 1 = {sen}^{'} (0)$ , por lo que $h (z) = g (z)$ para todo $z \in C$ , es decir, $g$ es entera.

Definición 42.2. (Serie de Laurent.)
Sea ${c_{n}}_{n \in Z} \subset C$ una suecesión de números complejos doblemente infinita y $z_{0} \in C$ fijo. Una serie de números complejos doblemente infinita:
$\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n},$ es llamada una serie de Laurent centrada en $z_{0}$ .

De acuerdo con el Lema 27.1, sabemos que la convergencia de una serie de Laurent está garantizada por la convergencia de las series:
$\sum_{n = 1}^{\infty} c_{- n} {(z - z_{0})}^{- n} = \sum_{n = 1}^{\infty} \frac{c_{- n}}{{(z - z_{0})}^{n}}, \sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n},$ las cuales son llamadas, respectivamente, la parte singular o principal y la parte regular o analítica, de la serie de Laurent.

En tal caso se cumple que:
$\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n} = \sum_{n = 1}^{\infty} \frac{c_{- n}}{{(z - z_{0})}^{n}} + \sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n} .$

Dado que:
$\sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n} = c_{0} + \sum_{n = 1}^{\infty} c_{n} {(z - z_{0})}^{n},$ en ocasiones resulta conveniente expresar a una serie de Laurent como:
$\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n} = \sum_{n = - \infty}^{- 1} c_{n} {(z - z_{0})}^{n} + \sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n} .$

Observación 42.3.
Notemos que haciendo $ζ := (z - z_{0})^{- 1}$ en la parte singular de una serie de Laurent, obtenemos la serie de potencias:
$\sum_{n = 1}^{\infty} c_{- n} ζ^{- n},$ para la cual existe $0 \leq R_{1} \leq \infty$ , proposición 29.2, tal que la serie converge absolutamente si:
$| ζ | < R_{1} ⟺ R_{1} < | z - z_{0} | .$

Más aún, la convergencia es absoluta y uniforme en el complemento de todo disco abierto $B (z_{0}, r_{1})$ , con $r_{1} > R_{1}$ , es decir, en:
$C ∖ B (z_{0}, r_{1}) = {z \in C : r_{1} \leq | z - z_{0} |} .$

Por otra parte, para la parte regular de una serie de Laurent:
$\sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n},$ tenemos que existe $0 \leq R_{2} \leq \infty$ , proposición 29.2, tal que la serie de potencias converge absolutamente si $| z - z_{0} | < R_{2}$ , mientras que la convergencia es absoluta y uniforme en todo subdisco cerrado $\overset{―}{B} (z_{0}, r_{2})$ , con $r_{2} < R_{2}$ .

En resumen, para una serie de Laurent, su parte singular converge absolutamente en el complemento del disco cerrado $\overset{―}{B} (z_{0}, R_{1})$ , es decir, en:
$C ∖ \overset{―}{B} (z_{0}, R_{1}) = {z \in C : R_{1} < | z - z_{0} |},$ mientras que la parte regular converge absolutamente en el disco abierto $B (z_{0}, R_{2})$ , por lo que, si $R_{1} < R_{2}$ , entonces la serie de Laurent converge absolutamente en:
$D := {z \in C : R_{1} < | z - z_{0} | < R_{2}},$ y en $D$ define una función analítica, corolario 39.1.

Motivados en lo anterior tenemos la siguiente:

Definición 42.2. (Región anular o anillo.)
Sean $z_{0} \in C$ fijo y $0 \leq R_{1} < R_{2} \leq \infty$ . Se define a la región anular o anillo abierto centrado en $z_{0}$ y de radios $R_{1}$ y $R_{2}$ como:
$A (z_{0}, R_{1}, R_{2}) = {z \in C : R_{1} < | z - z_{0} | < R_{2}} .$

Mientras que, se define al anillo cerrado con centro en $z_{0}$ y de radios $R_{1}$ y $R_{2}$ como:
$\overset{―}{A} (z_{0}, R_{1}, R_{2}) = {z \in C : R_{1} \leq | z - z_{0} | \leq R_{2}} .$

Figura 148: Regiones anulares $A (z_{0}, R_{1}, R_{2})$ y $\overset{―}{A} (z_{0}, R_{1}, R_{2})$ , respectivamente, en el plano complejo $C$ .

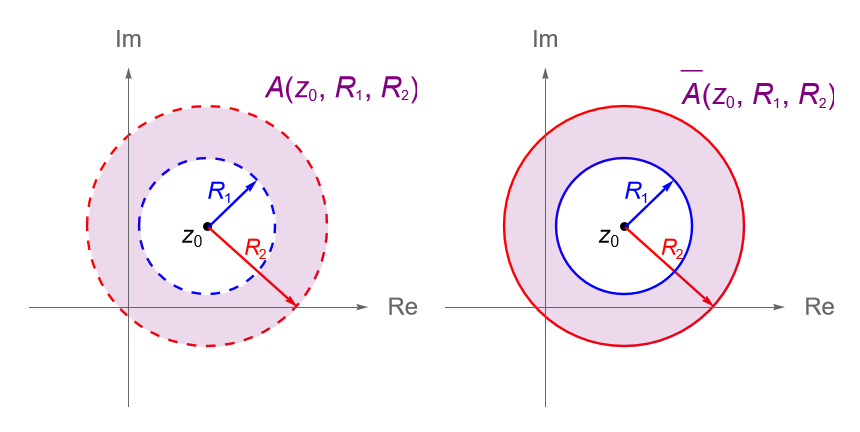
Observación 42.4.
Debe ser claro que si $R_{2} = \infty$ , entonces estaremos pensando en las regiones del plano complejo:
$\begin{aligned} A (z_{0}, R_{1}, \infty) & := {z \in C : R_{1} < | z - z_{0} | < \infty}, \\ \overset{―}{A} (z_{0}, R_{1}, \infty) & := {z \in C : R_{1} \leq | z - z_{0} | < \infty} . \end{aligned}$

También es posible considerar a los anillos degenerados correspondientes con los complementos de los discos $\overset{―}{B} (z_{0}, R_{1})$ y $B (z_{0}, R_{1})$ , respectivamente, es decir, las regiones del plano complejo:
$\begin{aligned} C ∖ \overset{―}{B} (z_{0}, R_{1}) & = {z \in C : R_{1} < | z - z_{0} |}, \\ C ∖ B (z_{0}, R_{1}) & = {z \in C : R_{1} \leq | z - z_{0} |} . \end{aligned}$

Ejemplo 42.6.
Sea $0 < R \leq \infty$ . Consideremos a la función $f (z) = \frac{1}{z^{3}} e^{z}$ . Es claro que la función $f$ no es analítica en $B (0, R)$ , ya que en $z = 0$ la función no es continua. Sin embargo, la función $f$ es analítica en el anillo abierto:
$B^{*} (0, R) = {z \in C : 0 < | z | < R} = A (0, 0, R) .$

De lo anterior se sigue que la función $f$ no tiene un desarrollo como serie de Maclauren. Notemos que para $z \neq 0$ , al considerar el desarrollo en serie de Maclauren de la función $g (z) = e^{z}$ , podemos dividir a cada término de dicha serie por $z^{3}$ y así obtener el siguiente desarrollo en serie de potencias de $f$ :
$\begin{aligned} f (z) & = \frac{1}{z^{3}} e^{z} \\ = \frac{1}{z^{3}} \sum_{n = 0}^{\infty} \frac{z^{n}}{n!} \\ = \frac{1}{z^{3}} + \frac{1}{z^{2}} + \frac{1}{2! z} + \frac{1}{3!} + \frac{z}{4!} + \frac{z^{2}}{5!} + \frac{z^{3}}{6!} + \dots, \end{aligned}$ el cual es válido para toda $z \in B^{*} (0, R)$ .

El desarrollo obtenido antes corresponde con la serie de Laurent de la función $f$ en el anillo $A (0, 0, R)$ , con $0 < R \leq \infty$ .

Proposición 42.1.
Sean $A (z_{0}, R_{1}, R_{2}) \subset C$ un anillo abierto y $\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n}$ una serie de Laurent. Si la serie de Laurent converge en el anillo $A (z_{0}, R_{1}, R_{2})$ , entonces la serie converge uniformemente en todo subanillo cerrado $\overset{―}{A} (z_{0}, r_{1}, r_{2})$ , donde $R_{1} < r_{1} < r_{2} < R_{2}$ .

Demostración. Se sigue de la observación 42.3 y la proposición 29.2, por lo que los detalles se dejan como ejercicio al lector.

Observación 42.5.
Notemos que para $R_{1} < r < R_{2}$ , la circunferencia $γ_{r} (t) = z_{0} + r e^{i t}$ , $t \in [0, 2 π]$ , orientada positivamente, está completamente contenida en el anillo $A (z_{0}, R_{1}, R_{2}) \subset C$ , entonces, para todo $z \in γ_{r} ([0, 2 π])$ la serie de Laurent $\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n}$ converge uniformemente a una función $f (z)$ analítica en $A (z_{0}, R_{1}, R_{2})$ , por lo que, proposición 39.1, podemos integrar término a término a la serie de Laurent a lo largo de $γ_{r}$ , es decir:
$\begin{aligned} \int_{γ_{r}} f (z) d z & = \int_{γ_{r}} \sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n} d z \\ = \sum_{n = - \infty}^{\infty} c_{n} \int_{γ_{r}} {(z - z_{0})}^{n} d z \\ = 2 π i c_{- 1}, \end{aligned}$ donde la última igualdad se sigue del ejemplo 34.2, ya que:
$\int_{γ_{r}} {(z - z_{0})}^{n} d z = {\begin{array}{lcc} 0 & si & n \neq - 1, \\ 2 π i & si & n = - 1. \end{array}$

Entonces:
$a_{- 1} = \frac{1}{2 π i} \int_{γ_{r}} f (z) d z .$

Procediendo de manera análoga para la función $(z - z_{0})^{k - 1} f (z)$ , con $k \in Z$ , en lugar de $f (z)$ , tenemos que:
$a_{k} = \frac{1}{2 π i} \int_{γ_{r}} \frac{f (z)}{(z - z_{0})^{k + 1}} d z .$

Por lo tanto, los coeficientes $c_{n}$ de una serie de Laurent están unívocamente determinados por la función $f (z)$ definida por dicha serie.

Proposición 42.2. (Teorema de Cacuhy para circunferencias concéntricas.)
Sean $z_{0} \in C$ fijo, $0 \leq R_{1} < R_{2} \leq \infty$ , $D := A (z_{0}, R_{1}, R_{2}) \subset C$ un anillo abierto y $f : D \to C$ una función analítica en $D$ . Para cada $R_{1} < r < R_{2}$ sea $γ_{r}$ la circunferencia con centro en $z_{0}$ y radio $r$ , orientada positivamente. Entonces:
$\int_{γ_{r}} f (z) d z,$ es independiente de $r$ .

Demostración. Dadas las hipótesis, sean $r_{1}$ y $r_{2}$ tales que $R_{1} < r_{i} < R_{2}$ , para $i = 1, 2$ . Dado que $γ_{r_{1}}$ y $γ_{r_{2}}$ son dos contornos cerrados homotópicos en $D$ , entonces del teorema de Cauchy, teorema 38.3, se sigue que:
$\int_{γ_{r_{1}}} f (z) d z = \int_{γ_{r_{2}}} f (z) d z .$

Proposición 42.3. (Fórmula integral de Cacuhy para anillos.)
Sean $z_{0} \in C$ fijo, $0 \leq R_{1} < R_{2} \leq \infty$ , $D := A (z_{0}, R_{1}, R_{2}) \subset C$ un anillo abierto y $f : D \to C$ una función analítica en $D$ . Para cada $R_{1} < r < R_{2}$ sea $γ_{r}$ la circunferencia con centro en $z_{0}$ y radio $r$ , orientada positivamente, es decir, $γ_{r} (t) = z_{0} + r e^{i t}$ , para $t \in [0, 2 π]$ . Si $R_{1} < r_{1} < | z - z_{0} | < r_{2} < R_{2}$ , entonces:
$f (z) = \frac{1}{2 π i} \int_{γ_{r_{2}}} \frac{f (ζ)}{ζ - z} d ζ - \frac{1}{2 π i} \int_{γ_{r_{1}}} \frac{f (ζ)}{ζ - z} d ζ .$

Demostración. Dadas las hipótesis, fijemos a $z \in D$ tal que $R_{1} < r_{1} < | z - z_{0} | < r_{2} < R_{2}$ . Definimos a la función $g : D \to C$ como:
$g (ζ) = {\begin{array}{lcc} \frac{f (ζ) - f (z)}{ζ - z} & si & ζ \neq z, \\ f^{'} (z) & si & ζ = z . \end{array}$

De la proposición 42.1 se sigue que $g$ es analítica en $D$ y por la proposición 42.2 se tiene que:
$\int_{γ_{r_{1}}} g (ζ) d ζ = \int_{γ_{r_{2}}} g (ζ) d ζ .$

Como lo anterior se cumple para todo $ζ \in γ_{r_{j}} ([0, 2 π])$ , con $j = 1, 2$ , entonces $ζ \neq z$ , por lo que:
$\int_{γ_{r_{1}}} \frac{f (ζ) - f (z)}{ζ - z} d ζ = \int_{γ_{r_{1}}} g (ζ) d ζ = \int_{γ_{r_{2}}} g (ζ) d ζ = \int_{γ_{r_{2}}} \frac{f (ζ) - f (z)}{ζ - z} d ζ .$

Entonces:
$\int_{γ_{r_{1}}} \frac{f (ζ)}{ζ - z} d ζ - f (z) \int_{γ_{r_{1}}} \frac{1}{ζ - z} d ζ = \int_{γ_{r_{2}}} \frac{f (ζ)}{ζ - z} d ζ - f (z) \int_{γ_{r_{2}}} \frac{1}{ζ - z} d ζ,$

de donde, considerando la definición 36.1, se sigue que:
$\begin{aligned} \int_{γ_{r_{2}}} \frac{f (ζ)}{ζ - z} d ζ - \int_{γ_{r_{1}}} \frac{f (ζ)}{ζ - z} d ζ & = f (z) [\int_{γ_{r_{2}}} \frac{1}{ζ - z} d ζ - \int_{γ_{r_{1}}} \frac{1}{ζ - z} d ζ] \\ = f (z) 2 π i [n (γ_{r_{2}}, z) - n (γ_{r_{1}}, z)] \\ = f (z) 2 π i [1 - 0] \\ = f (z) 2 π i, \end{aligned}$ ya que $z$ está fuera de la circunferencia $γ_{r_{1}}$ y dentro de la circunferencia $γ_{r_{2}}$ .

Por lo tanto:
$\begin{aligned} f (z) & = \frac{1}{2 π i} [\int_{γ_{r_{2}}} \frac{f (ζ)}{ζ - z} d ζ - \int_{γ_{r_{1}}} \frac{f (ζ)}{ζ - z} d ζ] \\ = \frac{1}{2 π i} \int_{γ_{r_{2}}} \frac{f (ζ)}{ζ - z} d ζ - \frac{1}{2 π i} \int_{γ_{r_{1}}} \frac{f (ζ)}{ζ - z} d ζ . \end{aligned}$

Teorema 42.2. (Teorema de Laurent.)
Sean $z_{0} \in C$ fijo, $0 \leq R_{1} < R_{2} \leq \infty$ , $D := A (z_{0}, R_{1}, R_{2}) \subset C$ un anillo abierto y $f : D \to C$ una función analítica en $D$ . Entonces $f$ tiene una única expansión en serie de Laurent en $D$ , es decir:
$f (z) = \sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n}, \forall z \in D,$ la cual converge absolutamente en el anillo $D$ y uniformemente en todo subanillo cerrado $\overset{―}{A} (z_{0}, r_{1}, r_{2})$ , con $R_{1} < r_{1}$ y $r_{2} < R_{2}$ . Más aún:
$c_{n} = \frac{1}{2 π i} \int_{C (z_{0}, r)} \frac{f (ζ)}{(ζ - z)^{n + 1}} d ζ, \forall n \in Z,$ donde $C (z_{0}, r)$ es la circunferencia con centro en $z_{0}$ y radio $r$ , orientada positivamente, con $R_{1} < r < R_{2}$ .

Demostración. Dadas las hipótesis, veamos que la serie de Laurent $\sum_{n = - \infty}^{\infty} c_{n} {(z - z_{0})}^{n}$ converge absolutamente en un subanillo cerrado $\overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ , con $R_{1} < ρ_{1}$ y $ρ_{2} < R_{2}$ , la convergencia uniforme se sigue de la proposición 42.1.

Sean $ρ_{1}$ y $ρ_{2}$ fijos, tales que $R_{1} < ρ_{1}$ y $ρ_{2} < R_{2}$ . Fijamos a $r_{1}$ y $r_{2}$ tales que:
$R_{1} < r_{1} < ρ_{1} \leq | z - z_{0} | \leq ρ_{2} < r_{2} < R_{2}$

Por la proposición 42.3, para todo $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ se cumple que:
$f (z) = \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{ζ - z} d ζ - \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{ζ - z} d ζ,$ donde $C (z_{0}, r_{j})$ es la circunferencia con centro en $z_{0}$ y radio $r_{j}$ , orientada positivamente, con $R_{1} < r_{j} < R_{2}$ , para $j = 1, 2$ .

Para $ζ \in C (z_{0}, r_{2})$ y $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ tenemos que:
$\frac{| z - z_{0} |}{| ζ - z_{0} |} \leq \frac{ρ_{2}}{r_{2}} < 1,$ entonces, como en la prueba del teorema de Taylor, tenemos que la siguiente serie geométrica es convergente:
$\sum_{n = 0}^{\infty} {(\frac{z - z_{0}}{ζ - z_{0}})}^{n} = \frac{1}{1 - \frac{z - z_{0}}{ζ - z_{0}}} .$

Por lo que, para $ζ \in C (z_{0}, r_{2})$ y $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ , se cumple que:
$\begin{aligned} \frac{1}{ζ - z} & = \frac{1}{(ζ - z_{0}) - (z - z_{0})} \\ = (\frac{1}{ζ - z_{0}}) \frac{1}{1 - \frac{z - z_{0}}{ζ - z_{0}}} \\ = (\frac{1}{ζ - z_{0}}) \sum_{n = 0}^{\infty} {(\frac{z - z_{0}}{ζ - z_{0}})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{{(ζ - z_{0})}^{n + 1}} . \end{aligned}$

Dado que $f$ es una función continua y acotada en $C (z_{0}, r_{2})$ , entonces existe $M_{2} > 0$ tal que $| f (ζ) | \leq M_{2}$ para todo $ζ \in C (z_{0}, r_{2})$ . Así:
$| \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) | \leq M_{2} \frac{ρ_{2}^{n}}{r_{2}^{n + 1}} = \frac{M_{2}}{r_{2}} {(\frac{ρ_{2}}{r_{2}})}^{n} := M_{n}^{(2)},$ para todo $ζ \in C (z_{0}, r_{2})$ y todo $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ .

Como $ρ_{2} < r_{2}$ , tenemos que la serie $\sum_{n = 0}^{\infty} M_{n}^{(2)}$ converge para todo $n \in N$ , por lo que, del criterio $M$ de Weierstrass, proposición 28.3, se sigue que la serie:
$\sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) = \frac{f (ζ)}{ζ - z},$ converge uniformemente para todo $ζ \in C (z_{0}, r_{2})$ .

Entonces, por el teorema de Weierstrass sobre integración término a término de una serie de funciones uniformemente convergente, proposición 39.1, y la fórmula integral de Cauchy para derivadas, proposición 36.5, tenemos que:
$\begin{aligned} \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{ζ - z} d ζ & = \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{(ζ - z_{0})^{n + 1}} f (ζ) d ζ \\ = \sum_{n = 0}^{\infty} (z - z_{0})^{n} \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ \\ = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n}, \end{aligned}$ donde:
$c_{n} = \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ .$

Análogamente, para $ζ \in C (z_{0}, r_{1})$ y $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ tenemos que:
$\frac{| ζ - z_{0} |}{| z - z_{0} |} \leq \frac{r_{1}}{ρ_{1}} < 1,$ entonces, la siguiente serie geométrica es convergente:
$\sum_{n = 0}^{\infty} {(\frac{ζ - z_{0}}{z - z_{0}})}^{n} = \frac{1}{1 - \frac{ζ - z_{0}}{z - z_{0}}} .$

Por lo que, para $ζ \in C (z_{0}, r_{1})$ y $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ , se cumple que:
$\begin{aligned} \frac{1}{ζ - z} & = \frac{1}{(ζ - z_{0}) - (z - z_{0})} \\ = (- \frac{1}{z - z_{0}}) \frac{1}{1 - \frac{ζ - z_{0}}{z - z_{0}}} \\ = (- \frac{1}{z - z_{0}}) \sum_{n = 0}^{\infty} {(\frac{ζ - z_{0}}{z - z_{0}})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{- (ζ - z_{0})^{n}}{{(z - z_{0})}^{n + 1}} \\ = \sum_{n = 1}^{\infty} \frac{- (ζ - z_{0})^{n - 1}}{{(z - z_{0})}^{n}} \end{aligned}$

Como $f$ es una función continua y acotada en $C (z_{0}, r_{1})$ , entonces existe $M_{1} > 0$ tal que $| f (ζ) | \leq M_{1}$ para todo $ζ \in C (z_{0}, r_{1})$ . Por lo que:
$| \frac{- (ζ - z_{0})^{n - 1}}{{(z - z_{0})}^{n}} f (ζ) | \leq M_{1} \frac{r_{1}^{n - 1}}{ρ_{1}^{n}} = \frac{M_{1}}{r_{1}} {(\frac{r_{1}}{ρ_{1}})}^{n} := M_{n}^{(1)},$ para todo $ζ \in C (z_{0}, r_{1})$ y todo $z \in \overset{―}{A} (z_{0}, ρ_{1}, ρ_{2})$ .

Como $r_{1} < ρ_{1}$ , tenemos que la serie $\sum_{n = 0}^{\infty} M_{n}^{(1)}$ converge para todo $n \in N$ , por lo que, del criterio $M$ de Weierstrass, se tiene que la serie:
$- \sum_{n = 1}^{\infty} \frac{(ζ - z_{0})^{n - 1}}{{(z - z_{0})}^{n}} f (ζ) = \frac{f (ζ)}{ζ - z},$ converge uniformemente para todo $ζ \in C (z_{0}, r_{1})$ .

Entonces, por la proposición 39.1 y la fórmula integral de Cauchy para derivadas, proposición 36.5, tenemos que:
$\begin{aligned} - \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{ζ - z} d ζ & = \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \sum_{n = 1}^{\infty} \frac{(ζ - z_{0})^{n - 1}}{{(z - z_{0})}^{n}} f (ζ) d ζ \\ = \sum_{n = 1}^{\infty} \frac{1}{{(z - z_{0})}^{n}} \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} (ζ - z_{0})^{n - 1} f (ζ) d ζ \\ = \sum_{n = 1}^{\infty} \frac{1}{{(z - z_{0})}^{n}} \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{(ζ - z_{0})^{1 - n}} d ζ \\ = \sum_{n = 1}^{\infty} \frac{c_{- n}}{{(z - z_{0})}^{n}}, \end{aligned}$ donde:
$c_{- n} = \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{(ζ - z_{0})^{1 - n}} d ζ,$ o equivalentemente:
$- \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{ζ - z} d ζ = \sum_{n = - \infty}^{- 1} c_{n} {(z - z_{0})}^{n},$ donde:
$c_{n} = \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ .$

Dado que para $r \in (R_{1}, R_{2})$ se cumple que $C (z_{0}, r_{1})$ , $C (z_{0}, r_{2})$ y $C (z_{0}, r)$ son tres contornos cerrados homótopicos en $D$ , del teorema integral de Cauchy, versión homotópica (teorema 38.3), se tiene que:
$\int_{C (z_{0}, r)} \frac{f (ζ)}{(ζ - z_{0})^{1 + n}} d ζ = \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ = \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ,$ por lo que:
$\begin{aligned} f (z) & = \frac{1}{2 π i} \int_{C (z_{0}, r_{2})} \frac{f (ζ)}{ζ - z} d ζ - \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{ζ - z} d ζ \\ = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n} + \sum_{n = - \infty}^{- 1} c_{n} {(z - z_{0})}^{n} \\ = \sum_{n = - \infty}^{\infty} c_{n} (z - z_{0})^{n}, \end{aligned}$ donde:
$c_{n} = \frac{1}{2 π i} \int_{C (z_{0}, r_{1})} \frac{f (ζ)}{(ζ - z_{0})^{n + 1}} d ζ, \forall n \in Z .$

Por último, para verificar la unicidad de la expansión de $f$ en serie de Laurent, supongamos que en $D$ se cumple que $f$ tiene dos expansiones en serie de Laurent, es decir:
$f (z) = \sum_{n = - \infty}^{\infty} a_{n} (z - z_{0})^{n} = \sum_{n = - \infty}^{\infty} b_{n} (z - z_{0})^{n} .$

Tenemos que ambas series convergen uniformemente en todo subanillo cerrado de $D$ , entonces, para $k \in Z$ arbitrario:
$\frac{1}{2 π i} \int_{C (z_{0}, r)} \sum_{n = - \infty}^{\infty} a_{n} (z - z_{0})^{n - k - 1} d z = \frac{1}{2 π i} \int_{C (z_{0}, r)} \sum_{n = - \infty}^{\infty} b_{n} (z - z_{0})^{n - k - 1} d z,$ donde $C (z_{0}, r)$ es una circunferencia contenida en cualquier subanillo cerrado de $D$ , entonces, por la convergencia uniforme de ambas series, se sigue de la proposición 39.1 que:
$\sum_{n = - \infty}^{\infty} \frac{1}{2 π i} \int_{C (z_{0}, r)} a_{n} (z - z_{0})^{n - k - 1} d z = \sum_{n = - \infty}^{\infty} \frac{1}{2 π i} \int_{C (z_{0}, r)} b_{n} (z - z_{0})^{n - k - 1} d z .$

Por el ejemplo 34.2 tenemos que:
$\int_{C (z_{0}, r)} a_{n} (z - z_{0})^{n - k - 1} d z = \int_{C (z_{0}, r)} b_{n} (z - z_{0})^{n - k - 1} d z = {\begin{array}{lcc} 0 & si & n \neq k, \\ 2 π i & si & n = k, \end{array}$ de donde:
$a_{k} 2 π i = b_{k} 2 π i ⟺ a_{k} = b_{k}, \forall k \in Z .$

Observación 42.6.
Dado que la convergencia de la serie de Laurent:
$f (z) = \sum_{n = 1}^{\infty} \frac{c_{- n}}{{(z - z_{0})}^{n}} + \sum_{n = 0}^{\infty} c_{n} {(z - z_{0})}^{n},$ en un anillo abierto $A (z_{0}, R_{1}, R_{2})$ , es uniforme en todo subanillo cerrado en $A (z_{0}, R_{1}, R_{2})$ y para cada $n \in Z$ , la función $c_{n} (z - z_{0})^{n}$ es analítica en dicho anillo abierto, entonces, teoremas de Weierstrass, podemos integrar y derivar a una serie de Laurent término a término.

Por lo que:
$f^{'} (z) = - \sum_{n = 1}^{\infty} \frac{n c_{- n}}{{(z - z_{0})}^{n + 1}} + \sum_{n = 1}^{\infty} n c_{n} {(z - z_{0})}^{n - 1} d z .$

En general, podemos continuar derivando a la función $f$ término a término para obtener a cualquier derivada de orden superior.

Por otra parte, para todo contorno $γ$ en el anillo $A (z_{0}, R_{1}, R_{2})$ tenemos que:
$\int_{γ} f (z) d z = \sum_{n = 1}^{\infty} c_{- n} \int_{γ} \frac{1}{{(z - z_{0})}^{n}} d z + \sum_{n = 0}^{\infty} c_{n} \int_{γ} {(z - z_{0})}^{n} .$

Ejemplo 42.7.
Determinemos la expansión en serie de Laurent de la función:
$f (z) = \frac{1}{z^{2} - 3 z + 2},$ en los anillos abiertos $A (0, 1, 2)$ y $A (- i, \sqrt{2}, \sqrt{5})$ .

Solución. Aplicando fracciones parciales, podemos reescribir la función $f (z)$ como:
$f (z) = \frac{1}{z^{2} - 3 z + 2} = \frac{1}{(1 - z) (2 - z)} = \frac{1}{1 - z} - \frac{1}{2 - z},$ de donde es claro que $f$ es analítica en $D := C ∖ {1, 2}$ y en particular en los anillos abiertos $A (0, 1, 2)$ y $A (- i, \sqrt{2}, \sqrt{5})$ contenidos en $D$ .

Para $z \in A (0, 1, 2)$ tenemos que $1 < | z | < 2$ , por lo que:
$\frac{1}{| z |} < 1 y \frac{| z |}{2} < 1.$

Entonces, considerando la serie geométrica tenemos que:
$\sum_{n = 0}^{\infty} {(\frac{1}{z})}^{n} = \frac{1}{1 - \frac{1}{z}} y \sum_{n = 0}^{\infty} {(\frac{z}{2})}^{n} = \frac{1}{1 - \frac{z}{2}} .$

Por lo que:
$\begin{aligned} \frac{1}{1 - z} & = (- \frac{1}{z}) \frac{1}{1 - \frac{1}{z}} \\ = (- \frac{1}{z}) \sum_{n = 0}^{\infty} {(\frac{1}{z})}^{n} \\ = - \sum_{n = 0}^{\infty} \frac{1}{z^{n + 1}} \\ = - \sum_{n = - \infty}^{- 1} z^{n} . \end{aligned}$
$\begin{aligned} \frac{1}{2 - z} & = (\frac{1}{2}) \frac{1}{1 - \frac{z}{2}} \\ = \frac{1}{2} \sum_{n = 0}^{\infty} {(\frac{z}{2})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{z^{n}}{2^{n + 1}} . \end{aligned}$

Entonces, para todo $z \in A (0, 1, 2)$ tenemos que:
$f (z) = - \sum_{n = - \infty}^{- 1} z^{n} - \sum_{n = 0}^{\infty} \frac{z^{n}}{2^{n + 1}} = \dots - \frac{1}{z^{2}} - \frac{1}{z} - \frac{1}{2} - \frac{z}{4} - \frac{z^{2}}{8} - \dots .$

Análogamente, para $z \in A (- i, \sqrt{2}, \sqrt{5})$ tenemos que $\sqrt{2} < | z + i | < \sqrt{5}$ , de donde:
$\frac{\sqrt{2}}{| z + i |} = \frac{| 1 + i |}{| z + i |} < 1 y \frac{| z + i |}{\sqrt{5}} = \frac{| z + i |}{| 2 + i |} < 1.$

Por lo que:
$\sum_{n = 0}^{\infty} {(\frac{1 + i}{z + i})}^{n} = \frac{1}{1 - \frac{1 + i}{z + i}} y \sum_{n = 0}^{\infty} {(\frac{z + i}{2 + i})}^{n} = \frac{1}{1 - \frac{z + i}{2 + i}} .$

Entonces:
$\begin{aligned} \frac{1}{1 - z} & = \frac{1}{(1 + i) - (z + i)} \\ = (- \frac{1}{z + i}) \frac{1}{1 - \frac{1 + i}{z + i}} \\ = (- \frac{1}{z + i}) \sum_{n = 0}^{\infty} {(\frac{1 + i}{z + i})}^{n} \\ = (- \frac{1}{z + i}) \sum_{n = - \infty}^{0} {(\frac{z + i}{1 + i})}^{n} \\ = - \sum_{n = - \infty}^{0} \frac{{(z + i)}^{n - 1}}{(1 + i)^{n}} \\ = - \sum_{n = - \infty}^{- 1} \frac{{(z + i)}^{n}}{(1 + i)^{n + 1}} . \end{aligned}$
$\begin{aligned} \frac{1}{2 - z} & = \frac{1}{(2 + i) - (z + i)} \\ = (\frac{1}{2 + i}) \frac{1}{1 - \frac{z + i}{2 + i}} \\ = \frac{1}{2 + i} \sum_{n = 0}^{\infty} {(\frac{z + i}{2 + i})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{{(z + i)}^{n}}{(2 + i)^{n + 1}} . \end{aligned}$

Por lo tanto, para todo $z \in A (- i, \sqrt{2}, \sqrt{5})$ tenemos que:
$f (z) = - \sum_{n = - \infty}^{- 1} \frac{{(z + i)}^{n}}{(1 + i)^{n + 1}} - \sum_{n = 0}^{\infty} \frac{{(z + i)}^{n}}{(2 + i)^{n + 1}} .$

Ejemplo 42.8.
Determinemos la expansión en serie de Laurent de la función $f (z) = e^{1 / z}$ , en el anillo $A (0, 0, \infty)$ .

Solución. Sabemos que $f$ es una función analítica en $D := C ∖ {0}$ , por lo que en particular es analítica en $A (0, 0, \infty) \subset D$ . Considerando la serie de Maclaurin de la exponencial compleja, ejemplo 42.4, tenemos que:
$e^{z} = \sum_{n = 0}^{\infty} \frac{z^{n}}{n!}, \forall z \in C .$

Para $z \in A (0, 0, \infty)$ tenemos que $0 < | z | < \infty$ , por lo que $z \neq 0$ , entonces:
$e^{1 / z} = \sum_{n = 0}^{\infty} \frac{(1 / z)^{n}}{n!} = \sum_{n = 0}^{\infty} \frac{1}{z^{n} n!} .$

Ejemplo 42.9.
Determinemos la serie de Laurent de la función $f (z) = (1 - z)^{- 3}$ , en el anillo $A (0, 1, \infty)$ .

Solución. Sabemos que $f$ es una función analítica en $D := C ∖ {1}$ , en particular es analítica en el anillo abierto $A (0, 1, \infty) \subset D$ . Considerando el ejemplo 42.7, para $z \in A (0, 1, \infty)$ tenemos que $| z |^{- 1} < 1$ , por lo que:
$\begin{aligned} \frac{1}{1 - z} & = (- \frac{1}{z}) \frac{1}{1 - \frac{1}{z}} \\ = (- \frac{1}{z}) \sum_{n = 0}^{\infty} {(\frac{1}{z})}^{n} \\ = - \sum_{n = 1}^{\infty} \frac{1}{z^{n}} . \end{aligned}$

Diferenciando dos veces de ambos lados de la igualdad, tenemos que:
$\frac{d}{z} \frac{1}{1 - z} = \frac{1}{(1 - z)^{2}} = \sum_{n = 1}^{\infty} \frac{n}{z^{n + 1}} = \frac{d}{d z} (- \sum_{n = 1}^{\infty} \frac{1}{z^{n}}),$
$\frac{d}{z} \frac{1}{(1 - z)^{2}} = \frac{2}{(1 - z)^{3}} = - \sum_{n = 1}^{\infty} \frac{n (n + 1)}{z^{n + 2}} = \frac{d}{d z} (\sum_{n = 1}^{\infty} \frac{n}{z^{n + 1}}),$ de donde:
$f (z) = \frac{1}{(1 - z)^{3}} = - \frac{1}{2} \sum_{n = 1}^{\infty} \frac{n (n + 1)}{z^{n + 2}},$ para todo $z \in A (0, 1, \infty)$ .

Ejemplo 42.10.
Sea $γ$ la circunferencia unitaria orientada positivamente. Evaluemos la integral:
$\int_{γ} \frac{e^{1 / z}}{z} d z .$

Solución. Sea $f (z) = e^{1 / z} z^{- 1}$ . Es claro que $f$ es una función analítica en $D := C ∖ {0}$ y $γ$ está completamente contenido en $D$ , entonces $f$ es continua en el contorno $γ$ , por lo que la integral existe. Sin embargo, no podemos utilizar el teorema integral de Cauchy para evaluar la integral ya que la singularidad $z_{0} = 0$ está dentro de la circunferencia unitaria dada por $γ$ .

Consideremos al anillo abierto $A (0, 0, \infty) \subset D$ . Por el ejemplo 42.8, sabemos que para todo $z \in A (0, 0, \infty)$ se cumple que:
$e^{1 / z} = \sum_{n = 0}^{\infty} \frac{(1 / z)^{n}}{n!} = \sum_{n = 0}^{\infty} \frac{1}{z^{n} n!} .$

Por lo que, para todo $z \in A (0, 0, \infty)$ tenemos que:
$f (z) = \frac{e^{1 / z}}{z} = \frac{1}{z} \sum_{n = 0}^{\infty} \frac{1}{z^{n} n!} = \sum_{n = 0}^{\infty} \frac{1}{z^{n + 1} n!} .$

Del ejemplo 34.1 sabemos que:
$\int_{γ} \frac{1}{z^{n + 1}} d z = {\begin{array}{lcc} 0 & si & n \neq 0, \\ 2 π i & si & n = 0. \end{array}$

Entonces, como $γ$ es un contorno en el anillo abierto $A (0, 0, \infty)$ , tenemos que:
$\begin{aligned} \int_{γ} \frac{e^{1 / z}}{z} d z & = \int_{γ} \sum_{n = 0}^{\infty} \frac{1}{z^{n + 1} n!} d z \\ = \sum_{n = 0}^{\infty} \frac{1}{n!} \int_{γ} \frac{1}{z^{n + 1}} d z \\ = \frac{1}{0!} 2 π i \\ = 2 π i . \end{aligned}$

Tarea moral

Sean $z_{1}, z_{2} \in C$ tales que $z_{1} \neq z_{2}$ y $0 < | z_{1} | \leq | z_{2} |$ . Muestra que para $| z | < | z_{1} |$ , se cumple que:
$\frac{1}{(z_{1} - z) (z_{2} - z)} = \frac{1}{(z_{1} - z_{2})} \sum_{n = 0}^{\infty} \frac{(z_{1}^{n + 1} - z_{2}^{n + 1})}{(z_{1} z_{2})^{n + 1}} z^{n} .$
Determina la expansión en serie de Taylor de las siguientes funciones alrededor del punto dado.
a) $f (z) = \frac{4}{z^{2} + 2 z}$ , alrededor de $z_{0} = 1$ .
b) $f (z) = \frac{2}{1 - z^{2}}$ , alrededor de $z_{0} = i$ .
c) $f (z) = \frac{2 i}{3 - i z}$ , alrededor de $z_{0} = - 1$ .
d) $f (z) = z e^{3 z^{2}}$ , alrededor de $z_{0} = 0$ .
Muestra que las siguientes funciones son analíticas en $z_{0} = 0$ . Determina su desarrollo en serie de Maclaurin y su radio de convergencia.
a) $f (z) = {\begin{array}{lcc} \frac{\cos (z) - 1}{z} & si & z \neq 0, \\ 0 & si & z = 0. \end{array}$
b) $f (z) = {\begin{array}{lcc} \frac{e^{z} - 1}{z} & si & z \neq 0, \\ 1 & si & z = 0. \end{array}$
Determina la expansión en serie de Laurent de las siguientes funciones en los anillos abiertos dados.
a) $f (z) = z + \frac{1}{z}$ , en $A (1, 1, \infty)$ .
b) $f (z) = \frac{1}{(3 z - 1) (2 z + 1)}$ , en $A (0, 1 / 3, 1 / 2)$ .
c) $f (z) = \frac{1}{1 - z^{2}}$ , en $A (2, 1, 3)$ .
d) $f (z) = z + \frac{1}{z}$ , en $A (1, 1, \infty)$ .
Evalúa las siguientes integrales utilizando una serie de Laurent apropiada en cada caso. Todas las circunferencias están orientadas positivamente.
a) $\int_{C (0, 1)} sen (\frac{1}{z}) d z$ .
b) $\int_{C (0, 4)} Log (1 + \frac{1}{z}) d z$ .
c) $\int_{C (0, 1)} \frac{\cos (\frac{1}{z^{2}})}{z} d z$ .
d) $\int_{C (0, 1)} e^{z^{2} + \frac{1}{z}} d z$ .
Muestra que:
$\cosh (z + \frac{1}{z}) = \sum_{n = - \infty}^{\infty} c_{n} z^{n},$ donde:
$c_{n} = \int_{0}^{2 π} \cos (n t) \cosh (2 \cos (t)) d t .$ Hint: Integra a lo largo de la circunferencia unitaria $C (0, 1)$ .

Más adelante…

En esta entrada hemos probado dos resultados que son de suma importancia en la teoría de la Variable Compleja y que nos permiten caracterizar aún más a las funciones analíticas. Dichos resultados son el teorema de Taylor y el teorema de Laurent, y ambos nos permiten dar un recíproco a los resultados de la tercera unidad, en la cual vimos que una serie de potencias define a una función analítica en su disco de convergencia, mientras que con los resultados de esta entrada establecimos que toda función analítica en un dominio puede representarse a través de un desarrollo en series de potencias, ya sea en una expansión en serie de Taylor o en una expansión en serie de Laurent, dependiendo de la función analítica en cuestión.

La siguiente entrada corresponde con la última de estas notas, en ella daremos una clasificación de las singularidades de una función analítica y veremos uno de los resultados más importantes del curso, el cual engloba la mayoría de resultados establecidos hasta ahora y que nos es de mucha utilidad en la práctica al evaluar integrales, es decir, el teorema del residuo.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Técnicas para construir funciones analíticas.
Siguiente entrada del curso: Clasificación de ceros y singularidades de una función analítica.

Variable Compleja I: Teorema integral de Cauchy

Por Pedro Rivera Herrera

Deja un comentario

Introducción

El teorema integral de Cauchy es una de las piedras angulares del análisis complejo. Dicho resultado resuelve dos características aparentemente contradictorias de las integrales de contorno cuando $f$ es una función fija pero el contorno $γ$ , a lo largo del que se integrará a $f$ , puede cambiar. Por una parte, es posible modificar el contorno $γ$ de forma bastante drástica sin efecto en la integral, por ejemplo, reemplazando un contorno simple por un contorno no simple a trozos. Por otra parte, si cambiamos un contorno semicircular en el semiplano superior del plano complejo $C$ , que une a $- 1$ y $1$ , por un contorno semicircular en el semiplano inferior de $C$ , que une a $- 1$ y $1$ , tenemos que el resultado de la integral de $f (z) = z^{- 1}$ a lo largo de dichos contornos cambia completamente. Entonces, a través del teorema integral de Cauchy nos será posible explicar estas dos características y concluir que lo que realmente importa es el número de vueltas que un contorno $γ$ da alrededor de los puntos que se encuentran fuera del dominio de $f$ .

El teorema integral de Cauchy-Goursat establece que dentro de ciertos dominios la integral de una función analítica a lo largo de un contorno cerrado simple es cero. Una extensión de este teorema nos permitirá reemplazar integrales sobre ciertos contornos complicados con integrales sobre contornos que son fáciles de evaluar.

En esta entrada abordaremos una versión local del teorema integral de Cauchy para discos abiertos, la cual nos permitirá obtener un resultado general de dicho teorema.

Recordemos el siguiente resultado visto en nuestros cursos de Cálculo.

Teorema 36.1. (Teorema de Green.)
Sea $C$ una curva de clase $C^{1}$ , cerrada, simple y orientada positivamente, tal que es la frontera de una región $D \subset R^{2}$ . Si $P, Q : D \to R$ son dos funciones reales de clase $C^{1}$ , entonces:
$\int_{C} P d x + Q d y = \iint_{D} (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}) d x d y .$

Procedemos a enunciar una primera versión del teorema integral de Cauchy para rectángulos.

Teorema 36.2. (Primera versión del Teorema Integral de Cauchy.)
Sean $U \subset C$ un conjunto abierto, $f : U \to C$ una función de clase $C^{1}$ y $R \subset U$ un rectángulo cerrado con frontera $\partial R$ orientada positivamente. Entonces:
$\int_{\partial R} f (z) d z = 0.$

Demostración. Dadas las hipótesis, sea $f (z) = u (x, y) + i v (x, y)$ .

De la definición 17.2 se tiene que $f$ es de clase $C^{1}$ si y solo si $u, u : U \to R$ son dos funciones reales de clase $C^{1}$ . Más aún, por el teorema 17.1 se cumple que las funciones $u$ y $v$ satisfacen las ecuaciones de C-R, por ser $f$ una función analítica en $U$ . Entonces, para $d z = d x + i d y$ , por la observación 34.3 y el Teorema de Green, se tiene que:
$\begin{aligned} \int_{\partial R} f (z) d z & = \int_{\partial R} (u d x - v d y) + i \int_{\partial R} (v d x + u d y) \\ = \iint_{R} (- \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}) d x d y + i \iint_{R} (\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}) d x d y \\ = \iint_{R} (\frac{\partial u}{\partial y} - \frac{\partial u}{\partial y}) d x d y + i \iint_{R} (\frac{\partial u}{\partial x} - \frac{\partial u}{\partial x}) d x d y \\ = 0. \end{aligned}$

Bajo la hipótesis adicional de que $f^{'} (z)$ es continua para todo $z \in U$ , la demostración de esta primera versión del Teorema de Cauchy es clara. Aunque el Teorema de Green fue establecido hasta 1828, fue Augustin Cauchy quien en 1814 demostró por primera vez el teorema 36.1, bajo la hipótesis adicional de continuidad sobre $f^{'}$ , utilizando una formulación equivalente a la establecida en el Teorema de Green.

Observación 36.1.
Más adelante probaremos que las derivadas de una función analítica son también funciones analíticas y por tanto continuas, proposición 16.1, entonces la hipótesis de continuidad sobre $f^{'}$ resulta redundante e innecesaria.

Procedemos ahora a probar una versión local del Teorema integral de Cauchy para discos.

Teorema 36.3. (Teorema Integral de Cauchy-Goursat para discos.)
Sean $r > 0$ , $z_{0} \in C$ un punto fijo y $f : B (z_{0}, r) \to C$ una función analítica en el disco abierto $B (z_{0}, r)$ . Entonces:
$\int_{γ} f (z) d z = 0,$ para cualquier contorno cerrado $γ$ en $B (z_{0}, r)$ .

Demostración. Dadas las hipótesis, sea $z_{0} = x_{0} + i y_{0}$ el centro del disco $B (z_{0}, r)$ , $ζ = x + i y \in B (z_{0}, r)$ cualquier punto y $f (z) = u (x, y) + i v (x, y)$ . De acuerdo con la proposición 35.2 basta con probar que existe una primitiva de $f$ en $B (z_{0}, r)$ .

Sea $γ_{1}$ el contorno dado por el segmento de recta vertical que une a $z_{0}$ con $x_{0} + i y$ seguido del segmento de recta horizontal que une a $x_{0} + i y$ con $ζ$ , es decir, $γ_{1} := [z_{0}, x_{0} + i y] + [x_{0} + i y, ζ]$ . Análogamente, definimos al contorno $γ_{2}$ dado por el segmento de recta horizontal que une a $z_{0}$ con $x + i y_{0}$ seguido del segmento de recta vertical que une a $x + i y_{0}$ con $ζ$ , es decir, $γ_{2} := [z_{0}, x + i y_{0}] + [x + i y_{0}, ζ]$ , figura 134.

Es claro que el contorno $γ = γ_{2} + (- γ)$ es un contorno cerrado y coincide con la frontera $\partial R$ del rectángulo $R \subset B (z_{0}, r)$ con vértices $z_{0}, x + i y_{0}, ζ, x_{0} + i y \in B (z_{0}, r)$ . Por lo que, del lema de Goursat y la proposición 34.2, tenemos que:
$\begin{aligned} 0 & = \int_{\partial R} f (z) d z \\ = \int_{z_{0}}^{x + i y_{0}} f (z) d z + \int_{x + i y_{0}}^{ζ} f (z) d z + \int_{ζ}^{x_{0} + i y} f (z) d z + \int_{x_{0} + i y}^{z_{0}} f (z) d z \\ = \int_{γ_{2}} f (z) d z + \int_{- γ_{1}} f (z) d z . \end{aligned}$

Es decir:
$\int_{γ_{2}} f (z) d z = - \int_{- γ_{1}} f (z) d z = \int_{γ_{1}} f (z) d z .$

Figura 134: Rectángulo cerrado $R \subset B (z_{0}, r)$ .

Considerando lo anterior definimos a la función:
$F (z) := \int_{γ_{1}} f (z) d z = \int_{γ_{2}} f (z) d z .$

Veamos que $F$ es una primitiva de $f$ en $B (z_{0}, r)$ .

Como en los segmentos $[z_{0}, x + i y_{0}]$ y $[x_{0} + i y, ζ]$ el término imaginario es constante, entonces podemos parametrizar a dichos segmentos, respectivamente, como:
$\begin{aligned} β_{1} (t) & = t + i y_{0}, \forall t \in [x_{0}, x], \\ β_{2} (t) & = t + i y, \forall t \in [x_{0}, x] . \end{aligned}$

Análogamente, en los segmentos $[z_{0}, x_{0} + i y]$ y $[x + i y_{0}, ζ]$ el término real es constante, por lo que podemos parametrizar a dichos segmentos, respectivamente, como:
$\begin{aligned} β_{3} (t) & = x_{0} + i t, \forall t \in [y_{0}, y], \\ β_{4} (t) & = x + i t, \forall t \in [y_{0}, y] . \end{aligned}$

Entonces, de la definición 34.1 y la proposición 33.1, se sigue que:
$\begin{aligned} F (z) & = \int_{γ_{1}} f (z) d z \\ = \int_{β_{1}} f (z) d z + \int_{β_{4}} f (z) d z \\ = \int_{x_{0}}^{x} f (t + i y_{0}) d t + i \int_{y_{0}}^{y} f (x + i t) d t \\ = \int_{x_{0}}^{x} u (t + i y_{0}) d t + i \int_{x_{0}}^{x} v (t + i y_{0}) d t - \int_{y_{0}}^{y} v (x, t) d t + i \int_{y_{0}}^{y} u (x, t) d t . \end{aligned}$

Por el primer Teorema Fundamental del Cálculo tenemos que:
$\begin{aligned} \frac{\partial F (z)}{\partial y} & = \frac{\partial}{\partial y} \int_{x_{0}}^{x} u (t + i y_{0}) d t + i \frac{\partial}{\partial y} \int_{x_{0}}^{x} v (t + i y_{0}) d t \\ - \frac{\partial}{\partial y} \int_{y_{0}}^{y} v (x, t) d t + i \frac{\partial}{\partial y} \int_{x_{0}}^{x} u (x, t) d t \\ = 0 + i 0 - v (x, y) + i u (x, y) \\ = i [u (x, y) + i v (x, y)] \\ = i f (z) . \end{aligned}$

Procediendo de manera análoga tenemos que:
$F (z) = \int_{β_{2}} f (z) d z + \int_{β_{3}} f (z) d z,$ de donde:
$\frac{\partial F (z)}{\partial x} = f (z) .$

Tenemos que:
$0 = f (z) - f (z) = \frac{\partial F (z)}{\partial x} + i \frac{\partial F (z)}{\partial y},$ es decir, si $F (z) = U (x, y) + i V (x, y)$ , entonces:
$\frac{\partial U}{\partial x} = \frac{\partial V}{\partial y}, \frac{\partial U}{\partial y} = - \frac{\partial V}{\partial x},$ por lo que $U$ y $V$ satisfacen las ecuaciones de C-R. Más aún, como $f$ es analítica en $B (z_{0}, r)$ , en particular es continua, por lo que $U_{x}, U_{y}, V_{x}$ y $V_{y}$ son continuas, es decir, $F$ es una función de clase $C^{1} (B (z_{0}, r))$ , entonces por el teorema 18.1 tenemos que $F$ es una función analítica en $B (z_{0}, r)$ tal que:
$F^{'} (z) = \frac{\partial F (z)}{\partial x} = - i \frac{\partial F (z)}{\partial y} = f (z), \forall z \in B (z_{0}, r),$ es decir, $F$ es una primitiva de $f$ en $B (z_{0}, r)$ , por lo que de la proposición 35.2 se sigue que:
$\int_{γ} f (z) d z = 0,$ para cualquier contorno cerrado $γ$ en $B (z_{0}, r)$ .

Ejemplo 36.1.
Evaluemos la integral:
$\int_{γ} \frac{e^{z}}{z^{2} - 16} d z,$ donde $γ$ describe a la circunferencia $C (0, 2)$ orientada positivamente y recorrida una vez.

Solución. Es claro que la función:
$f (z) = \frac{e^{z}}{z^{2} - 16},$ es analítica en $D = C ∖ {- 4, 4}$ y en particular es analítica en el disco abierto $B (0, 3) \subset D$ .

Por otra parte, tenemos que el contorno cerrado $C (0, 2)$ , parametrizado por $γ (t) = 2 e^{i t}$ , con $t \in [0, 2 π]$ , está completamente contenido en el disco $B (0, 3)$ , figura fig:f135, por lo que del teorema 36.3 se sigue que:
$\int_{γ} \frac{e^{z}}{z^{2} - 16} d z = 0.$

Figura 135: Contorno cerrado $C (0, 2)$ completamente contenido en el disco $B (0, 3)$ .

Ejemplo 36.2.
Veamos que
$\int_{0}^{\infty} \cos (t^{2}) d t = \int_{0}^{\infty} sen (t^{2}) d t = \frac{\sqrt{2 π}}{4} .$

Solución. Es claro que ambas integrales son integrales reales impropias, por lo que debemos probar que:
$lim_{r \to \infty} \int_{0}^{r} \cos (t^{2}) d t = lim_{r \to \infty} \int_{0}^{r} sen (t^{2}) d t = \frac{\sqrt{2 π}}{4} .$

Dado que $e^{i t^{2}} = \cos (t^{2}) + sen (t^{2})$ , basta probar que:
$lim_{r \to \infty} \int_{0}^{r} e^{t^{2}} d t = \frac{(1 + i) \sqrt{2 π}}{4},$ y tomar la parte real e imaginaria para obtener el resultado.

Sea $f (z) = e^{i z^{2}}$ . Definimos al contorno cerrado $γ = γ_{1} + γ_{2} - γ_{3}$ , firgura 136, donde:
$\begin{aligned} γ_{1} (t) & = t, \forall t \in [0, r] \\ γ_{3} (t) & = t e^{i π / 4}, \forall t \in [0, r], \\ γ_{2} (t) & = r e^{i t}, \forall t \in [0, π / 4] . \end{aligned}$

Figura 136: Contorno $γ = γ_{1} + γ_{2} - γ_{3}$ del ejemplo 36.2.

Tenemos que $f$ es una función entera, por lo que es analítica en cualquier disco abierto, en particular si consideramos al disco abierto $B (0, R)$ , con $0 < r < R$ , entonces es claro que el contorno $γ$ está completamente contenido en $B (0, R)$ , por lo que del Teorema Integral de Cauchy-Goursat, para discos y de la proposición 34.2, se sigue que:
$0 = \int_{γ} e^{i z^{2}} d z = \int_{γ_{1}} e^{i z^{2}} d z + \int_{γ_{2}} e^{i z^{2}} d z - \int_{γ_{3}} e^{i z^{2}} d z,$ por lo que:
$\begin{aligned} \int_{0}^{r} e^{i t^{2}} d t & = \int_{γ_{1}} e^{i z^{2}} d z \\ = \int_{γ_{3}} e^{i z^{2}} d z - \int_{γ_{2}} e^{i z^{2}} d z \\ (36.1) & = \frac{(1 + i) \sqrt{2}}{2} \int_{0}^{r} e^{- t^{2}} d t - \int_{γ_{2}} e^{i z^{2}} d z . \end{aligned}$

Por el ejemplo 34.11 sabemos que:
$| \int_{γ_{2}} e^{i z^{2}} d z | \leq \frac{π (1 - e^{r^{2}})}{4 r},$ por lo que, tomando el límite cuando $r \to \infty$ tenemos que:
$| \int_{γ_{2}} e^{i z^{2}} d z | = 0, ⟹ \int_{γ_{2}} e^{i z^{2}} d z = 0.$

Entonces, tomando el límite cuando $r \to \infty$ en (36.1) tenemos que:
$lim_{r \to \infty} \int_{0}^{r} e^{i t^{2}} d t = \frac{(1 + i) \sqrt{2}}{2} lim_{r \to \infty} \int_{0}^{r} e^{- t^{2}} d t .$

De nuestros cursos de Cálculo sabemos que:
$\int_{0}^{\infty} e^{- t^{2}} d t = \frac{π}{2},$ por lo que:
$\int_{0}^{\infty} e^{i t^{2}} d t = lim_{r \to \infty} \int_{0}^{r} e^{i t^{2}} d t = \frac{(1 + i) \sqrt{2}}{2} \frac{π}{2} = \frac{(1 + i) \sqrt{2 π}}{4} .$

Por último, tomando la parte real e imaginaria de esta última igualdad tenemos el resultado.

Teorema 36.4. (Teorema Integral de Cauchy-Goursat generalizado para discos.)
Sean $r > 0$ , $z_{0} \in C$ un punto fijo, $z_{1}, z_{2}, \dots, z_{n} \in B (z_{0}, r)$ , $D := B (z_{0}, r) ∖ {z_{1}, z_{2}, \dots, z_{n}}$ y $f : D \to C$ una función analítica en $D$ tal que:
$lim_{z \to z_{j}} (z - z_{j}) f (z) = 0,$ para todo $j = 1, \dots, n$ . Entonces:
$\int_{γ} f (z) d z = 0,$ para cualquier contorno cerrado $γ$ en $D$ que no pasa por los puntos $z_{1}, z_{2}, \dots, z_{n}$ .

Demostración. Dadas las hipótesis, es suficiente con probar el caso para un único punto $z_{1} \in B (z_{0}, r)$ en el cual $f$ no es analítica y proceder por inducción.

De manera similar a la prueba anterior, basta mostrar que existe una primitiva de $f$ en $D = B (z_{0}, r) ∖ {z_{1}}$ . Para ello tomamos a $ζ \in D$ y consideramos al contorno poligonal $γ$ que une al centro $z_{0}$ del disco abierto $B (z_{0}, r)$ con $ζ$ , considerando segmentos de recta verticales y horizontales, sin pasar por $z_{1}$ y definimos a dicha primitiva como la función:
$F (z) = \int_{γ} f (z) d z,$ la cual está bien definida pues $B (z_{0}, r)$ es poligonal conexo, entonces el contorno poligonal $γ$ siempre existe. Solo basta considerar la ubicación del punto $z_{1} \in B (z_{0}, r)$ al definir a $γ$ . Si $z_{1}$ no cae en las rectas $x = x_{0}$ y $y_{0}$ , entonces bastan tres segmentos de recta para unir a $z_{0} = x_{0} + i y_{0}$ con el punto $ζ \neq z_{1}$ , en tal caso es fácil mostrar, de la misma manera que antes, que $F_{y} (z) = i f (z)$ y $F_{x} (z) = f (z)$ utilizando el lema de Goursat generalizado y concluir que $F$ es una primitiva de $f$ en $D$ , por lo que el resultado se sigue de la proposición 35.2.

Por último, si $z_{1}$ cae en alguna de las rectas $x = x_{0}$ ó $y = y_{0}$ , basta con fijar otro punto de inicio de $γ$ , distinto del centro del disco $B (z_{0}, r)$ , en la definición de $F$ y volver a plantear el análisis anterior.

Observación 36.2.
Notemos que el resultado anterior es equivalente a pedir que $f$ sea analítica en $B (z_{0}, r) ∖ {z_{1}, z_{2}, \dots, z_{n}}$ , con $z_{1}, z_{2}, \dots, z_{n} \in B (z_{0}, r)$ , y continua en $B (z_{0}, r)$ .

Corolario 36.1.
Sean $r > 0$ , $z_{0} \in C$ un punto fijo, $[a, b] \subset R$ , con $a < b$ , un intervalo cerrado, $f : B (z_{0}, r) \to C$ una función analítica en el disco abierto $B (z_{0}, r)$ , $ζ \in B (z_{0}, r)$ y $γ : [a, b] \to B (z_{0}, r)$ un contorno cerrado que no pasa por $ζ$ . Entonces:
$f (ζ) \int_{γ} \frac{d z}{z - ζ} = \int_{γ} \frac{f (z)}{z - ζ} d z .$

Demostración.Dadas las hipótesis, sea $ζ \in B (z_{0}, r)$ , como $f$ es analítica en el disco abierto $B (z_{0}, r)$ , en particular lo es en $ζ$ , por lo que:
$lim_{z \to ζ} \frac{f (z) - f (ζ)}{z - ζ} = f^{'} (ζ) .$

Considerando lo anterior definimos a la función:
$g (z) = {\begin{array}{lcc} \frac{f (z) - f (ζ)}{z - ζ} & si & z \neq ζ, \\ f^{'} (ζ) & si & z = ζ . \end{array}$

Claramente $g$ es una función analítica en $B (z_{0}, r) ∖ {ζ}$ y continua en $ζ$ , por lo que:
$lim_{z \to ζ} (z - ζ) g (z) = 0.$

Entonces, por el Teorema de Cauchy generalizado tenemos que:
$\begin{aligned} 0 & = \int_{γ} g (z) d z \\ = \int_{γ} \frac{f (z) - f (ζ)}{z - ζ} d z \\ = \int_{γ} \frac{f (z)}{z - ζ} d z - \int_{γ} \frac{f (ζ)}{z - ζ} d z \\ = \int_{γ} \frac{f (z)}{z - ζ} d z - f (ζ) \int_{γ} \frac{d z}{z - ζ} . \end{aligned}$

Por lo que:
$f (ζ) \int_{γ} \frac{d z}{z - ζ} = \int_{γ} \frac{f (z)}{z - ζ} d z,$ para cualquier contorno cerrado $γ$ en $B (z_{0}, r)$ que no pasa por $ζ$ .

Lema 36.1.
Sean $[a, b] \subset R$ , con $a < b$ , $γ : [a, b] \to C$ un contorno y $φ : C \to C$ una función que está definida y es continua en los puntos del contorno, es decir, en $γ ([a, b])$ . Para cada $n \in N^{+}$ se define a la función:
$F_{n} (z) := \int_{γ} \frac{φ (ζ)}{(ζ - z)^{n}} d ζ, z \notin γ ([a, b]) .$

Entonces, cada función $F_{n}$ es analítica en $C ∖ γ ([a, b])$ y $F_{n}^{'} (z) = n F_{n + 1} (z)$ , lo cual implica que cada $F_{n}$ tiene derivadas analíticas de todos los órdenes.

Demostración. Dadas las hipótesis, primero procedemos a verificar que cada función $F_{n}$ es continua. Sea $z_{0} \in D := C ∖ γ ([a, b])$ fijo. Como $[a, b] \subset R$ es compacto y la función $γ$ es continua, entonces, proposición 10.9, $γ ([a, b])$ es compacto, por lo que, proposición 10.10, $γ$ alcanza su valor mínimo, entonces definimos a $r := min_{t \in [a, b]} | γ (t) - z_{0} | > 0$ . Análogamente, como $γ ([a, b])$ es compacto y $φ$ es continua en dicho conjunto, entonces su imagen también es un conjunto compacto, en particular es un conjunto acotado, es decir, existe $M > 0$ tal que $| φ (ζ) | \leq M$ para todo $ζ \in γ ([a, b])$ .

Recordemos la factorización:
$x^{n} - y^{n} = (x - y) (x^{n - 1} + x^{n - 2} y + \dots + x y^{n - 2} + y^{n - 1}) .$

Entonces:
$\begin{aligned} \frac{1}{(ζ - z)^{n}} - \frac{1}{(ζ - z_{0})^{n}} & = [\frac{1}{ζ - z} - \frac{1}{ζ - z_{0}}] [\frac{1}{(ζ - z)^{n - 1}} + \frac{1}{(ζ - z)^{n - 2} (ζ - z_{0})} \\ + \dots + \frac{1}{(ζ - z) (ζ - z_{0})^{n - 2}} + \frac{1}{(ζ - z_{0})^{n - 1}}] \\ = (z - z_{0}) [\frac{1}{(ζ - z)^{n} (ζ - z_{0})} + \frac{1}{(ζ - z)^{n - 1} (ζ - z_{0})^{2}} \\ + \dots + \frac{1}{(ζ - z)^{2} (ζ - z_{0})^{n - 1}} + \frac{1}{(ζ - z) (ζ - z_{0})^{n}}] . \end{aligned}$

Multiplicando por $φ (ζ)$ e integrando a lo largo de $γ$ , en ambos lados de la igualdad anterior, tenemos que:
$\begin{aligned} F_{n} (z) - F_{n} (z_{0}) & = (z - z_{0}) \int_{γ} [\frac{φ (ζ)}{(ζ - z)^{n} (ζ - z_{0})} + \dots + \frac{φ (ζ)}{(ζ - z) (ζ - z_{0})^{n}}] d ζ \\ = (z - z_{0}) \int_{γ} \sum_{k = 0}^{n - 1} \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ \\ (36.3) & = (z - z_{0}) \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ, \end{aligned}$ donde $z \in B (z_{0}, r / 2)$ y $ζ \in γ ([a, b])$ . Por lo que $| z - z_{0} | < r / 2$ , $r / 2 < r \leq | ζ - z_{0} |$ y $r / 2 < | ζ - z |$ , entonces:
$| \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} | < M {(\frac{2}{r})}^{n + 1},$ para cada $0 \leq k \leq n - 1$ .

Por lo tanto, para $ε > 0$ , tomando $δ < r / 2$ se tiene que si $| z - z_{0} | < δ$ , entonces podemos acotar a (36.3) mediante la proposición 34.3(5) y la desigualdad del triángulo, es decir:
$\begin{aligned} | F_{n} (z) - F_{n} (z_{0}) | & = | z - z_{0} | | \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ | \\ \leq | z - z_{0} | \sum_{k = 0}^{n - 1} | \int_{γ} \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ | \\ \leq | z - z_{0} | \sum_{k = 0}^{n - 1} \int_{γ} | \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ | \\ < δ \sum_{k = 0}^{n - 1} M {(\frac{2}{r})}^{n + 1} \int_{γ} | d z | \\ = n δ M ℓ (γ) {(\frac{2}{r})}^{n + 1} . \end{aligned}$

Por lo que, para:
$δ := min {\frac{r}{2}, \frac{ε r^{n + 1}}{n M ℓ (γ) 2^{n + 1}}},$ se tiene que si $| z - z_{0} | δ$ , entonces $| F_{n} (z) - F_{n} (z_{0}) | < ε$ , por lo que $F_{n}$ es una función continua.

Dividiendo en ambos lados de la igualdad (36.3) por $z - z_{0}$ , tenemos que:
$\begin{aligned} \frac{F_{n} (z) - F_{n} (z_{0})}{z - z_{0}} & = \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ)}{(ζ - z)^{n - k} (ζ - z_{0})^{k + 1}} d ζ \\ = \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ) (ζ - z_{0})^{- (k + 1)}}{(ζ - z)^{n - k}} d ζ . \end{aligned}$

Dado que $z_{0} \notin γ ([a, b])$ , entonces para cada $0 \leq k \leq n - 1$ , la función:
$φ (ζ) (ζ - z_{0})^{- (k + 1)},$ es continua. Por lo tanto, de la primera parte de la prueba tenemos que la función:
$h (z) = \int_{γ} \frac{φ (ζ) (ζ - z_{0})^{- (k + 1)}}{(ζ - z)^{n - k}} d ζ,$ es una función continua para cada $0 \leq k \leq n - 1$ . Entonces:
$\begin{aligned} F_{n}^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{F_{n} (z) - F_{n} (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ) (ζ - z_{0})^{- (k + 1)}}{(ζ - z)^{n - k}} d ζ \\ = \sum_{k = 0}^{n - 1} \int_{γ} lim_{z \to z_{0}} \frac{φ (ζ) (ζ - z_{0})^{- (k + 1)}}{(ζ - z)^{n - k}} d ζ \\ = \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ)}{(ζ - z_{0})^{n + 1}} d ζ \\ = \sum_{k = 0}^{n - 1} \int_{γ} \frac{φ (ζ)}{(ζ - z_{0})^{n + 1}} d ζ \\ = n \int_{γ} \frac{φ (ζ)}{(ζ - z_{0})^{n + 1}} d ζ \\ = n F_{n + 1} (z_{0}) . \end{aligned}$

Definición 36.1. (Índice de un contorno cerrado respecto a un punto.)
Sean $[a, b] \subset R$ , con $a < b$ , un intervalo cerrado, $γ : [a, b] \to C$ un contorno cerrado y $z_{0} \in C ∖ γ ([a, b])$ , es decir, $z_{0} \in C$ es un punto que no está en el contorno $γ$ . Se define al índice de $γ$ con respecto de $z_{0}$ como:
$n (γ, z_{0}) = \frac{1}{2 π i} \int_{γ} \frac{d z}{z - z_{0}} .$

Proposición 36.1.
Sean $[a, b] \subset R$ , con $a < b$ , un intervalo cerrado, $γ : [a, b] \to C$ un contorno cerrado y $z_{0} \in C ∖ γ ([a, b])$ . Entonces:
$\begin{matrix} (36.3) & \int_{γ} \frac{1}{z - z_{0}} d z = 2 π k i, \end{matrix}$ para algún $k \in Z$ . Es decir, la integral (36.3) es un múltiplo entero de $2 π i$ .

Demostración. Dadas las hipótesis, por la definición 34.1 tenemos que:
$h (z) := \int_{γ} \frac{1}{z - z_{0}} d z = \int_{a}^{b} \frac{γ^{'} (t)}{γ (t) - z_{0}} d t .$

Considerando lo anterior definimos a la función híbrida $F : [a, b] \to C$ como:
$F (x) := \int_{a}^{x} \frac{γ^{'} (t)}{γ (t) - z_{0}} d t, a \leq x \leq b .$

Por construcción es claro que $F$ es una función continua en $[a, b]$ y que $F (a) = 0$ y $F (b) = h (z)$ . Veamos que $F (b) = 2 π k i$ , para algún $k \in Z$ .

Dado que $γ^{'}$ es continua en $[a, b]$ , salvo quizás en un número finito de puntos, entonces $F$ es diferenciable en los puntos de continuidad de $γ^{'}$ y su derivada está dada por el Teorema Fundamental del Cálculo:
$\begin{matrix} (36.4) & F^{'} (x) = \frac{γ^{'} (x)}{γ (x) - z_{0}}, \end{matrix}$ para los puntos donde $γ^{'}$ existe.

Sea $G : [a, b] \to C$ la función híbrida dada por:
$G (t) = e^{- F (t)} [γ (t) - z_{0}], a \leq t \leq b .$

Por construcción tenemos que $G$ es también continua en $[a, b]$ . Más aún, para cada $t \in [a, b]$ donde $γ^{'}$ es continua, por (36.4) y como $γ (a) = γ (b) \neq z_{0}$ , tenemos que:
$\begin{aligned} G^{'} (t) & = e^{- F (t)} γ^{'} (t) - F^{'} (t) e^{- F (t)} [γ (t) - z_{0}] \\ = e^{- F (t)} (γ^{'} (t) - F^{'} (t) [γ (t) - z_{0}]) \\ = e^{- F (t)} (γ^{'} (t) - \frac{γ^{'} (t)}{γ (t) - z_{0}} [γ (t) - z_{0}]) \\ = e^{- F (t)} [γ^{'} (t) - γ^{'} (t)] \\ = 0. \end{aligned}$

Lo anterior nos dice que $G$ es una función constante en cada subintervalo donde $γ^{'}$ existe y como $G$ es continua entonces $G$ es una función constante en $[a, b]$ , por lo que $G (a) = G (b)$ , es decir:
$e^{- F (a)} [γ (a) - z_{0}] = e^{- F (b)} [γ (b) - z_{0}] .$

Dado que $F (a) = 0$ y $γ (a) = γ (b) \neq z_{0}$ , tenemos que:
$e^{- F (b)} = 1,$ lo cual implica, por la proposición 20.2(10), que para algún $k \in Z$ :
$F (b) = 2 π k i .$

Entonces:
$2 π k i = F (b) = h (z) = \int_{γ} \frac{1}{z - z_{0}} d z,$ para algún $k \in Z$ .

Corolario 36.2.
El índice de un contorno cerrado $γ$ respecto a un punto $z_{0}$ es un número entero.

Demostración. Es inmediato de la definición de $n (γ, z_{0})$ y la proposición 36.1.

Observación 36.3.
Claramente $f (z) = \frac{1}{z - z_{0}}$ es una función analítica en $D := C ∖ {z_{0}}$ . Si pudiéramos encontrar una función analítica $F : D \to C$ tal que $F^{'} (z) = f (z)$ para todo $z \in D$ , entonces tendríamos que $n (γ, z_{0}) = 0$ para toda curva cerrada $γ$ en $D$ , que no pase por $z_{0}$ . Sin embargo, de acuerdo con el ejemplo 34.1 y la proposición 35.3 sabemos que $f$ no tiene primitiva en $D$ , por lo que $n (γ, z_{0}) \neq 0$ para toda curva cerrada $γ$ en $D$ , que no pase por $z_{0}$ .

Para continuar, en este punto es importante introducir el siguiente resultado, el cual intuitivamente es claro, pero cuya demostración es bastante complicada y se escapa de los objetivos de estas notas, por lo que en el curso lo tomaremos como válido, aunque puede consultarse una prueba formal de este hecho en:

Complex Analysis: The Argument Principle in Analysis and Topology, de Alan F. Beardon.
An Introduction to Classical Complex Analysis, de Robert B. Burckel.

Teorema 36.5. (Teorema de la curva de Jordan.)
Los puntos en cualquier contorno cerrado simple $C \subset C$ son la frontera de dos dominios distintos, uno de los cuales es el interior de $C$ , denotado por $I$ , y está acotado. El otro, es el exterior de $C$ , denotado por $E$ , y no es acotado. En tal caso, $I \cup E \cup C$ es igual al plano complejo $C$ .

Ejemplo 36.3.
Sean $r > 0$ y $z_{0} \in C$ un punto fijo. Consideremos a los conjuntos disjuntos $S_{1} = {z \in C : | z - z_{0} | < r}$ y $S_{2} = {z \in C : | z - z_{0} | > r}$ , los cuales son abiertos en $C$ . Geométricamente es claro que la circunferencia $C (z_{0}, r) = {z \in C : | z - z_{0} | = r}$ es un contorno cerrado simple y los puntos en $C (z_{0}, r)$ son la frontera de $S_{1}$ y $S_{2}$ . El interior de $C (z_{0}, r)$ es $S_{1}$ , el cual es un conjunto acotado y el exterior de $C (z_{0}, r)$ es $S_{2}$ , el cual es un conjunto no acotado.

Observación 36.4.
Por la proposición 10.9 sabemos que al ser $[a, b] \subset R$ , con $a < b$ , un conjunto compacto y $γ : [a, b] \to C$ una trayectoria, es decir, $γ$ es una función continua en $[a, b]$ , entonces la curva $γ ([a, b])$ en el plano complejo, es un conjunto compacto, es decir, una curva en $C$ es un conjunto cerrado y acotado. Entonces el conjunto $U = C ∖ γ ([a, b])$ es un conjunto abierto no vacío, por lo que, ejercicio 9 de la entrada 10, podemos ver a $U$ como la unión disjunta numerable de dominios, correspondientes con las componentes conexas de $U$ .

El siguiente lema enuncia algunas de las propiedades clave del índice de un contorno.

Lema 36.2.
Sean $γ$ un contorno cerrado en el plano complejo y $U = C ∖ γ ([a, b])$ . Se cumplen las siguientes propiedades.

$n (γ, z)$ permanece constante conforme $z$ toma valores en cualquiera de las componentes conexas de $U$ .
$n (γ, z) = 0$ para cualquier $z$ en la componente no acotada de $U$ .
Si $γ$ es simple, entonces $n (γ, z) = 1$ ó $n (γ, z) = - 1$ , para todo $z$ en la componente acotada de $U$ .

Demostración. Dadas las hipótesis, únicamente probaremos las primeras dos propiedades. La última afirmación está sustentada en el teorema de la curva de Jordan y por lo extenso de su prueba la omitiremos, pero se puede consultar una prueba detallada en An Introduction to Complex Function Theory, de Bruce P. Palka.

Sea $φ : γ ([a, b]) \to C$ dada por:
$φ (ζ) = \frac{1}{2 π i} .$ Por lo que, del lema 36.1 para $n = 1$ y la definición 36.1, tenemos que:
$n (γ, z) = \int_{γ} \frac{1}{ζ - z} d ζ,$ es una función analítica, de $z$ , en $U$ , cuya derivada está dada por:
$n^{'} (γ, z) = \int_{γ} \frac{1}{(ζ - z)^{2}} d ζ .$ Por otra parte, si fijamos a $z \in C$ , entonces la función:
$f (ζ) = \frac{1}{(ζ - z)^{2}},$ es una función analítica, de $ζ$ , en $C ∖ {z}$ y tiene como primitiva, en dicho conjunto, a la función:
$F (ζ) = - \frac{1}{ζ - z} .$ Si $z \in U$ , entonces $γ$ es un contorno cerrado en $C ∖ {z}$ , por lo que del TFC para integrales de contorno, proposición 35.1, para $z \in U$ tenemos que:
$\int_{γ} \frac{1}{(ζ - z)^{2}} d ζ = \int_{γ} f (ζ) d ζ = 0.$ Por lo que $n^{'} (γ, z) = 0$ en $U$ , entonces de la proposición 19.2 concluimos que $n (γ, z)$ es una función constante en cada componente de $U$ .
Sea $r > 0$ tal que el conjunto compacto $γ ([a, b])$ está contenido en el disco abierto $B (0, r)$ . Tenemos que el conjunto $C ∖ B (0, r)$ es un subconjunto conexo de $U$ , entonces por la proposición 10.6(1) se cumple que dicho conjunto conexo está contenido en alguna componente conexa $D$ de $U$ . Notemos que la componente conexa $D$ es la única componente no acotada de $U$ , ya que todas las demás componentes claramente subconjuntos de $B (0, r)$ .

Como el punto $z_{0} = 2 r \in D$ y la función $f (ζ) = (ζ - z_{0})^{- 1}$ es analítica en $B (0, r)$ , por el teorema (local) integral de Cauchy, teorema 36.3, tenemos que:
$n (γ, z_{0}) = \frac{1}{2 π i} \int_{γ} \frac{1}{ζ - z} d ζ = 0.$ Entonces, por el inciso anterior tenemos que $n (γ, z) = 0$ para todo $z \in D$ .

Observación 36.5.
De acuerdo con lo anterior, el índice de un contorno $n (γ, z_{0})$ tiene una interpretación geométrica clara, ya que nos dice el número de vueltas que el contorno cerrado $γ$ le da al punto $z_{0}$ y su signo está determinado por la orientación del contorno, es decir, si $γ$ tiene orientación positiva entonces $n (γ, z_{0})$ es positivo, mientras que si $γ$ tiene orientación negativa entonces $n (γ, z_{0})$ es negativo.

Más aún, si el contorno cerrado $γ$ es simple y el punto $z_{0}$ está en el interior de $γ$ , entonces $n (γ, z_{0}) = 1$ , mientras que si $z_{0}$ está fuera del contorno entonces $n (γ, z_{0}) = 0$ .

Motivados en lo anterior establecemos la siguiente definición, la cual es consistente con el teorema de la curva de Jordan.

Definición 36.2. (Interior de un contorno cerrado simple.)
Sean $[a, b] \subset R$ , con $a < b$ , y $γ : [a, b] \to C$ un contorno cerrado simple en $C$ . Se define al interior de $γ$ como el conjunto:
$I (γ) := {z \in C : n (γ, z) \neq 0} .$

Algunas de las propiedades más elementales del índice de un contorno están dadas en la siguiente:

Proposición 36.2. (Propiedades del índice de un contorno.)
Sean $[a, b] \subset R$ , con $a < b$ , y $γ, β : [a, b] \to C$ dos contornos cerrados en $C$ con el mismo punto inicial. Se cumplen las siguientes propiedades.

$n (- γ, z) = - n (γ, z)$ , para todo $z \in C ∖ γ ([a, b])$ .
$n (γ + β, z) = n (γ, z) + n (β, z)$ , para todo $z \in C ∖ (γ ([a, b]) \cup β ([a, b]))$ .
$n (\overset{―}{γ}, \overset{―}{z}) = - n (γ, z)$ , para todo $z \in C ∖ γ ([a, b])$ .
n(a\gamma+b,az+b) = n(\gamma,z) $, p a r a t o d o$ z\in\mathbb{C}\setminus\gamma([a,b]) $, c o n$ a\neq 0 $y$ b$ dos constantes.

Demostración. Se deja como ejercicio al lector.

Ejemplo 36.4.
Sean $r > 0$ y $z_{0} \in C$ un punto fijo. Consideremos a la circunferencia $C (z_{0}, r)$ y al disco abierto $B (z_{0}, r)$ .

a) Sea $γ : [0, 2 π] \to C$ dada por $γ (t) = z_{0} + r e^{i t}$ , es decir, $γ$ parametriza a la circunferencia $C (z_{0}, r)$ positivamente. Si $z \in B (z_{0}, r)$ , entonces por el lema 36.2(1), la definición 36.1 y el ejemplo 34.1(a) tenemos que:
$\begin{aligned} n (γ, z) & = n (γ, z_{0}) \\ = \frac{1}{2 π i} \int_{γ} \frac{1}{ζ - z_{0}} d ζ \\ = \frac{1}{2 π i} 2 π i \\ = 1. \end{aligned}$

Más aún, por el lema 36.2(2), tenemos que si $z \in C ∖ B (z_{0}, r)$ , entonces $n (γ, z) = 0$ .

b) Sea $γ : [0, 2 π] \to C$ dada por $γ (t) = z_{0} + r e^{- i t}$ , es decir, $γ$ parametriza a la circunferencia $C (z_{0}, r)$ negativamente. Si $z \in B (z_{0}, r)$ , entonces por el lema 36.2(1), la definición 36.1 y la definición 34.1 tenemos que:
$\begin{aligned} n (γ, z) & = n (γ, z_{0}) \\ = \frac{1}{2 π i} \int_{γ} \frac{1}{ζ - z_{0}} d ζ \\ = \frac{1}{2 π i} \int_{0}^{2 π} \frac{γ^{'} (t)}{γ (t) - z_{0}} d t \\ = \frac{1}{2 π i} \int_{0}^{2 π} \frac{- i r e^{- i t}}{z_{0} + r e^{- i t} - z_{0}} d t \\ = - \frac{i}{2 π i} \int_{0}^{2 π} d t \\ = - \frac{i}{2 π i} 2 π \\ = - 1. \end{aligned}$

Del lema 36.2(2), se sigue que para $z \in C ∖ B (z_{0}, r)$ , se cumple que $n (γ, z) = 0$ .

c) Sea $γ : [0, 2 π n] \to C$ , con $n \in N^{+}$ , dada por $γ (t) = z_{0} + r e^{i t}$ , es decir, $γ$ parametriza a la circunferencia $C (z_{0}, r)$ positivamente, pero la recorre $n$ -veces. Si $z \in B (z_{0}, r)$ , entonces por el lema 36.2(1), la definición 36.1 y la definición 34.1 tenemos que:
$\begin{aligned} n (γ, z) & = n (γ, z_{0}) \\ = \frac{1}{2 π i} \int_{γ} \frac{1}{ζ - z_{0}} d ζ \\ = \frac{1}{2 π i} \int_{0}^{2 π n} \frac{γ^{'} (t)}{γ (t) - z_{0}} d t \\ = \frac{1}{2 π i} \int_{0}^{2 π n} \frac{i r e^{- i t}}{z_{0} + r e^{- i t} - z_{0}} d t \\ = \frac{i}{2 π i} \int_{0}^{2 π n} d t \\ = \frac{i}{2 π i} 2 π n \\ = n . \end{aligned}$

Más aún, por el lema 36.2(2), tenemos que si $z \in C ∖ B (z_{0}, r)$ , entonces $n (γ, z) = 0$ .

De acuerdo con los resultados previos, estamos listos para establecer una de las primeras consecuencias del teorema integral de Cauchy generalizado, para discos, mediante el cual podremos obtener una representación fundamental de una función analítica.

Proposición 36.3. (Fórmula integral de Cauchy para discos.)
Sean $r > 0$ , $z_{0} \in C$ un punto fijo, $f : B (z_{0}, r) \to C$ una función analítica en el disco abierto $B (z_{0}, r)$ y $γ$ un contorno cerrado en $B (z_{0}, r)$ . Entonces:
$n (γ, z) f (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{ζ - z} d ζ,$ para todo $z \in B (z_{0}, r) ∖ γ ([a, b])$ .

Demostración. Dadas las hipótesis, fijamos un punto $z \in B (z_{0}, r) ∖ γ ([a, b])$ . Definimos a la función:
$g : B (z_{0}, r) \to C,$ como:
$g (ζ) = {\begin{array}{lcc} \frac{f (ζ) - f (z)}{ζ - z} & si & ζ \neq z, \\ f^{'} (z) & si & ζ = z, \end{array}$ donde $ζ$ es una variable independiente.

Es claro que $g$ es una función analítica en $B (z_{0}, r) ∖ {z}$ . Más aún, como $f$ es analítica en $B (z_{0}, r)$ , entonces:
$lim_{ζ \to z} g (ζ) = lim_{ζ \to z} \frac{f (ζ) - f (z)}{ζ - z} = f^{'} (z) = g (z),$ es decir, $g$ es continua en $z$ , por lo que:
$lim_{ζ \to z} (ζ - z) g (ζ) = 0.$

Como $z$ no está en el contorno cerrado $γ$ , del teorema 36.4 y la definición 36.1, tenemos que:
$\begin{aligned} 0 & = \int_{γ} g (ζ) d ζ \\ = \int_{γ} \frac{f (ζ) - f (z)}{ζ - z} d ζ \\ = \int_{γ} \frac{f (ζ)}{ζ - z} d ζ - \int_{γ} \frac{f (z)}{ζ - z} d ζ \\ = \int_{γ} \frac{f (ζ)}{ζ - z} d ζ - 2 π i n (γ, z) f (z), \end{aligned}$ es decir:
$n (γ, z) f (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{ζ - z} d ζ .$ Dado que $z \in B (z_{0}, r) ∖ γ ([a, b])$ es arbitrario, entonces se tiene el resultado.

Observación 36.6.
Un aspecto importante de la fórmula integral de Cauchy es que para un punto $z \in C$ para el cual $n (γ, z) \neq 0$ , podemos expresar el valor de la función $f (z)$ de manera explícita en términos de los valores de $f$ que se encuentran en el contorno $γ$ , a cierta distancia de $z$ .

La aplicación más usual de la fórmula integral de Cauchy se tiene para el caso en que $n (γ, z) = 1$ , ya que bajo dicha condición se tiene que:
$f (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{ζ - z} d ζ .$

Ejemplo 36.5.
Evaluemos la integral:
$\int_{γ} \frac{e^{π z}}{z^{3} + z} d z,$ donde $γ$ parametriza positivamente a la circunferencia $C (0, 2)$ .

Solución. Primeramente parametrizamos a la circunferencia $C (0, 2)$ como $γ (t) = 2 e^{i t}$ , con $0 \leq t \leq 2 π$ .

Aplicando fracciones parciales tenemos que:
$\frac{e^{π z}}{z^{3} + z} = \frac{e^{π z}}{z} - \frac{e^{π z}}{2 (z - i)} - \frac{e^{π z}}{2 (z + i)} .$

Notemos que para todo $z \in B (0, 2)$ , por el ejemplo 36.4(a), se cumple que:
$n (γ, z) = n (γ, 0) = 1.$

Sea $f (z) = e^{π z}$ . Claramente $f$ es una función entera, por lo que para $r > 2$ , se cumple que $C (0, 2) \subset B (0, r)$ y $f$ es analítica en $B (0, r)$ . Entonces, de la fórmula integral de Cauchy para discos, como $0, i, - i \in B (0, 2) \subset B (0, r)$ , tenemos que:
$\begin{aligned} \int_{γ} \frac{e^{π ζ}}{ζ} d ζ = \int_{γ} \frac{e^{π ζ}}{ζ - 0} d ζ & = 2 π i n (γ, 0) f (0) \\ = 2 π i (1) (e^{0}) \\ = 2 π i . \end{aligned}$
$\begin{aligned} \int_{γ} \frac{e^{π ζ}}{2 (ζ - i)} d ζ = \frac{1}{2} \int_{γ} \frac{e^{π ζ}}{ζ - i} d ζ & = \frac{2 π i n (γ, i) f (i)}{2} \\ = \frac{2 π i (1) (e^{i π})}{2} \\ = - π i . \end{aligned}$
$\begin{aligned} \int_{γ} \frac{e^{π ζ}}{2 (ζ + i)} d ζ = \frac{1}{2} \int_{γ} \frac{e^{π ζ}}{ζ + i} d ζ & = \frac{2 π i n (γ, - i) f (- i)}{2} \\ = \frac{2 π i (1) (e^{- i π})}{2} \\ = - π i . \end{aligned}$

De la proposición 34.2(1) tenemos que:
$\begin{aligned} \int_{γ} \frac{e^{π ζ}}{ζ^{3} + ζ} d ζ & = \int_{γ} \frac{e^{π ζ}}{ζ} d ζ - \int_{γ} \frac{e^{π ζ}}{2 (ζ - i)} d ζ - \int γ \frac{e^{π ζ}}{2 (ζ + i)} d ζ \\ = 2 π i - (- i π) - (- i π) \\ = 4 π i . \end{aligned}$

Por lo que:
$\int_{γ} \frac{e^{π z}}{z^{3} + z} d z = 4 π i .$

Ejemplo 36.6.
Veamos que:
$\int_{γ} \frac{e^{i π z}}{2 z^{2} - 5 z + 2} d z = \frac{2 π}{3},$ donde $γ$ es la circunferencia unitaria $C (0, 1)$ , orientada positivamente.

Solución. Tenemos que $γ (t) = e^{i t}$ , para $0 \leq t \leq 2 π$ , parametriza a la circunferencia unitaria $C (0, 1)$ , positivamente. Factorizando el denominador del integrando, tenemos que $2 z^{2} - 5 z + 2 = (2 z - 1) (z - 2)$ , es decir, $z_{0} = 1 / 2$ y $z_{1} = 2$ son las raíces de dicho polinomio complejo. Como $1 / 2$ está en el interior de $γ$ , por el lema 36.2(1) y el ejemplo 36.4(a), concluimos que:
$n (γ, 1 / 2) = n (γ, 0) = 1.$

Sea $f (z) = \frac{e^{i π z}}{z - 2}$ . Claramente $f$ es analítica en $D = C ∖ {2}$ , por lo que es analítica en $B (0, 2) \subset D$ y $γ$ está completamente contenida en $D$ , entonces, por la fórmula integral de Cauchy (para discos), tenemos que:
$\begin{aligned} \int_{γ} \frac{e^{i π z}}{2 z^{2} - 5 z + 2} d z & = \int_{γ} \frac{e^{i π z}}{(2 z - 1) (z - 2)} d z \\ = \int_{γ} \frac{f (z)}{2 z - 1} d z \\ = \frac{1}{2} \int_{γ} \frac{f (z)}{z - 1 / 2} d z \\ = π i n (γ, 1 / 2) f (1 / 2) \\ = π i (1) \frac{e^{i π / 2}}{\frac{1}{2} - 2} \\ = \frac{2 π}{3} . \end{aligned}$

Procedemos ahora a establecer una consecuencia de la fórmula integral de Cauchy, la cual nos deja ver claramente las diferencias entre el Cálculo Complejo y el Cálculo Real.

Proposición 36.4.
Sean $U \subset C$ un conjunto abierto y $f : U \to C$ una función analítica en $U$ . Entonces $f^{'}$ también es analítica en $U$ . En particular $f \in C^{1} (U)$ .

Demostración. Dadas las hipótesis, basta probar que cada $z_{0} \in U$ es el centro de algún disco abierto $D$ en el cual $f^{'}$ es analítica, por lo que $f^{(2)} (z_{0}) = (f^{'})^{'} (z_{0})$ existe.

Sean $z_{0} \in U$ fijo y $r > 0$ tal que $B (z_{0}, r) \subset U$ . Fijamos a $s$ tal que $0 < s < r$ y definimos a $D = B (z_{0}, s)$ . Por la fórmula integral de Cauchy para discos, aplicada al disco $B (z_{0}, r)$ y al contorno $γ = \partial D$ orientado positivamente, es decir, $γ (t) = z_{0} + s e^{i t}$ , con $0 \leq t \leq 2 π$ , tenemos que:
$f (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{ζ - z} d ζ, \forall z \in D .$

Del lema 36.2(1) se sigue que:
$n (γ, z) = n (γ, z_{0}) = \frac{1}{2 π i} \int_{0}^{2 π} \frac{i s e^{i t}}{s e^{i t}} d t = 1,$ para todo $z \in D$ .

Sea $φ : γ ([0, 2 π]) \to C$ dada por:
$φ (ζ) = \frac{f (ζ)}{2 π i} .$

Del lema 36.1, aplicado a $φ$ para el caso $n = 1$ , tenemos que:
$F_{1} (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{ζ - z} d ζ = f (z), \forall z \in D,$ por lo que:
$f^{'} (z) = \frac{1}{2 π i} \int_{γ} \frac{f (ζ)}{(ζ - z)^{2}} d ζ,$ para todo $z \in D$ . Aplicando el lema 36.1, para el caso $n = 2$ , tenemos que:
$f^{'} (z) = F_{1}' (z) = F_{2} (z),$ donde $F_{2}$ es una función analítica en $C ∖ γ ([0, 2 π])$ . Por lo tanto, $f^{'}$ es analítica en $D \subset C ∖ γ ([0, 2 π])$ .

Como $z_{0} \in U$ es arbitrario, entonces $f$ es analítica en $U$ .

Por último, dado que $f$ es analítica en $U$ , para $f (z) = u (x, y) + i v (x, y)$ , por el teorema 17.1 tenemos que existen las derivadas parciales $u_{x}, u_{y}, v_{x}$ y $v_{y}$ y satisfacen las ecuaciones de C-R en $U$ , es decir:
$f^{'} (z) = f_{x} = i f_{y},$ y como $f^{'}$ es analítica en $U$ , en particular es continua en $U$ , por lo que las derivadas parciales $u_{x}, u_{y}, v_{x}$ y $v_{y}$ son continuas en $U$ y por tanto $f \in C^{1} (U)$ .

Corolario 36.3.
Sean $U \subset C$ un conjunto abierto y $f : U \to C$ una función analítica en $U$ . Entonces $f$ es indefinidamente diferenciable en $U$ y todas las derivadas $f^{'}, f^{(2)}, \dots, f^{(k)}, \dots$ , también son funciones analíticas en $U$ . En particular $f \in C^{\infty} (U)$ .

Demostración. Se sigue del resultado anterior al aplicar inducción, por lo que los detalles se dejan como ejercicio al lector.

Proposición 36.5. (Fórmula integral de Cauchy para derivadas, en discos.)
Sean $[a, b] \subset R$ , con $a < b$ , un intervalo cerrado, $z_{0} \in C$ fijo, $r > 0$ , $f : B (z_{0}, r) \to C$ una función analítica en el disco abierto $B (z_{0}, r)$ y $γ : [a, b] \to B (z_{0}, r)$ un contorno cerrado en $B (z_{0}, r)$ . Entonces, para todo $n \in N$ :
$n (γ, z) f^{(n)} (z) = \frac{n!}{2 π i} \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 1}} d ζ,$ para todo $z \in B (z_{0}, r) ∖ γ ([a, b])$ .

Demostración. Dadas las hipótesis, procedemos por inducción sobre $n$ . Para $n = 0$ tenemos que $f^{(0)} = f$ , por lo que el resultado se sigue de la fórmula integral de Cauchy (para discos), proposición 36.3, para toda función analítica en $B (z_{0}, r)$ . Supongamos que el resultado se cumple para algún $n \in N$ fijo. Verifiquemos que el resultado se cumple para $n + 1$ .

Como $f$ es analítica en $B (z_{0}, r)$ , por la proposición 36.4, tenemos que $f^{'}$ también es analítica en $B (z_{0}, r)$ . Sea $z \in B (z_{0}, r) ∖ γ ([a, b])$ fijo, entonces por hipótesis de inducción, aplicada a $f^{'}$ , tenemos que:
$\begin{matrix} (36.5) & n (γ, z) f^{(n + 1)} (z) = n (γ, z) (f^{'})^{(n)} (z) = \frac{n!}{2 π i} \int_{γ} \frac{f^{'} (ζ)}{(ζ - z)^{n + 1}} d ζ . \end{matrix}$

Sea $g : B (z_{0}, r) ∖ {z} \to C$ dada por:
$g (ζ) = \frac{f (ζ)}{(ζ - z)^{n + 1}} .$

Es claro que $g$ es analítica en $B (z_{0}, r) ∖ {z}$ y su derivada es:
$g^{'} (ζ) = \frac{f^{'} (ζ)}{(ζ - z)^{n + 1}} - \frac{(n + 1) f (ζ)}{(ζ - z)^{n + 2}} .$

Notemos que $g^{'}$ es una función continua en $B (z_{0}, r) ∖ {z}$ y tiene como primitiva a $g$ , por lo que del TFC para integrales de contorno, proposición 35.1, y la proposición 34.2(1), tenemos que:
$\begin{aligned} 0 & = \int_{γ} g^{'} (ζ) d ζ \\ = \int_{γ} \frac{f^{'} (ζ)}{(ζ - z)^{n + 1}} d ζ - (n + 1) \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 2}} d ζ, \end{aligned}$ es decir:
$\begin{matrix} (36.6) & \int_{γ} \frac{f^{'} (ζ)}{(ζ - z)^{n + 1}} d ζ = (n + 1) \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 2}} d ζ . \end{matrix}$

Entonces, de (36.5) y (36.6) se sigue que:
$\begin{aligned} n (γ, z) f^{(n + 1)} (z) & = \frac{n!}{2 π i} \int_{γ} \frac{f^{'} (ζ)}{(ζ - z)^{n + 1}} d ζ \\ = \frac{n!}{2 π i} (n + 1) \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 2}} d ζ \\ = \frac{(n + 1)!}{2 π i} \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 2}} d ζ . \end{aligned}$

Dado que $z \in B (z_{0}, r) ∖ γ ([a, b])$ es arbitrario y $f$ una función arbitraria, analítica en $B (z_{0}, r)$ , entonces para todo $n \in N$ y $z \in B (z_{0}, r) ∖ γ ([a, b])$ se cumple que:
$n (γ, z) f^{(n)} (z) = \frac{n!}{2 π i} \int_{γ} \frac{f (ζ)}{(ζ - z)^{n + 1}} d ζ .$

Ejemplo 36.7.
Sea $B (z_{0}, r) \subset C$ un disco abierto y $f : B (z_{0}, r) \to C$ una función analítica en dicho disco. Si $γ$ es un contorno cerrado contenido en $B (z_{0}, r)$ y $ζ$ es un punto en el interior de $γ$ veamos que:
$\frac{1}{n!} \int_{γ} \frac{f^{(n)} (z)}{z - ζ} d z = \int_{γ} \frac{f (z)}{(z - ζ)^{n + 1}} d z .$

Solución. Como la función $f$ es analítica en $B (z_{0}, r)$ , entonces $f^{(n)}$ es analítica $B (z_{0}, r)$ . Por la fórmula integral de Cauchy tenemos que:
$n (γ, ζ) f^{(n)} (ζ) = \frac{1}{2 π i} \int_{γ} \frac{f^{(n)} (z)}{z - ζ} d z .$

Por otra parte, de la fórmula integral de Cauchy para derivadas tenemos que:
$n (γ, ζ) f^{(n)} (ζ) = \frac{n!}{2 π i} \int_{γ} \frac{f (z)}{(z - ζ)^{n + 1}} d z .$

Entonces:
$\frac{1}{n!} \int_{γ} \frac{f^{(n)} (z)}{z - ζ} d z = \int_{γ} \frac{f (z)}{(z - ζ)^{n + 1}} d z .$

Ejemplo 36.8.
Veamos que:
$\int_{γ} \frac{e^{z^{2}}}{(z - i)^{4}} d z = - \frac{4 π}{3 e},$ donde $γ$ es la circunferencia $C (0, 2)$ con orientación positiva.

Solución. Tenemos que $γ (t) = 2 e^{i t}$ , para $0 \leq t \leq 2 π$ , parametriza a la circunferencia $C (0, 2)$ , positivamente. Como $i$ está en el interior de $γ$ , por el lema 36.2(1) y el ejemplo 36.4(a), concluimos que:
$n (γ, i) = n (γ, 0) = 1.$

Sea $f (z) = e^{z^{2}}$ . Claramente $f$ es una función entera, por lo que en particular es analítica en cualquier disco abierto $B (0, r)$ , con $r > 2$ . Utilizando las reglas de derivación tenemos que:
$f^{(3)} (z) = (12 z + 8 z^{3}) e^{z^{2}} .$

Como $γ$ está completamente contenida en el disco abierto $B (0, r)$ , con $r > 2$ , entonces, por la fórmula integral de Cauchy para derivadas (en discos), tenemos que:
$\begin{aligned} \int_{γ} \frac{e^{z^{2}}}{(z - i)^{4}} d z & = \frac{2 π i}{3!} n (γ, i) f^{(3)} (i) \\ = \frac{π i}{3} (1) [12 i + 8 i^{3}] e^{i^{2}} \\ = \frac{π i}{3 e} (4 i) \\ = - \frac{4 π}{3 e} . \end{aligned}$

Tarea moral

Determina el valor de las siguientes integrales, donde cada circunferencia está orientada positivamente.
a) $\int_{C (0, 1)} (z^{2} + 2 z)^{- 1} d z$ .
b) $\int_{C (- i, 3 / 2)} (z^{4} + z^{2})^{- 1} d z$ .
Sea $b > 0$ . Muestra que:
$\int_{- \infty}^{\infty} e^{- t^{2}} \cos (2 b π t) d t = \sqrt{π} e^{- b^{2} π^{2}} .$
Hint: Considera la integral:
$\int_{\partial R} e^{- z^{2}} d z,$ donde $R$ es el rectángulo con vértices en $- c, c, c + b π i$ y $- c + b π i$ , para $c > 0$ .
Evalúa las siguientes integrales, donde cada circunferencia está orientada positivamente.
a) $\int_{C (0, 1)} Log (z + e) z^{- 1} d z$ .
b) $\int_{C (0, 2)} e^{z} (z + 1)^{- 2} d z$ .
Muestra que:
$\int_{0}^{\infty} t^{- 1} sen (t) d t = \frac{π}{2} .$
Hint: Considera la integral:
$\int_{γ} z^{- 1} e^{i z} d z,$ ,donde el contorno de integración está dado por $γ = [s, r] + γ_{r} + [- r, - s] - γ_{s}$ , para $0 < s < r < \infty$ , $γ_{r} (t) = r e^{i t}$ y $γ_{s} (t) = s e^{i t}$ , ambas con $t \in [0, π]$ .
Para $k \in N^{+}$ , define:
$I_{k} := \int_{γ_{k}} \frac{sen (z)}{z} d z,$ donde $γ_{k} (t) = e^{t + i t}$ , para $t \in [- 2 π k, 2 π k]$ . Determina el $lim_{k \to \infty} I_{k}$ .
Hint: Usa el ejercicio anterior.
Demuestra la proposición 36.2.
Sea $γ = γ_{1} + γ_{2} + γ_{3}$ , donde $γ_{1} (t) = e^{i t}$ , con $0 \leq t \leq 2 π$ , $γ_{2} (t) = - 1 + 2 e^{- 2 i t}$ , con $0 \leq t \leq 2 π$ y $γ_{3} (t) = 1 - i + e^{i t}$ , con $π / 2 \leq t \leq 9 π / 2$ . Determina todos los valores que toma $n (γ, z)$ para $z \in C ∖ γ$ .

Más adelante…

En esta entrada hemos probado algunos resultado importantes sobre las integrales de contorno como el Teorema Fundamental del Cálculo para el caso complejo y el lema de Goursat, que como veremos nos permitirá probar el Teorema de Cauchy para el caso en que se tiene un contorno cerrado arbitrario.

En la siguiente entrada probaremos algunas versiones del Teorema integral de Cauchy y abordaremos algunas de sus consecuencias más importantes, como la Fórmula Integral de Cauchy, el Teorema de Liouville, el Teorema Fundamental del Álgebra, entre otros. Además veremos un recíproco del Teorema de Cauchy conocido como el Teorema de Morera.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Integrales de contorno II.
Siguiente entrada del curso: Consecuencias del teorema integral de Cauchy.

Variable Compleja I: Series de potencias y funciones

Por Pedro Rivera Herrera

Deja un comentario

Introducción

Las funciones vistas como series de potencias tienen un comportamiento bueno, en el sentido de que son funciones continuas y diferenciables, aunque aquí es donde radica una propiedad importante y es que la derivada de una serie de potencias es también una serie de potencias, por lo que resultará que las funciones dadas como series de potencias son infinitamente diferenciables.

Por el corolario 16.1 tenemos que la derivada de un polinomio complejo, digamos:
$p (z) = c_{0} + c_{1} z + \dots + c_{n} z^{n},$ está dada por el polinomio complejo:
$p^{'} (z) = c_{1} + 2 c_{2} z + \dots + n c_{n} z^{n - 1} .$ Intuitivamente, esto nos dice que la función suma $f$ , definición 28.6, dada por una serie de potencias, es decir:
$\begin{matrix} (30.1) & f (z) = \sum_{n = 0}^{\infty} c_{n} z^{n}, \end{matrix}$ debería tener como derivada:
$f^{'} (z) = \sum_{n = 0}^{\infty} n c_{n} z^{n - 1} .$ Si esto se cumple, entonces tendríamos que $f$ sería una función diferenciable término a término, pero ¿cuándo es posible esto? Para responder esta pregunta recurriremos a los conceptos de la entrada anterior sobre lo que es una serie de potencias así como los conceptos de convergencia de series de números complejos y de series de funciones vistos en las entradas anteriores, pues como veremos a continuación, para que la función suma $f$ propuesta en (30.1) satisfaga lo anterior, bastará con que la serie de potencias que la define sea convergente en algún dominio.

Proposición 30.1. (Continuidad de una serie de potencias.)
Sea $\sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n}$ una serie de potencias con radio de convergencia $R > 0$ y disco de convergencia $B (z_{0}, R)$ . Definimos:
$f (z) := \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n}, \forall z \in B (z_{0}, R) .$ Entonces $f$ es continua en $B (z_{0}, R)$ .

Demostración. Dadas las hipótesis, sea $a \in B (z_{0}, R)$ . Definimos:
$r := \frac{R - | z_{0} - a |}{2} > 0,$ entonces $\overset{―}{B} (a, r) \subset B (z_{0}, R)$ .

Dado que la serie converge uniformemente en $\overset{―}{B} (a, r)$ , proposición 29.2, y para cada $n \in N$ la función $f_{n} (z) = c_{n} (z - z_{0})^{n}$ es continua en $C$ , entonces se sigue del corolario 28.2 que $f$ es continua en $\overset{―}{B} (a, r)$ .

Como $a$ es un punto interior de $\overset{―}{B} (a, r)$ , entonces $f$ es continua en $a \in B (z_{0}, R)$ . Dado que $a$ era aribitrario, entonces $f$ es continua en $B (z_{0}, R)$ .

Lema 30.1.
Sea $\sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n}$ una serie de potencias con radio de convergencia $R > 0$ . Entonces la serie de potencias:
$\sum_{n = 1}^{\infty} n c_{n} z^{n - 1},$ tiene el mismo radio de convergencia $R > 0$ .

En general, para cada $k \geq 1$ la serie de potencias:
$\sum_{n = k}^{\infty} n (n - 1) \dots (n - k + 1) c_{n} z^{n - k} = \sum_{n = k}^{\infty} \frac{n!}{(n - k)!} c_{n} z^{n - k},$ también tiene el mismo radio de convergencia $R > 0$ .

Demostración. Sin pérdida de generalidad probaremos el resultado para $z_{0} = 0$ .

El resultado general se sigue fácilmente al aplicar inducción sobre $k$ , por ejemplo, el caso cuando $k = 2$ se obtiene al aplicar el resultado para $k = 1$ a la serie $\sum_{n = 1}^{\infty} n c_{n} z^{n - 1}$ , por lo que esta última parte del resultado se deja como ejercicio al lector.

Dadas las hipótesis, procedemos entonces a probar el caso cuando $k = 1$ . Para $z \in B (0, R)$ , tomamos $r = \frac{| z | + R}{2} > 0$ , tal que $| z | < r < R$ , entonces del lema de Abel se sigue que la serie $\sum_{n = 0}^{\infty} c_{n} r^{n}$ converge absolutamente, por lo que existe $K > 0$ tal que $| c_{n} r^{n} | \leq K$ para todo $n \in N$ . Sea:
$q := \frac{| z |}{r} < 1,$ entonces:
$| n c_{n} z^{n - 1} | = n | c_{n} | {| \frac{z}{r} |}^{n - 1} r^{n - 1} \leq \frac{n K}{r} q^{n - 1}, \forall n \geq 1.$ Dado que $0 \leq q < 1$ , tenemos que:
$lim_{n \to \infty} \frac{\frac{(n + 1) K q^{n}}{r}}{\frac{n K q^{n - 1}}{r}} = q lim_{n \to \infty} (1 + \frac{1}{n}) = q < 1,$ por lo que la serie $\sum_{n = 1}^{\infty} n K q^{n - 1} r^{- 1}$ converge, entonces la serie $\sum_{n = 0}^{\infty} | n c_{n} z^{n - 1} |$ converge, proposición 27.4(1), y por tanto, proposición 27.3, la serie $\sum_{n = 1}^{\infty} n c_{n} z^{n - 1}$ converge.

Por último, notemos que si $| z | > R$ , entonces la serie $\sum_{n = 0}^{\infty} | c_{n} z^{n} |$ diverge ya que la serie $\sum_{n = 0}^{\infty} c_{n} z^{n}$ diverge y dado que:
$| n c_{n} z^{n - 1} | \geq \frac{| c_{n} z^{n} |}{| z |}, \forall n \geq 1,$ entonces, proposición 27.4(2), la serie $\sum_{n = 1}^{\infty} n c_{n} z^{n - 1}$ diverge.

Por lo tanto, dichas series tienen el mismo radio de convergencia.

Observación 30.1.
Sean $z, z_{0} \in C$ distintos. Notemos que para todo $n \geq 2$ se cumple que: $\frac{z^{n} - z_{0}^{n}}{z - z_{0}} - n z_{0}^{n - 1} = (z - z_{0}) \sum_{m = 1}^{n - 1} m z_{0}^{m - 1} z^{n - m - 1} .$

Proposición 30.2.
Sean $z_{0} \in C$ fijo y $f : B (z_{0}, R) \to C$ una función dada por la serie de potencias:
$f (z) = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n},$ con radio de convergencia $R > 0$ . Entonces $f$ puede diferenciarse término a término dentro de su dominio de convergencia, es decir:
$f^{'} (z) = \sum_{n = 1}^{\infty} n c_{n} (z - z_{0})^{n - 1} .$

Demostración. Sin pérdida de generalidad probaremos el resultado para $z_{0} = 0$ , ya que en otro caso basta con que consideremos a la función:
$F (z) = \sum_{n = 0}^{\infty} c_{n} z^{n},$ la cual cumple que $f (z) = F (z - z_{0})$ , entonces $f$ es diferenciable si y solo si lo es la función $F$ y las derivadas de $f$ en $z_{0}$ son las derivadas de $F$ en $0$ .

Dadas las hipótesis, por el lema anterior tenemos que la serie $g (z) = \sum_{n = 1}^{\infty} n c_{n} z^{n - 1}$ es absolutamente convergente para $| z | < R$ .

Veamos que para $z_{0} \in B (0, R)$ se cumple que:
$f^{'} (z_{0}) = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} = g (z_{0}),$ o equivalentemente que:
$lim_{z \to z_{0}} [\frac{f (z) - f (z_{0})}{z - z_{0}} - g (z_{0})] = 0.$ Una vez fijo $z_{0} \in B (0, R)$ , tomemos $r = \frac{| z_{0} | + R}{2}$ , entonces $| z_{0} | < r < R$ y sea $z \in B (0, r) ∖ {z_{0}}$ . Dado que las series que definen a las funciones $f$ y $g$ son convergentes, entonces de la proposición 27.2 y la observación 30.1 tenemos que:
$\begin{aligned} \frac{f (z) - f (z_{0})}{z - z_{0}} - g (z_{0}) & = \frac{\sum_{n = 0}^{\infty} c_{n} z^{n} - \sum_{n = 0}^{\infty} c_{n} z_{0}^{n}}{z - z_{0}} - \sum_{n = 1}^{\infty} n c_{n} z_{0}^{n - 1} \\ = \sum_{n = 0}^{\infty} c_{n} (\frac{z^{n} - z_{0}^{n}}{z - z_{0}}) - \sum_{n = 1}^{\infty} n c_{n} z_{0}^{n - 1} \\ = \sum_{n = 1}^{\infty} c_{n} (\frac{z^{n} - z_{0}^{n}}{z - z_{0}} - n z_{0}^{n - 1}) \\ = \sum_{n = 2}^{\infty} c_{n} (\frac{z^{n} - z_{0}^{n}}{z - z_{0}} - n z_{0}^{n - 1}) \\ = \sum_{n = 2}^{\infty} c_{n} (z - z_{0}) \sum_{m = 1}^{n - 1} m z_{0}^{m - 1} z^{n - m - 1} . \end{aligned}$ Dado que $z, z_{0} \in B (0, r)$ , entonces se cumple que:
$\begin{aligned} | (z - z_{0}) \sum_{m = 1}^{n - 1} m z_{0}^{m - 1} z^{n - m - 1} | & \leq | z - z_{0} | \sum_{m = 1}^{n - 1} m | z_{0} |^{m - 1} | z |^{n - m - 1} \\ < | z - z_{0} | r^{n - 2} \sum_{m = 1}^{n - 1} m \\ = | z - z_{0} | r^{n - 2} (\frac{n (n - 1)}{2}) . \end{aligned}$ Por lo que:
$| \frac{f (z) - f (z_{0})}{z - z_{0}} - g (z_{0}) | < \frac{| z - z_{0} |}{2} \sum_{n = 2}^{\infty} n (n - 1) | c_{n} | r^{n - 2}, \forall z \in B^{*} (0, r) .$ Por el lema 30.1 tenemos que la series:
$\sum_{n = 0}^{\infty} c_{n} z^{n} y \sum_{n = 2}^{\infty} n (n - 1) c_{n} z^{n - 2},$ tienen el mismo radio de convergencia, es decir, $R > 0$ , y en particular ambas son absolutamente convergentes. Puesto que $r < R$ , entonces la serie $\sum_{n = 2}^{\infty} n (n - 1) | c_{n} | r^{n - 2}$ converge. Por lo tanto, dado que $z \in B (0, r) ∖ {z_{0}}$ al tomar el límite tenemos:
$lim_{z \to z_{0}} | \frac{f (z) - f (z_{0})}{z - z_{0}} - g (z_{0}) | < lim_{z \to z_{0}} \frac{| z - z_{0} |}{2} \sum_{n = 2}^{\infty} n (n - 1) | c_{n} | r^{n - 2} = 0,$ de donde se sigue el resultado.

Ejemplo 30.2.
Estudiemos la convergencia de la serie:
$\sum_{n = 1}^{\infty} \frac{n}{5^{n}} (z - i)^{n - 1} .$ Solución. Notemos que dicha serie resulta de derivar a la serie:
$\sum_{n = 0}^{\infty} \frac{1}{5^{n}} (z - i)^{n},$ la cual es una serie geométrica convergente si:
$| \frac{z - i}{5} | < 1 ⟺ | z - i | < 5,$ es decir, su dominio de convergencia es el disco $B (i, 5)$ . Entonces, de la proposición 30.2, al ser una serie geométrica, se sigue que ambas series tienen el mismo dominio de convergencia.

Por último, para obtener la suma de la serie dada tenemos que:
$\begin{aligned} f (z) & = \sum_{n = 0}^{\infty} \frac{1}{5^{n}} (z - i)^{n} \\ = \frac{1}{1 - \frac{z - i}{5}} \\ = \frac{5}{5 + i - z}, \forall z \in B (i, 5), \end{aligned}$ por lo que: $\begin{aligned} f^{'} (z) & = \sum_{n = 1}^{\infty} \frac{n}{5^{n}} (z - i)^{n - 1} \\ = \frac{5}{(5 + i - z)^{2}}, \forall z \in B (i, 5) . \end{aligned}$

Observación 30.2.
Aunque una serie de potencias y su derivada tienen el mismo radio de convergencia, es importante hacer énfasis en que su dominio de convergencia no necesariamente es el mismo.

Ejemplo 30.3.
Consideremos a las series:
$\sum_{n = 1}^{\infty} \frac{z^{n}}{n} y \sum_{n = 1}^{\infty} z^{n - 1} .$ De acuerdo con el ejercicio 7(a) de la entrada anterior, sabemos que la primera serie de potencias tiene radio de convergencia $R = 1$ y su dominio de convergencia es el conjunto:
$\overset{―}{B} (0, 1) ∖ {1} = {z \in C : | z | \leq 1 y z \neq 1} .$ Mientras que la segunda serie, que es su derivada, también tiene radio de convergencia $R = 1$ , pero al ser una serie geométrica su dominio de convergencia es el disco abierto $B (0, 1)$ , que es distinto al dominio de la primera serie.

Corolario 30.1 (Existencia de las derivadas de todos los órdenes de una serie de potencias.)
Sean $z_{0} \in C$ fijo y $f : B (z_{0}, R) \to C$ una función dada por la serie de potencias:
$f (z) = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n},$ con radio de convergencia $R > 0$ . Entonces todas las derivadas de orden superior de $f$ , es decir:
$f^{'}, f^{(2)}, f^{(3)}, \dots, f^{(k)}, \dots$ existen para todo $z$ en su dominio de convergencia y dichas derivadas están dadas por:
$\begin{aligned} f^{(k)} (z) & = \sum_{n = k}^{\infty} n (n - 1) \dots (n - k + 1) c_{n} (z - z_{0})^{n - k} \\ = \sum_{n = k}^{\infty} \frac{n!}{(n - k)!} c_{n} (z - z_{0})^{n - k} . \end{aligned}$ En particular:
$c_{k} = \frac{f^{(k)} (z_{0})}{k!}, k \in N .$

Demostración. Se deja como ejercicio al lector.

Corolario 30.2. (Unicidad del desarrollo en series de potencias.)
Sean $R > 0$ y $z_{0} \in C$ fijo. Si para todo $z \in C$ tal que $| z - z_{0} | < R$ se cumple que:
$\sum_{n = 0}^{\infty} a_{n} (z - z_{0})^{n} = \sum_{n = 0}^{\infty} b_{n} (z - z_{0})^{n},$ entonces $a_{n} = b_{n}$ para todo $n \in N$ . En particular, si $\sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n} = 0$ , entonces $c_{n} = 0$ para todo $n \in N$ .

Demostración. Se deja como ejercicio al lector.

Ejemplo 30.4.
Para todo $| z | < 1$ definimos a la función:
$f (z) = \sum_{n = 0}^{\infty} z^{n} = \frac{1}{1 - z} .$ De acuerdo con el corolario 30.1, derivando repetidamente y cambiando los índices de las sumas, es fácil verificar que para todo $k \in N$ y todo $| z | < 1$ se cumple que:
$f^{(k)} (z) = \sum_{n = 0}^{\infty} (n + k) (n + k - 1) \dots (n + 1) z^{n} = \frac{k!}{(1 - z)^{k + 1}} .$ Entonces, para todo $| z | < 1$ :
$\begin{aligned} f^{'} (z) & = \frac{1}{(1 - z)^{2}} = \sum_{n = 0}^{\infty} (n + 1) z^{n}, \\ f » (z) & = \frac{2}{(1 - z)^{3}} = \sum_{n = 0}^{\infty} (n + 2) (n + 1) z^{n}, \\ f^{(3)} & = \frac{6}{(1 - z)^{4}} = \sum_{n = 0}^{\infty} (n + 3) (n + 2) (n + 1) z^{n} . \end{aligned}$ Además:
$f^{(k)} (0) = k! ⟹ c_{k} = 1, \forall k \in N .$

Ejemplo 30.5.
Determinemos la función suma y el dominio de convergencia de la siguiente serie:
$\sum_{n = 0}^{\infty} n^{2} z^{n} .$

Solución. Notemos que para todo $n \in N$ se cumple que:
$n^{2} = (n + 2) (n + 1) - 3 (n + 1) + 1.$ De acuerdo con el ejemplo anterior, tenemos que para $| z | < 1$ las series:
$\sum_{n = 0}^{\infty} z^{n}, \sum_{n = 0}^{\infty} (n + 1) z^{n} y \sum_{n = 0}^{\infty} (n + 2) (n + 1) z^{n},$ son convergentes, entonces, de la proposición 27.2(2) se sigue:
$\begin{aligned} \sum_{n = 0}^{\infty} n^{2} z^{n} & = \sum_{n = 0}^{\infty} [(n + 2) (n + 1) - 3 (n + 1) + 1] z^{n} \\ = \sum_{n = 0}^{\infty} (n + 2) (n + 1) z^{n} - 3 \sum_{n = 0}^{\infty} (n + 1) z^{n} + \sum_{n = 0}^{\infty} z^{n} \\ = \frac{2}{(1 - z)^{3}} - \frac{3}{(1 - z)^{2}} + \frac{1}{1 - z} \\ = \frac{z^{2} + z}{(1 - z)^{3}} . \end{aligned}$ Por lo tanto, para todo $z \in B (0, 1)$ la función suma de la serie dada es:
$f (z) = \frac{z^{2} + z}{(1 - z)^{3}} .$

Definición 30.1. (Funciones par e impar.)
Sea $f (z) = \sum_{n = 0}^{\infty} c_{n} z^{n}$ una serie con radio de convergencia $R > 0$ . Se define a la serie:
$f (- z) = \sum_{n = 0}^{\infty} c_{n} (- z)^{n} = \sum_{n = 0}^{\infty} (- 1)^{n} c_{n} z^{n} .$ Se dice que $f$ es par si $c_{n} = 0$ para todo $n$ impar y que $f$ es impar si $c_{n} = 0$ para todo $n$ par.

Ejemplo 30.6.
De acuerdo con la definición 30.1, veamos que $f$ es par si y solo si $f (- z) = f (z)$ .

Solución. Dadas las hipótesis tenemos lo siguiente.

$\Rightarrow)$ Si $f$ es par, tenemos que $c_{n} = 0$ para todo $n$ impar. Además $(- 1)^{n} = 1$ si $n$ es par, entonces:
$f (- z) = \sum_{n = 0}^{\infty} (- 1)^{n} c_{n} z^{n} = \sum_{n par} (- 1)^{n} c_{n} z^{n} = \sum_{n par} c_{n} z^{n} = f (z) .$

$(\Leftarrow$ Si $f (- z) = f (z)$ entonces:
$\sum_{n = 0}^{\infty} (- 1)^{n} c_{n} z^{n} = \sum_{n = 0}^{\infty} c_{n} z^{n} .$ De acuerdo con el ejercicio 8(d) de la entrada anterior, tenemos que ambas series tienen el mismo radio de convergencia, por lo que ambas son series convergentes, entonces:
$\sum_{n = 0}^{\infty} [1 - (- 1)^{n}] c_{n} z^{n} = 0.$ Como $1 - (- 1)^{n} = 2$ si $n$ es impar tenemos que:
$\sum_{n impar} 2 c_{n} z^{n} = 0,$ entonces, corolario 30.2, $c_{n} = 0$ para todo $n$ impar.

Ejemplo 30.7.
Determinemos la serie de potencias y el dominio de convergencia de la función:
$f (z) = \frac{1}{(1 - z) (2 - z)} .$

Solución. Aplicando fracciones parciales tenemos que:
$\begin{aligned} f (z) & = \frac{1}{(1 - z) (2 - z)} \\ = \frac{1}{1 - z} - \frac{1}{2 - z} \\ = \frac{1}{1 - z} - \frac{1}{2} \frac{1}{1 - \frac{z}{2}} . \end{aligned}$ Notemos que si $| z | < 1$ entonces:
$\begin{aligned} f (z) & = \sum_{n = 0}^{\infty} z^{n} - \frac{1}{2} \sum_{n = 0}^{\infty} {(\frac{z}{2})}^{n} \\ = \sum_{n = 0}^{\infty} [1 - {(\frac{1}{2})}^{n + 1}] z^{n} . \end{aligned}$

En este punto es crucial que recordemos la observación 16.4 en la cual mencionamos que es posible definir de manera equivalente el concepto de función analítica a través del desarrollo en serie de potencias, ya que de acuerdo con el corolario 30.1 tenemos que una función dada a través de una serie de potencias es infinitamente diferenciable

Definición 30.2. (Función analítica.)
Sea $U \subset C$ un conjunto abierto. Una función $f : U \to C$ es analítica en $U$ si y solo si para cada $z_{0} \in U$ existe una sucesión de números complejos ${c_{n}}_{n \geq 0} \subset U$ y un número real $r > 0$ tal que:
$f (z) = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n}, \forall z \in B (z_{0}, r) .$

Observación 30.3.
Notemos que en la definición 30.2 no hemos asumido que $B (z_{0}, r)$ es necesariamente el mayor disco de convergencia en $U$ con centro en $z_{0}$ . Además, los números $c_{0}, c_{1}, \dots,$ en $U$ dependen de $z_{0}$ .

Observación 30.4.
Debe ser claro que una consecuencia inmediata de la definición 30.2 es que una función analítica $f$ hereda todas las propiedades locales de una serie de potencias como las operaciones entre series, entre otras propiedades importantes estudiadas en la unidad anterior.

Corolario 30.3.
Sean $f$ y $g$ dos funciones analíticas en algún dominio $D$ y $c \in C$ una constante. Entonces $c f$ , $f + g$ y $f g$ son funciones analíticas en $D$ . Más aún, la suma finita, el producto finito y las combinaciones lineales finitas de funciones analíticas son también analíticas.

Demostración. Se sigue de la definición anterior y de las propiedades de las series vistas en la entrada 27.

Ejemplo 30.7.
Si $p : C \to C$ es un polinomio complejo, entonces $p$ una función analítica en $C$ .

Verificar este hecho es sencillo si consideramos que para todo $n \in N$ se cumple que $z^{n} = (z - z_{0} + z_{0})^{n}$ , con $z_{0} \in C$ fijo y utilizamos la fórmula binomial:
$(z + z_{0})^{n} = \sum_{k = 0}^{n} \frac{n!}{k! (n - k)!} z^{k} z_{0}^{n - k},$ por lo que se deja como ejercicio al lector.

Asimismo cada función racional, digamos $r = p / q$ , donde $p$ y $q$ son dos polinomios complejos, es analítica en $C ∖ Q$ , con $Q$ el conjunto de los ceros del polinomio $q$ .

Ejemplo 30.8.
Sea $U = C ∖ {1}$ . Definimos a la función $f : U \to C$ como:
$f (z) = \frac{1}{1 - z} .$ Veamos que $f$ es analítica de acuerdo con la definición 30.2.

Solución. Sabemos que para todo $z \in B (0, 1)$ y $z_{0} = 0$ podemos ver a $f$ como la serie geométrica:
$f (z) = \frac{1}{1 - z} = \sum_{n = 0}^{\infty} z^{n} .$ Sea $z_{0} \in U$ , entonces tenemos que:
$\begin{aligned} f (z) = \frac{1}{1 - z} & = \frac{1}{1 - z_{0}} (\frac{1}{1 - \frac{z - z_{0}}{1 - z_{0}}}) \\ = \frac{1}{1 - z_{0}} \sum_{n = 0}^{\infty} {(\frac{z - z_{0}}{1 - z_{0}})}^{n} \\ = \sum_{n = 0}^{\infty} \frac{(z - z_{0})^{n}}{(1 - z_{0})^{n + 1}}, \end{aligned}$ para todo $z \in B (z_{0}, r) \subset U$ , donde $r = | 1 - z_{0} |$ .

Por lo tanto, $f$ es analítica en $U$ .

Tarea moral

Demuestra los corolarios 30.1 y 30.2.
Completa la demostración del lema 30.1.
Verifica la observación 30.1.
Sea $f$ una función analítica en un dominio $D$ y supón que:
$f (z_{1}) = f (z_{2}) = \dots = f (z_{n}) = w,$ para distintos puntos $z_{1}, z_{2}, \dots, z_{n} \in D$ . Muestra que:
$F (z) = \frac{f (z) - w}{(z - z_{1}) \dots (z - z_{n})},$ es una función analítica en $D$ con una definición adecuada de $F$ en $z_{1}, z_{2}, \dots, z_{n} \in D$ .
Sea $f$ una función analítica y distinta de cero en un dominio $D$ . Prueba que $1 / f$ es analítica en $D$ .
Hint: Procede de la siguiente forma.

Toma a $z_{0} \in D$ fijo y define:
$f (z) = \sum_{n = 0}^{\infty} c_{n} (z - z_{0})^{n},$ para todo $z \in B (z_{0}, ρ) \subset D$ , con $ρ > 0$ .

Define la sucesión de coeficientes ${b_{n}}_{n \geq 0} \subset D$ recursivamente como $b_{0} = 1 / c_{0}$ y para $n \geq 1$ :
$c_{0} b_{n} + c_{1} b_{n - 1} + \dots + c_{n} b_{0} = 0.$

Define a la función:
$g (z) = \sum_{n = 0}^{\infty} b_{n} (z - z_{0})^{n} .$ Elige a $r$ , con $0 < r < ρ$ , tal que:
$\sum_{n = 1}^{\infty} | a_{n} | r^{n} \leq | a_{0} | .$ a) Prueba por inducción que $| b_{n} | r^{n} \leq | b_{0} |$ .
b) Muestra que $g$ converge en $B (z_{0}, r)$ .
c) Prueba que $f (z) g (z) = 1$ en $B (z_{0}, r)$ , de donde:
$(\frac{1}{f}) (z) = \sum_{n = 0}^{\infty} b_{n} (z - z_{0})^{n} .$
Supón que la serie de potencias $f (z) = \sum_{n = 0}^{\infty} c_{n} z^{n}$ tiene radio de convergencia $R > 0$ y $f^{'} (0) = c_{1} \neq 0$ . Demuestra que para algún $0 < r \leq R$ la función $f$ es inyectiva en $B (0, r)$ .

Hint: Procede como en la prueba de la proposición 30.2, observa que si $0 < r < R$ y $z, w \in B (0, r)$ , entonces:
$f (z) - f (w) = c_{1} (z - w) + (z - w) \sum_{n = 2}^{\infty} c_{n} \sum_{m = 1}^{n} w^{m - 1} z^{n - m},$ de donde:
$| f (z) - f (w) | > \frac{| c_{1} |}{2} | z - w | .$
Determina la función suma y el dominio de convergencia de las siguientes series de potencias.
a) $\sum_{n = 0}^{\infty} (3 + 4 i)^{n} z^{n}$ .
b) $\sum_{n = 1}^{\infty} n (n + 1) z^{n}$ .
c) $\sum_{n = 0}^{\infty} (n^{3} - 1) z^{n}$ .
Hint: Considera el ejemplo 30.4, el inciso anterior y observa que para todo $n \in N$ se cumple que: $n^{3} = (n + 3) (n + 2) (n + 1) - 6 n (n + 1) - 5 (n + 1) - 1.$ d) $\sum_{n = 1}^{\infty} (- 1)^{n} (n + 1) z^{n}$ .
Considera las siguientes series y en cada caso prueba lo que se te pide.
a) $f (z) = \sum_{n = 0}^{\infty} \frac{z^{2 n}}{(2 n)!} .$ Muestra que su radio de convergencia es $R = \infty$ y prueba que $f (z) = f » (z)$ .
b) $f (z) = \sum_{n = 0}^{\infty} \frac{z^{2 n}}{(n!)^{2}} .$ Muestra que su radio de convergencia es $R = \infty$ y prueba que $z^{2} f » (z) + z f^{'} (z) = 4 z^{2} f (z)$ .
c) $f (z) = z - \frac{z^{3}}{3} + \frac{z^{5}}{5} - \frac{z^{7}}{7} + \dots .$ Muestra que su radio de convergencia es $R = 1$ y prueba que $f^{'} (z) = 1 / (z^{2} + 1)$ .
Considera la definición 30.1 y prueba que una función $f (z) = \sum_{n = 0}^{\infty} c_{n} z^{n}$ es impar si y solo si $f (- z) = - f (z)$ .
Determina la serie de potencias y su dominio de convergencia de la función:
$f (z) = \frac{1}{(1 + z) (2 + z)} .$

Más adelante…

En esta entrada hemos probado uno de los resultados más importantes referentes a las funciones analíticas y es que dichas funciones tienen un desarrollo como serie de potencias. Este hecho es crucial pues nos garantiza que una función analítica es de clase $C^{\infty}$ , lo cual nos será de gran utilidad en la última unidad de este curso al hablar de series de Taylor y series de Laurent que serán claves en la teoría de las funciones complejas pues nos permitirán dar de manera explícita un desarrollo en series de potencias para toda función compleja analítica.

La siguiente entrada corresponde con la última de esta tercera unidad y en ella abordaremos algunas de las funciones complejas elementales vistas como series de potencias, en particular de la función exponencial compleja que como hemos visto en la unidad anterior resulta fundamental para la definición de las demás funciones complejas elementales, por lo que a través de su desarrollo en series de potencias justificaremos su definición así como el uso de la notación $e^{z}$ y $\exp (z)$ de manera indistinta al hacer una extensión de la función real para el caso complejo.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Series de potencias. Introducción y criterios de convergencia.
Siguiente entrada del curso: Funciones complejas elementales como series de potencias.

Variable Compleja I: Consecuencias de las ecuaciones de Cauchy-Riemann

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En las entradas anteriores hemos determinado condiciones necesarias y suficientes para garantizar la analicidad de una función compleja. En particular hemos deducido las ecuaciones de C-R y hemos visto que dichas condiciones nos permiten caracterizar por completo la diferenciabilidad en el sentido complejo. Además, a través de dichas ecuaciones hemos probado que la diferenciabilidad en el sentido real de una función vectorial de dos variables no es equivalente a la diferenciabilidad de una función compleja, por lo que debe ser claro que no toda función vectorial de dos variables resultará ser una función analítica.

En esta entrada abordaremos algunos resultados que son consecuencia directa de las ecuaciones de C-R y veremos que es posible extender algunas resultados vistos en nuestros cursos de Cálculo para las funciones complejas a través de las funciones reales correspondientes con las partes real e imaginaria de una función compleja.

Observación 19.1.
De nuestros cursos de Cálculo sabemos que para una función $u : U \to R$ de clase $C^{1}$ , con $U \subset R^{2}$ una región, se cumple que $u$ no depende de la variable $x$ si y solo si $\partial u / \partial x = 0$ para todo punto en $U$ . Análogamente para la variable $y$ . Más aún, tenemos que: $\begin{array}{r} \frac{\partial}{\partial x} x = 1, \frac{\partial}{\partial y} x = 0, \\ \frac{\partial}{\partial x} y = 0, \frac{\partial}{\partial y} y = 1. \end{array}$

Para motivar los siguientes planteamientos consideremos el siguiente:

Ejemplo 19.1.
Determinemos si la función compleja $f (z) = 2 x y + i (y^{2} - x^{2})$ es analítica o no.

Solución. Es claro que podemos estudiar la analicidad de esta función a través de los resultados de la entrada anterior, sin embargo notemos que operando un poco a la función, para $z = x + i y \in C$ , tenemos que: $\begin{aligned} f (z) & = 2 x y + i (y^{2} - x^{2}) \\ = - i (i 2 x y) + i (y^{2} - x^{2}) \\ = - i [- (y^{2} - x^{2}) + i 2 x y] \\ = - i (x^{2} - y^{2} + i 2 x y) \\ = - i {(x + i y)}^{2} \\ = - i z^{2}, \end{aligned}$ es decir que para todo $z \in C$ se tiene que $f (z) = - i z^{2}$ , la cual es una función polinómica y por tanto analítica en todo $C$ . Es importante notar que en la función anterior no aparecen términos que dependan del conjugado de $z$ .

Debe ser claro que el conjugado de un número complejo $z$ , es decir $\overset{―}{z}$ , resulta ser una función compleja de la variable $z$ . En el ejemplo 17.2, de la entrada 17, hemos visto que la función $f (z) = \overset{―}{z}$ no es analítica en $C$ desde que no se cumplen las ecuaciones de C-R en ningún punto. Sin embargo, esta función en particular cumple que $u_{x} = - v_{y}$ y $u_{y} = v_{x}$ para todo $z = x + i y \in C$ .

De acuerdo con la observación 12.5 de la entrada 12, estamos interesados en caracterizar a las funciones complejas que solo dependen de la variable $z$ , es decir que no tienen términos que dependan de su conjugado.

Lo anterior nos motiva a considerar a $\overset{―}{z} = x - i y$ como una variable «independiente» de $z = x + i y$ . Entonces, nuestro objetivo es determinar un criterio similar al de la observación 19.1 para garantizar la analicidad de una función compleja $f$ cuando esta dependa únicamente de la variable $z$ . Tenemos que si $z$ y $\overset{―}{z}$ son variables independientes, entonces: $\begin{array}{r} \frac{\partial}{\partial z} z = 1, \frac{\partial}{\partial \overset{―}{z}} z = 0, \\ \frac{\partial}{\partial z} \overset{―}{z} = 0, \frac{\partial}{\partial \overset{―}{z}} \overset{―}{z} = 1. \end{array}$

Como para todo $z = x + i y \in C$ se cumple que: $\begin{matrix} (19.1) & x = \frac{z + \overset{―}{z}}{2}, y = \frac{z - \overset{―}{z}}{2 i}, \end{matrix}$ entonces, dada una función compleja $f (z) = u (x, y) + i v (x, y)$ definida en un conjunto abierto $U \subset C$ de clase $C^{1}$ , podemos pensarla como una función de las variables independientes $x$ e $y$ o bien de las variables «independientes» $z$ y $\overset{―}{z}$ , y así definir: $g (z, \overset{―}{z}) = \hat{f} (x, y) := f (z) = u (\frac{z + \overset{―}{z}}{2}, \frac{z - \overset{―}{z}}{2 i}) + i v (\frac{z + \overset{―}{z}}{2}, \frac{z - \overset{―}{z}}{2 i}) .$

Lo anterior resulta de gran utilidad al considerar a $z$ y $\overset{―}{z}$ como variables independientes, ya que bajo este supuesto podemos obtener a las derivadas parciales complejas $g_{z}$ y $g_{\overset{―}{z}}$ mediante la regla de la cadena como sigue: $\begin{array}{r} g_{z} = \frac{\partial g}{\partial z} = \frac{\partial g}{\partial x} \frac{\partial x}{\partial z} + \frac{\partial g}{\partial y} \frac{\partial y}{\partial z} = \frac{1}{2} (\frac{\partial g}{\partial x} - i \frac{\partial g}{\partial y}), \\ g_{\overset{―}{z}} = \frac{\partial g}{\partial \overset{―}{z}} = \frac{\partial g}{\partial x} \frac{\partial x}{\partial \overset{―}{z}} + \frac{\partial g}{\partial y} \frac{\partial y}{\partial \overset{―}{z}} = \frac{1}{2} (\frac{\partial g}{\partial x} + i \frac{\partial g}{\partial y}) . \end{array}$

De lo anterior obtenemos la siguiente:

Definición 19.1. (Operadores diferenciales complejos de Wirtinger.)
Sea $U \subset C$ un conjunto abierto y $f (z) = u (x, y) + i v (x, y)$ una función compleja definida en $U$ de clase $C^{1}$ . Definimos los operadores direrenciales complejos de Wirtinger como: $\begin{array}{r} f_{z} := \frac{\partial f}{\partial z} = \frac{1}{2} (\frac{\partial f}{\partial x} - i \frac{\partial f}{\partial y}) = \frac{1}{2} (\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) + \frac{i}{2} (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}), \\ f_{\overset{―}{z}} := \frac{\partial f}{\partial \overset{―}{z}} = \frac{1}{2} (\frac{\partial f}{\partial x} + i \frac{\partial f}{\partial y}) = \frac{1}{2} (\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}) + \frac{i}{2} (\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}) . \end{array}$

Observación 19.2.
Notemos que la condición $\frac{\partial f}{\partial \overset{―}{z}} = 0$ , intuitivamente nos dice que la función $f$ no depende de la variable $\overset{―}{z}$ como lo planteamos inicialmente. Más aún, considerando la definición anterior se tiene el siguiente:

Lema 19.1.
Sean $U \subset C$ un conjunto abierto y $f (z) = u (x, y) + i v (x, y)$ una función definida en $U$ de clase $C^{1}$ . Entonces $u$ y $v$ satisfacen las ecuaciones de C-R en $U$ si y solo si $\frac{\partial f}{\partial \overset{―}{z}} = 0$ para todo $z = x + i y \in U$ .

Demostración. Se deja como ejercicio al lector.

Ejemplo 19.2.
Sea $z \in C$ . Consideremos a la función $f (z) = | z |$ . Determinemos a la función $g (z, \overset{―}{z})$ y a las derivadas parciales $f_{z}$ y $f_{\overset{―}{z}}$ .

Solución. Tenemos que $f (z) = | z | = {(z \overset{―}{z})}^{1 / 2}$ , por lo que $g (z, \overset{―}{z}) = {(z \overset{―}{z})}^{1 / 2}$ .

Por otra parte, si $z \neq 0$ , entonces: $\begin{array}{r} f_{z} (z) = \frac{\partial g}{\partial z} (z, \overset{―}{z}) = \frac{1}{2} {(z \overset{―}{z})}^{- 1 / 2} \overset{―}{z} = \frac{\overset{―}{z}}{2 | z |}, \\ f_{\overset{―}{z}} (z) = \frac{\partial g}{\partial \overset{―}{z}} (z, \overset{―}{z}) = \frac{1}{2} {(z \overset{―}{z})}^{- 1 / 2} z = \frac{z}{2 | z |} . \end{array}$

Observación 19.2.
De acuerdo con el ejercicio 7 de la entrada 16, sabemos que la función $f (z) = | z |$ no es analítica en ningún punto de $C$ . Podemos analizar esto mediante el lema anterior.

Para $z = 0$ es claro que $f$ no es diferenciable en dicho punto desde que no existe: $lim_{h \to 0} \frac{f (0 + h) - f (0)}{h} = lim_{h \to 0} \frac{| h |}{h} .$

Por otra parte, para $z \neq 0$ se tiene que: $\frac{\partial f}{\partial \overset{―}{z}} = 0 ⟺ \frac{z}{2 | z |} = 0 ⟺ z = 0,$ lo cual claramente no es posible, por lo que no se satisfacen las ecuaciones de C-R para ningún $z \neq 0$ , es decir que $f$ no es analítica en ningún punto de $C$ .

El ejemplo anterior motiva la siguiente:

Proposición 19.1.
Sean $U \subset C$ un conjunto abierto y $f (z) = u (x, y) + i v (x, y)$ una función definida en $U$ de clase $C^{1}$ . Las siguientes condiciones son equivalentes:

$f$ es analítica en $U$ .
$\frac{\partial f}{\partial \overset{―}{z}} = 0$ para todo $z_{0} \in U$ . En tal caso: $f^{'} (z_{0}) = \frac{\partial f}{\partial z} (z_{0}) = \frac{\partial f}{\partial x} (z_{0}) = - i \frac{\partial f}{\partial y} (z_{0}), z_{0} \in U .$

Demostración. Se deja como ejercicio al lector.

Observación 19.3.
La trascendencia de este resultado radica en que podemos pensar a las funciones analíticas como «auténticas funciones complejas» en el sentido de que si $f (z) = u (x, y) + i v (x, y)$ es una función analítica, entonces al sustituir a las variables $x$ e $y$ por $\frac{z + \overset{―}{z}}{2}$ y $\frac{z - \overset{―}{z}}{2 i}$ respectivamente, dicha función no depende de la variable $\overset{―}{z}$ como mencionamos en la observación 19.2.

Ejemplo 19.3.
Consideremos a la función compleja $f (z) = | z |^{2} + \frac{z}{\overset{―}{z}}$ . Veamos que $f$ no es analítica en ningún punto en $C$ , determinemos dónde $f$ es al menos diferenciable y obtengamos a las derivadas parciales $f_{z}$ y $f_{\overset{―}{z}}$ .

Solución. La función $f$ está definida en el dominio $U = C ∖ {0}$ . Para $z = x + i y \in U$ tenemos que: $\begin{aligned} f (z) & = | z |^{2} + \frac{z}{\overset{―}{z}} \\ = | z |^{2} + \frac{z^{2}}{| z |^{2}} \\ = x^{2} + y^{2} + \frac{x^{2} + 2 i x y - y^{2}}{x^{2} + y^{2}} \\ = (x^{2} + y^{2} + \frac{x^{2} - y^{2}}{x^{2} + y^{2}}) + i (\frac{2 x y}{x^{2} + y^{2}}) \\ := u (x, y) + i v (x, y) . \end{aligned}$

Para mostrar la utilidad de obtener las derivadas parciales complejas pensando a $f$ como una función $g$ de las variables $z$ y $\overset{―}{z}$ , primeramente procedemos a obtener las derivadas parciales $f_{z}$ y $f_{\overset{―}{z}}$ mediante la definición 19.1.

Derivamos parcialmente a las funciones $u$ y $v$ . Sea $z = x + i y \neq 0$ , entonces:
$\begin{array}{r} \frac{\partial u}{\partial x} = \frac{2 x^{5} + 4 x^{3} y^{2} + 2 x y^{4} + 4 x y^{2}}{(x^{2} + y^{2})^{2}}, \\ \frac{\partial u}{\partial y} = \frac{2 y^{5} + 4 y^{3} x^{2} + 2 y x^{4} - 4 y x^{2}}{(x^{2} + y^{2})^{2}}, \end{array}$ $\begin{array}{r} \frac{\partial v}{\partial x} = \frac{2 y^{3} - 2 y x^{2}}{(x^{2} + y^{2})^{2}}, \\ \frac{\partial v}{\partial y} = \frac{2 x^{3} - 2 x y^{2}}{(x^{2} + y^{2})^{2}} . \end{array}$

Por tanto, para $z \neq 0$ tenemos que: $\begin{aligned} \frac{\partial f}{\partial z} & = \frac{1}{2} (\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) + \frac{i}{2} (\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}), \\ = (x + \frac{x}{x^{2} + y^{2}}) - i (y - \frac{y}{x^{2} + y^{2}}), \end{aligned}$ $\begin{aligned} \frac{\partial f}{\partial \overset{―}{z}} & = \frac{1}{2} (\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}) + \frac{i}{2} (\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}) \\ = (x + \frac{3 x y^{2} - x^{3}}{(x^{2} + y^{2})^{2}}) + i (y - \frac{3 x^{2} y - y^{3}}{(x^{2} + y^{2})^{2}}) . \end{aligned}$

Considerando las igualdades dadas en (19.1), tenemos que: $f_{z} = \overset{―}{z} + \frac{1}{\overset{―}{z}}, y f_{\overset{―}{z}} = z - \frac{z}{{\overset{―}{z}}^{2}} .$

Notemos que podemos evitar todo el desarrollo anterior si consideramos que: $\begin{aligned} f (z) & = | z |^{2} + \frac{z}{\overset{―}{z}} \\ = z \overset{―}{z} + \frac{z}{\overset{―}{z}} \\ := g (z, \overset{―}{z}), \forall z \neq 0, \end{aligned}$

entonces para todo $z \neq 0$ existen las derivadas parciales complejas: $\begin{array}{r} f_{z} = \frac{\partial g}{\partial z} = \overset{―}{z} + \frac{1}{\overset{―}{z}}, \\ f_{\overset{―}{z}} = \frac{\partial g}{\partial \overset{―}{z}} = z - \frac{z}{{\overset{―}{z}}^{2}} . \end{array}$

De estas últimas expresiones es claro que las funciones $f_{z}$ y $f_{\overset{―}{z}}$ son continuas en $U = C ∖ {0}$ , por lo que lo son también las derivadas parciales $u_{x}$ , $u_{y}$ , $v_{x}$ y $v_{y}$ , es decir que $f$ es de clase $C^{1} (U)$ .

Por otra parte, dado que: $\frac{\partial f}{\partial \overset{―}{z}} = 0 ⟺ z - \frac{z}{{\overset{―}{z}}^{2}} = 0 ⟺ {\overset{―}{z}}^{2} = 1 ⟺ z = \pm 1,$ entonces $f$ solo es diferenciable en los puntos $z = 1$ y $z = - 1$ . Puesto que no existe disco abierto alrededor de dichos puntos donde $f$ sea diferenciable, concluimos que $f$ no es analítica en ningún punto en $C$ .

Observación 19.4.
Debe ser claro que si tenemos una función compleja $f$ diferenciable en un punto $z_{0}$ , entonces se cumple que $f_{\overset{―}{z}} (z_{0}) = 0$ . Sin embargo, debemos enfatizar en que la existencia de $f_{\overset{―}{z}} (z_{0})$ no garantiza la existencia de $f^{'} (z_{0})$ , desde que las ecuaciones de C-R no son una condición suficiente para la diferenciabilidad en el sentido complejo.

Ejemplo 19.4.
Consideremos el ejercicio 6 de la entrada 17. Tenemos que la función: $f (z) = {\begin{array}{lcc} \frac{z^{5}}{| z |^{4}} & si & z \neq 0, \\ 0 & si & z = 0, \end{array}$ satisface las ecuaciones de C-R en $z = 0$ , pero $f^{'} (0)$ no existe.

Notemos que para $z = x + i y \neq 0$ tenemos que: $f (z) = \frac{x^{5} - 10 x^{3} y^{2} + 5 x y^{4}}{(x^{2} + y^{2})^{2}} + i (\frac{x^{4} - 10 x^{2} y^{3} + y^{5}}{(x^{2} + y^{2})^{2}}),$ por lo que: $\begin{array}{r} \frac{\partial u}{\partial x} (0, 0) = lim_{h \to 0} \frac{u (h, 0) - u (0, 0)}{h} = 0 \\ \frac{\partial u}{\partial y} (0, 0) = lim_{k \to 0} \frac{u (0, k) - u (0, 0)}{k} = 0 \\ \frac{\partial v}{\partial x} (0, 0) = lim_{h \to 0} \frac{v (h, 0) - v (0, 0)}{h} = 0 \\ \frac{\partial v}{\partial y} (0, 0) = lim_{k \to 0} \frac{v (0, k) - u (0, 0)}{k} = 0, \end{array}$

entonces, considerando la definición 19.1, tenemos que: $\begin{array}{r} \frac{\partial f}{\partial z} (0, 0) = \frac{1}{2} (\frac{\partial u}{\partial x} (0, 0) + \frac{\partial v}{\partial y} (0, 0)) + \frac{i}{2} (\frac{\partial v}{\partial x} (0, 0) - \frac{\partial u}{\partial y} (0, 0)) = 0, \\ \frac{\partial f}{\partial \overset{―}{z}} (0, 0) = \frac{1}{2} (\frac{\partial u}{\partial x} (0, 0) - \frac{\partial v}{\partial y} (0, 0)) + \frac{i}{2} (\frac{\partial v}{\partial x} (0, 0) + \frac{\partial u}{\partial y} (0, 0)) = 0, \end{array}$

es decir que $f_{z} (0, 0) = f_{\overset{―}{z}} (0, 0) = 0$ . Sin embargo, notemos que para $z \neq 0$ se tiene que: $\begin{aligned} lim_{z \to 0} \frac{f (z) - f (0)}{z - 0} & = lim_{z \to 0} \frac{z^{4}}{| z |^{4}} \\ = lim_{z \to 0} \frac{z^{2}}{{\overset{―}{z}}^{2}}, \end{aligned}$ pero dicho límite no existe pues si nos aproximamos a $0$ a través de la recta $y = x$ tenemos que: $\begin{aligned} lim_{z \to 0} \frac{f (z) - f (0)}{z - 0} & = lim_{x \to 0} \frac{x^{2} {(1 + i)}^{2}}{x^{2} {(1 - i)}^{2}} & = {(\frac{1 + i}{1 - i})}^{2} = - 1, \end{aligned}$

mientras que si nos aproximamos a $0$ a través del eje $x$ tenemos que: $lim_{z \to 0} \frac{f (z) - f (0)}{z - 0} = lim_{x \to 0} \frac{{(x + i 0)}^{2}}{{(x - i 0)}^{2}} = 1,$ por lo que $f^{'} (0)$ no existe.

El resultado obtenido en este ejemplo no contradice el teorema 18.1 de la entrada anterior ni a la proposición 19.1 de esta entrada, sino que en ambos casos no se cumple la hipótesis de continuidad de las derivadas parciales de las funciones $u$ y $v$ que determinan a $f$ .

Lema 19.2.
Sea $D \subset R^{2}$ un conjunto abierto y conexo. Si $u : D \to R$ es una función real tal que $u_{x} (z) = u_{y} (z) = 0$ para todo $z = (x, y) \in D$ , entonces $u$ es una función constante en $D$ .

Demostración. Dadas las hipótesis, tomemos a $z_{0} = (x_{0}, y_{0}) \in D$ fijo, entonces existe algún $r > 0$ tal que $B (z_{0}, r) \subset D$ . Sea $z = (x, y) \in B (z_{0}, r)$ , procediendo como en la prueba del teorema 18.1 de la entrada anterior, concluimos, por el teorema del valor intermedio para funciones reales, que existen $α, β \in (0, 1)$ , tales que:
$\begin{aligned} u (z) - u (z_{0}) & = u (x, y) - u (x_{0}, y_{0}) \\ (19.2) & = (x - x_{0}) u_{x} (x_{0} + α (x - x_{0}), y) + (y - y_{0}) u_{y} (x_{0}, y_{0} + β (y - y_{0})) . \end{aligned}$

Sean $ζ_{1} = (x_{0} + α (x - x_{0}), y)$ y $ζ_{2} = (x_{0}, y_{0} + β (y - y_{0}))$ , para algunos $α, β \in (0, 1)$ . Es claro que, figura 75: $| ζ_{1} - z_{0} | \leq | z - z_{0} | < r, | ζ_{2} - z_{0} | \leq | z - z_{0} | < r,$ por lo que, la igualdad en (19.2) es equivalente a decir que existen $ζ_{1}, ζ_{2} \in B (z_{0}, r)$ tales que: $\begin{matrix} (19.3) & u (z) - u (z_{0}) = (x - x_{0}) u_{x} (ζ_{1}) + (y - y_{0}) u_{y} (ζ_{2}) . \end{matrix}$

Figura 75: $ζ_{1}, ζ_{2} \in B (z_{0}, r)$ dados por el segmento de recta $[z_{0}, z]$ contenido en el disco abierto con centro en $z_{0}$ y radio $r > 0$ .

De acuerdo con la igualdad (19.3), como $ζ_{1}, ζ_{2} \in D$ , entonces por hipótesis se cumple que: $u (z) - u (z_{0}) = (x - x_{0}) \cdot 0 + (y - y_{0}) \cdot 0 = 0,$ por lo que para todo $z \in B (z_{0}, r)$ se cumple que $u (z) = u (z_{0})$ , es decir que $u$ es una función constante en todo disco abierto completamente contenido en $D$ .

Para $z_{0} \in D$ un punto fijo, definimos los siguientes conjuntos: $U = {z \in D : u (z) = u (z_{0})} y V = {z \in D : u (z) \neq u (z_{0})} .$

Probemos que $U$ y $V$ son conjuntos abiertos en $D$ .

Sea $z \in U$ , entonces $u (z) = u (z_{0})$ . Por otra parte, como $D$ es abierto entonces existe $r > 0$ tal que $B (z, r) \subset D$ . Veamos que $B (z, r) \subset U$ .

De acuerdo con lo que probamos antes, es claro que para todo $z^{*} \in B (z, r)$ la función $u$ es constante en dicho disco, por lo que $u (z) = u (z^{*})$ , entonces para todo $z^{*} \in B (z, r)$ se cumple que $u (z^{*}) = u (z_{0})$ , es decir, $z^{*} \in U$ , entonces: $B (z, r) \subset U,$ por lo que concluimos que $U$ es un conjunto abierto. De manera análoga se verifica que $V$ es un conjunto abierto, por lo que se deja como ejercicio al lector.

Tenemos entonces que $D = U \cup V$ y $U \cap V = \emptyset$ , pero como $D$ es un conjunto conexo, entonces uno de los dos conjuntos $U$ o $V$ debe ser vacío. Por construcción es claro que $z_{0} \in U$ , por lo que $V = \emptyset$ , por lo tanto $D = U$ , entonces para todo $z \in D$ se cumple que $u (z) = u (z_{0})$ , es decir que $u$ es una función constante en $D$ .

Proposición 19.2.
Sean $D \subset C$ un dominio y $f : D \to C$ una función analítica en $D$ . Si $f^{'} (z) = 0$ para todo $z \in D$ , entonces $f$ es una función constante en $D$ .

Demostración. Dadas las hipótesis, tomemos a $f (z) = u (x, y) + i v (x, y)$ definida en $D$ . Como $f$ es una función analítica en $D$ , entonces las funciones $u$ y $v$ satisfacen las ecuaciones de C-R en $D$ y se cumple que: $f^{'} (z) = u_{x} (z) + i v_{x} (z), \forall z = x + i y \in D .$

Por hipótesis tenemos que: $0 = f^{'} (z) = u_{x} (z) + i v_{x} (z) = v_{y} (z) - i u_{y} (z),$ para todo $z \in D$ , es decir que para todo punto en $D$ se cumple que: $u_{x} (x, y) = u_{y} (x, y) = v_{x} (x, y) = v_{y} (x, y) = 0.$

Considerando el lema 19.2 concluimos que las funciones $u$ y $v$ son constantes en $D$ y por tanto que $f$ es una función constante en $D$ .

Corolario 19.1.
Sean $D \subset C$ un dominio y $f, g \in F (D)$ dos funciones analíticas en $D$ . Si $f$ y $g$ coinciden en un punto y tienen la misma derivada en $D$ , entonces $f$ y $g$ son idénticas.

Demostración. Se deja como ejercicio al lector.

Observación 19.5.
La propiedad de conexidad del dominio $D$ es necesaria. Notemos que en la prueba de la proposición 19.2, de manera implícita, usamos fuertemente el hecho de que $D$ era un conjunto conexo, pero si $D$ solo es un conjunto abierto el resultado no es válido.

Ejemplo 19.5.
Consideremos al conjunto $U = {z = x + i y \in C : x \neq 0}$ , el cual es abierto en $C$ . Definimos a la función: $f (z) = {\begin{array}{lcc} 1 & si & Re (z) > 0, \\ 2 & si & Re (z) < 0. \end{array}$ Claramente la función $f (z)$ es analítica en $U$ y $f^{'} (z) = 0$ para todo $z \in U$ , sin embargo $f$ no es una función constante.

Procedemos ahora a probar un resultado en el cual podemos ver que la analicidad de una función compleja es una propiedad más restrictiva que la diferenciabilidad en el sentido real.

Proposición 19.3.
Sean $D \subset C$ un dominio y $f (z) = u (x, y) + i v (x, y)$ una función analítica en $D$ .

Si $u$ ó $v$ son constantes en $D$ , entonces $f$ también es una función constante en $D$ .
Si $| f |$ es constante en $D$ , entonces $f$ también es una función constante en $D$ .

Dadas las hipótesis, como $f$ es una función analítica en $D$ , entonces las funciones $u$ y $v$ satisfacen las ecuaciones de C-R en $D$ y se tiene que: $\begin{matrix} (19.4) & f^{'} (z) = u_{x} (z) + i v_{x} (z) = v_{y} (z) - i u_{y} (z), \forall z \in D \end{matrix}$

Probaremos el resultado considerando a la función $u$ como constante, el caso en el que la función $v$ es constante es completamente análogo.

Si suponemos que $u$ es una función constante en $D$ , entonces se cumple que: $u_{x} (z) = u_{y} (z) = 0, \forall z = x + i y \in D .$

De acuerdo con (19.4) tenemos que: $f^{'} (z) = u_{x} (z) - i u_{y} (z) = 0,$ para todo $z = x + i y \in D$ , por lo que se sigue de la proposición 19.2 que $f$ es constante en $D$ .

Supongamos ahora que $| f |$ es una función constante en $D$ , entonces tenemos que: $\begin{matrix} (19.5) & | f (z) |^{2} = u^{2} (x, y) + v^{2} (x, y) = c, \end{matrix}$ para todo $z = x + i y \in D$ y para alguna constante real $c \geq 0$ .

Si $c = 0$ , entonces es claro que $f (z) = 0$ para todo $z = x + i y \in D$ , por lo que en tal caso $f$ es constante.

Supongamos que $c > 0$ , entonces tomando derivadas parciales en (19.5), con respecto a $x$ e $y$ , para todo $z = x + i y \in D$ tenemos que: $\begin{array}{r} 2 u (x, y) u_{x} (x, y) + 2 v (x, y) v_{x} (x, y) = 0, \\ 2 u (x, y) u_{y} (x, y) + 2 v (x, y) v_{y} (x, y) = 0, \end{array}$

Por hipótesis sabemos que se cumplen las ecuaciones de C-R en $D$ , por lo que para todo $z = x + i y \in D$ se tiene que: $\begin{array}{r} u (x, y) u_{x} (x, y) - v (x, y) u_{y} (x, y) = 0, \\ u (x, y) u_{y} (x, y) + v (x, y) u_{x} (x, y) = 0. \end{array}$

Multiplicando por las funciones $u (x, y)$ y $v (x, y)$ , respectivamente, en las igualdades anteriores, procedemos a sumarlas y restarlas, entonces para todo $z = x + i y \in D$ tenemos que: $\begin{array}{r} u_{x} (x, y) (u^{2} (x, y) + v^{2} (x, y)) = 0, \\ u_{y} (x, y) (u^{2} (x, y) + v^{2} (x, y)) = 0, \end{array}$ de donde $u_{x} (x, y) = u_{y} (x, y) = 0$ para todo $z = x + i y \in D$ . De manera análoga podemos obtener que $v_{x} (x, y) = v_{y} (x, y) = 0$ en $D$ . Considerando el lema 19.2 concluimos que $u$ es una función constante en $D$ , por lo que, de acuerdo con la primera parte de la prueba, $f$ es una función constante en $D$ .

Tarea moral

Demuestra el lema 19.1 y la proposición 19.1.
Sea $D \subset C$ un dominio. Supón que $f$ y $| f |$ son funciones analíticas en $D$ . Prueba que $f$ es una función constante en $D$ .
Obtén las derivadas parciales $f_{z}$ y $f_{\overset{―}{z}}$ para las siguientes funciones complejas:
a) $f (z) = 2 x^{3} y^{2} + i (x^{2} - y)$ .
b) $f (z) = \frac{x - 1 - i y}{(x - 1)^{2} + y^{2}}$ .
c) $f (z) = x^{2} + y^{2} + 3 x + 1 + i 3 y$ .
d) $f (z) = x^{2} - y^{2} + i 3 x y$ .
e) $f (z) = (x + i y) (x^{2} + y^{2})$ .
¿Son analíticas? ¿Son diferenciables?
Sea $U \subset C$ un conjunto abierto y $f : U \to C$ una función de clase $C^{1}$ . Muestra que para todo $z \in U$ se cumple que:
a) $(\overset{―}{f})_{z} = \overset{―}{f_{\overset{―}{z}}}$ .
b) $(\overset{―}{f})_{\overset{―}{z}} = \overset{―}{f_{z}}$ .
Sean $D \subset C$ un dominio y $f \in F (D)$ una función analítica. Supón que existen $a, b, c \in R$ , constantes reales con $a^{2} + b^{2} > 0$ , tales que: $a Re f (z) + b Im f (z) = c, \forall z \in D .$ Prueba que la función $f$ es constante en $D$ .
Sea $f : C \to C$ un polinomio. Supón que: $\frac{\partial f}{\partial z} = 0 = \frac{\partial f}{\partial \overset{―}{z}}, \forall z \in C .$ Prueba que la función $f$ es constante.
Demuestra el corolario 19.1.
Sea $U \subset C$ un conjunto abierto y sean $f, g : U \to C$ dos funciones de clase $C^{1}$ . Muestra que para cualesquiera constantes $a, b \in C$ se cumple que:
a) $\frac{\partial}{\partial z} (a f + b g) = a \frac{\partial f}{\partial z} + b \frac{\partial g}{\partial z}$ .
b) $\frac{\partial}{\partial \overset{―}{z}} (a f + b g) = a \frac{\partial f}{\partial \overset{―}{z}} + b \frac{\partial g}{\partial \overset{―}{z}}$ .
c) $\frac{\partial}{\partial z} (f g) = g \frac{\partial f}{\partial z} + f \frac{\partial g}{\partial z}$ .
d) $\frac{\partial}{\partial \overset{―}{z}} (f g) = g \frac{\partial f}{\partial \overset{―}{z}} + f \frac{\partial g}{\partial \overset{―}{z}}$ .
Sean $U, V \subset C$ dos conjuntos abiertos. Supón que $f : U \to C$ y $g : V \to C$ son dos funciones de clase $C^{1}$ y que $f (U) \subset V$ . Muestra que: $\begin{array}{r} {(g \circ f)}_{z} = (g_{z} \circ f) f_{z} + (g_{\overset{―}{z}} \circ f) {(\overset{―}{f})}_{z}, \\ {(g \circ f)}_{\overset{―}{z}} = (g_{z} \circ f) f_{\overset{―}{z}} + (g_{\overset{―}{z}} \circ f) {(\overset{―}{f})}_{\overset{―}{z}} . \end{array}$ Concluye que:
a) Si $f$ es analítica en $U$ , entonces: ${(g \circ f)}_{z} = (g_{z} \circ f) f^{'}, {(g \circ f)}_{\overset{―}{z}} = (g_{\overset{―}{z}} \circ f) \overset{―}{f^{'}} .$
b) Si $g$ es analítica en $V$ , entonces: ${(g \circ f)}_{z} = (g^{'} \circ f) f_{z}, {(g \circ f)}_{\overset{―}{z}} = (g^{'} \circ f) f_{\overset{―}{z}} .$

Más adelante…

En esta entrada hemos deducido una serie de resultados que son consecuencia directa de las ecuaciones de C-R, además de caracterizar aún más a la diferenciabilidad compleja a través del concepto de analicidad de una función, que como vimos resulta ser un concepto más restrictivo que el de diferenciabilidad real. Mediante los resultados de esta entrada hemos concluido que las «genuinas» funciones complejas que resultan ser analíticas son aquellas que solo están dadas en términos de la variable compleja $z$ , es decir que no dependen de $\overset{―}{z}$ .

La siguientes entradas definiremos algunas de las funciones complejas elementales para la teoría. Mediante estas funciones haremos una extensión de las funciones reales como la exponencial, el logaritmo y las funciones trigonométricas. Veremos que para el caso complejo muchas de las propiedades que satisfacen dichas funciones reales se seguirán cumpliendo, aunque como es de esperarse veremos que en el caso complejo estas funciones cumplen otras propiedades como la periodicidad y retomaremos nuevamente el concepto de funciones multivaludas.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Ecuaciones de Cauchy-Riemann. Condiciones suficientes para la diferenciabilidad compleja.
Siguiente entrada del curso: Exponencial compleja.

Variable Compleja I: Diferenciabilidad en el sentido complejo

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En esta entrada abordaremos el concepto de diferenciabilidad desde un enfoque complejo, es decir, definiremos lo que entenderemos por la derivada de una función compleja, lo cual nos será de gran utilidad para caracterizar a $C$ y a las funciones complejas que posean derivadas en el sentido complejo, con lo cual quedará claro que la diferenciabilidad compleja es más estricta que la diferenciabilidad estudiada sobre $R^{2}$ .

Al hablar de funciones complejas y sus derivadas, algunos textos usan los términos «holomorfa» y «analítica» de forma indistinta, al referirse a la diferenciabilidad de dichas funciones, mientras que otros utilizan «diferenciable» o «complejo diferenciable» y «holomorfa» de forma indistinta. El uso del término «analítica» se debe al hecho de que una función «holomorfa» tiene una expansión en series de potencias locales en cada punto de su dominio. De hecho, esta propiedad de la expansión en series de potencias es una caracterización completa de las funciones holomorfas, la cual se discutirá a detalle más adelante. Por otra parte, el uso del término «complejo diferenciable» surge por las propiedades relacionadas con la derivada compleja. En otros textos más antiguos se suelen utilizar los términos «regular» y «monogénica».

Las funciones holomorfas son una generalización de los polinomios complejos, pero resultan ser objetos matemáticos mucho más flexibles que los polinomios. El conjunto de los polinomios complejos es cerrado bajo la suma y la multiplicación, mientras que el conjunto de las funciones holomorfas es cerrado no solo bajo la suma y la multiplicación, sino también bajo recíprocos, inversas, exponenciación, logarítmos, raíces cuadradas y muchas otras operaciones.

Otro término que suele usarse al hablar de funciones holomorfas es el de «conforme» o «trasformación conforme», el cual se debe a una propiedad geométrica muy importante de dichas funciones que estudiaremos a detalle en las siguientes entradas. La conformidad es una propiedad que permite modelar el flujo de los fluidos incompresibles y otros fenómenos físicos mediante las funciones holomorfas.

Definición 16.1. (Diferenciabilidad compleja.)
Sea $U \subset C$ un conjunto abierto, sea $z_{0} \in U$ y sea $f : U \to C$ una función. Diremos que $f$ es complejo diferenciable o $C$ -diferenciable en $z_{0}$ si existe el límite: $\begin{matrix} (16.1) & lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}}, \end{matrix}$ y en caso de existir, a dicho límite se le llama la derivada compleja, o simplemente la derivada, de $f$ en $z_{0}$ , la cual se denota como $f^{'} (z_{0})$ , $\frac{d f}{d z} (z_{0})$ o $\frac{d}{d z} f (z_{0})$ . Si $f$ posee derivada en todo punto de $U$ , entonces diremos que $f$ es holomorfa en $U$ y denotamos al conjunto de funciones holomorfas en $U$ como: $H (U) = {f : U \to C : f es holomorfa en U} .$

Observación 16.1.
Para definir el concepto de derivada compleja no es necesario pedir que $U$ sea un conjunto abierto, sino que basta con considerar a $z_{0} \in U \cap U^{'}$ para que la definición anterior sea válida. Sin embargo esta generalización carece de importancia para la teoría, por lo que en general siempre que se hable de funciones diferenciables en el sentido complejo se considerarán conjuntos abiertos en $C$ .

Observación 16.2.
Tomando $z = z_{0} + h$ , podemos reescribir el límite (16.1) como: $\begin{matrix} (16.2) & lim_{h \to 0} \frac{f (z_{0} + h) - f (z_{0})}{h}, \end{matrix}$ notemos que tanto en (16.1) como en (16.2) se observa una definición similar a la de la derivada de una función real, sin embargo debe ser claro que en el caso real utilizando (16.1) tenemos que $x$ solo puede aproximarse a $x_{0}$ en dos direcciones, por la izquierda o por la derecha, análogamente si consideramos (16.2) tenemos que $h$ solo puede aproximarse a $0$ en dichas direcciones, mientras que en el caso complejo esto no se cumple, ya que sin importar cual de los dos límites utilicemos, es claro que $z$ puede aproximarse a $z_{0}$ y/o $h$ puede aproximarse a $0$ en más de dos direcciones, por lo que la existencia de la derivada de una función compleja no dependerá de la dirección en que $z$ se aproxime a $z_{0}$ y/o $h$ se aproxime a $0$ , figura 71.

Figura 71: Gráfica de tres posibles direcciones por las que $z$ se aproxima a $z_{0}$ y $h$ se aproxima a $0$ .

Definición 16.2. (Analicidad.)
Sean $S \subset C$ y $f : S \to C$ una función.

Si $z_{0}$ es un punto interior de $S$ , entonces diremos que $f$ es analítica en $z_{0} \in S$ , si $f$ es holomorfa en $B (z_{0}, ρ) \subset S$ para algún $ρ > 0$ , es decir si en $S$ existe algún $ρ$ -vecindario de $z_{0}$ , donde $f$ es holomorfa. Diremos que $f$ es analítica en $S$ si existe algún conjunto abierto totalmente contenido en $S$ donde $f$ es analítica.
Si $S = C$ , entonces diremos que $f$ es entera si $f$ es analítica en $C$ .

Observación 16.3.
A partir de las definiciones 16.1 y 16.2 es claro que para $U \subset C$ un conjunto abierto, una función $f : U \to C$ será analítica en $U$ si es analítica en cada punto $z \in U$ , por lo que durante el curso utilizaremos de manera indistinta los términos analítica y holomorfa para referirnos a funciones $C$ -diferenciables en conjuntos abiertos en $C$ . Sin embargo, más adelante veremos que la definición 16.2 será de gran utilidad al trabajar con funciones dadas por series de potencias.

Observación 16.4.
Notemos que si una función $f (z)$ es holomorfa en $U \subset C$ , entonces $f^{'} (z)$ define una función $f^{'} : U \to C$ . Si $f^{'} (z)$ es continua, entonces se dice que $f (z)$ es continuamente diferenciable. Si $f^{'} (z)$ es holomorfa en $U$ , entonces se dice que $f (z)$ es dos veces diferenciable en $U$ . Continuando de esta manera, tenemos que una función $f$ tal que cada una de sus derivadas sucesivas es nuevamente diferenciable es llamada infinitamente diferenciable. Este concepto es de suma importancia pues de manera equivalente se puede definir a una función $f : U \to C$ como analítica en $U$ si $f (z)$ es continuamente diferenciable en $U$ . De hecho, más adelante veremos que a diferencia de las funciones reales, en el caso complejo la existencia de $f^{'} (z)$ garantiza la existencia de todas las derivadas de $f (z)$ , lo cual no sucede en el caso real, por ejemplo para la función $f (x) = | x | x$ es claro que $f^{'} (x) = 2 | x |$ existe para todo $x \in R$ , pero $f^{”} (x)$ no existe para $x = 0$ .

Ejemplo 16.1.
a) Sea $f : C \to C$ tal que $f (z) = c$ , con $c \in C$ constante, entonces $f$ es entera en $C$ .

Solución. Sea $z_{0} \in C$ , entonces: $\begin{aligned} f^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{c - c}{z - z_{0}} \\ = 0. \end{aligned}$

b) Sea $f : C \to C$ tal que $f (z) = (3 - i) z$ , entonces $f$ es entera en $C$ .

Solución. Sea $z_{0} \in C$ , entonces: $\begin{aligned} f^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{(3 - i) z - (3 - i) z_{0}}{z - z_{0}} \\ = 3 - i . \end{aligned}$

c) Sea $f : C \to C$ tal que $f (z) = z^{3}$ , entonces $f$ es entera en $C$ .

Solución. Sea $z_{0} \in C$ , entonces: $\begin{aligned} f^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{z^{3} - z_{0}^{3}}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{(z - z_{0}) (z^{2} + z z_{0} + z_{0}^{2})}{z - z_{0}} \\ = 3 z_{0}^{2} . \end{aligned}$

Del inciso a) tenemos que para $f (z) = c$ , con $c \in C$ constante, se tiene que $f^{'} (z) = 0$ , para todo $z \in C$ .

Por otra parte, del inciso b) tenemos que en general para $c \in C$ constante, se cumple que si $f (z) = c z$ , entonces $f^{'} (z) = c$ , para todo $z \in C$ .

Veamos ahora que el concepto de diferenciabilidad y analicidad no son intercambiables, es decir puede pasar que una función sea diferenciable en $z_{0}$ , pero que no sea analítica en dicho punto.

Ejemplo 16.2.
Sea $f : C \to C$ dada por $f (z) = {\overset{―}{z}}^{2}$ . Veamos que dicha función es diferenciable en $z_{0} = 0$ y que no es diferenciable en ningún $z_{0} \neq 0$ , en particular veamos que $f$ no es analítica en $z_{0} = 0$ .

Solución. Si $z_{0} = 0$ , entonces: $\begin{aligned} f^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} \\ = lim_{z \to 0} \frac{{\overset{―}{z}}^{2} - 0}{z - 0} \\ = lim_{z \to 0} \frac{{\overset{―}{z}}^{2}}{z} \\ = 0. \end{aligned}$ Veamos que si $z_{0} \neq 0$ , entonces el límite que define a la derivada no existe. Primeramente, si nos aproximamos a $z_{0}$ a través de la recta que pasa por $0$ y que tiene dirección $z_{0}$ , figura 72, es decir: $z = t z_{0}, t \in R,$ entonces: $\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 1} \frac{{\overset{―}{t z_{0}}}^{2} - {\overset{―}{z_{0}}}^{2}}{t z_{0} - z_{0}} \\ = lim_{t \to 1} \frac{{(\overset{―}{z_{0}})}^{2} (t^{2} - 1)}{z_{0} (t - 1)} \\ = \frac{{\overset{―}{z_{0}}}^{2}}{z_{0}} lim_{t \to 1} (t + 1) \\ = 2 \frac{{\overset{―}{z_{0}}}^{2}}{z_{0}} . \end{aligned}$ Por otra parte tenemos que si nos aproximamos a $z_{0}$ a través de la recta paralela al eje real que pasa por $z_{0}$ , figura 72, es decir: $z = z_{0} + t, t \in R,$ entonces:
$\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 0} \frac{{\overset{―}{(z_{0} + t)}}^{2} - {\overset{―}{z_{0}}}^{2}}{t} \\ = lim_{t \to 0} \frac{(\overset{―}{z_{0}} + t)^{2} - {\overset{―}{z_{0}}}^{2}}{t} \\ = lim_{t \to 0} \frac{2 t \overset{―}{z_{0}} + t^{2}}{t} \\ = lim_{t \to 0} (2 \overset{―}{z_{0}} + t) \\ = 2 \overset{―}{z_{0}} . \end{aligned}$ Desde que estos dos límites son distintos y $z_{0} \neq 0$ es arbitrario, concluimos que para $z_{0} \neq 0$ la función no es diferenciable, por lo que en $z_{0} = 0$ la función no es analítica ya que no existe vecindad de $z_{0} = 0$ donde $f^{'} (z_{0})$ exista.

Figura 72: Gráfica de las dos direcciones por las que $z$ se aproxima a $z_{0}$ en el ejemplo 14.2.

Ejemplo 16.3.
Veamos que las siguientes funciones no son analíticas en ningún punto de $C$ .
a) $f (z) = \overset{―}{z}$ .
b) $f (z) = Re (z)$ .

Solución. Sea $z_{0} \in C$ . Para verificar la afirmación basta con mostrar que el límite que define a la derivada no existe para todo $z_{0} \in C$ , para ello nos aproximaremos a $z_{0}$ a lo largo de las rectas utilizadas en el ejemplo 16.2, figura 72.

a) Si nos aproximamos a $z_{0}$ a través de la recta $z = t z_{0}$ , con $t \in R$ , tenemos que: $\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 1} \frac{\overset{―}{t z_{0}} - \overset{―}{z_{0}}}{t z_{0} - z_{0}} \\ = lim_{t \to 1} \frac{\overset{―}{z_{0}} (t - 1)}{z_{0} (t - 1)} \\ = \frac{\overset{―}{z_{0}}}{z_{0}} . \end{aligned}$ Mientras que si nos aproximamos a $z_{0}$ a través de la recta $z = z_{0} + t$ , con $t \in R$ , tenemos que: $\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 0} \frac{\overset{―}{(z_{0} + t)} - \overset{―}{z_{0}}}{t} \\ = lim_{t \to 0} \frac{\overset{―}{z_{0}} + t - \overset{―}{z_{0}}}{t} \\ = 1. \end{aligned}$ Como estos límites son distintos y $z_{0} \in C$ es arbitrario, entonces concluimos que no existe $f^{'}$ para ningún punto de $C$ , por lo que $f (z) = \overset{―}{z}$ no es analítica en $C$ .

b) Si nos aproximamos a $z_{0}$ a través de la recta $z = t z_{0}$ , con $t \in R$ , tenemos que: $\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 1} \frac{Re (t z_{0}) - Re (z_{0})}{t z_{0} - z_{0}} \\ = lim_{t \to 1} \frac{Re (z_{0}) (t - 1)}{z_{0} (t - 1)} \\ = \frac{Re (z_{0})}{z_{0}} . \end{aligned}$ Mientras que si nos aproximamos a $z_{0}$ a través de la recta $z = z_{0} + t$ , con $t \in R$ , tenemos que: $\begin{aligned} lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} & = lim_{t \to 0} \frac{Re (z_{0} + t) - Re (z_{0})}{t} \\ = lim_{t \to 0} \frac{Re (z_{0}) + t - Re (z_{0})}{t} \\ = 1. \end{aligned}$ Dado que estos límites son distintos y $z_{0} \in C$ es arbitrario, entonces concluimos que no existe $f^{'}$ para ningún punto de $C$ , por lo que $f (z) = Re (z)$ no es analítica en $C$ .

Proposición 16.1.
Sean $U \subset C$ un conjunto abierto y $f : U \to C$ una función analítica, entonces $f$ es continua en $U$ .

Demostración. Dado que $f$ es analítica en $U$ , sabemos que $f^{'} (z)$ existe para todo $z \in U$ , entonces de acuerdo con la proposición 14.3(2) se cumple que el límite de un producto es el producto de los límites, por lo que: $\begin{aligned} lim_{z \to z_{0}} (f (z) - f (z_{0})) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} (z - z_{0}) \\ = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} lim_{z \to z_{0}} (z - z_{0}) \\ = f^{'} (z_{0}) \cdot 0 \\ = 0, \end{aligned}$ de donde se tiene que $f$ es continua en $z_{0}$ .

Proposición 16.2. (Reglas de diferenciación.)
Sean $U \subset C$ un conjunto abierto, $g, f : U \to C$ dos funciones analíticas y $c_{1}, c_{2} \in C$ dos constantes, entonces:

La función $c_{1} f + c_{2} g$ es analítica en $U$ y para todo $z \in U$ se tiene que: $(c_{1} f (z) \pm c_{2} g (z))^{'} = c_{1} f^{'} (z) \pm c_{2} g^{'} (z) .$
La función $f g$ es analítica en $U$ y para todo $z \in U$ se tiene que: $(f (z) g (z))^{'} = f^{'} (z) g (z) + f (z) g^{'} (z) .$
La función $\frac{f}{g}$ es analítica en $W = U ∖ {z \in U : g (z) = 0}$ y para todo $z \in W$ se tiene que: ${(\frac{f (z)}{g (z)})}^{'} = \frac{f^{'} (z) g (z) - f (z) g^{'} (z)}{(g (z))^{2}} .$

Demostración.

Se deja como ejercicio al lector.
Dadas las hipótesis, para $z_{0} \in U$ tenemos, por la proposición 14.3(2) y la proposición 16.1, que: $\begin{aligned} (f (z_{0}) g (z_{0}))^{'} & = lim_{z \to z_{0}} \frac{f (z) g (z) - f (z_{0}) g (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{f (z) g (z) - f (z_{0}) g (z) + f (z_{0}) g (z) - f (z_{0}) g (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{g (z) [f (z) - f (z_{0})] + f (z_{0}) [g (z) - g (z_{0})]}{z - z_{0}} \\ = lim_{z \to z_{0}} g (z) \frac{f (z) - f (z_{0})}{z - z_{0}} + lim_{z \to z_{0}} f (z_{0}) \frac{g (z) - g (z_{0})}{z - z_{0}} \\ = g (z_{0}) f^{'} (z_{0}) + f (z_{0}) g^{'} (z_{0}) . \end{aligned}$
Dadas las hipótesis, procedemos a realizar la prueba considerando $f (z) = 1$ para todo $z \in U$ , el caso general {\bf se deja como ejercicio al lector.} Sea $z_{0} \in W$ , entonces $g (z_{0}) \neq 0$ . Por la proposición 16.1 sabemos que $g$ es continua en $W$ , por lo que, para $ε = | g (z_{0}) | / 2 > 0$ existe $δ > 0$ tal que si $| z - z_{0} | < δ$ , entonces: $| g (z) - g (z_{0}) | < \frac{| g (z_{0}) |}{2},$ de donde: $0 < \frac{| g (z_{0}) |}{2} < | g (z) |,$ por lo que $g (z) \neq 0$ .

Entonces, para todo $z \in B (z_{0}, δ)$ , por la proposición 14.3(2) y la proposición 16.1, tenemos que: $\begin{aligned} {(\frac{1}{g (z_{0})})}^{'} & = lim_{z \to z_{0}} \frac{\frac{1}{g (z)} - \frac{1}{g (z_{0})}}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{- 1}{g (z) g (z_{0})} \frac{g (z) - g (z_{0})}{z - z_{0}} \\ = - \frac{g^{'} (z_{0})}{g (z_{0})^{2}} . \end{aligned}$

Ejemplo 16.4.
Sea $f : C \to C$ dada por $f (z) = z^{n}$ , con $n \in N^{+}$ , veamos que $f$ es una función entera y que: $\begin{matrix} (16.3) & \frac{d}{d z} z^{n} = n z^{n - 1} . \end{matrix}$

Demostración. Realizamos la prueba por inducción sobre $n$ . Sea $n = 1$ , entonces $f (z) = z$ , por lo que para $z_{0} \in C$ tenemos que: $\begin{aligned} f^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{z - z_{0}}{z - z_{0}} \\ = 1, \end{aligned}$ de donde (16.3) se cumple para $n = 1$ .

Supongamos que (16.3) se cumple para $n = k$ con $k \in N$ fijo. Veamos que (16.3) se cumple para $n = k + 1$ . Notemos que para $n = k + 1$ se tiene que $f (z) = z^{k + 1} = z^{k} z$ , entonces para todo $z \in C$ , por la proposición 16.2(2), tenemos que: $\begin{aligned} f^{'} (z) & = \frac{d}{d z} (z^{k + 1}) \\ = z \frac{d}{d z} (z^{k}) + z^{k} \frac{d}{d z} z \\ = k z^{k - 1} z + z^{k} \\ = (k + 1) z^{k} . \end{aligned}$ Por lo que para todo $n \in N^{+}$ se tiene que $f (z) = z^{n}$ es entera y su derivada está dada por (16.3).

De hecho se puede mostrar que si $f : C ∖ {0} \to C$ está dada por $f (z) = z^{n}$ y $n \in Z$ , entonces $f$ es analítica y su derivada está dada por (16.3), lo cual se deja como ejercicio al lector.

Ejemplo 16.5.
Sea $f_{0} (z)$ la rama principal de la función multivaluada $F (z) = \sqrt{z}$ , es decir:
$f_{0} (z) = \sqrt{z} = \sqrt{r} cis (\frac{θ (z)}{2}),$ donde $r = | z |$ , $θ (z) = Arg (z)$ y $z \in C ∖ (- \infty, 0]$ .

Veamos que $f_{0}$ es analítica en el dominio $D = C ∖ (- \infty, 0]$ y determinemos su derivada.

Solución. De acuerdo con el ejemplo 15.7, sabemos que $f_{0}$ no es continua en $(- \infty, 0]$ , por lo que se sigue de la proposición 16.1 que en dicho conjunto $f_{0}$ no puede ser analítica.

Más aún, por la continuidad de $f_{0}$ en $D$ , para $z_{0} \in D$ fijo tenemos que: $\begin{aligned} f_{0}' (z_{0}) & = lim_{z \to z_{0}} \frac{\sqrt{z} - \sqrt{z_{0}}}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{\sqrt{z} - \sqrt{z_{0}}}{(\sqrt{z} - \sqrt{z_{0}}) (\sqrt{z} + \sqrt{z_{0}})} \\ = lim_{z \to z_{0}} \frac{1}{\sqrt{z} + \sqrt{z_{0}}} \\ = \frac{1}{2 \sqrt{z_{0}}} . \end{aligned}$

Desde que $z_{0} \in D$ era arbitrario y $D$ es un dominio, en particular un conjunto abierto, concluimos que $f_{0}$ es analítica en $D$ .

Es interesante notar que la derivada de la rama principal $f_{0}$ corresponde con la derivada de la función real $f (x) = \sqrt{x}$ con la que estamos familiarizados.

Corolario 16.1.
Sea $n \in N$ y sean $c_{i} \in C$ , con $i \in {0, 1, \dots, n}$ , constantes con $c_{n} \neq 0$ . Entonces:

Todo polinomio de grado $n$ , digamos $p (z) = c_{0} + c_{1} z + c_{2} z^{2} + \dots + c_{n} z^{n}$ , es una función entera y su derivada es: $\begin{matrix} (16.4) & p^{'} (z) = c_{1} + 2 c_{2} z + \dots + (n - 1) c_{n - 1} z^{n - 2} + n c_{n} z^{n - 1} . \end{matrix}$
Toda función racional $f (z) = \frac{p (z)}{g (z)}$ , donde $p (z)$ y $g (z)$ son polinomios, es una función analítica para todos los puntos $z$ tales que $g (z) \neq 0$ y su derivada es: $\begin{matrix} (16.5) & f^{'} (z) = \frac{p^{'} (z) g (z) + p (z) g^{'} (z)}{g (z)^{2}} . \end{matrix}$

Demostración.

Dadas las hipótesis, procedemos a realizar la prueba por inducción sobre $n$ . Si $n = 0$ entonces $p (z) = c_{0}$ es una función constante y por tanto es una función entera tal que $p^{'} (z) = 0$ . Si $n = 1$ , entonces tenemos que $p (z) = c_{0} + c_{1} z$ . De acuerdo con el ejemplo 16.4 y la proposición 16.2, tenemos que $p (z)$ es una función entera y su derivada es: $p^{'} (z) = 0 + c_{1} (1) z^{1 - 1} = c_{1},$ por lo que para $n = 1$ se cumple (16.4). Supongamos que el resultado es válido para $n = k$ , con $k \in N$ fijo. Para $n = k + 1$ tenemos que: $\begin{aligned} p (z) & = c_{0} + \sum_{n = 1}^{k + 1} c_{n} z^{n} \\ = c_{0} + \sum_{n = 1}^{k} c_{n} z^{n} + c_{k + 1} z^{k + 1}, \end{aligned}$ por hipótesis de inducción sabemos que $c_{0} + \sum_{n = 1}^{k} c_{n} z^{n}$ es una función entera cuya derivada está dada por (16.4) y por el ejemplo 16.4 y la proposición 16.2 tenemos que $c_{k + 1} z^{k + 1}$ es también una función entera cuya derivada es $(k + 1) c_{k + 1} z^{k}$ , entonces: $p^{'} (z) = c_{1} + 2 c_{2} z + \dots + (k - 1) c_{k - 1} z^{k - 2} + k c_{k} z^{k - 1} + (k + 1) c_{k + 1} z^{k},$ por lo que el resultado es válido para todo $n \in N$ .
De acuerdo con la proposición 16.2(3) y considerando el inciso anterior, es claro que una función racional $f (z) = \frac{p (z)}{g (z)}$ , con $p (z)$ y $g (z)$ polinomios, es una función analítica en su dominio de definición, es decir en $S = {z \in C : g (z) \neq 0}$ , cuya derivada está dada por (16.5).

Ejemplo 16.6.
Determina la derivada de las siguientes funciones y en caso de ser necesario especifica en dónde es analítica la función.

a) $f (z) = 3 z^{4} - 5 z^{3} + 2 z$ .

Solución. De acuerdo con el corolario 16.1 tenemos que $f$ es una función entera y su derivada es: $f^{'} (z) = 2 (1) - 5 (3 z^{2}) + 3 (4 z^{3}) = 12 z^{3} - 15 z^{2} + 2.$ b) $f (z) = \frac{(z + 1) (z + i)^{2}}{z + 1 - 3 i}$ .

Solución. De acuerdo con la proposición 16.2 tenemos que: $\begin{aligned} f^{'} (z) & = \frac{((z + i)^{2} + 2 (z + 1) (z + i)) (z + 1 - 3 i) - (z + 1) (z + i)^{2}}{(z + 1 - 3 i)^{2}} \\ = \frac{2 z^{3} + (4 - 7 i) z^{2} + (14 - 2 i) z + 5 i + 6}{(z + 1 - 3 i)^{2}} . \end{aligned}$ Por el corolario 16.1 tenemos que esta función es analítica en $S = C ∖ {- 1 + 3 i}$ , ya que en $z = - 1 + 3 i$ el denomidador de $f$ se anula.

c) $f (z) = \frac{z^{2}}{4 z + 1}$ .

Solución. Por la proposición 16.2 tenemos que: $\begin{aligned} f^{'} (z) & = \frac{(4 z + 1) (2 z - z^{2} (4))}{(4 z + 1)^{2}} \\ = \frac{4 z^{2} + 2 z}{(4 z + 1)^{2}} . \end{aligned}$ De acuerdo con el corolario 16.1 tenemos que esta función es analítica en $S = C ∖ {- \frac{1}{4}}$ , ya que en $z = - \frac{1}{4}$ el denomidador de $f$ se anula.

Proposición 16.3. (Carathéodory.)
Sean $U \subset C$ un conjunto abierto, $z_{0} \in U$ y $f : U \to C$ una función. Entonces, $f$ es analítica en $z_{0}$ si y solo si existe una función $φ : U \to C$ continua en $z_{0}$ tal que para todo $z \in U$ : $f (z) = f (z_{0}) + φ (z) (z - z_{0}) .$ En este caso $φ (z_{0}) = f^{'} (z_{0})$ .

Demostración. Dadas las hipótesis, tenemos que:

$\Rightarrow)$
Si $f$ es analítica en $z_{0}$ , entonces existe: $f^{'} (z_{0}) = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} .$ Sea $φ : U \to C$ dada por: $φ (z) = {\begin{array}{lcc} \frac{f (z) - f (z_{0})}{z - z_{0}} & si & z \neq z_{0}, \\ f^{'} (z_{0}) & si & z = z_{0} . \end{array}$ Es claro que para todo $z \in U$ , incluso para $z = z_{0}$ , se tiene que: $f (z) = f (z_{0}) + φ (z) (z - z_{0}) .$ Por otra parte notemos que:
$lim_{z \to z_{0}} φ (z) = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}} = f^{'} (z_{0}) = φ (z_{0}),$ por lo que $φ$ es continua en $z_{0}$ y $f^{'} (z_{0}) = φ (z_{0})$ .

$(\Leftarrow$
Sea $φ : U \to C$ una función continua en $z_{0}$ tal que para todo $z \in U$ : $f (z) = f (z_{0}) + φ (z) (z - z_{0}) .$ Por la continuidad de $φ$ tenemos que: $φ (z_{0}) = lim_{z \to z_{0}} φ (z) = lim_{z \to z_{0}} \frac{f (z) - f (z_{0})}{z - z_{0}},$ por lo que el límite que define a $f^{'} (z_{0})$ existe y $f^{'} (z_{0}) = φ (z_{0})$ , entonces $f$ es analítica en $z_{0}$ .

De nuestros cursos de Cálculo, sabemos que otra de las reglas de diferenciación importantes es la regla de la cadena, por lo que podemos preguntarnos si dicho resultado es válido para funciones complejas dado que hemos visto que la composición de funciones es una operación posible para las funciones complejas, por lo que nos disponemos a responder a esta pregunta mediante el siguiente resultado.

Proposición 16.4. (Regla de la cadena.)
Sean $U_{1}, U_{2} \subset C$ dos conjuntos abiertos, $g : U_{1} \to C$ una función analítica en $U_{1}$ y $f : U_{2} \to C$ una función analítica en $U_{2}$ , tales que $g (U_{1}) \subset U_{2}$ . Entonces $f \circ g$ es una función analítica en $U_{1}$ y para $z_{0} \in U_{1}$ se tiene que: $\begin{matrix} (16.6) & (f \circ g)^{'} (z_{0}) = f^{'} (g (z_{0})) g^{'} (z_{0}) . \end{matrix}$

Demostración. Dadas las hipótesis, por la proposición 16.3 tenemos que si $g$ es analítica en $z_{0} \in U_{1}$ y $f$ es analítica en $w_{0} = g (z_{0}) \in U_{2}$ , entonces existen funciones $φ_{1} : U_{1} \to C$ y $φ_{2} : U_{2} \to C$ continuas en $z_{0}$ y $w_{0}$ , respectivamente, tales que: $\begin{array}{r} g (z) = g (z_{0}) + φ_{1} (z) (z - z_{0}), \forall z \in U_{1}, \\ f (w) = f (w_{0}) + φ_{2} (w) (w - w_{0}), \forall w \in U_{2}, \end{array}$ con $φ_{1} (z_{0}) = g^{'} (z_{0})$ y $φ_{2} (w_{0}) = f^{'} (w_{0})$ .

Notemos que para todo $z \in U_{1}$ , $w = g (z) \in U_{2}$ , se tiene que: $\begin{aligned} (f \circ g) (z) & = f (g (z)) \\ = f (g (z_{0})) + φ_{2} (g (z)) (g (z) - g (z_{0})) \\ = (f \circ g) (z_{0}) + φ_{2} (g (z)) φ_{1} (z) (z - z_{0}), \forall z \in U_{1}, \end{aligned}$ entonces, por la continuidad de $φ_{1} (z)$ y $φ_{2} (g (z))$ en $z_{0}$ , tenemos que: $\begin{aligned} lim_{z \to z_{0}} \frac{(f \circ g) (z) - (f \circ g) (z_{0})}{z - z_{0}} & = lim_{z \to z_{0}} \frac{φ_{2} (g (z)) φ_{1} (z) (z - z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} φ_{2} (g (z)) φ_{1} (z) \\ = φ_{2} (g (z_{0})) φ_{1} (z_{0}) \\ = f^{'} (g (z_{0})) g^{'} (z_{0}) . \end{aligned}$ Como $z_{0} \in U_{1}$ era arbitrario, entonces es claro que $f \circ g$ es analítica en $U_{1}$ y su derivada está dada por (16.6).

Ejemplo 16.7.
Determina la derivada de las siguientes funciones y en caso de ser necesario especifica en dónde es analítica la función.

a) $f (z) = (i z^{2} + 3 z)^{5}$ .

Solución. De acuerdo con la regla de la cadena tenemos que: $f^{'} (z) = 5 (i z^{2} + 3 z)^{4} (2 i z + 3) .$ b) $f (z) = \frac{(z^{2} + 1)^{4}}{z^{4}}$ .

Solución. Considerando la proposición 16.2(3) y la regla de la cadena tenemos que: $\begin{aligned} f^{'} (z) & = \frac{4 (z^{2} + 1)^{3} (2 z) (z^{4}) - (z^{2} + 1)^{4} (4 z^{3})}{(z^{4})^{2}} \\ = \frac{4 (z^{2} + 1)^{3} (z^{2} - 1)}{z^{5}} . \end{aligned}$ c) $f (z) = (z^{3} + 1)^{10}$ .

Solución. Por la regla de la cadena tenemos que: $f^{'} (z) = 10 (z^{3} + 1)^{9} (3 z) = 30 z (z^{3} + 1)^{9} .$

Otro resultado importante, con el que estamos familiarizados por nuestros cursos de Cálculo, es el de la regla de L’Hôpital. Como consecuencia de la analicidad de funciones complejas, tenemos una versión de esta regla para calcular límites de cocientes que consideren indeterminaciones de la forma $0 / 0$ .

Proposición 16.5. (Regla de L’Hôpital.)
Sean $U \subset C$ un conjunto abierto y $z_{0} \in U$ . Si $f$ y $g$ son dos funciones analíticas en $z_{0}$ tales que $f (z_{0}) = 0 = g (z_{0})$ y $g^{'} (z_{0}) \neq 0$ , entonces: $lim_{z \to z_{0}} \frac{f (z)}{g (z)} = \frac{f^{'} (z_{0})}{g^{'} (z_{0})} .$

Demostración. Se deja como ejercicio al lector.

Ejemplo 16.8.
Considera las siguientes funciones y determina los siguientes límites:

a) $lim_{z \to 2 + i} \frac{f (z)}{g (z)}$ , donde $f (z) = z^{2} - 4 z + 5$ y $g (z) = z^{3} - z - 10 i$ .

Solución. Es fácil verificar que $f (2 + i) = g (2 + i) = 0$ , por lo que evaluar el límite dado nos lleva a una indeterminación de la forma $0 / 0$ . Dado que $f$ y $g$ son funciones polinómicas, es claro que son funciones enteras, cuyas derivadas son: $\begin{array}{r} f^{'} (z) = 2 z - 4, \\ g^{'} (z) = 3 z^{2} - 1 \end{array}$ y $g^{'} (i) \neq 0$ , por lo que de acuerdo con la regla de L’Hôpital tenemos que: $\begin{aligned} lim_{z \to 2 + i} \frac{f (z)}{g (z)} & = lim_{z \to 2 + i} \frac{z^{2} - 4 z + 5}{z^{3} - z - 10 i} \\ = \frac{2 (2 + i) - 4}{3 (2 + i)^{2} - 1} \\ = \frac{2 i}{12 i + 8} \\ = \frac{3}{26} + \frac{1}{26} i . \end{aligned}$ b) $lim_{z \to i} \frac{f (z)}{g (z)}$ , donde $f (z) = z^{14} + 1$ y $g (z) = z^{7} + i$ .

Solución. Claramente $f (i) = g (i) = 0$ , por lo que evaluar el límite dado nos lleva a una indeterminación de la forma $0 / 0$ . Dado que $f$ y $g$ son funciones polinómicas, es claro que son funciones enteras con derivadas: $\begin{array}{r} f^{'} (z) = 14 z^{13}, \\ g^{'} (z) = 7 z^{6} \end{array}$ y $g^{'} (i) \neq 0$ , por lo que de acuerdo con la proposición 14.5 tenemos que: $\begin{aligned} lim_{z \to i} \frac{f (z)}{g (z)} & = lim_{z \to i} \frac{z^{14} + 1}{z^{7} + i} \\ = \frac{14 i^{13}}{7 i^{6}} \\ = 2 i^{7} \\ = - 2 i . \end{aligned}$

Proposición 16.6. (Teorema de la función inversa.)
Sean $U, G \subset C$ dos conjuntos abiertos, $f : U \to G$ una función biyectiva, $g : G \to U$ la inversa de $f$ y $z_{0} \in G$ . Si $f$ es analítica en $g (z_{0})$ con $f^{'} (g (z_{0})) \neq 0$ y $g$ es continua en $z_{0}$ , entonces $g$ es analítica en $z_{0}$ y su derivada es: $g^{'} (z_{0}) = \frac{1}{f^{'} (g (z_{0}))} .$

Demostración. Dadas las hipótesis, como $f (g (z)) = z$ para todo $z \in G$ , entonces tenemos que: $\begin{aligned} g^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{g (z) - g (z_{0})}{z - z_{0}} \\ = lim_{z \to z_{0}} \frac{g (z) - g (z_{0})}{f (g (z)) - f (g (z_{0}))} \\ = lim_{z \to z_{0}} \frac{1}{\frac{f (g (z)) - f (g (z_{0}))}{g (z) - g (z_{0})}} . \end{aligned}$

Sea $w = g (z)$ , definimos: $φ (w) = {\begin{array}{lcc} \frac{f (w) - f (w_{0})}{w - w_{0}} & si & w \neq w_{0}, \\ f^{'} (w_{0}) & si & w = w_{0} . \end{array}$

Dado que $f$ es analítica en $w_{0} = g (z_{0})$ , entonces: $\begin{aligned} φ (w_{0}) = f^{'} (w_{0}) & = lim_{w \to w_{0}} \frac{f (w) - f (w_{0})}{w - w_{0}} \\ = lim_{w \to w_{0}} φ (w), \end{aligned}$ por lo que $φ$ es una función continua en $w_{0}$ . Por otra parte, como $g$ es continua en $z_{0}$ , entonces $lim_{z \to z_{0}} g (z) = g (z_{0}) = w_{0} \in U$ . Así, por la proposición 15.4 de la entrada anterior, tenemos que: $\begin{aligned} g^{'} (z_{0}) & = lim_{z \to z_{0}} \frac{1}{φ (g (z))} \\ = \frac{1}{φ (lim_{z \to z_{0}} g (z))} \\ = \frac{1}{f^{'} (w_{0})} \\ = \frac{1}{f^{'} (g (z_{0}))} . \end{aligned}$

Definición 16.3. (Singularidad o punto singular.)
Si una función compleja $f$ no es analítica en un punto $z_{0} \in C$ , pero es analítica en algún punto de cada disco abierto $B (z_{0}, r) \subset C$ , $r > 0$ , entonces $z_{0}$ se llama un punto singular o singularidad de $f$ .

Ejemplo 16.9.
De acuerdo con el ejemplo 16.6(b) el punto $z_{0} = - 1 + 3 i$ es un punto singular de la función $f (z) = \frac{(z + 1) (z + i)^{3}}{z + 1 - 3 i}$ .

Por otra parte, por el el ejemplo 16.3(a) sabemos que la función $f (z) = \overset{―}{z}$ no es analítica en ningún punto de $C$ , por lo que $f$ no tiene puntos singulares.

Tarea moral

Mediante la definición 16.1 obtén la derivada de las siguientes funciones.
a) $f (z) = z - \frac{1}{z}$ .
b) $f (z) = - z^{- 2}$ .
c) $f (z) = \frac{1}{i 2 z}$ .
Sean $a, b \in C$ constantes y $n \in N^{+}$ . Determina dónde existen las derivadas de las siguientes funciones y utiliza las reglas de diferenciación para obtener sus derivadas.
a) $f (z) = \frac{1}{(z - a)^{n}}$ .
b) $f (z) = \frac{i z^{2} - 2 z}{3 z - i + 1}$ .
c) $f (z) = {(\frac{z - a}{z - b})}^{n}$ .
d) $f (z) = z + \frac{1}{z (z^{2} - b)}$ .
Considera a la función $f : C ∖ 0 \to C$ dada por $f (z) = z^{n}$ . Prueba que $f$ es analítica en $C ∖ {0}$ , para toda $n \in Z$ , y que su derivada está dada por (16.3).
Demuestra la proposición 16.5. Hint: Considera que: $\frac{f (z)}{g (z)} = \frac{f (z) - f (z_{0})}{z - z_{0}} \frac{1}{\frac{g (z) - g (z_{0})}{z - z_{0}}} .$
Considera a la función $f (z) = | z |^{2}$ , la cual es continua en el punto $z = 0$ .
a) Prueba que $f (z)$ es diferenciable en el origen.
b) Prueba que $f (z)$ no es diferenciable en nigún punto $z \neq 0$ .
Calcula los siguientes límites.
a) $lim_{z \to \sqrt{2} i} \frac{z^{3} + 5 z^{2} + 2 z + 10}{z^{5} + 2 z^{3}}$ .
b) $lim_{z \to 1 + i} \frac{z^{5} + 4 z}{z^{2} - 2 z + 2}$ .
c) $lim_{z \to \sqrt{2} (1 + i)} \frac{z^{4} + 16}{z^{2} - 2 \sqrt{2} z + 4}$ .
Hint: Utiliza la regla de L’Hôpital.
Prueba que la función $f (z) = | z |$ no es diferenciable en ningún punto.

Más adelante…

Como hemos visto con los ejemplos anteriores, las reglas de diferenciación, en el sentido complejo, para la suma, el producto y el cociente de funciones, al igual que para las potencias enteras, parecen ser simplemente una extensión de las reglas de diferenciación para funciones reales, sin embargo como hemos mencionado antes, la derivada en el caso complejo es más restrictiva. A pesar de que parezca que simplemente estamos trabajando con la variable $z$ , no debemos olvidar que dicha variable depende a su vez de dos variables, su parte real y su parte imaginaria, por lo que las reglas de diferenciación obtenidas hasta ahora puede que no nos permitan obtener la derivada de algunas funciones complejas, incluso aunque estas funciones sí posean derivadas, por ejemplo si consideramos a las funciones $f (z) = 4 x^{2} - i y$ y $g (z) = x y + i (x + y)$ , es claro que no podemos utilizar la proposición 16.2 para intentar obtener sus derivadas, en caso de existir.

Es importante remarcar que a diferencia del caso real en el que dabamos distintas interpretaciones a la derivada de una función, en el caso complejo no nos centraremos en darle una interpretación a la derivada, sino que nos enfocaremos en saber si una función compleja tiene o no derivada, ya que la existencia de la misma nos dice mucho sobre la función compleja. Por ello en la siguiente entrada caracterizaremos la diferenciabilidad compleja mediante las ecuaciones de Cauchy-Riemann, las cuales resultan ser una condición necesaria para asegurar la diferenciabilidad de una función compleja y veremos que bajo ciertas condiciones podemos garantizar que también son una condición suficiente.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Continuidad en $C$ .
Siguiente entrada del curso: Ecuaciones de Cauchy-Riemann. Condiciones necesarias para la diferenciabilidad compleja.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: función analítica

Variable Compleja I: Series de Taylor y series de Laurent

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Teorema integral de Cauchy

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Series de potencias y funciones

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Consecuencias de las ecuaciones de Cauchy-Riemann

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Diferenciabilidad en el sentido complejo

Introducción

Tarea moral

Más adelante…

Entradas relacionadas