Introducción

Ya hemos visto que el campo de los números reales cumple con la propiedad de ser completos, esta propiedad la vimos enunciada con el Axioma del Supremo en la entrada pasada. Ahora veremos que utilizando Cortaduras de Dedekind podemos dar una equivalencia.

Una idea intuitiva

Previamente vimos que existe una relación biunívoca entre el conjunto de los números reales $\r$ y la recta: a cada punto en la recta le corresponde un único número real y viceversa.

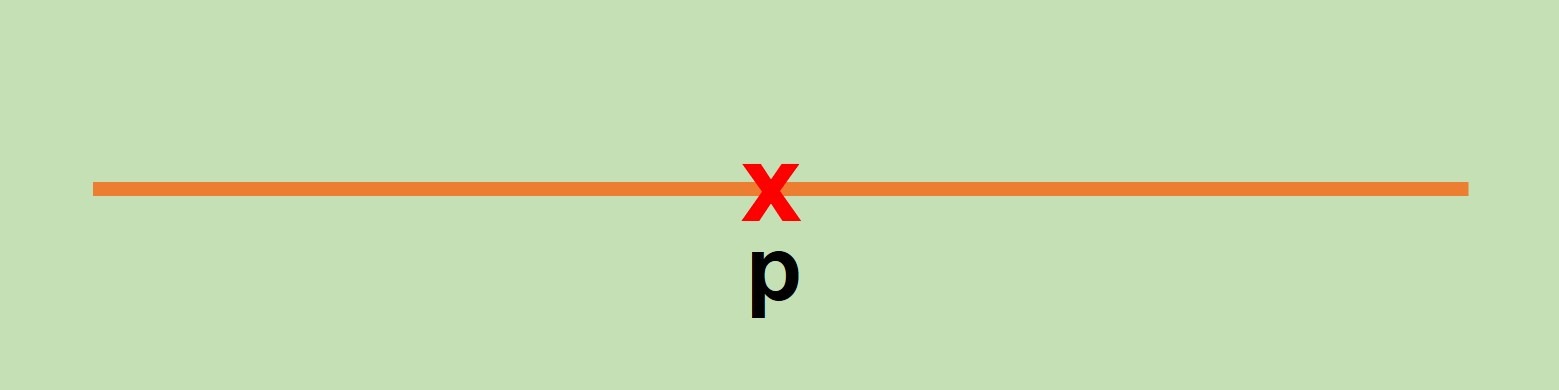
Imaginemos que tomamos un punto $p$ en la recta:

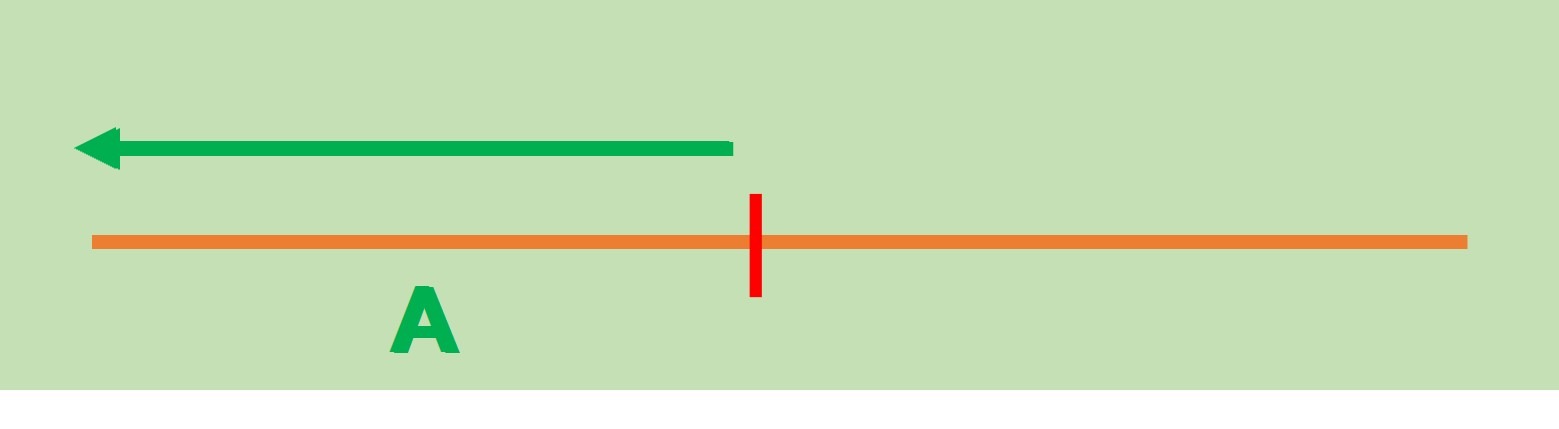
Observemos que ahora la recta queda dividida en dos secciones. La primera conformada por todos los elementos menores (o iguales) que $p$ a la que llamaremos $A$:

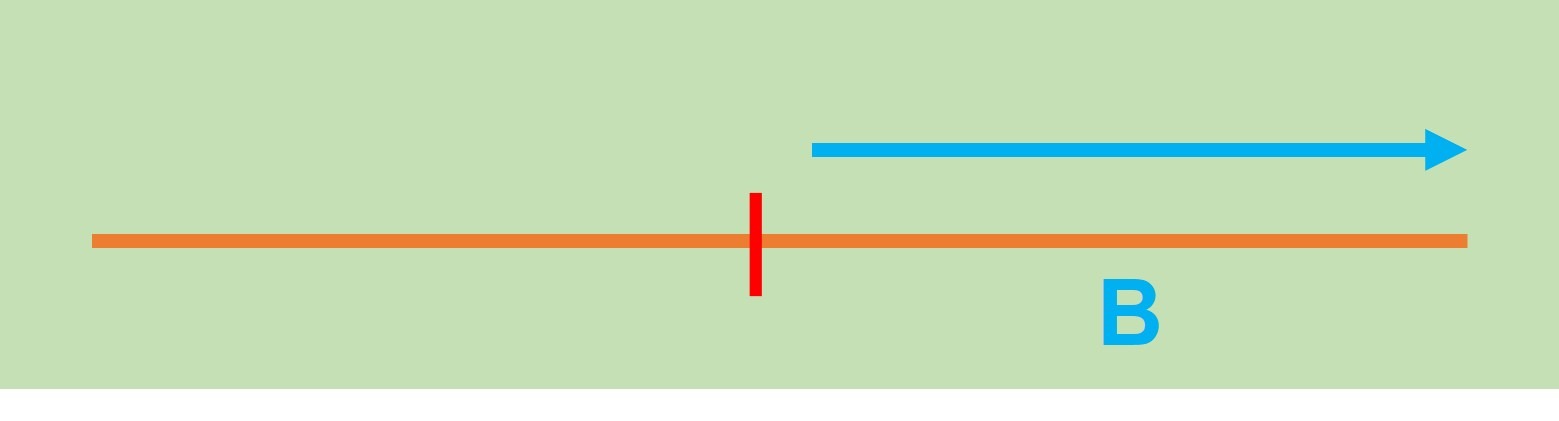
Y la segunda por los elementos mayores (o iguales) que $p$ que será $B$:

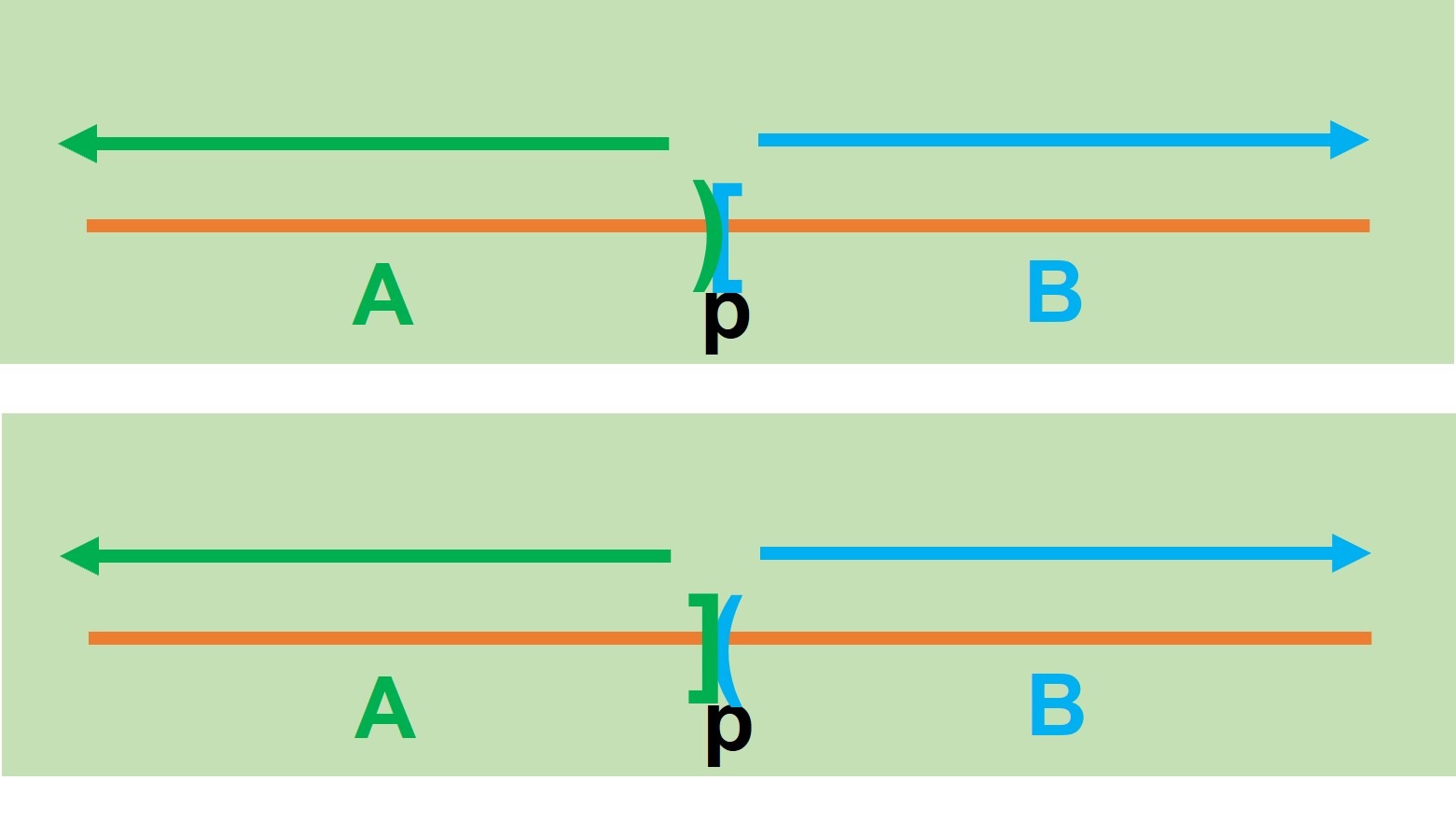
De este modo vemos que tenemos las siguientes posibilidades:

Cada una cumple que $A$ y $B$ no son vacíos además de ser ajenos. En la próxima sección veremos formalmente su definición.

Definición de Cortadura

Definición: Sean $A, B \subseteq \r$. Decimos que la pareja $(A,B)$ forma una cortadura de un campo ordenado $\mathbb{U} \Leftrightarrow$

• $A$ y $B$ son distintos del vacío.
• Para todo $x \in A$ y $y \in B$ ocurre que $x \leq y$.
• $A \cup B = \mathbb{U}$
  $A \cap B = \emptyset$.

Completitud por Cortaduras de Dedekind

Principio de Completitud por Cortaduras de Dedekind: Para toda cortadura $(A,B)$ de $\r$ existe un único $p \in \r$ tal que $\forall x \in A, \forall y \in B$:
$$x \leq p \leq y.$$

Este principio no lo cumplen los números racionales. A continuación veremos la razón:
Consideremos al campo como $\mathbb{U} = \mathbb{Q}$. Proponemos a los conjuntos $A$ y $B$ siguientes:
$$ A = \left\{ x \in \mathbb{Q} : x^{2} \leq 2 \quad \text{o} \quad x < 0 \right\}$$
$$ B = \left\{ y \in \mathbb{Q} : y^{2} > 2 \quad \text{y} \quad y > 0 \right\}$$

Primero debemos probar que son una cortadura de $\mathbb{Q}$:

• $A \neq \emptyset$ ya que $-1 <0$. Por lo que $-1 \in A$.
  $B \neq \emptyset$ pues $2 <3^{2}$. Así $2 \in B$.
• Vemos que $A,B \subseteq \mathbb{Q}$ ya que así fueron definidos.
  • Para $x \in A$ observamos que $x^{2} \leq 2$ o $x<0$.
    $\Rightarrow |x| \leq \sqrt{2}$ o $x <0$.
    $\therefore x \in [- \sqrt{2}, \sqrt{2}] \cup (-\infty, 0) = (- \infty, \sqrt{2}) \cap \mathbb{Q}$.
    Por lo que concluimos $A=(- \infty, \sqrt{2}] \cap \mathbb{Q}$ que vemos es un subconjunto de $\mathbb{Q}$.
  • Ahora si $y \in B$ tenemos que $y^{2} > 2$ y $y>0$.
    $\Rightarrow |y| > \sqrt{2}$ y $y >0$.
    $\therefore y \in ((-\infty, -\sqrt{2}) \cup (\sqrt{2},\infty)) \cap (0,\infty) = (\sqrt{2}, \infty) \cap \mathbb{Q}$.
    Así $B = (\sqrt{2}, \infty) \cap \mathbb{Q}$ y vemos que también es un subconjunto de los racionales.
• Notemos que para toda $x \in A$ y para toda $y \in B$ ocurre:
  $-\sqrt{2} \leq x \leq \sqrt{2}\quad$ o $\quad x<0$, $\sqrt{2}<y\quad$ y $\quad y>0$.
  $\Rightarrow x \leq \sqrt{2}\quad$ o $\quad x<0<y$.
  $\therefore x\leq y$.
• Además de que:
  • \begin {align*}
    A \cup B&=((- \infty, \sqrt{2}] \cap \mathbb{Q}) \cup ((\sqrt{2}, \infty) \cap \mathbb{Q})\\
    &= ((-\infty, \sqrt{2}] \cup (\sqrt{2}, \infty)) \cap \mathbb{Q}\\
    &= \mathbb{Q}\\
    \end{align*}
  • \begin{align*}
    A \cap B&=((- \infty, \sqrt{2}] \cap \mathbb{Q}) \cap ((\sqrt{2}, \infty) \cap \mathbb{Q})\\
    &=(- \infty, \sqrt{2}] \cap (\sqrt{2}, \infty) \cap \mathbb{Q}\\
    &= \emptyset\\
    \end{align*}

Así probamos que $A$ y $B$ son una cortadura de $\mathbb{Q}$.

Veamos que el único número $p$ que cumple la desigualdad $x \leq p \leq y$ para cualesquiera $x \in A$ y $y \in B$ es $p = \sqrt{2} \notin \mathbb{Q}$.
$\therefore \mathbb{Q}$ no es completo.

$\square$

Notemos que anteriormente afirmamos que $\sqrt{2} \notin \mathbb{Q}$, a continuación, veremos su prueba:
Afirmación: $\sqrt{2}$ es irracional.
Demostración: Procederemos por contradicción. Supongamos que $\sqrt{2}$ es racional, es por ello que podemos expresar dicha raíz como una fracción irreducible:
$$\sqrt{2}=\frac{a}{b}.$$

De este modo, $a$ y $b\in \mathbb{Z}$ no tienen ningún factor en común distinto de $1$.

Ahora bien, elevando al cuadrado la igualdad anterior:
\begin{align*}
2=\frac{a^{2}}{b^{2}} &\Rightarrow 2b^{2}= a^{2}\\
&\Rightarrow a^{2} \text{ es par}\\
&\Rightarrow a \quad\text{es par} \tag{por Lema auxiliar}\\
&\therefore a=2q.
\end{align*}

Sustituyendo $a=2q$ nos queda:
\begin{align*}
2b^{2}= a^{2}&\Rightarrow 2b^{2}= (2q)^{2}\\
&\Rightarrow 2b^{2}= 4q^{2}\\
&\Rightarrow b^{2}= 2q^{2}\\
&\Rightarrow b^{2} \text{ es par}\\
&\Rightarrow b \quad\text{es par}. \tag{por Lema auxiliar}\\
\end{align*}
Concluimos que $2$ es un factor común de $a$ y $b \contradiccion$ lo cual es una contradicción.

$\square$

Lema auxiliar: Si consideramos $p \in \mathbb{Z}$ tenemos que:

• $ p^{2}$ es par $\Leftrightarrow p$ es par.
• $ p^{2}$ es impar $\Leftrightarrow p$ es impar.

Equivalencia

Ahora veremos que el Axioma del Supremo y el Principio de Completitud por Cortaduras de Dedekind son equivalentes:

Teorema: Axioma del Supremo $\Leftrightarrow$ Principio de Completitud por Cortaduras de Dedekind
Demostración:
$\Rightarrow ):$ Tomemos $(A,B)$ una cortadura de Dedekind de $\r$ cualquiera, así por definición sabemos que se cumple:
$$x \leq y,$$
para cualquier $x \in A$ y cualquier $y \in B$.

Observemos que $A$ es un conjunto acotado superiormente, entonces aplicando el Axioma del Supremo se sigue que:
$\exists \alpha \in \r$ tal que $\alpha = sup(A).$
Por lo que $\alpha$ cumple ser la menor de las cotas superiores de $A$ y $x \leq \alpha$ para toda $x \in A$.
Ya que para todo $y \in B$ ocurre que $y$ es cota superior de $A$ y $\alpha$ supremo de $A$
$\Rightarrow \alpha \leq y.$
Así concluimos que $\forall x \in A$ y $\forall y \in B$:
$$x \leq \alpha \leq y.$$

$\Leftarrow ):$ Consideremos a un conjunto de reales $C$ no vacío y acotado superiormente. Así tenemos que existe $M \in \r$ cota superior de $C$ por lo que si tomamos:
$$B = \left\{ cotas \quad superiores \quad de \quad C \right\},$$
podemos afirmar que $B \neq \emptyset$. Definamos al conjunto $A = B^{c}$ y hagamos las siguientes observaciones:

• $A\neq \emptyset$. Si suponemos lo contrario se seguiría:
  $A= \emptyset \Rightarrow A^{c}= (B^{c})^{c} \Rightarrow B= \r$.
  Por lo que $C = \emptyset \quad \contradiccion$ lo que es una contradicción.
  $\therefore A, B$ son no vacíos.
• $A \cup B= B^{c} \cup B= \r$
  $A \cap B= B^{c} \cap B= \emptyset$
• Para cualquier $x \in A$ y para cualquier $y \in B$ se cumple la desigualdad $x \leq y$. De lo contrario tendríamos que:
  $\Rightarrow \exists x_{0} \in A$ y $\exists y_{0} \in B$ donde $y_{0} < x_{0}$.
  Como $y_{0}$ es cota superior de $C$, para cualquier $x \in C$ se cumple que:
  $$x \leq y_{0} < x_{0} \Rightarrow x < x_{0}.$$
  $\therefore x_{0}$ es cota superior de $C$.
  Por lo que $x_{0} \in B=A^{c}$ y $x_{0} \in A \quad \contradiccion.$

De todo lo anterior concluimos que los conjuntos $A$ y $B$ son una cortadura de Dedekind de $\r$.

Por el Principio de Completitud por Cortaduras de Dedekind existe un único $p \in \r$ tal que para todo $x \in A$ y para todo $y \in B$ cumple que:
$$x \leq p \leq y.$$
Queremos probar que $p =sup(C)$, es decir:

1. $p$ es cota superior de $C$.
2. $p$ es la menor de todas las cotas superiores.

Comenzaremos probando el punto 1 procediendo por contradicción:
Supongamos que $p$ no es una cota superior de $C$, así existe $x’ \in C$ donde $p<x’$.
Aplicando la densidad de los reales se sigue que existe $y’ \in \r$ tal que:
$$p<y'<x’.$$
Por hipótesis toda $x \in A$ cumple $x \leq p$ entonces $x < y’$. Por lo que concluiríamos que $y’ \in B$ por ser cota superior de $C$ y $y'<x$ con $x \in C \quad \contradiccion$.
$\therefore p$ es cota superior de $C$.

Ahora debemos probar que $p$ es la menor de las cotas superiores. Si suponemos que no lo es entonces existe $M \in B$ con $M<p \quad \contradiccion$ lo que contradice que $p \leq y$ para toda $y \in B$.
$\therefore p= sup(C)$.

$\square$

Más adelante

En la siguiente entrada veremos como tema adicional para esta unidad a los Conjuntos infinitos. Para ello daremos las definiciones necesarias y revisaremos teoremas útiles.

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Axioma del Supremo y sus aplicaciones.
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Conjuntos infinitos.
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»