Archivo de la etiqueta: Completitud

Cálculo Diferencial e Integral I: Sucesiones de Cauchy

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores vimos las propiedades de una sucesión convergente para lo cual era necesario conocer su límite. En esta ocasión estudiaremos a las sucesiones de Cauchy, éstas cumplen una propiedad particular: dado un valor positivo arbitrario, existe un momento a partir del cual la distancia entre dos términos cualesquiera de la sucesión es menor al valor arbitrario establecido. Además, probaremos la relación entre este tipo de sucesiones y las sucesiones convergentes.

Sucesiones de Cauchy

La definición formal de sucesión de Cauchy se da a continuación.

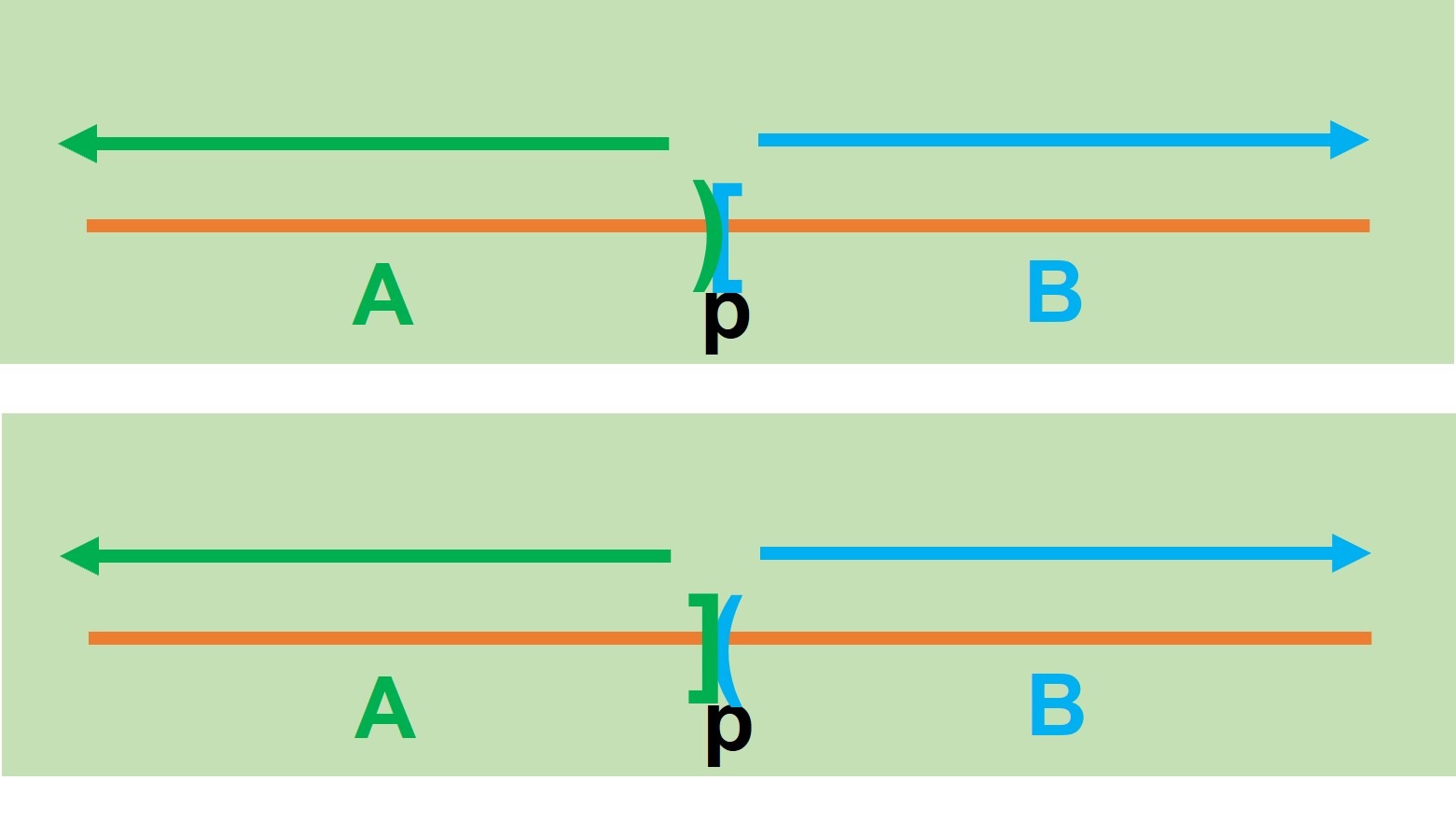
Definición. Se dice que una sucesión $\{a_n\}$ de números reales es una sucesión de Cauchy si para todo $\varepsilon > 0$ existe un número natural $k$ tal que para todos los números naturales $n$, $m \geq k$ se satisface que $|a_n – a_m| < \varepsilon.$

En esta entrada demostraremos la equivalencia entre que una sucesión sea de Cauchy y que sea convergente. La gran ventaja que presenta el concepto de sucesión de Cauchy es que podremos probar que una sucesión converge sin necesidad de conocer su límite, puesto que la definición no hace uso de él. Pero antes de probarlo, veremos un par de ejemplos para familiarizarnos con la definición.

Ejemplo 1. La sucesión $\{\frac{1}{n}\}$ es una sucesión de Cauchy.

Demostración.

Sea $\varepsilon > 0$.

Tomemos $k > \frac{2}{\varepsilon}$. Si $n$, $m > k$, entonces $\frac{1}{n} < \frac{1}{k} < \frac{\varepsilon}{2}$. Análogamente se tiene que $\frac{1}{m} < \frac{\varepsilon}{2}.$

Por lo anterior, si $n$, $m > k$, entonces

\begin{align*}
\left\lvert \frac{1}{n}-\frac{1}{m} \right\rvert & \leq \frac{1}{n} + \frac{1}{m} \\
& < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \\
& = \varepsilon.
\end{align*}

$$\therefore \left\lvert \frac{1}{n}-\frac{1}{m} \right\rvert < \varepsilon.$$

Se concluye que $\{\frac{1}{n}\}$ es una sucesión de Cauchy.

$\square$

Ejemplo 2. Prueba que la sucesión $\{ \frac{n}{n+1} \}$ es de Cauchy.

Demostración.

Sea $\varepsilon > 0.$ Consideremos $k \in \mathbb{N}$ tal que $k > \frac{2}{\varepsilon}$, y por tanto $ \frac{1}{k} < \frac{\varepsilon}{2}$. Además, si $n$, $m > k$, entonces se sigue que

\begin{align*}
\left| \frac{n}{n+1} – \frac{m}{m+1} \right| & = \left| \frac{nm+n-nm-m}{(n+1)(m+1)} \right| \\ \\
& = \left| \frac{n-m}{(n+1)(m+1)} \right| \\ \\
& \leq \left| \frac{n-m}{nm} \right| , \text{ pues } (n+1)(m+1) > nm \\ \\
& = \left| \frac{n}{nm} – \frac{m}{nm} \right| \\ \\
& = \left| \frac{1}{m} – \frac{1}{n} \right| \\ \\
& \leq \frac{1}{n} + \frac{1}{m} \\ \\
& < \frac{1}{k} + \frac{1}{k}, \text{ pues } n,m > k \\ \\
& < \frac{\varepsilon}{2} + \frac{\varepsilon}{2}, \text{ pues } \frac{1}{k} < \frac{\varepsilon}{2} \\ \\
& = \varepsilon.
\end{align*}

Por tanto, $\{ \frac{n}{n+1} \}$ es de Cauchy.

$\square$

Ejemplo 3. Demuestra que la sucesión $\{ (-1)^n \}$ no es de Cauchy.

Demostración.

Debemos probar que existe $\varepsilon > 0$ tal que para todo $k \in \mathbb{N}$, existe al menos un $n > k$ y al menos un $m > k$, tales que $|a_n-a_m| \geq \varepsilon$.

Notemos que la sucesión toma el valor $1$ cuando $n$ es par y $-1$ cuando $n$ es impar. Así, consideremos $\varepsilon = 2$ y sea $k \in \mathbb{N}$. Tomemos cualquier número par $n$ tal que $n > k$ y sea $m = n+1$, $m$ impar. Entonces se tiene que

$$|a_n-a_m| = |1-(-1)| = 2 = \varepsilon.$$

Por tanto, se puede concluir que $\{(-1)^n\}$ no es de Cauchy.

$\square$

Proposición. Si $\{a_n\}$ y $\{b_n\}$ son sucesiones de Cauchy, entonces la sucesión $\{a_n+b_n\}$ también es de Cauchy.

Demostración.

Sea $\varepsilon > 0$. Como $\{a_n\}$ es de Cauchy, para $\frac{\varepsilon}{2} > 0$ existe $k_1$ tal que si $n$, $m > k_1$, se tiene que $$|a_n-a_m| < \frac{\varepsilon}{2}.$$

Como $\{b_n\}$ es de Cauchy, para $\frac{\varepsilon}{2} > 0$ existe $k_2$ tal que si $n$, $m > k_2$, se tiene que $$|b_n-b_m| < \frac{\varepsilon}{2}.$$

Consideremos $k = max\{k_1, k_2 \}$, si $n$, $m > k$, entonces

\begin{align*}
|(a_n+b_n)-(a_m+b_m)| & = |(a_n-a_m)+(b_n-b_m)| \\
& \leq |a_n-a_m| + |b_n-b_m| \\
& < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.
\end{align*}

$$\therefore |(a_n+b_n)-(a_m+b_m)| < \varepsilon.$$

Por lo tanto, la sucesión $\{a_n+b_n\}$ también es de Cauchy.

$\square$

Una de las propiedades naturales de las sucesiones de Cauchy es que son sucesiones acotadas; esto derivado directamente de la definición donde debe existir un punto $k$ a partir de donde cualesquiera dos términos deben distar menos de $\varepsilon$. A continuación demostraremos tal propiedad.

Proposición. Toda sucesión de Cauchy está acotada.

Demostración.

Sea $\{a_n\}$ una sucesión de Cauchy. Entonces para $\varepsilon = 1$, existe $k \in \mathbb{N}$ tal que para $n \geq k$, se tiene que $|a_n – a_k| < \varepsilon = 1$. De la desigualdad del triángulo se tiene que

\begin{gather*}
& |a_n|-|a_k| \leq |a_n-a_k| < 1. \\
\Rightarrow & |a_n| \leq 1 + |a_k|.
\end{gather*}

Notemos que $1+|a_k|$ es una cota para los términos subsecuentes de $a_k$. Para extender la cota a los primeros $k-1$ términos, consideremos $M = max\{ |a_1|, |a_2|, \ldots, |a_{k-1}|, 1+|a_k|\}$. De esta forma, para todo $n \in \mathbb{N}$ se tiene que $|a_n| < M$. Por tanto, la sucesión está acotada.

$\square$

Es importante resaltar que no es equivalente que una sucesión sea de Cauchy a que cumpla que la distancia entre dos términos consecutivos sea cada vez menor, y lo veremos en el siguiente ejemplo.

Ejemplo 4. Sea $\{a_n\}$ tal que $a_n = \sqrt{n}$. Prueba que la sucesión $\{a_n\}$ satisface que

$$\lim_{n \to \infty} |a_{n+1}-a_n| = 0.$$

Pero que no es una sucesión de Cauchy.

Demostración.

Notemos que

\begin{align*}
|a_{n+1}-a_n| & = \left\lvert \sqrt{n+1}-\sqrt{n} \right\rvert \\ \\
& = \left( \sqrt{n+1}-\sqrt{n} \right) \cdot \frac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}} \\ \\
& = \frac{n+1-n}{\sqrt{n+1}+\sqrt{n}} \\ \\ & = \frac{1}{\sqrt{n+1}+\sqrt{n}}.
\end{align*}

Por lo anterior, se sigue que
$$\lim_{n \to \infty} |a_{n+1}-a_n| = \frac{1}{\sqrt{n+1} + \sqrt{n}} = 0.$$

Por otro lado, se tiene que la sucesión $\{a_n\}$ no está acotada, por lo cual no puede ser una sucesión de Cauchy.

$\square$

Relación entre sucesiones convergentes y de Cauchy

Como se menciona anteriormente, dentro del conjunto de los números reales, que una sucesión sea de Cauchy es equivalente a que sea convergente y a este hecho se le suele llamar Completitud de $\mathbb{R}$. Este tema se estudiará en cursos más avanzados, pero de forma intuitiva, que $\mathbb{R}$ sea completo quiere decir que «no deja huecos en la recta numérica». Es decir, a cada punto de la recta le corresponde un número real.

Teorema. Si $\{a_n\}$ es una sucesión convergente de números reales, entonces es de Cauchy.

Demostración

Sea $\varepsilon > 0$. Dado que $\{a_n\}$ es convergente, digamos a $L$, entonces para $\frac{\varepsilon}{2}$ existe un número $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ se satisface que $|a_n – L | < \frac{\varepsilon}{2}.$

Consideremos $k = n_0$. Si $n$, $m \geq k$, entonces

\begin{align*}
|a_n-a_m| & = |a_n-L+L-a_m| \\
& \leq|a_n-L| + |L-a_m| \\
& = |a_n-L| + |a_m – L| \\
& < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \\
& = \varepsilon.
\end{align*}

$$\therefore |a_n-a_m| < \varepsilon.$$

Por lo tanto, $\{a_n\}$ es de Cauchy.

$\square$

Teorema. Toda sucesión de Cauchy es convergente.

Demostración.

Sea $\{a_n\}$ una sucesión de Cauchy. Por la proposición revisada anteriormente, $\{a_n\}$ está acotada. Además, por el teorema de Bolzano-Weierstrass, existe una subsucesión $\{a_{n_r}\}$ convergente y llamemos $L$ al límite de tal subsucesión. Probaremos que $\{a_n\}$ también converge a $L$.

Sea $\varepsilon > 0$. Como la sucesión $\{a_n\}$ es de Cauchy, entonces existe $k \in \mathbb{N}$ tal que
$$|a_n-a_m| < \varepsilon \quad \forall n,m \geq k. \tag{1}$$

Por otro lado, como $\{a_{n_r} \}$ converge a $L$, existe $n_0 \in \mathbb{N}$ tal que

$$|a_{n_l} – L| < \varepsilon \quad \forall n_l \geq n_0. \tag{2}$$

Consideremos $M = max\{k, n_0\}$. Si $s \geq M \geq n_0$, entonces se cumple $(2)$ y además sabemos que $n_s \geq s \geq M \geq k$, pues $n_l$ es una sucesión creciente de números naturales. Por tanto, también se cumple $(1)$. De esto se sigue que

\begin{align*}
|a_s-L|& = |a_s-a_{n_s}+a_{n_s}-L| \\
& \leq |a_s-a_{n_s}|+|a_{n_s}-L| \\
& \leq \frac{\varepsilon}{2} +\frac{\varepsilon}{2} \\
& = \varepsilon.
\end{align*}

$$\therefore |a_s-L| < \varepsilon \quad \forall s \geq M.$$

Se concluye que $\{a_n\}$ es convergente.

$\square$

Más adelante…

Uno de los números más famosos en matemáticas y que probablemente has escuchado hablar de él es el número de Euler: $e$. En la siguiente entrada estudiaremos este número a través de sucesiones y probaremos algunas de sus propiedades.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Da un ejemplo de una sucesión de Cauchy.
  • Da un ejemplo de una sucesión acotada que no sea una sucesión de Cauchy.
  • Prueba mediante la definición que la sucesión $\{ \frac{n+1}{n} \}$ es de Cauchy.
  • Demuestra mediante la definición que la sucesión $\{ (-1)^n \}$ no es de Cauchy.
  • Demuestra mediante la definición que si $\{a_n\}$ y $\{b_n\}$ son sucesiones de Cauchy, entonces la sucesión $\{a_n \cdot b_n\}$ también es de Cauchy.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Cortaduras de Dedekind (Adicional)

Por Karen González Cárdenas

Deja un comentario

Introducción

Ya hemos visto que el campo de los números reales cumple con la propiedad de ser completos, esta propiedad la vimos enunciada con el Axioma del Supremo en la entrada pasada. Ahora veremos que utilizando Cortaduras de Dedekind podemos dar una equivalencia.

Una idea intuitiva

Previamente vimos que existe una relación biunívoca entre el conjunto de los números reales $\r$ y la recta: a cada punto en la recta le corresponde un único número real y viceversa.

Imaginemos que tomamos un punto $p$ en la recta:

Observemos que ahora la recta queda dividida en dos secciones. La primera conformada por todos los elementos menores (o iguales) que $p$ a la que llamaremos $A$:

Y la segunda por los elementos mayores (o iguales) que $p$ que será $B$:

De este modo vemos que tenemos las siguientes posibilidades:

Cada una cumple que $A$ y $B$ no son vacíos además de ser ajenos. En la próxima sección veremos formalmente su definición.

Definición de Cortadura

Definición: Sean $A, B \subseteq \r$. Decimos que la pareja $(A,B)$ forma una cortadura de un campo ordenado $\mathbb{U} \Leftrightarrow$

  • $A$ y $B$ son distintos del vacío.
  • Para todo $x \in A$ y $y \in B$ ocurre que $x \leq y$.
  • $A \cup B = \mathbb{U}$
    $A \cap B = \emptyset$.

Completitud por Cortaduras de Dedekind

Principio de Completitud por Cortaduras de Dedekind: Para toda cortadura $(A,B)$ de $\r$ existe un único $p \in \r$ tal que $\forall x \in A, \forall y \in B$:
$$x \leq p \leq y.$$

Este principio no lo cumplen los números racionales. A continuación veremos la razón:
Consideremos al campo como $\mathbb{U} = \mathbb{Q}$. Proponemos a los conjuntos $A$ y $B$ siguientes:
$$ A = \left\{ x \in \mathbb{Q} : x^{2} \leq 2 \quad \text{o} \quad x < 0 \right\}$$
$$ B = \left\{ y \in \mathbb{Q} : y^{2} > 2 \quad \text{y} \quad y > 0 \right\}$$

Primero debemos probar que son una cortadura de $\mathbb{Q}$:

  • $A \neq \emptyset$ ya que $-1 <0$. Por lo que $-1 \in A$.
    $B \neq \emptyset$ pues $2 <3^{2}$. Así $2 \in B$.
  • Vemos que $A,B \subseteq \mathbb{Q}$ ya que así fueron definidos.
    • Para $x \in A$ observamos que $x^{2} \leq 2$ o $x<0$.
      $\Rightarrow |x| \leq \sqrt{2}$ o $x <0$.
      $\therefore x \in [- \sqrt{2}, \sqrt{2}] \cup (-\infty, 0) = (- \infty, \sqrt{2}) \cap \mathbb{Q}$.
      Por lo que concluimos $A=(- \infty, \sqrt{2}] \cap \mathbb{Q}$ que vemos es un subconjunto de $\mathbb{Q}$.
    • Ahora si $y \in B$ tenemos que $y^{2} > 2$ y $y>0$.
      $\Rightarrow |y| > \sqrt{2}$ y $y >0$.
      $\therefore y \in ((-\infty, -\sqrt{2}) \cup (\sqrt{2},\infty)) \cap (0,\infty) = (\sqrt{2}, \infty) \cap \mathbb{Q}$.
      Así $B = (\sqrt{2}, \infty) \cap \mathbb{Q}$ y vemos que también es un subconjunto de los racionales.
  • Notemos que para toda $x \in A$ y para toda $y \in B$ ocurre:
    $-\sqrt{2} \leq x \leq \sqrt{2}\quad$ o $\quad x<0$, $\sqrt{2}<y\quad$ y $\quad y>0$.
    $\Rightarrow x \leq \sqrt{2}\quad$ o $\quad x<0<y$.
    $\therefore x\leq y$.
  • Además de que:
    • \begin {align*}
      A \cup B&=((- \infty, \sqrt{2}] \cap \mathbb{Q}) \cup ((\sqrt{2}, \infty) \cap \mathbb{Q})\\
      &= ((-\infty, \sqrt{2}] \cup (\sqrt{2}, \infty)) \cap \mathbb{Q}\\
      &= \mathbb{Q}\\
      \end{align*}
    • \begin{align*}
      A \cap B&=((- \infty, \sqrt{2}] \cap \mathbb{Q}) \cap ((\sqrt{2}, \infty) \cap \mathbb{Q})\\
      &=(- \infty, \sqrt{2}] \cap (\sqrt{2}, \infty) \cap \mathbb{Q}\\
      &= \emptyset\\
      \end{align*}

Así probamos que $A$ y $B$ son una cortadura de $\mathbb{Q}$.

Veamos que el único número $p$ que cumple la desigualdad $x \leq p \leq y$ para cualesquiera $x \in A$ y $y \in B$ es $p = \sqrt{2} \notin \mathbb{Q}$.
$\therefore \mathbb{Q}$ no es completo.

$\square$

Notemos que anteriormente afirmamos que $\sqrt{2} \notin \mathbb{Q}$, a continuación, veremos su prueba:
Afirmación: $\sqrt{2}$ es irracional.
Demostración: Procederemos por contradicción. Supongamos que $\sqrt{2}$ es racional, es por ello que podemos expresar dicha raíz como una fracción irreducible:
$$\sqrt{2}=\frac{a}{b}.$$

De este modo, $a$ y $b\in \mathbb{Z}$ no tienen ningún factor en común distinto de $1$.

Ahora bien, elevando al cuadrado la igualdad anterior:
\begin{align*}
2=\frac{a^{2}}{b^{2}} &\Rightarrow 2b^{2}= a^{2}\\
&\Rightarrow a^{2} \text{ es par}\\
&\Rightarrow a \quad\text{es par} \tag{por Lema auxiliar}\\
&\therefore a=2q.
\end{align*}

Sustituyendo $a=2q$ nos queda:
\begin{align*}
2b^{2}= a^{2}&\Rightarrow 2b^{2}= (2q)^{2}\\
&\Rightarrow 2b^{2}= 4q^{2}\\
&\Rightarrow b^{2}= 2q^{2}\\
&\Rightarrow b^{2} \text{ es par}\\
&\Rightarrow b \quad\text{es par}. \tag{por Lema auxiliar}\\
\end{align*}
Concluimos que $2$ es un factor común de $a$ y $b \contradiccion$ lo cual es una contradicción.

$\square$

Lema auxiliar: Si consideramos $p \in \mathbb{Z}$ tenemos que:

  • $ p^{2}$ es par $\Leftrightarrow p$ es par.
  • $ p^{2}$ es impar $\Leftrightarrow p$ es impar.

Equivalencia

Ahora veremos que el Axioma del Supremo y el Principio de Completitud por Cortaduras de Dedekind son equivalentes:

Teorema: Axioma del Supremo $\Leftrightarrow$ Principio de Completitud por Cortaduras de Dedekind
Demostración:
$\Rightarrow ):$ Tomemos $(A,B)$ una cortadura de Dedekind de $\r$ cualquiera, así por definición sabemos que se cumple:
$$x \leq y,$$
para cualquier $x \in A$ y cualquier $y \in B$.

Observemos que $A$ es un conjunto acotado superiormente, entonces aplicando el Axioma del Supremo se sigue que:
$\exists \alpha \in \r$ tal que $\alpha = sup(A).$
Por lo que $\alpha$ cumple ser la menor de las cotas superiores de $A$ y $x \leq \alpha$ para toda $x \in A$.
Ya que para todo $y \in B$ ocurre que $y$ es cota superior de $A$ y $\alpha$ supremo de $A$
$\Rightarrow \alpha \leq y.$
Así concluimos que $\forall x \in A$ y $\forall y \in B$:
$$x \leq \alpha \leq y.$$

$\Leftarrow ):$ Consideremos a un conjunto de reales $C$ no vacío y acotado superiormente. Así tenemos que existe $M \in \r$ cota superior de $C$ por lo que si tomamos:
$$B = \left\{ cotas \quad superiores \quad de \quad C \right\},$$
podemos afirmar que $B \neq \emptyset$. Definamos al conjunto $A = B^{c}$ y hagamos las siguientes observaciones:

  • $A\neq \emptyset$. Si suponemos lo contrario se seguiría:
    $A= \emptyset \Rightarrow A^{c}= (B^{c})^{c} \Rightarrow B= \r$.
    Por lo que $C = \emptyset \quad \contradiccion$ lo que es una contradicción.
    $\therefore A, B$ son no vacíos.
  • $A \cup B= B^{c} \cup B= \r$
    $A \cap B= B^{c} \cap B= \emptyset$
  • Para cualquier $x \in A$ y para cualquier $y \in B$ se cumple la desigualdad $x \leq y$. De lo contrario tendríamos que:
    $\Rightarrow \exists x_{0} \in A$ y $\exists y_{0} \in B$ donde $y_{0} < x_{0}$.
    Como $y_{0}$ es cota superior de $C$, para cualquier $x \in C$ se cumple que:
    $$x \leq y_{0} < x_{0} \Rightarrow x < x_{0}.$$
    $\therefore x_{0}$ es cota superior de $C$.
    Por lo que $x_{0} \in B=A^{c}$ y $x_{0} \in A \quad \contradiccion.$

De todo lo anterior concluimos que los conjuntos $A$ y $B$ son una cortadura de Dedekind de $\r$.

Por el Principio de Completitud por Cortaduras de Dedekind existe un único $p \in \r$ tal que para todo $x \in A$ y para todo $y \in B$ cumple que:
$$x \leq p \leq y.$$
Queremos probar que $p =sup(C)$, es decir:

  1. $p$ es cota superior de $C$.
  2. $p$ es la menor de todas las cotas superiores.

Comenzaremos probando el punto 1 procediendo por contradicción:
Supongamos que $p$ no es una cota superior de $C$, así existe $x’ \in C$ donde $p<x’$.
Aplicando la densidad de los reales se sigue que existe $y’ \in \r$ tal que:
$$p<y'<x’.$$
Por hipótesis toda $x \in A$ cumple $x \leq p$ entonces $x < y’$. Por lo que concluiríamos que $y’ \in B$ por ser cota superior de $C$ y $y'<x$ con $x \in C \quad \contradiccion$.
$\therefore p$ es cota superior de $C$.

Ahora debemos probar que $p$ es la menor de las cotas superiores. Si suponemos que no lo es entonces existe $M \in B$ con $M<p \quad \contradiccion$ lo que contradice que $p \leq y$ para toda $y \in B$.
$\therefore p= sup(C)$.

$\square$

Más adelante

En la siguiente entrada veremos como tema adicional para esta unidad a los Conjuntos infinitos. Para ello daremos las definiciones necesarias y revisaremos teoremas útiles.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Axioma del supremo y sus aplicaciones

Por Karen González Cárdenas

Deja un comentario

Introducción

Durante toda esta unidad hemos visto una serie de propiedades que cumple el conjunto de los reales $\r$, sin embargo, debemos añadir a la lista una relacionada con la completitud de $\r$: el Axioma del Supremo. Para ello comenzaremos hablando de la completitud de $\r$, lo enunciaremos y veremos algunas de sus consecuencias.

Una idea de completitud en $\r$

La completitud de los reales afirma que el conjunto $\r$ rellena a toda la recta numérica sin dejar agujeros. Por lo que cada número real tiene asignado un punto de la recta real:
$$punto \quad en \quad la \quad recta = número \quad real$$
Previamente hemos hecho uso de esta idea al representar gráficamente al conjunto $\r$ utilizando una recta. En el curso veremos dos enunciados que enunciarán esta propiedad: el Axioma del Supremo y Completitud por Cortaduras de Dedekind.

Consideramos como parte de nuestro conjunto de propiedades al Axioma del Supremo, por lo que el enunciado de Cortaduras de Dedekind será un tema adicional para esta unidad.

Axioma del Supremo

En la entrada anterior ya empezamos a platicar de algunas de las impliciciones del siguiente axioma.

Axioma del Supremo: Si $A \subseteq \r$ es no vacío y $A$ es acotado superiormente entonces existe $\alpha \in \r$ tal que:
$$\alpha = sup(A)$$

Pese a lo simple que pueda parecer, más adelante veremos su importancia, ya que muchos resultados y propiedades de $\r$ son consecuencia de este.

Hablemos del ínfimo

Veremos que el enunciado anterior tiene como una de sus consecuencias a su análogo, hablando ahora del ínfimo de un conjunto.

Teorema del ínfimo: Si $A \subseteq \r$ no vacío y $A$ es acotado inferiormente entonces existe $\beta \in \r$ tal que:
$$\beta= inf(A)$$

Demostración:
Sea $A \neq \emptyset$ acotado inferiormente. Ahora consideremos el siguiente conjunto:
$$ B = \left\{ -x \in \r | x \in A \right\}$$

Como $A$ es acotado inferiormente entonces existe $m \in \r$ que es cota inferior de $A$. Así se cumple la siguiente desigualdad para todos los $x \in A$:

$m \leq x \Leftrightarrow -m \geq -x$ para toda $-x \in B$.
Por tanto, $-m$ es cota superior de $B$. Concluimos así que $B$ es no vacío y acotado superiormente. Aplicando el Axioma del Supremo tenemos que existe $\alpha = sup(B)$.

Recordemos que por definición $\alpha$ cumple:

  1. $\alpha$ es cota superior de $B$ para cualquier $-x \in B$.
  2. Es la menor de las cotas superiores de $B$, por lo que si $\alpha_0$ es cota superior de $B$
    $\Rightarrow \alpha < \alpha_0$
  3. Además $-x \leq \alpha$.

Del punto $3$ observamos que:
$$x \geq -\alpha \quad \forall x \in A.$$
$\Rightarrow -\alpha$ cota inferior de $A$.


Nos falta ver qué $- \alpha$ es la mayor de las cotas inferiores de $A$. Notemos que del punto $2$ tenemos que:
$$ -\alpha>-\alpha_0.$$
donde $-\alpha_0$ es cota inferior de $A$.
$$\therefore -\alpha=inf(A).$$

$\square$

$\mathbb{N}$ y $\r$ no acotados superiormente

Teorema: El conjunto $\mathbb{N}$ no es acotado superiormente.

Demostración: Procederemos por contradicción. Supongamos que $\mathbb{N}$ es acotado superiormente por lo que existe $M \in \r$ tal que $M$ es cota superior de $\mathbb{N}$. Aplicando el Axioma del Supremo existe:
$$\alpha = sup(\mathbb{N})$$

entonces:

  • $\alpha$ es cota superior de $\mathbb{N}$
  • $\alpha$ es la menor de las cotas superiores de $\mathbb{N}$

Como para toda $n \in \mathbb{N}$:
$$n \leq \alpha$$
Y $n+1 \in \mathbb{N}$ entonces:
$$n+1 \leq \alpha \Leftrightarrow n \leq \alpha -1$$

Ya que para toda $n \in \mathbb{N}$ se cumple:
$$n \leq \alpha -1$$

donde vemos que $\alpha -1$ es cota superior de $\mathbb{N}$ y además:
$$\alpha -1 < \alpha \quad \contradiccion$$
lo que contradice la definición de $\alpha$.

$\square$

Corolario: El conjunto $\r$ no es acotado superiormente.

Demostración: Procederemos por contradicción, por lo que supongamos que $\r$ es un conjunto acotado superiormente. Ya que sabemos $\mathbb{N} \subseteq \r$ y $\r$ es acotado tendríamos que:
$\mathbb{N}$ es acotado $\contradiccion$ lo cual es una contradicción al teorema anterior.

$\square$

Propiedad de Arquímedes

Teorema (Propiedad de Arquímedes): Si $x >0$ y $y \in \r$ entonces existe $N \in \mathbb{N}$ tal que $$y < Nx$$

Demostración (Por contradicción): Suponemos que no se cumple, es decir,
$\exists x >0$ y $y \in \r$ tal que $\forall n \in \mathbb{N}$ ocurre que $y > nx$
Ya que $x>0$ entonces para cualquier $n \in \mathbb{N}$:
$$\frac{y}{x} > n$$
por lo que $\frac{y}{x}$ es cota superior de $\mathbb{N}$.

Concluimos que $\mathbb{N}$ es acotado superiormente lo que sabemos es una contradicción.

$\square$

Corolario: Para todo $x >0$ existe $n \in \mathbb{N}$ tal que
$$ \frac{1}{n} < x$$

Demostración: Ejercicio como Tarea moral.

Ejercicio

Sean $A \subseteq \r$ y $\lambda >0$ con $\alpha = sup(A)$. Para el conjunto
$$\lambda A := \left\{ x:x=\lambda a \quad\text{con}\quad a \in A \right\}$$
Es decir, el conjunto $\lambda A$ consiste en los reales $x$ que son de la forma $x= \lambda a$ para algún $a$ en $A$.
Prueba que existe $sup(\lambda A)$ y que $sup(\lambda A)= \lambda \alpha$.
Demostración:

Sea $a \in A$ entonces se sigue que $a \leq \alpha$ así al multiplicar por $\lambda >0$:
$$\Rightarrow \lambda a \leq \lambda \alpha$$

Ya que $\lambda a =x \in \lambda A \Rightarrow \lambda A$ es acotado superiormente y $\lambda \alpha$ es cota superior.

Aplicando el Axioma del Supremo afirmamos que existe $\beta := sup(\lambda A)$ y además:
$$\beta \leq \lambda \alpha.$$

Falta probar que $\beta \geq \lambda \alpha$
Si tomamos $x \in \lambda A$ entonces $x = \lambda a$ y $\lambda a \leq \beta$:
$$\Rightarrow a \leq \frac{\beta}{\lambda}$$

Y por la definición de supremo se sigue:
$$\alpha \leq \frac{\beta}{\lambda} \Leftrightarrow \lambda \alpha \leq \beta$$
Así concluimos:
$$\therefore \beta = \lambda \alpha$$
$$\therefore \lambda sup(A) = sup(\lambda A)$$

$\square$

Otras aplicaciones

A continuación sólo enunciaremos un teorema en el cual el Axioma del Supremo es aplicado. Dado que en este punto no hemos revisado los conceptos de sucesión ni de límite, más adelante se verá su demostración.

Teorema: Si $\{ a_n \}$ es una sucesión en $\mathbb{R}$ no decreciente y acotada superiormente entonces es una sucesión convergente.

Más adelante

En la próxima entrada veremos un poco sobre las Cortaduras de Dedekind y la completitud de $\r$, éste será considerado como un tema adicional para esta unidad.

Tarea moral

  • Demuestra que para todo $x >0$ existe $n \in \mathbb{N}$ tal que
    $$ \frac{1}{n} < x$$
  • Prueba que si $a<b$ e $I=(a,b)$ es un intervalo en $\r$ entonces $sup(I)=b$ y $inf(I)=a$.
    Sugerencia: Utiliza el resultado anterior y procede haciendo uso de las respectivas definiciones.
  • Sean $A,B \subseteq \r$ con $\alpha = sup(A)$ y $\beta=sup(B)$. Definimos el siguiente conjunto
    $$ A+B := \left\{ x:x=a+b; a \in A, b \in B \right\}$$
    Demuestra que existe $sup(A+B)$ y que $sup(A+B)= \alpha + \beta$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»