Archivo de la etiqueta: cardinalidad de un conjunto

Álgebra Superior I: Cardinalidad de conjuntos finitos

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

¿Qué es lo que entiendes cuando alguien te dice: «En esta canasta hay cinco manzanas»? Probablemente te llegue a la mente una imagen similar a la siguiente:

Y es que para nosotros es muy natural el decir «cuántas» cosas hay dentro de un conjunto. De hecho los primeros usos que dieron lugar al nacimiento de las matemáticas datan de hace más de $5000$ años en mesopotamia con los primeros sistemas para contar. Esto remarca la necesidad de contar objetos que a su vez trata de diferenciar unos de otros.

Imagínate que te pidieran contar cuántos Pingüinos Rey hay en un zoológico. Para ello primero habría que saber distinguir a cuáles son este tipo de pingüinos y cuáles no. En un principio puede resultar fácil, y es que veremos que el distinguir elementos unos de otros puede llegar a complicarse cuando más consideraciones hacemos como el saber cuántos pingüinos hay que sean machos, o cuántos machos hay que no tengan más de un año, por ejemplo. Con este tipo de ejercicios los matemáticos fueron descubriendo con el tiempo que hacía falta poder estudiar un poco más a detalles este concepto de «diferenciar» y «contar» elementos de un conjunto. En las siguientes entradas vamos a desarrollar un poco más este concepto de diferenciar y contar.

Cardinalidad de un conjunto

Como todo en matemáticas, necesitaríamos hacer una definición de lo que significa que «un conjunto tenga $3$ elementos» y cómo es diferente a «un conjunto con $5$ elementos», por poner un ejemplo. Es con esto que damos la siguiente definición entre cardinalidad de un conjunto finito.

Definición. Sea $X$ un conjunto. Diremos que $X$ tiene cardinalidad finita o es finito si existe $n \in \mathbb{N}$ y una función biyectiva entre $X$ y $n$. En este caso escribiremos $|X|=n$.

Detengámonos un poco a analizar esta definición.

Recordemos que por ejemplo el número $2$ es escrito como conjunto como
$$ \{\emptyset,\{\emptyset\}\}$$.

Ahora pensemos en un conjunto con un plátano y una manazana. Entonces podemos definir la siguiente función $f: X \rightarrow \mathbb{N}$ como $f(manzana)= \emptyset$ y $f(plátano)=\{\emptyset\}$:

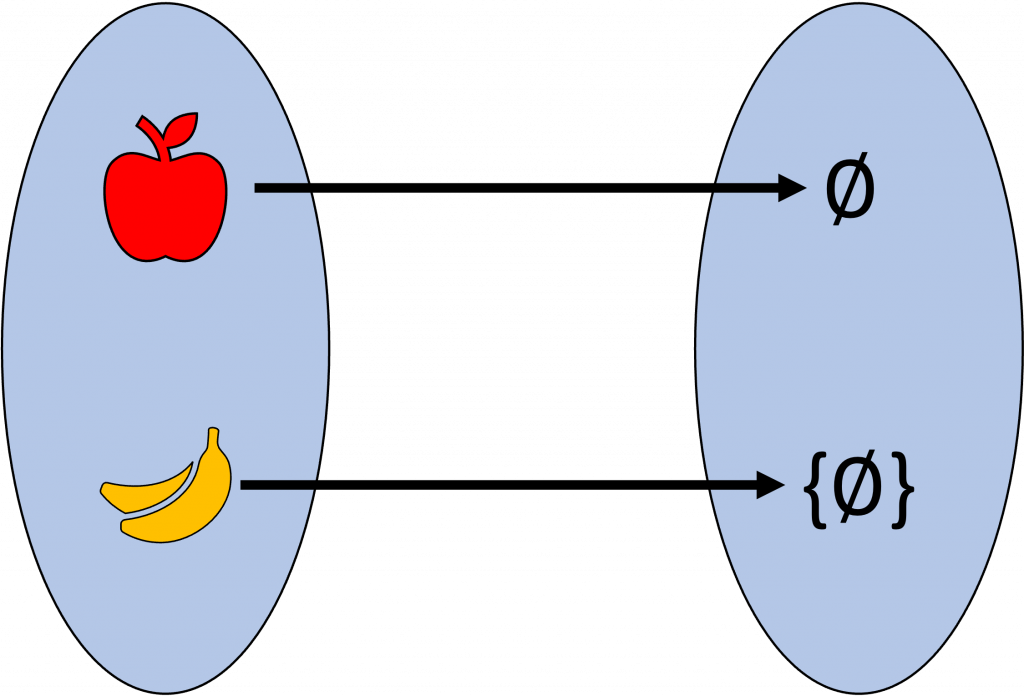
Puedes comprobar que esta función es biyectiva, y es solo una forma de biyectar el conjunto $X$ con el $2$. Dicho esto, entonces podemos decir que $|X|=2$. Ahora ¿Qué pasa con un conjunto que también tenga cardinalidad $2$? Digamos el conjunto $Y$ de un perro y un gato.

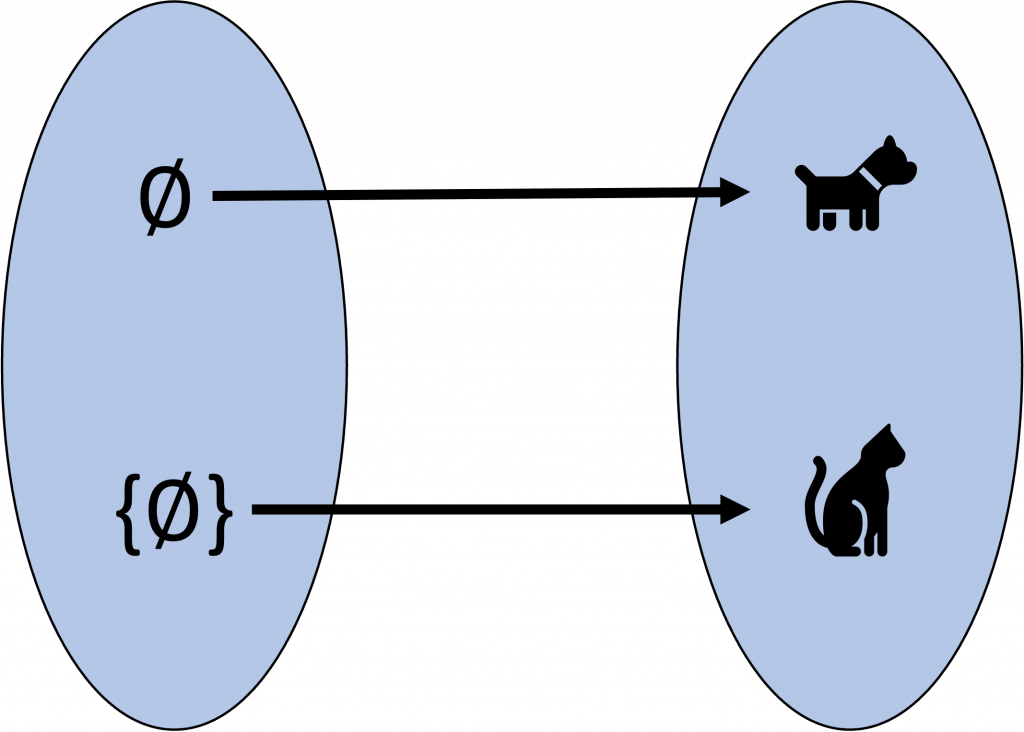
Entonces podríamos decir que igual puede haber una biyección entre los dos conjuntos $X$ y $Y$.

Ahora ¿Qué pasa si unimos los conjuntos de animales con los de ls frutas? Pues nuestra razón nos dirá que si en un conjunto tenemos dos elementos y en el otro dos, si los combinamos tendremos cuatro elementos, y esto es justamente otra de las bondades de la cardinalidad, pues se comporta de acuerdo a lo que nuestra razón nos dice.

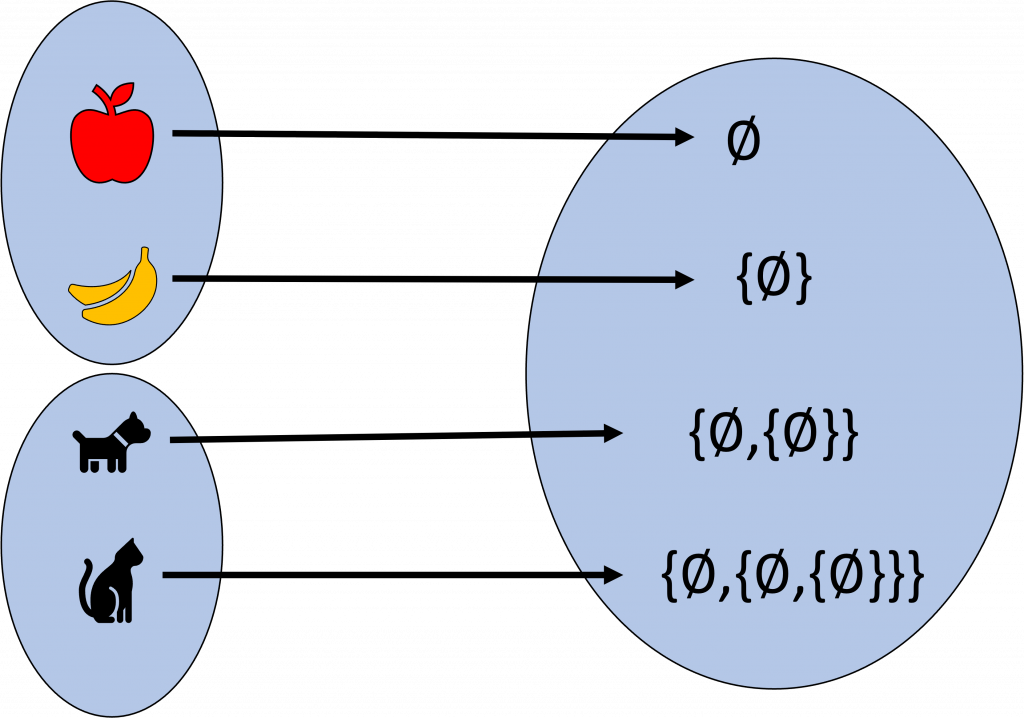
Proposición Sean $X,Y$ dos conjuntos disjuntos. Si $|X|=n, |Y|=m$ entonces $|X \cup Y| = n+m$.

Demostración. Por definición de cardinalidad, existen dos funciones $g:X \rightarrow n$ y $f: Y \rightarrow m$ biyectivas. Notemos ahora que la función $h: X \cup Y \rightarrow n+m $ dada por $$h(x) = \begin{cases} &f(x), x \in X \\ g(x) + n, x \in Y \end{cases} $$ es biyectiva. Para demostrar que esta función es biyectiva, demostraremos la inyectividad y suprayectividad.

Es inyectiva. Considera dos elementos $x,y$ distintos. Existen tres casos, el primero es que $x,y \in X$, en este caso, $h(x)=f(x), h(y)=f(y)$ y como $f$ es inyectiva, sus imágenes son distintas.
El segundo caso es $x , y \in Y$. En este caso, recordemos que $h(x)=n+g(x)$ y $h(y) = n + g(y)$ Si las imágenes fueran iguales entonces $g(x)=g(y)$ pero esto solo sucede si $x=y$, pues $g$ es inyectiva, y esto contradiciendo la hipótesis de que los elementos son distintos.
Finalmente en el caso de que un elemento pertenezca a $X$, digamos $x$ y el otro a $Y$, digamos $y$, sucede que $h(x)=f(x)$, mientras que $h(y)=n+g(y)$, ahora notemos que $f: X \rightarrow n$, entonces ningún elemento es más grande que $n$, mientras que $h(y)$ sí es más grande que $n$, pues estamos uniendo números naturales al más grande número natural que compone al conjunto $X$, es decir, siempre sucederá que $h(x)<h(y)$ y en particular $h(x) \neq h(y)$, siendo la función inyectiva.

Además la función es suprayectiva, ya que para cualquier elemento $k \in n+m$ se tienen dos casos: Si $k <= n$ entonces existe $x \in X$ tal que $h(x)=f(x)=k$, mientras que si$k>n$ existe $l \in. \mathbb{N}$ tal que $n+l=k$. Por otro lado, como $g$ es suprayectiva, existe $y \in Y$ tal que $g(y)=l$. Así $h(y)=n+g(y)=n+l=k$. Por lo tanto la función es biyetiva.

Y más aún, hemos demostrado que los conjuntos disjuntos tienen cardinalidad $n+m$.

$\square$

El principio de las casillas

Una de las propiedades más importantes sobre cardinalidad que es intuitiva es la siguiente:

Proposición. (El principio de las casillas). Sean $X,Y$ dos conjuntos tales que $|X|=s(n)$ y $|Y|=n$. Entonces si $f:X \rightarrow Y$, $f$ no es inyectiva.

A esta se le llama principio de las casillas o de los palomares y se explica con el siguiente ejemplo:

Supón tienes $9$ casillas para palomas:

Naturalmente, solo cabrá a lo más una paloma en cada una de las casillas, entonces si lega al menos una paloma más, forzosamente tendría que haber más de una paloma en alguna de las casillas. En general para $n$ casillas, caben a lo más $n$ paloma para que quede solo una paloma en cada casilla. Es decir, podríamos hacer una inyección entre el número de palomas y el de casillas siempre y cuando haya menos palomas que casillas.

Demostración. Para ello deberíamos mostrar que no existe una inyección entre un conjunto de $n$ elementos y otro de $s(n)$.

Base de inducción. Sea $|X|=s(0)$ y $|Y|=0$. Notemos entonces que $Y$ tiene que ser el vacío, pues $0$ es el vacío y si $Y$ no fuera vacío, entonces existiría una función $f$ y un elemento $y \in Y$ tal que $f(y) \in \emptyset$. Lo cual es una contradicción. Ahora notemos que por vacuidad el enunciado se cumple, pues de no ser así, existiría una función $g:X \rightarrow Y$ inyectiva, pero esto supondría que $Im[g] \subset \emptyset$ tiene al menos un elemento.

Hipótesis de inducción. Ahora supongamos que para cualesquiera dos conjuntos $|X|=s(n)$ y $|Y|=n$ se cumple la condición.

Paso inductivo. Consideremos ahora dos conjuntos $X,Y$ con $|X|=s(s(n))$ y $|Y|=s(n)$. Ahora consideremos cualquier función $f: X \rightarrow Y$, bastará probar que esta función no es inyectiva. Para ello, notemos que si le quitamos cualquier elemento $x \in X$ a $X$, su cardinalidad será $s(n)$. Además si quitamos el elemento $y \in Y$ tal que $f(x)=y$ entonces $Y$ tiene cardinalidad $n$. Así volvemos al caso de la hipótesis de inducción donde la función $f’: X/\{x\} \rightarrow Y/{y}$ definida como $f'(x)=f(x)$ no es inyectiva, esto significa que existen dos elementos $y,z \in X/\{x\}$ tales que $f'(x)=f'(y)$. Más aún, la función $f$ tampoco es inyectiva por la existencia de estos dos elementos.

Así hemos demostrado el principio de las casillas.

$\square$

La cardinalidad de dos conjuntos

Una definición ahora sobre la cardinalidad de dos conjuntos es consecuencia de

Definición Dos conjuntos $X$ y $Y$ tienen la misma cardinalidad si existe una función biyectiva $f: X \rightarrow Y$ y lo escribiremos como $|X|=|Y|$

Y ahora veamos cómo es que en el caso finito, esta es una definición que no contradice la primera definición que dimos

Proposición En el caso finito, Son equivalentes para cualesquiera dos conjuntos finitos $X,Y$ y cualquier número natural $n$:

  1. $|X| = n \land |Y| = n$
  2. $|X| = |Y|$

Demostración.

$\Rightarrow$

Supongamos primero que $|X| = n$ y $|Y|=n$. Ahora, notemos que existen dos funciones biyectivas $f: X \rightarrow n$ y $g: Y \rightarrow n$ Ahora consideremos la siguiente función $g^{-1} \circ f : X \rightarrow Y$. Y notemos que es una biyección, pues como $g$ es biyectiva, en particular es suprayectiva y eso significa que $Im[g] = n$ Siendo entonces la función $g{-1}: Im[g] =n \rightarrow Y$ con el mismo dominio que el contradominio de $f$, es decir la composición es una función bien definida. Además como $f$ también es biyectiva, entonces $g^{-1} \circ f$ también es biyectiva.

$\Leftarrow$

Demostremos ahora por contradicción que $|X| = n \land |Y| = n$ cuando $|X|=|Y|$.

Para ello supongamos primero que existen dos naturales distintos $n,m$ tales que $|X|=n$ y $|Y|=m $, y esto es posible pues $X,Y$ son finitos. Y también $|X|=|Y|$ Ahora sin perdida de la generalidad supongamos que $n>m$. Pero esto es una contradicción al principio de las casillas, pues toda función de $X$ a $Y$ no sería inyectiva, y en general tampoco será biyectiva. Cumpliéndose así la condición deseada.

$\square$

Algunas propiedades más de la cardinalidad

Veamos ahora otras propiedades sobre las cardinalidades de los conjuntos. Para ello supón que $X$ es finito de cardinalidad $n$ y $Y$ es finito de cardinalidad $m$.

  • Proposición. $|X /Y| = |X| – |X \cap Y|$
    Demostración. Esto es consecuencia del hecho de que $X/Y$ y $X \cap Y$ son conjuntos disjuntos, entonces:
    $$ |X/Y| + |X \cap Y| = |X/Y \cup (X \cap Y)| = |X|$$

$\square$

  • Proposición. $|X \cup Y| = |X| + |Y| – |X \cap Y|$
    Demostración. Por el inciso anterior, sabemos que $$ |X \cup Y| = |X/Y \cup Y| = |X|- |X \cap Y| + |Y|$$

$\square$

  • Proposición. $|P({X)|=2^{|X|}$
    Demostración. Por inducción sobre el número de elementos en el conjunto $X$.
    Base de inducción. Si $X$ tiene $0$ elementos, entonces es el vacío, mientras que $P(X)={\emptyset}$ el cuál tiene cardinalidad $1=2^{0}$.
    Hipótesis de inducción. Ahora supongamos que si $|X|=n$ para algún número $n$ natural, entonces $|P(X)|=2^{n}$.
    Paso inductivo. Sea $|X|=n+1$. Consideremos ahora un elemento $x$ de $X$ y notemos que el conjunto $X/\{x\}$ es un conjunto con $n$ elementos, por lo cual sabemos que $|P(X/\{x\})|=2^n$. Ahora veamos que este conjunto describe todos los posibles subconjuntos de $X$ en los que $x$ no está incluído, por lo que si definimos el conjunto $P(X/\{x\}) \cup x := {A \cup x : A \in P(X/\{x\})}$, se tiene que $$(P(X/\{x\}) \cup x) \cup P(X/\{x\}) = P(X) $$ Pues el primer conjunto son todos los subconjuntos de $X$ que sí tienen a $x$ y el segundo aquellos que no. Como estos dos son conjuntos disjuntos y tienen exactamente $n$ elementos, entonces $$|P(X)| = |(P(X/\{x\}) \cup x) \cup P(X/\{x\})| = 2^n + 2^n = 2^{n+1}$$.

$\square$

Más adelante…

Ahora que hemos introducido el concepto de cardinalidad, veremos cómo es que podemos escalar este concepto del caso finito al caso infinito. Es decir ¿Qué pasa cuando ya no podemos hablar de conjuntos que podemos «contar»?

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que $(P(X/\{x\}) \cup x) \cup P(X/\{x\}) = P(X)$
  2. Demuestra que $|X|=|Y|$ si y solo si $|Y|=|X|$
  3. Demuestra que la relación «tener la misma cardinalidad» es de equivalencia.
  4. ¿Cuál es la cardinalidad de |X \cup Y \cup Z|?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Moderna I: Paridad de una permutación

Por Cecilia del Carmen Villatoro Ramos

4 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior descubrimos que toda permutación se puede factorizar en producto de transposiciones. Mas aún, el polinomio de Vandermonde nos permite saber que, aunque hayan varias factorizaciones, en realidad, todas siempre tienen una cantidad par (o un cantidad impar) de transposiciones. Con esto, podemos definir el signo de una permutación. La secuencia que se seguirá para abordar el signo de una permutación es la presentada en el libro de Avella, Mendoza, Sáenz y Souto, es decir se usarán los resultados de la entrada previa de acuerdo al enfoque de Herstein, para introducir la función signo y probar que es multiplicativa, y con ello obtener la fórmula del signo que aparece en el libro de Rotman (todos estos libros son los que se mencionan en la bibliografía).

Ya teniendo una noción de la paridad de una permutación podemos jugar con las consecuencias: podemos deducir qué pasa si multiplicamos dos permutación con la misma paridad, qué sucede cuando tienen distinta paridad y además, como es raro en los cursos de matemáticas… ¡podemos agrupar por paridad! En esta entrada, descubrimos que el conjunto de transposiciones con signo par, es en realidad un grupo con $\frac{n!}{2}$ elementos. Este conjunto es llamado el grupo alternante.

¿Pares o impares?

Definición. Sea $\alpha \in S_n$, $\alpha$ es par si $\alpha = \text{id}$ o si $\alpha$ es un producto de un número par de transposiciones. Por otro lado, $\alpha$ es impar si es un producto de un número impar de transposiciones.

La función signo es $sgn: S_n \to \{+1, -1\}$ definida como
\begin{align*}
sgn \; \alpha = \begin{cases} +1 & \text{si } \alpha \text{ es par} \\
-1 & \text{si } \alpha \text{ es impar}
\end{cases}
\end{align*}

Observación. Sean $\alpha = \tau_{1} \cdots \tau_r \in S_n$, con $\tau_{1}, \cdots, \tau_r$ transposiciones. Entonces $sgn\;\alpha = (-1)^r$.

Demostración.
La definición nos asegura que $sgn\;\alpha = +1$ si y sólo si $r$ es par.

$\blacksquare$

Proposición. Sean $\alpha, \beta \in S_n$. Entonces $$sgn \;(\alpha \, \beta) = sgn\, \alpha \; sgn \, \beta.$$

Esto nos dice que la función signo ($sgn$) es multiplicativa. Esto lo hace más sencilla de trabajar.

Demostración.

Esto es bastante fácil de demostrar, para usar lo que vimos tenemos que expresar a estas permutaciones como producto de transposiciones.

Sean $\alpha, \beta \in S_n$, con $\alpha = \tau_{1} \cdots \tau_r$, $\beta = \rho_1 \cdots \rho_t$. Donde, $\tau_1, \cdots, \tau_r, \rho_{1}, \cdots, \rho_t$ son transposiciones.

Si calculamos el signo del producto $\alpha\,\beta$ y usando la observación anterior, obtenemos lo siguiente:
\begin{align*}
sgn(\alpha \, \beta) &= sgn(\tau_1 \cdots \tau_r \, \rho_1 \cdots \rho_t) \\
& = (-1)^{r+t} & \text{Observación anterior}\\
& = (-1)^r \, (-1)^t & \text{Propiedades de las potencias}\\
& = sgn\, \alpha \; sgn\, \beta &\text{Observación anterior}
\end{align*}

Esto es precisamente lo que queríamos probar.

$\blacksquare$

Podemos concluir que para calcular el signo de un producto, basta entender el signo de cada uno de los factores.

Calculando el signo de una permutación

Seguiremos puliendo la idea que nos dio la proposición anterior hasta llegar a una fórmula para sacar el signo de una permutación. Pero por ahora, veamos qué sucede con los $r$-ciclos.

Lema. Sea $\sigma = (i_1 \cdots i_r) \in S_n$ un $r$-ciclo. Entonces $sgn\, \sigma = (-1)^{r-1}$.

Demostración.
Recordemos que en la entrada anterior vimos que podemos ver a $\sigma$ como producto de transposiciones:
\begin{align*}
\sigma &= (i_1 \cdots i_r) = (i_1\,i_r) \cdots (i_1 \, i_2).
\end{align*}
Intuitivamente, estamos intercambiando a $i_1$ con los elementos que le siguen, esto nos da $r-1$ transposiciones. Por lo tanto, $\sigma$ es un producto de $r-1$ transposiciones. De acuerdo con la observación, podemos concluir que $sgn \, \sigma = (-1)^{r-1}$.

$\blacksquare$

Estamos listos para enunciar y probar  la fórmula del signo que aparece en el libro de Rotman que se menciona en la bibliografía, y que resulta muy útil para calcular el signo de una permutación.

Teorema. Sea $\alpha \in S_n$, $\alpha = \beta_1 \cdots \beta_t$ una factorización completa de $\alpha$. Entonces $sgn\,\alpha = (-1)^{n-t}$, donde $t$ es la cantidad de factores que tiene la factorización completa de $\alpha$.

Demostración.
Como el signo es multiplicativo,
\begin{align*}
sgn\,\alpha = \prod_{i=1}^t sgn\,\beta_i.
\end{align*}
Estamos tomando una factorización completa de $\alpha$, entonces todos los $\beta_i$ son ciclos disjuntos. Así que su signo está dado por la longitud del ciclo (de acuerdo al lema dado):
\begin{align*}
sgn\,\beta_i = (-1)^{\text{long}\,\beta_i-1} \qquad \forall i\in\{1,\dots,t\}.
\end{align*}
Juntando ambas ecuaciones y sumando los $t$ exponentes obtenemos las siguientes igualdades
\begin{align*}
sgn\,\alpha &= \prod_{i = 1}^{t} sgn \,\beta_i & \text{Proposición}
\\&= \prod_{i = 1}^t (-1)^{\text{long}\,\beta_i – 1} &\text{Lema}\\
& = (-1)^{\left(\sum_{i = 1}^t \text{long}\,\beta_i \right) -\;\large{ t}} = (-1)^{n-t}. &\text{Leyes de exponentes}
\end{align*}

Como la factorización es completa, la siguiente igualdad se cumple: $$\sum_{i = 1}^t \text{long}\,\beta_i = n.$$

Por lo tanto $sgn\,\alpha = (-1)^{n-t}$.

$\blacksquare$

Esta forma resulta útil porque ya no necesito descomponer una permutación en producto de transposiciones, nos basta con encontrar una factorización completa. Veamos esto con un ejemplo.

Ejemplo.
Consideremos $\alpha \in S_{10}$ como
\begin{align*}
\alpha = \begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\
2 & 4 & 7 & 5 & 1 & 8 & 3 & 9 & 6 & 10
\end{pmatrix}.
\end{align*}

También podemos escribirla como $\alpha = (1\;2\;4\;5)(3\;7)(6\;8\;9)(10)$. Esto nos muestra que $\alpha$ es una factorización completa con 4 factores.

Entonces, de acuerdo con el teorema que acabamos de probar, $$sgn\,\alpha = (-1)^{10-4} = (-1)^6 = +1.$$

Por otro lado podemos sacar una factorización de $\alpha$ en transposiciones: $\alpha = (1 \; 5)(1 \; 4)(1 \; 2)(3 \; 7)(6 \; 9)(6 \; 8)$ que tiene 6 transposiciones. Entonces, efectivamente $\alpha$ es un producto de un número par de transposiciones.

Hora de Agrupar

Hemos visto que la función $sgn$ es una función mutliplicativa. Esto nos da como consecuencia que al multiplicar dos permutaciones con la misma paridad, te da como resultado una permutación par. En caso contrario, el resultado es impar. Ahora nos fijaremos solamente en las permutaciones pares.

Definición. El grupo alternante para $n$ elementos está definido como

$$A_n = \{\alpha \in S_n | sgn \, \alpha = +1\}.$$

Observación. $A_n$ efectivamente es un subgrupo de $S_n$.

Demostración.
Si $\alpha = \text{id}$, por definición del signo, $sgn\,\text{id} = +1$. Así, $\text{id}\in A_n$.

Sean $\alpha, \beta \in A_n$.
Como la función signo es multiplicativa:
\begin{align*}
sgn\,\alpha\beta = sgn \, \alpha \; sgn \, \beta = (+1)(+1) = +1.
\end{align*}
Así, $\alpha\beta \in A_n$. Es decir, $A_n$ es cerrada bajo el producto.

Por último, sea $\alpha \in A_n$.

Por un lado, usando la propiedad multiplicativa del signo obtenemos:
\begin{align*}
sgn\,(\alpha\alpha^{-1}) = sgn \, \alpha \; sgn \, \alpha^{-1} = (+1)\, sgn\, \alpha^{-1}.
\end{align*}

Por otro lado, como $\alpha \,\alpha^{-1} = \text{id}$, tenemos:
\begin{align*}
sgn\,(\alpha\,\alpha^{-1}) = sgn\, \text{id} = +1.
\end{align*}

Por lo tanto $sgn\,(\alpha\, \alpha^{-1}) = +1$, así $\alpha^{-1} \in A_n$. Es decir, $A_n$ es cerrada bajo inversos.

Por lo tanto $A_n$ es un subgrupo de $S_n$.

$\blacksquare$

El siguiente resultado nos muestra que el grupo alternante $A_n$ «parte en dos» a las permutaciones, es decir, la mitad de permutaciones son pares.

Proposición. Sea $n>1$, entonces $|A_n| = \frac{n!}{2}$.

Demostración. Podemos ver a $S_n$ como la unión de las permutaciones pares e impares, esto se expresa así $$S_n = A_n \cup (S_n\setminus A_n).$$
Pero, podemos dar una biyección definida como $\phi: A_n \to S_n\setminus A_n$, definida como $\phi \, \alpha = (1\;2)\alpha$.

Entonces, $|A_n| = \# S_n \setminus A_n$.

Así, como dijimos que

$n! = |S_n| = |A_n| + \# S_n\setminus A_n = 2 |A_n|$.

Por lo tanto $|A_n| = \frac{n!}{2}$.

Notación. Para denotar la cardinalidad u orden de un conjunto $A$, usamos dos notaciones:
\begin{align*}
|A| \to & \;\text{Si $A$ es un grupo.}\\
\# A \to & \;\text{Si $A$ no es un grupo (o si no sabemos si $A$ es un grupo o no).}
\end{align*}

Tarea moral

  1. Considera el elemento $\alpha \in S_{12}$ como
    \begin{align*}
    \alpha = \begin{pmatrix}
    1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 &10&11&12\\
    2 & 11&4& 1 & 8 &12& 3 & 6 & 9 & 5 & 7 & 10
    \end{pmatrix}
    \end{align*}
    1. Encuentra $\alpha^{-1}$, el signo de $\alpha$ y el de $\alpha^{-1}$.
    2. En general, ¿qué pasará con el signo de una permutación y de su inversa?
  2. Sea $\alpha$ un $r$ ciclo en $S_n$. ¿Podemos determinar el signo de $\alpha$ a partir de la paridad de $r$?
  3. Dada $\alpha \in S_n$ decimos que los números $i,j \in \{1,2,\dots,n\}$ forman una inversión si $i<j$ pero $\alpha(i) > \alpha(j)$. ¿Qué relación existe entre la paridad y el número de inversiones de $\alpha$?
  4. Encuentra todos los elementos de $A_4$.

Más adelante…

Esta entrada nos sirvió para construir los cimientos, es importante que lo tengamos claro antes de avanzar. En la siguiente entrada definiremos el producto de $S$ con $T$, veremos en qué situaciones el producto de los subconjuntos conmuta, cuándo se cumple que $ST$ es un subgrupo de $G$. Esto nos ayudará para definir las clases laterales. Más adelante, estas clases nos ayudarán a definir una nueva relación de equivalencia.

Entradas relacionadas