$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
En secciones anteriores vimos que las sucesiones de Cauchy no siempre son convergentes en un espacio métrico, pero cuando todas lo son decimos que el espacio es completo.
Si tenemos un espacio que no es completo, intuitivamente podemos pensar en agregar puntos a los que las sucesiones de Cauchy converjan, produciendo así, un espacio métrico más grande que sí sea completo. Habrá que tener cuidado en definir adecuadamente las distancias con los nuevos elementos. Podríamos preguntarnos entonces si dicha completación es posible, y más aún, si es única.
Comencemos con la siguiente:
Definición. Completación de un espacio métrico: Sea $(X,d)$ un espacio métrico. Diremos que un espacio métrico completo $(X^*,d^*)$ es una completación del espacio $X$ si cumple que:
- $X$ es subespacio métrico de $X^*.$ Así $d$ es la métrica restringida en $X.$
- $X$ es denso en $X^*,$ es decir $\overline{X}=X^*.$
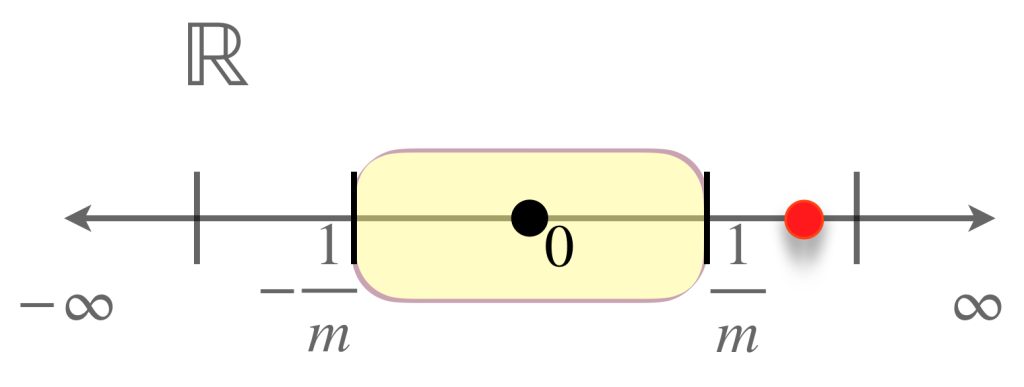
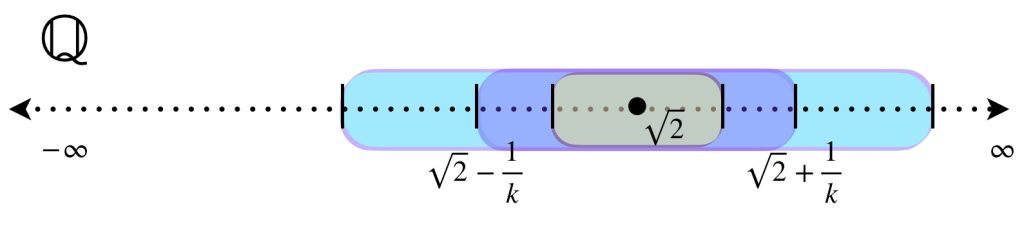
Ejemplo: El espacio métrico $(\mathbb{R},|\cdot|)$ es una completación de $(\mathbb{Q},|\cdot|).$
Proposición: Todo espacio métrico $(X,d)$ tiene una completación y esta completación es única, salvo una aplicación isométrica que envía los puntos de $X$ en sí mismos. (Aquí vimos la definición de isometría).
Prueba unicidad
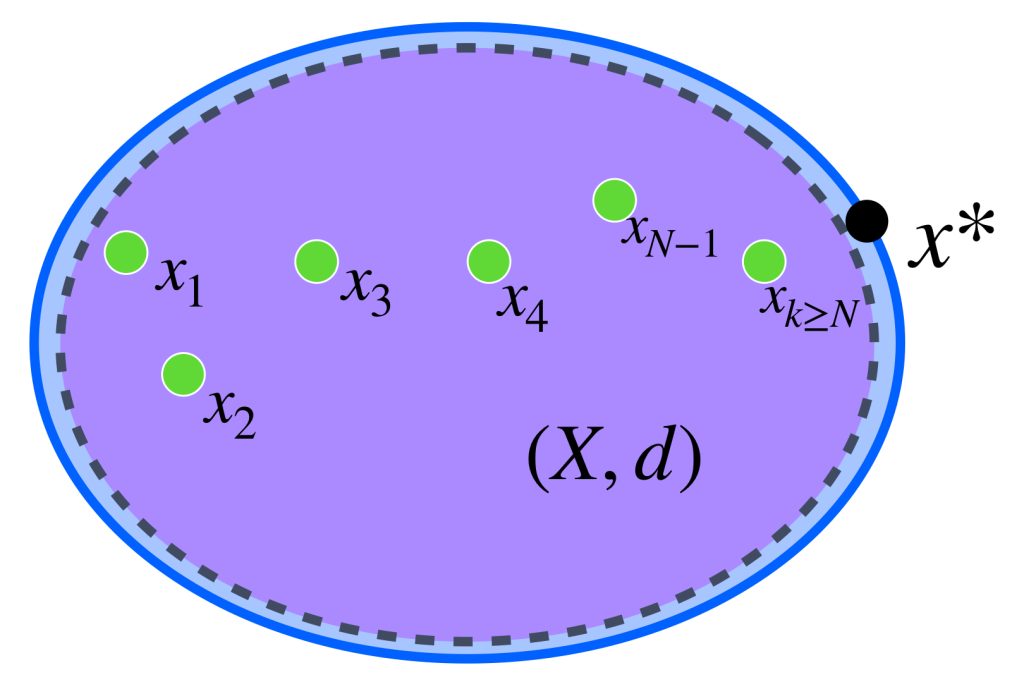
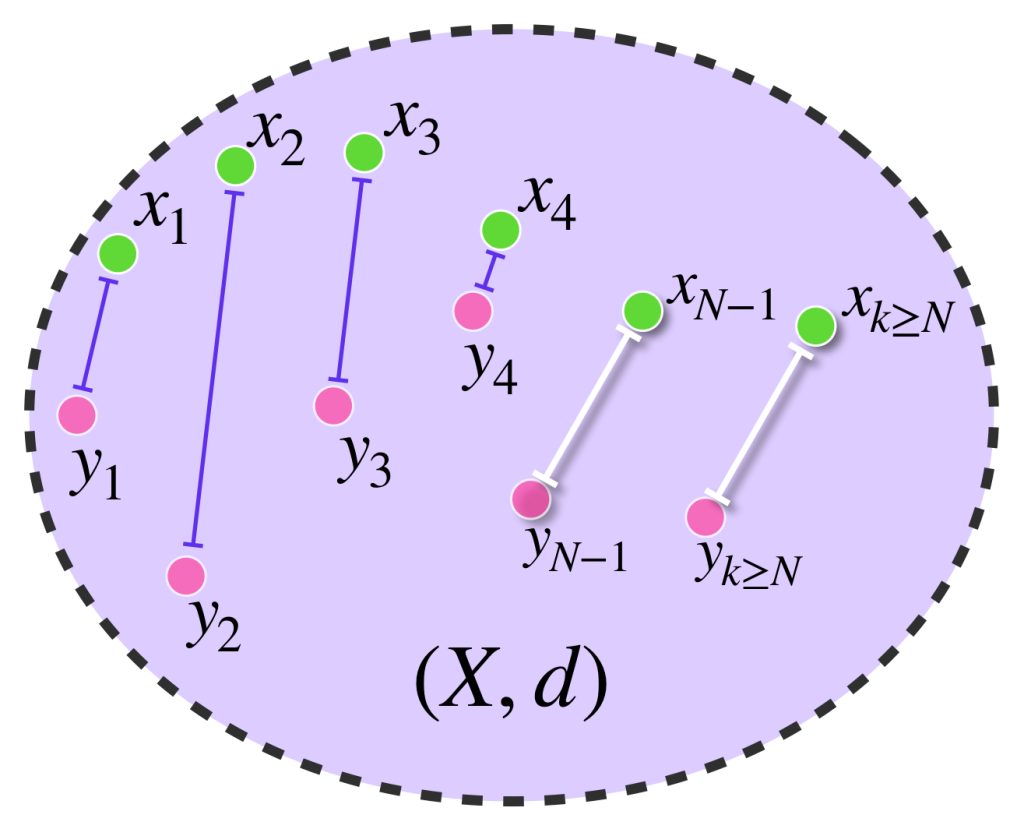
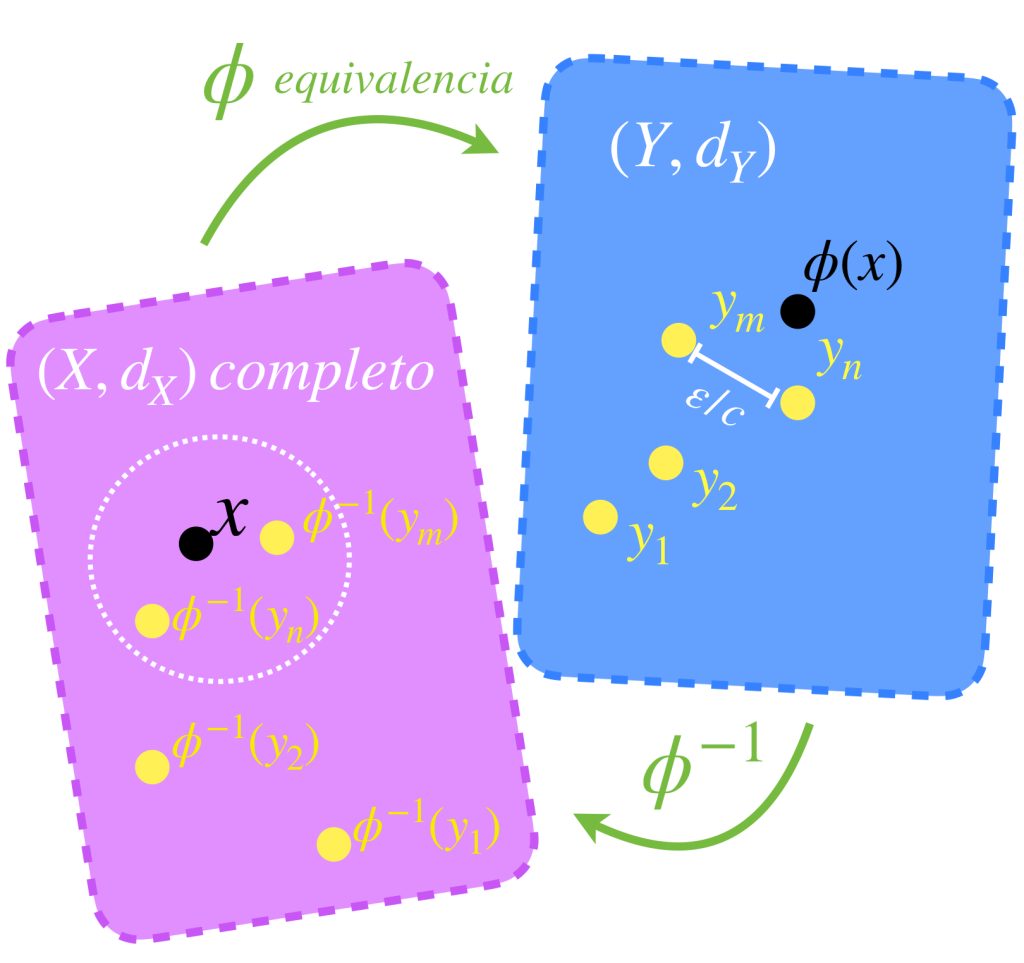
Considera $X$ un espacio métrico y dos completaciones $(X^*,d^*)$ y $(X^{**},d^{**})$ de este espacio. Para probar que son iguales salvo isometrías debemos demostrar que existe una isometría biyectiva entre ambas completaciones. La isometría se construye como sigue:
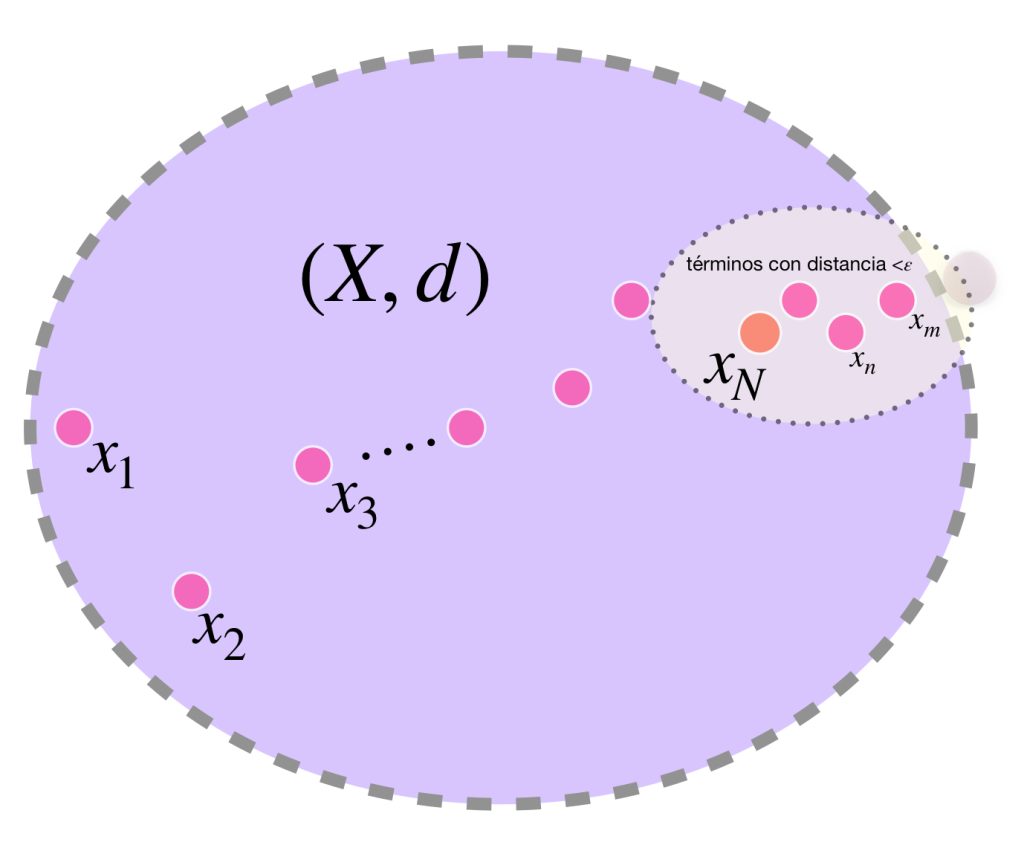
Sea $x^* \in X^*,$ como $X^*$ es completación de $X$ entonces, de acuerdo con la definición $\overline{X}=X^*,$ en consecuencia $x^* \in \overline{X}$ y existe una sucesión $(x_n)_{n \in \mathbb{N}}$ de puntos en $X,$ que converge a $x^*.$ (Resultado visto en Convergencia). Nota que la convergencia permite concluir que $(x_n)$ es de Cauchy en $X^*$ (pues $X \subset X^*$) y por tanto también lo es en $X,$ debido a que la completación debe preservar las distancias para cualesquiera dos puntos de $X.$
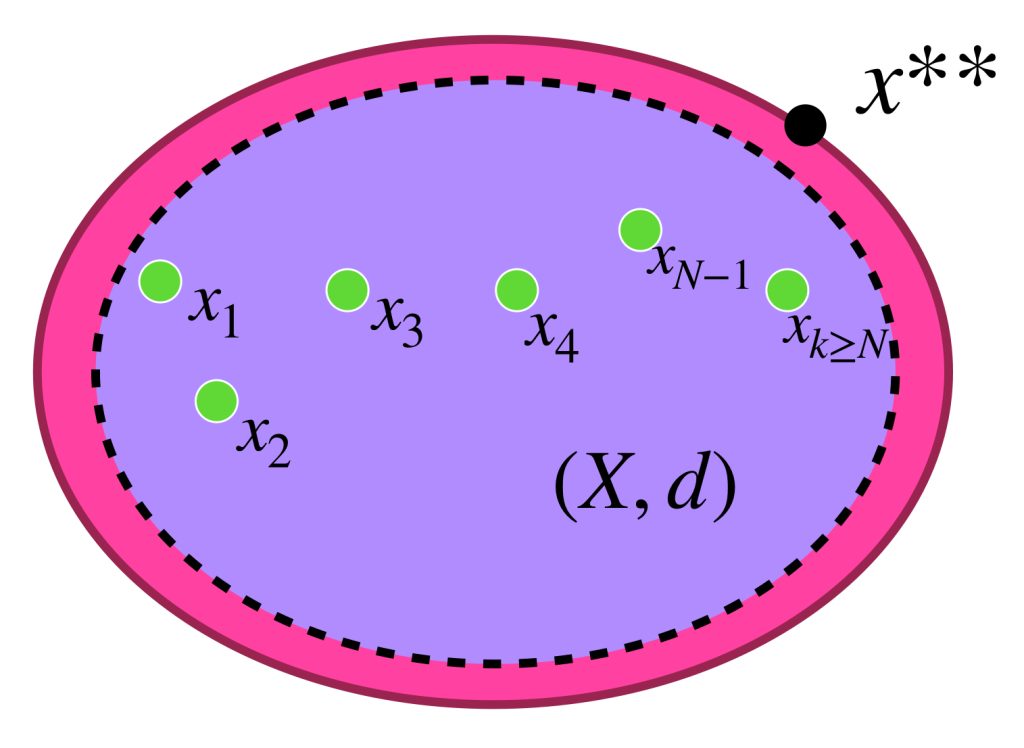
Como también $X \subset X^{**}$ se sigue que los términos de $(x_n)$ también pertenecen a $X^{**}$ que, al ser completo, implica que $x_n \to x^{**}$ para algún $x^{**} \in X^{**},$ (pues si la sucesión es de Cauchy en $X$ también lo es en la completación $X^{**}$).
Afirmación: El punto $x^{**}$ no depende de la sucesión elegida $(x_n)$ que converge en $x^*.$ Esto es, cualquier otra que también converja en $x^*$ en el espacio $X^*,$ igualmente convergerá a $x^{**}$ en el espacio $X^{**}.$ ¿Por qué? $\textcolor{orange}{\text{(Ejercicio como tarea moral).}}$
Para cada $x^* \in X^*$ sea $\phi(x^*)=x^{**}.$ Demostraremos que $\phi$ es la isometría buscada:
Se cumple que para todo $x \in X, \, \phi(x)=x.$ ¿Por qué? $\textcolor{orange}{\text{(Ejercicio como tarea moral).}}$ Por otra parte, si suponemos que tenemos sucesiones $(x_n), (y_n)$ cuyos términos están en $X,$ tales que:
$x_n \to x^*$ en $X^*\, $ y $\, x_n \to x^{**}$ en $X^{**};$
$y_n \to y^*$ en $X^*\, $ y $\, y_n \to y^{**}$ en $X^{**}$
entonces:
$d^*(x^*,y^*)=\underset{n \to \infty}{lim}\, d^*(x_n,y_n)=\underset{n \to \infty}{lim}\, d(x_n,y_n)$
así mismo
$d^{**}(x^{**},y^{**})=\underset{n \to \infty}{lim}\, d^{**}(x_n,y_n)=\underset{n \to \infty}{lim}\, d(x_n,y_n)$ ¿Por qué? $\textcolor{orange}{\text{(Ejercicio como tarea moral).}}$
Por lo tanto,
\begin{align*}
d^*(x^*,y^*)&=d^{**}(x^{**},y^{**})\\
&=d^{**}(\phi(x^*),\phi(y^*)).
\end{align*}
Lo cual demuestra que $\phi$ es una isometría. ¿Por qué se le puede considerar biyectiva? $\textcolor{orange}{\text{(Ejercicio como tarea moral).}}$
Prueba existencia
Antes de probar la existencia veamos la siguiente:
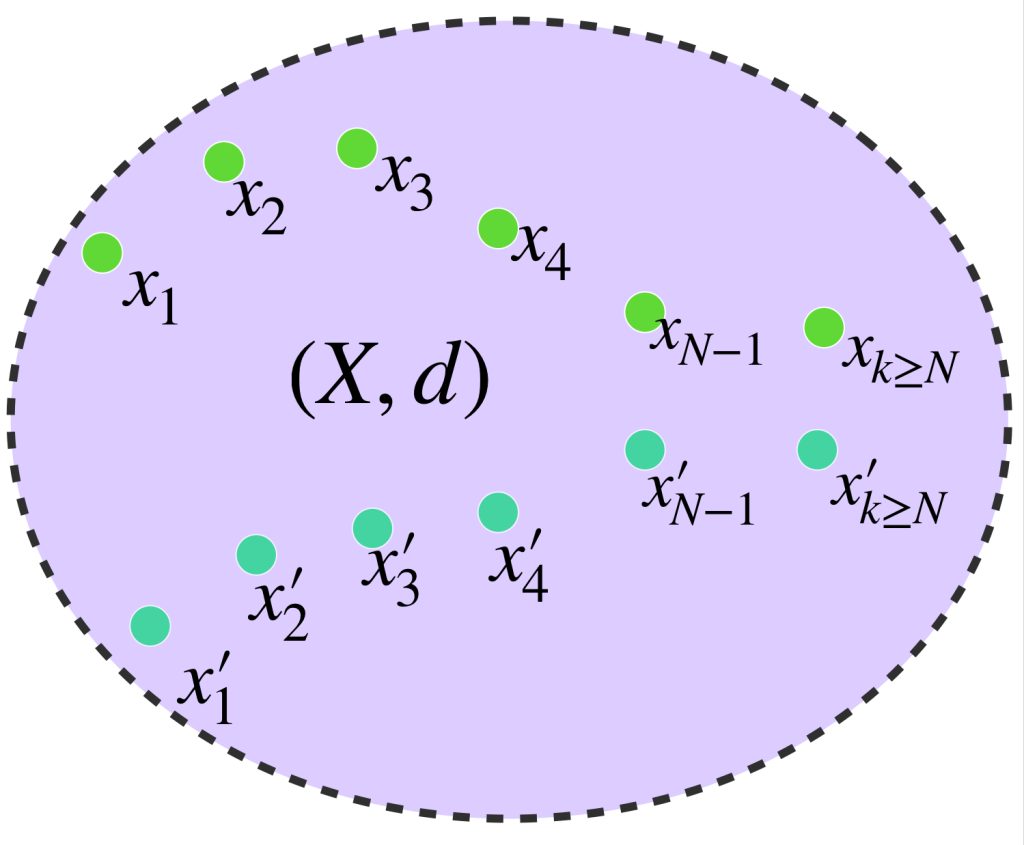
Definición. Sucesiones equivalentes: Sean $(x_n)_{n \in \mathbb{N}}\,$ y $\,(x’_n)_{n \in \mathbb{N}}$ sucesiones de Cauchy en el espacio métrico $X.$ Si ocurre que $\underset{n \to \infty}{lim} \, d(x_n,x’_n)=0$ diremos que las sucesiones son equivalentes y lo denotaremos como:
$$(x_n)\sim (x’_n)$$
Se deja como $\textcolor{orange}{\text{ejercicio como tarea moral}}$ probar que esta relación es de equivalencia (reflexiva, simétrica y transitiva). Para recordar, te recomendamos visitar Álgebra Superior I: Relaciones de equivalencia y clases de equivalencia.
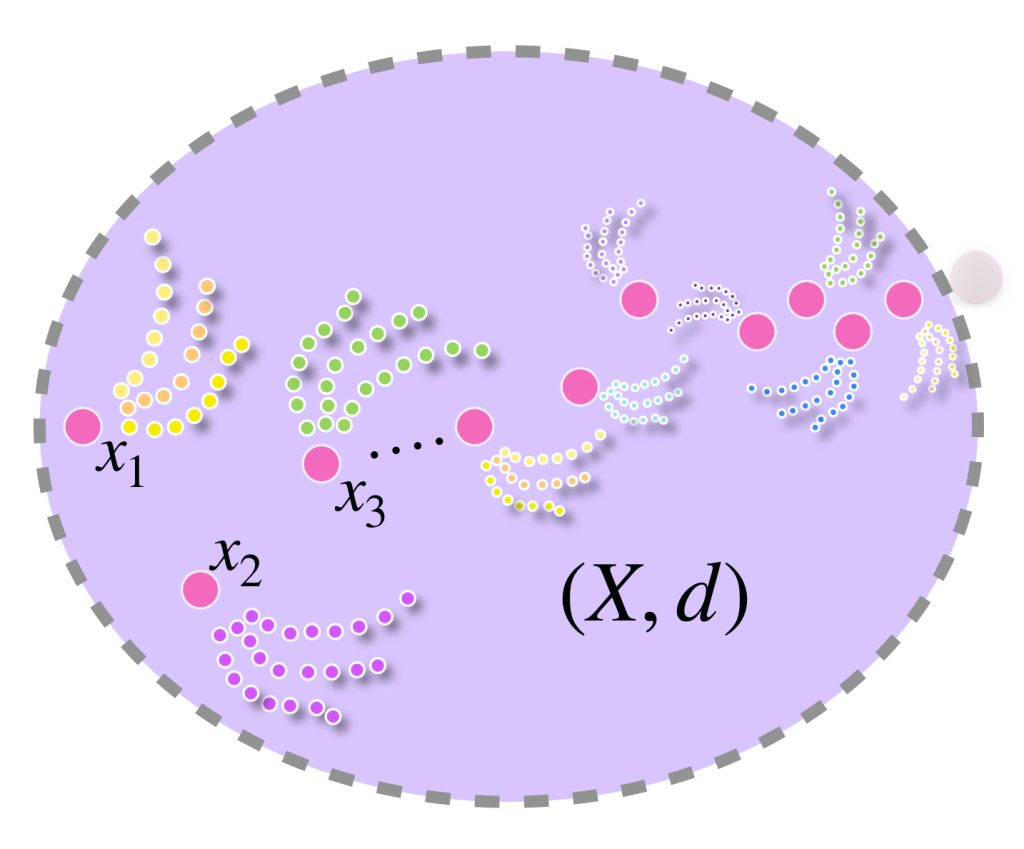
Con esto se define un conjunto de clases de equivalencia, agrupando según la relación, las sucesiones de Cauchy en $X.$ Veremos que es una completación de $X.$ Probablemente esto cause confusión en este momento, pues mientras $X$ es un conjunto de puntos, la completación que proponemos tiene como elementos conjuntos de sucesiones de Cauchy. No obstante, aunque el tipo de elementos entre ambos conjuntos parezcan muy diferentes, en las próximas líneas veremos que la magia del isomorfismo admitirá considerarlos equivalentes.
Sean $[(x_n)] \,$ y $\, [(y_n)]$ dos clases de equivalencia y sean $(x_n)$ y $(y_n)$, respectivamente, representantes de clase. Definimos la distancia entre ambas clases como:
$$d^*([(x_n)],[(y_n)])=\underset{n \to \infty}{lim} \, d(x_n,y_n).$$
Entonces se considera la distancia entre un término de la sucesión $(x_n)$ y el término correspondiente en $(y_n).$ Hablar de que existe el límite de las distancias cuando $n \to \infty$ indica que en algún momento, la distancia entre pares de términos se estabiliza.
Por supuesto que habrá que demostrar que este límite existe y que esta distancia es invariante, no depende del representante de clase elegido en cada clase de equivalencia.
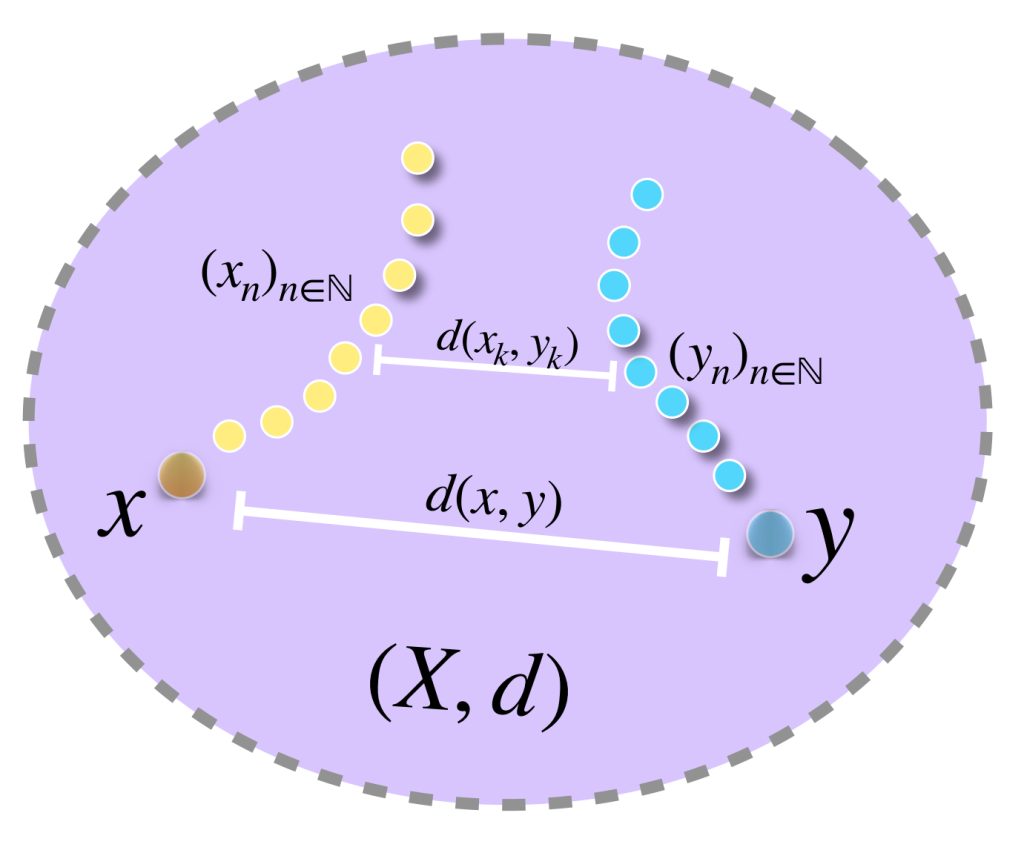
Probemos primero que la sucesión dada por $(d(x_n,y_n))_{n \in \mathbb{N}}$ es convergente en $\mathbb{R}$. Bastará con demostrar que es de Cauchy.
Sea $\varepsilon >0.$ Como $(x_n),(y_n)$ son de Cauchy, existen $N_1$ y $N_2 \in \mathbb{N}$ tales que
\begin{align}
\text{si } \, n,m \geq N_1 \text{ entonces } d(x_n,x_m) < \dfrac{\varepsilon}{2}\\
\text{si } \, n,m \geq N_2 \text{ entonces } d(y_n,y_m) < \dfrac{\varepsilon}{2}.
\end{align}
Sea $N=\text{máx} \, \{N_1,N_2\}.$ Se sigue que $\forall \, n,m \geq N$ se cumple que:
\begin{align*}
|d(x_n,y_n)-d(x_m,y_m)|&=|d(x_n,y_n) \textcolor{magenta}{- d(x_n,y_m)+ d(x_n,y_m)}-d(x_m,y_m)| &\textcolor{gray}{\text{(sumando un cero estratégico)}}\\
&\leq |d(x_n,y_n)- d(x_n,y_m)|+ |d(x_n,y_m)-d(x_m,y_m)| &\textcolor{gray}{\text{(desigualdad del triángulo)}}
\end{align*}
Es sencillo probar que si $u,v,w$ son elementos de un espacio métrico $(Y,d_Y)$ se satisface que
\begin{align}
|d_Y(u,v)-d_Y(u,w)|\leq d_Y(v,w). \, \textcolor{orange}{\text{ (Ejercicio como tarea moral).}}
\end{align}
Con este resultado es posible continuar con la cadena de igualdades:
\begin{align*}
|d(x_n,y_n)- d(x_n,y_m)|+ |d(x_n,y_m)-d(x_m,y_m)|&\leq d(y_n,y_m) + d(x_n,x_m) \\
&\leq \frac{\varepsilon}{2}+ \frac{\varepsilon}{2} &\textcolor{gray}{\text{(desigualdades (1) y (2) )}}\\
&= \varepsilon
\end{align*}
Entonces la sucesión $(d(x_n,y_n))_{n \in \mathbb{N}}$ es de Cauchy en $\mathbb{R}$ y converge cuando $n \to \infty.$
Ahora demostremos que la distancia entre clases no depende del representante elegido. Sean $(x_n) \sim (x’_n)$ y sean $(y_n) \sim (y’_n)$. En efecto
$$d^*([(x_n)],[(y_n)])\, \textbf{=} \, d^*([(x’_n)],[(y’_n)])$$
pues al calcular la diferencia entre estas magnitudes tenemos:
\begin{align*}
|d^*([(x_n)],[(y_n)]) \, \textbf{-} \, d^*([(x’_n)],[(y’_n)])|&=|\underset{n \to \infty}{lim} \, d(x_n,y_n)-\underset{n \to \infty}{lim} \,d(x’_n,y’_n)| &\textcolor{gray}{\text{(por definición)}}\\
&=|\underset{n \to \infty}{lim} \, (d(x_n,y_n)- \,d(x’_n,y’_n))| &\textcolor{gray}{\text{(propiedad de límites)}}\\
&=|\underset{n \to \infty}{lim}(d(x_n,y_n)\textcolor{magenta}{- d(x_n,y’_n)+ d(x_n,y’_n)}-d(x’_n,y’_n))|&\textcolor{gray}{\text{(sumando un cero estratégico)}} \\
&=|\underset{\textcolor{ForestGreen}{n \to \infty}}{\textcolor{ForestGreen}{lim}}(d(x_n,y_n)- d(x_n,y’_n))+ \underset{\textcolor{RoyalBlue}{n \to \infty}}{\textcolor{RoyalBlue}{lim}}(d(x_n,y’_n)-d(x’_n,y’_n))| &\textcolor{gray}{\text{(propiedad de límites)}}\\
&\leq |\underset{\textcolor{ForestGreen}{n \to \infty}}{\textcolor{ForestGreen}{lim}} (d(x_n,y_n)- d(x_n,y’_n))| + |\underset{\textcolor{RoyalBlue}{n \to \infty}}{\textcolor{RoyalBlue}{lim}} (d(x_n,y’_n)-d(x’_n,y’_n))| &\textcolor{gray}{\text{(desigualdad del triángulo)}}\\
&\leq \underset{\textcolor{ForestGreen}{n \to \infty}}{\textcolor{ForestGreen}{lim}} |(d(x_n,y_n)- d(x_n,y’_n))| + \underset{\textcolor{RoyalBlue}{n \to \infty}}{\textcolor{RoyalBlue}{lim}} |(d(x_n,y’_n)-d(x’_n,y’_n))| &\textcolor{gray}{\text{(propiedad de límites y $|\cdot|$)}}\\
&\leq \underset{\textcolor{ForestGreen}{n \to \infty}}{\textcolor{ForestGreen}{lim}} d(y_n,y’_n) + \underset{\textcolor{RoyalBlue}{n \to \infty}}{\textcolor{RoyalBlue}{lim}} d(x_n,x’_n) &\textcolor{gray}{\text{(desigualdad (3) )}}\\
&= 0+0 &\textcolor{gray}{\text{(por ser sucesiones equivalentes)}}\\
&= 0
\end{align*}
Por lo tanto la distancia entre clases está bien definida.
El conjunto de clases de equivalencias de sucesiones es un espacio métrico
Sean $[(x_n)], [(y_n)], [(z_n)]$ clases de equivalencia de la relación descrita arriba. Se satisfacen los axiomas:
- $d^*([(x_n)], [(y_n)])=0$ si y solo si $[(x_n)]= [(y_n)]$
- $d^*([(x_n)], [(y_n)])=d^*([(y_n)], [(x_n)])$
- $d^*([(x_n)], [(y_n)]) \leq d^*([(x_n)], [(z_n)]) +d^*([(z_n)], [(y_n)])$
Dejaremos como $\textcolor{orange}{\text{ejercicio como tarea moral}}$ probar $1)$ y $2)$
Para probar $3)$ partimos de tomar representantes de clase $(x_n) \in [(x_n)], \, (y_n) \in [(y_n)] \text{ y } \,(z_n) \in [(z_n)].$ Lo siguiente es consecuencia de la desigualdad del triángulo en $d$ y la distancia entre clases definida.
\begin{align*}
&&d(x_n,y_n) &\leq d(x_n,z_n) + d(z_n,y_n)\\
&\Rightarrow & \underset{n \to \infty}{lim}d(x_n,y_n) &\leq \underset{n \to \infty}{lim}d(x_n,z_n) + \underset{n \to \infty}{lim}d(z_n,y_n)\\
&\Rightarrow& d^*([(x_n)], [(y_n)]) &\leq d^*([(x_n)], [(z_n)]) +d^*([(z_n)], [(y_n)]).
\end{align*}
Que es lo que queríamos demostrar.
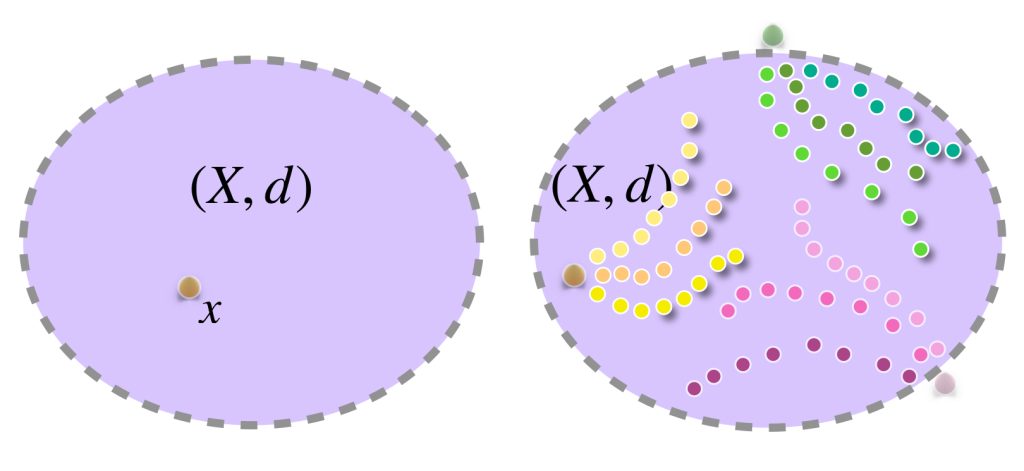
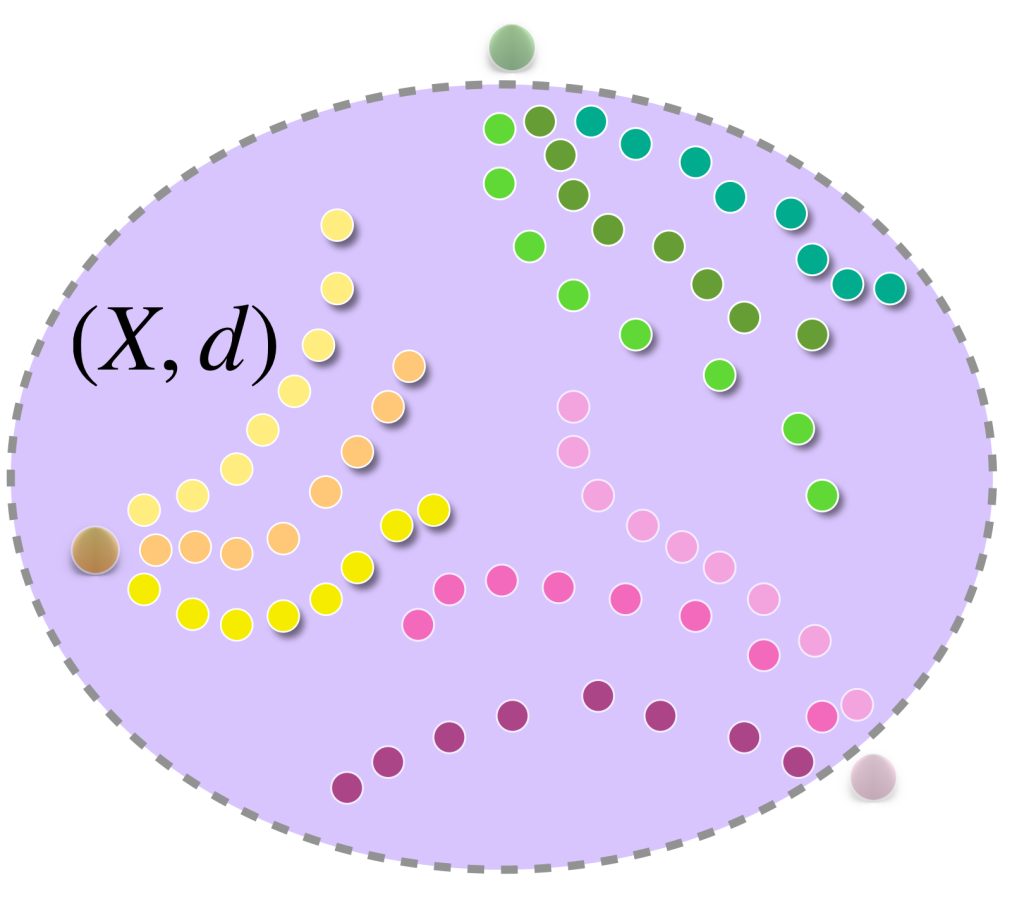
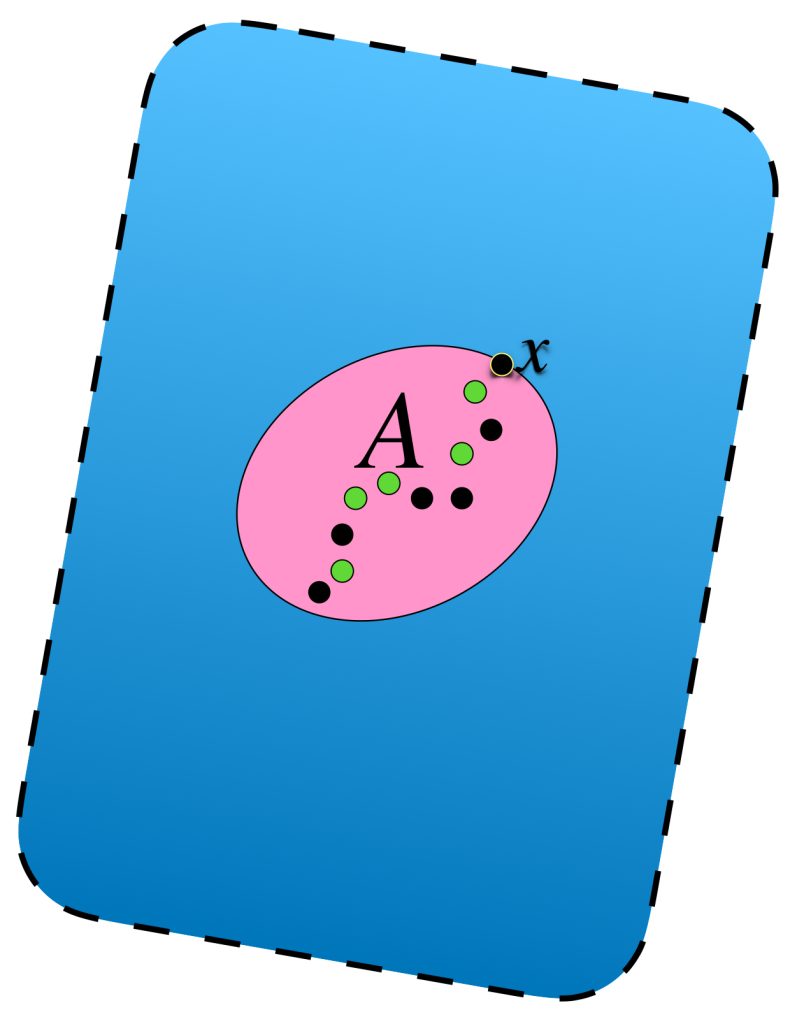
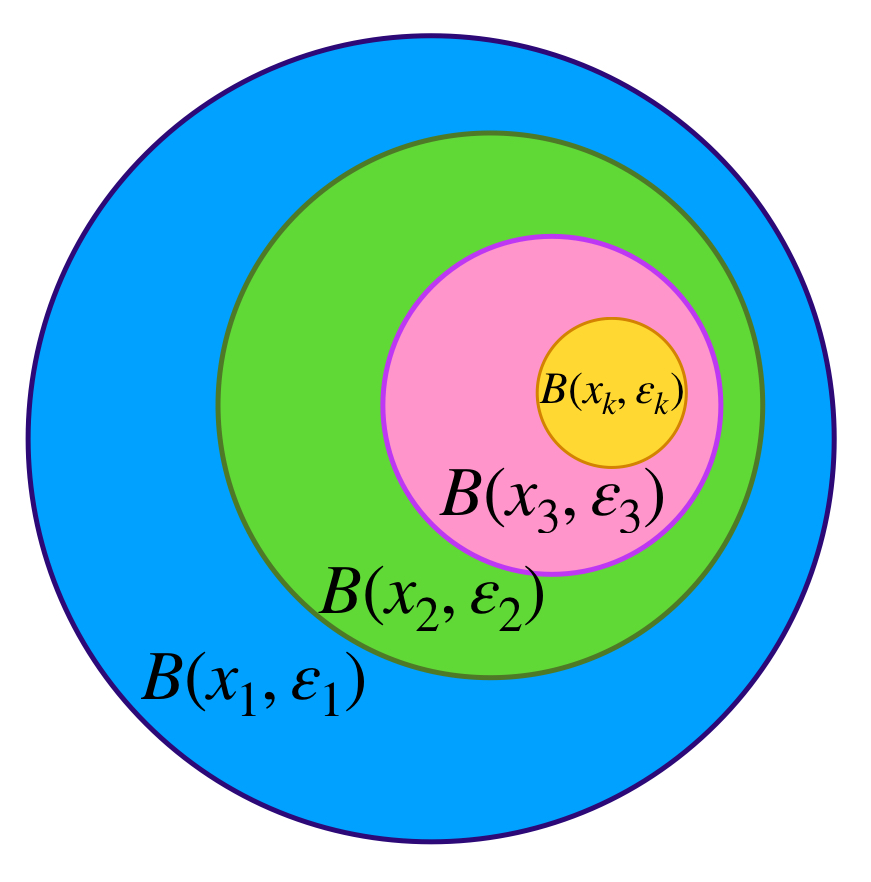
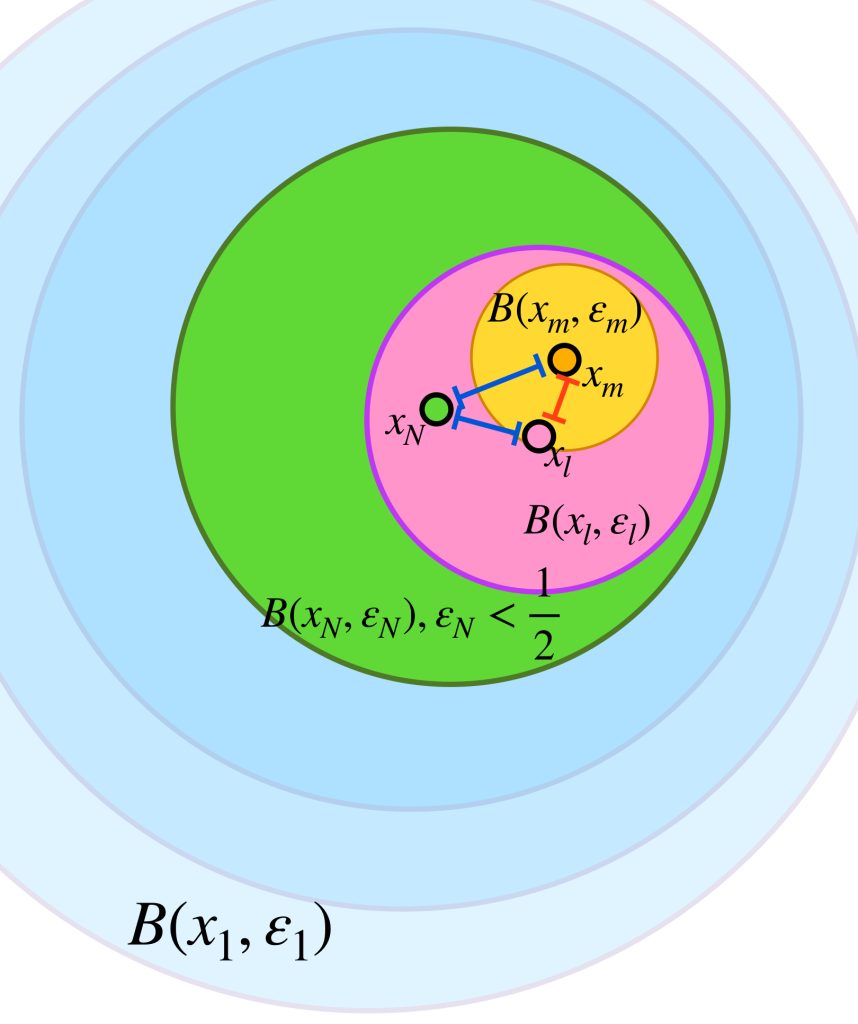
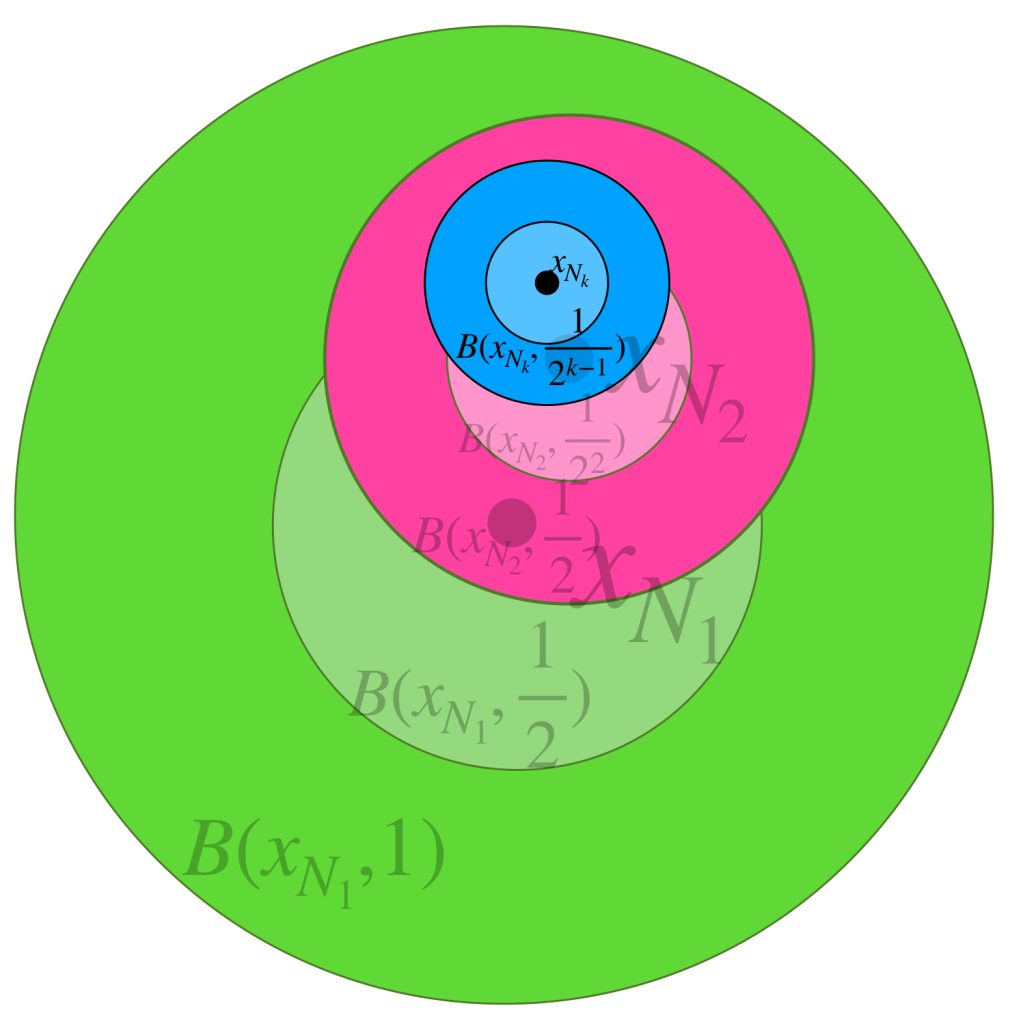
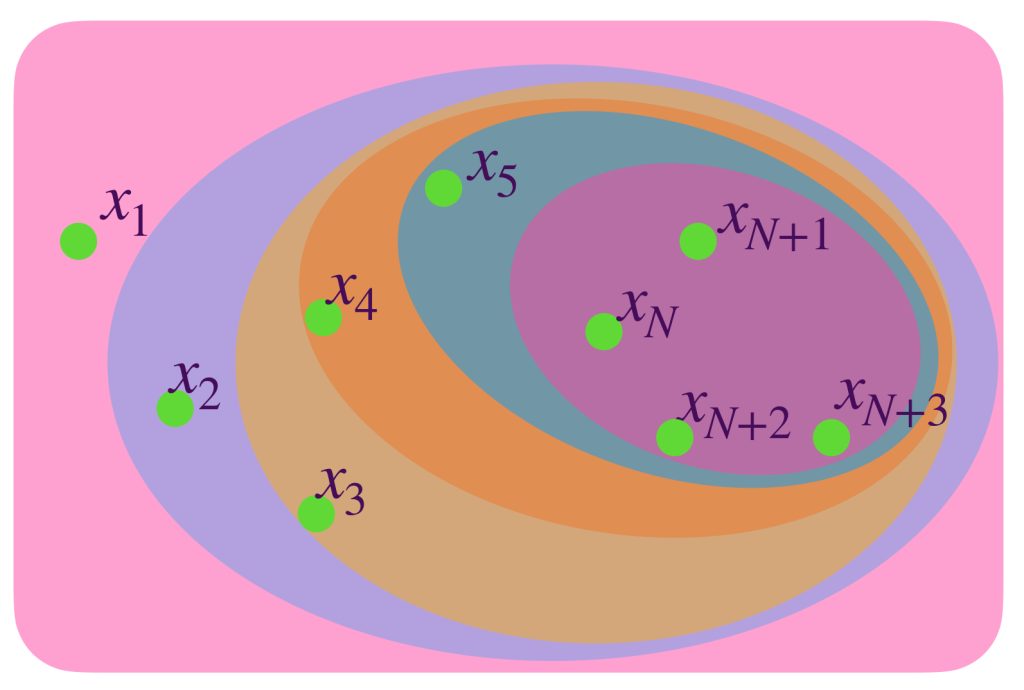
En el dibujo cada clase de equivalencia está representada por sucesiones de colores similares. Al ser de Cauchy y tener distancias entre ellas que “se reducen a cero” podemos pensar en que todas las sucesiones de una clase convergen a un punto del espacio $X$ cuando de hecho son convergentes;
o bien, si no convergen en $X$ lo harán en un punto “afuerita” de $X,$ (en la cerradura respecto al espacio completo que lo contiene). Esta misma idea nos deja imaginar la distancia entre clases como la distancia entre esos “puntos de convergencia.”
El conjunto de clases de equivalencia es una completación de $X$
Sea $X^*$ el conjunto de clases de equivalencia de sucesiones de Cauchy en $X.$ Definimos $\phi:X \to X^*$ tal que para cada punto $x \in X, \,$ $\phi(x)$ es la clase de sucesiones de Cauchy que convengen en $x.$
Sean $x,y \in X$ y dos sucesiones $(x_n), (y_n)$ en $X$ tales que:
$$\underset{n \to \infty}{lim}x_n=x \, \text{ y } \, \underset{n \to \infty}{lim}y_n =y.$$
Entonces se cumple que:
\begin{align*}
d(x,y)&=\underset{n \to \infty}{lim}d(x_n,y_n) &\textcolor{orange}{\text{(ejercicio)}}\\
&=d^*([(x_n)], [(y_n)]).
\end{align*}
Por lo tanto $\phi$ es una isometría entre $X$ y $X^*$
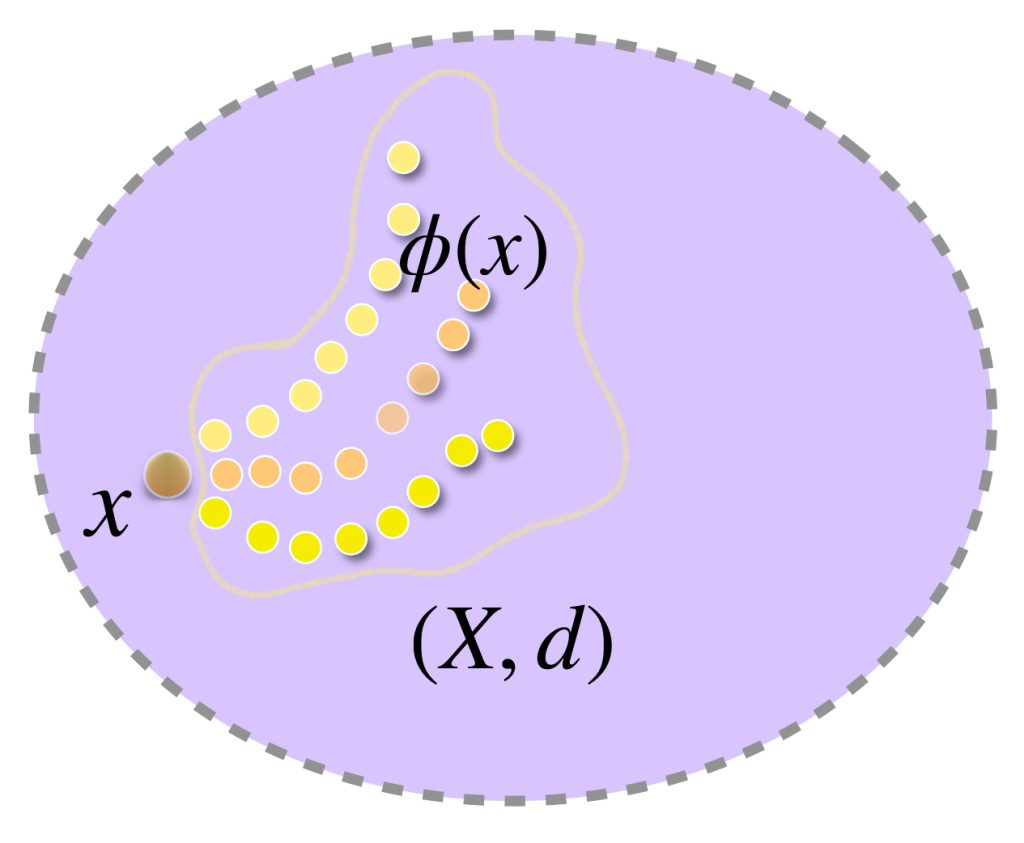
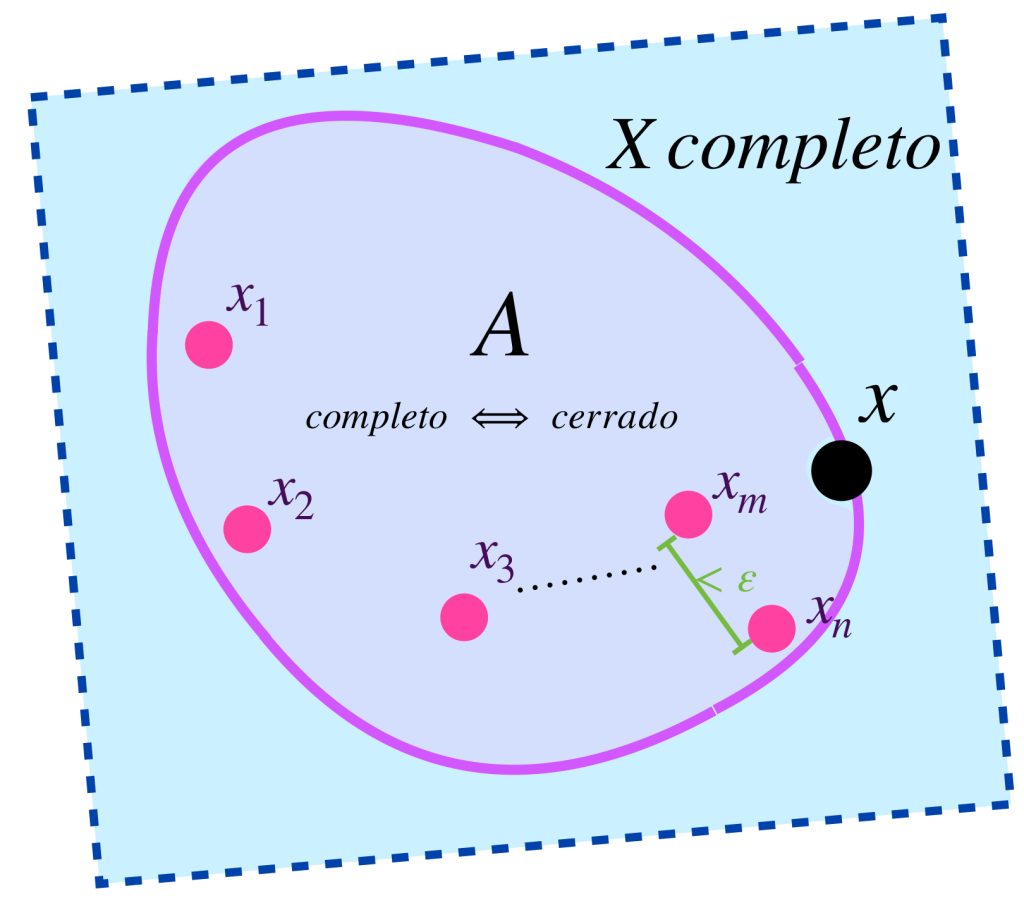
Ahora que podemos considerar a $X$ como $\phi(X),$ demostremos que $\overline{\phi(X)}=X^*.$ En consecuencia, el espacio métrico $(X^*, d^*)$ será isométrico al espacio métrico $(\overline{\phi(X)}, d^*).$
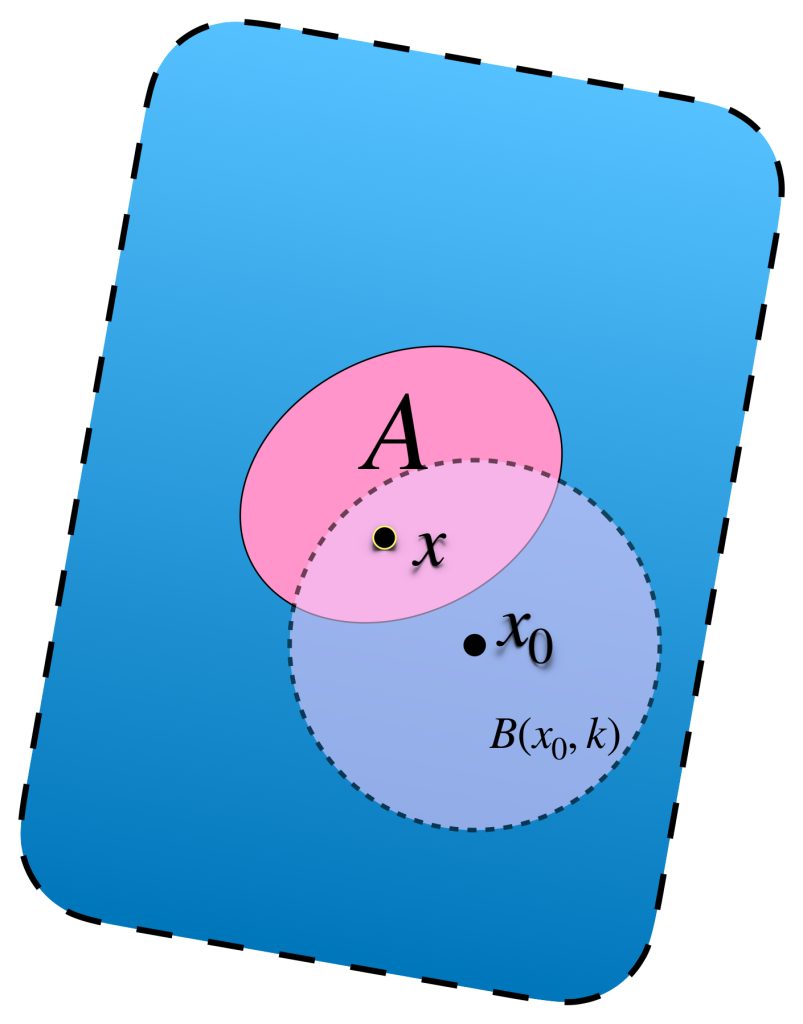
Sea $[(x_n)] \in X^*$ y sea $\varepsilon>0.$
Buscamos demostrar que existe un elemento de $\phi(X)$ en la bola de radio $\varepsilon$ con centro en $[(x_n)],$ es decir, que su distancia a $[(x_n)]$ sea menor que $\varepsilon.$
Sea $(x_n)$ un representante de clase de $[(x_n)]$. Como es de Cauchy, existe $N \in \mathbb{N}$ tal que $\forall \, n,m \geq N$ se cumple que
$$d(x_n,x_m)< \varepsilon.$$
Entonces si consideramos la sucesión constante $(x_N),$ donde todos sus términos son $x_N,$ se sigue:
$$d^*([(x_N)],[(x_n)])= \underset{k \to \infty}{lim} \, d(x_N,x_k)< \varepsilon$$
Lo cual demuestra que $[(x_N)] \in \phi(X)$ está en la bola de radio $\varepsilon$ con centro en $[(x_n)].$ Por lo tanto $\overline{\phi(X)}$ es denso en $X^*.$
$X^*$ es completo
Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $X^*.$ Si todos los términos de la sucesión están en $\phi(X)$ entonces cada una de las clases, términos de $(x_n),$ converge en puntos de $X$ formando así una sucesión de Cauchy en $X.$
Luego, por como fue construido $X^*,$ la sucesión converge a su clase de equivalencia $[(x_n)]$ en $X^*.$
En el caso general, si la sucesión en $X^*$ es de la forma $(x^*_n)_{n \in \mathbb{N}}$ donde cada $(x^*_n)$ es una clase de equivalencia que no necesariamente tiene una sucesión constante de puntos en $X$, dada la densidad de $X$ (visto como $\phi(X)),$ para cada $n \in \mathbb{N}$ es posible elegir $x_n \in X$ tal que $x_n \in B(x^*_n,\frac{1}{n}).$ Queda como $\textcolor{orange}{\text{ ejercicio }}$ argumentar que la sucesión $(x_n)$ es de Cauchy y por tanto, vista como sucesión de clases, converge a algún $x^* \in X^*$. $\textcolor{orange}{\text{ Argumenta también }}$ por qué podemos concluir que $(x^*_n)$ también converge a $x^*.$
Con esto queda demostrada la proposición.
Más adelante…
Seguiremos trabajando con la convergencia de sucesiones, pero ahora tendrán, como términos, los valores asignados en un punto por una sucesión de funciones. Hablaremos de los valores a los que una sucesión de funciones converge y veremos los términos de límite puntual y límite uniforme.
Tarea moral
- Argumenta los detalles que quedaron pendientes en la demostración de la completación de un espacio métrico.