Archivo de la etiqueta: acciones

Álgebra Moderna I: Órbita de $x$ y tipos de acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

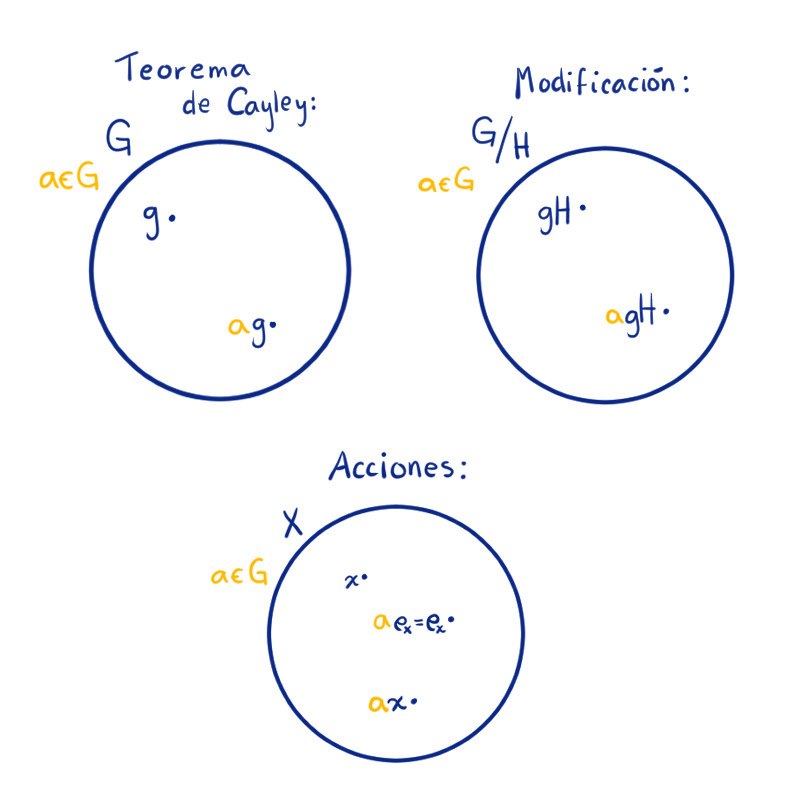
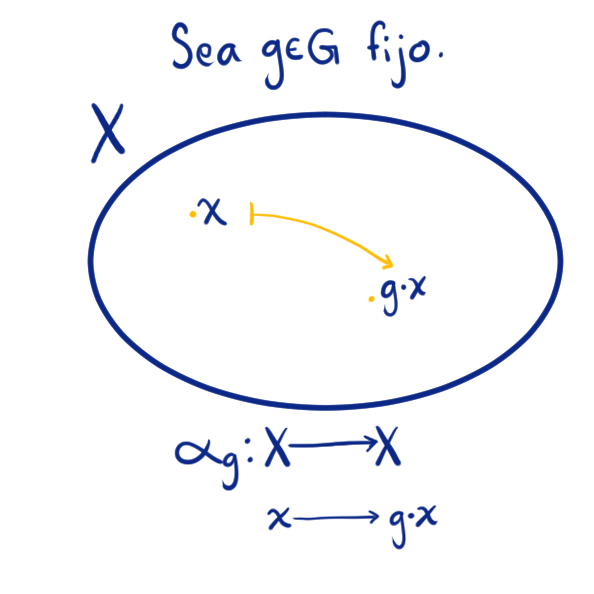
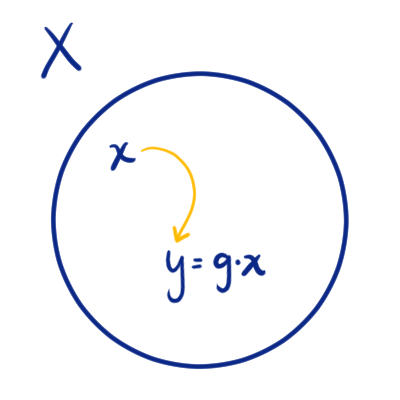
Tomemos un grupo $G$ y $X$ un $G$-conjunto. A lo largo de esta entrada consideraremos la relación de equivalencia en $X$ inducida por esta acción y que fue definida en la entrada anterior de la siguiente manera:

$x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$.

Continuemos entonces con esta idea, comenzando por definir las clases de equivalencia inducidas por esa relación.

Después, definiremos nuevos tipos de acciones, por ejemplo, ¿qué pasa si la relación sólo induce una clase de equivalencia? o ¿qué sucede con el conjunto de objetos que dejan fijo a los elementos de $G$?

Órbita de un elemento de $X$

Dada la importancia de esta manera de relacionar a los elementos de un grupo de acuerdo a una acción, daremos un nombre a sus clases de equivalencia.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Para cada $x\in X$, la órbita de $x$ es
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g \in G\},
\end{align*}

es decir, todos los objetos que podemos obtener haciendo actuar a $G$ sobre $x$.

Observación. Sean $G$ un grupo, $X$ un $G$-conjunto. Tenemos que $\mathcal{O}(x)$ es la clase de equivalencia de $x$ con respecto a la relación inducida por la acción de $G$ en $X$.

Demostración.

Sea $x\in G$. Sabemos que la clase de equivalencia de $x$, denotada por $[x]$, se define como:
\begin{align*}
[ x ] &= \{y\in X |x\sim y\} &\text{Definición de clase de equivalencia} \\
&= \{y\in X|\exists g\in G \text{ con }g\cdot x = y\} &\text{Definición de la relación }\sim\\
&= \{g\cdot x| g\in G\} = \mathcal{O}(x) &\text{Definición de órbita.}
\end{align*}

$\blacksquare$

De cursos anteriores sabemos que la colección de clases de equivalencia inducidas por una relación es una partición del conjunto. El siguiente teorema se da como consecuencia de las propiedades de una partición.

Teorema. Sean $G$ un grupo, $X$ un $G$-conjunto. Entonces

  1. $\mathcal{O}(x) \neq \emptyset $ para toda $x\in X$.
  2. Sean $x,y\in X$. Si $\mathcal{O}(x)\cap \mathcal{O}(y)\neq \emptyset$, entonces $\mathcal{O}(x) = \mathcal{O}(y)$.
  3. $\displaystyle X = \bigcup_{x\in X}\mathcal{O}(x)$.

Este teorema sólo enlista las propiedades de una partición en el caso particular en el que estamos trabajando, por lo que no hay nada nuevo que demostrar.

Una acción transitiva

Las órbitas están determinadas por varios factores: el conjunto $X$, el grupo $G$ y la acción de $G$ en $X$. En algunos casos existe una única órbita.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Si $\mathcal{O}(x) = X$ para alguna $x\in X$, decimos que la acción es transitiva.

Esta definición nos dice que podemos obtener cualesquier elemento de $X$ haciendo actuar algún elemento del grupo en el objeto $x$.

Ejemplos de acciones transitivas

Ejemplo 1. Dado $G$ un grupo, $X=G$ definimos la acción de $G$ en sí mismo mediante la operación de $G$, es decir $a\cdot x = a x$ para todas $a\in G$, $x\in X.$

Consideremos cualquier $x\in X$. Sea $y\in X$. Siempre tenemos una manera de obtener $y$ a través de $x$:
\begin{align*}
y = y(x^{-1}x) = (yx^{-1})x = (yx^{-1})\cdot &x \in \mathcal{O}(x). \\
\text{Entonces } &y \in \mathcal{O}(x).
\end{align*}

Por lo tanto $\mathcal{O}(x) = X$ y así la acción es transitiva.

Ejemplo 2. Sean $G$ un grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH) = agH$ para todas $a,g\in G.$

Consideremos cualquier $gH \in X.$ Sea $tH \in X$ con $t\in G.$ Podemos reescribir al representante como:
\begin{align*}
t H &= t(g^{-1}g) H = (tg^{-1})gH \\
&= (tg^{-1})\cdot gH \in \mathcal{O}(gH).
\end{align*}

Por lo tanto $\mathcal{O}(gH) = X$. Así, la acción es transitiva.

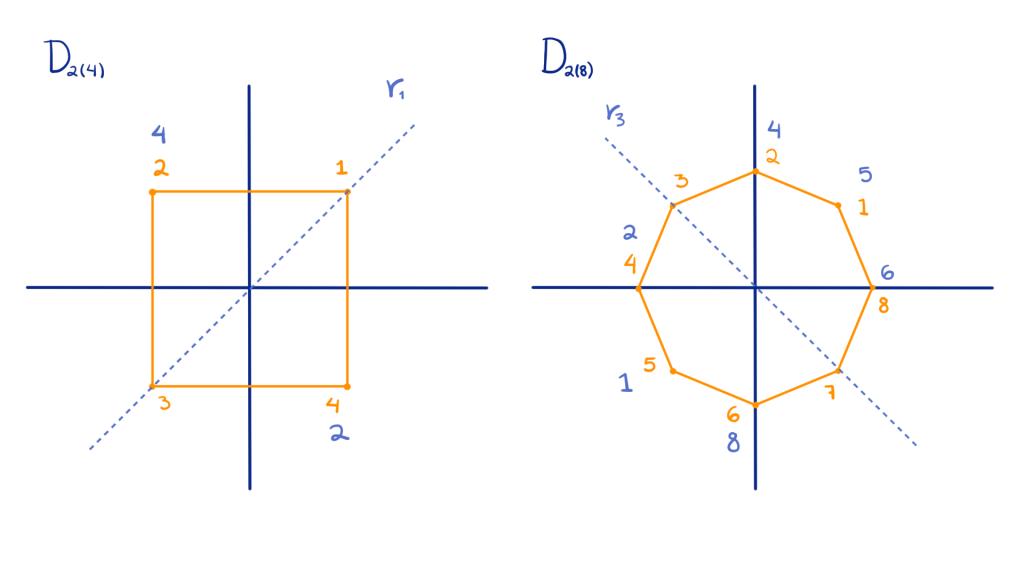
Ejemplo 3. Sea $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

La acción que ya habíamos trabajado: dados $g\in G$, $i\in X$ definimos $g\cdot i = g(i)$.

Dada $a\in G$ la rotación $\displaystyle\frac{2\pi}{n}$ y $1\in X$, tenemos que
\begin{align*}
\text{id}\cdot 1 &= 1, \\
a\cdot 1 = a(1) &= 2,\\
a^2 \cdot 1 = a^2(1) &= 3, \\
&\vdots \\
a^{n-1} \cdot 1 = a^{n-1} (1) &= n.
\end{align*}

Entonces $X = \{1,2,\cdots,n\}\subseteq \mathcal{O}(1) \subseteq X$. Así, $\mathcal{O}(1) = X$. Por lo tanto la acción es transitiva.

Ejemplo 4. Ahora veamos un ejemplo nuevo.

Sea $G$ un grupo, $X= G$. Dados $a\in G$, $x\in X$ definimos
\begin{align*}
a\cdot x &= a x a^{-1}.
\end{align*}

Demostremos que es una acción:
\begin{align*}
e\cdot x &= exe^{-1} = x &\forall x\in X.\\
a\cdot(b\cdot x) &= a(b\cdot x)a^{-1} = a(bxb^{-1})a^{-1} = (ab)x(ab)^{-1}& \text{Asociando diferente}\\
&= (ab)\cdot x &\forall a,b\in G, \forall x\in X.
\end{align*}

Así, $G$ actúa en sí mismo por conjugación.

Dado $x\in X$,
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g\in G\} = \{gxg^{-1}| g\in G\}
\end{align*}
que son todos los conjugados de $x$.

En este caso, la acción no siempre es transitiva: Si $ G\neq \{e\}$ consideremos $x\in G\setminus\{e\}.$ Si $e\in \mathcal{O}(x)$ entonces $e = g\cdot x = gxg^{-1}$ para algún $g\in G$ y entonces $e = x$, esto es una contradicción porque $x\in G\setminus\{e\}$. Así, $\mathcal{O}(x)\neq X$ y la acción no es transitiva.

Más definiciones de acciones

En toda acción el neutro del grupo actúa de forma trivial en todos los elementos del conjunto pero puede ser que existan otros elementos del grupo con esa propiedad. Si no es el caso decimos que la acción es fiel:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto. Decimos que la acción es fiel si $g\cdot x = x$, con $g\in G$, para todo $x\in X$, implica que $g=e.$

Consideremos ahora los elementos del grupo que fijan a algún elemento específico del conjunto:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. El estabilizador de $x$ es
\begin{align*}
G_x = \{g\in G | g\cdot x = x\}.
\end{align*}

Es decir, la colección de todos los elementos de $G$ que dejan fijo a $x$.

Ejemplos de acción fiel y estabilizador

Ejemplo 1. Sea $G$ un grupo, $X = G$ y $g\cdot x = gx$ para todo $g,x \in G.$

Si $g\in G$ es tal que $g\cdot x = x$ para toda $x\in X$, entonces $gx = x$ para toda $x\in X$, en particular $g = ge = e.$

Así $g=e$ y la acción es fiel.

Dado $x\in X$,
\begin{align*}
G_x = \{g\in G | g\cdot x = x\} = \{g\in X| gx = x\}.
\end{align*}

Pero si $gx = x$,por cancelación $g=e$. Así $G_x = \{e\}$ para toda $x\in X,$ de modo que los estabilizadores son triviales.

Ejemplo 2. Sean $G$ grupo, $H$ subgrupo de $G$, $X = \{xH | x\in G\}$ con $g\cdot(xH) = gx H$ para toda $g,x\in G.$

Si $g\in G$ es tal que $g\cdot (xH) = xH$ para toda $x\in G$, entonces
\begin{align*}
gxH &= xH &\forall x\in G\\
\Rightarrow \, x^{-1} g x &\in H & \forall x\in G\\
\Rightarrow \, g&\in xHx^{-1} & \forall x\in G.
\end{align*}

Si $H\unlhd G$ esto se cumple para toda $g\in H$. Por lo tanto la acción no necesariamente es fiel.

Ahora, dada una clase lateral $xH \in X$.
\begin{align*}
G_{xH} &= \{g\in G | g\cdot (xH) = xH\}\\
&= \{g\in G| gxH = xH\}\\
&= \{g\in G | x^{-1}gx\in H\} \\
&= \{g\in G | g\in xHx^{-1}\}\\
&= xHx^{-1}.
\end{align*}

Así $G_{xH} = xHx^{-1}$ para toda $x\in G.$

Ejemplo 3. Sean $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

Dados $g\in G, i \in X$ definimos $g\cdot i = g(i)$.

Si $g\in G$ es tal que $g\cdot i = i$ para toda $i \in X$, entonces $g(i) = i$ para toda $i\in X$. Así, $g$ sería una transformación lineal en el plano, que fija a los vértices $1$ y $2,$ los cuales forman una base del plano. Por lo tanto $g = \text{id}$ y la acción es fiel.

Dado $i\in X$,
\begin{align*}
G_i &= \{g \in G | g\cdot i = i\}\\
&= \{g\in G | g(i) = i\}\\
&= \{\text{id},r_i\}
\end{align*}
con $r_i$ la reflexión con respecto a la recta que pasa por $(0,0)$ y $i.$

Por último, veremos una observación.

Ilustración de lo que sucede con $r_i$ de $D_{2(n)}.$ Usamos $D_{2(4)}$ representado con un cuadrado y $D_{2(8)}$ representado con un octágono. En el dibujo, $r_1$ mantiene fijo a 1 y 3, y $r_3$ mantiene fijo a 3 y 7.

Observación. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. $G_x$ es un subgrupo de $G$.

Demostración.
Sean $G$ grupo, $X$ un $G$-conjunto, $x\in X.$

El neutro de $G$ siempre está en el estabilizador porque:
\begin{align*}
e\cdot x = x \quad \forall x\in X,
\end{align*}

entonces $e\in G_x.$

Si $a,b\in G_x$, entonces $(ab)\cdot x = a\cdot (b\cdot x) = a\cdot x = x = x$. Así, $ab\in G_x$. Es decir, el estabilizador es cerrado bajo producto.

Finalmente si $a\in G_x$, $a\cdot x = x$, entonces $a^{-1}\cdot x = a^{-1}\cdot (a\cdot x) = (a^{-1}a)\cdot x = e\cdot x = x$, así $a^{-1} \in G_x$.

Por lo tanto $G_x \leq G$.

$\blacksquare$

Tarea moral

  1. En cada uno de los incisos del ejercicio 1 de la entrada de acciones, en donde haya una acción, describe cómo son las órbitas y determina si se trata de una acción transitiva.
  2. Considera el conjunto $X = \{1,2,3,4,5,6,7,8\}$ y el grupo $G = \left< a \right>$ con $a\in S_8$. Define $a^{i}\cdot j = a^{i}(j)$ para cada $a^{i} \in G$ y cada $j\in X$.
    • Verifica que es una acción de $G$ en $X$.
    • Si $a = (2 \; 4 \; 1 \; 7 \; 8)$ describe las órbitas y determina si se trata de una acción transitiva.
    • Si $a = (6 \; 1 \; 5 \; 8)(3 \; 4)$ describe órbitas y determina si se trata de una acción transitiva.
  3. Sea $G$ un grupo y $X$ un $G$-conjunto. Si la acción de transitiva prueba o da un contraejemplo para las siguientes afirmaciones:
    • $\mathcal{O}(x) = X$ para todo $x\in X$.
    • Para cada $x,y \in X$ existe $g\in G$ tal que $g\cdot x = y$.
  4. Considera el grupo diédrico $D_{2(n)}$ actuando sobre sí mismo con conjugación.
    • Determina si la acción es fiel.
    • Encuentra el estabilizador de $a$, con $a$ la rotación de $\displaystyle\frac{2\pi}{n}$, y el de $b$ con $b$ la reflexión con respecto al eje $x$.
  5. Sea $G$ un grupo y $X$ un $G$-conjunto.
    • Determina si el hecho de que exista $x\in G$ tal que $G_x = \{e\}$ implica que la acción es fiel.
    • Determina si el hecho de que la acción sea fiel implica que exista $x\in G$ tal que $G_x=\{e\}$.

Más adelante…

Continuaremos estudiando las propiedades de las órbitas, en particular, el orden de las órbitas, ¿cómo se relaciona éste con el orden del grupo $G$? Daremos respuesta a ello en la siguiente entrada.

Entradas relacionadas

Álgebra Moderna I: Acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Antes de comenzar con el tema que nos compete, repasemos lo que hemos visto del Teorema de Cayley y su modificación de la entrada anterior. Primero, en el Teorema de Cayley, comenzamos tomando un grupo $G$, un $a$ en el grupo y actuamos con ese $a$ sobre el grupo, es decir multiplicamos los elementos. En resumen, nos permite mover los elementos del mismo grupo.

Con la modificación avanzamos en la abstracción. En el teorema nos tomamos el conjunto de clases laterales y ahora, $G$ actúa sobre las clases laterales. Detente un minuto para pensar, si cada vez somos más generales ¿cuál es el siguiente paso? ¿sobre quién queremos que actúe $G$ ahora?

La respuesta es: sobre un conjunto cualquiera $X$. Ahora queremos pensar que usamos los elementos de $G$ para mover elementos de $X$. Para eso necesitamos una especie de producto, además de algunos matices. Por ejemplo, para un $x\in X$ cuando $a = e$, el elemento $a\cdot x = x$ se quede fijo y que si se multiplica por $a$ y luego por $b$, que sea lo mismo que multiplicar por $ab$, es decir $a\cdot(b\cdot x) = ab\cdot x$. Si se cumplen estas dos condiciones diremos que $a$ es una acción de $G$ en el conjunto $X$.

Diagrama de qué es una acción.

Luces, cámara, ¡acción!

Como verás, hemos estado usando el verbo actuar para referirnos a esta transformación que sucede al operar un $a\in G$ y otro elemento, sea del mismo $G$ o de las clases laterales. Aunque no hayamos definido formalmente qué es una acción, la realidad es que ya usar actuar da una idea de lo que estamos queriendo decir. Estamos usando un elemento de un grupo para transformar un elemento de otro. A continuación definiremos formalmente a una acción.

Definición. Sea $G$ un grupo, $X$ un conjunto. Si existe una función:
\begin{align*}
G \times X &\to X\\
(a,x) &\mapsto a\cdot x
\end{align*}
para todos $a\in G, x\in X$, tal que:

  1. $e \cdot x = x$ para toda $x\in X$.
  2. $a \cdot (b\cdot x) = (ab)\cdot x $ para todas $a,b\in G, x\in X$,

decimos que la función es una acción de $G$ en $X$, y que $G$ actúa en $X$ o que $X$ es un $G$-conjunto.

Ejemplos.

Veamos algunos ejemplos nuevos y retomemos algunos otros, para verificar que esto es una generalización para lo que se hizo en el Teorema de Cayley y en su modificación.

Ejemplo 1. Sean $G$ grupo, $X=G$ definimos $a\cdot x = ax$ para todas $a\in G, x\in X$. Es decir, definimos una acción sobre sí mismo. Probemos las dos condiciones:

\begin{align*}
&e\cdot x = ex = x &\forall x\in X\\
&a\cdot(b\cdot x) = a\cdot(bx) = a(bx) = (ab)x = (ab)\cdot x &\forall a,b\in G,\; x\in X.
\end{align*}

Así, todo grupo $G$ actúa en sí mismo mediante su operación binaria. Como vimos en la entrada del Teorema de Cayley.

Ejemplo 2. Sean $G$ grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH)= agH$ para toda $a,g\in G$. Ahora, probemos las dos condiciones de una acción:

\begin{align*}
&e\cdot(gH) = egH = gH &\forall g\in G
\end{align*}
\begin{align*}
a\cdot(b\cdot(gH)) &= a\cdot(bgH) = a(bg)H = (ab)gH \\
&= ab\cdot (gH) &\forall a,b,g\in G
\end{align*}

Así se tiene una acción de $G$ en las clases laterales de $H$ en $G$. Este ejemplo lo vimos en la entrada de la modificación al Teorema de Cayley.

Por último, podemos ver un ejemplo nuevo.

Ejemplo 3. Sea $G = D_{2n}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices de polígono regular de $n$ lados.

Dados $g\in G, i\in X$ definimos $g\cdot i = j$ si $g$ manda el vértice $i$ en el vértice $j$. Recordemos que los elementos de un grupo diédrico son las simetrías del polígono regular de $n$ lados, es decir, son transformaciones lineales del plano que mandan del polígono en sí mismo. En particular, los vértices van a dar a vértices bajo estas transformaciones.

Representación de una grupo diédrico.

Entonces, como son transformaciones del plano nuestra acción quedaría como una evaluación $g \cdot i = g(i)$. Así, para todos $i\in X, g,h\in G$,
\begin{align*}
\text{id}\cdot i &= \text{id}(i) = i \\
g\cdot (h\cdot i )& = g\cdot (h(i)) = g(h(i)) = (gh) (i) = (gh) \cdot i.
\end{align*}

Así, $D_{2n}$ actúa en el conjunto de vértices.

Recordemos que al escribir $(gh)\cdot i$, la operación que ocurre entre $g$ y $h$ es la composición. En este momento se omitió el símbolo $\circ$ para evitar confusiones con el símbolo $\cdot$ de acción.

Otra definición de Acción

Anteriormente hemos visto la noción de que los elementos de un grupo dan lugar a permutaciones. Usaremos esta idea para dar una definición de acción equivalente a la definición que acabamos de dar.

Teorema. Sean $G$ un grupo, $X$ un conjunto. Toda acción de $G$ en $X$ induce un homomorfismo de $G$ en $S_X$ y viceversa.

Demostración.

Sean $G$ un grupo y $X$ un conjunto.
Supongamos que $G\times X \to X$ es una acción de $G$ en $X$ tal que $(g,x)\mapsto g\cdot gx$. Para cada $g\in G$ definimos $\alpha_g : X\to X$ dada por $\alpha_g(x) = g\cdot x$ para toda $x\in X$.

Ilustración del efecto de $\alpha_g$.

Analicemos las funciones $\alpha_g$, veamos que son biyectivas:

\begin{align*}
\alpha_g\circ\alpha_{g^{-1}}(x) & = \alpha_g(\alpha_{g^{-1}}) = \alpha_g(g^{-1}\cdot x) = g\cdot(g^{-1}\cdot x)\\
&= (gg^{-1})\cdot x &\text{Condición 2 de acción}\\
&= e\cdot x = x &\text{Condición 1 de acción}.
\end{align*}

Entonces $\alpha_g\circ\alpha_{g^{-1}} = \text{id}_X$.

Anáogamente $\alpha_{g^{-1}}\circ \alpha_g = \text{id}_X$, entonces $\alpha_g$ es biyectiva, es decir $\alpha_g \in S_X$.

Definimos $\psi: G \to S_X$ con $\psi (g) = \alpha_g$ para toda $g\in G$.

Veamos que $\psi$ es un homomorfismo. Tomemos $g,h\in G$,
\begin{align*}
\psi(gh)(x) &= \alpha_{gh}(x) = (gh)\cdot x = g\cdot(h\cdot x) = \alpha_g(\alpha_h(x)) & \text{Condición 2}\\
&= \alpha_g \circ \alpha_g(h) = \psi(g) \psi(h)(x) &\forall x\in X.
\end{align*}

Entonces $\psi(gh) = \psi(g)\psi(h)$ para todos $g,h\in G$.

Por lo tanto $\psi$ es un homomorfismo.

Ahora de regreso. Supongamos ahora que se tiene un homomorfismo $\psi: G\to S_X$. Entonces, para cada $g\in G, \psi(g) \in S_x$.

Definimos la función $G\times X \to X$ donde $(g,x)\mapsto g\cdot x$. Entonces $g\cdot x = \psi(g)(x)$ para toda $g\in G, x\in X$. Además, $\psi(g)(x) \in X$.

Ahora veamos que esta función es una acción. La primera condición para ser acción se cumple de la siguiente manera:

Como $\psi$ es un homomorfismo, $\psi(e) = \text{id}_X$. Así,
\begin{align*}
e\cdot x& = \psi(e)(x) = \text{id}_X(x) = x &\forall x\in X
\end{align*}

Probemos la segunda condición de acción:

\begin{align*}
g\cdot (h\cdot x) &= \psi(g) (\psi(h)(x)) = \psi(g)\circ \psi(h)(x) \\
&= \psi(gh)(x) = (gh) \cdot x & \psi\text{ es un homomorfismo}.
\end{align*}
Para todas $g,h\in G, x\in X$. Así $G$ actúa en $X$.

$\blacksquare$

Una relación de equivalencia

Si tenemos un grupo $G$ actuando sobre un conjunto $X$, entonces podemos considerar $g\in G$ y $x,y\in X$. Con los dos elementos $x,y$ de $X$, podemos preguntarnos ¿es posible llegar de $x$ a $y$ usando a $g$?, algo como $y = g\cdot x$. En realidad esto no es siempre posible, entonces podemos crear una relación de $x$ con $y$ si existe tal $g\in G$. Esto lo veremos en el siguiente resultado.

¿Es posible llegar de $x$ a $y$ usando a $g$?

Lema. Sean $G$ un grupo, $X$ un $G$-conjunto. Para todo $x,y\in X$, la relación en $X$: $x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$ es una relación de equivalencia.

Demostración.
Sean $G$ un grupo, $X$ un $G$-conjunto. Definimos la relación en $X$ donde para todo $x,y\in X$.
\begin{align*}
x\sim y \Leftrightarrow g\cdot x = y \text{ para algún }g\in G.
\end{align*}

Primero, por la condición 1 de acción, $e\cdot x = x$ para toda $x\in X$ con $e\in G$, entonces $x\sim x$ para toda $x\in X$. Por lo que nuestra relación es reflexiva.

Si $x,y\in X$ son tales que $x\sim y$, entonces existe $g\in G$ tal que $g\cdot x = y$. Así,
\begin{align*}
g^{-1} \cdot y &= g^{-1}\cdot (g\cdot x) \\
&= (g^{-1}g)\cdot x & \text{por condición } 2\\
&= (e\cdot x )\\
&= x & \text{por condición } 1
\end{align*}

con $g^{-1} \in G$, entonces $y\sim x$. Por lo que tenemos una relación simétrica.

Si $x,y,z\in X$ son tales que $x\sim y$ y $y\sim z$, entonces existen $g,h\in G$ tales que $g\cdot x = y$, $h\cdot y = z$. Así
\begin{align*}
(hg)\cdot x &= h\cdot (g\cdot x) &\text{condición } 2\\
&= h \cdot y = z
\end{align*}
con $hg\in G$. Entonces $x\sim z$. Así, nuestra relación es transitiva.

Por lo tanto $\sim$ es una relación de equivalencia.

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. En los siguientes incisos determina si la función dad es una acción de $G$ en $X$:
    • Considera un campo $K$ y $V$ un $K$-espacio vectorial. Sea $G= K^*$ con el producto y $X= V$. Definimos $\lambda\cdot v = \lambda v$ para cada $\lambda\in K^*$ y $v\in V$. (Nota que $K^*$ es el campo sin el neutro aditivo).
    • Sea $G$ un grupo y $X=G$. Definimos $g\cdot x = g^{-1}xg$ para cada $g\in G$ y cada $x\in X$.
    • Sea $G$ un grupo y $X = \{H|H\leq G\}$. Definimos $g\cdot H = gHg^{-1}$ para cada $g\in G$ y cada $H\in X$.
    • Sea $G$ un grupo y $X=N$ un subgrupo normal de $G$. Definimos $g\cdot n= gng^{-1}$ para cada $g\in G$ y cada $n\in N$.
  2. Sea $G$ un grupo y $X$ un $G$ conjunto. Considera el homomorfismo $\psi: G\to S_X$ asociado. ¿Es necesariamente $\psi$ un monomorfismo? Si lo es, pruébalo y si no, establece qué condiciones debería cumplir la acción para que lo sea.
  3. Para repasar lo que hemos visto desde el Teorema de Cayley, puedes consultar el video en inglés de Mathemaniac.

Más adelante…

Hemos expandido la idea de que un grupo puede mover a los elementos de otro hasta llamarlo una acción. Luego, encontramos una relación de equivalencia a partir de la acción. Como es usual en este tipo de cursos, estudiaremos la partición inducida por esta relación de equivalencia y a partir de estos conjuntos, definiremos otros tipos de acciones.

Entradas relacionadas