Esta entrada está motivada por una pregunta en el grupo de Matemáticos de Facebook. Palabras más, palabras menos, alguien preguntaba por qué «derivar es el inverso de integrar», si uno tiene que ver con sacar un área y el otro tiene que ver con sacar una pendiente. La idea formal que está detrás de esto de que sean «inversas» son los teoremas fundamentales del cálculo (TFC). Pero en esta entrada no me quiero meter con definiciones de límite ni cosas por el estilo. A fin de cuentas es un blog y estamos navegando tranquilos. Así que déjenme trabajar «al ahí se va», osea, informalmente. La idea es entender por qué derivar e integrar son operaciones inversas «con dibujitos» y en un caso más sencillo: el caso discreto. Veremos los teoremas fundamentales de los cuadraditos (TFC). ¡Oh no! ¡Se confunden las siglas! Bueno, ni modo.

Los cuadraditos

Todo empieza con algunos cuadraditos ordenados en columnas. De izquierda a derecha, tenemos 1, 2, 5, 3, 2, 4 y 2 cuadraditos en cada columna. Le voy a llamar $C_j$ a la cantidad de cuadraditos en la columna $j$. Por ejemplo, $C_3=5$.

El área de cuadraditos y la diferencia de cuadraditos

Ahora imagina que queremos ver todos los cuadraditos que quedan acumulados hasta la columna $j$. Es decir, queremos el área hasta la columna $j$ y por eso le llamaremos $A_j$ a la cantidad de cuadritos en las primeras $j$ columnas. Por ejemplo, el área naranja tiene los cuadraditos hasta la columna 5 y por tanto $A_5=1+2+5+3+2=13$. Otra idea que también va a ser importante es la diferencia de cuadraditos, es decir, cuántos necesitamos para pasar de una columna a otra.  A la cantidad de cuadraditos para pasar de la columna $j$ a la $j+1$ le llamamos $D_j$. Observa que justo $D_j=C_{j+1}-C_j$. Por ejemplo, en la siguiente figura, $D_5=4-2=2$, osea hay que agregar dos cuadraditos. Por otro lado, $D_4=2-3=-1$, osea de la columna 4 a la 5 quitamos un cuadradito.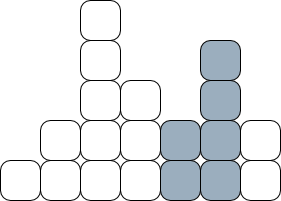

El primer TFC

Observa el siguiente dibujo: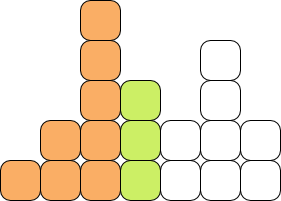 Si consideramos el área hasta donde está en naranja, tenemos $A_3$. Si consideramos hasta la columna verde, tenemos $A_4$. Justo para pasar de un área a otra, tenemos que agregar $C_4$. Esto es un hecho más general, que enuncio a continuación.

Primer teorema fundamental de los cuadraditos:

«La diferencia entre $A_j$ y $A_{j+1}$ justo es $C_{j+1}$, en símbolos: $A_{j+1}-A_j=C_{j+1}$»

El segundo TFC

Nuestros numeritos $D_j$ están buenos para saber cómo cambia la cantidad de cuadraditos de una columna a la siguiente. Pero a lo mejor queremos saber cuánto cambiamos desde el principio hasta el final como en la figura. O de la columna $m$ a la columna $n$. ¡Aprovechemos que sabemos cómo cambiar de uno en uno! Lo que cambiamos en total de principio a fin es la suma de todos los cambios de uno en uno. Es decir, podemos escribir: $C_7-C_1=(C_7-C_6)+(C_6-C_5)+\ldots+(C_2-C_1)=D_6+D_5+\ldots+D_1$ Esta idea nos lleva al siguiente teorema

Segundo teorema fundamental de los cuadraditos:

«Para encontrar la diferencia de cuadritos de la columna $m$ a la $n$, basta sumar las diferencias $D_m, D_{m+1},\ldots, D_{n-1}$, en símbolos: $\sum_{j=m}^{n-1} D_j = C_n-C_m$.»

Y le metemos infinitos y…

Bueno, pues ahí están los TFC. En realidad si uno lo piensa, son ideas sencillas. Pero pensemos un poco qué sucede cuando metemos infinitos. La suma y diferencia de cuadraditos son los equivalentes discretos a la integral y la derivada. O dicho al revés, la integral y la derivada es lo que sucede cuando metemos una infinidad de columnas. Recordemos que si tenemos una función $f$, entonces usamos los símbolos $F$ y $f’$ para hablar de la integral y la derivada. Saltándonos hipótesis y otras cosas latosas, comparemos los TFCuadraditos con los TFCálculo. Las primeras versiones de ambos son $A_{j+1}-A_j=C_{j+1}$ y $F'(x)=f(x)$. En ambos casos nos está diciendo «si vemos la diferencia inmediata de sumar cosas, entonces obtenemos el último sumando». Las segundas versiones de ambos son $\sum_{j=m}^{n-1} D_j = C_n-C_m$ y $\int_a^b f'(x)\, dx = f(b)-f(a)$. Ambos nos dicen «al sumar las pequeñas diferencias inmediatas, obtenemos la diferencia total». ¡Los teoremas fundamentales del cálculo son los teoremas fundamentales de cuadraditos! Bueno, pero son más fufufu y hay que tenerles más respeto por que requieren la noción de límite y más madurez matemática.

Extra

Voy a dejarle hasta aquí, pero este cambio de lenguaje entre sucesiones y funciones va más allá de los teoremas fundamentales del cálculo. También se pueden hacer analogías similares entre las ecuaciones en diferencias y las ecuaciones diferenciales. O entre la integración por partes y las sumas de Abel. O intentar dar una definición de continuidad para sucesiones de enteros (por ejemplo $|a_{n+1}-a_n|\leq 1$) y encontrarle su teorema del valor intermedio. Bueno, ya que me puse a hacer dibujitos para esta entrada, también hice otro, que es algo así como una teselación hexagonal. Más o menos. Se las dejo: ¿Qué otras analogías entre funciones discretas y contínuas conoces?

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

• Una demostración del teorema de la función inversa
• Un ejemplo de aplicación del teorema de la función inversa
• Un problema de probabilidad y escuchar música
• Mariposa de siete equivalencias de invertibilidad de matrices