$\textit{MATERIAL EN REVISIÓN}$
Introducción
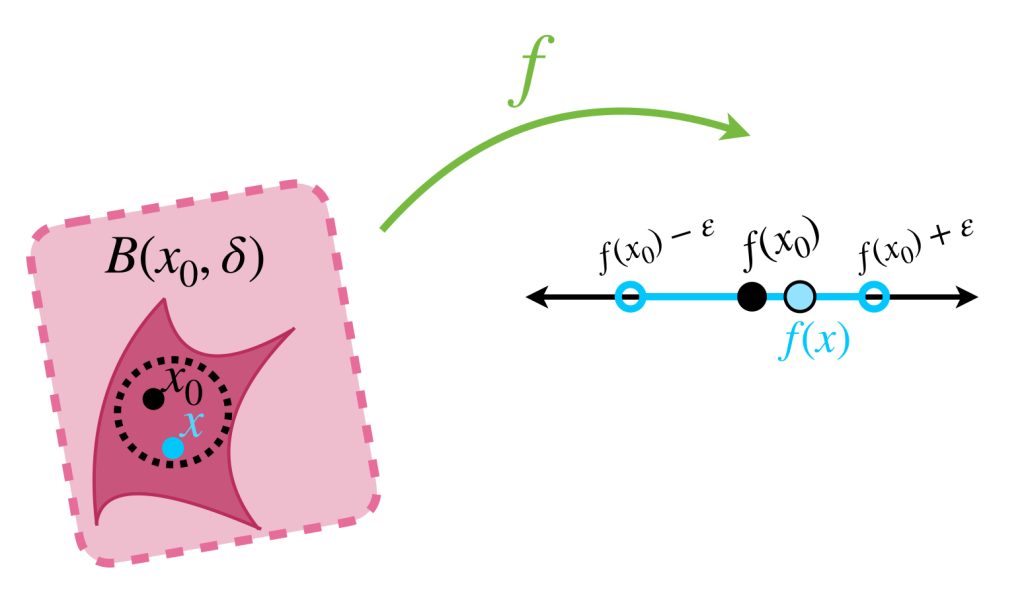
En la entrada Funciones continuas en espacios métricos vimos que una función $f: X \to \mathbb{R}\, $ con $X$ espacio métrico, es continua en un punto $x_0 \in X$ si dado $\varepsilon >0$ existe $\delta >0$ tal que si $x$ está en la bola abierta $B(x_0, \delta)$ entonces $f(x) \in B(f(x_0), \varepsilon).$
Nota que esto significa que existe una bola abierta con centro $x_0$ que cumple que cualquiera de sus elementos $x$ satisface las siguientes desigualdades:
\begin{align}
f(x_0) \, – \, \varepsilon < &f(x). \\
&f(x) < f(x_0)+ \varepsilon.
\end{align}
Si bien, una función que no cumple ambas desigualdades en $x_0$ no es continua en $x_0, \,$ es posible concluir propiedades si hace valer al menos una de las dos desigualdades:
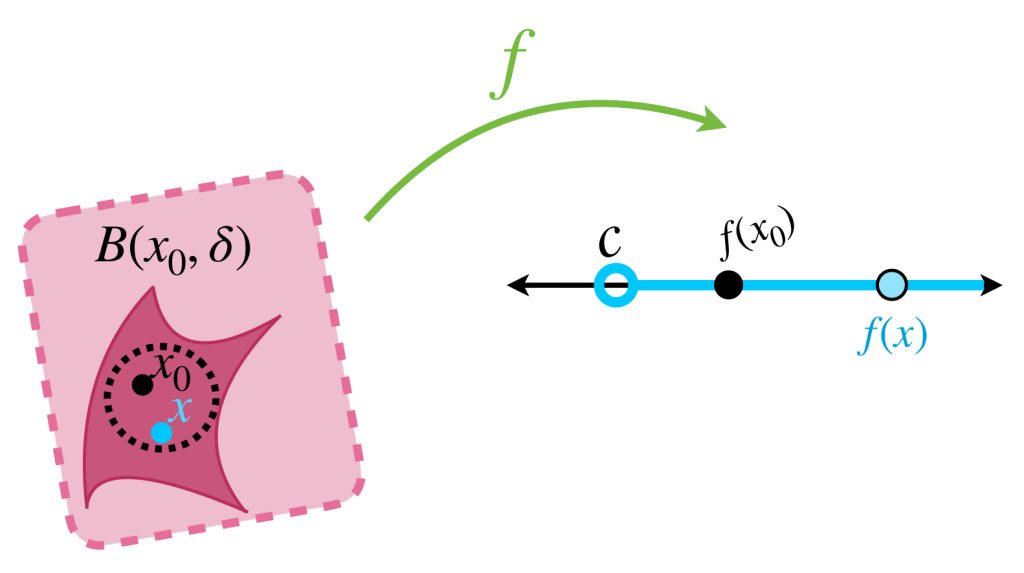
Supongamos que una función $f$ satisface en el punto $x_0, \,$ para cualquier $\varepsilon >0\,$ la desigualdad (1). Entonces
$$f(x_0) \, – \, \varepsilon < f(x).$$
Como estamos considerando $\varepsilon >0$ se sigue que $f(x_0) – \varepsilon$ es siempre un número $\, c \,$ menor que $f(x_0),$ entonces que se cumpla la desigualdad (1) significa que
$$c < f(x).$$
Esto muestra que el valor de la función $f$ en puntos muy cercanos a $x_0$ darán saltos arriba de $f(x_0)$ (cuando hay discontinuidad). Dicho formalmente, tenemos:
Definición. Función semicontinua inferiormente. Sea $f:X \to (-\infty, \infty]$ una función, (nota que admite el valor $\infty$). Decimos que $f$ es semicontinua inferiormente en el punto $x_0 \in X$ si para toda $c<f(x_0)$ existe $\delta>0$ tal que si $d_X(x,x_0)< \delta$ entonces $c<f(x).$
Diremos que $f$ es semicontinua inferiormente si lo es en todo punto de $X.$
Nota que esta definición permite valores infinitos.
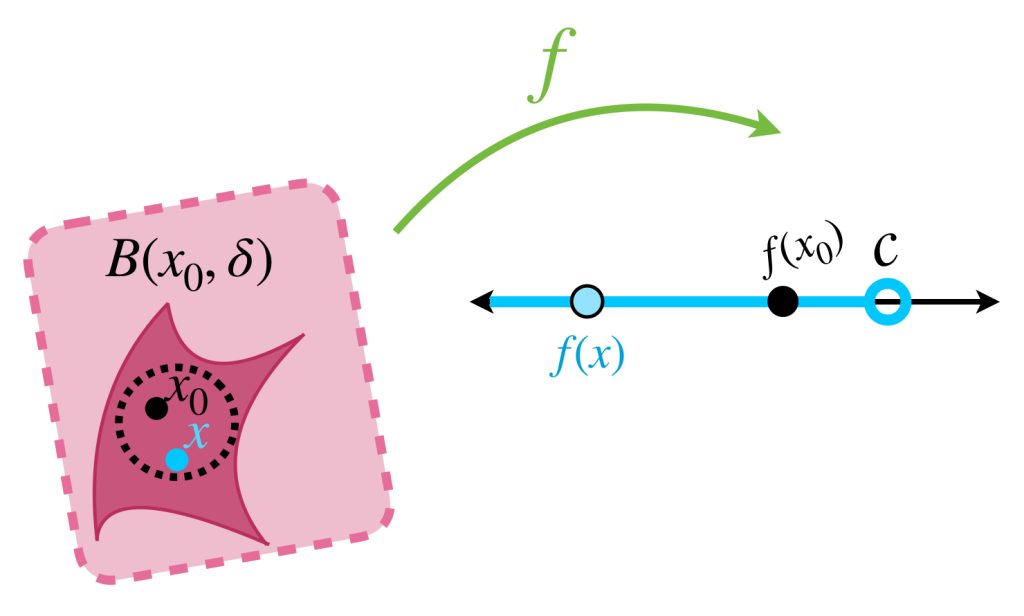
Por otro lado, si una función $f$ satisface en el punto $x_0, \,$ para cualquier $\varepsilon >0\,$ la desigualdad (2). Entonces
$$f(x)< f(x_0) \, + \, \varepsilon.$$
Como estamos considerando $\varepsilon >0$ se sigue que $f(x_0) + \varepsilon$ es siempre un número $\, c \,$ mayor que $f(x_0),$ entonces que se cumpla la desigualdad (2) significa que
$$f(x) < c.$$
Esto muestra que el valor de la función $f$ en puntos muy cercanos a $x_0$ darán saltos abajo de $f(x_0)$ (cuando hay discontinuidad). Dicho formalmente, tenemos:
Definición. Función semicontinua superiormente. Sea $f:X \to [-\infty, \infty)$ una función, (nota que admite el valor $-\infty$). Decimos que $f$ es semicontinua superiormente en el punto $x_0 \in X$ si para toda $c>f(x_0)$ existe $\delta>0$ tal que si $d_X(x,x_0)< \delta$ entonces $f(x)<c.$
Diremos que $f$ es semicontinua superiormente si lo es en todo punto de $X.$
Ejemplos:
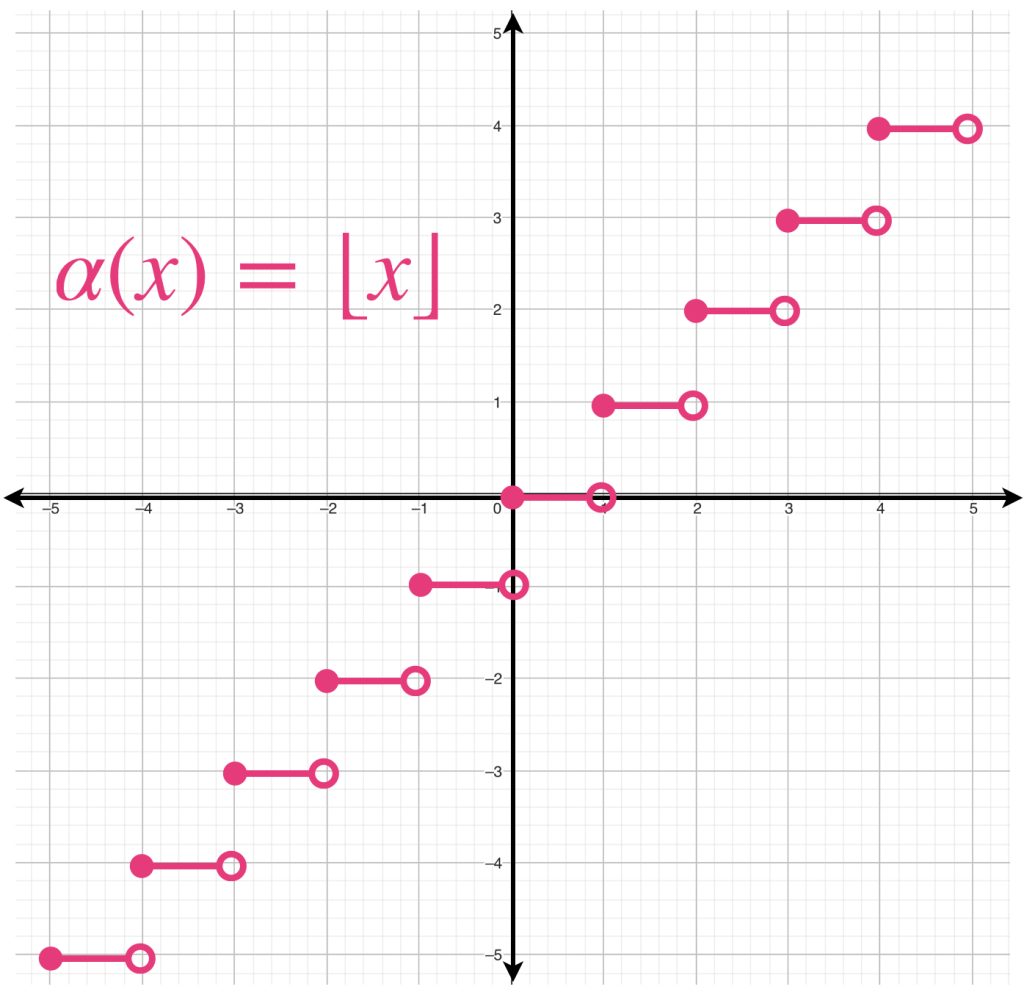
- La función piso
$f(x) = \lfloor x \rfloor: \mathbb{R} \to \mathbb{R},$ donde
\begin{align*}
\lfloor x \rfloor = {\text{máx} \,} \{k \in \mathbb{Z} : k \leq x\}
\end{align*}
Es semicontinua superiormente.
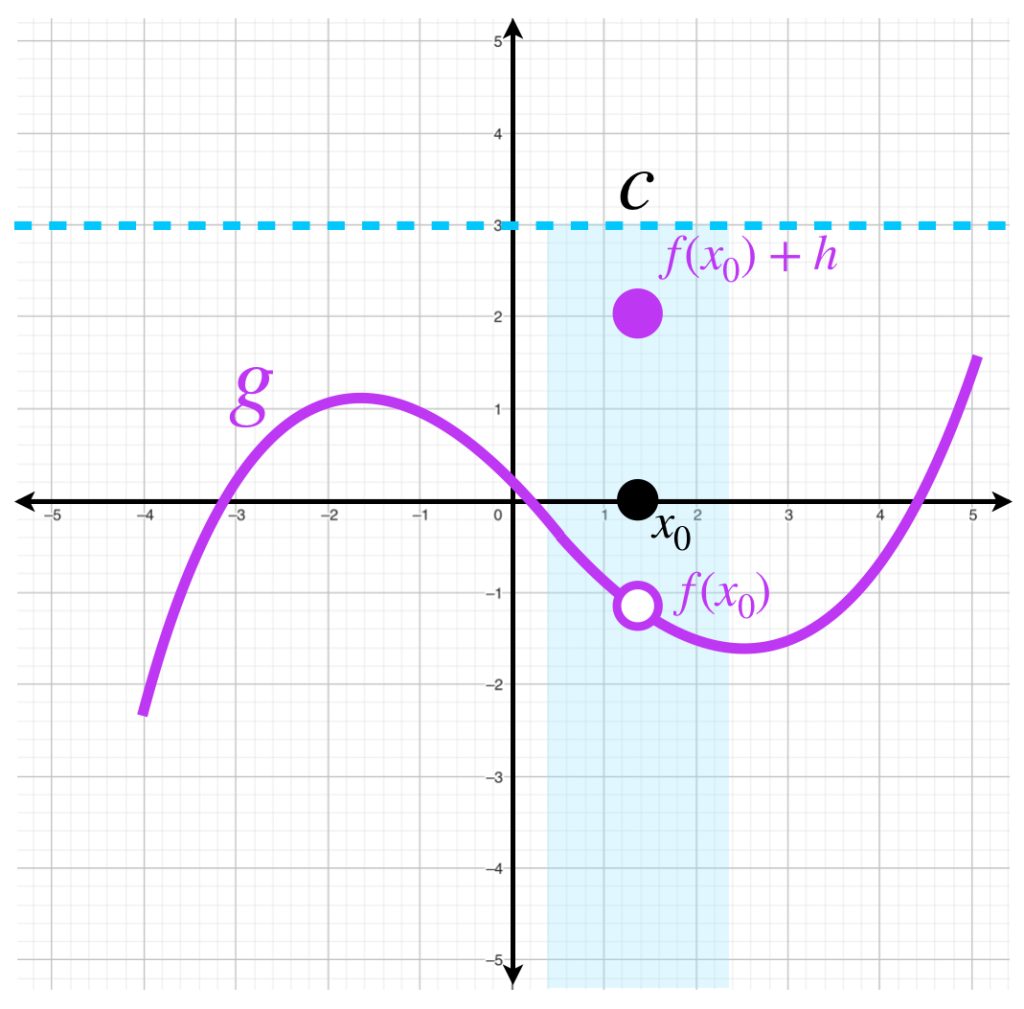
- $f$ aumentada en un punto de continuidad.
Sea $f: X \to \mathbb{R}$ tal que $f$ es continua en $x_0.$ Sea $h>0.$ Considera la función \begin{equation*}
g(x) = \begin{cases}
f(x) &\text{si $x \neq x_0$}\\
f(x_0) + h &\text{si $x = x_0$}
\end{cases}
\end{equation*}
Entonces $g$ es una función semicontinua superiormente en $x_0.$
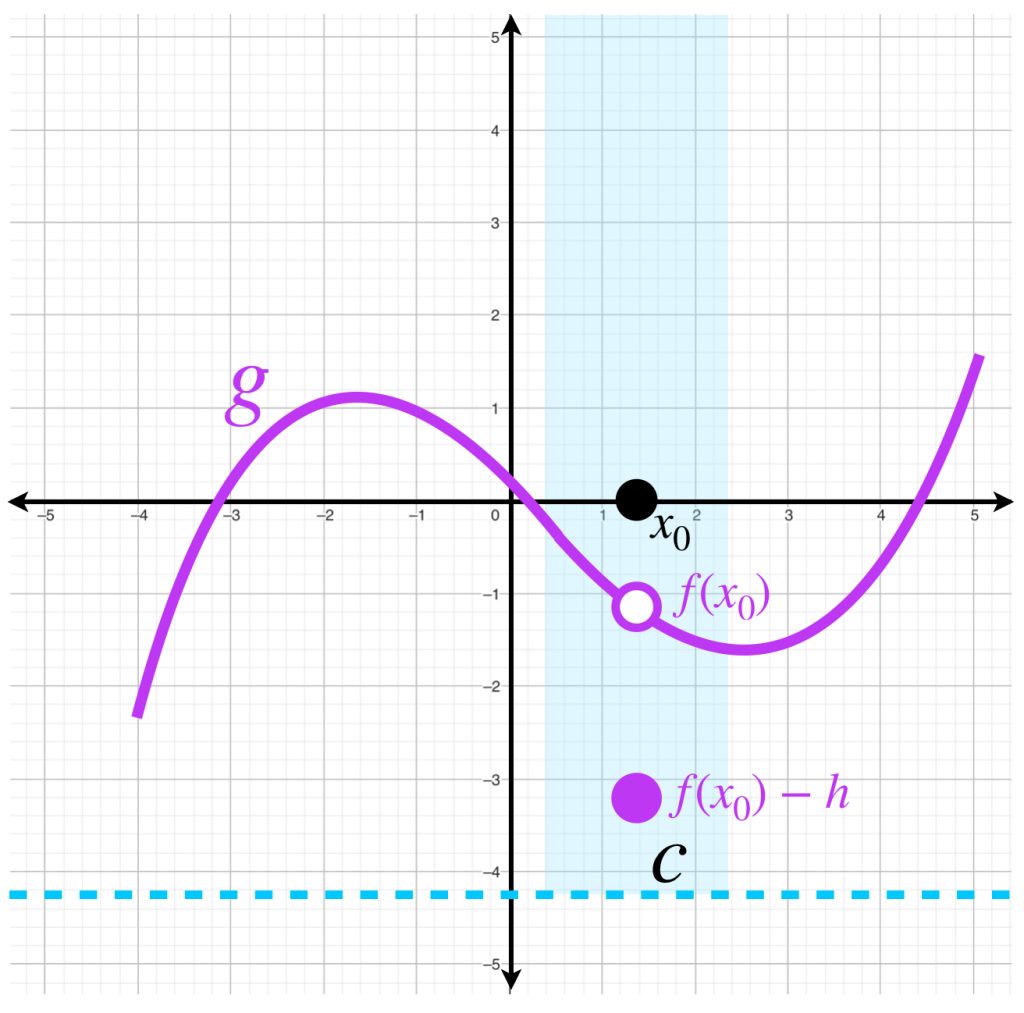
- $f$ disminuida en un punto de continuidad.
Sea $f: X \to \mathbb{R}$ tal que $f$ es continua en $x_0.$ Sea $h>0.$ Considera la función \begin{equation*}
g(x) = \begin{cases}
f(x) &\text{si $x \neq x_0$}\\
f(x_0) \, – \, h &\text{si $x = x_0$}
\end{cases}
\end{equation*}
Entonces $g$ es una función semicontinua inferiormente en $x_0.$
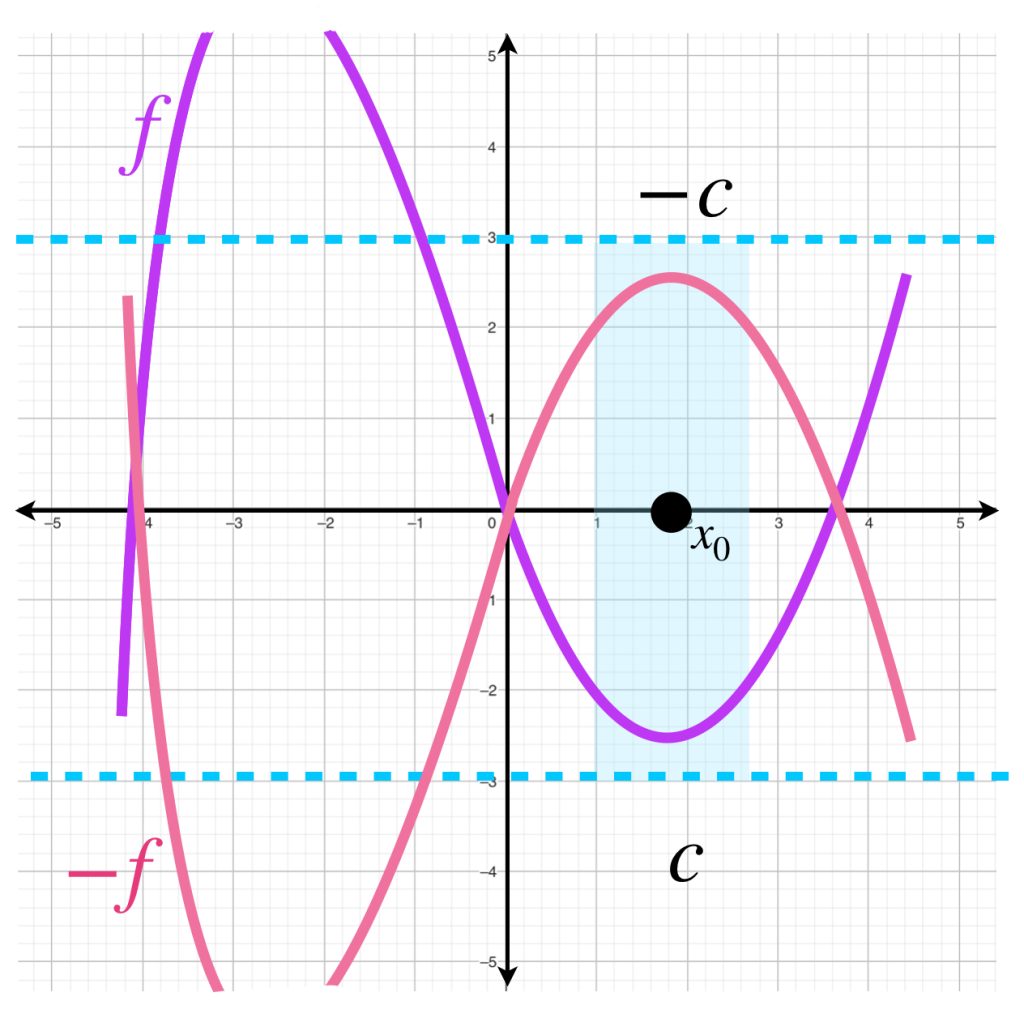
- Si $f:X \to [-\infty, \infty)$ es una función semicontinua inferiormente en $x_0$, entonces la función $-f$ es semicontinua superiormente en $x_0$.
$\textcolor{orange}{\text{Queda como ejercicio al lector verificar que las funciones mencionadas son semicontinuas.}}$
Definición. Límite superior y límite inferior de $f$ en un punto $x_0.$ Considera $f:X \to \mathbb{R}.\, $ Sea $x_0 \in X.$ Pensemos en todos los valores que toma la función $f$ en puntos «muy cerquita» de $x_0 \,$ identificando así que es «lo más» que podría valer. Nos referimos al valor de
$$\overline{f}(x_0)= \underset{\varepsilon \to 0}{lim}\, \left[ \underset{x \in B(x_0, \varepsilon)}{sup} \, f(x) \right]$$
que podría ser finito o infinito y recibe el nombre de límite superior de $f$ en $x_0.$
Análogamente, si pensamos en todos los valores que toma la función $f$ en puntos «muy cerquita» de $x_0 \,$ identificando así que es «lo menos» que podría valer. Nos referimos al valor de
$$\underline{f}(x_0)= \underset{\varepsilon \to 0}{lim}\, \left[ \underset{x \in B(x_0, \varepsilon)}{inf} \, f(x) \right]$$
que podría ser finito o infinito y recibe el nombre de límite inferior de $f$ en $x_0.$
Definición. Oscilación de la función $f$ en el punto $x_0.$ Sean $f:X \to \mathbb{R} \,$ y $\, x_0 \in X.$ La diferencia
$$\omega f(x_0) = \overline{f}(x_0) \, – \, \underline{f}(x_0)$$
si es que tiene sentido, es decir si al menos uno de los números $\overline{f}(x_0)$ o bien $\underline{f}(x_0)$ es finito, se llama oscilación de la función $f$ en el punto $x_0.$
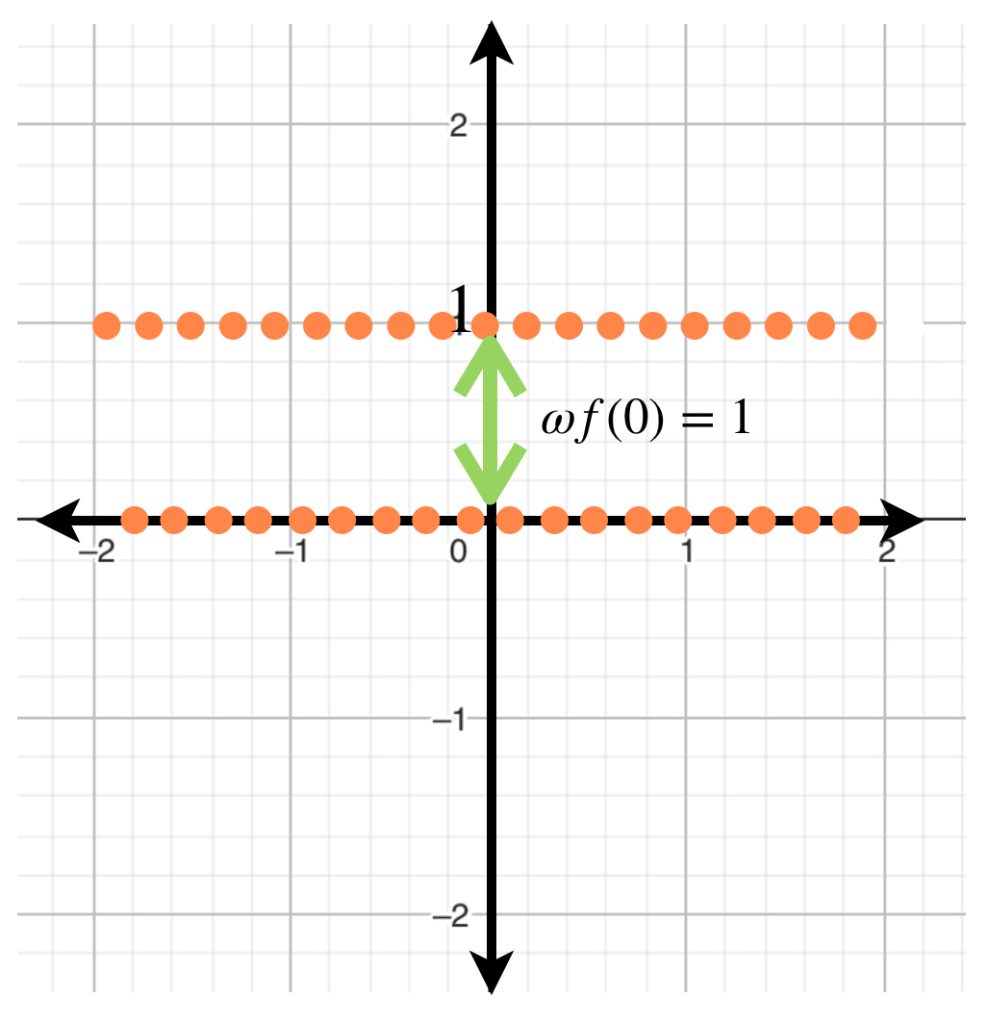
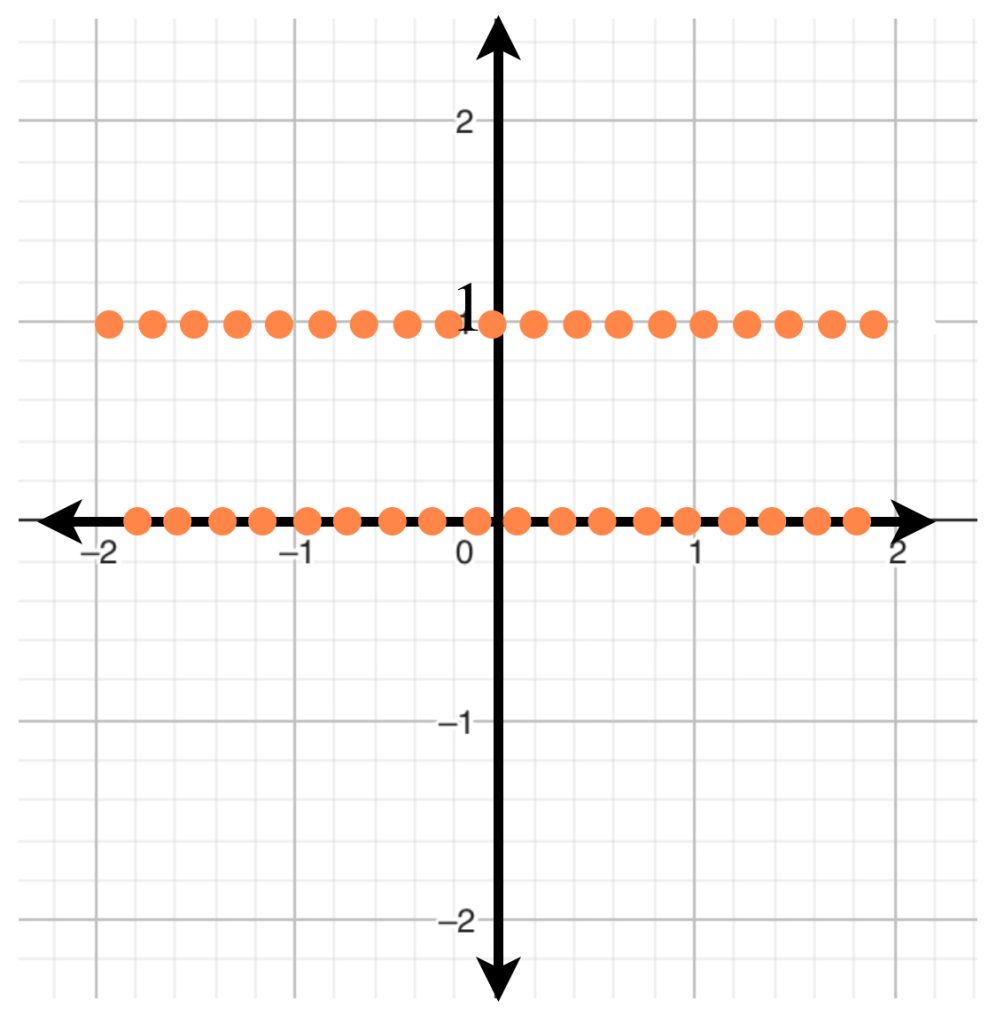
Ejemplo
Si $f$ es la función de Dirichlet, la oscilación de $f$ en cualquier punto de $\, \mathbb{R} \,$ es $1.$
Proposición: Sean $f:X \to \mathbb{R} \,$ y $\, x_0 \in X.$ Entonces $f$ es continua en $x_0 \,$ si y solo si $\omega f(x_0) = 0,$ es decir
$$-\infty < \underline{f}(x_0) \,= \, \overline{f}(x_0) < \infty.$$
$\textcolor{orange}{\text{La demostración queda como ejercicio al lector.}}$
Nota que para cualquier función $f:X \to \mathbb{R} \,$ la función $\overline{f}(x)$ es semicontinua superiormente mientras que la función $\underline{f}(x)$ es semicontinua inferiormente. $\textcolor{orange}{\text{La demostración de estos hechos también se deja como ejercicio.}}$
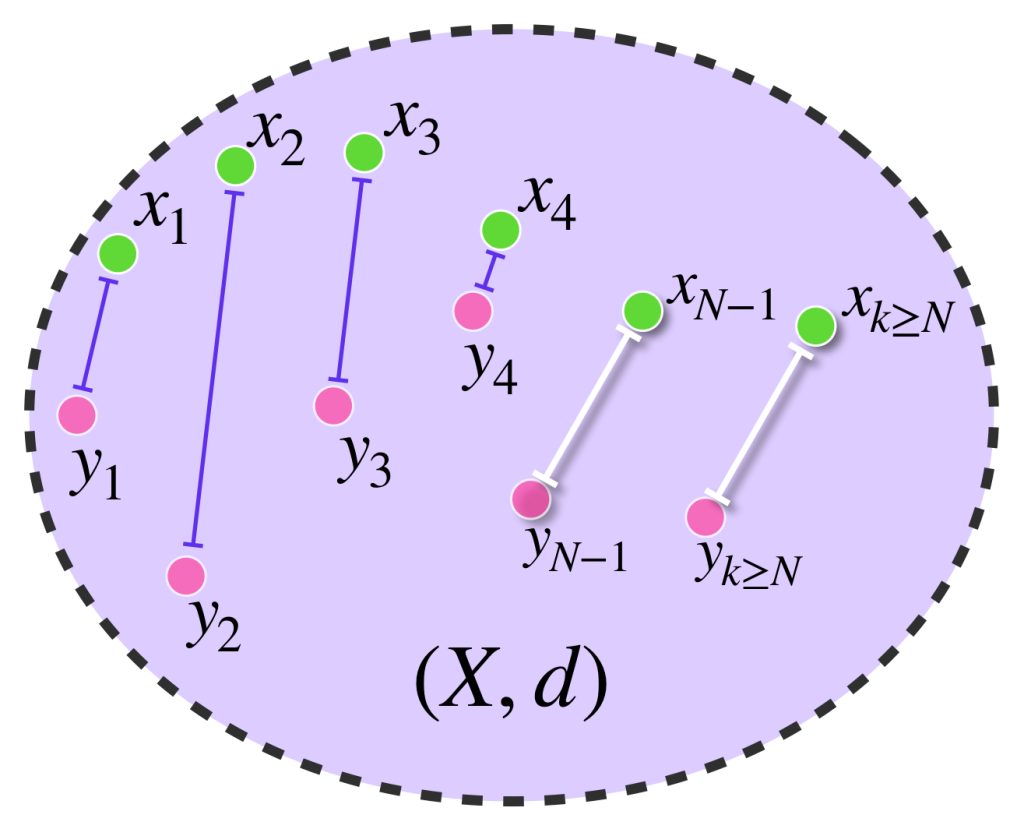
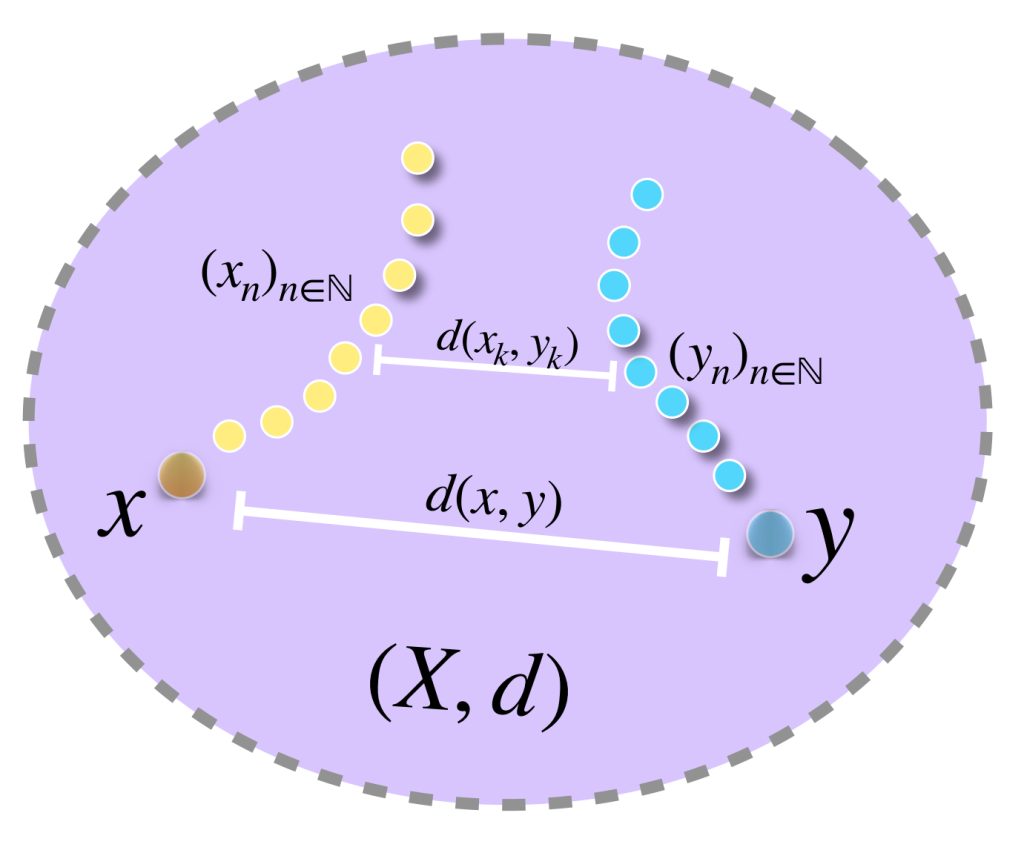
Antes de continuar recordemos la entrada Espacios métricos de caminos. Vimos que un camino es una función continua $\gamma: [a,b] \to X$ con $X$ un espacio topológico. En algunos libros, como el de Mónica Clapp, esta definición se indica como trayectoria.
Si $X$ es un espacio métrico entonces a cada trayectoria $\gamma:[a,b] \to X$ se le puede asociar el valor dado por
$$L(\gamma) : = sup \left\{ \sum_{k=1}^{n} d(\gamma(t_{k-1}), \gamma(t_k)) : a=t_0 \leq t_1 \leq …\leq t_n = b, \, n \in \mathbb{N} \right\}$$
lo cual define una función $L:(\mathcal{C}^0[a,b],X) \to (-\infty, \infty]$ que satisface los axiomas de una longitud de caminos.
Otra cosa que podemos observar de $L$ es que no es continua cuando $X = \mathbb{R}^2.$ Como ejemplo un ejercicio al final de esta sección. La cuestión es que dada una trayectoria $\gamma$ puede haber trayectorias con longitud muy grande pese a ser cercanas a $\gamma$ en la métrica uniforme. No obstante, puede asegurarse que si las trayectorias son suficientemente cercanas a $\gamma$ entonces su longitud no podrá ser arbitrariamente menor que la de $\gamma$. En otras palabras:
La función $L$ es semicontinua inferiormente en $(\mathcal{C}^0[a,b],X)$
Proposición: Sean $\gamma \in (\mathcal{C}^0[a,b],X)\,$ y $c < L(\gamma).$ Entonces existe $\delta>0$ tal que si $d_\infty(\gamma,\sigma) < \delta$ se satisface
$$c < L(\sigma).$$
Demostración:
Tomemos $d_0 >0$ tal que $c+ \delta_0 < L(\gamma).$ Por definición de $L,$ existen $a=t_0, \leq t_1 \leq … \leq t_n = b\,$ en $\mathbb{R}$ tales que
$$c + \delta_0 < \sum_{k=1}^{n} d(\gamma(t_{k-1}), \gamma(t_k)).$$
Sea $\delta := \frac{\delta_0}{2m}. \,$ Si $\delta_\infty (\gamma, \sigma,) < \delta$ se sigue
\begin{align*}
d(\gamma(t_{k-1}), \gamma(t_k)) &\leq d(\gamma(t_{k-1}), \sigma(t_{k-1})) + d(\sigma(t_{k-1}),\gamma(t_k)) \\
&\leq d(\gamma(t_{k-1}), \sigma(t_{k-1})) + d(\sigma(t_{k-1}),\sigma (t_k)) + d(\sigma(t_k),\gamma(t_k)) \\
< \delta + d(\sigma(t_{k-1}),\sigma (t_k)) + \delta \\
= d(\sigma(t_{k-1}),\sigma (t_k)) + 2 \delta\\
= d(\sigma(t_{k-1}),\sigma (t_k)) + \frac{\delta_0}{m}.
\end{align*}
Si sumamos las desigualdades para todo $k = 1,…,n$ tenemos lo siguiente
\begin{align}
c + \delta_0 &< \sum_{k=1}^{n} d(\gamma(t_{k-1}), \gamma(t_k))\\
&< \sum_{k=1}^{n} d(\sigma(t_{k-1}), \sigma(t_k)) + \delta_0 \\
&\leq L(\sigma) + \delta_0.
\end{align}
De modo que $\, c< L(\sigma)$ que es lo que queríamos demostrar.
En la entrada Funciones en espacios topológicos compactos vimos que toda función continua $\, f:A \to \mathbb{R} \,$ en un espacio compacto $A$ alcanza su mínimo y máximo en $A.$ Los resultados siguientes muestran la generalización al caso de funciones semicontinuas.
Proposición: Sea $f:A \to \mathbb{R} \,$ una función semicontinua inferiormente sobre un espacio métrico compacto $A, \, $ entonces la imagen de $f$ está acotada inferiormente.
Demostración:
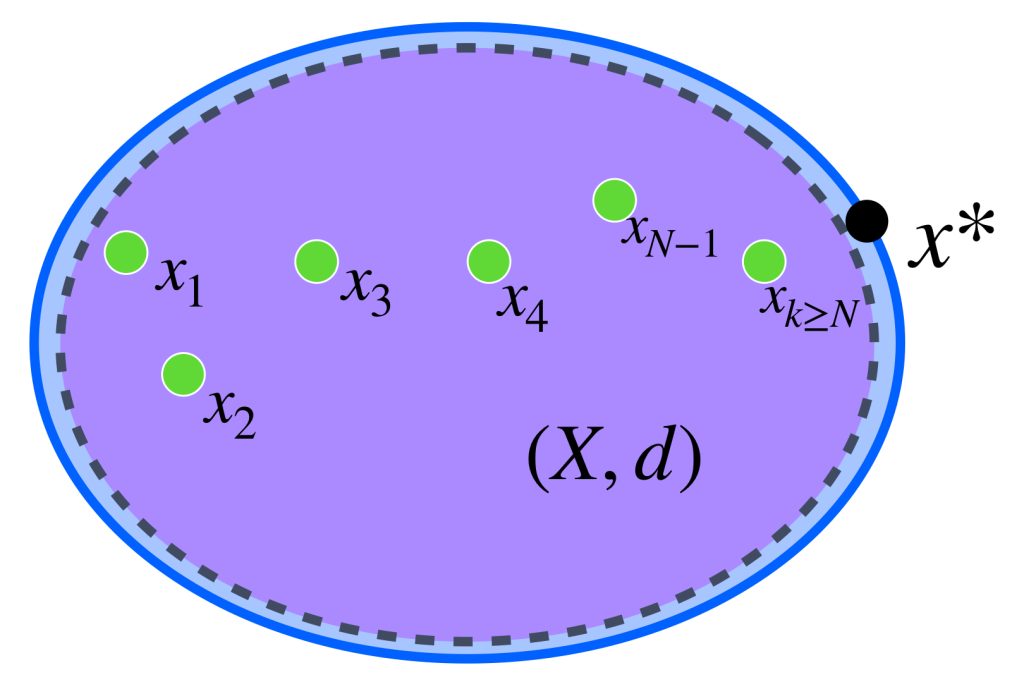
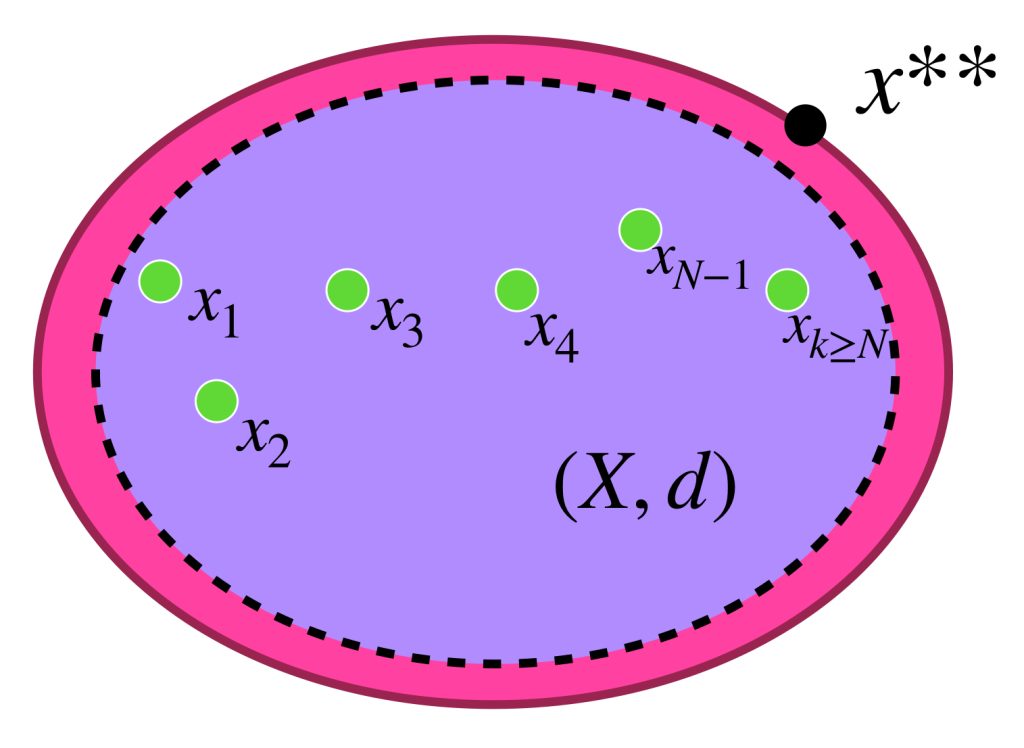
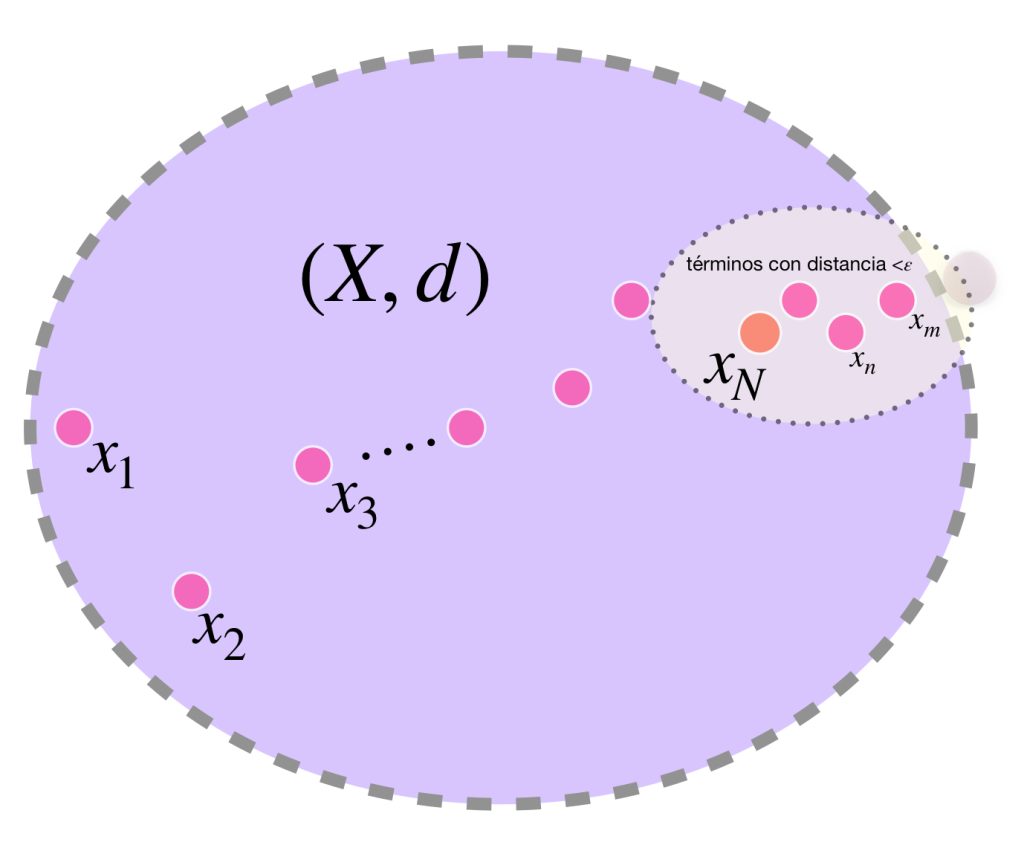
Supón por el contrario que $\underset{x \in A}{\text{ínf}} \, f(x) = – \infty.$ Entonces existe una sucesión $\{x_n\}_{n \in \mathbb{N}} \,$ de elementos en $A$ tal que para cada $n \in \mathbb{N}, \, f(x_n) < -n.$ Puesto que el espacio $A$ es compacto, el subconjunto infinito $\{x_n: n \in \mathbb{N}\} \,$ tiene al menos un punto de acumulación $x_0, \,$ en $A. \,$(Recuerda el problema 3 de la tarea moral de la entrada Compacidad en espacios métricos). Ya que $f$ es semicontinua inferiormente en $x_0, \,$ existe $\delta >0$ tal que para cada $x \in B(x_0, \delta)$ se cumple que $f(x) > f(x_0) \, – \, 1.$ Observa que $B(x_0, \delta)$ contiene a lo más una cantidad finita de puntos de la sucesión, pero esto contradice que $x_0$ sea punto de acumulación de $\{x_n: n \in \mathbb{N}\} \,$ por lo tanto la imagen de $f$ está acotada inferiormente.
Se puede probar el resultado análogo para una función semicontinua superiormente. $\textcolor{orange}{\text{Queda como ejercicio.}}$
Proposición: Sea $f:A \to \mathbb{R} \,$ una función semicontinua inferiormente sobre un espacio métrico compacto $A, \, $ entonces $f$ alcanza su mínimo en $A.$
Demostración:
Como $f$ es semicontinua inferiormente y por el resultado anterior, $f(A)$ tiene ínfimo en $\mathbb{R},$ podemos construir una sucesión $(x_n)_{n \in \mathbb{N}}$ de elementos en $A$ tal que para cada $n \in \mathbb{N}, \, f(x_n) \leq \underset{x \in A}{\text{ínf}} \, f(x) \, + \, \frac{1}{n}.$
Como $A$ es compacto, el conjunto $\{x_n: n \in \mathbb{N}\} \,$ tiene un punto de acumulación $x_0 \in A.$
Vamos a probar que $f$ alcanza su mínimo en $x_0,$ es decir que $f(x_0) = \underset{x \in A}{\text{ínf}} \, f(x).$
Supón por el contrario que $f(x_0) > \underset{x \in A}{\text{ínf}} \, f(x).$ Entonces existe $\varepsilon>0$ tal que $\underset{x \in A}{\text{ínf}} \, f(x) + \varepsilon \leq f(x_0).$ Como $f$ es semicontinua inferiormente en $x_0,$ existe $\delta>0$ tal que para cada $x \in B(x_0, \delta), \, f(x > \underset{x \in A}{\text{ínf}} \, f(x) + \varepsilon).$ Observa que $B(x_0, \delta)$ contiene a lo más una cantidad finita de puntos de la sucesión, pero esto contradice que $x_0$ sea punto de acumulación de $\{x_n: n \in \mathbb{N}\} \,$ por lo tanto $f(x_0) = \underset{x \in A}{\text{ínf}} \, f(x)$ y así, $f$ alcanza su mínimo en $A.$
Se puede probar el resultado análogo para una función semicontinua superiormente. $\textcolor{orange}{\text{Queda como ejercicio.}}$
Más adelante…
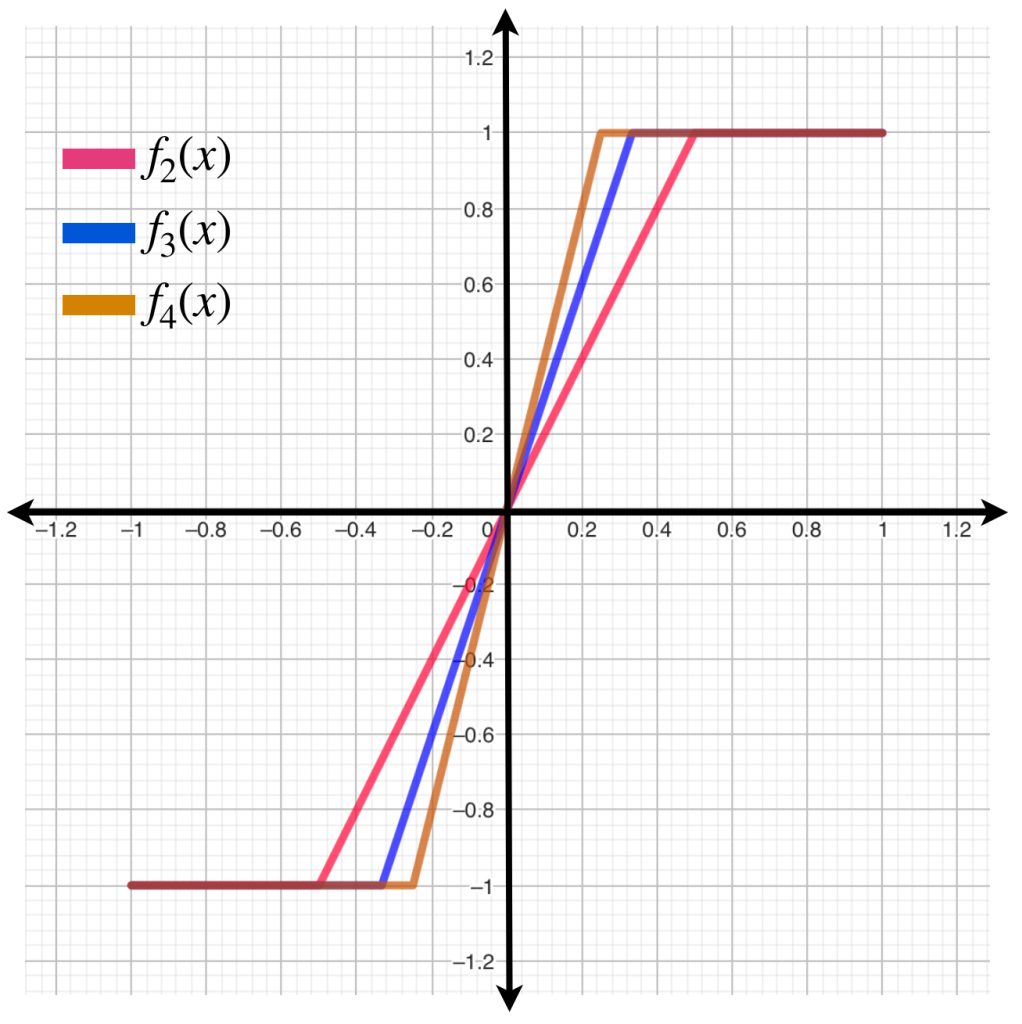
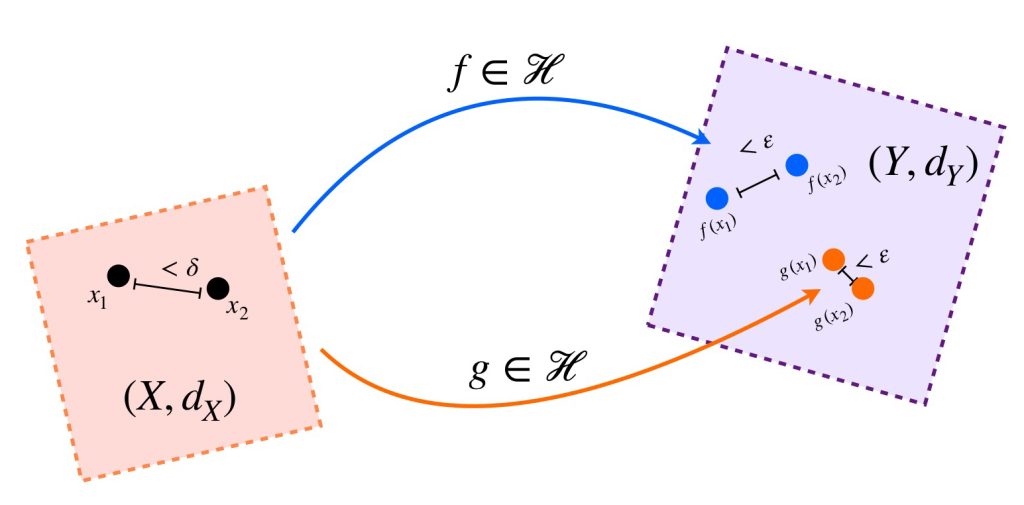
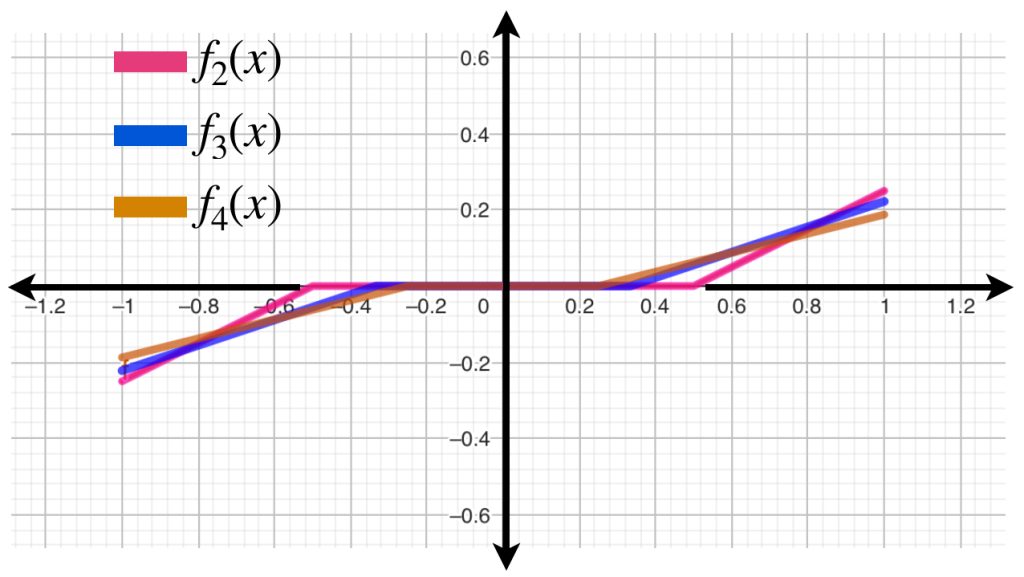
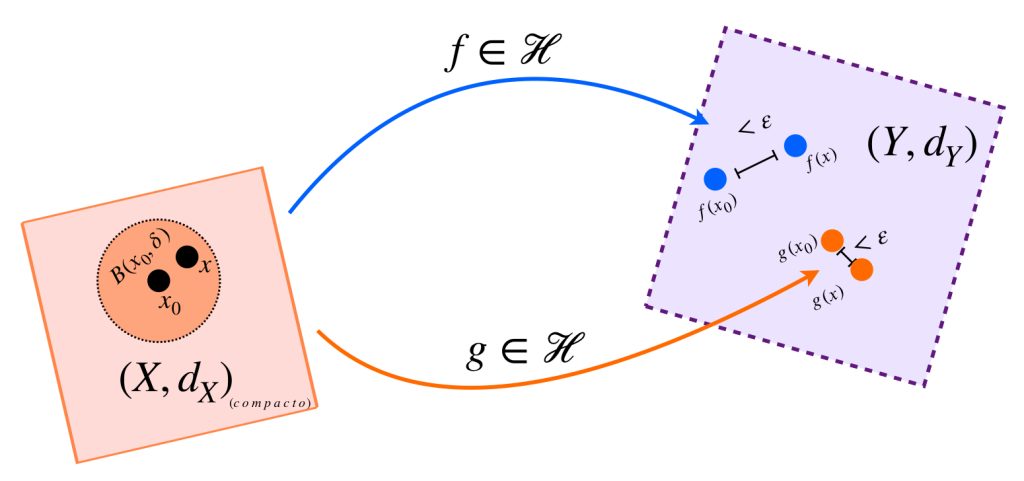
Conoceremos otro «tipo de continuidad» en las funciones. Esta vez lo haremos con una colección de ellas cuando la misma bola de radio $\delta$ y centro en $x_0$ asegura la cercanía con los puntos que cada función asigna a $x_0.$ Este concepto es equicontinuidad y se verá formalmente en la siguiente entrada.
Tarea moral
- Demuestra los resultados que se fueron indicando a lo largo de esta entrada.
- a) Prueba que la sucesión de trayectorias $\gamma_k: [0,1] \to \mathbb{R}^2,$
$$\gamma_k = \left(x, \frac{1}{\sqrt{k}}sen(\pi k x) \right),$$
converge a la trayectoria $\gamma(x) = (x,0)$ en el conjunto de funciones acotadas de $[0,1]$ en $\mathbb{R}^2$
b) Prueba que $L(\gamma_k) \to \infty$
c) Concluye que $L$ no es continua en $\mathcal{C}^0([a,b], \mathbb{R}).$