Introducción
En las dos entradas anteriores revisamos los conceptos esenciales para poder estudiar el plano fase del sistema de ecuaciones de primer orden homogéneas con coeficientes constantes $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Revisamos el campo vectorial asociado al sistema, que para los sistemas que estamos considerando se reduce al campo $\textbf{F}(x,y)=(ax+by, cx+dy)$. A cada $(x,y)$, el campo asocia un vector anclado en dicho punto, que además será tangente a las curvas solución. Si observamos el campo vectorial en el plano, entonces podemos darnos una idea aproximada de cómo se verían las curvas solución, y por tanto, el plano fase completo. Por otra parte estudiamos la estabilidad de los puntos de equilibrio, que son aquellos donde el campo vectorial se anula, es decir, cuando $\textbf{F}(x,y)=(0,0)$. De ellos depende el comportamiento del resto de las soluciones en el plano fase.
Con estos ingredientes, estamos listos para poder dibujar los planos fase de casi cualquier sistema de dos ecuaciones con coeficientes constantes. Como sabemos, la solución general a estos sistemas depende de los valores propios de la matriz asociada. Analizaremos el comportamiento de dichas soluciones, comenzando en esta entrada con el caso cuando los valores propios del sistema son reales distintos y no nulos. Después de cada análisis podremos hacer un dibujo esquemático de cómo se ven las soluciones en el plano fase.
¡Vamos a comenzar!
Plano fase para sistemas con valores propios reales distintos no nulos
En el primer video analizamos de manera general el comportamiento de las soluciones a sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando estos tienen valores propios reales distintos y no nulos. Dependiendo del signo de los valores propios será la forma del plano fase.
En el segundo video resolvemos un ejemplo por cada caso analizado en el video anterior.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.
- Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Prueba que si el determinante de la matriz asociada es cero, entonces el sistema tiene al menos un valor propio $\lambda=0$.
- Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 4 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
- Encuentra la solución general al sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 5 & -1 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Posteriormente grafica la curva correspondiente a la condición inicial $$\textbf{X}(0)=\begin{pmatrix} 2 \\ 1 \end{pmatrix}.$$
- Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
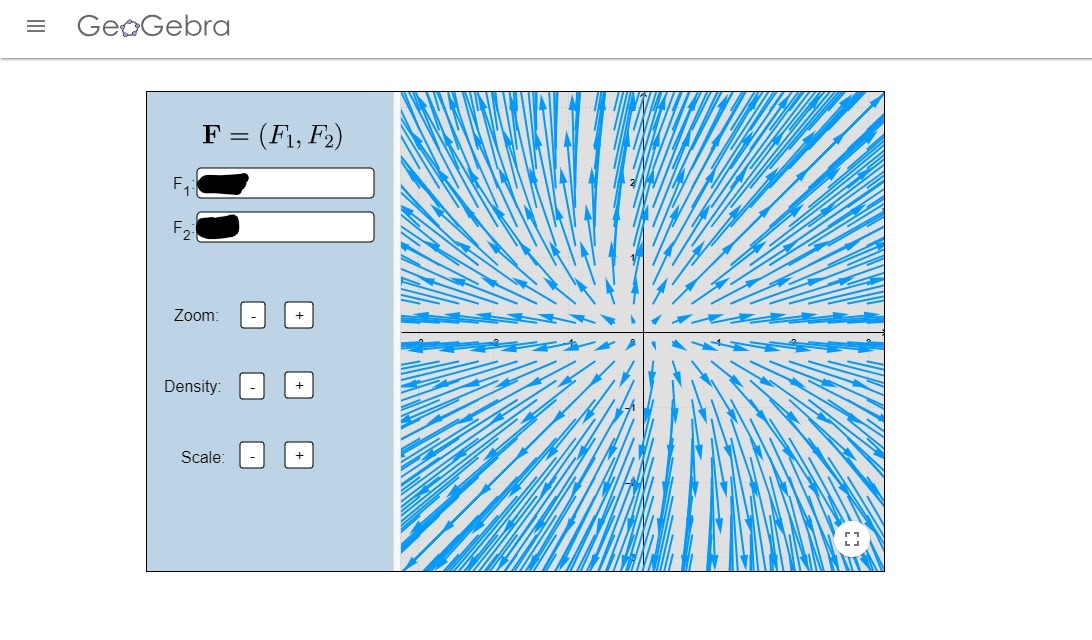
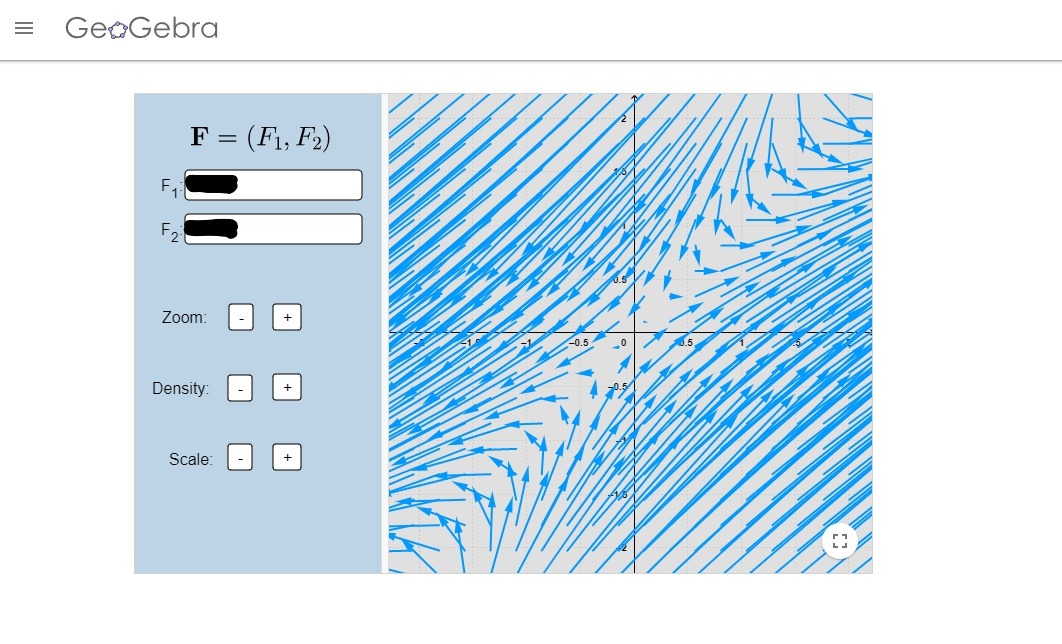
- Relaciona cada sistema de ecuaciones con la imagen correspondiente a su plano fase:
- $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 3 & -2 \\ 2 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
- $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
- $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -1 & 1 \\ 0 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$

Más adelante
En esta entrada logramos dibujar el plano fase para sistemas cuyos valores propios son reales distintos y no nulos. El siguiente paso será considerar aquellos sistemas que tienen valores propios complejos. Nuevamente dividiremos el análisis en tres casos, dependiendo del signo de la parte real de los valores propios. Eso lo haremos en la siguiente entrada.
¡No te la pierdas!
Entradas relacionadas
- Ir a Ecuaciones Diferenciales I
- Entrada anterior del curso: Puntos de equilibrio y estabilidad para sistemas de dos ecuaciones de primer orden
- Siguiente entrada del curso: Plano fase para sistemas lineales con valores propios complejos
- Notas escritas relacionadas con el tema: Teoría cualitativa de los sistemas lineales homogéneos. Valores propios reales y distintos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
