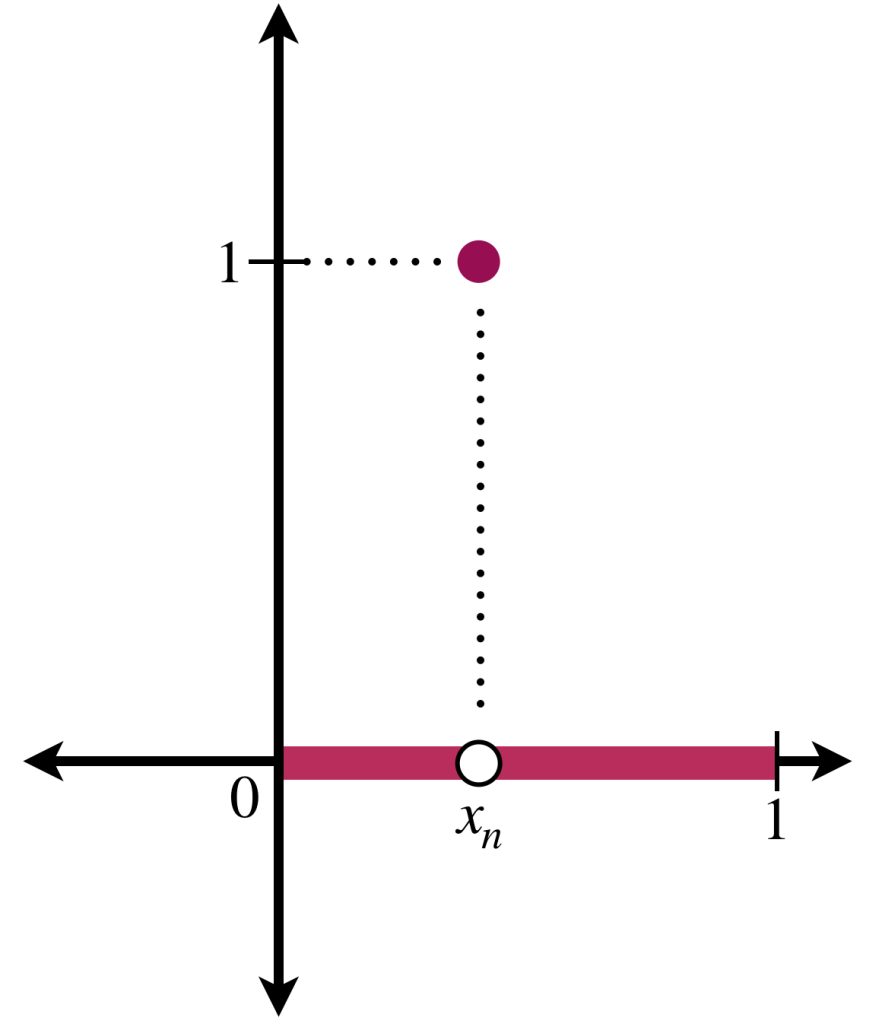
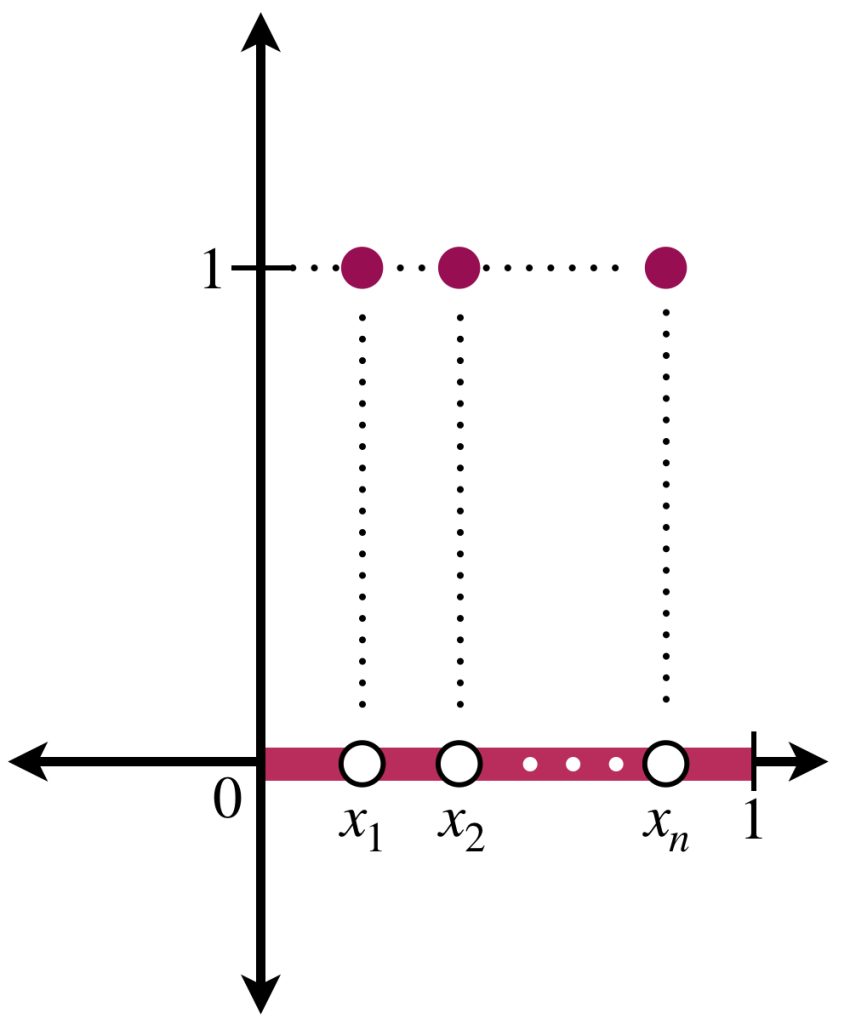
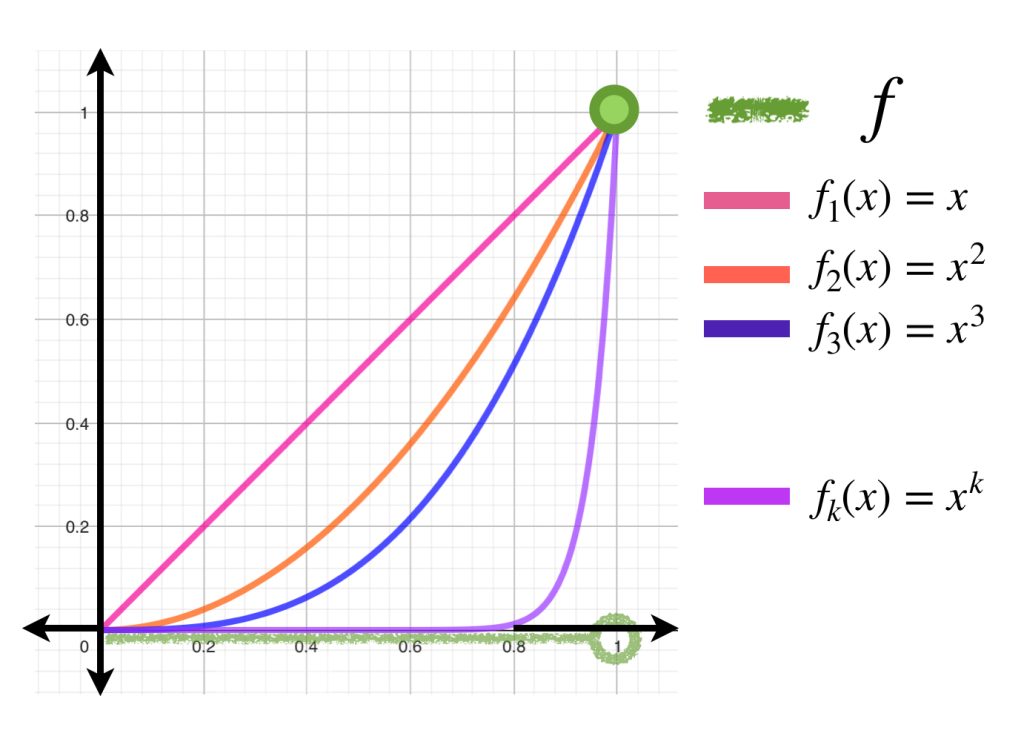
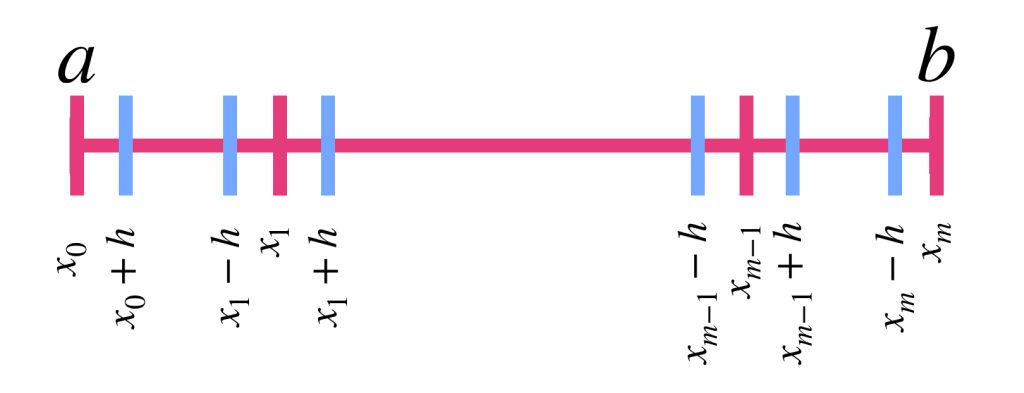
Teorema de la Función Inversa (sistema $f_{i}:\mathbb{R}^{n}\rightarrow\mathbb{R}$)

Teorema 1. Sea $U\subset\mathbb{R}^{n}$ un abierto y sean
$$\begin{matrix}
f_{1}:U\rightarrow\mathbb{R} \\
\vdots \\
f_{n}:U\rightarrow\mathbb{R}
\end{matrix}$$
con derivadas parciales continuas. Considerar las ecuaciones
$$\begin{array}{c}
f_1(x_1,x_2,…,x_n)= y_1\\
f_2(x_1,x_2,…,x_n)= y_2\\
\vdots\\
f_n(x_1,x_2,…,x_n)= y_n
\end{array}$$ Tratamos de resolver las n-ecuaciones para $x_1,x_2,… x_n$como funciones de $y_1,y_2,… y_n$.
La condición de existencia para la solución en una vecindad del punto $x_0$ es que el determinante de la matriz $Df(x_0)$ y $f=(f_1,f_2,… f_n)$ sean distintos de cero.

La condición de existencia para la solución en una vecindad del punto $x_0$ es que el determinante de la matriz $Df(x_0)$ y $f=(f_i,f_2,… f_n)$ sean distintos de cero. Explicitamente:

$[\left. \begin{array}{c}
\displaystyle\frac{\partial(f_1,f_2,…,f_n)}{\partial(x_1,x_2,…,x_n)}
\end{array}\right|_{x=x_0}= J(f)(x_0)= \left| \begin{array}{ccc}
\displaystyle\frac{\partial f_1}{\partial x_1}(x_0)&\ldots&\displaystyle\frac{\partial f_1}{\partial x_1}(x_0)\\
\vdots & & \vdots\\
\displaystyle\frac{\partial f_n}{\partial x_1}(x_0)&\ldots&\displaystyle\frac{\partial f_n}{\partial x_n}(x_0)
\end{array}\right| \neq 0
]$

entonces el sistema anterior se puede resolver de manera ‘unica como $x=g(y)$ para $x$ cerca de $x_{0}$ y y cerca de $y_{0}$ $\square$

Nota. La cuestión de existencia se responde por medio del teorema general de la función implícita aplicado a las funciones $y_i-f_i(x_1,x_2,…,x_n)$ con las incognitas $x_1,x_2,…,x_n$.

Ejemplo. El problema de factorizar un polinomio $x^{n}+a_{n-1}x^{n-1}+\cdots+a_{0}$ en factores lineales es, en cierto sentido un problema de función inversa. Los coeficientes $a_{i}$ son funciones conocidas de las n raices $r_{j}$. ¿Se podran expresar las raices como funciones de los coeficientes en alguna región?. Con $n=3$ , aplicar el teorema de la función inversa a este problema y enunciar la conclusión acerca de la posibilidad de hacer lo planteado.

Solución. Para el caso n=3 tenemos que podemos factorizar el polinomio de la siguiente forma
$$x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=(x-r_{1})(x-r_{2})(x-r_{3})$$
desarrolando el lado derecho tenemos que
$$(x-r_{1})(x-r_{2})(x-r_{3})=x^{3}-r_{3}x^{2}-r_{2}x^{2}+r_{2}r_{3}x-r_{1}x^{2}+xr_{1}r_{3}+r_{1}r_{2}x-r_{1}r_{2}r_{3}$$
que se puede escribir
$$x^{3}+x^{2}(-r_{3}-r_{2}-r_{1})+x(r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2})-r_{1}r_{2}r_{3}$$
igualando las expresiones
$$x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=x^{3}+x^{2}(-r_{3}-r_{2}-r_{1})+x(r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2})-r_{1}r_{2}r_{3}$$
por lo tanto igualando coeficientes
$$\begin{matrix}a_{0}=-r_{1}r_{2}r_{2}\\a_{1}=r_{2}r_{3}+r_{1}r_{3}+r_{1}r_{2}\\a_{2}=-r_{1}-r_{2}-r_{3}\end{matrix}$$

Al sistema anterior le aplicamos el teorema de la función implicita para comprobar si las raices se pueden expresar en términos de los coeficientes, para ello calculamos el determinante de jacobiano del sistema que en este caso es

$$J=\left(\begin{matrix}\frac{\partial a_{0}}{\partial r_{1}}&\frac{\partial a_{0}}{\partial r_{2}}&\frac{\partial a_{0}}{\partial r_{3}}\\\frac{\partial a_{1}}{\partial r_{1}}&\frac{\partial a_{1}}{\partial r_{2}}&\frac{\partial a_{2}}{\partial r_{3}}\\\frac{\partial a_{2}}{\partial r_{1}}&\frac{\partial a_{2}}{\partial r_{2}}&\frac{\partial a_{3}}{\partial r_{3}}\end{matrix}\right)=\left(\begin{matrix}-r_{2}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right)$$

de esta manera el determinante del jacobiano es
$$\det\left(\begin{matrix}-r_{1}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right)=\left|\begin{matrix}-r_{1}r_{3}&-r_{1}r_{3}&-r_{1}r_{2}\\r_{3}+r_{2}&r_{3}+r_{1}&r_{2}+r_{1}\\-1&-1&-1\end{matrix}\right|=$$
$$\textcolor{Green}{(-r_{2} r_{3})\times
\left|\begin{array}{cc}
r_{3}+r_{1} & r_{2}+r_{1} \\
-1 & -1\end{array}\right|}-\textcolor{Red}{(-r_{1}r_{3})\times
\left|\begin{array}{cc}
r_{3}+r_{2} & r_{2}+r_{1} \\
-1 &- 1\end{array}\right|}+\textcolor{Blue}{(-r_{1}r_{2})\times
\left|\begin{array}{cc}
r_{3}+r_{2} & r_{3}+r {1}\\ 3 & 1\end{array}\right|}=$$ $$\textcolor{Green}{(-r{2}r_{3})\times(r_{2}-r_{3})}+\textcolor{Red}{(r_{1}r_{3})\times(r_{1}-r_{3})}-\textcolor{Blue}{(r_{1}r_{2})\times(r_{1}-r_{2})}=-r_{2}r_{3}r_{2}+r_{2}r_{3}r_{3}+r_{1}r_{3}r_{1}-r_{1}r_{3}r_{3}-r_{1}r_{2}r_{1}+r_{1}r_{2}r_{2}$$

que se puede escribir
$$=r_{3}r_{1}r_{1}-r_{3}r_{1}r_{3}-r_{3}r_{2}r_{1}+r_{3}r_{2}r_{3}-r_{2}r_{1}r_{1}+r_{2}r_{1}r_{3}+r_{2}r_{2}r_{1}-r_{2}r_{2}r_{3}$$
$$=(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})r_{1}-(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})r_{3}=(r_{3}r_{1}-r_{3}r_{2}-r_{2}r_{1}+r_{2}r_{2})(r_{1}-r_{3})$$
$$=((r_{3}-r_{2})r_{1}-(r_{3}-r_{2})r_{2})(r_{1}-r_{3})=(r_{3}-r_{2})(r_{1}-r_{2})(r_{1}-r_{3})$$

Este último término no es cero si el polinomio tiene raices distintas. Así el teorema de la función inversa muestra que las raices se pueden hallar como funciones de los coeficientes en alguna vecindad de cualquier punto en el que las raices sean distintas. Esto es, si las rices $r_{1},~r_{2},~r_{3}$ de $x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$ son todas diferentes, entonces hay vecindades V de $(r_{1},~r_{2},~r_{3})$ y $W$ de $(a_{0},~a_{1},~a_{2})$ tales que las raices en V son funciones de los coeficientes en $W$.

Funciones de $\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición 1. Una función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ denotada $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, es una relación que asigna a cada vector del espacio $\mathbb{R}^{n}$ un único vector del espacio $\mathbb{R}^{m}$\Si f es una función de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$, entonces f se expresa
$$f=(f_{1},f_{2},\cdots,f_{m})$$ en donde $f_{k}~~k=1,…,m$ es la k-ésima función componente y $f_{k}:\mathbb{R}^{n}\rightarrow \mathbb{R}$ $k=1,…,m$

Definición 2. Si $A\subset \mathbb{R}^{n}$, la imagen bajo la función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ se denota $f(A)$, y se define
$$f(A)={f(x)\in \mathbb{R}^{m}~|~x\in A}$$

Definición 3. El dominio de una función f de $\mathbb{R}^{n}$ en $\mathbb{R}^{m}$ es la intersección de los dominios de las funciones componentes $f_{k}$ es decir
$$Dom_{f}=\bigcap_{k=1}^{m}Dom_{f_{k}}=Dom_{f_{1}}\bigcap Dom_{f_{2}}\bigcap Dom_{f_{3}}\bigcap\cdots \bigcap Dom_{f_{m}}$$

Ejemplo. Encontrar el dominio y la imagen de la recta $y=3x$ para la función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ dada por $$\displaystyle{f(x,y)=\left(\frac{4x+2y}{5},\frac{2x+y}{5}\right)}$$
\item[Solución] En este caso $$f_{1}=\left(\frac{4x+2y}{5}\right)~\Rightarrow~Dom_{f_{1}}=\mathbb{R}^{2}$$
$$f_{2}=\left(\frac{2x+y}{5}\right)~\Rightarrow~Dom_{f_{2}}=\mathbb{R}^{2}$$
por lo tanto
$$Dom_{f}=Dom_{f_{1}}\bigcap Dom_{f_{}}=\mathbb{R}^{2}\bigcap \mathbb{R}^{2}=\mathbb{R}^{2}$$
Para la imagen de la recta $y=3x$ procedemos de la siguiente manera
$$f(x,y)=\left(\frac{4x+2y}{5},\frac{2x+y}{5}\right)=(x’,y’)~ \Rightarrow ~f(x,3x)=\left(\frac{4x+2(3x)}{5},\frac{2x+(3x)}{5}\right)=(x’,y’)~\Rightarrow~$$
$$x’=\frac{4x+2(3x)}{5}yy’=\frac{2x+(3x)}{5}~ \Rightarrow ~x’=2xyy’=x \Rightarrow y’=\frac{x’}{2}$$
por lo tanto la imagen de la recta $y=3x$ sera:
$$f(3x)=\left\{(x’,y’)\in\mathbb{R}^{2}~|~y’=\frac{x’}{2}\right\}$$

$\textbf{Definición 4.}$ Sean $f:A\subset\mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ y $D\subset\mathbb{R}^{m}$. Definimos la $\textbf{imagen inversa}$ de $D$ bajo $f$, que denotamos $f^{-1}(D)$, como el conjunto dado por:
$$f^{-1}(D)=\left\{\hat{x}\in A~|~f(\hat{x})\in D\right\}$$

Definición 5. Sean $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ y $D\subset\mathbb{R}^{m}$, $B\subset A$. Definimos la $\textbf{imagen directa}$ de $B$ bajo $f$, que denotamos $f(B)$, como el conjunto dado por:
$$f(B)=\left\{f(\hat{x})\in \mathbb{R}^{m}~|~\hat{x}\in B\right\}$$

Proposición 1. Sean $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, $A_{\alpha},~B,C\subset A$ y $D_{\alpha},~D,~E\subset\mathbb{R}^{m}$, con $\alpha\in I$ I un conjunto de indices. Pruebe que:
$$\begin{matrix}
1.& D\subset E~\Rightarrow~f^{-1}(D)\subset f^{-1}(E) \\
2. & f^{-1}\left(\bigcup_{\alpha \in I}D_{\alpha}\right)=\bigcup_{\alpha\in I}f^{-1}(D_{\alpha})\
3.& f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)=\bigcap_{\alpha\in I}f^{-1}(D_{\alpha}) \\
4.&f^{-1}(D^{c})=(f^{-1}(D))^{c} \\
5.&B\subset C~\Rightarrow~f(B)\subset f(C)\\
6.&f\left(\bigcup_{\alpha\in I}A_{\alpha}\right)=\bigcup_{\alpha\in I}f(A_{\alpha}) \\
7.&f\left(\bigcap_{\alpha\in I}A_{\alpha}\right)\subset\bigcap_{\alpha\in I}f(A_{\alpha}) \\
8.&f(A)-f(B)\subset f(A-B) \\
9.&B\subset f^{-1}(f(B)) \\
10.&f(f^{-1})(D)\subset D
\end{matrix}$$

Demostración. $\textcolor{Blue}{(1). D\subset E~\Rightarrow~f^{-1}(D)\subset f^{-1}(E)}$
$$x\in f^{-1}(D)~\Rightarrow~f(x)\in D$$
$$~\underbrace{\Rightarrow}{D\subset E}~f(x)\in E$$ $$~\Rightarrow~x\in f^{-1}(E)$$ $\textcolor{Blue}{(2). f^{-1}\left(\bigcup{\alpha \in I}D_{\alpha}\right)=\bigcup_{\alpha\in I}f^{-1}(D_{\alpha})}$
$$x\in f^{-1}\left(\bigcup_{\alpha \in I}D_{\alpha}\right)~\Leftrightarrow~f(x)\in \bigcup_{\alpha \in I}D_{\alpha}$$
$$~\Leftrightarrow~f(x)\in D_{\alpha_{i}}p.a.~i\in I$$ $$~\Leftrightarrow~x\in f^{-1}(D_{\alpha_{i}})p.a.~i\in I$$
$$~\Leftrightarrow~x\in (\bigcup_{\alpha \in I}f^{-1}(D_{\alpha})$$
$\textcolor{Blue}{(3). f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)=\bigcap_{\alpha\in I}f^{-1}(D_{\alpha}) }$
$$x\in f^{-1}\left(\bigcap_{\alpha \in I}D_{\alpha}\right)~\Leftrightarrow~f(x)\in \bigcap_{\alpha \in I}D_{\alpha}$$
$$~\Leftrightarrow~f(x)\in D_{\alpha_{i}}\forall~i\in I$$ $$~\Leftrightarrow~x\in f^{-1}(D_{\alpha_{i}})\forall~i\in I$$
$$~\Leftrightarrow~x\in (\bigcap_{\alpha \in I}f^{-1}(D_{\alpha})$$
$\textcolor{Blue}{(4). f^{-1}(D^{c})=(f^{-1}(D))^{c} }$
$$x\in f^{-1}(D^{c})~\Leftrightarrow~f(x)\in D^{c}$$
$$~\Leftrightarrow~f(x)\notin D$$
$$~\Leftrightarrow~x\notin f^{-1}(D)$$
$$~\Leftrightarrow~x\in (f^{-1}(D))^{c}$$
$\textcolor{Blue}{(5). B\subset C~\Rightarrow~f(B)\subset f(C)}$
$$f(x)\in f(B)~\Rightarrow~x\in B$$
$$~\underbrace{\Rightarrow}{B\subset C}~x\in C$$ $$~\Rightarrow~f(x)\in f(C)$$ $\textcolor{Blue}{(6). f\left(\bigcup{\alpha\in I}A_{\alpha}\right)=\bigcup_{\alpha\in I}f(A_{\alpha})}$
$$f(x)\in f\left(\bigcup_{\alpha \in I}A_{\alpha}\right)~\Leftrightarrow~x\in \bigcup_{\alpha \in I}A_{\alpha}$$
$$~\Leftrightarrow~x\in A_{\alpha}p.a~\alpha\in~I$$ $$~\Leftrightarrow~f(x)\in~f(A_{\alpha})~p.a~\alpha\in~I$$ $$~\Leftrightarrow~f(x)\in \bigcup_{\alpha\in I}f(A_{\alpha})$$

$\textcolor{Blue}{(7). f\left(\bigcap_{\alpha\in I}A_{\alpha}\right)\subset\bigcap_{\alpha\in I}f(A_{\alpha})}$ $$f(x)\in f\left(\bigcap_{\alpha \in I}A_{\alpha}\right)~\Rightarrow~x\in \bigcap_{\alpha \in I}A_{\alpha}$$ $$~\Rightarrow~x\in A_{\alpha}\forall~\alpha\in~I$$
$$~\Rightarrow~f(x)\in~f(A_{\alpha})~\forall~\alpha\in~I$$
$$~\Rightarrow~f(x)\in \bigcap_{\alpha\in I}f(A_{\alpha})$$
$\textcolor{Blue}{(8). f\left(A\right)-f(B)\subset f(A-B)}$
$$f(A)-f(B)=f(A)\bigcap (f(B))^{c}$$
$$~ \Rightarrow ~f(x)\in f(A)-f(B)$$
$$~ \Rightarrow ~f(x)\in f(A)\bigcap (f(B))^{c}$$
$$~ \Rightarrow ~f(x)\in f(A)yf(x)\in (f(B))^{c}$$
$$~ \Rightarrow ~x\in Ayf(x)\notin f(B)$$
$$~ \Rightarrow x\in Ayx\notin B$$ $$~ \Rightarrow x\in Ayx\in B^{c}$$
$$~ \Rightarrow ~x\in A\bigcap B^{c}$$
$$~ \Rightarrow ~x\in A-B$$
$$~ \Rightarrow ~f(x)\in f(A-B)$$
$\textcolor{Blue}{(9). B\subset f^{-1}(f(B))}
$$x\in B~\Rightarrow~f(x)\in f(B)$$
$$~\Rightarrow~x\in f^{-1}(f(B))$$

$\textcolor{Blue}{(10).f(f^{-1}(D))\subset D}$
$$f(x)\in f(f^{-1}(D))~\Rightarrow~x\in f^{-1}(D)$$
$$~ \Rightarrow ~f(x)\in D$$ $\square$

Diferenciación de funciones $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$

Definición. Considere la función $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ definida en un conjunto abierto A de $\mathbb{R}^{n}$ y sea $x_{0}\in A$. Se dice que esta función es diferenciable si

$$f(x_{0}+h)=f(x_{0})+f'(x_{0})\cdot h+r(h)$$
cumple
$$\lim_{h\rightarrow0}\frac{r(h)}{|h|}=\hat{0}$$

Ejemplo. Compruebe que la función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}^{3}$ definida por
$$f(x,y)=\left(e^{xy},x^{2}+y,2x^{3}y^{2}\right)$$ es diferenciable en $(1,3)$
$\textbf{Solución}$ En este caso
$$\lim_{h\rightarrow0}\frac{r(h)}{|h|}=$$
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{f(1+h_{1},3+h_{2})-f(1,3)-\left((3e^{3},e^{3})\cdot\binom{h_{1}}{h_{2}},(2,1)\cdot\binom{h_{1}}{h_{2}},(54,12)\cdot\binom{h_{1}}{h_{2}}\right)}{|(h_{1},h_{2})|}$$
$$=\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{\left(e^{(1+h_{1})(3+h_{2})},(1+h_{1})^{2}+(3+h_{2}),2(1+h_{1})^{3}(3+h_{2})^{2}\right)-\left(e^{3},4,18\right)}{|(h_{1},h_{2})|}$$
$$\frac{-\left((3e^{3},e^{3})\cdot\binom{h_{1}}{h_{2}},(2,1)\cdot\binom{h_{1}}{h_{2}},(54,12)\cdot\binom{h_{1}}{h_{2}}\right)}{|(h_{1},h_{2})|}$$
$$=\left(\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{e^{(1+h_{1})(3+h_{2})}-e^{3}-3e^{3}h_{1}-e^{3}h_{2}}{|(h_{1},h_{2})|},\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{(1+h_{1})^{2}+(3+h_{2})-4-2h_{1}-h_{2}}{|(h_{1},h_{2})|},\right.$$
$$\left.\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{2(1+h_{1})^{3}(3+h_{2})^{2}-18-54h_{1}-12h_{2}}{|(h_{1},h_{2})|}\right)$$
$$=(0,0,0)$$
por lo que la función es diferenciable.

En el ejemplo anterior se tiene que
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{f(1+h_{1},3+h_{2})-f(1,3)-\left((3e^{3},e^{3})\cdot\binom{h_{1}}{h_{2}},(2,1)\cdot\binom{h_{1}}{h_{2}},(54,12)\cdot\binom{h_{1}}{h_{2}}\right)}{|(h_{1},h_{2})|}$$
se puede expresar
$$\lim_{(h_{1},h_{2})\rightarrow (0,0)}\frac{f(1+h_{1},3+h_{2})-f(1,3)-\left( \begin{matrix}
3e^{3}&e^{3}\\
2&1\\ 54&12
\end{matrix}\right)\left[ \begin{array}{ll}
h_{1}\\ h_{2} \end{array}\right]}{\sqrt{h_{1}^{2}+h_{2}^{2}}}$$
lo que nos lleva a la siguiente definición.

Definición. A la matriz de $m\times n$ se le llama Matriz Jacobiana de la función $f$ en $x_{0}$ y se le denota $Jf(x_{0})$.

Definición. Sea $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ definida en el abierto $\Omega$ de $\mathbb{R}^{n}$ y $x_{0}\in \Omega$. Se dice que $f$ es diferenciable en $x_{0}\in\Omega$ si y solo si existe una matriz T de $m\times n$ tal que $$\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})-T(x_{0})\cdot h}{|h|}=0$$donde $T(x_{0})$ es la matriz jacobiana denotada por $Jf(x_{0})$ ó $Df(x_{0})$. En notación matricial:
$$T(x_{0})\cdot h=\left( \begin{matrix}
\frac{\partial f_{1}(x_{0})}{\partial x_{1}}&\cdot\cdot\cdot& \frac{\partial f_{1}(x_{0})}{\partial x_{n}}\\
\cdot&\cdot&\cdot\\
\cdot&\cdot&\cdot\\
\cdot&\cdot&\cdot\\
\frac{\partial f_{m}(x_{0})}{\partial x_{1}}&\cdot\cdot\cdot&\frac{\partial f_{m}(x_{0})}{\partial x_{n}}
\end{matrix}\right)\cdot \left( \begin{matrix}
h_{1}\\
\cdot\\
\cdot\\
\cdot\
h_{n}
\end{matrix}\right)$$

En términos $\epsilon-\delta$ se tiene que si $0<|h|<\delta$ entonces $$\frac{|f(x_{0}+h)-f(x_{0})-T(x_{0})\cdot h|}{|h|}<\epsilon$$

Teorema 1. Supónga que $f:\Omega\subset\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ es diferenciable en $x_{0}\in \mathbb{R}^{n}$. Entonces la matriz $T$ es única

Demostración. Supongamos que existen $T_{1}$ y $T_{2}$ que cumplen $$\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})-T_{1}(x_{0})\cdot h}{|h|}=0\quad y\quad \lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})-T_{2}(x_{0})\cdot h}{|h|}=0$$
$\therefore$
$$\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})-T_{1}(x_{0})\cdot h}{|h|}-\frac{f(x_{0}+h)-f(x_{0})-T_{2}(x_{0})\cdot h}{|h|}=0$$
$$\Rightarrow \lim_{h\rightarrow 0}\frac{T_{2}(x_{0})\cdot h-T_{1}(x_{0})\cdot h}{|h|}=0$$
Sea $x$ un vector unitario en la dirección del vector $h$ y hacemos $h=tx$ con $t\in\mathbb{R}$
$\therefore$
$$ 0=\lim_{h\rightarrow 0}\frac{T_{2}(x_{0})\cdot h-T_{1}(x_{0})\cdot h}{|h|}= \lim_{t\rightarrow 0}\frac{T_{2}(x_{0})\cdot tx-T_{1}(x_{0})\cdot tx}{|tx|}=\lim_{t\rightarrow 0}t\frac{T_{2}(x_{0})\cdot x-T_{1}(x_{0})\cdot x}{|t||x|}$$
$$ \Rightarrow 0=T_{2}(x_{0})\cdot x-T_{1}(x_{0})\cdot x \Rightarrow T_{2}(x_{0})\cdot x=T_{1}(x_{0})\cdot x\Rightarrow T_{2}(x_{0})=T_{1}(x_{0})\Rightarrow T_{2}=T_{1}$$ $\square$

Operadores: Divergencia, Rotacional y Laplaciano

Considere la función $f:\mathbb{R}^{3}\rightarrow\mathbb{R}^{3}$ dada por
$$f(x,y,z)=\left(f_{1}(x,y,z),f_{2}(x,y,z),f_{3}(x,y,z)\right)$$
cuya matriz jacobiana es
$$\left( \begin{matrix}
\frac{\partial f_{1}}{\partial x}&\frac{\partial f_{1}}{\partial y}&\frac{\partial f_{1}}{\partial z}\\
\frac{\partial f_{2}}{\partial x}&\frac{\partial f_{2}}{\partial y}&\frac{\partial f_{2}}{\partial z}\\
\frac{\partial f_{3}}{\partial x}&\frac{\partial f_{3}}{\partial y}&\frac{\partial f_{3}}{\partial z}\
\end{matrix}\right)$$
Con los elementos de esta matriz se forman importantes combinaciones que son la divergencia y el rotacional, conocidos también como invariantes de primer orden de esta matriz. La razón por la que se llaman invariantes es porque el valor de dichas combinaciones no se altera al efectuar un cambio de coordenadas.

Definición. Dada la matriz Jacobiana $$\left( \begin{matrix}
\textcolor{Red}{\frac{\partial f_{1}}{\partial x}}&\frac{\partial f_{1}}{\partial y}&\frac{\partial f_{1}}{\partial z}\\
\frac{\partial f_{2}}{\partial x}&\textcolor{Red}{\frac{\partial f_{2}}{\partial y}}&\frac{\partial f_{2}}{\partial z}\\
\frac{\partial f_{3}}{\partial x}&\frac{\partial f_{3}}{\partial y}&\textcolor{Red}{\frac{\partial f_{3}}{\partial z}}\
\end{matrix}\right)$$
Se define la divergencia de f como
$$div~(f)=\textcolor{Red}{\frac{\partial f_{1}}{\partial x}+\frac{\partial f_{2}}{\partial y}+\frac{\partial f_{3}}{\partial z}}$$
Se puede ver que es igual a la suma de los elementos de la diagonal principal, es decir, que constituye la traza de la matriz jacobiana de f. La defnición de divergencia puede darse también mediante el operador $\nabla$ (nabla)
$$\nabla\cdot f=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\cdot \left(f_{1},f_{2},f_{3}\right)=\frac{\partial f_{1}}{\partial x}+\frac{\partial f_{2}}{\partial y}+\frac{\partial f_{3}}{\partial z}$$

Dada la matriz Jacobiana
$$\left( \begin{matrix}
\frac{\partial f_{1}}{\partial x}&\textcolor{Green}{\frac{\partial f_{1}}{\partial y}}&\textcolor{Red}{\frac{\partial f_{1}}{\partial z}}\
\textcolor{Green}{\frac{\partial f_{2}}{\partial x}}&\frac{\partial f_{2}}{\partial y}&\textcolor{Blue}{\frac{\partial f_{2}}{\partial z}}\
\textcolor{Red}{\frac{\partial f_{3}}{\partial x}}&\textcolor{Blue}{\frac{\partial f_{3}}{\partial y}}&\frac{\partial f_{3}}{\partial z}\
\end{matrix}\right)$$
se define el rotacional como
$$rot~(f)=\left(\textcolor{Blue}{\frac{\partial f_{3}}{\partial y}-\frac{\partial f_{2}}{\partial z}},\textcolor{Red}{\frac{\partial f_{3}}{\partial x}-\frac{\partial f_{1}}{\partial z}},\textcolor{Green}{\frac{\partial f_{2}}{\partial x}-\frac{\partial f_{1}}{\partial y}}\right)$$
Y podemos ver que las componentes del rotacional están definidas por las diferencias de los elementos situados simétricamente con respecto a la diagonal principal de la matriz Jacobiana.
La defnición de rotacional puede darse también mediante el operador $\nabla$ (nabla)
$$\nabla\times f=\left|\begin{matrix}\hat{i}&\hat{j}&\hat{k}\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\f_{1}&f_{2}&f_{3}\end{matrix}\right|=\left(\frac{\partial f_{3}}{\partial y}-\frac{\partial f_{2}}{\partial z},\frac{\partial f_{3}}{\partial x}-\frac{\partial f_{1}}{\partial z},\frac{\partial f_{2}}{\partial x}-\frac{\partial f_{1}}{\partial y}\right)$$

Definición. Sea $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ definida en el abierto $\Omega$ de $\mathbb{R}^{n}$ tal que $f$ es de clase $C^{2}$ en $\Omega$. La expresión
$$\nabla^{2}f=\frac{\partial^{2}f}{\partial x^{2}}+\frac{\partial^{2}f}{\partial y^{2}}$$
es llamada Laplaciano de f. La ecuación
$$\frac{\partial^{2}f}{\partial x^{2}}+\frac{\partial^{2}f}{\partial y^{2}}=0$$
es llamada la ecuación de Laplace. Las funciones f de clase $C^{2}$ que cumplen la ecuación de Laplace se llaman funciones Armónicas.

Ejercicio. Sean $f,g:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}^{3}$ dos funciones diferenciables en una región $A\subset\mathbb{R}^{3}$ y $\varphi:\mathbb{R}^{3}\rightarrow\mathbb{R}$
Pruebe que

(a) $div~(f+g)=div~f+div~g$

(b) $div~(\varphi f)=\varphi~div~(f)+grad~(\varphi)\cdot f$
(c) $rot~(f+g)=rot~(f)+rot~g$
(d) Sean $\phi,\psi:A\subset \mathbb{R}^{2}\rightarrow\mathbb{R}$ dos funciones $\psi=\psi(x,y),~\phi=\phi(x,y)$ tales que $$\frac{\partial \phi}{\partial x}=\frac{\partial \psi}{\partial y},~~\frac{\partial \phi}{\partial y}=-\frac{\partial \psi}{\partial x}$$
Demuestre que $\phi,~\psi$ son armónicas.

Solución. Para el inciso (a) se tiene
$$div~(f+g)=\nabla\cdot (f+g)$$
$$=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\cdot (f+g)$$
$$=\frac{\partial}{\partial x}(f+g)+\frac{\partial}{\partial y}(f+g)+\frac{\partial}{\partial z}(f+g)$$
$$=\frac{\partial}{\partial x}f+\frac{\partial}{\partial x}g+\frac{\partial}{\partial y}f+\frac{\partial}{\partial y}g+\frac{\partial}{\partial z}f+\frac{\partial}{\partial z}g$$
$$=\frac{\partial}{\partial x}f+\frac{\partial}{\partial y}f+\frac{\partial}{\partial z}f+\frac{\partial}{\partial x}g+\frac{\partial}{\partial y}g+\frac{\partial}{\partial z}g$$
$$=\nabla\cdot f+\nabla\cdot g$$

Para el inciso (a) se tiene
$$div~(f+g)=\nabla\cdot (f+g)$$
$$=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\cdot (f+g)$$
$$=\frac{\partial}{\partial x}(f+g)+\frac{\partial}{\partial y}(f+g)+\frac{\partial}{\partial z}(f+g)$$
$$=\frac{\partial}{\partial x}f+\frac{\partial}{\partial x}g+\frac{\partial}{\partial y}f+\frac{\partial}{\partial y}g+\frac{\partial}{\partial z}f+\frac{\partial}{\partial z}g$$
$$=\frac{\partial}{\partial x}f+\frac{\partial}{\partial y}f+\frac{\partial}{\partial z}f+\frac{\partial}{\partial x}g+\frac{\partial}{\partial y}g+\frac{\partial}{\partial z}g$$
$$=\nabla\cdot f+\nabla\cdot g$$

Para el inciso (c) se tiene
$$\nabla\times (f+g)=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\times(f_{1}+g_{1},f_{2}+g_{2},f_{3}+g_{3})$$
$$=\left(\frac{\partial (f_{3}+g_{3})}{\partial y}-\frac{\partial (f_{2}+g_{2})}{\partial z},\frac{\partial (f_{3}+g_{3})}{\partial x}-\frac{\partial (f_{1}+g_{1})}{\partial z},\frac{\partial (f_{2}+g_{2})}{\partial x}-\frac{\partial (f_{1}+g_{1})}{\partial y}\right)$$
$$=\left[\left(\frac{\partial f_{3}}{\partial y}-\frac{\partial f_{2}}{\partial z}\right)+\left(\frac{\partial g_{3}}{\partial y}-\frac{\partial g_{2}}{\partial z}\right),\left(\frac{\partial f_{3}}{\partial x}-\frac{\partial f_{1}}{\partial z}\right)+\left(\frac{\partial g_{3}}{\partial x}-\frac{\partial g_{1}}{\partial z}\right),\left(\frac{\partial f_{2}}{\partial x}-\frac{\partial f_{1}}{\partial y}\right)+\left(\frac{\partial g_{2}}{\partial x}-\frac{\partial g_{1}}{\partial y}\right)\right]$$
$$=\nabla\times f+\nabla\times g$$

Para el inciso (d) se tiene
$$\frac{\partial \phi}{\partial x}=\frac{\partial \psi}{\partial y},~~~~\frac{\partial \phi}{\partial y}=-\frac{\partial \psi}{\partial x}$$
por lo que
$$\frac{\partial^{2} \phi}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial \psi}{\partial y}\right)$$
$$=\frac{\partial^{2}\psi}{\partial x\partial y}$$
por otro lado
$$\frac{\partial^{2} \phi}{\partial y^{2}}=\frac{\partial}{\partial y}\left(-\frac{\partial \psi}{\partial x}\right)$$
$$=-\frac{\partial^{2}\psi}{\partial y\partial x}$$
por lo tanto
$$\frac{\partial^{2} \phi}{\partial x^{2}}+\frac{\partial^{2} \phi}{\partial y^{2}}=\frac{\partial^{2}\psi}{\partial x\partial y}-\frac{\partial^{2}\psi}{\partial y\partial x}=0$$
Analogamente se tiene
$$\frac{\partial^{2} \psi}{\partial x^{2}}=\frac{\partial}{\partial x}\left(-\frac{\partial \phi}{\partial y}\right)$$
$$=-\frac{\partial^{2}\phi}{\partial x\partial y}$$
por otro lado
$$\frac{\partial^{2} \psi}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial \phi}{\partial x}\right)$$
$$=\frac{\partial^{2}\phi}{\partial y\partial x}$$
por lo tanto
$$\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}=-\frac{\partial^{2}\phi}{\partial x\partial y}+\frac{\partial^{2}\phi}{\partial y\partial x}=0$$
como las funciones $\psi,~\phi$ satisfacen la ecuación de Laplace entonces ambas funciones son armónicas.

Introducción

Así como ya hicimos comparaciones de continuidad o diferenciabilidad del límite de una sucesión de funciones a partir de sus términos, en esta ocasión lo haremos con funciones integrables.

Partimos de una sucesión de funciones donde para cada $n \in \mathbb{N}, \, f_n:[a,b] \to \mathbb{R}, \, a,b \in \mathbb{R}.$ Supón además que $(f_n)_{n \in \mathbb{N}}$ converge puntualmente a una función $f$ en $[a,b].$

Si cada una de las funciones $f_n$ son integrables, ¿será $f$ también integrable?

¿La sucesión de integrales converge? ¿Su límite coincide con la integral del límite? Veamos el siguiente:

Ejemplo.

Considera el conjunto $\mathbb{Q} \cap [0,1].$ Como es numerable, podemos identificarlo como $\mathbb{Q} \cap [0,1] = \{ x_n: n \in \mathbb{N} \}.$ Para cada $n \in \mathbb{N}$ definimos $\mathcal{X}_{\{x_n\}}$ como la función característica dada por:

Ahora, para cada $n \in \mathbb{N}$ definimos $f_n = \mathcal{X}_{\{x_1\}}+…+\mathcal{X}_{\{x_n\}}.$

Entonces la función $f_n$ es integrable en $[a,b]$ y la sucesión $(f_n)_{n \in \mathbb{N}}$ converge puntualmente a la función:

\begin{equation*}
\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} = \begin{cases}
1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
\end{cases}
\end{equation*}

Pero $\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]}$ no es integrable en $[0,1].$ Por lo tanto la convergencia puntual podría no bastar para que el límite sea integrable. ¿Y si la convergencia es uniforme?

Proposición: Sea $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones integrables en $[a,b]$ que converge uniformemente a una función $f$ en $[a,b].$ Entonces $f$ es integrable y
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$

Demostración:
Para cada $n \in \mathbb{N}$ sea $\large{\varepsilon_n} := \underset{a \leq x \leq b}{sup}|f_n(x) – f(x)|.$
Entonces $f_n \, – \, \large{\varepsilon_n} \leq f \leq f_n + \varepsilon_n,$ de modo que las integrales superior e inferior de $f$ satisfacen:
$\int_{a}^{b} (f_n \, – \, \large{\varepsilon_n}) \, dx \leq \underline{\int} f \, dx\leq \overline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx$

Entonces $0 \leq \overline{\int} f \, dx – \underline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx – \int_{a}^{b} (f_n – \large{\varepsilon_n}) \, dx = 2\large{\varepsilon_n}[b-a].$
Dado que $\large{\varepsilon_n} \to 0$ porque $(f_n)_{n \in \mathbb{N}} \to f$ de manera uniforme, se sigue que $\overline{\int} f=\underline{\int} f.$ Por lo tanto $f$ es integrable.

Podemos ver también que
$\left| \int_{a}^{b} f \, dx \, – \, \int_{a}^{b} f_n \, dx \right| \leq \large{\varepsilon_n}[b-a] \to 0$ lo que demuestra que
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$

Es importante mencionar que la convergencia uniforme no es una condición necesaria para que se de esta igualdad. Veamos el siguiente:

Ejemplo.

Para cada $n \in \mathbb{N}$ sea $f_n(x) = x^n$ con $x \in [0,1].$ En la entrada Convergencia uniforme y continuidad mostramos que la sucesión $(x^n)_{n \in \mathbb{N}} \, $ converge puntualmente a la función:

\begin{equation*}
f(x)= \begin{cases}
0 & \text{ si $0\leq x<1$}\\
1 & \text{ si $x=1$}
\end{cases}
\end{equation*}

Si calculamos las integrales tenemos que para cada $n \in \mathbb{N}:$

$\large{\int_{0}^{1}x^n} \, dx = \dfrac{1}{n+1} \to 0 = \large{\int_{0}^{1} f(x)} \, dx.$

Por lo tanto
$$ \int_{0}^{1}f(x) \, dx =\underset{n \to \infty}{lim} \, \int_{0}^{1}f_n(x) \, dx.$$

Las condiciones de este ejemplo pueden generalizarse. Antes conozcamos algunas definiciones:

Definición. Sucesión uniformemente acotada: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}$. Diremos que es uniformemente acotada en $A$ si existe $M >0 \in \mathbb{R}$ tal que $|f_n(x)| \leq M$ para cualquier $x \in A$ y cualquier $n \in \mathbb{N}.$

Definición. Sucesión acotadamente convergente: Una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}$ es acotadamente convergente en $A$ si converge puntualmente y es uniformemente acotada en $A.$

Proposición: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión acotadamente convergente en $[a,b]$ donde cada función es integrable en $[a,b],$ y que la función límite $f$ es integrable en $[a,b].$ Supongamos también que existe una partición $P$ de $[a,b],$ a saber, $P=\{x_0,x_1,…,x_m\},$ tal que la sucesión $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente convergente hacia $f$ en cada subintervalo $[c,d] \subset [a,b]$ que no contenga ninguno de los puntos $x_k \in P.$ Entonces:

$$ \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n(x) \, dx = \int_{a}^{b} f(x) \, dx.$$

Demostración:
Dado que $f$ es acotada y $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada, existe $M >0$ tal que $|f(x)| \leq M$ para cada $x \in [a,b]$ y para cualquier $n \in \mathbb{N}.$
Sea $\varepsilon > 0$ tal que $2 \varepsilon < \norm{P},$
sea $h = \frac{\varepsilon}{2m},$ donde $m$ es el múmero de subintervalos de $P,$
considera una nueva partición $P’$ de $[a,b]$ dada por:
$P’=\{x_0, \, x_0+h,\, x_1-h,\, x_1+h, \, … \, ,x_{m-1}-h, \, x_{m-1}+h, \, x_m-h, \, x_m\}$

Nota que la función $|f-f_n|$ es integrable en $[a,b]$ y es acotada por $2M.$ Consideremos la integral de esta función en cada uno de los intervalos de la nueva partición $P’.$

Por un lado, consideremos la suma de las integrales de $|f-f_n|$ tomadas sobre los intervalos que sí tienen algún punto de $P,$ es decir los intervalos
$[x_0,x_0+h], \, [x_1-h,x_1+h],…,[x_{m-1}-h,x_{m-1}+h], \, [x_m-h,x_m].$

La suma está dada por:

\begin{align*}
&\int_{x_0}^{x_0+h} |f-f_n|(x)\, dx + \int_{x_1-h}^{x_1+h} |f-f_n|(x)\, dx +…+ \int_{x_{m-1}-h}^{x_{m-1}+h} |f-f_n|(x)\, dx + \int_{x_m-h}^{x_m} |f-f_n|(x)\, dx \\
\leq & 2M(x_0+h-x_0) + 2M(x_1+h-(x_1-h))+…+2M(x_{m-1}+h-(x_{m-1}-h))+2M(x_m-(x_m-h)) \\
=&2Mh+2M(2h)+…+2M(2h)+2Mh \\
=&2M(2hm) \\
=&2M \varepsilon
\end{align*}

El subconjunto restante de $[a,b]$ lo llamaremos $S.$ Está formado por un número finito de intervalos cerrados en los que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente hacia $f$ (pues no tiene ningún punto de $P$). Por consiguiente, existe $N \in \mathbb{N}$ tal que para cada $x \in S,$ si $n \geq N \,$ se cumple que
$$|f(x)-f_n(x)| < \varepsilon$$

De modo que la suma de las integrales de $|f-f_n|$ sobre los intervalos de $S$ es a lo sumo $\large{\varepsilon} (b-a),$ luego para cada $n \geq N:$

$\int_{a}^{b}|f(x)-f_n(x)|dx \leq (2M + b-a) \large{\varepsilon} \, \to \, 0.$

Esto demuestra que $\int_{a}^{b}f_n(x)dx \to \int_{a}^{b}f(x)dx$ cuando $n \to \infty .$

En la última sección de Análisis Matemático I hablaremos de la integral de Riemann-Stieltjes, que es un concepto que generaliza la integral de Riemann. La proposición vista aquí se puede expresar como sigue:

Proposición. Sucesión de funciones Riemann-Stieltjes: Sea $\alpha$ monótona en $[a,b].$ Supón que para cada $n \in \mathbb{N}, \, f_n \in \mathcal{R}(\alpha)$ en $[a,b].$ Si $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f$ en $[a,b]$ entonces $f \in \mathcal{R}(\alpha)$ en $[a,b]$ y:

$$\int_{a}^{b} f \, d \alpha = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n \, d \alpha .$$

Más adelante…

Hablaremos de series de funciones y del límite de ellas. Así conoceremos el concepto de convergencia uniforme pero ahora en sumas infinitas.

Tarea moral

1. Sea $f_n$ como en el primer ejemplo. Prueba que en efecto la sucesión $(f_n)_{n \in \mathbb{N}} \,$ no converge uniformemente a la función:
   \begin{equation*}
   \mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} = \begin{cases}
   1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
   0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
   \end{cases}
   \end{equation*}
2. Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones acotadas con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}, \,$ tal que converge uniformemente a una función $f:A \to \mathbb{R}.$ Demuestra que $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada en $A.$
3. Regresa luego de ver la integral de Riemann-Stieljes y demuestra la última proposición de esta sección.

Enlaces:

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

Cuando los puntos de un espacio métrico son enviados al mismo espacio a través de una función, conviene saber si habrá algún punto que se envíe a sí mismo, es decir, que se conserve fijo. Las próximas entradas nos mostrarán cuándo esa situación ocurre y resultados interesantes derivados de ello. Comencemos con la primera:

Definición. Función contracción: Sea $(X,d)$ un espacio métrico y $ \phi: X \to X$ una función. Diremos que $\phi$ es una contracción si existe $\alpha \in (0,1)$ tal que para cualesquiera $x,y \in X$ se cumple que:
$$d(\phi(x),\phi(y)) \leq \alpha \, d(x,y)$$

Podemos pensar entonces, que una función contracción, justamente hace que los puntos sean más cercanos entre sí de lo que eran originalmente.

Nota que una contracción es también una función Lipschitz continua con constante de Lipschitz $c<1.$ Este concepto se vio en la entrada Más conceptos de continuidad. Demos paso a otra:

Definición. Punto fijo: Sea $X$ un espacio métrico y $x^* \in X.$ Decimos que $x^*$ es punto fijo de la función $\phi:X \to X$ si $\phi(x^*)=x^*.$

Para ejemplificar estas ideas, veamos dos funciones que son contracciones y cómo existe un punto fijo en los casos a mencionar:

Ejemplos. $f(x)=\dfrac{x}{2},$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
d(f(x),f(y))&=|f(x)-f(y)| \\
&=\left|\frac{x}{2}-\frac{y}{2} \right| \\
&=\left|\frac{1}{2}(x-y) \right| \\
&=\frac{1}{2}|x-y| \\
&=\frac{1}{2}d(x,y)
\end{align*}

Por lo tanto $d(f(x),f(y)) \leq \frac{1}{2}d(x,y)$ lo que demuestra que $f$ es una contracción con $\alpha = \frac{1}{2}$.

La siguiente imagen representa la diferencia de las distancias antes y después de aplicar la función en dos puntos $x$ y $y.$ Basta con observar las proyecciones de la gráfica de $f$ en los ejes coordenados.

Ahora busquemos un punto fijo:

\begin{align*}
f(x)&=x \\
\iff \frac{x}{2}&=x \\
\iff x&=2x \\
\iff 0&=2x-x \\
\iff 0&=x
\end{align*}

Es decir, $0$ es el único punto fijo de $f.$

A continuación, vamos a construir una sucesión de la siguiente manera:

Toma cualquier $x_0 \in X$

$x_1:=f(x_0)=\dfrac{x_0}{2}$

$x_2 :=f(x_1)=\dfrac{\dfrac{x_0}{2}}{2}=\dfrac{x_0}{2^2}$

$x_3:=f(x_2)=\dfrac{\dfrac{x_0}{2^2}}{2}=\dfrac{x_0}{2^3}$
.
.
.
$x_k:=f(x_{k-1})=\dfrac{x_0}{2^k}$

Entonces la sucesión se define como $(x_n)_{n \in \mathbb{N}} \, $ donde $x_n = \dfrac{x_0}{2^n}.$
Nota que tiende a $0$ en $\mathbb{R}.$

En las siguientes gráficas podemos observar el comportamiento de la sucesión:

Sea $x_0 \in X.$ Mostramos la gráfica de la función $f(x)=\dfrac{x}{2}$ y la función identidad $ \, \mathcal{I}(x)=x.$
Señalamos los términos $x_0$ y $x_1 =f(x_0)=\dfrac{x_0}{2}$ y la distancia entre $f(x_0) \,$ y $\, f(x_1)$ vistos como proyecciones de las gráficas de los puntos sobre los ejes del plano cartesiano:

Si continuamos, generamos el punto $x_2=f(x_1).$ Gráficamente también es visible que las distancias entre dos puntos disminuyen en el eje vertical al continuar con las iteraciones.

Podemos observar que los puntos convergen a $0$ que recordemos, es también el punto fijo de $f$.

Veamos otro caso:

Ejemplo. $f(x)=\dfrac{x}{2}+6,$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}+6$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
|f(x)-f(y)|&=\left|\frac{x}{2}+6- \left(\frac{y}{2}+6 \right) \right| \\
&= \left|\frac{1}{2}(x-y) \right| \\
&= \frac{1}{2}|x-y|
\end{align*}

De modo que $d(f(x),f(y))\leq \frac{1}{2}d(x,y)$ lo cual prueba que $f$ es una contracción con $\alpha = \frac{1}{2}.$

Busquemos puntos fijos:

\begin{align*}
&f(x)&=x \\
\iff &\frac{x}{2}+6 &=x \\
\iff &6 &\, = \frac{x}{2} \\
\iff &12 & = x
\end{align*}

Entonces $12$ es el único punto fijo de $f.$

El siguiente gráfico nos confirma estos resultados para la sucesión generada a partir de un punto $x_0 \in X$ donde para cada $n \in \mathbb{N}, \, x_n=f(x_{n-1}).$

Queda como ejercicio al lector demostrar que $(x_n)_{n \in \mathbb{N}} \to 12$ en $\mathbb{R}.$

Esto da pie para enunciar el:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}}$ converge a un punto $x^* \in X.$ $\, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0, \phi (x_0)).$$

Por lo pronto demostremos que si una contracción tiene un punto fijo entonces este es único.

Sean $x, y \in X$ tales que $\phi(x)=x \,$ y $\, \phi(y)=y.$ Como $\phi$ es una contracción se tiene que:

$$d(x,y) = d(\phi(x),\phi(y)) \leq \alpha d(x,y) $$

Como $\alpha <1$ se sigue que:
$$\alpha d(x,y) \leq d(x,y)$$
Por lo tanto $d(x,y)=d(x,y),$ y en consecuencia $x=y.$

Más adelante…

Continuaremos con la demostración del teorema de punto fijo de Banach. En la siguiente entrada comprobaremos que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy.

Tarea moral

1. Sea $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = \dfrac{x}{2} +6$ en el espacio euclidiano. Sea $x_0 \in \mathbb{R}, \,$ prueba que la sucesión $(f^n(x_0))_{n \in \mathbb{N}} \, $ converge a $12.$
2. Sea $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ una función continua. Demuestra que tiene al menos un punto fijo.
3. Da un ejemplo de una función continua $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ con una infinidad de puntos fijos.
4. Prueba que si $f: \mathbb{R} \to \mathbb{R}$ y para cada $x \in \mathbb{R}, \, |f'(x)| \leq M<1$ entonces $f$ es una contracción.
5. Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X \,$ que satisface que para todo $x \neq y \in X, \, d(\phi(x), \phi(y)) < d(x,y)$ pero que no tenga ningún punto fijo.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Ejemplo. Se da el nivel cero de una función diferenciable $F:\mathbb{R}^{4}\rightarrow \mathbb{R}$ y un punto P perteneciente a este nivel. Diga en cada caso si en los alrededores del punto p es posible ver la gráfica de F como la gráfica de una función diferenciable del tipo

$$a)~u=u(x,y,z)$$ $$b)~z=z(x,y,u)$$$$c)~y=y(x,u,z)$$ $$d)~x=x(y,z,u)$$ para $x^{2}+y^{2}+z^{2}+u^{u}=4$ en $p=(1,1,1,1)$

Solución. En este caso para todos los incisos podemos definir $f(x,y,z,u)=x^{2}+y^{2}+z^{2}+u^{u}-4=0$ y para el inciso a, se tiene
$$\frac{\partial F}{\partial u}=2u\left.\right|_{(1,1,1,1)}=2\neq0$$ por lo tanto es posible ver a la gráfica de F como una función diferenciable del tipo $u=u(x,y,z)$ y sus derivadas parciales seran:

$$\frac{\partial u}{\partial x}(1,1,1,1)=-\frac{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial u}\left.\right|{(1,1,1,1)}}=-\frac{2x}{2u}=-1$$
$$\frac{\partial u}{\partial y}(1,1,1,1)=-\frac{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial u}\left.\right|{(1,1,1,1)}}=-\frac{2y}{2u}=-1$$
$$\frac{\partial u}{\partial z}(1,1,1,1)=-\frac{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial u}\left.\right|{(1,1,1,1)}}=-\frac{2z}{2u}=-1$$

para el inciso b, se tiene

$$\frac{\partial F}{\partial z}=2z\left.\right|{(1,1,1,1)}=2\neq0$$ por lo tanto es posible ver a la gráfica de F como una función diferenciable del tipo $z=z(x,y,u)$ y sus derivadas parciales seran: $$\frac{\partial z}{\partial x}(1,1,1,1)=-\frac{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}=-\frac{2x}{2z}=-1$$ $$\frac{\partial z}{\partial y}(1,1,1,1)=-\frac{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}=-\frac{2y}{2z}=-1$$ $$\frac{\partial z}{\partial z}(1,1,1,1)=-\frac{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial z}\left.\right|_{(1,1,1,1)}}=-\frac{2u}{2z}=-1$$

para el inciso c, se tiene

$$\frac{\partial F}{\partial y}=2y\left.\right|{(1,1,1,1)}=2\neq0$$ por lo tanto es posible ver a la gráfica de F como una función diferenciable del tipo $y=y(x,z,u)$ y sus derivadas parciales seran: $$\frac{\partial y}{\partial x}(1,1,1,1)=-\frac{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}=-\frac{2x}{2y}=-1$$ $$\frac{\partial y}{\partial z}(1,1,1,1)=-\frac{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}=-\frac{2z}{2y}=-1$$ $$\frac{\partial y}{\partial u}(1,1,1,1)=-\frac{\frac{\partial F}{\partial u}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}=-\frac{2u}{2y}=-1$$ para el inciso d, se tiene $$\frac{\partial F}{\partial x}=2x\left.\right|{(1,1,1,1)}=2\neq0$$ por lo tanto es posible ver a la gráfica de F como una función diferenciable del tipo $x=x(y,z,u)$ y sus derivadas parciales seran:
$$\frac{\partial x}{\partial y}(1,1,1,1)=-\frac{\frac{\partial F}{\partial y}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}=-\frac{2x}{2y}=-1$$
$$\frac{\partial x}{\partial z}(1,1,1,1)=-\frac{\frac{\partial F}{\partial z}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}=-\frac{2z}{2y}=-1$$
$$\frac{\partial x}{\partial u}(1,1,1,1)=-\frac{\frac{\partial F}{\partial u}\left.\right|{(1,1,1,1)}}{\frac{\partial F}{\partial x}\left.\right|{(1,1,1,1)}}=-\frac{2u}{2y}=-1$$

Teorema de la Función Implicita (version (4))

Consideremos ahora el sistema
$$au+bv-k_{1}x=0$$ $$cu+dv-k_{2}y=0$$
con $a,b,c,d,k_{1},k_{2}$ constantes. Nos preguntamos cuando podemos resolver el sistema para $u$ y $v$ en términos de $x$ y $y$.
Si escribimos el sistema como
$$au+bv=k_{1}x$$ $$cu+dv=k_{2}y$$
y sabemos que este sistema tiene solución si $det \left|\begin{array}{cc} a&b \\c&d\end{array}\right|\neq0$ en tal caso escribimos
$u=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b \\c&d\end{array}\right|}(k_{1}dx-k_{2}by)$, $~~~$ $v=\displaystyle \frac{1}{det \left|\begin{array}{cc} a&b \\c&d\end{array}\right|}(k_{2}ay-k_{1}cx)$.
Esta solución no cambiaria si consideramos
$$au+bv=f_{1}(x,y)$$ $$cu+dy=f_{2}(x,y)$$

donde $f_{1}$ y $f_{2}$ son funciones dadas de $x$ y $y$. La posibilidad de despejar las variables $u$ y $v$ en términos de $x$ y $y$ recae sobre los coeficientes de estas variables en las ecuaciones dadas.

Ahora si consideramos ecuaciones no lineales en $u$ y $v$ escribimos el sistema como
$$g_{1}(u,v)=f_{1}(x,y)$$ $$g_{2}(u,v)=f_{2}(x,y)$$

nos preguntamos cuando del sistema podemos despejar a $u$y $v$ en términos de $x$ y $y$. Mas generalmente, consideramos el problema siguiente, dadas las funciones $F$ y $G$ de las variables $u,v,x,y$ nos preguntamos cuando de las expresiones

$$F(x,y,u,v)=0$$ $$G(x,y,u,v)=0$$

podemos despejar a $u$ y $v$ en términos de $x$ y $y$ en caso de
ser posible diremos que las funciones $u=\varphi_{1}(x,y)$ y
$v=\varphi_{2}(x,y)$ son funciones implícitas dadas. Se espera que
$\exists’$n funciones $u=\varphi_{1}(x,y)$ y
$v=\varphi_{2}(x,y)$ en
$$F(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$$ $$G(x,y,\varphi_{1}(x,y),\varphi_{2}(x,y)$$
con $(x,y)$ en alguna vecindad $V$. Suponiendo que existen $\varphi_{1}$ y $\varphi_{2}$ veamos sus derivadas

$$\displaystyle \frac{\partial F}{\partial x}\displaystyle \frac{\partial x}{\partial
x}+\displaystyle \frac{\partial F}{\partial y}\displaystyle \frac{\partial y}{\partial x}+\displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial
x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0 \Rightarrow \displaystyle \frac{\partial F}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial F}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial F}{\partial x}$$

$$\displaystyle \frac{\partial G}{\partial x}\displaystyle \frac{\partial x}{\partial x}+\displaystyle \frac{\partial G}{\partial y}\displaystyle \frac{\partial y}{\partial x}+\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=0 ~~ \Rightarrow ~~ \displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial x}+\displaystyle \frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial x}=-\displaystyle \frac{\partial G}{\partial x}$$

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas $\displaystyle \frac{\partial u}{\partial x}$ y $\displaystyle \frac{\partial v}{\partial x}$. Aquí se ve que para que el sistema tenga solución

$det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|\neq0$ en $(P)$ (el $det$ Jacobiano) y según la regla de Cramer

$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
x}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial x}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{\det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$, $~~ $ $\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial x} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial x}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ (con los dos $det$ Jacobianos).

Análogamente si derivamos con respecto a $y$ obtenemos
$$\displaystyle \frac{\partial F}{\partial
u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial F}{\partial v}\displaystyle \frac{\partial
v}{\partial y}=-\displaystyle \frac{\partial F}{\partial y}$$ ,$$\displaystyle \frac{\partial G}{\partial u}\displaystyle \frac{\partial u}{\partial y}+\displaystyle
\frac{\partial G}{\partial v}\displaystyle \frac{\partial v}{\partial y}=-\displaystyle \frac{\partial G}{\partial y}$$
de donde

$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{array}{cc} \displaystyle -\frac{\partial F}{\partial
y}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle -\frac{\partial G}{\partial y}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}{det
\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}$,$~~$ $\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle -\frac{\partial F}{\partial y} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle -\frac{\partial G}{\partial y}\end{array}\right|}{det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|}$ (con los dos $det$ Jacobianos).

Al determinante $det \left|\begin{array}{cc} \displaystyle
\frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial G}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|$ lo llamamos Jacobiano y lo denotamos por $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}$.

Teorema de la Función Implícita (Versión 4)

Teorema 1. Considere las funciones $z_{1}=F(x,y,u,v)$ y $z_{2}=G(x,y,u,v)$. Sea $P=(x,y,u,v) \in \mathbb{R}^{4}$ un punto tal que $F(P)=G(P)=0$.
Suponga que en una bola $\textit{B} \in \mathbb{R}^{4}$ de centro $P$ las funciones $F$ y $G$ tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano $\displaystyle \frac{\partial (F,G)}{\partial (u,v)}(P)\neq0$ entonces las expresiones
$F(x,y,u,v)=0$ y $G(x,y,u,v)=0$ definen funciones (implícitas) $u=\varphi_{1}(x,y)$ y $v=\varphi_{2}(x,y)$ definidas en una vecindad $v$ de $(x,y)$ las cuales tienen derivadas parciales continuas en $v$ que se pueden calcular como se menciona arriba.

Demostración. Dado que $$det \left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial v}\end{array}\right|\neq 0$$ entonces $\displaystyle{\frac{\partial F}{\partial u}(p)}$, $\displaystyle{\frac{\partial F}{\partial v}(p)}$, $\displaystyle{\frac{\partial G}{\partial u}(p)}$, $\displaystyle{\frac{\partial G}{\partial v}(p)}$ no son cero al mismo tiempo, podemos suponer sin pérdida de generalidad que $\displaystyle{\frac{\partial G}{\partial v}(p)}\neq0$. Entonces la función $z_{1}=G(x,y,u,v)$ satisface las hipótesis del T.F.I y en una bola abierta con centro p, v se puede escribir como $v=\psi(x,y,u)$. Hacemos ahora $$H(x,y,u)=F(x,y,u,\psi(x,y,u))$$ y tenemos que $$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial F}{\partial u}\frac{\partial u}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}$$ por otro lado
$$\frac{\partial \psi}{\partial u}=-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}$$ por lo tanto $$\frac{\partial H}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\frac{\partial \psi}{\partial u}=\frac{\partial F}{\partial u}+\frac{\partial F}{\partial v}\left(-\frac{\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\right)=\frac{\frac{\partial F}{\partial u}\frac{\partial G}{\partial v}-\frac{\partial F}{\partial v}\frac{\partial G}{\partial u}}{\frac{\partial G}{\partial v}}\neq0$$por lo tanto para $H(x,y,u)=0$ tenemos que existe una función $u=\varphi_{1}(x,y)$ y por lo tanto $v=\psi(x,y,u)=\psi(x,y,\varphi_{1}(x,y,u))=\varphi_{2}(x,y)$ y por tanto $u,v $ se pueden expresar en términos de $x,y$ en una vecindad de $p$ $\square$

Ejemplo. Analizar la solubilidad del sistema
$$e^{u}+e^{v}=x+ye$$ $$ue^{u}+ve^{v}=xye$$

Solución. En este caso definimos
$$F(x,y,u,v)=e^{u}+e^{v}-x-ye=0$$ $$G(x,y,u,v)=ue^{u}+ve^{v}-xye=0$$
por lo que el sistema tendrá solución si $\displaystyle{\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|}\neq 0$
En este caso
$$\det\left|\begin{array}{cc} \displaystyle \frac{\partial F}{\partial
u}&\displaystyle \frac{\partial F}{\partial v}
\\ \displaystyle \frac{\partial F}{\partial u}&\displaystyle \frac{\partial G}{\partial
v}\end{array}\right|=\det\left|\begin{array}{cc} \displaystyle e^{u}&\displaystyle e^{v}\\ ue^{u}+e^{e^{u}}&ve^{v}+e^{v}\end{array}\right|=e^{u}\left(ve^{v}+e^{v}\right)-e^{v}\left(ue^{u}+e^{u}\right)=ve^{u+v}-ue^{v+u}\neq 0$$
por lo tanto u y v se pueden ver en términos de x,y $\therefore$ se pueden calcular sus parciales en $u=0,~v=1,~x=1, ~y=1$ que es este caso dan

$$\displaystyle \frac{\partial u}{\partial x}=-\frac{\det
\left|\begin{matrix}-1&-ye\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-(ve^{v}+e^{v})+e^{v}ye}{ve^{u+v}-ue^{v+u}}\left.\right|{(1,1,1,1)}=\frac{2e-e^{2}}{e}=2-e$$ $$\displaystyle \frac{\partial v}{\partial x}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-1&-ye\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-ye^{u}e+ue^{u}+e^{u}}{ve^{u+v}-ue^{v+u}}\left.\right|{(1,1,1,1)}=\frac{e-1}{e}=1-e^{-1}$$ $$\displaystyle \frac{\partial u}{\partial y}=-\frac{\det
\left|\begin{matrix}-e&-xe\\e^{v}&ve^{v}+e^{v}\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e(ve^{v}+e^{v})+e^{v}xe}{ve^{u+v}-ue^{v+u}}\left.\right|{(1,1,1,1)}=\frac{e^{2}+e^{2}-e^{2}}{e}=e$$ $$\displaystyle \frac{\partial v}{\partial y}=-\frac{\det \left|\begin{matrix}e^{u}&ue^{u}+e^{u}\\-e&-xe\end{matrix}\right|}{ve^{u+v}-ue^{v+u}}=-\frac{-e^{u}xe+e(ue^{u}+e^{u})}{ve^{u+v}-ue^{v+u}}\left.\right|{(1,1,1,1)}=\frac{e-e}{e}=0$$