Diferenciales de funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$

Tenemos que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es diferenciable si
$$f(x_{o}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
cumple
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Esto se puede escribir como
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$

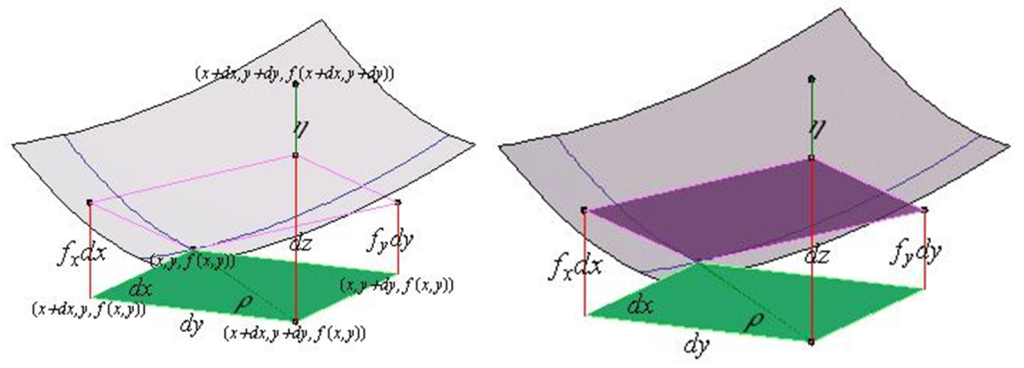
tomando
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z$$
$$\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x$$
$$\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}=\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
tenemos que
$$\triangle z=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y+r(\triangle x,\triangle y)$$
haciendo $\triangle x,~\triangle y\rightarrow 0$ tenemos
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$
$\textbf{Definición.}$Si $z=f(x,y)$ es una función diferenciable, la diferencial de f denotada $dz$ se define
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$

$\textbf{Ejemplo.}$ Calcular la diferencial de $z=4x^{2}-xy$\En este caso
$$dz=\frac{\partial (4x^{2}-xy)}{\partial x}dx+\frac{\partial (4x^{2}-xy)}{\partial y}dy=(8x-y)dx-xdy$$

Ahora bien
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z\approx \frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
expresa el cambio aproximado de $z=f(x,y)$ cuando $(x,y)$ pasa a $(x+\triangle x,y+\triangle y)$

Ejemplo. Aproximar el cambio de $z=4x^{2}-xy$ cuando $(x,y)$ pasa de $(2,1)$ a $(2.1,1.5)$\
En este caso tomamos $x_{0}=2$, $y_{0}=1$, $\triangle x=0.1$ y $\triangle y=.5$ y el valor de cambio será
$$\frac{\partial f}{\partial x}(2,1)\triangle x+\frac{\partial f}{\partial y}(2,1)\triangle y=(15)(0.1)-2(0.5)=1.5$$
mientras que
$$f(2.1,1.5)-f(2,1)=14.49-14=0.49$$
por lo tanto en la aproximacion se cometió un error de $0.01$

Ejemplo. Usando diferenciales se quiere calcular aproximadamente
$$A=\frac{0.97}{\sqrt{15.05}+\sqrt[3]{0.98}}$$

Solución. Considerando la función
$$f(x,y,z)=\frac{x}{\sqrt{y+\sqrt[3]{z}}}$$
con $x=1$, $y=15$, $z=1$, $dx=-0.03$, $dy=0.05$ y $dz=-0.02$ se tiene
$$f(x+dx,y+dy,z+dz)=f(x,y,z)+df(x,y,z)$$
en este caso
$$f(x,y,z)=f(1,15,1)=\frac{1}{4}$$
$$\frac{\partial f}{\partial x}=\frac{1}{\sqrt{y}+\sqrt[3]{z}},~\frac{\partial f}{\partial y}=-\frac{x}{2}\left(y+\sqrt[3]{z}\right)^{\frac{-3}{2}},~\frac{\partial f}{\partial z}=-\frac{x}{2}(y+\sqrt[3]{z})^{\frac{-3}{2}}\frac{1}{3}z^{\frac{-2}{3}}$$
evaluando en $(1,15,1)$ se tiene
$$\frac{\partial f}{\partial x}(1,15,1)=\frac{1}{4},~\frac{\partial f}{\partial y}(1,15,1)=-\frac{1}{128},~\frac{\partial f}{\partial z}(1,15,1)=-\frac{1}{384}$$
de modo que
$$df(1,15,1)=\frac{1}{4}(-0.03)-\frac{1}{128}(0.05)-\frac{1}{384}(-0.02)=-\frac{3.01}{384}$$
por lo que
$$A=\frac{1}{4}-\frac{3.01}{384}=0.242161$$
(el valor es $0.2421726$)

Diferencial de orden 2

Si $\displaystyle{df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy}$ entonces una diferencial de orden 2 seria:
$$d^{2}f=d(df)=d\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dy$$
$$=\left(\frac{\partial^{2} f}{\partial x^{2}}dx+\frac{\partial^{2} f}{\partial x\partial y}dy\right)dx+\left(\frac{\partial^{2} f}{\partial y\partial x}dx+\frac{\partial^{2} f}{\partial y^{2}}dy\right)dy=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y\partial x}dydx+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
$$=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
Por lo tanto

$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$

Ejemplo. Hallar la diferencial de orden 2 para $f(x,y)=e^{x^{2}+y^{y}}$

Solución. En este caso tenemos la fórmula
$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
vamos a calcular las derivadas parciales correspondientes
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}=2xe^{x^{2}+y^{2}}$$
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}=2ye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial(2xe^{x^{2}+y^{2}})}{\partial x}=4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial(2ye^{x^{2}+y^{2}})}{\partial y}=4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial (2xe^{x^{2}+y^{2}})}{\partial y}=4xye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x\partial y}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial (2ye^{x^{2}+y^{2}})}{\partial x}=4xye^{x^{2}+y^{2}}$$
y la diferencial de orden 2 sería:
$$d^{2}f=\left(4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dx^{2}+8xye^{x^{2}+y^{2}}dxdy+\left(4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dy^{2}$$

Diferencial de orden 3

Si $\displaystyle{d^{2}f=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}}$ entonces una diferencial de orden 3 seria:
$$d^{3}f=d(d^{2}f)=d\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)=$$
$$\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dy=$$

$$\left(\frac{\partial^{3} f}{\partial x^{3}}dx^{2}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dxdy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dy^{2}\right)dx+\left(\frac{\partial^{3} f}{\partial x^{2} \partial y}dx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy+\frac{\partial^{3} f}{\partial y^{3}}dy^{2}\right)dy=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial x^{2} \partial y}dydx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$
Por lo tanto
$$d^{3}f=d(d^{2}f)=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$

Diferencial de orden 3

Si $\displaystyle{d^{3}f=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}}$ entonces una diferencial de orden 4 seria:
$$d^{4}f=d(d^{3}f)=\frac{\partial^{4} f}{\partial x^{4}}dx^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}dx^{3}dy+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}dx^{2}dy^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}dxdy^{3}+\frac{\partial^{4} f}{\partial y^{4}}dy^{4}$$

Diferencial de orden n

$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$

que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$