Introducción

Definición. Sea ${\overline{x_{k}}}$ una sucesión de puntos de $\mathbb{R}^{n}$. Se dice que ${\overline{x_{k}}}$ es una sucesión de Cauchy si dado $\epsilon>0$ $\exists N_{0}\in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x_{l}}|<\epsilon$ $\forall k,l\geq N_{0}$

Teorema 1. Una sucesión $\overline{x_{k}}\in \mathbb{R}^{n}$ es convergente si y solo si cumple el criterio de Cauchy

Demostración. $\Rightarrow$ Suponemos que ${\overline{x_{k}}}\rightarrow \overline{x}$ $\therefore$ $|\overline{x_{k}}-\overline{x}|<\epsilon$ $\forall k>N_{0}$. Se tiene entonces que $$|\overline{x_{k}}-\overline{x_{l}}|=|\overline{x_{k}}-\overline{x}+\overline{x}-\overline{x_{l}}|\leq |\overline{x_{k}}-\overline{x}|+|\overline{x}-\overline{x_{l}}|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon$$ $\forall k,l>N_{0}$ $\therefore$ ${\overline{x_{k}}}$

$\Leftarrow$ Supongamos que ${\overline{x_{k}}}$ cumple la condición de Cauchy por tanto se tiene que: $$|\overline{x_{k}}-\overline{x_{l}}|<\epsilon\Rightarrow |x_{i,k}-x_{i,l}|<\epsilon\quad \forall i\Rightarrow {x_{i,k}}\quad cumple\quad Cauchy$$ $\therefore$ $x_{i,k}$ es convergente $\forall i$ $\therefore$ ${\overline{x_{k}}}$ es convergente. $\square$

Teorema 2. (Bolzano-Wierstrass) Toda sucesión $\overline{x_{k}}$ en $\mathbb{R}^{n}$ acotada tiene un punto limite. Dicho de otro modo, toda sucesión en $\mathbb{R}^{n}$ tiene una subsucesión convergente

Demostración. Sea $\overline{x_{k}}$ en $\mathbb{R}^{n}$ suponiendo $\overline{x_{k}}$ es acotada, entonces cada $x_{i,k}$ es acotada $\therefore$ según el teorema de Bolzano-Wierstrass para sucesiones en $\mathbb{R}$, ${x_{i,k}}$ tiene una subsucesión convergente $\alpha_{i,k}$ la cual es una sucesión convergente, $\therefore$ podemos formar la sucesiòn $\overline{x_{\alpha,k}}={x_{\alpha,1,k},x_{\alpha,2,k},…,x_{\alpha,n,k}}$ la cual es una sucesión convergente, pero $\overline{x_{\alpha,k}}$ es subsucesión de $\overline{x_{k}}$ $\therefore$ $\overline{x_{k}}$ tiene una subsucesión convergente. $\square$

Criterio de Convergencia de Cauchy

Una colección $g$ de conjuntos abiertos cuya unión contiene a $K$ con frecuencia se llama cubierta de $K$. De modo que el requisito para que $K$ sea compacto es que toda cubierta $g$ de $K$ se pueda sustituir por una cubierta finita $g$ de $K$.

Ejemplo. Sea $k={x_{1},x_{2},…,x_{m}}$ un subconjunto finito de $\mathbb{R}^{n}$ si $G={G_{\alpha}}$ es una colección de abiertos tal que $k\subset{G_{\alpha}}$ y si todo punto de k pertenece a algún subconjunto de ${G_{\alpha}}$ entonces cuando más m subconjuntos de ${G_{\alpha}}\supset k$ $\therefore$ k es un subconjunto compacto de $\mathbb{R}^{n}$.

Ejemplo. Considere al subconjunto $H=\left\{x\in \mathbb{R}| x\geq0\right\}$. Sea $G_{n}=(-1,n)$ $n\in \mathbb{N}$ de tal manera que ${G_{n}| n\in \mathbb{N}}$ sea una colección de subconjuntos abiertos de $\mathbb{R}$ cuya union contenga a $H$. Si ${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}|n\in\mathbb{N}}$. Sea $M=sup\left\{n_{1},n_{2},…,n_{k}\right\}$ de tal manera que $G_{n_{j}} \subset G_{n_{k}}$ de aquí deducimos que $G_{M}$ es la unión de
${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$. Sin embargo el número real $M$ no pertenece a $G_{M}$ y por lo tanto no pertenece a $\bigcup_{j=1}^{k}G_{n_{j}}$. En consecuencia, ninguna unión finita de ${G_{n}|n\in\mathbb{N}}$ puede contener a $H$.$\therefore$ $H$ no es compacto.

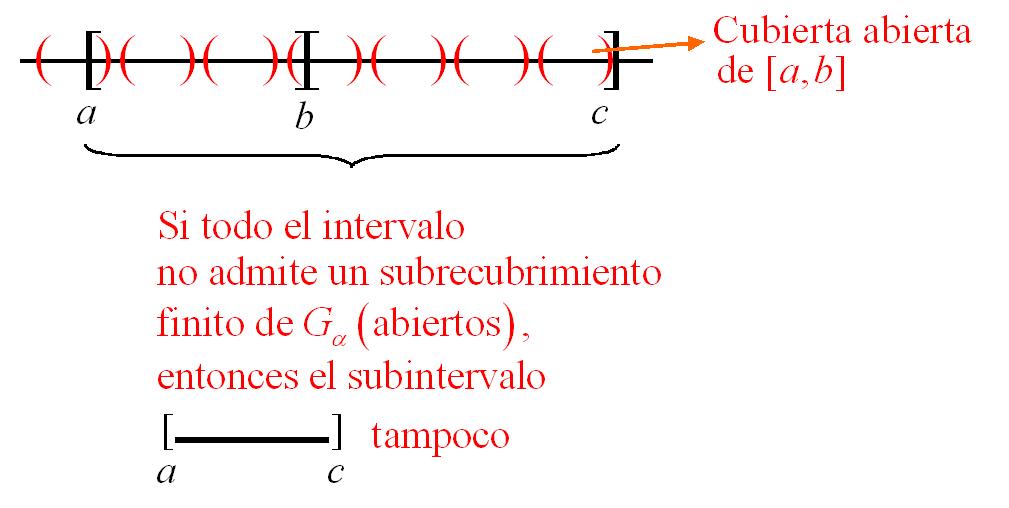
Ejemplo. Demuestrese que todo intervalo cerrado $[a, b]$ de $\mathbb{R}$ es compacto.
Demostración. Supongamos un recubrimiento abierto $[a, b]$ tal que no admite subrecubrimiento finito. Entonces tampoco existe un subrecubrimiento finito para

$[a, c]$ $[c; b]$ con $c$ punto medio. Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $p$ el punto de intersección y sea $U$ el recubrimiento que contiene a $p$ y sea $[p-\varepsilon,p+\varepsilon]\subset U$. Entonces existe $r \in \mathbb{N}$ tal que $\forall n > r$,$\frac{b-a}{2^n} < \varepsilon$ y $\forall \, n\geq r$ $[a_n,b_n]\subset U \underset{\circ}{\bigtriangledown}$ ya que ningun $[a_k, b_k]$ admitía un subrecubrimiento finito.

Ejemplo. Sea $H=(0,1)$ en $\mathbb{R}$. Si $G_{n}={\frac{1}{n},1-\frac{1}{n}}$ para $n>0$ entonces la colección${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}| n>2}$. Sea $M=sup{n_{1},…,n_{k}}$ de tal manera que $G_{n_{j}} \subset G_{M}$ se ifiere que $G_{M}$ es la unión de ${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ sin embargo el número real $\frac{1}{m}$ pertenece a $H$ pero no pertenece a $G_{M}$ $\therefore$ ninguna subcolecciónfinita de $\left\{G_{n}~|~ n>2\right\}$ puede formar una subcolección finita para $H$ $\therefore$ $H$ no es compacto.

Compactos por Sucesiones

Teorema 3. Sea $A\subset \mathbb{R}^{n}$ tal que para todo recubrimiento abierto $\left\{A_{i}\right\}_{i\in I}$ admite un subrecubrimiento finito es decir $\displaystyle{A\subset \bigcup_{i}^{n}A_{i}}$ entonces toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$

Demostración. Supongamos que exite una sucesión $\overline{x}{n}\in A$ que no tuviera una subsucesión convergente (en este caso $\overline{x}_{n}$ tiene infinitos elementos). Sea $\overline{x}\in A$ como $\lim_{n\rightarrow\infty}\overline{x}{n}\neq \overline{x}$, existe $\delta{x}>0$ tal que en la bola abierta $B(\overline{x},\delta_{x})$ solo hay a lo más un número finito de elementos de $\overline{x}_{n}$. Entonces la familia de abiertos ${B(\overline{x},\delta{x})}$ es un recubrimiento abierto de A; por hipótesis este recubrimiento admite un subrecubrimiento finito $A_{x_{1}},A_{x_{2}},…,A_{x_{n}}$ de estos abiertos. Por lo tanto los infinitos elementos de $\overline{x}_{n}$ que estan en $A$ pueden ser cubiertos por un número finito de conjuntos abiertos $\underset{\circ}{\bigtriangledown}$ pues cada $A{x_{i}}$ cubre a lo mas un número finito de elementos de $A$.

Teorema 4. Si toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$ entonces $A$ es cerrado y acotado.

Demostración. A es cerrado. Sea $\overline{a}\in\mathbb{R}^{n}$ tal que $\overline{a}\in \partial A$ vamos a ver que $\overline{a}\in A$. Como $\overline{a}\in \partial A$ entonces $\forall~r>0$ $B(\overline{a},r)\bigcap A\neq \emptyset$ consideremos ahora $r=\frac{1}{n}$ y en cada bola abierta $\displaystyle{(\overline{a},\frac{1}{n}}$ hay algún punto de $A$ al que podemos llamar $\overline{x}{n}$ de esta manera construimos una sucesión de puntos de $A$ que convergen a $\overline{a}$ por lo tanto por hipótesis $\overline{a}\in A$ por tanto $A$ es cerrado.

A es acotado. Si $A$ no fuera acotado, existiria una sucesión $\overline{x}_{n}$ de puntos de $A$ tal que $\lim_{n\rightarrow\infty}\overline{x}_{n}=\infty$ y este límite no estaría en $A$ $\underset{\circ}{\bigtriangledown}$ por tanto $A$ es acotado.

Teorema. Heine-Borel. Todo subconjunto cerrado y acotado es compacto.

$1.-$ $K$ compacto implica que $K$ es cerrado.

Demostración. Sea $\bar{x} \in K^c$ y sea $G_m =\left\{y \in \mathbb{R}^n | |y-x | > \frac{1}{m}, m \in \mathbb{N}\right\}$ entonces $y \in Ext B(\bar{x}, \frac{1}{m})$ cada $G_m$ es abierta, la unión de todas las $G_m$ consta de todos los puntos de $\mathbb{R}^n$ excepto $x$. Dado que $x \in K$ cada punto de $K$ pertenece a algún $G_m$. Debido a la compacidad de $K$, se infiere que existe $M \in \mathbb{N}$ tal que $K \subset \bigcup_1^m G_i$. Dado que los conjuntos $G_m$ incrementan con $m$, $K \subset G_m$ de donde la vecindad ${z \in \mathbb{R}^n | |z-x| < \frac{1}{m}}$ no intercepta a $K$ demostrando que $K^c$ es abierto $\therefore$ $K$ es cerrado.

$2.-$ $K$ compacto implica que $K$ es acotado.

Demostración. Sea $H_m = \left\{ x \in \mathbb{R}^n | \left\| x\right\| < m\right\}$ todo el espacio $\mathbb{R}^n$ y por tanto $K$ está contenido en la unión de los conjuntos crecientes, $H_m$ $m\in \mathbb{N}$. Dado que $K$ es compacto existe $M \in \mathbb{N}$ tal que $K \subset H_m$ por lo que $K$ esta acotado.

Para completar la demostración de este teorema se necesita probar que si $K$ es un subconjunto cerrado y acotado contenido en la unión de una colección $g {G_{\alpha}}$
de conjuntos abiertos en $\mathbb{R}^n$, entonces está contenido en la unión de
algún número finito de conjuntos de $g$.

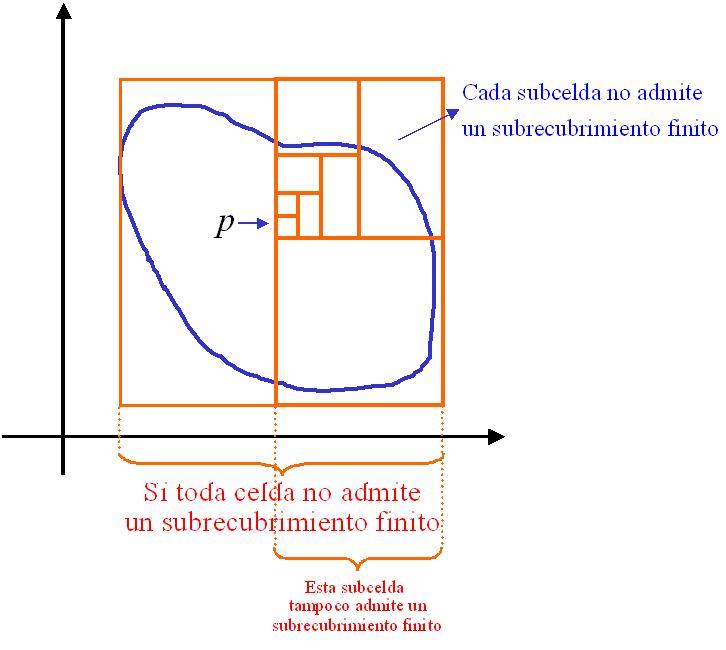
Dado que $K$ esta acotado, encontramos un punto de acumulación de $K$, como $K$ es cerrado $y \in K$ y esta en alguna celda abierta, por lo tanto existe $\varepsilon > 0$ tal que para cada $w$ con $|y -w| < \varepsilon $ en la celda abierta y si suponemos que $g ={G_{\alpha}}$ no admite un subrecubrimiento finito llegamos a una contradicción.

Teorema 6. Si $S$ es un conjunto cerrado y acotado en $\mathbb{R}^{n}$ entonces $S$ es compacto por sucesiones

Demostración. Suponga que $S$ es cerrado y acotado, sea ${x_{k}}$ una sucesión de puntos de $S$, se tiene entonces que $S$ es acotada y por el teorema de Bolzano- Weierstrass ${x_{k}}$ tiene una subsucesión convergente ${x_{k_{\alpha}}}$ tal que $x_{k_{\alpha}}\rightarrow x$ y como $S$ es cerrado $x\in S$. $\square$