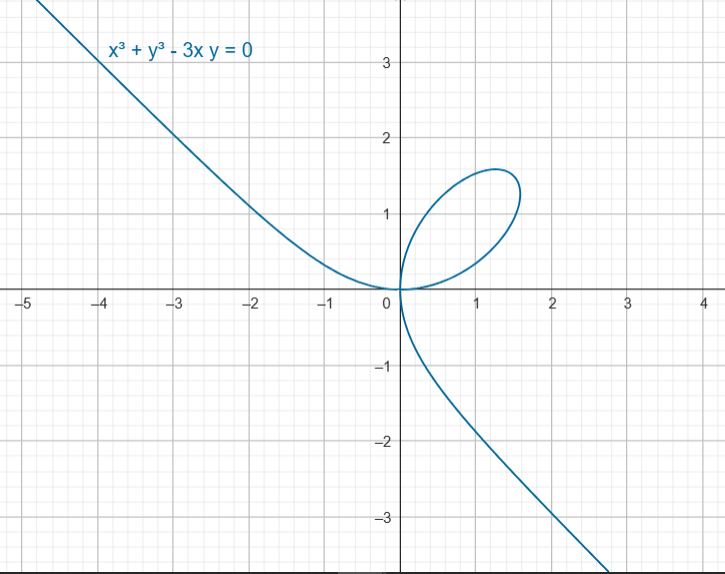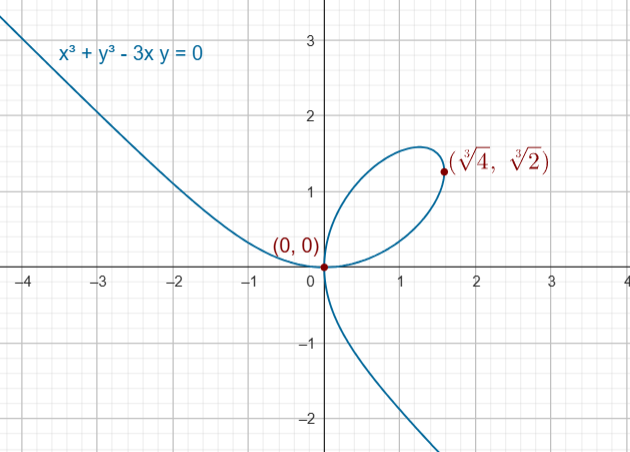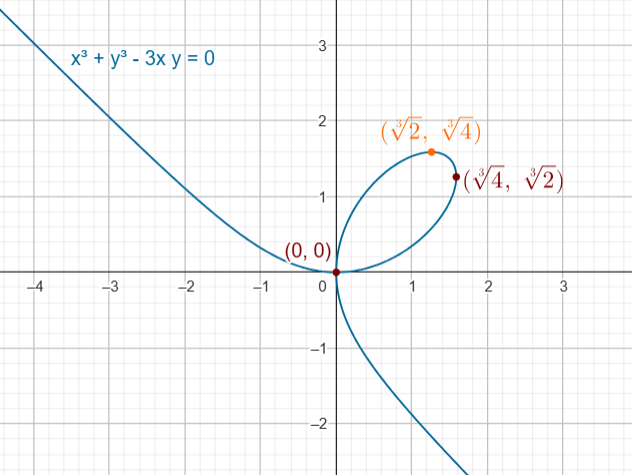Teorema de la función implícita:

Sea $F : \mathcal{U} \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$ con derivadas parciales continuas $F_x$, $F_y$ en una vecindad de un punto $(x_0, y_0)$ tal que $F (x_0, y_0) = 0$ y además $F_y (x_0, y_0) \neq 0$, entonces existe un rectángulo $\big[ x_0 \, – \, \alpha , x_0 \, + \, \alpha \big] \times \big[ y_0 \, – \, \beta , y_0 \, + \, \beta \big]$ tal que para cada $x$ en el intervalo $\big[ x_0 \, – \, \alpha , x_0 \, + \, \alpha \big]$ la ecuación $F ( x, y) = 0$ tiene una solución $ y = f (x)$ con $ y_0 \, – \, \beta \leq y \leq y_0 \, + \, \beta. $

Dicha función $ f : \big[ x_0 \, – \, \alpha , x_0 \, + \, \alpha \big] \rightarrow \big[ y_0 \, – \, \beta , y_0 \, + \, \beta \big]$ satisface la condición $f (x_0) = y_0$ y para toda $ x \in \big[ x_0 \, – \, \alpha , x_0 \, + \, \alpha \big] $ cumple que

$F ( x, f (x) ) = 0$

$F_y ( x, f (x) ) \neq 0$

Más aún, $f$ es continua con derivada continua, y está dada por la ecuación

$$ f’ (x) = \, – \, \dfrac{F_x ( x, f (x) )}{F_y ( x, f (x) )}$$

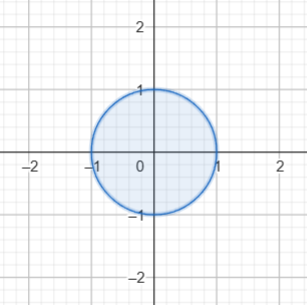
EJEMPLO: La circunferencia unitaria

Si $f (x) $ es una función diferenciable tal que $F (x, f (x) ) \equiv 0$, entonces $ h (x) = F (x, f (x) )$ es diferenciable y $h’ (x) \equiv 0.$

$ h (x) = ( F \, o \, \alpha) (x) $ , con $\alpha (x) = (x, f (x) )$

Entonces

$ \begin{align*} h’ (x) &= ( F \, o \, \alpha)’ (x) \\ &= \nabla F ( \alpha (x) ) \cdot {\alpha}’ (x) \end{align*}$ . . . (1)

Tenemos que

$ \alpha’ (x) = ( 1, f’ (x) )$ . . . (2)

$\nabla F ( x, y) = \Big( \dfrac{\partial F}{\partial x} (x, y), \dfrac{\partial F}{\partial y} (x, y) \Big)$ . . . (3)

Luego, sustituyendo (2) y (3) en (1) tenemos que

$\begin{align*} \nabla F ( \alpha (x) ) \cdot {\alpha}’ (x) &= \nabla F ( x, f (x) ) \cdot (1, f’ (x) ) \\ &= \Big( \dfrac{\partial F}{\partial x} (x, f (x)), \dfrac{\partial F}{\partial y} (x, f (x)) \Big) \cdot (1, f’ (x) ) \\ &= \dfrac{\partial F}{\partial x} (x, f (x)) \, + \, f’ (x) \dfrac{\partial F}{\partial y} (x, f (x)) = 0 \end{align*}$

Despejando $f’ (x)$ de la última igualdad, tenemos que

$$\textcolor{Purple}{f’ (x) = \dfrac{- \, \dfrac{\partial F}{\partial x} (x, f (x)) }{\dfrac{\partial F}{\partial y} (x, f (x)) }}$$

EJEMPLO

$f (x) = \sqrt{ 1 \, – \, x^2 \, } = ( 1 \, – \, x^2 )^{1/2} $

Entonces

$f’ (x) = \dfrac{1}{\cancel{2}} ( 1 \, – \, x^2 )^{-1/2} (-\, \cancel{2}x) = \dfrac{- \, x}{\sqrt{ 1 \, – \, x^2 \, }}$

$F_x (x, y) = 2x$ $F_y (x, y) = 2y$

$ \dfrac{- \, \dfrac{\partial F}{\partial x} (x, f (x)) }{\dfrac{\partial F}{\partial y} (x, f (x)) } = \dfrac{ – \, 2x}{2y} = \dfrac{- \, x}{f (x)} = \dfrac{ – \, x}{\sqrt{ 1 \, – \, x^2 \, }} = f’ (x)$

Observaciones:

(*) Podríamos aproximar $f (x)$ con su polinomio de Taylor $ f (x_0) + f’ (x_0) ( x \, – \, x_0)$ ya que

$f (x_0) = y_0$ que lo conocemos.

Y además también conocemos $ f’ (x) = \dfrac{- \, F_x (x_0, y_0) }{F_y (x_0, y_0) }$

(*) Podríamos calcular ${f’}’ (x) $ como sigue:

$\begin{align*} {f’}’ (x) &= \dfrac{d}{dx} \Bigg( \dfrac{- \, F_x (x, f (x)) }{ F_y (x, f (x)) } \Bigg) \\ &= \dfrac{d}{dx} \Bigg( \dfrac{- \, F_x (x, f (x)) }{ F_y (x, f (x)) } \Bigg) \\ &= \, – \; \dfrac{ F_y (x, f (x)) \dfrac{d}{dx} F_x (x, f (x)) \, – \, F_x (x, f (x)) \dfrac{d}{dx} F_y (x, f (x))}{\Big( F_y (x, f (x)) \Big)2} \\ &= \, – \; \dfrac{ F_y (x, f (x)) \Big( F_{xx} (x, f (x)).1 \, + \, F_{xy} (x, f (x)) (f’ (x)) \Big) \, – \, F_x (x, f (x)) \Big( F_{xy} (x, f (x)).1 \, + \, F_{yy} (x, f (x)) (f’ (x)) \Big) }{\Big( F_y (x, f (x)) \Big)^2} \end{align*}$

Entonces

$ {f’}’ (x) = \, – \; \dfrac{ F_y F_{xx} \, + \, F_{xy} \Big(- \, \dfrac{F_x}{\cancel{F_y}} \cancel{F_y} \Big) \, – \, F_x F_{xy} \, + \, F_x F_{yy} \Big(- \, \dfrac{F_x}{F_y} \Big) }{\Big( F_y \Big)^2}$

multiplicando por $\dfrac{F_y}{F_y}$

$ {f’}’ (x) = \, – \; \dfrac{ F^2_y F_{xx} \, + \, F_{xy} \big(- \, F_x \big) F_y \, – \, F_x F_{xy} F_y \, + \, F_x F_{yy} \Big(- \, \dfrac{F_x}{\cancel{F_y}} \cancel{F_y} \Big) }{\Big( F_y \Big)^3}$

Por lo tanto

$$\textcolor{BrickRed}{ {f’}’ (x) = \, – \; \dfrac{ F^2_y F_{xx} \, – \, 2 F_{xy} F_x F_y \, – \, F^2_x F_{yy} }{\Big( F_y \Big)^3}}$$

${}$

En la siguiente entrada https://blog.nekomath.com/64-1-material-en-revision-teorema-de-la-funcion-implicita/ demostramos este teorema.

Ejemplo

Sea $f (x, y) = ( y \, – \, 3x^2) (y \, – \, x^2)$

(a) El origen es punto crítico.

(b) En cada recta que pasa por el origen $\alpha ( t) = (at , bt)$ , $( f \, \circ \, \alpha) (t) $ tiene un mínimo relativo en $0$.

(c) El origen no es mínimo relativo.

(*) Calcule el polinomio de Taylor de 2° grado de $f$ alrededor del origen.

$\dfrac{\partial f}{\partial x} = -\, 6x (x \, – \, y^2 ) + (y \, – \, 3x^2 ) (\, – \, 2x)$

$\dfrac{\partial f}{\partial y} = (y \, – \, x^2 ) + (y \, – \, 3x^2 ) $

$\nabla f (0, 0) = (0 , 0) $

De aquí concluimos que el origen es un punto crítico de $f$.

(**) $f (\alpha (t)) = f (at, bt) = (bt \, – \, 3(at)^2 ) (bt \, – \, (at)^2 ) = b^2 t^2 \, – \, 4 a^2 b t^3 + 3 a^4 t^4 $

$ ( f \, \circ \, \alpha)’ (t) = 2 b^2 t \, – \, 12 a^2 b t^2 + 12 a^4 t^3 $ entonces $( f \, \circ \, \alpha)’ (0) = 0$

${( f \, \circ \, \alpha)}^{\prime \prime} (t) = 2 b^2 \, – \, 24 a^2 b t + 36 a^4 t^2 $ entonces ${( f \, \circ \, \alpha)}^{\prime \prime} (0) = 2 b^2 > 0 $. Si $ b \neq 0$. Entonces $ f \, o \, \alpha $ alcanza un mínimo relativo en 0.

Si $ b = 0 $ , $a = 1$ $ f ( \alpha ( t)) = 3 t^4$ que también tiene mínimo en $(0, 0)$.

De aquí concluimos que si restringimos el movimiento de las variables independientes a lo largo de rectas que pasan por el origen, entonces $f$ alcanza un valor mínimo.

(***) Ahora vamos a ver que $f$ no alcanza un mínimo local en el origen.

Para ello usaremos la negación de la definición de que $ f $ alcanza mínimo local en el punto $(x_0 , y_0)$.

Es decir queremos negar que:

existe una bola de radio $\delta$ con centro en el punto $(x_0 , y_0)$ en la cual todos los puntos $(x,y)$ cumplen que $f(x,y) \geq f(x_0 , y_0)$.

Es decir que para toda bola $B_{\delta} (x_0, y_0) $ existe algún punto $(x,y)$ en esa vecindad tal que $f (x, y) < f (x_0 , y_0)$

Sea $\delta > 0$, consideremos la parábola $ 2x^2$, tomemos un punto en esta parábola dentro de $B_{\delta} (0, 0) $ distinto del $(0, 0) $. En este punto $f (x, y) < 0 = f (0, 0)$, entonces $ f $ no alcanza un valor mínimo local en $(0, 0)$.

Consideremos $\alpha (t) = (t, 2t^2)$, luego $ \alpha ( \alpha (t) ) = (2t^2 \, – \, 3t^2) ( 2t^2 \, – \, t^2) = \, – \, t^4$ , de hecho, alcanza máximo.

(****) El polinomio de Taylor de 2° grado alrededor de $(0, 0)$

Sabemos que $ f (0, 0) = 0$, $\nabla f (0, 0) = (0, 0)$

$ H = \begin{pmatrix} f_{xx} (0, 0) & f_{xy} (0, 0) \\ \\ f_{yx} (0, 0) & f_{yy} (0, 0) \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ \\ 0 & 2 \end{pmatrix}$

$det(H) = 0$

Luego $p (x, y) = \dfrac{1}{2} 2 y^2 = y^2$

En el enlace siguiente puedes ver la gráfica de $f$ y la gráfica de $p$, y compararlas:

https://www.geogebra.org/classic/ymhfe9fv

${}$

Teorema

Sea $ f : \mathcal{U} \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}$ tal que existen las segundas derivadas parciales.

Si son continuas, entonces el polinomio de Taylor de 2° grado es el único $p (x, y)$ tal que

$$\lim\limits_{(h,k) \to (0,0)} \dfrac{f (x_0 + h, y_0 + k) \, – \, p (x_0 + h, y_0 + k)}{\|(h,k)\|^2} = 0 $$

Observación: si NO son continuas la demostración no sería válida.

Demostración:

$p (x_0 + h, y_0 + k) = Ah^2 + B hk + C k^2 + Dh + Ek + F$ para algunas $A, B, C, D, E, F \in \mathbb{R}$ constantes.

$ F = f (h, k)$ ya que $ \lim\limits_{(h,k) \to (0,0) } f (x_0 + h, y_0 + k) \, – \, p (x_0 + h, y_0 + k) = f (x_0 , y_0 ) \, – \, F = 0$

Tenemos que $D = \dfrac{\partial f}{\partial x} (x_0, y_0)$, y $ E = \dfrac{\partial f}{\partial y} (x_0, y_0)$ porque

$\lim\limits_{(h,k) \to (0,0)} \dfrac{\big| f (x_0 + h, y_0 + k) \, – \, p (x_0 + h, y_0 + k) \big| }{\| (h,k)\|} = 0$

En particular, si tomamos el límite con puntos de la forma $(h, 0)$ y $(0, k)$ entonces

$\lim\limits_{h \to 0} \dfrac{\big| f (x_0 + h, y_0 ) \, – \, p (x_0 + h, y_0 ) \big| }{\big| (h,k) \big|} = 0$

$\lim\limits_{h \to 0} \dfrac{\big| f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, Dh \, – \, Ah^2 \big| }{\big| h \big|} = 0$

$\iff$

$\lim\limits_{h \to 0} \dfrac{ f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 )}{h} \, – \, D \, – \, \cancel{A\lim\limits_{h \to 0} |h|}^0 = 0$

$\iff$

$\lim\limits_{h \to 0} \dfrac{ f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 )}{h} = D$

$\iff$

$D = \dfrac{\partial f}{\partial x} (x_0, y_0)$

Análogamente $E = \dfrac{\partial f}{\partial y} (x_0, y_0)$

Ahora bien,

$$\lim\limits_{(h,k) \to (0,0)} \dfrac{f (x_0 + h, y_0 + k) \, – \, p (x_0 + h, y_0 + k)}{\|(h,k)\|^2} = \lim\limits_{(h,k) \to (0,0)} \dfrac{\big| f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h \, – \, \dfrac{\partial f}{\partial y} (x_0, y_0) k \, – \, Ah^2 \, – \, 2B hk \, – \, C k^2 \big| }{\big\|( h, k) \big\|^2} $$

En particular, si tomamos puntos de la forma $(h, 0)$

$\lim\limits_{h \to 0} \dfrac{\big| f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h \, – \, Ah^2 \big| }{\big| h \big|^2} = 0 $

$\iff$

$\lim\limits_{h \to 0} \dfrac{ f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h \, – \, Ah^2 }{ h^2 } = 0 $

$\iff$

$\lim\limits_{h \to 0} \dfrac{ f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h }{ h^2 } = A $

Aplicando la regla de L’Hôpital

$\lim\limits_{h \to 0} \dfrac{ f (x_0 + h, y_0 ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h }{ h^2 } = \lim\limits_{h \to 0} \dfrac{ \dfrac{\partial f}{\partial x} (x_0 + h, y_0 ) \, – \, \dfrac{\partial f}{\partial y} (x_0 , y_0 ) }{ 2h } = \lim_{h \to 0} \frac{G (h)}{2h} $ . . . (*)

Aplicaremos L’Hôpital por segunda vez a la expresión anterior (*), entonces tenemos

$\lim\limits_{h \to 0 } \dfrac{G’ (h)}{2}$

Necesitamos que $\lim\limits_{h \to 0 } G (h) = 0 $ , es decir ,

$ \lim\limits_{h \to 0} \dfrac{\partial f}{\partial x} (x_0 + h, y_0 ) \, – \, \dfrac{\partial f}{\partial y} (x_0 , y_0 ) = 0$

Esto lo garantizamos si $\dfrac{\partial f}{\partial x} (x, y) $ es continua en $(x_0, y_0)$.

Luego

$G’ (h) = \dfrac{\partial^2 f}{\partial x^2} (x_0 + h, y_0)$ por continuidad, entonces cuando $h \rightarrow 0 , G’ (0) = \dfrac{\partial^2 f}{\partial x^2} (x_0 , y_0)$

Por lo tanto, $A = \dfrac{1}{2} \dfrac{\partial^2 f}{\partial x^2} (x_0, y_0)$

Análogamente usando trayectorias $(x_0, y_0 + k)$, cuando $ k \rightarrow 0$ tenemos que $ C = \dfrac{1}{2} \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0)$

Reuniendo la información anterior , tenemos que

$\lim\limits_{(h,k) \to (0,0)} \dfrac{\big| f (x_0 + h, y_0 + k ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h \, – \, \dfrac{\partial f}{\partial y} (x_0, y_0) k \, – \, \dfrac{1}{2} \dfrac{\partial^2 f}{\partial x^2} (x_0, y_0) h^2 \, – \, 2B hk \, – \, \dfrac{1}{2} \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0) k^2 \big| }{\big\|( h, k) \big\|^2} = 0 $

En particular cuando tomamos $h = k$

$\lim\limits_{(h,h) \to (0,0)} \dfrac{\big| f (x_0 + h, y_0 + h ) \, – \, f (x_0 , y_0 ) \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) h \, – \, \dfrac{\partial f}{\partial y} (x_0, y_0) h \, – \, \dfrac{1}{2} \dfrac{\partial^2 f}{\partial x^2} (x_0, y_0) h^2 \, – \, 2B h^2 \, – \, \dfrac{1}{2} \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0) h^2 \big| }{ 2h^2} = 0 $

$\iff$

$\lim\limits_{ h \to 0} \dfrac{ f (x_0 + h, y_0 + h ) \, – \, f (x_0 , y_0 ) \, – \, h \Big( \dfrac{\partial f}{\partial x} (x_0, y_0) \, – \, \dfrac{\partial f}{\partial y} (x_0, y_0) \Big) \, – \, \dfrac{1}{2} h^2 \Big( \dfrac{\partial^2 f}{\partial x^2} (x_0, y_0) \, – \, \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0) \Big) }{ 2h^2} = 2 B $

$\iff$ Aplicando L’Hôpital

$\lim\limits_{ h \to 0} \dfrac{ \dfrac{\partial f}{\partial x} (x_0 + h, y_0 + h ).1 \, – \, \dfrac{\partial f}{\partial y} (x_0 , y_0 ).1 \, – \, \dfrac{\partial f}{\partial x} (x_0, y_0) \, – \, \dfrac{\partial f}{\partial y} (x_0, y_0) h \, – \, \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0) h }{ 4h} = B $

Aplicamos L’Hôpital nuevamente, entonces tenemos que:

$\lim\limits_{ h \to 0} \dfrac{ \dfrac{\partial^2 f}{\partial x^2} (x_0 + h, y_0 + h ) \, + \, \dfrac{\partial^2 f}{\partial y \; \partial x} (x_0 + h, y_0 + h ) \, +\, \dfrac{\partial^2 f}{\partial x \; \partial y} (x_0 + h, y_0 + h) \, + \, \dfrac{\partial^2 f}{\partial y^2} (x_0 + h, y_0 + h )\, – \, \dfrac{\partial^2 f}{\partial x^2} (x_0, y_0) \, – \, \dfrac{\partial^2 f}{\partial y^2} (x_0, y_0) h }{ 4} = B $

Si las segundas derivadas parciales son continuas, el último límite es igual a

$\dfrac{\dfrac{\partial^2 f}{\partial y \; \partial x} (x_0 , y_0 )}{4} = B$

y por tanto

$$B = \dfrac{1}{2} \dfrac{\partial^2 f}{\partial x \; \partial y } (x_0, y_0)$$

Decir que $p (x, y)$ es la mejor aproximación de 2° grado de $f (x, y)$ cerca del punto $(x_0 , y_0)$, es decir que

$$\lim\limits_{(h,k) \to (0,0)} \dfrac{\Big| f (x_0 + h, y_0 + k) \, – \, p (x_0 + h, y_0 + k) \Big|}{\Big\|(h,k) \Big\|^2} = 0 \; \; \; _{\blacksquare}$$

La matriz simétrica que define la parte de segundo grado de este polinomio $p(x,y)$ recibe el nombre de Matriz Hessiana de $f$ en el punto $(x_0, y_0)$.

${}$

Dada $f (x , y) = \ln ( 1 + x^2 + y^2 ) $

Analicemos cuando las derivadas parciales valen cero.

$\dfrac{\partial f}{\partial x} = \dfrac{1}{1+x^2+y^2} 2x = 0 \Rightarrow \dfrac{2x}{1+x^2+y^2} = 0 \Rightarrow x = 0$

$\dfrac{\partial f}{\partial y} = \dfrac{1}{1+x^2+y^2} 2y = 0 \Rightarrow \dfrac{2y}{1+x^2+y^2} = 0 \Rightarrow y = 0$

Por lo que el punto $(0, 0)$ es el único punto crítico.

El valor crítico correspondiente es

$f (0, 0) = \ln ( 1 + (0)^2 + (0)^2 ) = \ln (1) = 0$

Segundas derivadas parciales

$\dfrac{\partial^2 f}{\partial x^2} = \dfrac{2 (1 + x^2 + y^2) \, – \, 2x (2x)}{(1 + x^2 + y^2)^2} = \dfrac{2+2x^2+2y^2 \, – \, 4x^2}{(1 + x^2 + y^2)^2} $

Por lo tanto $\dfrac{\partial^2 f}{\partial x^2} = \dfrac{2+2y^2 \, – \, 2x^2}{(1 + x^2 + y^2)^2}$

Luego $f_{xx} (0, 0) = 2$

Análogamente

$\dfrac{\partial^2 f}{\partial y^2} = \dfrac{2 (1 + x^2 + y^2) \, – \, 2y (2y)}{(1 + x^2 + y^2)^2} = \dfrac{2+2x^2+2y^2 \, – \, 4y^2}{(1 + x^2 + y^2)^2} $

Por lo tanto $\dfrac{\partial^2 f}{\partial x^2} = \dfrac{2+2y^2 \, – \, 2y^2}{(1 + x^2 + y^2)^2}$

Luego $f_{yy} (0, 0) = 2$

Además

$\dfrac{\partial^2 f}{\partial y \, \partial x} = \dfrac{2 x(2 y) \, – \, 0}{(1 + x^2 + y^2)^2} = \dfrac{ 4 xy}{(1 + x^2 + y^2)^2} $

Luego $f_{xy} (0, 0) = 0$

Entonces el polinomio de Taylor de 2° grado de $f$ alrededor del punto $( 0, 0)$ es

$$p ( x, y) = \dfrac{1}{2} \big( 2 ( x^2 + y^2 ) \big) = x^2 + y^2 $$

EL punto crítico es NO degenerado, porque el determinante

$$\begin{vmatrix} f_{xx} & f_{xy} \\ \\ f_{xy} & f_{yy} \end{vmatrix} \neq 0$$

Por lo tanto, $f$ alcanza un valor mínimo en $ ( 0, 0).$

Observación:

En coordenadas polares

$$ f ( r, \theta ) = \ln ( 1 + r^2) $$

Las curvas de nivel son circunferencias.

(*) Curva de nivel 1

$\big\{ (x, y) \in \mathbb{R}^2 \big| \ln (1+x^2+y^2) = 1 \big\}$

$ 1+x^2+y^2 = e \; \; \iff \; \; x^2+y^2 = e \, – \, 1$ circunferencia de radio $ \sqrt{e \, – \, 1 \, }$

(*) Curva de nivel $\mathcal{c}$ ( con $\mathcal{c} > 1 $) es

$\big\{ (x, y) \in \mathbb{R}^2 \big| \ln (1+x^2+y^2) = \mathcal{c} \big\}$

$ 1+x^2+y^2 = e^{\mathcal{c}} \; \; \iff \; \; x^2+y^2 = e^{\mathcal{c}} \, – \, 1$ circunferencia de radio $ \sqrt{e^{\mathcal{c}} \, – \, 1 \, }$

Cerca de $ r = 0 $ , $ \ln ( 1 + r^2) $ se aproxima a su polinomio de Taylor.

$ f (r) = \ln (1+r^2)$

$ f (0) = 0$

$f’ (r) = \dfrac{2r}{1+r^2} $

$ f’ (0) = 0$

${f}^{\prime \prime} (r) = \dfrac{(1+r^2) 2 \, – \, 2r (2r) }{(1+r^2)^2} = \dfrac{2 + 2r^2 \, – \, 4r^2}{(1+r^2)^2} = \dfrac{ 2 \, – \, 2r^2 }{(1+r^2)^2} $

${f}^{\prime \prime} (0) = 2$

$ p (r) = \dfrac{1}{2} 2 r^2 = r^2$

Cerca de $ r = 0$ , $\ln (1+r^2) \approx r^2$

$\ln ( 1+x^2 + y^2) \approx x^2 + y^2 $ cuando $(x , y) $ está cerca del $ ( 0, 0) .$

Lejos de $ r = 0 $, $r$ es grande entonces, $ \ln (1+r^2) \approx \ln (r^2) = 2 \ln r $

https://www.geogebra.org/classic/wqm6krex

La gráfica de $f$ es $ \big\{ (x, y, z) \in \mathbb{R}^3 \Big| z = \ln (1 + x^2 + y^2) \big\} $ , una superficie de revolución girando la curva $ z = \ln (1 + x^2) $ alrededor del eje $z$.

${}$

Consideremos una curva parametrizada $$\alpha : I \subseteq \mathbb{R} \rightarrow \mathbb{R}^2$$ $$\alpha (t) = \big( x (t), y (t) \big)$$

Supongamos que $ t = 0 $

$ x ( 0 ) = 0 $

$ y ( 0 ) = 0 $

$\alpha ( 0 ) = ( 0 , 0 )$

Supongamos además que $x $, $ y $ son funciones derivables de $ t $ y que $\big( x’ (t), y’ (t) \big) \neq ( 0, 0) $ vector velocidad.

Llamemos $\vec{v} = \big( x’ (0), y’ (0) \big)$

Consideremos una reparametrización de $\alpha$ $$\beta (s) = \alpha ( h (s) )$$

con $\beta = \alpha \, \circ \, h$, para algún $ h : J \subseteq \mathbb{R} \rightarrow \mathbb{R}$.

Sin pérdida de generalidad, supongamos también $ h (0) = 0$

${\beta \,}’ (s) = \alpha’ ( h (s) ) \cdot h’ ( s )$

${\beta \,}’ (s) = \big( x’ (h (s)), y’ (h (s)) \big) \cdot h’ ( s )$

$\vec{w} = {\beta \,}’ (0) = \big( x’ (0), y’ (0) \big) \cdot h’ (0) = h’ (0) \cdot \vec{v}$

Pedimos que $ h’ (0) \neq 0$

$ \vec{w} $ es el vector velocidad usando $\beta$ como parametrización.

Los dos vectores velocidad $ \vec{v}$ y $\vec{w} $ son colineales. Además, si

$ h’ (0) > 0 $ tienen el mismo sentido, y si

$h’ (0) < 0 $ tienen sentidos contrarios.

${}$

Supongamos que $ \gamma (t) = \big( x (t), y (t) \big)$ es una curva parametrizada, y que $ x (t)$ , $y (t) $ son de clase $\mathcal{C}^2$.

Además

$\gamma’ (0) \neq \vec{0}$

${\gamma}^{\prime \prime} (0) \neq \vec{0}$

Se dice que la circunferencia osculatriz a una curva en un punto $P$ es la circunferencia que más se parece a la curva cerca del punto.

¿Cómo saber cuál es la circunferencia osculatriz en el punto $P$?

Si $\gamma $ estuviera parametrizada por longitud de arco, entonces el centro de la circunferencia osculatriz es $$ \gamma (0) + \dfrac{1}{\mathcal{K} (0)} \vec{n} (0)$$

donde $\vec{n} (0) $ es el vector normal unitario.

Y el radio de la circunferencia osculatriz es $\dfrac{1}{\mathcal{K} (0)}$

Sabiendo la curvatura y el vector normal tenemos toda la información necesaria. (no necesariamente tiene que ser en el punto CERO, puede ser un punto $t_0$ con $\gamma’ (t_0) $ y ${\gamma}^{\prime \prime} (t_0)$ distintas de CERO)

(*) Tenemos una fórmula para calcular $\mathcal{K} (t_0)$

(*) a. En el plano, basta conocer el vector tangente unitario $T (t_0) = \dfrac{ \gamma’ (t_0)}{ \big\| \gamma’ (t_0) \big\|}$. Solo hay dos opciones para $(u, v)$ puede ser $ (- \, v, u ) $ o también $ (v, \, – \, u) $

b. En el espacio

$$ \overrightarrow{N} (t) = \dfrac{\dfrac{d}{dt} \overrightarrow{T} (t) }{\Bigg\| \dfrac{d}{dt} \overrightarrow{T} (t) \Bigg\|}$$