Introducción
En la entrada 16 abordamos algunas de las funciones elementales en el estudio de la variable compleja. Vimos que todas las funciones de dicha entrada estaban motivadas por la extensión de las funciones reales a $\mathbb{C}$, además de que todas las funciones definidas en dicha entrada estuvieron dadas en términos de la función exponencial compleja, por lo que nos resulta de gran interés estudiar a detalle las propiedades de dicha función y justificar el por qué la definición dada para dicha función realmente extiende a la función exponencial real.
En esta entrada abordaremos de nueva cuenta a algunas de las funciones elementales desde el sentido complejo, pero utilizando series de potencias. Como veremos, esta caracterización nos permitirá entender mejor la analicidad de dichas funciones.
Primeramente consideremos la definición de la función exponencial como una serie de potencias dada en nuestros cursos de cálculo. Si $x \in \mathbb{R}$, entonces:
\begin{equation*}
\operatorname{exp}(x) = e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \tag{31.1}.
\end{equation*}
De acuerdo con la definición 20.1, tenemos que si $z=x+iy\in\mathbb{C}$, entonces la función exponencial compleja está dada por:
\begin{equation*}
\operatorname{exp}(z) = e^x\left[\operatorname{cos}(y) + i \operatorname{sen}(y)\right]. \tag{31.2}
\end{equation*}
Por la fórmula de Euler tenemos que si $z\in\mathbb{C}$ es un número complejo puro, es decir, $z=iy$ con $y\in\mathbb{R}$, entonces:
\begin{equation*}
\operatorname{exp}(iy) =\operatorname{cos}(y) + i \operatorname{sen}(y). \tag{31.3}
\end{equation*}
Motivados en la definición de la función exponencial para el caso real (31.1), veamos que mediante series de potencias podemos dar una definición similar para el caso complejo, que extienda de manera natural a la exponencial real a su versión compleja. Más aún, veamos que a través de dicha definición podemos justificar la definición (31.2) y todos los resultados de la entrada 20, como la fórmula de Euler (31.1), que resultarán ser consecuencia de esta expansión en series y sus propiedades.
Entonces, la pregunta fundamental es ¿cómo podemos llegar a una expresión similar a la de (31.1) para el caso complejo?
Sea $z\in\mathbb{C}$. Definimos a la función:
\begin{equation*}
f(z) = \sum_{n=0}^\infty c_n z^n.
\end{equation*}
Dado que $f$ es nuestra función candidata a ser la exponencial compleja, de acuerdo con las propiedades de la exponencial compleja vistas en la entrada 20, planteamos la siguiente ecuación diferencial con condición inicial.
\begin{equation*}
f(z) = f'(z), \quad f(0) = 1 \tag{31.4}
\end{equation*}
La respuesta a nuestra pregunta está dada por la solución de la ecuación diferencial anterior.
Tenemos que:
\begin{equation*}
f(z) = c_0 + c_1 z + c_2 z^2 + c_3 z^3 + \cdots,
\end{equation*}como la función exponencial es entera, entonces el radio de convergencia de la serie que define a $f$ debe ser infinito, entonces, por la proposición 30.2 tenemos que el de su derivada también es infinito y $f’$ deberá estar dada por la derivada término a término de la serie que la define, es decir:
\begin{align*}
f(z) = c_0 + c_1 z + c_2 z^2 + c_3 z^3 + \cdots,\\
f'(z) = c_1 + 2c_2 z + 3c_3 z^2 + 4 c_4 z^3 + \cdots .
\end{align*}
Como $f(z) = f'(z)$, entonces, por el corolario 30.2, los coeficientes de ambas series deben ser iguales, es decir:
\begin{equation*}
c_0 = c_1, \,\, c_1 = 2 c_2, \,\, c_2 = 3 c_3, \,\, \ldots, c_{n-1} = n c_n,
\end{equation*}de donde $c_n = \dfrac{1}{n} c_{n-1}$, para todo $n\geq 1$.
Considerando lo anterior y la condición inicial $f(0) = 1$, entonces $c_0 = 1$, por lo que:
\begin{equation*}
c_1 = 1, \,\, c_2 = \frac{1}{2} = \frac{1}{2!}, \,\, c_3 = \left(\frac{1}{3}\right) \left(\frac{1}{2}\right) = \frac{1}{3!}, \,\, \ldots \,\, , c_{n} = \left( \frac{1}{n}\right)\left( \frac{1}{(n-1)!}\right) = \frac{1}{n!}.
\end{equation*}
Por lo que, la solución a la ecuación diferencial (31.4) es:
\begin{equation*}
f(z) = \sum_{n=0}^\infty \frac{z^n}{n!}, \forall z\in\mathbb{C}.
\end{equation*}
Definición 31.1. (Exponencial compleja como serie de potencias.)
Sea $z \in\mathbb{C}$, entonces definimos a la exponencial compleja como la serie de potencias:
\begin{equation*}
\operatorname{exp}(z) = \sum_{n=0}^\infty \frac{z^n}{n!}. \tag{31.5}
\end{equation*}
Observación 31.1.
En el ejemplo 27.8 hemos probado que la serie de potencias que define a la exponencial compleja es absolutamente convergente para todo $z\in\mathbb{C}$. Por lo que la función exponencial compleja está bien definida para todo $z\in\mathbb{C}$.
Podemos mencionar algunas de las propiedades más importantes de esta función, dada como series de potencias, en la siguiente:
Proposición 31.1. (Propiedades de la exponencial compleja.)
La función exponencial compleja definida como en (31.5) satisface las siguientes propiedades.
- Es una función entera y para todo $z\in\mathbb{C}$ se cumple que $\dfrac{d}{dz} \operatorname{exp}(z) = \operatorname{exp}(z)$.
- $\operatorname{exp}(0) = 1$.
- $\operatorname{exp}(z_1 + z_2) = \operatorname{exp}(z_1) \operatorname{exp}(z_2)$ para todo $z_1, z_2 \in\mathbb{C}$.
- $\operatorname{exp}(z) \neq 0$ para todo $z\in\mathbb{C}$.
- $\operatorname{exp}(-z) = \dfrac{1}{\operatorname{exp}(z)}$ y $\operatorname{exp}(z_1 – z_2) = \dfrac{\operatorname{exp}(z_1)}{\operatorname{exp}(z_2)}$, para cualesquiera $z, z_1, z_2 \in\mathbb{C}$.
- $\overline{\operatorname{exp}(z)} = \operatorname{exp}\left(\overline{z}\right)$ para todo $z\in\mathbb{C}$.
- Para todo $z\in\mathbb{C}$ se cumple que $|\operatorname{exp}(z)| = \operatorname{exp}\left(\operatorname{Re}(z)\right)$, de donde:
\begin{equation*}
|\operatorname{exp}(i\theta)| = 1 \quad \Longleftrightarrow \quad \theta \in\mathbb{R} \quad \text{y} \quad |\operatorname{exp}(z)| \leq \operatorname{exp}(|z|).
\end{equation*}
Demostración.
- Sea $z\in\mathbb{C}$, entonces, por la proposición 30.2 se cumple que:
\begin{equation*}
\dfrac{d}{dz} \operatorname{exp}(z) = \dfrac{d}{dz} \sum_{n=0}^\infty \frac{z^n}{n!} = \sum_{n=1}^\infty \frac{n z^{n-1}}{n (n-1)!} = \sum_{n=0}^\infty \frac{z^n}{n!} = \operatorname{exp}(z).
\end{equation*} - Es inmediata de la definición de la función exponencial compleja.
- Sean $z_1, z_2 \in\mathbb{C}$, entonces:
\begin{equation*}
\operatorname{exp}(z_1) = \sum_{n=0}^\infty \frac{z_1^n}{n!} \quad \text{y} \quad \operatorname{exp}(z_2) = \sum_{n=0}^\infty \frac{z_2^n}{n!}.
\end{equation*}Por el ejemplo 27.8 sabemos que ambas series son absolutamente convergentes. Del ejemplo 27.11, tenemos que el producto de Cauchy de dichas series es:
\begin{equation*}
\sum_{n=0}^\infty c_n = \sum_{n=0}^\infty \frac{(z_1 + z_2)^n}{n!}.
\end{equation*}Por último, por el ejemplo 27.12, sabemos que el producto de estas series absolutamente convergentes, converge a su producto de Cauchy, es decir:
\begin{align*}
\operatorname{exp}(z_1) \operatorname{exp}(z_2) & = \left(\sum_{n=0}^\infty \frac{z_1^n}{n!}\right) \left(\sum_{n=0}^\infty \frac{z_2^n}{n!}\right)\\
& = \sum_{n=0}^\infty \frac{(z_1 + z_2)^n}{n!}\\
& = \operatorname{exp}(z_1 + z_2).
\end{align*}Por inducción es fácil verificar que:
\begin{equation*}
\prod_{i=1}^n \operatorname{exp}(z_i) = \operatorname{exp}\left( \sum_{i=1}^n z_i\right), \quad \forall n\geq 2.
\end{equation*} - Se sigue de los incisos 2 y 3, por lo que los detalles se dejan como ejercicio al lector.
- Se sigue de los incisos 2 y 3, por lo que los detalles se dejan como ejercicio al lector.
- El resultado se sigue de la proposición 27.2(2).
- Sea $z\in\mathbb{C}$. Sabemos que:
\begin{equation*}
\operatorname{Re}(z) = \frac{z + \overline{z}}{2} \quad \text{y} \quad |z|^2 = z \overline{z}.
\end{equation*}De los incisos 3, 4 y 6 tenemos que:
\begin{equation*}
|\operatorname{exp}(z)|^2 = \operatorname{exp}(z) \overline{\operatorname{exp}(z)} = \operatorname{exp}(z) \operatorname{exp}\left(\overline{z}\right) = \operatorname{exp}\left(z+\overline{z}\right) = \operatorname{exp}\left(2 \operatorname{Re}(z)\right) = \left[\operatorname{exp}\left(\operatorname{Re}(z)\right)\right]^2 >0,
\end{equation*}de donde:
\begin{equation*}
|\operatorname{exp}(z)| = \operatorname{exp}\left(\operatorname{Re}(z)\right).
\end{equation*}La parte restante del resultado se sigue de esta última igualdad, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Es claro que si $z=x\in\mathbb{R}$, entonces las definiciones (31.5) y (31.1), correspondientes con la exponencial compleja y la exponencial real, coinciden. Sin embargo, procedemos a verificar que en efecto la exponencial compleja extiende a la exponencial real de manera formal.
Recordemos los siguientes resultados de Cálculo.
Teorema 31.1. (Teorema del Valor Intermedio.)
Sea $f:[a, b] \to \mathbb{R}$ una función continua en $[a, b]$. Entonces, para todo $y$ entre $f(a)$ y $f(b)$ existe $c\in [a, b]$ tal que $f(c) = y$.
Teorema 31.2. (Teorema del Valor Medio.)
Sea $f:[a,b] \to \mathbb{R}$ una función continua en $[a, b]$ y diferenciable en $(a, b)$. Entonces, existe $c\in (a, b)$ tal que:
\begin{equation*}
f'(c) = \frac{f(b) – f(a)}{b – a}.
\end{equation*}
Lema 31.1.
Si $f:(a,b) \to \mathbb{R}$ es una función diferenciable en $(a, b)$ tal que $f'(x)>0$ para todo $x\in(a, b)$, entonces $f$ es estrictamente creciente en $(a, b)$.
Demostración. Es una consecuencia de teorema del valor medio, por lo que se deja como ejercicio al lector.
$\blacksquare$
Lema 31.2.
Si $f:[a,b] \to \mathbb{R}$ es una función estrictamente creciente en $[a, b]$, entonces $f$ es inyectiva.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Lema 31.3.
Sea $I\subset\mathbb{R}$ un intervalo. Si $f:I \to \mathbb{R}$ es una función continua e inyectiva. Entonces $f^{-1}$ es continua.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Puede consultarse la prueba de estos resultados en alguno de los siguientes textos:
- Elementary Analysis: The Theory of Calculus de Kenneth A. Ross.
- An Introduction to Analysis de William R. Wade.
- An Introduction to Analysis de James R. Kirkwood.
Procedemos con el resultado.
Corolario 31.1. ($\pmb{e^x = \operatorname{exp}|_{\mathbb{R}}(x)}$.)
Si $z = x+i0 \in\mathbb{C}$, con $x\in\mathbb{R}$, entonces la función $u(x) = \operatorname{exp}|_{\mathbb{R}}(x)$, es decir, la exponencial compleja restringida a $\mathbb{R}$, satisface lo siguiente:
- $u$ es una función real, continua y estrictamente creciente en su dominio $\mathbb{R}$.
- $u(\mathbb{R}) = (0, \infty)$.
- $u$ es un homeomorfismo, definición 9.2, entre $\mathbb{R}$ y $(0, \infty)$ y la única solución de la ecuación $u(0)=1$ es $x=0$.
Demostración. Dadas las hipótesis.
- De acuerdo con la definición 30.1, es claro que al evaluar la expresión (31.5) con $z=x\in\mathbb{R}$, la función $u(x) = \operatorname{exp}(x)$ es una función real de variable real. La continuidad de la función $u$ se sigue de la proposición 31.1(1), pues la exponencial compleja es una función entera y por tanto continua en $\mathbb{C}$, proposición 16.1, en particular es continua en $\mathbb{R}\subset\mathbb{C}$.
Por otra parte, de la proposición 31.1(4) sabemos que para todo $z\in\mathbb{C}$ se cumple que $\operatorname{exp}(z) \neq 0$, y por el inciso 2, de la misma proposición, para todo $z=x\in\mathbb{R}$ tenemos que:
\begin{equation*}
u(x) = \operatorname{exp}(x) = \operatorname{exp}\left(\frac{x}{2} + \frac{x}{2} \right) = \left[\operatorname{exp}\left(\frac{x}{2}\right)\right]^2 >0.
\end{equation*}Dado que $u'(x) = u(x) > 0$, proposición 31.1(1), entonces se sigue del lema 31.1 que la función $u$ es estrictamente creciente en $\mathbb{R}$. - Como $u$ es continua y $\mathbb{R}$ es un conjunto conexo, entonces de la proposición 10.3 se sigue que $u(\mathbb{R}) = \operatorname{exp}(\mathbb{R}) \subset{\mathbb{R}}$ debe ser un conjunto conexo, por lo tanto, proposición 10.1, es un intervalo. Puesto que para todo $z=x\in\mathbb{R}$ se cumple que $u(x)>0$, entonces $u(\mathbb{R}) \subset (0, \infty)$.
Probemos la otra contención. De acuerdo con la definición de $u$, es claro que para $z = x>0$ se cumple que:
\begin{equation*}
u(x) = \operatorname{exp}(x) > 1 + x,
\end{equation*}por lo que:
\begin{equation*}
\lim_{x \to\infty} u(x) = \infty. \tag{31.6}
\end{equation*}Dado que para todo $z\in\mathbb{C}$ se cumple que $\operatorname{exp}(z) = 1/\operatorname{exp}(-z)$, proposición 31.1(5), entonces, para $z=t\in\mathbb{R}$ tal que $t<0$, es claro que:
\begin{equation*}
\lim_{t \to -\infty} u(t) = \lim_{-t \to \infty} \frac{1}{u(-t)} = \lim_{x \to\infty} \frac{1}{u(x)} = 0. \tag{31.7}
\end{equation*}Sea $L>0$. De acuerdo con la definición del límite, de (31.6) se sigue que si $K=L>0$, entonces existe $M>0$ tal que:
\begin{equation*}
f(x) > K, \quad \text{si} \quad x>M.
\end{equation*}En particular, para $x=M+1$ tenemos que $u(M+1) > L$.
Análogamente, considerando la definición del límite (31.7), si $\varepsilon=L>0$, entonces existe $N<0$ tal que:
\begin{equation*}
|u(x) – 0| = |u(x)| = u(x) < L, \quad \text{si} \quad x < N.
\end{equation*}Entonces, para $x=N-1$ tenemos que $u(N-1) < L$. Por lo tanto, dado $L>0$ existen $a=N-1<0$ y $b = M+1>0$ tales que:
\begin{equation*}
u(a) < L < u(b).
\end{equation*}Como $u$ es continua en $\mathbb{R}$, en particular lo es en $(a, b)$, entonces, del teorema del valor intermedio se sigue que existe $c\in(a, b)$ tal que $u(c) = L$, lo cual prueba la contención restante, por lo que $u(\mathbb{R}) = (0, \infty)$. - Dado que $u$ es estrictamente creciente, entonces, del lema 31.2 se sigue que es una función inyectiva. Por otra parte, del inciso anterior tenemos que $u:\mathbb{R} \to (0,\infty)$ es una función suprayectiva, por lo que $u$ es una función biyectiva y por tanto invertible. Denotamos a $u^{-1}(y)=x$ como la función inversa, entonces $u^{-1}$ es continua, lema 31.3, ya que $u$ es continua e inyectiva, por lo que $\mathbb{R}$ y $(0, \infty)$ son homeomorfos, definición 9.2.
Como $u$ es inyectiva es claro que la única solución de la ecuación $u(0)=1$ es $x=0$.
$\blacksquare$
Observación 31.2.
De acuerdo con estos resultados, es claro que para $z=x\in\mathbb{R}$, la definición de la exponencial compleja dada en (31.5) se reduce al caso real dado por (31.1), por lo que de manera natural hemos hecho una extensión de la función exponencial real a $\mathbb{C}$, y como la serie que define a la exponencial converge absolutamente para todo $z\in\mathbb{C}$, entonces podemos utilizar las expresiones $e^z$ y $\operatorname{exp}(z)$ de manera indistinta para referirnos a la función exponencial compleja.
De nuestros cursos de cálculo, sabemos que las series de potencias de las funciones trigonométricas reales seno y coseno son:
\begin{align*}
\operatorname{sen}(x) = \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)!},\\
\operatorname{cos}(x) = \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{(2n)!}.
\end{align*}
Notemos que si $z = iy \in\mathbb{C}$, con $y\in\mathbb{R}$, entonces:
\begin{align*}
\operatorname{exp}(iy) & = \sum_{n=0}^\infty \frac{(iy)^n}{n!}\\
& = 1 + iy – \frac{y^2}{2!} – i\frac{y^3}{3!} + \frac{y^4}{4!} + i \frac{y^5}{5!} – \frac{y^6}{6!} – i
\frac{y^7}{7!} + \frac{y^8}{8!} + \cdots\\
& = \left( 1 – \frac{y^2}{2!} + \frac{y^4}{4!} – \frac{y^6}{6!} + \frac{y^8}{8!} – \cdots \right) + i \left( y – \frac{y^3}{3!} + \frac{y^5}{5!} – \frac{y^7}{7!} – \cdots \right)\\
& = \sum_{n=0}^\infty \frac{(-1)^n y^{2n}}{(2n)!} + i \sum_{n=0}^\infty \frac{(-1)^n y^{2n+1}}{(2n+1)!}\\
& = \operatorname{cos}(y) + i \operatorname{sen}(y).
\end{align*}
De acuerdo con la proposición 31.1(3), para $z = x+ iy \in\mathbb{C}$ se tiene que:
\begin{align*}
e^z = \operatorname{exp}(z) & = \operatorname{exp}(x + iy)\\
& = \operatorname{exp}(x) \operatorname{exp}(iy)\\
& = e^x \left[ \operatorname{cos}(y) + i \operatorname{sen}(y)\right],
\end{align*}lo cual justifica la definición 20.1 y por tanto todos los resultados de las entradas 20, 21, 22 y 23 son válidos.
De manera análoga, se puede utilizar la definición en series de potencias de la función exponencial compleja y las definiciones de las funciones trigonométricas e hiperbólicas, dadas en la entrada 22, para obtener sus correspondientes definiciones en series de potencias, que extienden de manera natural a $\mathbb{C}$ a sus versiones reales.
Proposición 31.2. (Series de las funciones trigonométricas e hiperbólicas seno y coseno.)
Sea $z\in\mathbb{C}$, entonces:
\begin{align*}
\operatorname{sen}(z) := \sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{(2n+1)!}, \tag{31.8} \\
\operatorname{cos}(z) := \sum_{n=0}^\infty \frac{(-1)^n z^{2n}}{(2n)!}, \tag{31.9}\\
\operatorname{senh}(z) := \sum_{n=0}^\infty \frac{z^{2n+1}}{(2n+1)!}, \tag{31.10} \\
\operatorname{cosh}(z) := \sum_{n=0}^\infty \frac{z^{2n}}{(2n)!}. \tag{31.11}
\end{align*}
Demostración. La demostración es análoga para las cuatro funciones y se sigue de las definiciones 22.1, 22.3, 31.1 y de la proposición 27.2(1). Para ejemplificar el procedimiento realicemos la prueba de la serie de la función coseno hiperbólico y el resto de las series se dejan como ejercicio al lector.
De las definiciones 22.3 y 30.1, para todo $z\in\mathbb{C}$, por la proposición 27.2(1) tenemos que:
\begin{align*}
\operatorname{cosh}(z) & = \frac{\operatorname{exp}(z) + \operatorname{exp}(-z)}{2}\\
& = \dfrac{\displaystyle \sum_{n=0}^\infty \dfrac{z^n}{n!} + \displaystyle \sum_{n=0}^\infty \dfrac{(-z)^n}{n!}}{2}\\
& = \displaystyle \sum_{n=0}^\infty \dfrac{z^n + (-z)^n}{2 \cdot n!}\\
& = \displaystyle \sum_{n=0}^\infty \dfrac{z^n \left[1 + (-1)^n\right]}{2 \cdot n!}.
\end{align*}
Sea $c_n = \dfrac{1 + (-1)^n}{2 \cdot n!}$, para todo $n\in\mathbb{N}$. Notemos que:
\begin{equation*}
c_n = \left\{ \begin{array}{lcc}
0 & \text{si} & n = 2k+1, \\
\\ \dfrac{1}{(2k)!} & \text{si} & n=2k,
\end{array}
\right.
\end{equation*} donde $k\in\mathbb{N}$.
Entonces:
\begin{equation*}
\operatorname{cosh}(z) = \sum_{n=0}^\infty \frac{z^{2n}}{(2n)!}.
\end{equation*}
$\blacksquare$
De manera análoga es posible deducir las series de potencias del resto de funciones trigonométricas e hiperbólicas, por lo que se deja como ejercicio al lector.
Observación 31.2.
De estas definiciones para las funciones trigonométricas e hiperbólicas seno y coseno es claro que para todo $z\in\mathbb{C}$ se cumple que:
\begin{equation*}
\operatorname{sen}(-z) = -\operatorname{sen}(z) \quad \text{y} \quad \operatorname{cos}(-z) = \operatorname{cos}(z),
\end{equation*}
\begin{equation*}
\operatorname{senh}(-z) = -\operatorname{senh}(z) \quad \text{y} \quad \operatorname{cosh}(-z) = \operatorname{cosh}(z),
\end{equation*}ya que las series de potencias de las funciones $\operatorname{sen}$ y $\operatorname{senh}$ solo consideran a las potencias impares de $z$, mientras que las series de potencias de las funciones $\operatorname{cos}$ y $\operatorname{cosh}$ solo consideran potencias pares de $z$.
Observación 31.3.
De acuerdo con las definiciones en series de las funciones hiperbólicas seno y coseno es claro que si restringimos el dominio de estas funciones al conjunto de los números reales positivos, entonces estas funciones serán positivas y estrictamente crecientes.
Más aún, por la observación 22.5, sabemos que para todo $z=x+iy\in\mathbb{C}$ se cumplen las identidades:
\begin{align*}
|\operatorname{sen}(z)|^2 = \operatorname{sen}^2(x) + \operatorname{senh}^2(y),\\
|\operatorname{cos}(z)|^2 = \operatorname{cos}^2(x) + \operatorname{senh}^2(y),
\end{align*}de donde es claro que los únicos ceros de las series (31.8) y (31.9), que definen al seno y coseno complejos, son reales ya que $\operatorname{senh}(y) = 0$ si y solo si $y=0$.
Considerando las propiedades que hemos probado para las series de números complejos a lo largo de esta unidad, podemos probar fácilmente algunas de las identidades con las que estamos familiarizados para el caso real, mediante la manipulación algebraica de las series de potencias que definen a las funciones trigonométricas e hiperbólicas.
Ejemplo 31.1.
Verifiquemos que para todo $z\in\mathbb{C}$ se cumple que:
a) \begin{equation*}
\operatorname{cos}^2(z) = \frac{1+\operatorname{cos}(2z)}{2}.
\end{equation*}
b) \begin{equation*}
\operatorname{sen}(2z) = 2 \operatorname{sen}(z)\operatorname{cos}(z).
\end{equation*}
Solución.
a) Notemos que:
\begin{align*}
\frac{1+\operatorname{cos}(2z)}{2} & = \frac{1}{2} + \frac{\operatorname{cos}(2z)}{2}\\
& = \frac{1}{2} + \sum_{n=0}^\infty \frac{(-1)^n (2z)^{2n}}{2 (2n)!}\\
& = \frac{1}{2} + \sum_{n=0}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!}.
\end{align*}
Por otra parte:
\begin{align*}
\operatorname{cos}^2(z) & = \left(\frac{\operatorname{exp}(iz) + \operatorname{exp}(-iz)}{2}\right)^2\\
& = \frac{1}{4} \left[\operatorname{exp}(2iz) + 2 +\operatorname{exp}(-2iz)\right]\\
& = \frac{1}{2} + \sum_{n=0}^\infty \frac{(2iz)^n}{4 \cdot n!} + \sum_{n=0}^\infty \frac{(-2iz)^n}{4 \cdot n!}\\
& = \frac{1}{2} + \sum_{n=0}^\infty \frac{2^{n-2} \, i^n \, z^n}{n!} + \sum_{n=0}^\infty \frac{(-1)^n \, 2^{n-2} \, i^n \, z^n}{n!}\\
& = \frac{1}{2} + \sum_{n=0}^\infty \frac{2^{n-2} \, i^n \, z^n \left[1 + (-1)^n\right]}{n!}.
\end{align*}
Sea $c_n = \dfrac{2^{n-2} \, i^n \left[1 + (-1)^n\right]}{n!}$, para todo $n\in\mathbb{N}$. Notemos que:
\begin{equation*}
c_n = \left\{ \begin{array}{lcc}
0 & \text{si} & n = 2k+1, \\
\\ \dfrac{2^{2k-1} i^{2k}}{(2k)!} & \text{si} & n=2k,
\end{array}
\right.
\end{equation*}donde $k\in\mathbb{N}$.
Entonces:
\begin{equation*}
\frac{1+\operatorname{cos}(2z)}{2} = \frac{1}{2} + \sum_{n=0}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!} = \operatorname{cos}^2(z).
\end{equation*}b) De acuerdo con el inciso anterior tenemos que:
\begin{equation*}
\operatorname{cos}^2(z) = \frac{1}{2} + \sum_{n=0}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!},
\end{equation*}la cual es una serie con radio de convergencia infinito.
Derivando ambos lados de ésta última igualdad, por la proposición 30.2 tenemos que:
\begin{align*}
-2 \operatorname{sen}(z) \operatorname{cos}(z) & = \sum_{n=1}^\infty \frac{i^{2n} \, 2^{2n-1} \, 2n \, z^{2n-1}}{2n \, (2n-1)!}\\
& = \sum_{n=1}^\infty \frac{(-1)^{n} \, (2z)^{2n-1}}{(2n-1)!}\\
& = \sum_{n=0}^\infty \frac{(-1)^{n+1} \, (2z)^{2n+1}}{(2n+1)!}\\
& = – \operatorname{sen}(2z),
\end{align*}de donde:
\begin{equation*}
\operatorname{sen}(2z) = 2 \operatorname{sen}(z)\operatorname{cos}(z).
\end{equation*}
Ejemplo 31.2.
Las funciones complejas exponencial, seno y coseno son analíticas, definición 30.1, en $\mathbb{C}$.
Solución. Sea $z_0\in\mathbb{C}$ fijo. Tenemos que:
\begin{align*}
e^z = e^{z_0 + z-z_0} & = e^{z_0} e^{z-z_0}\\
&= e^{z_0} \sum_{n=0}^\infty \frac{(z-z_0)^n}{n!}\\
& = \sum_{n=0}^\infty e^{z_0} \frac{(z-z_0)^n}{n!}, \quad \forall z\in\mathbb{C}.
\end{align*}
Por otra parte, por la proposición 22.1 sabemos que para todo $z\in\mathbb{C}$ se cumple que:
\begin{align*}
\operatorname{sen}(z) = \operatorname{sen}(z_0+z-z_0) = \operatorname{sen}(z_0) \operatorname{cos}(z-z_0) + \operatorname{sen}(z-z_0) \operatorname{cos}(z_0),\\
\operatorname{cos}(z) = \operatorname{cos}(z_0+z-z_0)= \operatorname{cos}(z_0) \operatorname{cos}(z-z_0) – \operatorname{sen}(z_0) \operatorname{sen}(z-z_0).
\end{align*}
Entonces:
\begin{equation*}
\operatorname{sen}(z) = \operatorname{sen}(z_0) \sum_{n=0}^\infty \frac{(-1)^n(z-z_0)^{2n}}{(2n)!} + \operatorname{cos}(z_0) \sum_{n=0}^\infty \frac{(-1)^n(z-z_0)^{2n+1}}{(2n+1)!}, \quad \forall z\in\mathbb{C},
\end{equation*}
\begin{equation*}
\operatorname{cos}(z) = \operatorname{cos}(z_0) \sum_{n=0}^\infty \frac{(-1)^n(z-z_0)^{2n}}{(2n)!} – \operatorname{sen}(z_0) \sum_{n=0}^\infty \frac{(-1)^n(z-z_0)^{2n+1}}{(2n+1)!}, \quad \forall z\in\mathbb{C}.
\end{equation*}
Ejemplo 31.3.
Determinemos el radio de convergencia y la suma de la serie:
\begin{equation*}
\sum_{n=2}^\infty \frac{n}{(n-2)!} z^n.
\end{equation*}
Solución. Por la forma de la serie, al tener un factorial en el denominador, inferimos que la función suma que describe la serie dada debe estar en términos de la exponencial compleja.
Sabemos que la serie de potencias, centrada en $z_0 = 0$, de la exponencial es:
\begin{equation*}
f(z) = e^z = \sum_{n=0}^\infty \frac{z^n}{n!}, \quad \forall z\in\mathbb{C},
\end{equation*}entonces, al derivar dos veces de ambos lados de la igualdad, por el corolario 30.1 tenemos que:
\begin{equation*}
f»(z) = e^z = \sum_{n=2}^\infty \frac{n(n-1) z^{n-2}}{n!}= \sum_{n=2}^\infty \frac{z^{n-2}}{(n-2)!}, \quad \forall z\in\mathbb{C}.
\end{equation*}
Multiplicando ambos lados por $z^2$ tenemos:
\begin{equation*}
z^2 e^z = \sum_{n=2}^\infty \frac{z^{n}}{(n-2)!} = \sum_{k=0}^\infty c_k z^k, \quad \forall z\in\mathbb{C},
\end{equation*}de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{1}{(n-2)!}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n,\\
\\ 0, & \text{en otro caso.}\\
\end{array}
\right.
\end{equation*}
Por lo que $c_0 = c_1 =0$ y para todo $k\geq 2$:
\begin{equation*}
c_k = \dfrac{1}{(k-2)!}.
\end{equation*}
Considerando lo anterior no es difícil verificar que esta última serie tiene radio de convergencia infinito, por lo que podemos volver a aplicar la proposición 30.2 y derivar de ambos lados de la igualdad, de donde se sigue que:
\begin{align*}
\frac{d}{dz} z^2 e^z = 2ze^z + z^2 e^z & = \sum_{k=1}^\infty k c_k z^{k-1}\\
& = \sum_{n=2}^\infty \frac{n z^{n-1}}{(n-2)!}, \quad \forall z\in\mathbb{C}.
\end{align*}
Por último, si multiplicamos por $z$ ésta última igualdad tenemos que:
\begin{equation*}
e^z(2z^2 + z^3) = \sum_{n=2}^\infty \frac{n z^{n}}{(n-2)!}, \quad \forall z\in\mathbb{C},
\end{equation*}la cual es la función suma correspondiente a la serie dada y tiene también radio de convergencia infinito.
Para cerrar esta entrada analicemos ahora a la función multivaluada logaritmo complejo, para ello consideremos el siguiente:
Ejemplo 31.4.
Veamos que la serie de potencias para la función $\operatorname{Log}(1+z)$ es:
\begin{equation*}
\sum_{n=0}^\infty \frac{(-1)^n z^{n+1}}{n+1},
\end{equation*}y determinemos su dominio de convergencia.
Solución. De acuerdo con el ejercicio 10 de la entrada 21, sabemos que la función $\operatorname{Log}(1+z)$ es analítica en $\mathbb{C}\setminus(-\infty, -1]$ y para todo punto en dicho dominio su derivada es:
\begin{equation*}
\frac{d}{dz} \operatorname{Log}(1+z) = \frac{1}{1+z}. \tag{31.12}
\end{equation*}
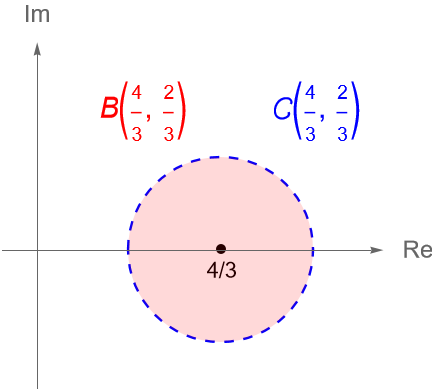
En particular, dicha función es analítica en $B(0,1)$ y para $|z|<1$ se cumple (31.12).
Por otra parte, considerando la serie geométrica, tenemos que:
\begin{equation*}
\sum_{n=0}^\infty (-z)^n = \sum_{n=0}^\infty (-1)^n z^n = \frac{1}{1+z}, \quad \text{si} \,\, |z|<1.
\end{equation*}
Entonces:
\begin{equation*}
\frac{d}{dz} \operatorname{Log}(1+z) = \sum_{n=0}^\infty (-1)^n z^n = \frac{1}{1+z}, \quad \text{si} \,\, |z|<1.
\end{equation*}
Notemos que si definimos a una función $f$ considerando la serie de potencias dada, tenemos que:
\begin{equation*}
f(z) = \sum_{n=0}^\infty \frac{(-1)^n z^{n+1}}{n+1} = \sum_{k=0}^\infty c_k z^k,
\end{equation*}de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{(-1)^{n}}{n+1}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n+1,\\
\\ 0, & \text{en otro caso.}\\
\end{array}
\right.
\end{equation*}
Por lo que, $c_0 = 0$ y para $k\geq 1$ se tiene que:
\begin{equation*}
c_k = \frac{(-1)^{k-1}}{k}.
\end{equation*}
Es claro que para $k\geq 1$ se tiene que $c_k \neq 0$ y como:
\begin{equation*}
\lambda = \lim_{k\to\infty} \frac{|c_{k+1}|}{|c_{k}|} = \lim_{k\to\infty} \left|\frac{k (-1)^{k}}{(k+1) (-1)^{k-1}}\right| = \lim_{k\to\infty} \frac{k}{k+1} = 1,
\end{equation*}entonces, del corolario 29.3 se sigue que $R = 1/ \lambda = 1$, es decir, la serie que define a $f$ tiene radio de convergencia 1, por lo que su dominio de convergencia es el disco $B(0,1)$.
Lo anterior nos garantiza que tanto $f(z)$ como $\operatorname{Log}(1+z)$ están bien definidas en el disco abierto $B(0,1)$.
De acuerdo con la proposición 30.2 y la definición 30.1, tenemos que $f$ es analítica en $B(0,1)$ y su derivada es:
\begin{align*}
f'(z) & = \sum_{k=1}^\infty k c_k z^{k-1}\\
& = \sum_{k=1}^\infty k \left(\frac{(-1)^{k-1}}{k}\right) z^{k-1}\\
& = \sum_{n=0}^\infty (-1)^n z^{n}\\
& = \frac{1}{1+z}, \quad \text{si} \,\, |z|<1.
\end{align*}
Sea $g(z) = f(z) – \operatorname{Log}(1+z)$. Claramente $g$ es analítica en $B(0,1)$ y su derivada es:
\begin{equation*}
g'(z) = \dfrac{d}{dz} \left [f(z) – \operatorname{Log}(1+z)\right] = 0, \quad \forall z\in B(0,1),
\end{equation*}por lo que $g$ es una función constante en $B(0,1)$, proposición 19.2. Para $z=0$ tenemos que:
\begin{equation*}
g(0) = f(0) – \operatorname{Log}(1+0) = 0,
\end{equation*}entonces:
\begin{equation*}
f(z) – \operatorname{Log}(1+z) = 0 \quad \Longrightarrow \quad f(z) = \operatorname{Log}(1+z).
\end{equation*}
Por lo tanto:
\begin{equation*}
\operatorname{Log}(1+z) = \sum_{n=0}^\infty \frac{(-1)^n z^{n+1}}{n+1}, \quad \text{si} \,\, |z|<1.
\end{equation*}
Observación 31.4.
Notemos que si sustituimos a $z$ por $z-1$ en el resultado anterior, entonces:
\begin{equation*}
\operatorname{Log}(z) = \sum_{n=0}^\infty \frac{(-1)^n (z-1)^{n+1}}{n+1}, \quad \text{si} \,\, |z-1|<1.
\end{equation*}
Tarea moral
- Prueba los lemas 31.1, 31.2 y 31.3.
- Completa la demostración de la proposición 31.1.
- Completa la demostración de la proposición 31.2.
- Utilizando las definiciones en series de potencias de las funciones seno y coseno prueba la identidad Pitagórica $\operatorname{sen}^2(z) + \operatorname{cos}^2(z) = 1$ para todo $z\in\mathbb{C}$.
- Determina la serie de potencias de la función $\operatorname{Log}\left(\dfrac{1}{1-z}\right)$ y determina su región de convergencia.
Hint: Recuerda que para la rama principal del logaritmo se cumple que $\operatorname{Log}\left(w^{-1}\right) = -\operatorname{Log}(w)$ si $w\in\mathbb{C}\setminus(-\infty,0]$. - a) Considera el desarrollo en serie de potencias para la función $f(z) = \operatorname{Log}(z)$ dado en la observación 31.4 y muestra que $f'(z) = 1/z$.
b) Sea $z_0 \neq 0$. Para $z \in B(z_0, 1)$ define a la función:
\begin{equation*}
f(z) = \displaystyle\sum_{n=0}^\infty \dfrac{(-1)^{n-1}}{n} \left(\dfrac{z-z_0}{z_0}\right)^n.
\end{equation*} Muestra que $f'(z) = 1/z$. - Determina la función suma y el dominio de convergencia de las siguientes series de potencias.
a) $\displaystyle \sum_{n=0}^\infty \frac{(-1)^{n+1}}{n!} z^{3n}$.
b) $\displaystyle \sum_{n=1}^\infty \frac{z^{2n+1}}{(2n-1)!}$.
c) $\displaystyle \sum_{n=0}^\infty \frac{2^{n+1}(z-i)^{n+2}}{(n+1)!}$. - Se definen a los números de Bernoulli $B_n$ a través de la serie de potencias:
\begin{equation*}
\frac{z}{e^z -1} = \displaystyle \sum_{n=0}^\infty \frac{B_n}{n!} z^n.
\end{equation*}a) Prueba la fórmula recursiva:
\begin{equation*}
\frac{B_0}{n! \, 0!} + \frac{B_1}{(n-1)! \, 1!} + \cdots + \frac{B_{n-1}}{1! \, (n-1)!} = \left\{ \begin{array}{lcc}
1 & \text{si} & n=1, \\
\\ 0 & \text{si} & n>1.
\end{array}
\right.
\end{equation*}Entonces $B_0=1$.
b) Calcula $B_1$, $B_2$, $B_3$, $B_4$.
c) Muestra que $B_n=0$ si $n$ es un número impar distinto de $1$. - Define a la función $f:\mathbb{R} \to \mathbb{R}$ como:
\begin{equation*}
f(x) = \left\{ \begin{array}{lcc}
0 & \text{si} & x\leq 0, \\
\\ e^{-1/x} & \text{si} & x>0.
\end{array}
\right.
\end{equation*}Muestra que $f$ es infinitamente diferenciable y que $f^{(n)}=0$ para todo $n\in\mathbb{N}$.
Más adelante…
Esta entrada es la última de la tercera unidad, correspondiente al tema de series de números complejos. En ella hemos abordado de manera general algunas de las funciones complejas elementales vistas como series de potencias, cabe mencionar que muchas de las propiedades referentes a estas funciones las hemos estudiado a detalle en la segunda unidad. Es importante notar que muchas de las definiciones dadas en esta entrada coinciden con las definiciones de estas funciones como series para el caso real, por lo que resulta natural la extensión de estas funciones al caso complejo.
En la siguiente entrada iniciamos con la cuarta unidad, correspondiente con el tema de integración compleja, en la cual veremos algunos de los resultados más importantes para las funciones complejas que sin duda son fundamentales en la teoría de la variable compleja en sí, mismos que nos permitirán caracterizar de manera clara a las funciones complejas y distinguirlas de las funciones reales.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Sucesiones y series de funciones.
- Siguiente entrada del curso: Trayectorias, curvas y contornos en el plano complejo $\mathbb{C}$.