Introducción
En la entrada anterior definimos el concepto de transformación compleja, como una función $T$ del plano complejo en sí mismo y probamos algunos resultados básicos sobre estas transformaciones al considerar a $\mathbb{C}$ como un $\mathbb{R}$-espacio vectorial. Además, definimos algunas de las transformaciones del plano más elementales como la traslación, la homotecia, la reflexión y la rotación.
Nuestro objetivo en ésta entrada es trabajar con un tipo de transformación compleja muy particular, que nos permitirá entender mejor la geometría de las funciones complejas en la siguiente entrada.
Definición 25.1. (Transformaciones afines lineales.)
Sean $a,b\in\mathbb{C}$ con $a\neq 0$. A las transformaciones de la forma:
\begin{equation*}
T(z) = az + b, \tag{25.1}
\end{equation*} se les llama transformaciones afines lineales o simplemente transformaciones lineales, las cuales son transformaciones dadas por una homotecia, una rotación y una traslación.
Observación 25.1.
En nuestros cursos de Geometría a las transformaciones de la forma (25.1), comúnmente se les llama transformaciones afines, sin embargo, en la mayoría de textos referentes a transformaciones del plano complejo $\mathbb{C}$ se les suele llamar transformaciones lineales puesto que geométricamente a una expresión de la forma (25.1) se le puede asociar una recta en el plano. Tener esto en cuenta es de suma importancia para no confundir las definiciones 24.2 y 24.3 con la definición 25.1, puesto que las primeras dos definiciones, vistas en nuestros cursos de Álgebra Lineal, corresponden a una propiedad entre $\mathbb{R}$-espacios vectoriales, mientras que la última definición está dada por una interpretación geométrica.
De hecho, es fácil verificar que no toda transformación lineal, definición 25.1, es $\mathbb{C}$-lineal, ya que $T(0) = b$ y $b\in\mathbb{C}$ no necesariamente es la constante cero.
Ejemplo 25.1.
Las transformaciones elementales del plano complejo son una transformación lineal particular.
a) Si $a=1$ y $b\in\mathbb{C}$, entonces tenemos la traslación por $b$, $T_b(z) = z+b$.
b) Si $a=e^{i\theta} \in \mathbb{C}$, con $\theta\in\mathbb{R}$ y $b=0$, entonces tenemos una rotación, $R_\theta(z) = e^{i\theta} z$.
c) Si $b=0$ y $a=k\in\mathbb{R}$, entonces tenemos una homotecia, $T(z)=kz$.
d) Si $a=e^{i\theta} \in \mathbb{C}$, con $\theta\in\mathbb{R}$ y $b\in\mathbb{C}$, entonces tenemos una reflexión respecto a una recta $L$, $r_\mathcal{L}(z) = e^{i\theta}\overline{z}+b$.
Procedemos ahora a establecer algunas propiedades sobre las transformaciones lineales.
Lema 25.1.
Sean $z_1, z_2, z_3\in\mathbb{C}$ tres puntos no colineales. El ángulo $\alpha$, figura 95, formado entre los vectores $z_2 – z_1$ y $z_3 – z_1$ está dado por:
\begin{equation*}
\alpha = \operatorname{arg}\left(\frac{z_3 – z_1}{z_2 – z_1}\right).
\end{equation*}
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Proposición 25.1.
Sea $T:\mathbb{C}\to\mathbb{C}$ una transformación lineal, entonces:
- $T$ envía rectas en rectas.
- $T$ envía circunferencias en circunferencias.
Demostración. Sea $T(z) = az + b$, con $a,b\in\mathbb{C}$ y $a\neq 0$.
- Sea $\mathcal{L}$ una recta en $\mathbb{C}$ con ecuación: \begin{equation*} c\overline{z} + \overline{c}z + d =0, \tag{25.2} \end{equation*} para algún $c\in\mathbb{C}$, $c\neq 0$, y $d\in\mathbb{R}$.
Veamos que $T\left(\mathcal{L}\right)$ es también una recta. Notemos que cualquier $z\in\mathcal{L}$, bajo $T$ es de la forma $w = az+b$. Dado que $a\neq 0$, entonces: \begin{equation*} z = \frac{1}{a}\left(w-b\right), \end{equation*} por lo que, al ser $z$ un punto de $\mathcal{L}$ satisface (25.2), es decir: \begin{align*} 0 & = c\overline{\left(\frac{1}{a}\left(w-b\right)\right)} + \overline{c} \left(\frac{1}{a}\left(w-b\right)\right) + d\\ & = c \, \overline{\left(\frac{w}{a}\right)} + \overline{c} \left(\frac{w}{a}\right) + d – \left( c \overline{\left(\frac{b}{a}\right)} + \overline{c} \left(\frac{b}{a}\right)\right). \end{align*} Dado que: \begin{equation*} c \, \overline{\left(\frac{b}{a}\right)} + \overline{c} \left(\frac{b}{a}\right) = c \overline{\left(\frac{b}{a}\right)} + \overline{c \, \overline{\left(\frac{b}{a}\right)}} = 2 \operatorname{Re}\left(c \, \overline{\left(\frac{b}{a}\right)}\right), \end{equation*} entonces: \begin{equation*} d – \left( c \overline{\left(\frac{b}{a}\right)} + \overline{c} \left(\frac{b}{a}\right)\right) \in \mathbb{R}, \end{equation*} por lo que todos los puntos $w\in T\left(\mathcal{L}\right)$ satisfacen la ecuación de una recta, es decir, $T\left(\mathcal{L}\right)$ es una recta. - Se deja como ejercicio al lector.
$\blacksquare$
Proposición 25.2.
Toda transformación lineal preserva ángulos.
Demostración. Sea $T$ una transformación lineal, es decir, $T(z) = az + b$, con $a,b\in\mathbb{C}$ y $a\neq 0$.
Dado que $T$ envía rectas en rectas, basta probar que el ángulo formado entre dos rectas que se cortan en un punto es igual al de sus imágenes bajo $T$.
Sean $\mathcal{L}_1$ y $\mathcal{L}_2$ dos rectas que se cortan en un punto $z_0\in\mathbb{C}$. Sean $z_1 \in\mathcal{L}_1$ y $z_2 \in\mathcal{L}_2$. Veamos que:
\begin{equation*}
\angle\left(\mathcal{L}_1, \mathcal{L}_2\right) = \angle\left(T(\mathcal{L}_1), T(\mathcal{L}_2)\right).
\end{equation*}
Por el lema 24.1 tenemos que:
\begin{align*}
\angle\left(T(\mathcal{L}_1), T(\mathcal{L}_2)\right) & = \operatorname{arg}\left(\frac{T(z_2) – T(z_0)}{T(z_1) – T(z_0)}\right)\\
& = \operatorname{arg}\left(\frac{az_2 + b – az_0-b}{az_1 + b – az_0-b}\right)\\
& = \operatorname{arg}\left(\frac{z_2 – z_0}{z_1-z_0}\right)\\
& = \angle\left(\mathcal{L}_1, \mathcal{L}_2\right).
\end{align*}
$\blacksquare$
Observación 25.2.
En general, es posible definir a una transformación compleja para la cual las transformaciones lineales son un caso particular. Dichas transformaciones resultan de gran interés en el estudio de las funciones complejas pues nos dicen mucho sobre su comportamiento geométrico.
Definición 25.2. (Transformaciones fraccionarias lineales.)
Sean $a,b,c,d\in\mathbb{C}$, con al menos $c$ ó $d$ distinto de cero. Una transformación de la forma:
\begin{equation*}
T(z) = \frac{az + b}{cz+d}, \tag{25.3}
\end{equation*} recibe el nombre de transformación fraccionaria lineal.
Observación 25.3.
Debe ser claro que una función $T$ dada por (25.3) está bien definida para todo $z\in\mathbb{C}$ tal que $cz+d\neq 0$. De hecho $T$ es una función analítica en $\mathbb{C}\setminus A$, donde:
\begin{equation*}
A = \{z\in\mathbb{C} : cz + d = 0\}.
\end{equation*}
Más aún, bajo la condición $c\neq0$, la función $T$ se restringe de $\mathbb{C}\setminus\left\{-\frac{d}{c}\right\}$ en $\mathbb{C}\setminus\left\{\frac{a}{c}\right\}$.
Definición 25.3. (Transformaciones de Möbius.)
Sean $a,b,c,d\in\mathbb{C}$. Una transformación de la forma (25.3) tal que $ad – bc\neq 0$ recibe el nombre de transformación de Möbius.
Observación 25.4.
La condición $ad – bc\neq 0$, impuesta sobre las constantes $a,b,c,d\in\mathbb{C}$, nos permite garantizar lo siguiente:
1) Las expresiones $az + b$ y $cz + d$ no se anulan para los mismos valores de $z$.
2) La transformación $T$ no puede ser constante, ya que $a$ y $c$ no pueden ser ambas cero, al igual que $b$ y $d$ no pueden ser ambas cero.
3) En general, el denominador no puede ser un múltiplo constante del numerador, es decir que $az + b$ y $cz + d$ no tienen un factor común.
Además, no es difícil verificar que $T$ es biyectiva si y solo si $ad – bc\neq 0$, por lo que se deja como ejercicio al lector.
Observación 25.5.
Notemos que toda transformación de la forma:
\begin{equation*}
w = T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc\neq 0,
\end{equation*} es equivalente a una expresión de la forma:
\begin{equation*}
Azw + Bz + Cw + D = 0, \,\,\,\text{con} \,\,AD – BC\neq 0,
\end{equation*} donde $A = c$, $B=-a$, $C =d$ y $D=-b$.
Dado que ésta última expresión es lineal en $z$ y es lineal en $w$, entonces es bilineal en $z$ y $w$, por lo que una transformación de Möbius también suele llamarse una transformación bilineal.
Ejemplo 25.2.
Notemos que algunas de las transformaciones definidas antes, son un una transformación de Möbius particular.
a) Si $a=1=d$ y $b=0=c$, entonces tenemos la transformación identidad, $T(z) = z$.
b) Si $c=0$ y $d=1$, entonces tenemos una transformación lineal, $T(z) = az + b$.
c) Si $a = d = 0$ y $b=c$, entonces tenemos la transformación inversión, $T(z)=\dfrac{1}{z}$, dada en el ejemplo 24.1.
Es común trabajar con las transformaciones de Möbius como funciones sobre el plano complejo extendido, por lo que, considerando la observación 15.5 y el ejercicio 4 de la entrada 12, podemos definir a una transformación de Möbius como una función continua en $\mathbb{C}_\infty$, como sigue:
Definición 25.4. (Transformaciones de Möbius en $\mathbb{C}_\infty$.)
Sean $a,b,c,d\in\mathbb{C}$. Si $ad – bc\neq 0$, entonces diremos que una función racional $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ dada como:
\begin{equation*}
T(z)= \left\{ \begin{array}{lcc}
\dfrac{az+b}{cz+d}, & \text{si} & z \neq -\frac{d}{c}, \,\, z\neq \infty, \\
\\ \infty, & \text{si} & z = -\frac{d}{c}, \\
\\ \dfrac{a}{c}, & \text{si} & z = \infty,
\end{array}
\right.
\end{equation*} es una transformación de Möbius en el plano complejo extendido.
Observación 25.6.
Como hemos mencionado anteriormente, la condición $ad – bc\neq 0$ se impone para evitar que trabajemos con una transformación constante. Sin embargo, podemos utilizar dicha condición para plantear de una forma equivalente a la definición 25.4 considerando los siguientes casos:
1) Si $c=0$, entonces la condición $ad – bc\neq 0$ se reduce a $ad \neq 0$, en dicho caso tenemos que $T(\infty) = \infty$ y:
\begin{equation*}
T(z) = \frac{az+b}{d} = \frac{a}{d} \, z + \frac{b}{d}.
\end{equation*} 2) Si $c\neq 0$, tenemos $ad – bc\neq 0$, entonces $T(\infty) = a/c$, $T\left(-d/c\right) = \infty$ y:
\begin{equation*}
T(z) = \frac{az+b}{cz+d} = \frac{a}{c} + \frac{bc-ad}{c}\frac{1}{cz+d}.
\end{equation*}
Ejemplo 25.3.
La transformación:
\begin{equation*}
f(z) = \frac{z-1}{iz+i},
\end{equation*} es una transformación de Möbius desde que $a=1$, $b=-1$, $c=i=d$ y $ad – bc = i – (-i) = 2i \neq 0$.
Dado que $c=i\neq 0$, entonces la transformación de Möbius $f$ es una función restringida, es decir:
\begin{equation*}
f:\mathbb{C}\setminus\{-1\} \to \mathbb{C}\setminus\{-i\}.
\end{equation*}
Podemos extender dicha transformación de Möbius al plano complejo extendido como sigue:
\begin{equation*}
f(z) = \frac{z-1}{iz+i}, \quad \text{si} \quad z\neq -1 \quad \text{y} \quad z\neq \infty,
\end{equation*}
mientras que:
\begin{equation*}
f(-1) = \infty \quad \text{y} \quad f(\infty) = -i.
\end{equation*}
Proposición 25.3.
Sean $T_1$ y $T_2$ dos transformaciones de Möbius dadas por:
\begin{equation*}
T_1(z) = \frac{a_1 z + b_1}{c_1 z + d_1} \quad \text{y} \quad T_2(z) = \frac{a_2 z + b_2}{c_2 z + d_2}
\end{equation*}
con $a_1d_1 – b_1c_1 \neq 0$ y $a_2d_2 – b_2c_2 \neq 0$. Entonces su composición es también una transformación de Möbius.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Proposición 25.4.
Toda transformación de Möbius es una biyección de $\mathbb{C}_\infty$ en $\mathbb{C}_\infty$. En particular la inversa de una transformación de Möbius es también una transformación de Möbius.
Demostración. Sea $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ una transformación de Möbius dada por:
\begin{equation*}
T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc \neq 0.
\end{equation*}
De acuerdo con la observación 25.6 tenemos que si $c = 0$, entonces $T(\infty) = \infty$ y si $c\neq 0$, entonces $T(\infty) = a/c$ y $T\left(-d/c\right) = \infty$.
Primeramente verifiquemos que $T$ es inyectiva. Supongamos que $T(z_1) = T(z_2)$. Notemos que si $c \neq 0$, entonces tenemos la condición $ad – bc\neq 0$, por lo que:
\begin{align*}
\frac{az_1 + b}{cz_1+d} &= \frac{az_2 + b}{cz_2+d}\\ & \Longleftrightarrow \quad adz_1 + bcz_2 = adz_2 + bcz_1\\
& \Longleftrightarrow \quad (ad-bc)(z_1 – z_2) = 0\\
& \Longleftrightarrow \quad z_1 = z_2.
\end{align*}
Por otra parte, notemos que si $c=0$, entonces tenemos la condición $ad\neq 0$, por lo que:
\begin{align*}
\frac{az_1 + b}{d} &= \frac{az_2 + b}{d}\\ & \Longleftrightarrow \quad az_1 + b= az_2 + b\\
& \Longleftrightarrow \quad z_1 = z_2.
\end{align*}
Verifiquemos ahora que $T$ es suprayectiva. Sea $w\in\mathbb{C}_\infty$. Veamos que existe $z\in\mathbb{C}_\infty$ tal que $T(z) = w$. Notemos que si $w = \infty$, entonces $z = -d/c$ corresponde con dicho valor si $c = 0$. Sin pérdida de generalidad supongamos que $w\neq \infty$, entonces tenemos que $c\neq 0$ y por tanto se cumple la condición $ad – bc\neq 0$, por lo que planteamos la ecuación:
\begin{equation*}
w = \frac{az+b}{cz+d}.
\end{equation*}
Resolviendo para $z$ tenemos que:
\begin{equation*}
z = T^{-1}(w) = \frac{-dw+b}{cw-a},
\end{equation*} por lo que $T$ es suprayectiva.
Dado que $T$ es biyectiva entonces existe $T^{-1}$ tal que $T \circ T^{-1} = T^{-1} \circ T = \mathbb{I}_\mathbb{C}$ para todo $z\in\mathbb{C}_\infty$, la cual está dada por:
\begin{equation*}
T^{-1}(z) = \frac{-dz+b}{cz-a},\,\,\,\text{con} \,\,ad – bc \neq 0,
\end{equation*} tal que si $c = 0$, entonces $T^{-1}(\infty) = \infty$ y si $c\neq 0$, entonces $T^{-1}(a/c) = \infty$ y $T^{-1}\left(\infty\right) = -d/c$. Es claro que $T^{-1}$ es también una transformación de Möbius.
$\blacksquare$
Observación 25.7.
De acuerdo con las proposiciones 25.3 y 25.4 no es díficil verificar que el conjunto de todas las transformaciones de Möbius dotado con la operación de composición de funciones forma un grupo.
Proposición 25.5.
Toda transformación de Möbius $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ se puede expresar como la composición de transformaciones lineales (homotecias, rotaciones y traslaciones) y la inversión.
Demostración. Sea $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ una transformación de Möbius dada por:
\begin{equation*}
T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc \neq 0,
\end{equation*} tal que si $c = 0$, entonces $T(\infty) = \infty$ y si $c\neq 0$, entonces $T(\infty) = a/c$ y $T\left(-d/c\right) = \infty$.\\
Por la observación 25.6(1) tenemos que, para $c=0$ la transformación $T$ se puede ver como la composición $T_2 \circ T_1$, donde:
\begin{equation*}
T_1(z) = \frac{a}{d}\,z, \quad \quad T_2(z) = z + \frac{b}{d},
\end{equation*} con $ad\neq 0$, por lo que en dicho caso se cumple el resultado.
Por otra parte, por la observación 25.6(2), para $c\neq 0$ tenemos que la transformación $T$ se puede ver como la composición $T_3 \circ T_2 \circ T_1$, donde:
\begin{equation*}
T_1(z) = cz + d, \quad \quad T_2(z) = \frac{1}{z}, \quad \quad T_3(z) = \frac{a}{c} + \frac{bc-ad}{c} z,
\end{equation*} con $ad – bc\neq 0$, por lo que en dicho caso también se cumple el resultado.
$\blacksquare$
Procedemos a analizar algunas propiedades geométricas importantes de las transformaciones de Möbius. Para ello nos apoyaremos de algunos resultados para la transformación inversión.
Tenemos que la transformación:
\begin{equation*}
w = T(z) = \frac{1}{z}, \tag{25.4}
\end{equation*} establece una biyección entre los puntos distintos de cero de los planos $z$ y $w$. Dado que $z \, \overline{z} = |\,z\,|^2$, entonces podemos reescribir a (25.4) mediante la composición de las siguientes transformaciones:
\begin{equation*}
T_1(z) = \frac{1}{\overline{z}} = \frac{z}{|\,z\,|^2}, \quad \quad T_2(z) = \overline{z}, \tag{25.5}
\end{equation*} entonces es claro que $T(z) = (T_2 \circ T_1)(z)$.
Notemos que la primer transformación en (25.5) nos describe una inversión con respecto a la circunferencia unitaria $C(0,1)$, es decir, la imagen de un punto $z\neq 0$ es el punto $w_1 = T_1(z)$ con las siguientes propiedades:
\begin{equation*}
|\,w_1\,| = \frac{1}{|\,z\,|}, \quad \quad \operatorname{arg} w_1 = \operatorname{arg} z.
\end{equation*}
Por lo que los puntos fuera de la circunferencia unitaria $|\,z\,|=1$ serán mapeados, mediante $T_1$, en los puntos $w_1\neq 0$ dentro de dicha circunferencia y viceversa. Mientras que los puntos que caigan sobre la circunferencia unitaria $|\,z\,|=1$, bajo $T_1$, serán mapeados en ellos mismos. Por otra parte, la segunda transformación dada en (16.2) es simplemente una reflexión a través del eje real de cada $w_1 = T_1(z) \neq 0$, es decir $w = \overline{w_1}$, figura 96.

Podemos visualizar lo anterior en el siguiente applet de GeoGebra: https://www.geogebra.org/m/z3cf2kyt.
Desde que:
\begin{equation*}
\lim_{z\to 0} \frac{1}{z} = \infty, \quad \lim_{z\to \infty} \frac{1}{z} = 0,
\end{equation*} entonces podemos definir una biyección entre los planos $z$ y $w$ extendidos, es decir entre $\mathbb{C}_\infty$ y $\mathbb{C}_\infty$, mediante:
\begin{equation*}
T(z) = \left\{ \begin{array}{lcc}
\dfrac{1}{z}, & \text{si} & z\neq 0, z\neq \infty,\\
\\0, & \text{si} & z = \infty, \\
\\ \infty, & \text{si} & z=0.
\end{array}
\right.
\end{equation*}
Es claro que la transformación $T$, definida previamente, es una función continua en $\mathbb{C}_\infty$.
Considerando lo anterior, estamos listos para probar la siguiente:
Proposición 25.6.
La transformación inversión mapea el conjunto de circunferencias y rectas en el conjunto de circunferencias y rectas.
Demostración. Sea $T(z) = 1/z$ la transformación inversión. De nuestros cursos de geometría analítica sabemos que para $A,D,E,F$ números reales tales que $D^2+E^2 > 4AF$, la ecuación:
\begin{equation*}
A(x^2 + y^2) + Dx + Ey + F = 0, \tag{25.6}
\end{equation*} representa una circunferencia o una recta, si $A\neq 0$ ó $A = 0$, respectivamente.
Dado que $z\, \overline{z} = |\,z\,|^2$, tenemos que si $w = u + iv$ es la imagen de $z=x+iy\neq 0$ bajo la transformación inversión, es decir:
\begin{equation*}
w=T(z) = \frac{1}{z} = \frac{\overline{z}}{|\,z\,|^2},
\end{equation*}entonces:
\begin{equation*}
u=\frac{x}{x^2+y^2}, \quad v = -\frac{y}{x^2+y^2}. \tag{25.7}
\end{equation*}
Considerando que la transformación inversión establece una biyección entre los planos $z$ y $w$, entonces podemos plantear:
\begin{equation*}
z= T^{-1}(w) = \frac{1}{w} = \frac{\overline{w}}{|\,w\,|^2},
\end{equation*} de donde:
\begin{equation*}
x=\frac{u}{u^2+v^2}, \quad y = -\frac{v}{u^2+v^2}.\\ \tag{25.8}
\end{equation*}
Supongamos que $z=x+iy\neq 0$ satisface (25.6), veamos que $w=u+iv = T(z) \neq 0$ también satisface una ecuación similar. Sustituyendo las ecuaciones dadas en (25.8) tenemos que:
\begin{align*}
0 & = A\left[\frac{u^2+v^2}{(u^2+v^2)^2}\right] + D\left(\frac{u}{u^2+v^2}\right) + E\left(-\frac{v}{u^2+v^2}\right) + F\\
& = A\left(\frac{1}{u^2+v^2}\right) + Du\left(\frac{1}{u^2+v^2}\right) -Ev\left(\frac{1}{u^2+v^2}\right) + F,
\end{align*} de donde se sigue que $w=u+iv$ satisface la ecuación:
\begin{equation*}
F(u^2 + v^2) + Du – Ev + A = 0, \tag{25.9}
\end{equation*}la cual corresponde con la ecuación de una circunferencia o una recta, si $F\neq 0$ ó $F = 0$, respectivamente.
De manera análoga se puede mostrar que si $w=u+iv$ satisface (25.9), entonces, utilizando (25.7), $z=x+iy$ satisface (25.6).
$\blacksquare$
Observación 25.8.
Si consideramos a $T$ la transformación inversión, entonces de las ecuaciones (25.6) y (25.9) tenemos que:
1) Si $A\neq0$ y $F\neq 0$, en el plano $z$ se tiene una circunferencia que no pasa a través del origen, la cual, bajo $T$, será mapeada en una circunferencia que tampoco pasa por el origen en el plano $w$.
2) Si $A\neq0$ y $F=0$, en el plano $z$ se tiene una circunferencia que pasa a través del origen, la cual, bajo $T$, será mapeada en una recta que no pasa por el origen en el plano $w$.
3) Si $A=0$ y $F\neq 0$, en el plano $z$ se tiene una recta que no pasa a través del origen, la cual, bajo $T$, será mapeada en una circunferencia que pasa por el origen en el plano $w$.
4) Si $A=0$ y $F= 0$, en el plano $z$ se tiene una recta que pasa a través del origen, la cual será mapeada, bajo $T$, en una recta que pasa por el origen en el plano $w$.
Podemos visualizar lo anterior en el siguiente applet de GeoGebra: https://www.geogebra.org/m/eqh4nbab.
De acuerdo con las proposiciones 25.1, 25.5 y 25.6 se tiene el siguiente:
Corolario 25.1.
Toda transformación de Möbius mapea el conjunto de rectas y circunferencias en el conjunto de rectas y circunferencias.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 25.4.
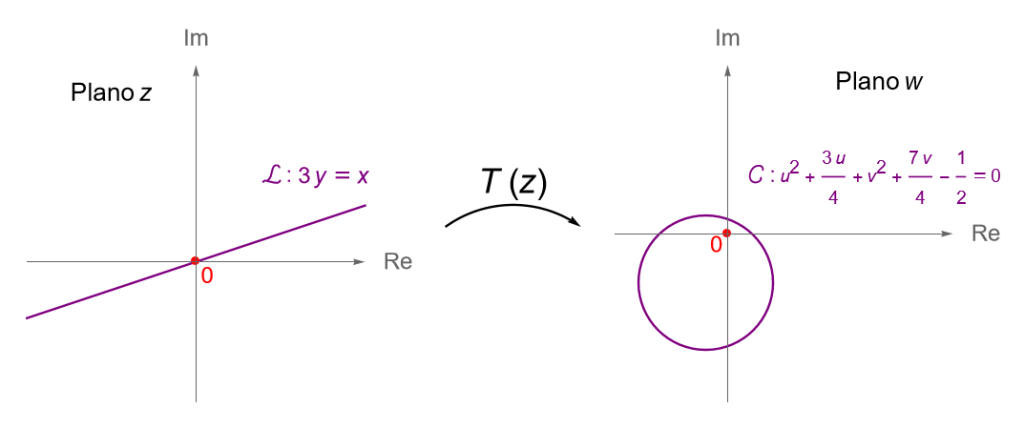
Muestra que la recta $\mathcal{L} : 3y=x$, en el plano $z$, es enviada en una circunferencia, en el plano $w$, bajo la transformación de Möbius:
\begin{equation*}
w = T(z) = \frac{i z+ 2}{4z+i}. \tag{25.10}
\end{equation*}
Solución. Sean $z=x+iy$ y $w=u+iv$. Para determinar la imagen de la recta $3y=x$ bajo $T$, debemos encontrar los valores de $x$ y de $y$ en términos de $u$ y de $v$.
Resolvemos (25.10) para $z$:
\begin{align*}
w = \frac{i z+ 2}{4z+i} \quad &\Longrightarrow \quad 4zw + iw = iz +2\\
&\Longrightarrow \quad z(4w-i) = 2-iw\\
&\Longrightarrow \quad z = \frac{2-iw}{4w-i}.
\end{align*}
Entonces:
\begin{align*}
x+iy & = \frac{v+2-iu}{4u+i(4v-1)} \frac{4u-i(4v-1)}{4u-i(4v-1)}\\
& = \frac{(v+2-iu)[4u+i(4v-1)]}{16u^2+(4v-1)^2}\\
& = \frac{9u – i(4u^2+4v^2+7v-2)}{16u^2+(4v-1)^2},
\end{align*} de donde:
\begin{equation*}
x = \frac{9u}{16u^2+(4v-1)^2}, \quad \quad y = -\frac{4u^2+4v^2+7v-2}{16u^2+(4v-1)^2}.
\end{equation*}
Sustituyendo en la ecuación de la recta tenemos que:
\begin{equation*}
\frac{9u}{16u^2+(4v-1)^2} = \frac{-3(4u^2+4v^2+7v-2)}{16u^2+(4v-1)^2},
\end{equation*} es decir:
\begin{equation*}
u^2 + v^2 + \frac{3}{4}u+\frac{7}{4}v-\frac{1}{2} = 0,
\end{equation*} la cual corresponde con la ecuación de una circunferencia, en el plano $w$, con centro en $\left(-3/8, -7/8\right)$ y radio $r = (3/8) \sqrt{10}$.
Podemos generalizar la definición 24.10, de punto fijo de una transformación, para las funciones complejas definidas sobre el plano complejo extendido.
Definición 25.5.(Punto fijo.)
Sea $S\subset\mathbb{C}_\infty$ y sea $f: S \to \mathbb{C}_\infty$ una función. Diremos que un punto $z_0 \in S$ es un punto fijo de $f$ si y solo si $f(z_0) = z_0$.
Ejemplo 25.5.
a) La función $f(z) = z^2$ fija a los puntos $0, 1$ e $\infty$.
b) La función $f(z) = \dfrac{1}{z}$ fija a los puntos $1$ y $-1$.
c) La función $f(z) = z+i$ fija al $\infty$.
Una pregunta interesante que podemos hacernos es ¿cuáles son los puntos fijos de una transformación de Möbius?
Para responder a esta pregunta consideremos los siguientes resultados.
Proposición 25.7.
Toda transformación de Möbius $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ deja fijo 1, 2 o todos los puntos de $\mathbb{C}_\infty$.
Demostración. Sea $T:\mathbb{C}_\infty \to \mathbb{C}_\infty$ una transformación de Möbius dada por:
\begin{equation*}
T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc\neq 0.
\end{equation*}
Para encontrar los puntos fijos de $T$ planteamos la siguiente ecuación:
\begin{equation*}
T(z) = \frac{az + b}{cz+d} = z,
\end{equation*} resolviendo para $z$ obtenemos la ecuación cuadrática:
\begin{equation*}
cz^2 + (d-a)z – b = 0.\tag{25.11}
\end{equation*}
Caso 1. Si $c\neq 0$, por la observación 25.6 tenemos que $T(\infty) = a/c$ y $T\left(-d/c\right) = \infty$, es decir, $T$ no fija al punto $z=\infty$. Por otra parte, es claro que la ecuación (25.11) tiene exactamente 1 ó 2 soluciones, por lo que en dicho caso tenemos que $T$ fija 1 ó 2 puntos de $\mathbb{C}_\infty$.
Caso 2. Si $c=0$, por la observación 25.6 tenemos que $T(\infty) = \infty$, es decir, $T$ fija al punto $z=\infty$. Por otra parte, para $c=0$ tenemos la condición $ad\neq 0$, por lo que $a \neq 0$ y $d \neq 0$, entonces procedemos a analizar los siguientes casos:
- Si $a\neq d$, entonces la transformación $T$ es de la forma: \begin{equation*} T(z) = \frac{az + b}{d}. \end{equation*} De (25.11) tenemos la solución: \begin{equation*} z = \frac{b}{d-a} \neq \infty, \end{equation*} la cual es otro punto fijo de $T$, por lo que tenemos exactamente 2 puntos fijos, es decir, $T$ deja fijos a 2 puntos de $\mathbb{C}_\infty$.
- Si $a = d$, entonces la ecuación (25.11) se reduce a $b=0$, por lo que la transformación $T$ es de la forma: \begin{equation*} T(z) = \frac{az + 0}{0z + a} = z, \end{equation*} la cual es la transformación identidad, por lo que claramente $T$ fija a todo punto de $\mathbb{C}_\infty$.
$\blacksquare$
Corolario 25.2.
Si $T$ es una transformación de Möbius que fija tres puntos distintos de $\mathbb{C}_\infty$, entonces $T$ es la identidad.
Demostración. Es inmediata del resultado anterior.
$\blacksquare$
Corolario 25.3.
Si $T_1$ y $T_2$ son dos transformaciones de Möbius que fijan a tres puntos distintos de $\mathbb{C}_\infty$, entonces $T_1=T_2$.
Demostración. Se sigue de las proposiciones 25.3, 25.4 y del corolario 25.3, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Observación 25.9.
El último resultado es de suma importancia pues nos dice que el comportamiento de una transformación de Möbius está completamente descrito por su acción sobre tres puntos distintos de $\mathbb{C}_\infty$.
Observación 25.10.
Notemos que si $T$ es una transformación de Möbius, digamos:
\begin{equation*}
T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc\neq 0,
\end{equation*} entonces para $\lambda\in\mathbb{C}$, tal que $\lambda\neq 0$, se cumple que:
\begin{equation*}
S(z) = \frac{\lambda a z +\lambda b}{\lambda c z + \lambda d}
\end{equation*} también es una transformación de Möbius desde que $\lambda^2(ad – bc) \neq 0$. Más aún, es claro que $T = S$.
Ejemplo 25.6.
Determina la transformación de Möbius que envía los puntos del plano $z$, en los puntos del plano $w$, respectivamente.
a) $-1\mapsto -i$, $0 \mapsto 1$ y $1 \mapsto i$.
b) $1\mapsto 0$, $i \mapsto 1$ y $-1 \mapsto \infty$.
c) $1\mapsto i$, $0 \mapsto \infty$ y $-1 \mapsto 1$.
Solución. Sea $T$ una transformación de Möbius, es decir:
\begin{equation*}
w = T(z) = \frac{az + b}{cz+d}, \,\,\,\text{con} \,\,ad – bc\neq 0.
\end{equation*}
a) Dado que $T(0)=1$, tenemos que:
\begin{equation*}
1 = \frac{b}{d} \quad \Longrightarrow \quad b = d,
\end{equation*} por lo que $b(a-c) \neq 0$, es decir $b\neq 0$ y $a\neq c$, entonces:
\begin{equation*}
T(z) = \frac{az + b}{cz+b}, \,\,\,\text{con} \,\,b(a-c) \neq 0.
\end{equation*} Como $T(-1) = -i$ y $T(1) = i$, tenemos el siguiente sistema de ecuaciones:
\begin{equation*}
\left\{ \begin{array}{c}
\dfrac{-a+b}{-c+b} = -i,\\
\\ \dfrac{a+b}{c+b} = i.
\end{array}
\right. \quad \Longrightarrow \quad \left\{ \begin{array}{c}
-a+b = ic-ib,\\
\\ a+b = ic+ib.
\end{array}
\right.
\end{equation*}Resolviendo tenemos $a = ib$ y $c = -ib$.
Como $b\neq 0$, entonces:
\begin{equation*}
T(z) = \frac{b(iz+1)}{b(-iz+1)} = \frac{iz+1}{-iz+1} = \frac{i-z}{i+z}.
\end{equation*}
b) Puesto que $T(-1)=\infty$, de la observación 25.6 tenemos que $c\neq 0$ y $-d/c = -1$, es decir, $c=d$.
Como $T(1) = 0$, entonces $a+b = 0$, es decir $a = -b$, entonces:
\begin{equation*}
T(z) = \frac{-b(z-1)}{d(z+1)}, \quad -2bd \neq 0.
\end{equation*}Por último, como $T(i)=1$, entonces:
\begin{equation*}
\frac{-b(i-1)}{d(i+1)} = 1 \quad \Longrightarrow \quad b = d \left(\frac{1+i}{1-i}\right) = id.
\end{equation*}Por lo tanto, como $d\neq 0$, tenemos que:
\begin{equation*}
T(z) = \frac{-id(z-1)}{d(z+1)}= -i\left(\dfrac{z-1}{z+1}\right).
\end{equation*}
c) Dado que $T(0)=\infty$, de la observación 25.6 tenemos que $c\neq 0$ y $d=0$, por lo que:
\begin{equation*}
T(z) = \frac{az + b}{cz}, \,\,\,\text{con} \,\,bc \neq 0.
\end{equation*}Como $T(1) = i$ y $T(-1) = 1$, tenemos el siguiente sistema de ecuaciones:
\begin{equation*}
\left\{ \begin{array}{c}
\dfrac{a+b}{c} = i,\\
\\ \dfrac{-a+b}{-c} = 1.
\end{array}
\right. \quad \Longrightarrow \quad \left\{ \begin{array}{c}
a+b = ic,\\
\\ -a+b = -c.
\end{array}
\right.
\end{equation*} Resolviendo tenemos $2a = c(1+i)$ y $2b = c(i-1)$.
De acuerdo con la observación 25.10 y considerando que $c\neq 0$, entonces tenemos que:
\begin{align*}
T(z) = \frac{az+b}{cz} & = \frac{2az+2b}{2cz}\\
&= \frac{c[(1+i)z+(i-1)]}{2cz}\\
&= \frac{(1+i)z+(i-1)}{2z}.
\end{align*}
Proposición 25.8.
Sean $z_1, z_2, z_3 \in\mathbb{C}_\infty$ tres puntos distintos. Entonces existe una única transformación de Möbius tal que:
\begin{equation*}
T(z_1) = 0, \quad T(z_2) = 1 \quad \text{y} \quad T(z_3) = \infty. \tag{25.12}
\end{equation*}
Demostración. Sean $z_1, z_2, z_3 \in\mathbb{C}_\infty$ tres puntos distintos. La unicidad se sigue del corolario 25.3.
Supongamos primeramente que los tres puntos son finitos, entonces para la existencia definimos a la transformación:
\begin{equation*}
T(z) = \frac{(z-z_1)(z_2 – z_3)}{(z-z_3)(z_2 – z_1)}, \quad \forall z\in\mathbb{C}. \tag{25.13}
\end{equation*} Primero veamos que $T$ es una transformación de Möbius. Notemos que:
\begin{align*}
T(z) &= \frac{(z-z_1)(z_2 – z_3)}{(z-z_3)(z_2 – z_1)}\\
& = \frac{(z_2 – z_3) z + z_1(z_3-z_2)}{(z_2 – z_1)z + z_3 (z_1 – z_2)}\\
& =: \frac{az+b}{cz+d},
\end{align*}de donde:
\begin{align*}
ad – bc & = z_3(z_2 – z_3)(z_1 – z_2) + z_1(z_3 – z_2)(z_1 – z_2)\\
& = (z_2 – z_3)(z_1 – z_2)(z_3 – z_1).
\end{align*}Dado que $z_1, z_2, z_3$ son distintos, entonces $z_2 – z_3 \neq 0$, $z_1 – z_2 \neq 0$ y $z_3 – z_1 \neq 0$, es decir, $ad – bc \neq 0$, por lo que $T$ es una transformación de Möbius.
Veamos ahora que $T$ cumple (25.12). Es claro que:
\begin{align*}
T(z_1) &= \frac{(z_1-z_1)(z_2 – z_3)}{(z_1-z_3)(z_2 – z_1)} = 0,\\
T(z_2) &= \frac{(z_2-z_1)(z_2 – z_3)}{(z_2-z_3)(z_2 – z_1)} = 1,\\
T(z_3) &= \frac{(z_3-z_1)(z_2 – z_3)}{(z_3-z_3)(z_2 – z_1)} = \infty.
\end{align*}
Por otra parte, si alguno de los $z_k$’s es $\infty$, definimos a $T(z)$ de modo que $z_k$ tienda a $\infty$ en (25.13). Sin pérdida de generalidad, supongamos que $z_1 = \infty$, entonces reescribimos el lado derecho de la igualdad en (25.13) como sigue:
\begin{equation*}
\dfrac{\dfrac{z}{z_1} – 1}{z-z_3} \dfrac{z_2-z_3}{\dfrac{z_2}{z_1} – 1},
\end{equation*}entonces:
\begin{equation*}
T(z) := \lim_{z_1 \to \infty} \dfrac{\dfrac{z}{z_1} – 1}{z-z_3} \dfrac{z_2-z_3}{\dfrac{z_2}{z_1} – 1} = \frac{z_2 – z_3}{z – z_3}.
\end{equation*}Claramente $T$ es una transformación de Möbius pues $z_3 – z_2 \neq 0$. Notemos que:
\begin{equation*}
T(\infty) = 0, \quad T(z_2) = 1 \quad \text{y} \quad T(z_3) = \infty.
\end{equation*}Análogamente, si $z_2 = \infty$ podemos definir:
\begin{equation*}
T(z) = \frac{z – z_1}{z – z_3},
\end{equation*}mientras que si $z_3 = \infty$ definimos:
\begin{equation*}
T(z) = \frac{z – z_1}{z_2 – z_1}.
\end{equation*}En ambos casos $T$ es una transformación de Möbius y se cumple (25.12).
$\blacksquare$
El resultado anterior nos motiva a dar la siguiente:
Definición 25.6. (Razón cruzada.)
Sean $z_1, z_2, z_3 \in\mathbb{C}_\infty$ tres puntos distintos y sea $z\in\mathbb{C}_\infty$. La {\bf razón cruzada} de $z, z_1, z_2$ y $z_3$, denotada como $(z; z_1, z_2, z_3)$, es el valor $T(z) \in\mathbb{C}_\infty$, donde $T$ es la única transformación de Möbius tal que $T(z_1)=0$, $T(z_2)=1$ y $T(z_3)=\infty$.
Observación 25.11.
De acuerdo con la proposición 25.8 es claro que:
\begin{equation*}
(z; z_1, z_2, z_3) = T(z)= \left\{ \begin{array}{lcc}
\dfrac{(z-z_1)(z_2 – z_3)}{(z-z_3)(z_2 – z_1)} & \text{si} & z_1, z_2, z_3 \in\mathbb{C}, \\
\\ \dfrac{z_2-z_3}{z-z_3} & \text{si} & z_1 = \infty, \\
\\ \dfrac{z-z_1}{z-z_3} & \text{si} & z_2 = \infty, \\
\\ \dfrac{z-z_1}{z_2-z_1} & \text{si} & z_3 = \infty.
\end{array}
\right.
\end{equation*}
Ejemplo 25.7.
Determina el valor de las siguientes razones cruzadas.
a) $(z;0,1,\infty)$.
b) $(z;1,\infty, 0)$.
c) $(z_2;z_1,z_2,z_3)$.
d) $(2;\infty, i,-1)$.
Solución. Tenemos que:
a) \begin{equation*}
(z;0,1,\infty) = \frac{z-0}{1-0} = z.
\end{equation*}b)
\begin{equation*}
(z;1,\infty,0) = \frac{z-1}{z-0} = \frac{z-1}{z}.
\end{equation*}c)
\begin{equation*}
(z_2;z_1,z_2,z_3) = \dfrac{(z_2-z_1)(z_2 – z_3)}{(z_2-z_3)(z_2 – z_1)} = 1.
\end{equation*}d)
\begin{equation*}
(2;\infty, i,-1) = \frac{i-(-1)}{2-(-1)} = \frac{1+i}{3}.
\end{equation*}
Ejemplo 25.8.
De acuerdo con la definición 25.6, la transformación de Möbius del ejemplo 25.6(b) puede escribirse como $T(z) = (z;1,i,-1)$.
Corolario 25.4.
Sean $z_1, z_2, z_3 \in\mathbb{C}_\infty$ tres puntos distintos y $w_1, w_2, w_3 \in\mathbb{C}_\infty$ tres puntos distintos. Entonces, existe una única transformación de Möbius tal que:
\begin{equation*}
H(z_1) = w_1, \quad H(z_2) = w_2 \quad \text{y} \quad H(z_3) = w_3.
\end{equation*}
Demostración. Dadas las hipótesis, sean $T(z) = (z; z_1, z_2, z_3)$ y $S(w) = (w; w_1, w_2, w_3)$. Definimos $H=S^{-1}\circ T$, entonces es claro que:
\begin{align*}
H(z_1) & = (S^{-1}\circ T)(z_1) = S^{-1}\left(T(z_1)\right) = S^{-1}\left(0\right) = w_1,\\
H(z_2) &= (S^{-1}\circ T)(z_2) = S^{-1}\left(T(z_2)\right) = S^{-1}\left(1\right) = w_2,\\
H(z_3) &= (S^{-1}\circ T)(z_3) = S^{-1}\left(T(z_3)\right) = S^{-1}\left(\infty\right) = w_3.
\end{align*} La unicidad se sigue del corolario 25.3.
$\blacksquare$
Proposición 25.9.
Toda transformación de Möbius preserva la razón cruzada.
Demostración. Sea $T$ una transformación de Möbius y sean $z_1, z_2, z_3 \in\mathbb{C}_\infty$ tres puntos distintos. Veamos que:
\begin{equation*}
\left(z; z_1, z_2, z_3\right) = \left(T(z); T(z_1), T(z_2), T(z_3)\right).
\end{equation*}
Sea $S(z) = \left(z; z_1, z_2, z_3\right)$. Definimos $H=S\circ T^{-1}$, la cual claramente es una transformación de Möbius. Tenemos que:
\begin{align*}
H(T(z_1)) & = S(z_1) = 0,\\
H(T(z_2)) &= S(z_2) = 1,\\
H(T(z_3)) &= S(z_3) = \infty,
\end{align*} por lo que, por la unicidad de la razón cruzada:
\begin{equation*}
H(z) = \left(z; T(z_1), T(z_2), T(z_3)\right), \quad \forall z\in\mathbb{C}_\infty.
\end{equation*}Entonces:
\begin{equation*}
S(z) = H(T(z)) = \left(T(z); T(z_1), T(z_2), T(z_3)\right), \quad \forall z\in\mathbb{C}_\infty.
\end{equation*}
$\blacksquare$
Observación 25.12.
Podemos reescribir el resultado anterior como:
\begin{equation*}
\dfrac{(z-z_1)(z_2 – z_3)}{(z-z_3)(z_2 – z_1)} = \dfrac{(w-w_1)(w_2 – w_3)}{(w-w_3)(w_2 – w_1)},
\end{equation*}donde $w = T(z)$ y $T$ es una transformación de Möbius. En caso de que algún $z_k$ ó algún $w_k$, con $k=1,2,3$, sea igual a $\infty$, entonces consideramos la definición de la observación 25.11.
Obtener una transformación de Möbius resulta sencillo mediante la razón cruzada.
Ejemplo 25.9.
Consideremos los incisos a) y c) del ejemplo 25.6.
Para el inciso a) queremos una transformación de Möbius tal que:
\begin{equation*}
-1\mapsto -i, \quad 0 \mapsto 1 \quad \text{y} \quad 1 \mapsto i.
\end{equation*}Considerando la observación 25.12 tenemos que:
\begin{equation*}
\dfrac{(z-(-1))(0 – 1)}{(z-1)(0 – (-1))} = \dfrac{(w-(-i))(1 – i)}{(w-i)(1 – (-i))},
\end{equation*}es decir:
\begin{equation*}
\dfrac{-(z+1)}{z-1} = \dfrac{(w+i)(1 – i)}{(w-i)(1 +i)},
\end{equation*}de donde:
\begin{equation*}
-2(z +i) = 2w(z+i) \quad \Longrightarrow \quad w = T(z) = \frac{i-z}{i+z}.
\end{equation*}
Por otra parte, para el inciso c) queremos una transformación de Möbius tal que:
\begin{equation*}
1\mapsto i, \quad 0 \mapsto \infty \quad \text{y} \quad -1 \mapsto 1.
\end{equation*}Considerando la observación 25.12 tenemos que:
\begin{equation*}
\dfrac{(z-1)(0 – (-1))}{(z-(-1))(0 – 1)} = \dfrac{w-i}{w-1},
\end{equation*}es decir:
\begin{equation*}
\dfrac{z-1}{-(z+1)} = \dfrac{w-i}{w-1},
\end{equation*}de donde:
\begin{equation*}
z(1 +i) + i – 1 = 2zw \quad \Longrightarrow \quad w = T(z) = \frac{(1+i)z +(i-1)}{2z}.
\end{equation*}
Ejemplo 25.10.
Determina la transformación de Möbius tal que:
\begin{equation*}
0\mapsto i, \quad 1 \mapsto 2 \quad \text{y} \quad -1 \mapsto 4.
\end{equation*}
Solución. Tenemos que:
\begin{equation*}
(z; 0, 1, -1) = \dfrac{(z-0)(1 – (-1)}{(z-(-1))(1 – 0)} = \frac{2z}{z+1},
\end{equation*}mientras que:
\begin{equation*}
(w; i, 2, 4) = \dfrac{(w-i)(2 – 4)}{(w-4)(2 – i)} = \dfrac{-2(w-i)}{(w-4)(2 – i)},
\end{equation*}por lo que:
\begin{equation*}
\frac{2z}{z+1} = \dfrac{-2(w-i)}{(w-4)(2 – i)},
\end{equation*}de donde, al resolver para $w$ tenemos:
\begin{equation*}
w\left[(6-2i)z+2\right] = \left[(16-6i)z+2i\right] \quad \Longrightarrow \quad w = T(z) = \frac{(16-6i)z+2i}{(6-2i)z+2}.
\end{equation*}
Corolario 25.5.
Sea $C \subset\mathbb{C}_\infty$ una circunferencia (o una recta), sean $z_1, z_2, z_3 \in C$ tres puntos distintos y $z\in\mathbb{C}_\infty$. Entonces $(z;z_1,z_2,z_3) \in \mathbb{R}$ si y solo si $z\in C$.
Demostración. Dadas las hipótesis, consideremos a $T(z) = (z;z_1,z_2,z_3)$. Dado que $T$ es una transformación de Möbius, del corolario 25.1 se sigue que $T$ mapea a $C$ en una circunferencia (o en una recta) en $\mathbb{C}_\infty$ que pasa por $0, 1$ e $\infty$, entonces $T(C) = \mathbb{R}\cup\{\infty\}$.
Por lo que:
\begin{align*}
T(z) = (z;z_1,z_2,z_3) \in \mathbb{R} \quad & \Longleftrightarrow \quad T(z) \in \mathbb{R} \cup\{\infty\} = T(C)\\
& \Longleftrightarrow \quad z \in C.
\end{align*}
$\blacksquare$
Tarea moral
- Completa la demostración de la proposición 25.1.
- Realiza la demostración de la proposición 25.3.
- Prueba la observación 25.7.
- Demuestra los corolarios 25.1 y 25.3.
- a) Muestra que la ecuación (25.6) se puede escribir de la forma: \begin{equation*} 2Az\,\overline{z} + (D-Ei)z + (D+Ei)\overline{z} + 2F = 0, \end{equation*} donde $z=x+iy$. b) Muestra que bajo la transformación inversión, $f(z)=1/z$, la ecuación del inciso anterior se convierte en: \begin{equation*} 2Fw\,\overline{w} + (D+Ei)w + (D-Ei)\overline{w} + 2A = 0. \end{equation*} Después prueba que si $w=u+iv$, entonces la ecuación anterior es la misma que la ecuación (25.9).
Hint: Utiliza coordenadas complejas conjugadas. - Determina de forma explícita la transformación de Möbius determinada por las siguientes correspondencias de puntos. Verifica tu resultado utilizando la razón cruzada.
a) $1+i \mapsto 0$, $2 \mapsto \infty$, $0 \mapsto i-1$.
b) $0 \mapsto 1$, $1 \mapsto 1+i$, $\infty \mapsto 2$.
c) $\infty \mapsto 0$, $1+i \mapsto 1$, $2 \mapsto \infty$.
d) $-2 \mapsto 1-2i$, $i \mapsto 0$, $2 \mapsto 1+2i$.
e) $1 \mapsto 1$, $i \mapsto 0$, $-1 \mapsto -1$. - Obtén los puntos fijos de las siguientes transformaciones.
a) $T(z) = \dfrac{iz+2}{z+1}$.
b) $T(z) = i\left(\dfrac{z-i}{z+i}\right)$.
c) $T(z) = \dfrac{z}{z+1}$.
d) $T(z) = \dfrac{1+i}{z+1}$. - a) Determina la transformación de Möbius tal que: \begin{equation*} 1 \mapsto 0, \quad i \mapsto -1 \quad \text{y} \quad 0 \mapsto -i. \end{equation*}
b) Considera la transformación $T$ del inciso anterior. ¿Cuál es la imagen de la circunferencia, en el plano $z$, que pasa por los puntos $z_1 = 1, z_2 = i$ y $z_3 = 0$, bajo $T$? ¿Cuál es la imagen del interior de dicha circunferencia bajo $T$? - Prueba que si el origen es un punto fijo de una transformación de Möbius $T$, entonces dicha transformación es de la forma: \begin{equation*} w=T(z)=\frac{z}{cz+d}, \quad d\neq 0. \end{equation*}
- Muestra que la transformación: \begin{equation*} w = T(z) = \frac{iz+2}{4z+i}, \end{equation*} envía el eje real, en el plano $z$, en una circunferencia en el plano $w$. Determina el centro y el radio de dicha circunferencia. ¿Cuál es el punto en el plano $z$ que es enviado en el centro de la circunferencia?
- Determina la transformación de Möbius tal que envía el punto $i$ en el punto $-i$ y que fija el punto $1+2i$.
Más adelante…
En esta entrada hemos definido el concepto de transformación de Möbius o bilineal y establecimos algunos resultados elementales, en el estudio de estas transformaciones del plano complejo (extendido), las cuales resultan de suma importancia para entender de manera clara la geometría de algunas de las funciones complejas más elementales, como veremos en la siguiente entrada.
En general, las transformaciones de Möbius tienen muchas aplicaciones en el análisis complejo. Dejando de lado la aparente simplicidad en su definición, éstas transformaciones son el corazón de algunas áreas matemáticas modernas de investigación, por su conexión con las geometrías no Euclidianas como la geometría hiperbólica. De hecho, éstas transformaciones están estrechamente ligadas con la teoría de la relatividad de Einstein.
La siguiente entrada es la última de ésta segunda unidad y en ella abordaremos una alternativa básica para poder estudiar el comportamiento geométrico de las funciones complejas más elementales.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Transformaciones del plano complejo $\mathbb{C}$.
- Siguiente entrada del curso: Funciones complejas como transformaciones. Técnicas de graficación.